2. 上海凯泉泵业(集团)有限公司,上海 201804
2. Shanghai Kaiquan Pump(Group)CO., Ltd., Shanghai 201804, China
世界经济的发展为能源生产带来了巨大压力,同时,飞速增长的能源消耗也带来了一系列的环境问题[1]。泵作为一种通用机械,被广泛应用于工业、农业、城市建设、居民生活等各个领域,其每年的能量消耗超过能源生产总值的22%[2]。然而,一份调查报告指出,仍有大量的泵(约40%)工作在效率低下的工况下,不仅造成了大量的能量浪费,同时也埋下了安全隐患[3]。目前,针对泵过流部件的优化设计被认为是提高泵工作效率及稳定性的有效方法。
叶轮作为离心泵的核心部件,其几何外型设计对离心泵的效率有着决定性影响。因此,对叶轮进行优化设计,能够显著提高离心泵的综合性能[4-5]。由于计算力缺乏,传统的离心泵优化设计方法主要是基于相似理论的半经验半理论方法[6]和试验设计方法[7],这种方法对设计者的经验水平要求高且优化成功率较差。近年来,随着计算机技术和计算流体力学(CFD)的发展,基于近似模型和智能算法的优化设计方法正逐步成为离心泵设计领域的主流技术,在大量研究过程中被证明具有良好的稳定性[8-9]。袁寿其等[10]选取了叶片出口宽度、叶片出口安放角和叶片包角3个参数作为优化变量,采用克里金模型结合多岛遗传算法对1台低比转速离心泵进行优化,优化后的模型在设计工况点效率提升了4.18%。姜丙孝等[11]采用6阶贝塞尔曲线对离心泵的叶片型线进行参数化建模,并选取其中的5个控制点为优化变量,利用支持向量机的表示方法建立近似模型,并通过遗传算法寻优得到了最优的叶片型线参数组合。王春林等[12]采用径向神经网络构建了双叶片离心泵叶轮3个设计参数与泵扬程、效率之间的预测模型,并通过多目标粒子群算法进行寻优,最终使得优化模型相较于原始模型水力效率提高了10.11%、扬程提高了5.5%。Zhao等[13]基于BP神经网络和NSGA-Ⅱ算法对1台超低比转速离心泵的叶轮进行优化设计,结果表明该优化方法可以有效地提高超低比转速离心泵的水力性能。然而,高比转速离心泵的设计变量与水力性能之间的相关性研究以及多参数优化方法还鲜有报道。
本文以1台KQL300-315-90高比转速离心泵为研究对象,基于Python编程及数值分析方法搭建了性能优化平台。通过参数化建模和相关性分析方法选取了叶轮的8个设计变量作为决策变量,并通过拉丁超立方抽样(Latin Hypercube Sampling,LHS)方法创建了数据样本库,最后,基于BP神经网络(Back Propagation Nerual Network,BPNN)和遗传算法(Genetic Algorithm,GA)对叶轮进行了优化设计,优化过程以提升水力效率作为目标并严格限制扬程波动。
1 计算模型与数值模拟 1.1 计算模型本文选取的模型为单级单吸立式高比转速离心泵,其性能参数为:设计流量Qd=720 m3/h,设计扬程Hd=31 m,叶轮转速n=1 480 r/min,泵比转速ns=184。原型离心泵叶轮及蜗壳的关键几何参数如表 1所示。
| 表 1 原型泵主要参数 Tab. 1 Prototype pump main parameters |
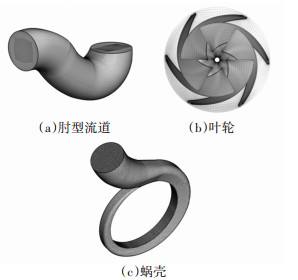
采用ANSYS BladeGen对叶轮进行参数化建模,其余部件则采用三维造型软件UG进行建模,同时在肘型流道进口和蜗壳出口处延长5倍直径的管路,以减少进出口回流涡旋对数值模拟计算收敛性的影响。整体计算域如图 1所示。

|
图 1 计算域 Fig. 1 Computational domains |
本文采用专门针对旋转机械网格划分的软件TurboGrid对叶轮进行高质量结构网格划分。由于蜗壳结构较为复杂,利用ICEM软件对其采用以六面体为核心的混合网格划分形式,并设置边界层。
对计算域进行网格无关性分析,结果如图 2所示。当总网格数大于300万时,扬程系数变化小于0.5%,基于此最终确定的计算网格数为316.8万,其中进口管、肘型流道、叶轮、蜗壳和出口管的网格数分别为19.15万、30.58万、118.52万、127.6万和20.95万。同时,叶轮壁面最大y+小于10,其余部件关键壁面平均y+小于20,可以满足SST k-ω湍流模型对近壁面网格的要求。网格细节如图 3所示。

|
图 2 网格无关性分析 Fig. 2 Analysis of grid independence |
|
图 3 主要计算域网格细节 Fig. 3 Mesh details of main computational domain |
采用ANSYS CFX对模型泵计算域进行定常数值模拟。湍流模型设置为SST k-ω,对流项的离散格式设置为二阶迎风(High Resolution)。参考压力设置为0 atm,边界条件分别为总压进口(1 atm)和质量流量出口(199.64 kg/s),动静交界面设置为“Frozen Rotor”,近壁区设置为光滑壁面,最大迭代步数为300步,时间步长设置为0.2/ω(0.001 3 s,ω为角速度即154.99 rad/s),收敛精度设置为10-5。
为了验证数值模拟的合理性和准确性,在上海凯泉泵业公司开式试验台上采用电测法对原型泵进行外特性试验(GB/T3216—2016规定的1级精度)。试验台细节如图 4所示,具体设备和仪器均在图 4(a)中标出。压力表型号均为3051TG,测量范围分别为0~200 kPa和0~0.7 MPa,精度为0.5%;电磁流量计型号为DN300,量程比为20:1,精度为0.5%。同时,为了保证试验的准确性,每个试验都重复了3次,最后使用平均值。根据测量不确定度B类计算方法,扬程及效率的不确定度小于1%。

|
图 4 试验台 Fig. 4 Test rig |
由于模拟得到的效率为水力效率,并没有考虑容积损失和机械损失,因此基于损失计算公式[14]对泵的总效率进行估算。扬程系数定义为
| $\mathit{\Psi } = \frac{{gH}}{{u_2^2}}$ | (1) |
式中:H为扬程,m;u2为叶轮出口的圆周速度,m/s;g为重力加速度,本文取9.84 m/s2。
图 5给出了试验结果和数值模拟结果的对比。设计工况点,模拟效率值与试验值分别为79.09%和75.97%,相对误差为4.11%;扬程系数分别为0.422和0.417,相对误差为1.18%。非设计工况下,计算结果与试验结果的误差有所上升,效率最大相对误差为7.71%,扬程系数最大相对误差为4.47%,但仍处于置信区间内,因此认为计算结果具有良好的可靠性,可以满足后续研究的要求。

|
图 5 试验与数值模拟外特性的对比曲线 Fig. 5 Performance comparison between computational and experimental results |
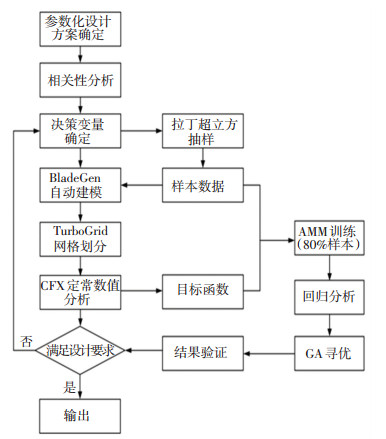
高比转速离心泵的优化过程如图 6所示,首先对叶轮的设计变量和泵的水力性能进行相关性分析,筛选出优化变量并确定决策域。以最大化泵设计工况下的效率作为目标函数,扬程波动小于5%作为限制条件,采用LHS方法在决策域内抽取了160组设计样本,并通过自动数值分析程序得到各个样本的定常效率和扬程。采用单隐层BP神经网络建立泵效率、扬程与决策变量之间的近似模型,并通过回归分析验证模型的可靠性,最后使用遗传算法对近似模型进行全局寻优,获得最优的叶轮设计变量。
|
图 6 叶轮优化流程图 Fig. 6 Flow chart of optimization procedure |
为了提高原型泵的水力性能,优化过程选用设计工况点的效率作为优化目标函数,同时考虑到后续工程应用的实际情况,将模型泵扬程作为限制条件,具体如式(2)所示:
| $\left\{ {\begin{array}{*{20}{l}} {\max \left( {{\eta _{1.0{Q_{\rm{d}}}}}} \right)}\\ {{\rm{ subject to }}\left( {1.05H_{1.0{Q_{\rm{d}}}}^{{\rm{ORI}}} \geqslant H_{1.0{Q_{\rm{d}}}}^{{\rm{OPT}}} \geqslant 0.95H_{1.0{Q_{\rm{d}}}}^{{\rm{ORI}}}} \right)} \end{array}} \right.$ | (2) |
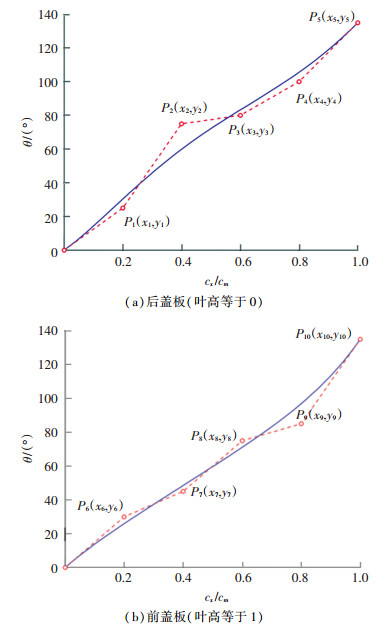
将原始叶轮计算域前/后盖板轴面投影和叶片高度为0、0.5和1时的叶片型线点集数据整理为.crv文件导入ANSYS BladeGen中,从而实现对原始叶轮的逆向建模。叶轮的轴面形状和叶片厚度与原始模型保持一致。同时,为了保证对叶片型线的精确控制,采用5阶贝塞尔曲线对前盖板和后盖处的叶片包角变化进行控制,其他流线上的叶片角度则按线性插值进行设计。考虑到叶片包角变化对泵性能影响的敏感性,设定叶片包角贝塞尔曲线的各个控制点在x方向和y方向上均自由(终点除外),具体如图 7所示。根据相关文献[15],叶片包角和叶片安放角可以通过式(3)进行互相转换,从而实现对叶片型线的整体控制。
| $\theta = \int_0^{{c_m}} {\frac{{\tan \beta }}{r}} \cdot {\rm{d}}{c_x}$ | (3) |
|
图 7 叶片包角曲线控制示意图 Fig. 7 Diagram of blade wrap angle curve control |
式中:θ为叶片包角;β为叶片安放角;r为当前位置的半径,m;cx为叶片进口边至当前位置的流线长度,m;cm为流线总长,m。
2.3 相关性分析首先采用拉丁超立方抽样方法,针对2.2小节中所述的18个设计变量随机生成160组不同的设计方案,具体变量取值范围如表 2所示。之后基于ANSYS Workbench平台与Python编程,利用ANSYS Scripting与Dos命令控制BladeGen、TurboGrid以及CFX,实现对不同叶轮设计方案的自动三维造型、网格划分和数值分析,具体流程如图 8所示。
| 表 2 叶轮设计变量取值范围 Tab. 2 Range of impeller design variables |

|
图 8 自动数值分析技术路线 Fig. 8 Technical route of automatic numerical analysis |
最后,提取计算结果,对数据进行Pearson相关性分析,进而得到各个参数对泵水力性能的影响,结果如表 3所示。从中可以看出,位于叶片前缘和叶片中段的控制点对泵效率和扬程的影响不大。但是,位于叶片尾缘附近的控制点对泵效率和扬程的影响却很显著,其中控制点x4对泵效率的影响最大,控制点y5对泵扬程的影响最大。此外值得注意的是,对大多数控制点而言,其数值大小改变之后,泵的效率和扬程变化是相反的,因此在寻优过程中限制扬程的波动是非常必要的。
| 表 3 叶轮设计变量取值范围 Tab. 3 Pearson correlation analysis of variables |
一般认为相关性系数∣r∣>0.2,两变量之间具有一定的相关关系。依照此标准对原有设计变量进行筛选,并根据前人研究和本文的实际情况,确定优化变量的取值范围,其余控制点则保持不变,最终结果如表 4所示。基于此结果,使用拉丁超立方抽样重新抽取160组设计样本,以此保证样本库具有良好的填充率和代表性,从而提高后续近似模型的拟合精度。
| 表 4 叶轮设计变量取值范围 Tab. 4 Range of optimization variables |
BP神经网络是一种基于监督学习的多层前馈网络,一般采用最速下降法进行训练,具有很强的自适应性,可实现从输入到输出的强非线性映射[16-17],其基本拓扑结构如图 9所示。

|
图 9 基本的三层BP神经网络 Fig. 9 Basic three-layer BP neural network |
本文利用三层BP神经网络同时建立优化变量与高比转速离心泵水力效率和扬程的近似模型。其中,BP神经网络输入层为8个神经元;隐含层为1层,具有6个神经元,使用sigmoid函数作为激活函数,如式(4)所示;输出层为1个神经元,使用线性函数作为激活函数,如式(5)所示。为了保证近似模型的准确性,样本库中80%的数据被用于训练BP神经网络,10%的数据被用于测试,10%的数据被用于验证。
| $f(p) = \frac{2}{{1 + {{\rm{e}}^{ - 2p}}}} - 1$ | (4) |
| $g(p) = {W_p} + b$ | (5) |
式中:p为输入值;Wp为权重;b为偏置。
2.5 遗传算法遗传算法[18](Genetic Algorithm,GA)是Holland提出的一种通过模拟自然选择和生物进化来搜索最优解的优化方法,其将问题的求解过程转化为类似生物进化中染色体基因交叉、变异等过程,具有较好的全局搜索能力和鲁棒性,因此被广泛应用于流体机械的优化设计领域。
本文定义遗传算法的种群数大小为100,最大遗传代数为30次,交叉概率为0.8,变异概率为0.01。经过遗传算法寻优计算之后得到的最优模型预测效率为83.31%,预测扬程为29.81 m。通过数值计算验证该最优模型,计算效率为82.11%,计算扬程为29.51 m,与预测值之间的相对误差分别为1.46%和1.02%,均在工程许可范围之内。
3 结果与讨论 3.1 近似模型精度分析采用回归分析验证BP神经网络拟合的近似模型的适应性和精确度,决定系数R2值越接近1,则表示模型拟合度越高。分析结果如图 10所示,效率模型R2值为0.9776,扬程模型R2值为0.998 5,均接近1,可以说明近似模型的预测值和真实值之间具有良好的吻合性,BP神经网络能准确地建立泵效率、扬程与优化变量之间的函数关系。

|
图 10 人工神经网络模型的回归分析 Fig. 10 Regression analysis of artificial neural network |
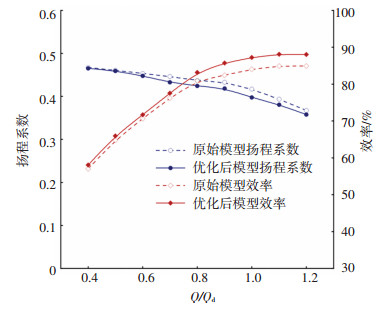
优化后模型设计变量与原始模型设计变量对比如表 5所示,优化前后叶片三维及泵外特性曲线对比如图 11和图 12所示。从中可以看出: 优化后叶片在前/后盖板处的型线过渡得更加光顺,同时叶片前缘和尾缘的形状也有较大的变化;设计工况下,效率提升达3.02%;大流量工况下,效率提升明显,幅度接近3%;小流量工况下,效率有小幅度的提升。因此可以说明,该型泵经过优化之后,其高效运行区得到了拓宽。优化后的模型扬程整体有所下降,但下降幅度均小于5%,在可接受范围之内。
| 表 5 设计变量对比 Tab. 5 Comparison between original and optimized cases |

|
图 11 优化前后叶片三维对比 Fig. 11 Comparison of blade 3D shapes between original and optimized models |
|
图 12 优化前后外特性对比 Fig. 12 Comparison of performance characteristics between original and optimized models |
湍动能是表征流体能量耗散程度的物理量,湍动能越大,流体的耗散也就越大。图 13给出了设计工况优化前后0.5倍叶高下叶轮的湍动能分布。从中可以看出,优化前的叶片吸力面附近存在一定面积的高能湍动能区,这是因为叶片进口来流存在正冲角,随着叶轮的旋转,流体会在叶片吸力面形成流动分离区,分离区内部由于惯性力与剪切力的作用,形成高速涡旋,从而造成了大量的水力损失。同时,由于叶轮-隔舌之间的动静干涉效应使得叶轮出口处湍动能数值也较大。优化后,叶轮来流与叶片安放角的吻合程度改善,从而有效提高了叶轮流道内的流动分布,降低了水力损失。因此,优化后的叶轮吸力面附近的湍动能强度相较于原始模型有了明显的降幅。另一方面,由于出口安放角的变化,动静干涉对叶轮内流造成的负面影响得到改善,因此,在优化模型出口处的湍动能强度有所下降。这就从能量转换的角度印证了优化后模型效率会高于原型泵效率。
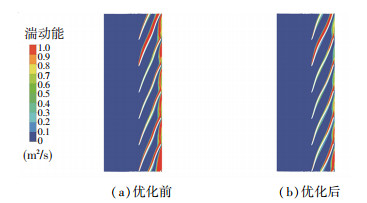
|
图 13 优化前后湍动能分布对比 Fig. 13 Comparison of turbulent kinetic energy distribution between original and optimized models |
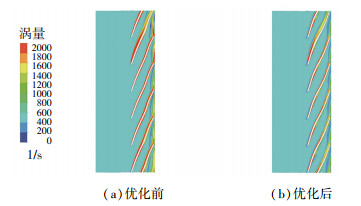
速度矢量的旋度称为涡量,离心泵内涡量集中的区域一般认为存在不稳定流动结构[19]。图 14对比了设计工况优化前后0.5倍叶高下叶轮的涡量分布情况。从中可以发现,相较于原始模型,优化后模型在叶片壁面和尾缘附近的高涡量区面积有所减少且涡量数值也有所下降,这说明优化后叶片壁面附近的不稳定流动结构有所减少,叶轮尾迹涡强度下降,从而会在一定程度上提高泵的运行稳定性。
|
图 14 优化前后涡量分布对比 Fig. 14 Comparison of vorticity distribution between original and optimized models |
针对高比转速离心泵的能效低下问题,本文提出了一种基于参数化设计与自动数值分析程序的优化设计方案,对于高比转速离心泵的正向水力设计具有借鉴意义。首先通过LHS方法在决策空间内选取了160组样本,并通过自动数值模拟程序获得了样本目标值,形成初始样本库。利用Pearson相关分析方法对初始样本库进行了研究,并根据研究结论对设计参数进行了降维,以降低优化问题复杂度。优化过程基于神经网络与遗传算法,其主要结论如下:
1) 根据Pearson相关性分析方法研究了叶轮设计变量对高比转速离心泵水力性能的影响,发现位于叶片尾缘附近的控制点对泵效率和扬程的影响最大,并降低了设计变量的维数。
2) 基于BP神经网络与遗传算法的优化设计方法在高比转速离心泵的优化问题上表现出了良好的可靠性。
3) 优化后,研究对象在设计工况及大流量下的效率得到了显著提升(设计工况下计算效率提升了3.02%),针对其内部流场的研究亦表明优化后的模型具有更好的运行稳定性。
| [1] |
SHANKAR V K A, UMASHANKAR S, PARAMASIVAM S, et al. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system[J]. Applied Energy, 2016, 181: 495. DOI:10.1016/j.apenergy.2016.08.070 |
| [2] |
BERTOLDI P, FALKNER H, REEVES D. European commission—europump guidance on efficiencies for pumps[C]//Energy Efficiency in Motor Driven Systems. [S.l.]: Springer, 2003: 520
|
| [3] |
WU Peng, LAI Zhounian, WU Dazhuan, et al. Optimization research of parallel pump system for improving energy efficiency[J]. Journal of Water Resources Planning and Management, 2015, 141(8): 04014094. DOI:10.1061/(ASCE)WR.1943-5452.0000493 |
| [4] |
司乔瑞, 林刚, 袁寿其, 等. 高效低噪无过载离心泵多目标水力优化设计[J]. 农业工程学报, 2016, 32(4): 69. SI Qiaorui, LIN Gang, YUAN Shouqi, et al. Multi-objective optimization on hydraulic design of non-overload centrifugal pumps with high efficiency and low noise[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(4): 69. DOI:10.11975/j.issn.1002-6819.2016.04.010 |
| [5] |
代翠, 孔繁余, 董亮, 等. 基于响应面法的离心泵作透平水力和声学性能优化[J]. 农业工程学报, 2015, 31(15): 45. DAI Cui, KONG Fanyu, DONG Liang, et al. Hydraulic and acoustic property optimization for centrifugal pump as turbine based on response surface method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(15): 45. DOI:10.11975/j.issn.1002-6819.2015.15.006 |
| [6] |
XU Jianzhong, WU Yulin, ZHANG Yangjun, et al. Fluid machinery and fluid mechanics[M]. [S.l.]: Springer Science & Business Media, 2010
|
| [7] |
陈建华, 周晨佳, 王雪, 等. 基于正交试验的高速井泵优化设计[J]. 排灌机械工程学报, 2021, 39(5): 458. CHEN Jianhua, ZHOU Chenjia, WANG Xue, et al. Optimization design of high-speed well pump based on orthogonal test[J]. Journal of Drainage and Irrigation Mechanical Engineering, 2021, 39(5): 458. DOI:10.3969/j.issn.1674-8530.19.0227 |
| [8] |
王延锋, 张连军, 段海鹏. 基于遗传算法-反向传播神经网络的径向式导叶多级泵水力性能优化[J]. 科学技术与工程, 2021, 21(4): 1378. WANG Yanfeng, ZHANG Lianjun, DUAN Haipeng, et al. Hydraulic performance optimization of radial diffuser multistage pump based on genetic algorithm-back propagation neural network[J]. Science Technology and Engineering, 2021, 21(4): 1378. |
| [9] |
童哲铭, 陈尧, 童水光, 等. 基于NSGA-Ⅲ算法的低比转速离心泵多目标优化设计[J]. 中国机械工程, 2020, 31(18): 2243. TONG Zheming, CHEN Yao, TONG Shuiguang, et al. Multi-objective parameters optimization of low specific speed centrifugal pump based on NSGA-Ⅲ genetic algorithm[J]. China Mechanical Engineering, 2020, 31(18): 2243. DOI:10.3969/j.issn.1004-132X.2020.18.012 |
| [10] |
袁寿其, 王文杰, 裴吉, 等. 低比转数离心泵的多目标优化设计[J]. 农业工程学报, 2015, 31(5): 50. YUAN Shouqi, WANG Wenjie, PEI Ji, et al. Multi-objective optimization of low-specific-speed centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(5): 50. DOI:10.3969/j.issn.1002-6819.2015.05.007 |
| [11] |
姜丙孝, 杨军虎, 白小榜, 等. 基于高维混合模型与遗传算法的离心泵叶片优化[J]. 华中科技大学学报(自然科学版), 2020, 48(7): 132. JIANG Bingxiao, YANG Junhu, BAI Xiaobang, et al. Optimization of centrifugal pump blade based on high-dimensional hybrid model and genetic algorithm[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2020, 48(7): 132. DOI:10.13245/j.hust.200722 |
| [12] |
王春林, 胡蓓蓓, 冯一鸣, 等. 基于径向基神经网络与粒子群算法的双叶片泵多目标优化[J]. 农业工程学报, 2019, 35(2): 31. WANG Chunlin, HU Beibei, FENG Yiming, et al. Multi-objective optimization of double vane pump based on radial basis neural network and particle swarm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2019, 35(2): 31. DOI:10.11975/j.issn.1002-6819.2019.02.004 |
| [13] |
ZHAO An, LAI Zhounian, WU Peng, et al. Multi-objective optimization of a low specific speed centrifugal pump using an evolutionary algorithm[J]. Engineering Optimization, 2015, 48(7): 1274. DOI:10.1080/0305215X.2015.1104987 |
| [14] |
关醒凡. 现代泵理论与设计[M]. 北京: 中国宇航出版社, 2011. GUAN Xingfan. Modern pump theory and design[M]. Beijing: China Aerospace Press, 2011. |
| [15] |
ANSYS. ANSYS turbo system user's guide[M]. Canonsburg: ANSYS, 2019.
|
| [16] |
YI Jianqiang, WANG Qian, ZHAO Dongbin, et al. BP neural network prediction-based variable-period sampling approach for networked control systems[J]. Applied Mathematics and Computation, 2007, 185(2): 988. DOI:10.1016/j.amc.2006.07.020 |
| [17] |
LI Zhaokun, ZHAO Xiaohui. BP artificial neural network based wave front correction for sensor-less free space optics communication[J]. Optics Communications, 2017, 385: 220. DOI:10.1016/j.optcom.2016.10.037 |
| [18] |
HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 68. |
| [19] |
张宁. 离心泵内部非稳态流动激励特性研究[D]. 镇江: 江苏大学, 2016 ZHANG Ning. Excitation characteristics induced by unsteady flow within a centrifugal pump[D]. Zhenjiang: Jiangsu University, 2016 |
 2022, Vol. 54
2022, Vol. 54


