海洋孕育着丰富的自然资源,这种得天独厚的巨大资源让其成为世界各国主权与权益的焦点所在[1]。各国对于海洋领域的探究越来越多,载人潜航、海洋探测层出不穷[2]。耐压外壳作为水下设备的重要部件,它承受着巨大的海水压力,同时也是浮力的主要提供者。研究表明耐压圆柱壳体的结构稳定性是水下设备正常工作的重要保证,同时也是水下设备研发的关键问题之一[3]。
有限元分析能够预测圆柱壳体的屈曲强度[4],对耐压壳体稳定性的研究有很大的助益。随着非线性有限元分析技术的发展,数值实验分析逐渐取代了模型实验。万福腾等[5]采用了弧长法、非线性稳定算法两种有限元数值模拟方法对圆柱壳体进行仿真,并通过与实验数据进行对比,表明弧长法和非线性稳定法都能准确地模拟真实情况。ZHANG等[6]利用Ansys的弧长法对圆柱形容器进行了屈曲分析,数值求解结果与实验结果有较好的相关性。张伯君[7]使用非线性稳定算法对圆柱壳体进行了仿真分析,结果表明非线性稳定算法有较好的预测精度。选择合理的分析方法,对屈曲研究非常重要。
在生产壳体时,由于加工方法而引起的壳体表面的小凹坑等缺陷,可以统称为初始缺陷[8]。实验与经典屈曲理论的结果之间有较大差异的主要原因就是初始缺陷,因此有限元模型对初始缺陷进行合理的表征是影响预测精度的重要因素。ZHANG[6]采用了实际测量的几何缺陷形状,因此计算结果与实验结果相差很小,偏差在14.5%以内。邓志军等[9]采用“一致缺陷模态法”对仿真模型施加初始几何偏差, 最终计算结果与实验结果相差较小。张建等[10]发现对于轴压柱形壳屈曲问题, 第1阶模态缺陷不是对结构承载能力损害最严重的缺陷(最不利模态缺陷)。XIONG等[11]选择了6种不同材料的圆柱壳进行研究,发现各种材料的最不利模态缺陷的阶数不相同。
基于实际测量的初始几何缺陷构造方法,需要进行大量的精确的测量。为减少成本,部分学者们尝试建立了真实缺陷的数据库。但尺寸、材料和加工方法等情况的改变,都会造成缺陷的变化,因而该方法所需数据太过庞大而难以行通。本文主要研究缺陷模态法,缺陷模态法认为模态缺陷是对结构最不利的缺陷形式,可以计算出最低的临界载荷。虽然前人对最不利单一模态缺陷进行了研究,却尚未对多模态组合缺陷进行研究。因此本文对模态缺陷法的最不利模态阶数进一步进行探究,并对多模态组合缺陷形式进行研究,最后设计实验进行验证。
1 模型的建立进行有限元分析计算之前,首先需要确定分析对象的非线性因素。对于耐压圆柱壳体,主要的非线性因素是材料非线性与几何非线性[12]。本研究中材料非线性主要考虑材料的弹塑性,几何非线性主要考虑结构的初始几何缺陷(模态缺陷法)与结构的变形影响。
1.1 几何模型耐压壳分为圆柱壳体和端盖两部分,本文主要关注点为圆柱壳体的屈曲失稳。如图 1所示,本研究采用的圆柱壳有效长度为265 mm,外径125 mm,壁厚6 mm。

|
图 1 耐压壳的结构示意图 Fig. 1 Schematic diagram of the structure of the pressure shell |
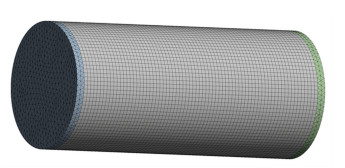
在有限元软件Ansys workbench中建立上述结构的有限元模型,模型端盖部分采用四面体单元solid187,筒体部分使用六面体单元solid186。为消除网格精度引起的计算误差,试算了不同的网格精度,最终确定网格大小为2 mm。图 2所示为耐压壳的有限元模型,边界条件使用简支的三点约束六个自由度的方法。该有限元模型用于计算结构的特征值屈曲模态,进行非线性分析时需要引入模态缺陷。
|
图 2 耐压壳的有限元模型 Fig. 2 Finite element model of pressure shell |
海洋的特殊环境对耐压壳材料提出了特殊要求,耐压壳应采用高比强度、物理性能稳定、成型工艺好的高性能材料[13]。铝合金密度小重量轻、有较高的强度[14],因此本研究的耐压壳采用铝合金AL6061。铝合金的强度属性由拉伸试验得到,属性如表 1所示。材料模型考虑了弹塑性,在模型中引入了切线模量。
| 表 1 AL6061属性表 Tab. 1 AL6061 attribute table |
应用经典屈曲荷载乘以一个折减系数对圆柱壳体的稳定性进行预测,由于其形式简单仍被广泛采用[15]。该方法准确性不足,但可为本研究做参考。由潜艇承压结构工程分析方法[16]可知,耐压外壳的屈曲压力为
| $ {P_{{\rm{cr}}}} = 0.75{C_s}{P_e} $ |
式中:Cs为材料物理非线性修正系数,查图得0.48;Pe为弹性临界压力,MPa。
| $ {P_e} = E{\left( {\frac{t}{R}} \right)^2}\frac{{0.6}}{{u - 0.37}} $ |
式中:E为弹性模量,N/mm2;t为壳板厚度,mm;R为圆柱壳体平均半径,mm;l为肋骨间距,mm;u为参数,由式u=0.643
代入数据可得,Pcr=20.25 MPa。
2 仿真分析 2.1 分析方法非线性稳定算法是使用人工阻尼的静态改良Newton-Raphson方法,这种人工阻尼是解算器内部产生的一组力,该力使用每个节点的速度(以其位移除以相应的时间增量测得的)乘以阻尼因子计算得出的,阻尼力总是施加在位移的相反方向上[17]。当载荷增量较小而位移增量较大时,分析难以收敛。而阻尼力的存在则可以帮助收敛,计算出临界屈曲载荷。
弧长法可以使Newton-Raphson迭代沿一段弧收敛,即便当正切刚度矩阵的斜率达到零或者是负值时,也可以阻止结果发散。因此弧长法是结构非线性分析中计算稳定高效的一种数值方法,能够有效地分析结构非线性前后屈曲并跟踪后屈曲路径,计算出临界屈曲载荷[18]。
非线性稳定法和弧长法均可以计算临界屈曲压力,因此在本研究中都被采用,并对这两种分析方法的结果进行对比。
2.2 单一模态缺陷分析单一模态缺陷法是将特征值屈曲分析得出的前N阶模态中的某一阶作为结构的初始缺陷的分布模式。在工程分析中常用一阶屈曲模态模拟圆柱壳体的初始几何缺陷,但一阶模态并不一定是最不利缺陷状态。本文对特征值屈曲前30阶模态对应的缺陷模型,分别进行了非线性屈曲分析。
1) 进行圆柱壳体的特征值屈曲分析,并提取前30阶屈曲模态。2)参考实际加工精度与相关规范,最大缺陷幅值确定为0.1 mm,并引入缺陷模型。3)分别采用非线性稳定法和弧长法对其进行非线性屈曲分析,得出临界屈曲载荷。
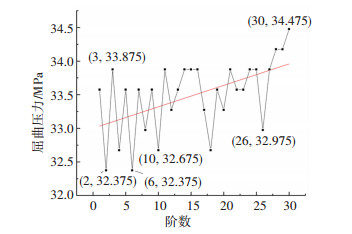
计算结果如图 3与图 4所示,图 3为非线性稳定法的分析结果,图 4为弧长法的分析结果。从图 3可以看出,临界屈曲压力在模态阶数为2阶时达到最小为32.375 MPa,在模态阶数为30阶时达到最大为34.475 MPa。在图 4中,最大与最小屈曲压力的模态阶数与图 3相同,但数值大小不同。由计算结果可知2阶模态才是该结构的最不利模态。对两图进行线性拟合后发现,弧长法的斜率略大于非线性稳定法,即弧长法所得计算结果对初始缺陷模态阶数的敏感度更高。
|
图 3 0.1 mm模型非线性稳定法的分析结果 Fig. 3 Analysis results of non-linear stabilization method of 0.1 mm model |

|
图 4 0.1 mm模型弧长法的分析结果 Fig. 4 Analysis results of arc-length method of 0.1 mm model |
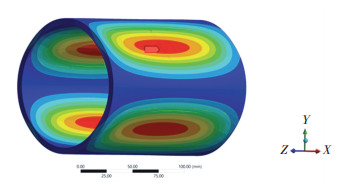
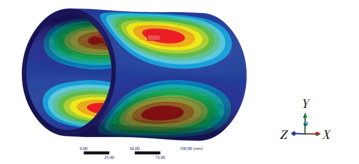
2阶模态缺陷模型计算得到的耐压壳位移云图,如图 5与图 6所示。图 5为非线性稳定法所得位移云图,图 6为弧长法所得位移云图。由图可知两种分析方法得到的失稳波数相同,即失稳模式相同。因此可知两种分析方法仅在计算精度上有差距。
|
图 5 2阶模态缺陷下非线性稳定法的位移云图 Fig. 5 Displacement cloud diagram of non-linear stabilization method under second-order modal defects |
|
图 6 2阶模态缺陷下弧长法的位移云图 Fig. 6 Displacement cloud diagram of arc-length method under second-order modal defects |
为研究缺陷幅值对模态缺陷的影响,将模态缺陷的幅值扩大到五倍(幅值大小为0.5 mm),再进行计算分析。
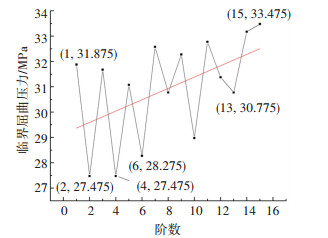
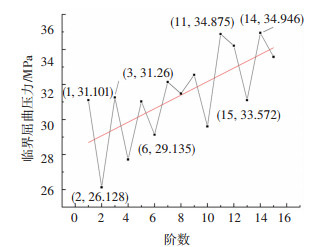
图 7与图 8所示分别为0.5 mm单一模态缺陷模型非线性稳定法和弧长法的分析结果。由图可知,对该结构承载能力影响最大的初始几何缺陷的模态阶数依旧为2阶。并且随着模态阶数的增大,临界屈曲压力大体呈增高趋势,所以最不利几何缺陷的模态阶数一般为低阶。该规律与初始几何缺陷幅值为0.1 mm时相同,因此可知缺陷幅值大小对最不利几何缺陷的模态阶数没有影响。对于缺陷幅值为0.1 mm的2阶模态缺陷模型,当其幅值增大到0.5 mm时临界屈曲压力降低了5 MPa左右。因此缺陷幅值的大小对结构承载能力影响很大。
|
图 7 0.5 mm模型非线性稳定法的分析结果 Fig. 7 Analysis results of non-linear stabilization method of 0.5 mm model |
|
图 8 0.5 mm模型弧长法的分析结果 Fig. 8 Analysis results of arc-length method of 0.5 mm model |
多模态组合缺陷就是将多个特征值屈曲模态同时引入一个模型中,从而形成具有多个模态缺陷形式的有限元模型。因此和单一模态缺陷模型相比,组合模态具有更多可能发生的失效形式。对其进行非线性屈曲分析,与2.2节中分析不同的是,需要在软件中利用命令将多个模态引入缺陷模型,缺陷幅值取0.1 mm。
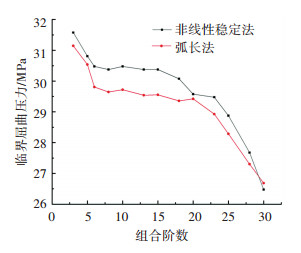
表 2所示为多模态组合缺陷形式的分析结果,图 9所示为多模态组合缺陷形式分析结果的折线统计图。
| 表 2 多模态组合缺陷形式的分析结果表 Tab. 2 Analysis results of multi-modal combined defect form |
|
图 9 多模态组合缺陷形式的分析结果 Fig. 9 Analysis results of multi-modal combined defect form |
由图 9可知,当使用弧长法且组合阶数为1~6至1~20之间时,临界屈曲压力值缓慢降低,变化幅度在3.04%以内。当组合阶数超过20阶时,临界屈曲压力下降明显。因此可知当组合总阶数大于20阶后,由于缺陷模态叠加的过多而对模型产生非常不利的影响,结果可信度不高。当组合阶数小于6阶时,变化幅度也较为明显。由于最不利模态一般低阶,因此多模态组合缺陷应该以低阶模态组合为主,且总阶数不宜超过20阶和低于6阶。
当使用非线性稳定法时,在组合阶数在1~6以内或1~23以外,临界屈曲压力同样下降明显。因此,非线性稳定法组合阶数的合理范围应为1~6至1~23。综合以上两种方法可知,多模态组合缺陷应以低阶模态组合为主,但总阶数不宜过大或过小。
3 实验验证为验证仿真的可靠性,建立了水压模拟实验。根据图 1,制造耐压圆柱壳体。本实验采用静水压力实验装置,对耐压壳的外表面施加均匀压力,实验装置如图 10所示。

|
图 10 试验装置 Fig. 10 Test device |
通过加压装置对压力仓进行施压,耐压壳承受的压力持续增大。实验装置设有压力表,可对水压力进行实时监控。压力每提升1 MPa,保压1~2 min。当压力缓慢升至28.7 MPa时,听到压力仓内发出一声巨响且水压剧烈下降。打开实验装置后发现耐压壳发生大形变,即耐压壳屈曲失效。试验后的耐压壳,如图 11所示。

|
图 11 失效后的耐压壳 Fig. 11 Pressure shell after failure |
通过实验得到耐压壳的临界屈曲载荷为28.7 MPa,因此可知:
1) 使用弧长法时,单一模态缺陷模型分析结果的误差为8.44%,多模态组合缺陷模型分析结果的误差为3.55%。
2) 使用非线性稳定法时,单一模态缺陷模型分析结果的误差为11.76%,多模态组合缺陷模型分析结果的误差为6.18%。
3) 工程分析方法的误差为29.4%。
4 结论1) 非线性有限元分析的计算精度远高于耐压壳的工程分析方法,工程分析方法非常保守。与非线性稳定法相比,弧长法对初始几何缺陷模态阶数的敏感度更高,预测精度也高于非线性稳定法(8.44%<11.76%)。
2) 随着初始几何缺陷模态阶数的变大,临界屈曲压力整体呈增大的趋势,因此耐压壳的最不利几何缺陷的模态阶数一般为低阶。缺陷幅值的大小对临界屈曲压力有较大的影响,但是对最不利几何缺陷的模态阶数没有影响。
3) 模态总阶数适宜的低阶多模态组合缺陷模型,具有非常高的预测精度。
| [1] |
庞连路, 张一鸣, 张心波, 等. 基于ANSYS Workbench的海洋承压舱辅助设计[J]. 船舶工程, 2017, 39(增刊1): 218. PANG Lianlu, ZHANG Yiming, ZHANG Xinbo, et al. Auxiliary design of marine pressure tank based on ANSYS Workbench[J]. Ship Engineering, 2017, 39(S1): 218. |
| [2] |
张亮, 刘大兴, 陈玉龙. 海洋探测仪耐压壳体结构强度特性研究[J]. 机械强度, 2015, 37(3): 508. ZAHNG Liang, LIU Daxing, CHEN Yulong. Study on the structural strength characteristics of the pressure-resistant shell of ocean sounder[J]. Mechanical Strength, 2015, 37(3): 508. |
| [3] |
沈克纯, 潘光, 姜军, 等. 静水压力下纤维缠绕圆柱壳体的稳定性分析[J]. 西北工业大学学报, 2018, 36(5): 839. SHEN Kechun, PAN Guang, JIANG Jun, et al. Stability analysis of filament wound cylindrical shell under hydrostatic pressure[J]. Journal of Northwestern Polytechnical University, 2018, 36(5): 839. DOI:10.3969/j.issn.1000-2758.2018.05.005 |
| [4] |
DAISUKE S, DAISUKE Y. Elastic local shell and stiffener-tripping buckling strength of ring-stiffened cylindrical shells under external pressure[J]. Thin-Walled Structures, 2020, 148(12): 106622. |
| [5] |
万福腾, 陈志平, 焦鹏, 等. 含初始几何缺陷薄壁圆柱壳屈曲载荷的数值模拟方法研究[J]. 压力容器, 2017, 34(3): 1. WAN Futeng, CHEN Zhiping, JIAO Peng, et al. Research on buckling load numerical method of cylindrical shells with initial imperfection[J]. Pressure Vessel Technology, 2017, 34(3): 1. |
| [6] |
ZHANG Zekun, HUI Peizi, GU Chaohua, et al. Buckling of cold-stretched cylindrical vessels under external pressure: experimental and numerical investigation[J]. Thin-Walled Structures, 2018, 131: 475. DOI:10.1016/j.tws.2018.07.009 |
| [7] |
张伯君. 山体滑坡区域内长输埋地油气管道强度研究[D]. 杭州: 浙江大学, 2013 ZHANG Bojun. Research on the strength of long-distance buried oil and gas pipelines in landslide area[D]. Hangzhou: Zhejiang University, 2013 |
| [8] |
KORUCUK F M, MAALI M, KILIC M, et al. Experimental analysis of the effect of dent variation on the buckling capacity of thin-walled cylindrical shells[J]. Thin-Walled Structures, 2019, 143: 106259. DOI:10.1016/j.tws.2019.106259 |
| [9] |
邓志军, 陈冰冰, 郑浣琪, 等. 外压模拟计算中圆筒初始几何偏差描述方法的研究[J]. 机械工程学报, 2015, 51(6): 66. DENG Zhijun, CHEN Bingbing, ZHENG Huanqi, et al. Research on the description method of cylinder initial geometric deviation in external pressure simulation calculation[J]. Chinese Journal of Mechanical Engineering, 2015, 51(6): 66. |
| [10] |
张建, 周通, 王纬波, 等. 模态缺陷条件下复合材料柱形壳屈曲特性[J]. 复合材料学报, 2017, 34(3): 588. ZHANG Jian, ZHOU Tong, WANG Weibo, et al. Buckling property of a composite cylindrical shell considering mode imperfections[J]. Acta Materiae Compositae Sinica, 2017, 34(3): 588. |
| [11] |
XIONG Zhixin, HUI Hanju, HUANG Zhiquan. The ultimate strength of ring stiffened cylindrical shell and its influence factors[J]. Journal of Theoretical and Applied Sciences, 2020, 3. |
| [12] |
蒲映超, 初艳玲, 洪英. 大深度载人潜水器极限承载能力非线性有限元分析方法研究[J]. 船舶工程, 2014, 36(3): 119. PU Yingchao, CHU Yanling, HONG Ying. Study on nonlinear finite element analysis method of ultimate carrying capacity of large depth manned submersible[J]. Ship Engineering, 2014, 36(3): 119. |
| [13] |
罗珊, 王纬波. 潜水器耐压壳结构研究现状及展望[J]. 舰船科学技术, 2019, 41(19): 7. LUO Shan, WANG Weibo. The research status and prospect of submersible pressure hull structure[J]. Ship Science and Technology, 2019, 41(19): 7. |
| [14] |
李文跃, 王帅, 刘涛, 等. 大深度载人潜水器耐压壳结构研究现状及最新进展[J]. 中国造船, 2016, 57(1): 210. LI Wenyue, WANG Shuai, LIU Tao, et al. The research status and latest progress of pressure hull structure of deep manned submersible[J]. China Shipbuilding, 2016, 57(1): 210. |
| [15] |
ABUBAKR E S, MUSA M A, HUSAIN J, et al. An equivalent imperfection-based FE simulation of the stability of dented cylindrical shells accounting for unintended imperfections[J]. Thin-Walled Structures, 2021, 158: 107159. |
| [16] |
潜艇结构设计计算方法: GJB/Z 21A—2011[S]. 北京: 国防科学技术工业委员会, 2001 Calulation method of submarine structure design: GJB/Z 21A—2011[S]. Beijing: The Commission of Science, Technology and Insudstry for National Defense of the PRCL, 2001 |
| [17] |
SAULLO G P, ROLF Z, MARIANO A A, et al. Geometric imperfections and lower-bound methods used to calculate knock-down factors for axially compressed composite cylindrical shells[J]. Thin-Walled Structures, 2014, 74: 118. |
| [18] |
杨帆, 岳珠峰, 李磊. 基于弧长法的加筋板后屈曲特性分析及试验[J]. 应用力学学报, 2015, 32(1): 119. YANG Fan, YUE Zhufeng, LI Lei. Analysis and experiment of post-buckling characteristics of stiffened plates based on arc-length method[J]. Chinese Journal of Applied Mechanics, 2015, 32(1): 119. |
 2022, Vol. 54
2022, Vol. 54


