为使仿人机器人这一多自由度、高耦合性的机构实现自如运动,世界各地的研究学者提出了诸如ZMP、角动量控制、落脚点控制等平衡控制策略,以及倒立摆模型、车桌模型等简化模型来进行运动控制和规划,使仿人机器人的运动指标不断地提高。但作为仿人机器人的模仿对象,人类本身的运动参数与运动模式也是仿人机器人设计与控制的重要参考。所以,另一种更为直接的进行仿人机器人运动规划与控制的方法是应用采集到的真实人体运动数据作为参考,将人体运动参数映射到仿人机器人的关节空间中。Dasgupta等[1]于1999年将人体步行时足部数据与ZMP稳定性判据相结合, 用于仿人机器人ZMP轨迹的生成,并提出了一种地面反力的解算方法。Aceves-Lopez等[2]于2007年对比了实际人体行走下肢关节曲线和规定足部运动轨迹为半圆时的机器人下肢关节曲线,得出了实际人体行走关节曲线更为平滑的结论。Sohn等[3]于2012年使用捕捉到的运动数据结合强化学习,实现了以节省能量为目的的小型机器人轨迹规划。Powell等[4]于2013年将运动人体捕捉数据结合混合零动力学用于NAO机器人的速度规划上。Sinnet等[5]于2014年提出一种利用人体运动捕捉数据规划双足机器人行走的理论框架。Wu等[6]于2017年将人体步行的运动捕捉数据处理后映射到机器人上,实现了双足机器人的跟随步行。Cornejo-Arismendi等[7]于2018年提出了一种将实际人体行走数据映射到机器人关节空间的方法。此外,也有大量针对于特定人群特定动作运动过程中的运动参数变化的研究。Cross[8]于1999年在测力平台上测量了人体在站立、行走、跑步和跳跃情况下足底所受的地面反力。Chen[9]于2011年使用高速摄像机对人体垂直跳跃过程中的质心速度和下肢关节角度进行了测量分析。Ibata等[10]使用无线惯性测量单元对跳远过程中人体下肢关节位置变化进行了测量分析。Chiu等[11]于2015年利用光学摄像机对人体训练前后跳跃情况下的下肢弯曲情况进行了测量分析。目前, 仿人机器人设计者通常是依照经验与部分运动形式下的局部范围的仿真结果作为参考, 设计者并不能够完全了解机器人的极限运动能力,而只能在制造装配完成后通过实验获得。作为大自然优胜劣汰的选择结果,人类的动作是最自然有效的运动模式。所以,为得到仿人机器人实现自然运动和高机动运动的设计准则,达到多种运动行为下的综合设计,需要对人体进行运动捕捉实验。
综上,现有实验研究还未能得出以人类为参照的,在走跑跳等多种运动行为下达到综合设计效果的设计准则。在仿人机器人设计阶段,最重要的驱动元件的选型应主要考虑其最大输出力矩和输出功率。所以,本文选取人体运动时的最大关节力矩和关节功率来评价人体极限驱动能力,分别对应前述两个指标。利用PhaseSpace三维运动捕捉系统和自行设计研制的大量程集成化测力鞋系统采集人体运动轨迹及足底受力数据,计算下肢关节力矩及关节功率,并对结果进行拟合;同时将人体在不同运动下的运动周期划分为不同阶段以分析运动特征。综合分析结果,得到仿人机器人设计参考准则。
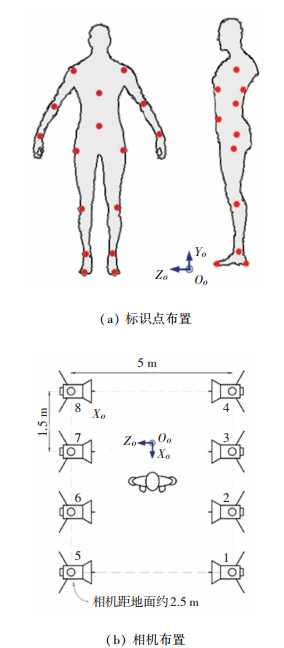
1 运动捕捉与力测量实验设备及数据处理 1.1 PhaseSpace三维运动捕捉系统及实验场景人体运动轨迹由PhaseSpace三维运动捕捉系统采集得到。测量对象的左右脚尖、左右脚跟、左右腿髋膝踝关节、胸前、腹部、左右臂肩肘腕关节各设置一个LED标识点,共18个,如图 1(a)所示。8台光学摄像机分成左右两列,每列各4台,距离地面高度约2.5 m,列间间距约5 m,列中间隔约1.5 m,如图 1(b)所示。
|
图 1 PS运动捕捉系统标识点布置及相机布置示意图 Fig. 1 Layout of PhaseSpace motion capture system markers and cameras |
不同动作实际捕捉场景如图 2所示。

|
图 2 不同动作运动捕捉实验截图 Fig. 2 Screenshots of motion capture experiments for different behaviors |
现有足底力测量技术以及相应产品或专利[12-13]存在量程过小难以承受走跑跳等运动行为下3~7倍人体自重冲击载荷、远距离大运动范围下的不易携带等技术问题。为此,本文研制了如图 3所示集成化可穿戴式大量程测力鞋系统[14]。实验中,测量对象不得倚靠或触碰其他物体。人体在运动过程中的受力情况,即足底力变化,由自研的测力鞋系统提供。

|
图 3 测力鞋系统原理示意及实物图 Fig. 3 Principle and picture of force-measuring shoes |
测力鞋部分总质量约2.5 kg,测力鞋系统最高采样频率200 Hz,单只测力鞋底部分布7个薄膜压力传感器,单点接触测力最大4 448 N,达人体自重5倍。单只测力鞋最大量程可达31 136 N(双脚最大量程62 272 N),可满足实际测量需求。同时,纵向和横向均设有伸缩装置,可满足脚长为255~280 mm(对应中国男鞋尺码41到45码)的实验对象进行实验测量。
1.3 数据处理流程PhaseSpace三维运动捕捉系统捕捉到的数据为各采样时刻各LED标识点在坐标系O0-X0Y0Z0中的坐标值,由于捕捉误差及人体抖动会造成运动轨迹不平滑,且捕捉期间某些LED标识点被遮挡使得相应轨迹不连续,因此,本文采用拉格朗日插值法对运动轨迹数据进行预处理。从处理后的数据中可以提取处关节位置数据,进而可以计算出关节角速度、角加速度等动力学参数。
测力鞋采集到的足底力数据经过低通滤波和坐标系转换,可得足底力大小与其在坐标系O0-X0Y0Z0的作用点。
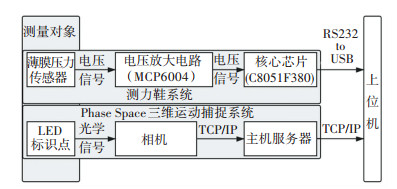
运动捕捉实验整体信号流程如图 4所示。
|
图 4 测量系统信号流程图 Fig. 4 Signal flow of measurement system |
根据牛顿欧拉法建立人体动力学模型,将下肢简化为刚性杆件,上肢简化为质点。单腿采样点从髋关节开始依次编号为髋关节1、膝关节2、踝关节3、脚尖4和脚跟5。髋关节、踝关节定义为三自由度回转关节,膝关节定义为二自由度回转关节,简化模型如图 5所示。

|
图 5 人体机构化的双足简化模型 Fig. 5 Bipedal model of mechanized human body |
由PS三维运动捕捉系统可获得各关节标记点运动轨迹pi(i=1, 2, …, 5),对应肢体i(定义肢体编号i=1, 2, 3分别对应大腿、小腿和足部)质心Ci在基坐标系中位置pci及相对质心惯性矩Ici可根据实验对象的身高、体重及各体段长度等数据,参考国标GB/T 17245—2004《成年人人体惯性参数》[15]确定。肢体i质心速度与加速度可根据如下公式计算:
| ${\mathit{\boldsymbol{v}}}_{ci}^t = \frac{{{\mathit{\boldsymbol{p}}}_{ci}^{t + 1} - {\mathit{\boldsymbol{p}}}_{ci}^t}}{{2{d_t}}}$ | (1) |
| $\mathop {{\dot{\mathit{\boldsymbol{v}}}} _{ci}}^t = \frac{{{\mathit{\boldsymbol{p}}}_{ci}^{t + 1} - 2{\mathit{\boldsymbol{p}}}_{ci}^t + {\mathit{\boldsymbol{p}}}_{ci}^{t - 1}}}{{d_t^2}}$ | (2) |
t时刻肢体i旋转角度可根据余弦定理计算:
| ${\theta _i}^t = \arccos \left( {\frac{{{{\mathit{\boldsymbol{Q}}}_i}^t \cdot {{\mathit{\boldsymbol{Q}}}_i}^0}}{{\left| {{{\mathit{\boldsymbol{Q}}}_i}^t} \right|\left| {{{\mathit{\boldsymbol{Q}}}_i}^0} \right|}}} \right)$ | (3) |
其中,Qi0为肢体i的初始位姿,Qit为肢体i在t时刻位姿,Qit=pi+1t-pit。足部位姿Q3t=p5t-p4t,为表述简洁,不再做额外区分。
对应旋转轴
| $\hat{\boldsymbol{r}}=\left(\boldsymbol{r}_{x}, \boldsymbol{r}_{y}, \boldsymbol{r}_{z}\right)=\frac{\boldsymbol{Q}_{i}{ }^{t} \times \boldsymbol{Q}_{i}{ }^{0}}{\left|\boldsymbol{Q}_{i}{ }^{t}\right|\left|\boldsymbol{Q}_{i}{ }^{0}\right|}$ | (4) |
根据罗德里格旋转公式(Rodrigues’ rotation formula),可得旋转矩阵:
| $\begin{array}{l} {{\tilde R}_r}\left( {{\theta _i}} \right) = \tilde r\sin {\theta _i} + \tilde r\left( {1 - \cos {\theta _i}} \right) = \\ \left[ {\begin{array}{*{20}{c}} {\cos {\theta _i} + r_x^2\left( {1 - \cos {\theta _i}} \right)}&{{r_x}{r_y}\left( {1 - \cos {\theta _i}} \right) - {r_z}\sin {\theta _i}}&{{r_y}\sin \theta + {r_x}{r_z}\left( {1 - \cos {\theta _i}} \right)}\\ {{r_z}\sin {\theta _i} + {r_x}{r_y}\left( {1 - \cos {\theta _i}} \right)}&{\cos {\theta _i} + r_y^2\left( {1 - \cos {\theta _i}} \right)}&{{r_y}{r_z}(1 - \cos \theta ) - {r_x}\sin {\theta _i}}\\ {{r_x}{r_z}\left( {1 - \cos {\theta _i}} \right) - {r_y}\sin {\theta _i}}&{{r_x}\sin {\theta _i} + {r_y}{r_z}\left( {1 - \cos {\theta _i}} \right)}&{\cos \theta + r_z^2\left( {1 - \cos {\theta _i}} \right)} \end{array}} \right] \end{array}$ | (5) |
其中,
设定描述肢体i欧拉角旋转的顺序为ZYX,则关于欧拉角αβγ的旋转矩阵为:
| $R = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma }&{\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma }\\ {\sin \alpha \cos \beta }&{\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma }\\ { - \sin \beta }&{\cos \beta \sin \gamma }&{\cos \beta \cos \gamma } \end{array}} \right]$ | (6) |
对比矩阵中相应元素可解算出欧拉角αβγ。
则肢体i角速度ωi=(ωxi, ωyi, ωzi)T可根据下式得,
| $\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\omega }}}_x}}\\ {{{\mathit{\boldsymbol{\omega }}}_y}}\\ {{{\mathit{\boldsymbol{\omega }}}_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\mathit{\boldsymbol{\beta }}}\cos {\mathit{\boldsymbol{\gamma }}}}&{ - \sin {\mathit{\boldsymbol{\gamma }}}}&0\\ {\cos {\mathit{\boldsymbol{\beta }}}\sin {\mathit{\boldsymbol{\gamma }}}}&{\cos {\mathit{\boldsymbol{\gamma }}}}&0\\ { - \sin {\mathit{\boldsymbol{\beta }}}}&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{\mathit{\boldsymbol{\alpha }}}}}{{{\rm{d}}{\mathit{\boldsymbol{t}}}}}}\\ {\frac{{{\rm{d}}{\mathit{\boldsymbol{\beta }}}}}{{{\rm{d}}{\mathit{\boldsymbol{t}}}}}}\\ {\frac{{{\rm{d}}{\mathit{\boldsymbol{\gamma }}}}}{{{\rm{d}}{\mathit{\boldsymbol{t}}}}}} \end{array}} \right]$ | (7) |
则肢体i角加速度根据
至此,牛顿欧拉法计算逆动力学所需全部参数计算完毕。
根据图 6分析分离体i受力,定义肢体靠近躯干端为近端,远离躯干端为远端。合力与合力矩可根据下式计算:
| $\begin{array}{c} {{\mathit{\boldsymbol{F}}}_i} = {{\mathit{\boldsymbol{m}}}_i}{\mathop {\dot{\mathit{\boldsymbol{v}}}} _i}\\ {{\mathit{\boldsymbol{N}}}_i} = {{\mathit{\boldsymbol{I}}}_{ci}}{\mathop {\dot {\mathit{\boldsymbol{\omega }}}} _i} + {{\mathit{\boldsymbol{\omega }}}_i} \times {I_{ci}}{{\mathit{\boldsymbol{\omega }}}_i} \end{array}$ | (8) |

|
图 6 分离体受力分析示意图 Fig. 6 Force analysis of free body |
根据受力平衡,又有:
| $\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{F}}}_i} = {{\mathit{\boldsymbol{f}}}_i} - {{\mathit{\boldsymbol{f}}}_{i + 1}} + {{\mathit{\boldsymbol{G}}}_i}}\\ {{{\mathit{\boldsymbol{N}}}_i} = {{\mathit{\boldsymbol{n}}}_i} - {{\mathit{\boldsymbol{n}}}_{i + 1}} + \left( {{{\mathit{\boldsymbol{p}}}_{ci}} - {{\mathit{\boldsymbol{p}}}_i}} \right) \times {{\mathit{\boldsymbol{f}}}_i} + \left( {{{\mathit{\boldsymbol{p}}}_{i + 1}} - {{\mathit{\boldsymbol{p}}}_{ci}}} \right) \times \left( { - {{\mathit{\boldsymbol{f}}}_{i + 1}}} \right)} \end{array}} \right.$ | (9) |
则肢体i近端力和力矩为:
| $\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{f}}}_i} = {{\mathit{\boldsymbol{f}}}_{i + 1}} + {{\mathit{\boldsymbol{F}}}_i} - {{\mathit{\boldsymbol{G}}}_i}}\\ {{{\mathit{\boldsymbol{n}}}_i} = {{\mathit{\boldsymbol{N}}}_i} + {{\mathit{\boldsymbol{n}}}_{i + 1}} + \left( {{{\mathit{\boldsymbol{p}}}_i} - {{\mathit{\boldsymbol{p}}}_{ci}}} \right) \times {{\mathit{\boldsymbol{f}}}_i} + \left( {{{\mathit{\boldsymbol{p}}}_{i + 1}} - {{\mathit{\boldsymbol{p}}}_{ci}}} \right) \times {{\mathit{\boldsymbol{f}}}_{i + 1}}} \end{array}} \right.$ | (10) |
至此,人体下肢逆动力学模型建立完成。逆动力学计算从肢体3即足部开始,依次计算踝关节、膝关节、髋关节力和力矩。足部受力(即f4)由测力鞋测量结果确定,若足部与支撑面无接触,则f4=0。
关节功率可根据下式计算:
| ${{\mathit{\boldsymbol{P}}}_i} = {{\mathit{\boldsymbol{n}}}_i} \cdot {{\mathit{\boldsymbol{\omega}}}_i}$ | (11) |
本实验共测量成年男性6名,体重55~78 kg,身高175~185 cm;共测量5种动作,获得有效数据149组。测量对象身体参数见表 1,动作编号及测量结果范围见表 2。
| 表 1 测量对象身体参数表 Tab. 1 Physical parameters of subjects |
| 表 2 运动编号及测量结果范围 Tab. 2 Action number and range of results |
为表达简洁,用Tij表示关节力矩,Pij表示关节功率;i=1, 2, …,5代表动作编号,具体定义见表 2;j=h, k, a,表示关节名称,h代表髋关节,k代表膝关节,a代表踝关节。例如,T1k表示步行(动作1)膝关节力矩,P3k表示向上跳跃(动作3)膝关节功率。
2.2 步行将人体步行周期分为单足支撑相和双足支撑相两个阶段,根据实验数据计算得到各相位占比(见表 3)。
| 表 3 不同运动方式下各相位占比汇总表 Tab. 3 Summary of phase proportions under different behaviors |
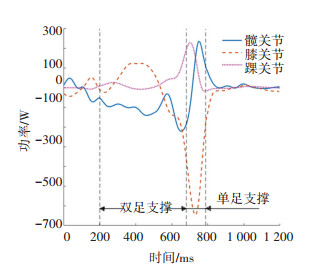
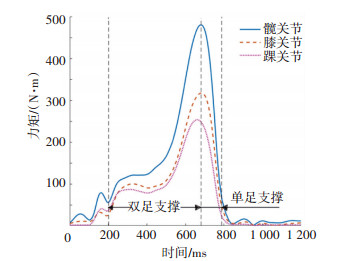
对步行过程中人体下肢进行逆动力学分析得,T1h、T1k和T1a均在单足支撑相达到最大。P1k在双足支撑相达到最大,此时膝关节做正功,移动质心位置,转换支撑脚;P1a和P1h在单足支撑相达到最大值,使游脚向前迈出,提供步行速度,且P1hmax略比P1amax滞后。
最大关节力矩与功率拟合方程以体重、身高和运动指标作为自变量,用最小二乘法进行多元非线性拟合,拟合曲面如附图 1所示。图 7、8为5号被测对象以0.96 m/s速度步行时,下肢各关节的功率和力矩变化曲线。
|
图 7 5号被测对象以0.96 m/s速度步行关节功率曲线图 Fig. 7 Joint power curves of lower limb during walking(Subject No.5, 0.96 m/s) |
|
图 8 5号被测对象以0.96 m/s速度步行关节力矩曲线 Fig. 8 Torque curves of lower limb during walking(Subject No.5, 0.96 m/s) |
将人体跑步周期分为着地相和腾空相两个阶段,各相位占比见表 3。对跑步过程中人体下肢进行逆动力学分析得,T2h、T2k和T2a均在着地相达到最大。P2a和P2h最大值出现在腾空相中,使游脚向前迈出并以正确的姿态着地,P2amax比P2hmax稍滞后;P2k在着地相达到最大值,此时膝关节做正功,提供跑步速度。最大关节力矩与功率拟合曲面如附图 2所示。如图 9为5号被测对象以1.5 m/s速度跑步时,下肢各关节的功率和力矩变化曲线。

|
图 9 5号被测对象以1.5 m/s速度跑步关节功率和力矩曲线图 Fig. 9 Joint power and torque curves of lower limb during running(Subject No.5, 1.5 m/s) |
将人体向上跳跃运动周期分为起跳、腾空和缓冲3个阶段,各相位占比见表 3。对向上跳跃过程中人体下肢进行逆动力学分析得,T3h、T3k和T3a均在起跳相达到最大。起跳相中膝关节做正功,踝关节与髋关节做负功;上升相中,髋关节做正功;缓冲相中,踝关节与髋关节做正功,膝关节做负功。P3hmax发生在腾空相;P3kmax发生在起跳相,P3amax发生在缓冲相。最大关节力矩与功率拟合曲面如附图 3所示。图 10为4号被测对象向上跳跃至600 mm高台时,下肢各关节的功率和力矩变化曲线。
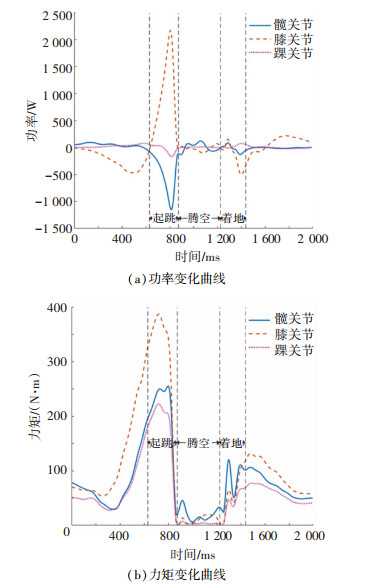
|
图 10 4号被测对象向上跳跃至600 mm高台关节功率和力矩曲线图 Fig. 10 Joint power and torque curves of lower limb during jumping up(Subject No.4, 600 mm) |
在向上跳跃过程中,髋关节主要负责腾空相中的屈髋动作,以确保足底高度大于高台高度;膝关节主要负责起跳时功率输出,提供人体离地时的初速度;踝关节则负责落地时的身体稳定性。根据附图 3中拟合曲面可知,P3h随运动指标的上升先下降,再上升,即当高度较低时,人体离地初速度不需要太大,靠屈髋即可保证足底高度大于台面;随着距离上升,膝关节为人体提供了较大初速度,屈髋动作幅度可适当减小;之后随着距离上升,跳上高台需要同时具备较大的离地初速度和屈髋幅度。P3k随运动指标的上升先上升,再小幅下降,原因是随着高台高度的增加,人体手臂的摆动提供了一部分离地初速度,使得膝关节做功减小。
2.4.2 向下跳跃人体向下跳跃运动周期从人体离开高台后质心到达最高点处开始计算,分为腾空与缓冲两个阶段,各相位占比见表 3。对向下跳跃过程中人体下肢进行逆动力学分析得,T4h、T4k和T4a均在缓冲相达到最大。缓冲时,髋关节与踝关节做正功,膝关节做负功。P4h和P4a在缓冲相达到最大,此时P4k为负值且最小。P4kmax发生在缓冲相之后,负责将人体由落地后稳定状态恢复至直立状态,与向下跳跃过程无关,故忽略。最大关节力矩与功率拟合曲面如附图 4所示。图 11为4号被测对象从600 mm高台上向下跳跃时,下肢各关节的功率和力矩变化曲线。
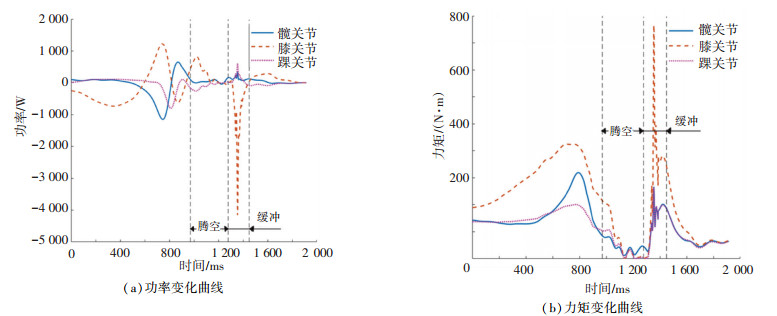
|
图 11 4号被测对象从600 mm高台上向下跳跃关节功率和力矩曲线图 Fig. 11 Joint power and torque curves of lower limb during jumping down(Subject No.4, 600 mm) |
向下跳跃落地瞬间,膝关节主要负责吸收冲击与人体动能,髋关节与踝关节则主要负责保持身体的平衡。需要指出的是,功率为负值时,表示人体对抗重力做功,将重力势能转化为动能、肌肉的弹性势能和振动损耗。对应仿人机器人则为原动机、缓冲机构和机械振动吸收能量。实际使用中应在关节处,尤其是膝关节处加入联轴器或弹性元件,或进行单独的缓冲机构设计,避免造成驱动元件或传动部件损坏。
2.4.3 原地跳跃将人体原地跳跃运动周期分为起跳、上升、下降和缓冲4个阶段,各相位占比见表 3。对向下跳跃过程中人体下肢进行逆动力学分析得,T5h、T5k和T5a均在缓冲相中达到最大。P5kmax发生在起跳相,P5hmax和P5amax发生在缓冲相,此时P5h值最小(负值)。最大关节力矩与功率拟合曲面附图 5所示。图 12为4号被测对象原地跳跃380 mm时,下肢各关节的功率和力矩变化曲线。
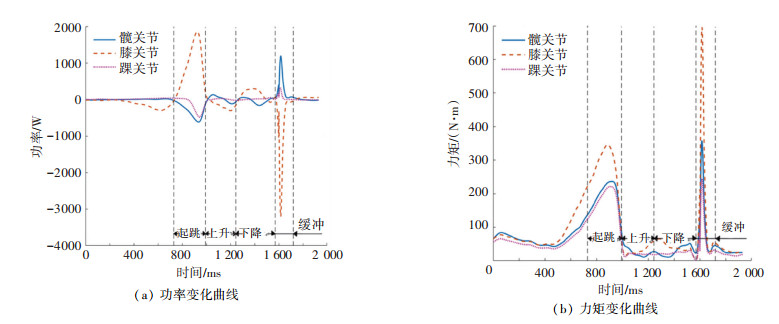
|
图 12 4号被测对象原地跳跃380mm下肢关节功率曲线图 Fig. 12 Joint power curves of lower limb during vertical jumping(Subject No.4, 380 mm) |
受到跳起高度和动作模式的限制,原地跳跃可近似看作高度较低的向上跳跃和向下跳跃的结合。膝关节在起跳相中负责提供人体离地的初速度,在缓冲相中负责吸收震动与能量;原地跳跃中基本不存在屈髋动作,髋关节与膝关节主要负责落地时刻人体的稳定性。与向下跳跃不同的是,在原地跳跃时,髋关节功率与踝关节功率之比大于向下跳跃,说明这时髋关节在保持身体稳定方面起到更大的作用。
综合3种跳跃方式可得出,髋关节在缓冲相与腾空相做功达到最大值,负责落地时维持身体的稳定性以及腾空状态中的屈髋动作(如果有的话);膝关节在起跳相做功达到最大值,负责提供人体跃起离地的初速度以及吸收落地时的动能;踝关节在缓冲相做功达到最大值,负责落地时维持人体身体的稳定性。
3 拟合公式汇总及应用示例对第2节中计算结果使用SPSS数据分析软件进行多元非线性拟合,得到不同动作下各关节最大关节力矩与关节功率拟合方程,如表 4和表 5所示。
| 表 4 最大关节力矩拟合公式汇总表 Tab. 4 Summary of fitting equations for maximum joint torque |
| 表 5 最大关节功率拟合公式汇总表 Tab. 5 Summary of fitting equations for maximum joint power |
下面给出一例前述拟合公式的应用实例。
假设机器人向上跳跃和向下跳跃的运动指标相等,将两种运动方式下对应关节力矩与关节功率拟合曲面相结合,得到类似如图 13(a)所示拟合曲面,图中所示为踝关节所受最大关节力矩拟合曲面。在确定仿人机器人全身身高为1.8 m的情况下,体重为50~80 kg,运动幅度范围在100~600 mm内的分界线如图 13(b)所示。在向上/向下跳跃运动指标相同情况下,当由运动指标与体重确定的坐标点在分界线包围的右下侧时,最大膝关节力矩可直接使用向上跳跃拟合公式计算;反之,则使用向下跳跃相应拟合公式计算,其余关节力矩与关节功率联合拟合分界线如表 6所示。设计者也可根据实际情况,参照表 4和5中结果,设计出不同运动指标下不同动作结合的联合拟合表。
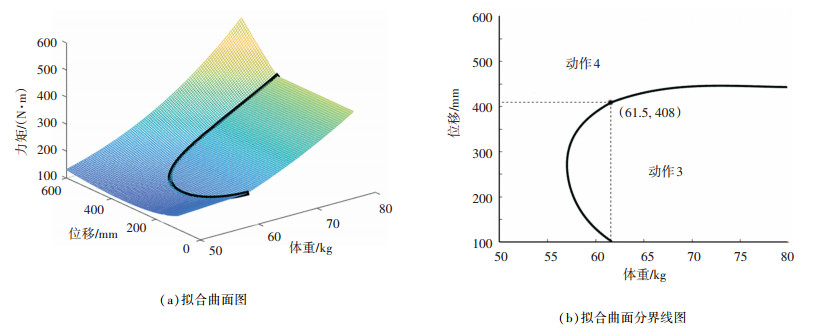
|
图 13 仿人机器人总高180 cm且向上/向下跳跃运动指标相等时踝关节力矩拟合结果 Fig. 13 Ankle joint torque fitting results when total height of humanoid robot is 180 cm and indexes of jumping up/down are equal |
| 表 6 仿人机器人总高180 cm且向上/向下跳跃运动指标相等时各关节力矩与关节功率拟合分界线汇总表 Tab. 6 Summary of fitting boundaries of joint torque and joint power when total height of humanoid robot is 180 cm and indexes of jumping up/down are equal |
本文选取人体运动中最大关节功率和关节力矩评价仿人机器人的极限驱动能力,采集了人体运动轨迹和足底力数据;利用机构化人体双足模型计算关节力矩和功率,得到了不同运动方式下各关节最大关节力矩和功率的拟合方程;并分析了各关节在不同运动方式下关节力矩和功率变化。综合分析结果,总结得到不同动作下仿人机器人设计参考准则如下:
1) 步行运动下,关节力矩均在单足支撑相中达到峰值;膝关节功率在双足支撑相达到峰值,踝关节与髋关节功率在单足支撑相达到峰值,且P1hmax略比P1amax滞后。最大关节功率与关节力矩均出现在髋关节。
2) 跑步运动下,关节力矩均在单足支撑相中达到峰值;踝关节与髋关节功率在腾空相达到峰值,P2amax比P2hmax稍滞后;膝关节功率在着地相达到峰值。最大关节功率与关节力矩均出现在膝关节。
3) 向上跳跃运动下,关节力矩均在起跳相中达到峰值。膝关节功率在起跳相中达到峰值,髋关节功率在腾空相中达到峰值,踝关节功率在缓冲相中达到峰值。最大关节功率与关节力矩均出现在膝关节。
4) 向下跳跃运动下,关节力矩及关节功率均在缓冲相中达到峰值。最大关节功率出现在髋关节与踝关节,最大关节力矩出现在髋关节与膝关节。
5) 原地跳跃运动下,关节力矩均在缓冲相中达到峰值。膝关节功率在起跳相中达到峰值,踝关节与髋关节功率在缓冲相中达到峰值。最大关节功率与关节力矩均出现在膝关节。
6) 对于多种行为动作综合设计,可通过查阅表 4、表 5中拟合公式,结合实际机器人运动指标进行设计计算。
相关设计人员可根据前述设计参考准则,并利用表 4和表 5中拟合方程,结合实际设计指标计算得到各关节应达到的极限驱动能力,实现多运动方式下双足机器人的综合设计。
本文仅计算与分析了人体下肢在运动中的关节力矩与功率的变化情况,未考虑上肢在运动中的作用。后续将进行人体上肢在运动中的作用分析,并实施更大规模、更多运动方式的测量实验,丰富样本库,以获得适应性更广、更精确的仿人机器人设计参考准则。
附录
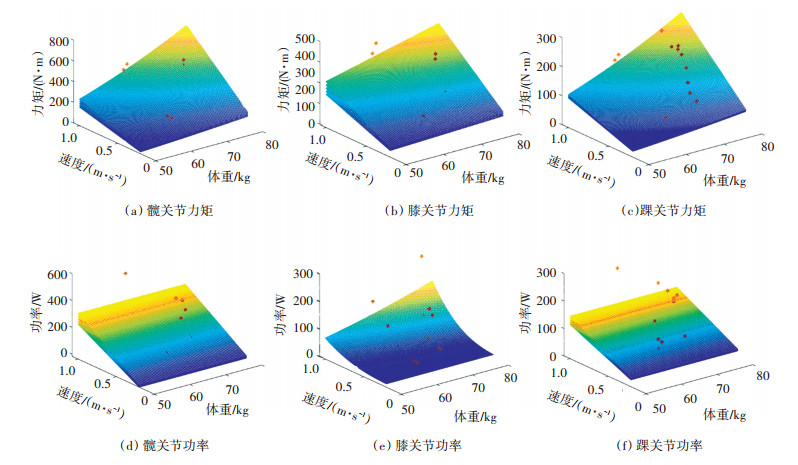
|
附图 1 步行关节力矩和关节功率拟合曲面图 Fig. 1 Fitting surface diagram of joint torque and joint power for walking |
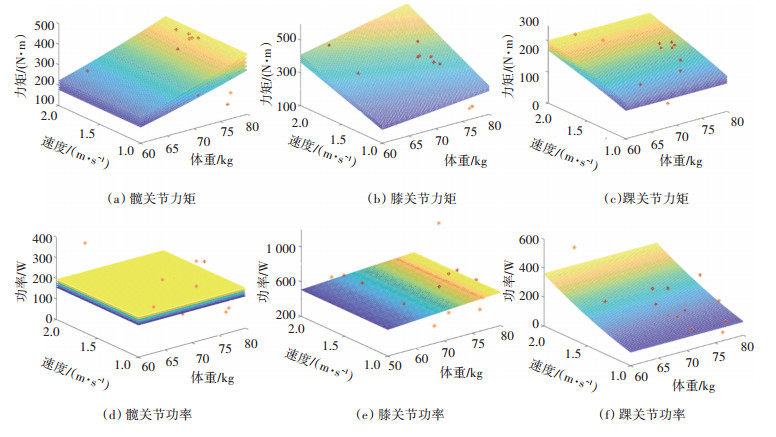
|
附图 2 跑步关节力矩和关节功率拟合曲面图 Fig. 2 Fitting surface diagram of joint torque and joint power for running |

|
附图 3 向上跳跃关节力矩和关节功率拟合曲面图 Fig. 3 Fitting surface diagram of joint torque and joint power for jumping up |

|
附图 4 向下跳跃关节力矩和关节功率拟合曲面图 Fig. 4 Fitting surface diagram of joint torque and joint power for jumping down |
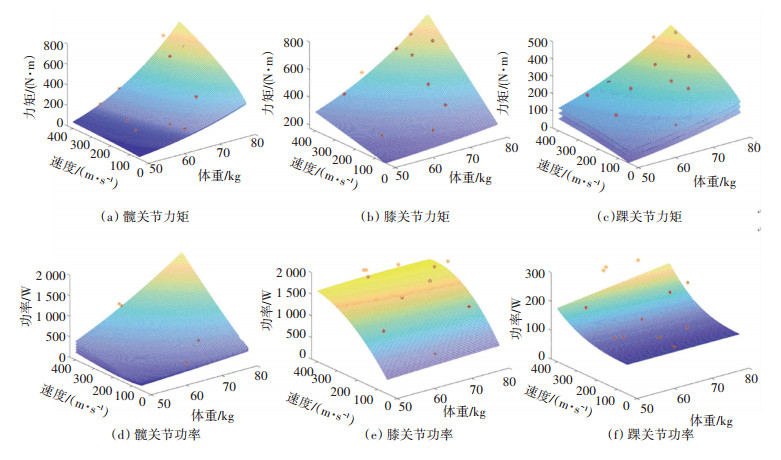
|
附图 5 原地跳跃关节力矩和关节功率拟合曲面图 Fig. 5 Fitting surface diagram of joint torque and joint power for vertical jumping |
| [1] |
DASGUPTA A, NAKAMURA Y. Making feasible walking motion of humanoid robots from human motion capture data[C]//Proceedings of 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C). Detroit: IEEE, 1999: 1044. DOI: 10.1109/ROBOT.1999.772454
|
| [2] |
ACEVES-LOPEZ A, MELENDEZ-CALDERON A. Human-inspired walking-style for a low-cost biped prototype[C]// 2006 IEEE 3rd Latin American Robotics Symposium. Santiago: IEEE, 2006: 141. DOI: 10.1109/LARS.2006.334339
|
| [3] |
SOHN K, OH P. Applying human motion capture to design energy-efficient trajectories for miniature humanoids[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura-Algarve: IEEE, 2012: 3425. DOI: 10.1109/IROS.2012.6385986
|
| [4] |
POWELL M J, HEREID A, AMES A D. Speed regulation in 3D robotic walking through motion transitions between human-inspired partial hybrid zero dynamics[C]// 2013 IEEE International Conference on Robotics and Actuation. Karlsruhe: IEEE, 2013: 4803
|
| [5] |
SINNET R W, JIANG S, AMES A D. A human-inspired framework for bipedal robotic walking design[J]. International Journal of Biomechatronics and Biomedical Robotics, 2014, 3(1): 20. DOI:10.1504/IJBBR.2014.059275 |
| [6] |
吴伟国, 栗华, 高力扬. 人体步行捕捉下的双足机器人跟随步行与实验[J]. 哈尔滨工业大学学报, 2017, 49(1): 21. WU Weiguo, LI Hua, GAO Liyang. Follow-walking motions of a biped robot and its experimental research based on human walking capturing[J]. Journal of Harbin Institute of Technology, 2017, 49(1): 21. DOI:10.11918/j.issn.0367-6234.2017.01.003 |
| [7] |
CORNEJO-ARISMENDI V, BARRIOS-ARANIBAR D. A mapping approach for real time imitation of human movements by a 22 DOF humanoid[C]//2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE). João Pessoa: IEEE, 2018: 420. DOI: 10.1109/LARS/SBR/WRE.2018.00081
|
| [8] |
CROSS R. Standing, walking, running, and jumping on a force plate[J]. American Journal of Physics, 1999, 67(4): 304. DOI:10.1119/1.19253 |
| [9] |
CHEN Y. Jumping mechanism and simulation of the humanoid robot[J]. Applied Mechanics and Materials, 2011, 80. DOI:10.4028/www.scientific.net/AMM.80-81.1176 |
| [10] |
IBATA Y, KITAMURA S, MOTOI K, et al. Measurement of three-dimensional posture and trajectory of lower body during standing long jumping utilizing body-mounted sensors[C]//2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Osaka: IEEE, 2013: 4891. DOI: 10.1109/EMBC.2013.6610644
|
| [11] |
CHIU L Z, MOOLYK A N. Segment kinematics differ between jump and drop landings regardless of practice[J]. Journal of Applied Biomechanics, 2015, 31(5): 357. DOI:10.1123/jab.2014-0101 |
| [12] |
王勇, 胡保华, 张方双, 等. 一种足底压力传感鞋: CN205671578U[P]. 2016-11-09 WANG Yong, HU Baohua, ZHANG Fangshuang, et al. A kind of plantar pressure sensing footwear: CN205671578U[P]. 2016-11-09 |
| [13] |
金昊龙, 宋慧新, 陈宇, 等. 一种用于下肢助力系统的足底力测量装置: CN103750848A[P]. 2015-08-26 JIN Haolong, SONG Huixin, CHEN Yu, et al. Foot applied force measuring device for lower limb assistance system: CN103750848A[P]. 2015-08-26 |
| [14] |
吴伟国, 张效, 林鹏程. 一种可适应不同脚长的集成化智能足底力测量系统: CN113349762A[P]. 2021-09-07 WU Weiguo, ZHANG Xiao, LIN Pengcheng. An integrated intelligent plantar force measurement system that can adapt to different foot lengths: CN113349762A[P]. 2021-09-07 |
| [15] |
全国人类工效学标准化技术委员会. 成年人人体惯性参数: GB/T 17245—2001[S]. 北京: 中国标准出版社, 2004 Inertialparameters of adult human body: GB/T 17245—2001[S]. Beijing: Standards Press of China, 2004 |
 2022, Vol. 54
2022, Vol. 54


