液滴撞击固体表面现象普遍存在于自然界和日常生活中,并且广泛应用于各类工业过程和技术中,如喷雾冷却[1]、喷墨打印[2]、农药喷洒[3-4]、血迹模式分析[5]等。液滴撞击固体壁面的动态过程是一个涉及气、液、固多相耦合的复杂流动问题,研究其动力学行为特性,不仅能了解自由表面多相流流动问题的本质,而且对相关技术应用具有非常重要的指导意义。例如,基于血迹覆盖模式可提取血滴撞击信息,有助于刑事案件调查;增大农药液滴的润湿面积能增强除草除虫效果。研究发现,液滴在固体壁面上的动态行为主要受撞击参数(液滴尺寸[6]、撞击速度[7-8])、液体性质(表面张力[9]、液体黏性力[10])、壁面参数(壁面粗糙度[3]、壁面温度[11-12]、壁面润湿性[13])、环境条件(温度及压强[14])等因素的综合影响。
复杂的动态液滴碰撞现象是惯性力、毛细力、黏性力三者相互作用的结果,为了表征各种作用力的强弱,通常采用韦伯数We=ρD0V02/σ和雷诺数Re=ρD0V0/μ来分别量化惯性力与表面张力、惯性力与黏性力的比率。在We
在液滴撞击动力学领域,分析及预测最大铺展因子是关键问题之一。通过改变液体密度、黏性、表面张力等物理性质,能有效控制液滴的铺展面积。例如,使用水和甘油的混合物,可研究液体黏性对铺展程度的影响。Lee等[15]的研究结果表明,由于黏性耗散快速消耗液滴动能,黏度大的液滴铺展面积更小,并且能更快速地形成最大铺展直径。然而,Qin等[10]发现,在相对较小的韦伯数下(We < 30),最大铺展因子随着黏度的增加呈现先上升后下降的趋势。这是因为在该工况下,液滴的变形和内部流动并不是由惯性力主导的,此时黏性力的作用较强。此外,许多学者采用乙醇[17]、添加活性剂的方式[18]来研究表面张力对液滴铺展过程的作用规律,结果表明,较小的表面张力会导致更小的能量耗散率,从而推迟最大铺展面积的形成[17]。
上述研究表明,液体黏度和表面张力显著影响液滴撞击的动力学行为。目前,大多研究采用不同液体或者两种液体的混合物来研究黏性和表面张力对液滴铺展行为的影响。当壁面温度改变时,尤其是壁温低于液滴的液固相变点时,液滴的表面张力和黏度均会发生变化,但针对壁面过冷度对液滴铺展过程的影响的认知仍较为有限,一些问题仍有待回答,例如液滴铺展是否随着壁面过冷度的增加而减弱?撞击韦伯数是如何影响过冷条件下的液滴铺展行为的?
基于上述问题,本文采用实验手段,针对大范围韦伯数下壁面过冷度对液滴铺展特性的影响展开研究,获得了过冷温区液滴铺展的作用规律,相关研究结果可为控制固-液接触面积提供理论支撑。
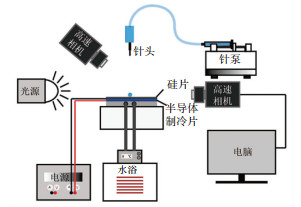
1 实验方法与装置图 1为液滴撞击冷表面的实验装置图,包括液滴发生系统、高速摄像系统以及壁面控温系统3部分。实验工质为22 ℃的去离子水,其密度为997.77 kg/m3,表面张力为72.48×10-3 N/m,黏度为0.954 4×10-3 Pa·s。在开始实验之前,首先使用超声波清洗仪清洁表面。微量针泵以缓慢的速度推动液体,当液体的重力大于表面张力时,液滴从针头滴落。通过改变针头尺寸,获得初始直径范围为2.21~3.10 mm的液滴,液滴撞击速度范围为2.21~2.62 m/s。为清晰观测液滴撞击壁面的动态行为,采用高速摄像机与冷光源对液滴撞击全过程进行了拍摄,拍摄速度为10 000帧/s。实验开始前调节冷光源角度及亮度,以及高速相机位置、焦距,确保视场中的液滴轮廓清晰。相机的高度和拍摄角度通过三脚架进行调节,冷光源主体的高度通过升降台控制,并且冷光源探头也具备一定伸缩调节功能,确保光从合适的角度照亮拍摄画面。高速相机与电脑连接,用于控制拍摄的开始、结束以及实时显示拍摄的内容。为校正拍摄画面尺寸,在每次实验过程中以相同的角度拍摄已知长度参照物,从而获得拍摄尺寸与实际尺寸之间的比例尺,经过计算得到图像中数据的实际值。
|
图 1 实验系统图 Fig. 1 Schematic diagram of experimental setup |
采用亲水硅片作为实验壁面,1 μL去离子水在该壁面上的静态接触角约为59.6°,该壁面的粗糙度Ra为0.52 nm,壁面温度由半导体制冷片和恒温浴仪进行控制。采用稳压电源为半导体制冷片供电并调节其功率,半导体制冷片的热端与恒温水浴仪的冷模块相接,通过及时散热使冷端温度降至更低。本研究采用K型热电偶实时检测壁面温度,该热电偶的测量误差为±0.3 K,壁温(θs)的变化范围为-36.6~-10.2 ℃,壁面导热系数随壁温发生变化,相应变化范围为232.06~198.48 W/(m·K)。为减少实验误差,每一实验工况重复进行3次并计算出3组数据的标准差,如式(1)所示,所有标准差的大小采用误差棒的形式在数据图中表示。环境温度和相对湿度分别控制在(22±1)℃和(38±2)%。
| $ \eta=\sqrt{\frac{1}{3}\left[\left(x_{1}-\bar{x}\right)^{2}+\left(x_{2}-\bar{x}\right)^{2}+\left(x_{3}-\bar{x}\right)^{2}\right]} $ | (1) |
式中:x1,x2,x3分别代表 3次重复实验的测量数据,x为3次测量数据的平均值。
2 结果与讨论 2.1 液滴碰撞动态铺展现象4组不同工况下的液滴动态撞击过程如图 2所示,实验工况分别为:

|
图 2 不同工况下液滴撞击过冷壁面的拍摄图 Fig. 2 Snapshots of water droplets impacting on supercooled surface under different experimental conditions |
(a) D0=2.21 mm,θs=-36.5 ℃,V0=2.21 m/s;
(b) D0=2.21 mm,θs=-36.5 ℃,V0=2.62 m/s;
(c) D0=2.21 mm,θs=-15.1 ℃,V0=2.62 m/s;
(d)D0=3.10 mm,θs=-36.5 ℃,V0=2.62 m/s。
将液滴接触壁面瞬间的时刻定义为初始时刻,t=0 s。从图 2中可以看出,在撞击之后的初始阶段(t=0.6 s),液滴的顶部继续保持球形,底部逐渐向外扩展。随着时间的推移,液滴继续向外铺展,由于黏性耗散和表面张力的限制,在2.0~2.4 ms左右到达最大铺展直径(Dmax),形成“披萨状”形态(中间为薄的液体层,四周具有花瓣状凸出)。由于壁面的亲水性质和液滴底部迅速结冰,液滴几乎不发生回缩现象,上层液体继续震荡直至平衡状态。
液滴铺展至最大程度时刻(tmax)的动态行为说明液滴铺展与撞击速度、壁温、液滴尺寸等参数相关。当θs=-36.5 ℃时,随着撞击速度的增加,液滴的四周出现了指状形态,如图 2(a)和(b)所示。在撞击速度相对较大的情况下,持续降低壁面温度会进一步强化指状形态,如图 2(b)和(c)所示。在壁温较低且撞击速度较大的工况下,随着液滴尺寸的增加,指状现象进一步加剧,指端脱离形成飞溅子液滴,如图 2(d)中t=2 ms时的红色圆圈所示。上述结果表明,足够大的撞击速度是形成指状形态的前提,高壁面过冷度和大液滴尺寸会强化这一现象,这与指状形态的形成机理一致。指状形态是由泰勒-瑞利不稳定性触发的,这种不稳定性出现在两种具有不同密度的流体之间。当密度低的流体推动密度高的流体时,该不稳定性则会发生。当V0较大时,更多的空气被限制在液滴和基板之间,这些空气即为低密度流体,可触发强烈的不稳定性,最终导致指状形态的产生。相反,在较低的V0下,被限制空气较少,不足以触发强烈的泰勒-瑞利不稳定性。较大的液滴会增加被限制空气,从而强化泰勒-瑞利不稳定性。另外,液膜边缘突然减速也会强化该不稳定性,增强指状形态。导致液膜边缘减速的原因说法不一,Allen等[19]发现黏性力导致减速的发生,而Thoroddsen等[20]则发现液体表面张力是减速的主要原因。这两个力均随壁面温度的降低而增加,所以较低的壁面温度会强化指状形态。
2.2 铺展阶段换热模型本研究在铺展过程中并未观测到明显的结冰现象,为了进一步检验结冰对铺展过程的影响,这里提出了一个简化的换热模型来估算液滴冻结开始的时刻,以典型工况(D0=3.10 mm,V0=2.21 m/s,θs=-36.6 ℃)为例,-36.6 ℃为本研究中最低壁面温度。如图 3所示,液滴在铺展过程中的几何形状假设为高度h(t)、直径D(t)的圆饼状,并均分为n=800层,每一层的高度为Δh(t)=h(t)/800,每一层“i”具有均匀的温度θi,上下相邻层“i+1”和“i-1”的温度分别为θi+1和θi-1,i=1和i=802层的温度分别等于壁面温度和室温。随着液滴的不断铺展,通过拍摄视频测得D(t)的变化范围是1.35~11.85 mm。通过体积守恒得到h(t)相应从10.90 mm减小至0.14 mm。为了简化模型,忽略密度、传热系数和导热系数随温度的变化。

|
图 3 模型示意图 Fig. 3 Schematic diagram of the model |
对与壁面直接接触的液体层而言,即i=2,换热方式主要包括水在壁面上流动产生的强制对流换热以及液滴与壁面之间的导热。该对流换热项为0.25αwtπD(t)2(θ2(t)-(θ2(t)+θ1(t))/2),其中αwt为水的强制对流换热系数,量级约为103[21],T(t)为铺展过程中每一个液体层的平均温度。导热项为0.25klπD(t)2[(θ2(t)-(θ2(t)+θ1(t))/2]/[2Δh(t)],其中kl为水在常温下的导热系数,为0.602 W/(m·K)。通过固液界面的对流换热量与导热量之比约为10-4~10-2,表明可忽略对流换热项。
对液滴的顶层而言,即i=801,换热方式主要包括作用在气液界面的空气强制对流换热以及从该层到下层液体的导热。该对流换热项为0.25αairπ·D(t)2((θ802(t)+θ801(t))/2-θ801(t)),其中αair为空气的强制对流换热系数,量级约为10[21]。导热项为klπD(t)2/4((θ801(t)-θ800(t))/Δh(t)),由于(θ802(t)-θ801(t))和(θ801(t)-θ800(t))处于相同量级,可得对流换热项与导热项之比约为10-6~10-4,表明可忽略气液界面的对流换热项。
对中间层i而言,换热方式主要包括作用在气液界面的空气强制对流换热,从上层液体i+1到该层的导热,以及从该层到下层液体i-1的导热。该对流换热项为αairπD(t)Δh(t)(θair(t)-θi(t)),该层与下层液体的导热项为klπD(t)2/4((θi(t)-θi-1(t))/Δh(t))。考虑极限条件下该层冷却至273.15 K,得到θair-θi(t)≤θair-273.15≈22 K,θi(t)-θi-1(t)近似视为(θair-θs)/n~10-2 K,并将铺展过程中D(t)和h(t)的变化情况纳入考虑范围,得到作用在气液界面的对流项与该层到下层的导热项的比值约为10-7~10-2,表明可忽略该对流项。经过时长Δt后,内能的变化量为ρlCp, l(πD(t+ Δt)2)/ 4· Δh(t+Δt)θi(t+Δt)-ρlCp, lπD(t)2/4Δh(t)θi(t),其中Cp, l为水在室温下的比热容,约为4 182.8 J/(kg·K)。
根据能量守恒,总的换热量等于内能的变化量,结合对顶层、底层和中间液体层的上述分析,可将i层的能量守恒表示为:
| $ \left\{ \begin{array}{l} {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t + \Delta t)}^2}}}{4}\Delta h(t + \Delta t){\theta _i}(t + \Delta t) - {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t)}^2}}}{4}\Delta h(t){\theta _i}(t) = {k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{{\theta _{i + 1}}(t) - {\theta _i}(t)}}{{\Delta h(t)}}\\ \;\;\;\;\;\;\; - {k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{{\theta _i}(t) - 0.5\left( {{\theta _i}(t) + {\theta _{i - 1}}(t)} \right)}}{{2\Delta h(t)}}, \quad i = 2\\ {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t + \Delta t)}^2}}}{4}\Delta h(t + \Delta t){\theta _i}(t + \Delta t) - {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t)}^2}}}{4}\Delta h(t){\theta _i}(t) = {k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{{\theta _{i + 1}}(t) - {\theta _i}(t)}}{{\Delta h(t)}} - \\ \;\;\;\;\;\;{k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{{\theta _i}(t) - {\theta _{i - 1}}(t)}}{{\Delta h(t)}}, \quad 2 < i < 801\\ {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t + \Delta t)}^2}}}{4}\Delta h(t + \Delta t){\theta _i}(t + \Delta t) - {\rho _1}{C_{p, 1}}\frac{{\pi D{{(t)}^2}}}{4}\Delta h(t){\theta _i}(t) = {k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{\frac{{{\theta _i}(t) + {\theta _{i + 1}}(t)}}{2} - {\theta _i}(t)}}{{2\Delta h(t)}} - \\ \;\;\;\;\;\;{k_1}\frac{{\pi D{{(t)}^2}}}{4}\Delta t\frac{{{\theta _i}(t) - {\theta _{i - 1}}(t)}}{{\Delta h(t)}}, \quad i = 801 \end{array} \right. $ | (2) |
式中:Δt为计算的步长,数值为1×10-8。
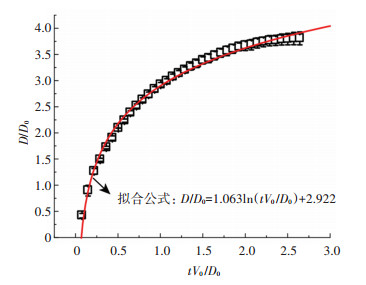
通过将实验数据进行拟合,如图 4所示,得
| $ D(t)=\left\{\begin{array}{l} \left(a \ln \left(\frac{V_{0}}{D_{0}} t\right)+b\right) D_{0}, \quad 0.001 \mathrm{~s} \leqslant t \leqslant t_{\max } \\ \left(a \ln \left(\frac{V_{0}}{D_{0}} t_{\max }\right)+b\right) D_{0}, \quad t_{\max } <t \end{array}\right. $ | (3) |
|
图 4 在V0=2.21 m/s,θs=-36.6 ℃的工况下,3.10 mm液滴的量纲一的铺展直径随量纲一的时间的变化情况 Fig. 4 Variation of dimensionless spreading diameter of 3.10 mm droplet with dimensionless time (θs=-36.6 ℃, V0=2.21 m/s) |
式中:a=1.036,b=2.922。
初始条件为:
| $ \theta(1 <i \leqslant n+1, t=0)=\theta_{\text {air }} $ | (4) |
边界条件为:
| $ \theta(1, t)=\theta_{\mathrm{s}} $ | (5) |
| $ \theta(802, t)=\theta_{\text {air }} $ | (6) |
底部“j”层的平均温度到达0 ℃(273.15 K)所需要的时间tic可用式(7)计算:
| $ \begin{array}{l} {{\bar \theta }_{2 \sim j}} = \frac{{{\theta _2}\left( {{t_{{\rm{ic}}}}} \right) + {\theta _3}\left( {{t_{{\rm{ic}}}}} \right) + \cdots + {\theta _{j - 1}}\left( {{t_{{\rm{ic}}}}} \right) + {\theta _j}\left( {{t_{{\rm{ic}}}}} \right)}}{{j - 1}} = \\ \;\;273.15 \end{array} $ | (7) |
通过在软件MATLAB中进行迭代求解,得到液滴底部1/10~1/5厚度的平均温度到达0 ℃所需时间为1.35~2.33 ms。该时间与tmax处于相同的数量级,但略小于tmax,这表明液滴底部在到达最大扩展状态时已达到0 ℃。假设一旦温度降到0 ℃,液滴底层开始冻结,那么在到达最大铺展时刻之前,液滴底部可能会形成一层薄冰。但是,流动的水的冻结温度通常低于静止的水[22],因此,由于液滴在铺展过程中不断流动,结冰可能受到抑制从而推迟。这也与以下事实相吻合:根据高速相机的可视化结果,在整个铺展过程中是无法显著区分结冰是否发生,这意味着冰层可能太薄而难以准确观测,或者结冰主要发生在到达最大铺展程度之后,因此其对动态铺展过程的影响可忽略不计。此外,Ruiter等[23]提出了一种判别液滴在铺展过程是否发生结冰的判据:如果液滴在铺展过程中发生结冰,液滴完全结冰后会在边缘形成自剥离现象,即内部的冰黏附于壁面而四周的冰形会向上翘起。在本研究的实验中并未观察到这种自剥离现象,再次验证了上述推论。
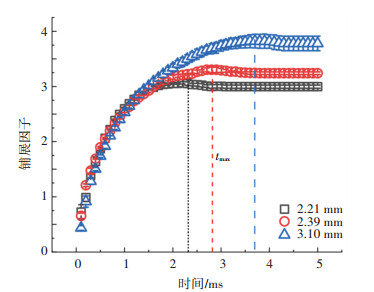
2.3 液滴尺寸对动态铺展过程的影响为定量描述液滴与壁面接触面积的动态变化过程,这里引入了一个量纲一参数——铺展因子(β),定义为液滴动态直径(D)与初始直径的比值。图 5对比了不同液滴尺寸下,铺展因子随时间的变化。从图 5中可以看出,不同实验条件下β均会快速增加直至最大值,然后几乎保持恒定,这与图 2中液滴的动态铺展结果一致。随着液滴尺寸的增加,最大铺展因子(βmax)显著增加,并且达到最大铺展因子所需的时间也明显增加。由于大尺寸液滴的初始动能更高,该动能被黏性耗散所需时间更长。
|
图 5 不同尺寸液滴以2.21 m/s的速度撞击-36.5℃壁面的铺展因子随时间的变化 Fig. 5 Variation of spreading factor of droplets of different sizes impacting on surface with time (θs=-36.5 ℃, V0=2.21 m/s) |
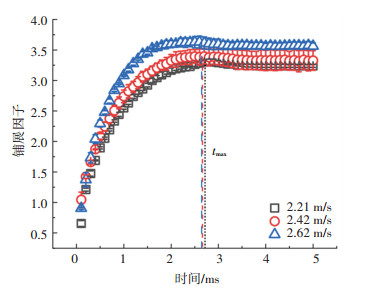
图 6给出了不同撞击速度下直径为2.39 mm液滴撞击-36.5 ℃壁面的铺展因子随时间的变化情况,随着撞击速度的增加,液滴铺展程度明显增加,而撞击速度对最大铺展时间的影响非常微弱,这与Wildeman等[24]的研究结果一致,他们基于实验结果提出最大铺展时间的拟合公式tmax=(βmax-1)D0/V0,当βmax和V0增加的程度可以抵消时,tmax几乎不随V0发生变化。
|
图 6 直径为2.39 mm的液滴以不同的速度撞击-36.5 ℃壁面的铺展因子随时间的变化曲线 Fig. 6 Variation of spreading factor of 2.39 mm droplet with time under θs=-36.5 ℃ and different velocities |
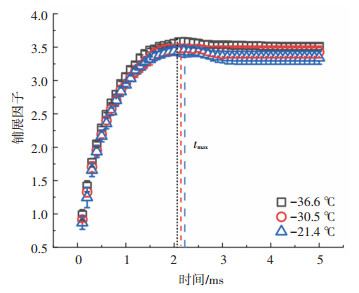
与液滴尺寸及撞击速度相比,壁面温度对于液滴动态铺展过程的影响相对较小。如图 7所示,随着壁面温度增加,tmax略微增加,这是由于液滴温度随着基板温度的上升而增大,从而导致液滴黏性力以及表面张力减小,动能以更慢的速度被耗散,最终使得液滴的最大铺展时间增加。但是,研究中发现βmax与壁面温度的关系呈现相反的趋势。随着壁面温度的升高,液滴铺展程度反而有所下降,下面对这一现象产生的原因和机理进行具体分析。
|
图 7 直径为2.21 mm的液滴以2.62 m/s的速度撞击不同温度壁面的铺展因子随时间的变化 Fig. 7 Variation of spreading factor of 2.21 mm droplet with time under V0=2.62 m/s and different temperatures |
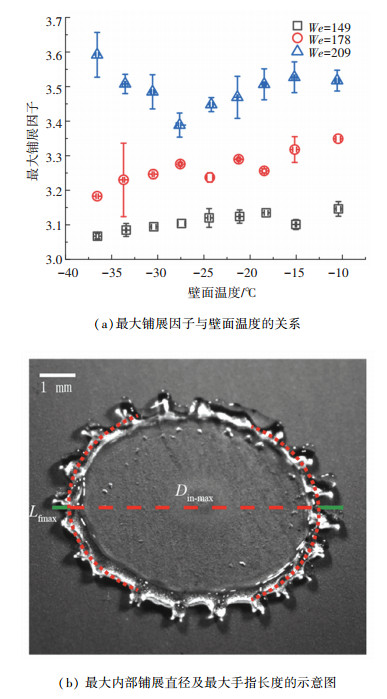
将液滴尺寸和撞击速度的影响用We表征。图 8(a)为不同We下最大铺展因子随温度的变化情况。最大铺展因子在不同We区域呈现出不同的规律。在We相对较小时,βmax随着θs的增加而明显增加而在We较大时(We=209),βmax与θs的关系呈现非单调趋势:随着θs的增加,βmax首先从3.59降低至最小值3.39,然后增大至3.52。从-36.6 ℃到-27.6 ℃,壁面温度增加了9 ℃,导致βmax降低了5.9%。
|
图 8 最大铺展因子的变化情况及组成部分 Fig. 8 Variation and components of maximum spreading factor |
为了更清晰地表明各个因素对最大铺展因子的影响,这里把βmax分为最大内部铺展因子βin-max=Din-max/D0和最大量纲一指状长度Lfinger=Lfmax/D0两个部分,即βmax=βin-max+2Lfinger。如图 8(b)所示,液滴中间虚线段和两端实线段分别表示最大内部铺展直径Din-max和最大手指状长度Lfmax。需要说明的是本研究以水平方向的手指状长度为基准进行比较,首先从指状长度根部确定圆弧,圆弧到指状顶部的距离即为指状长度,取左右两侧指状长度的平均值作为该工况下的实验值。
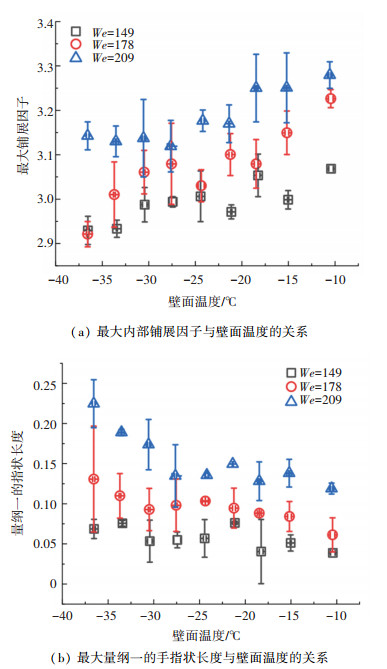
图 9(a)和(b)分别表示不同We下,βin-max和Lfinger随壁面温度的变化趋势。可以看出,无论We如何变化,βin-max均随θs的升高而增大,这是由于温度的上升导致了黏性耗散以及表面张力的下降。然而,Lfinger与θs的关系在不同We下呈现不同的情况。We较小时,Lfinger几乎不随壁面温度变化,数值接近于0,表明该工况下液滴边缘波动非常微弱,不产生手指状形态。当We较大时,Lfinger随着壁面温度的升高而减小。综上所述,随着壁面温度的上升,当Lfinger减小的程度大于βin-max增加的程度,βmax呈现下降趋势,反之,βmax则随之增加。
|
图 9 最大内部铺展因子与最大量纲一的指状长度变化情况 Fig. 9 Variation of maximum interior spreading factor and maximum dimensionless fingering length |
本文研究了较大范围韦伯数下,液滴在过冷壁面的动态铺展特性,并分析了液滴尺寸、撞击速度以及壁面温度对于动态铺展过程的影响,结果表明:
1) 增加液滴尺寸导致初始动能增加,从而加剧了液滴铺展程度,同时增大液滴形成最大铺展面积所需的时间。
2) 增加撞击速度有助于液滴铺展,但对最大铺展时刻的影响可忽略不计。
3) 在不同韦伯数下,最大铺展因子随壁温呈现不同变化趋势,韦伯数较大时,随着壁面温度的升高,由于最大量纲一的指状长度的减量与最大内部铺展因子的增量相互抗衡,所以最大铺展因子呈现先下降后上升的趋势,在韦伯数为209的工况下,壁面温度从-36.6 ℃上升至-27.6 ℃,导致最大铺展因子从3.59降低至3.39,减量为5.9%;当韦伯数较小时,最大铺展因子随着壁温升高而单调增加。
4) 较大的韦伯数有助于液滴与冷板之间捕捉更多的空气,从而引发液膜边缘剧烈的不稳定性,产生指状形态。壁面温度的降低会加剧液膜的减速,进而强化手指状现象。
| [1] |
ZHAO Yugang, ZHU Fangqi, ZHANG Hui, et al. Triple condensate halo from a single water droplet impacting upon a cold surface[J]. Applied Physics Letters, 2019, 114: 1. DOI:10.1063/1.5080356 |
| [2] |
ALMOHAMMADI H, AMIRFAZLI A. Asymmetric spreading of a drop upon impact onto a surface[J]. Langmuir, 2017, 33: 5957. DOI:10.1021/acs.langmuir.7b00704 |
| [3] |
HAO Jiguang. Effect of surface roughness on droplet splashing[J]. Physics of Fluids, 2017, 29: 1. DOI:10.1063/1.5005990 |
| [4] |
LIN Shiji, ZHAO Binyu, ZOU Song, et al. Impact of viscous droplets on different wettable surfaces: impact phenomena, the maximum spreading factor, spreading time and post-impact oscillation[J]. Journal of Colloid and Interface Science, 2018, 516: 87. DOI:10.1016/j.jcis.2017.12.086 |
| [5] |
LAAN N, BRUIN K G, BARTOLO D, et al. Maximum diameter of impacting liquid droplets[J]. Physical Review Applied, 2014, 2: 1. DOI:10.1103/PhysRevApplied.2.044018 |
| [6] |
刘联胜, 任蕰佳, 田亮, 等. 液滴撞击壁面铺展及换热过程数值模拟[J]. 低温与超导, 2021, 49(1): 47. LIU Liansheng, REN Wenjia, TIAN Liang, et al. Numerical simulation of spreading of droplet on wall and heat transfer process[J]. Cryogenics and Superconductivity, 2021, 49(1): 47. DOI:10.16711/j.1001-7100.2021.01.008 |
| [7] |
JIN Zheyan, ZHANG Huanhuan, YANG Zhigang. Experimental investigation of the impact and freezing processes of a water droplet on an ice surface[J]. International Journal of Heat and Mass Transfer, 2017, 109: 717. DOI:10.1016/j.ijheatmasstransfer.2017.02.055 |
| [8] |
XU Qing, LI Zhanyong, WANG Jin, et al. Characteristics of single droplet impact on cold plate surfaces[J]. Drying Technology, 2012, 30: 1757. DOI:10.1080/07373937.2012.708001 |
| [9] |
BEAK S, YONG K. Impact dynamics on SLIPS: effects of liquid droplet's surface tension and viscosity[J]. Applied Surface Science, 2020, 506: 2. DOI:10.1016/j.apsusc.2019.144689 |
| [10] |
QIN Mengxiao, TANG Chenglong, TONG Shangqing, et al. On the role of liquid viscosity in affecting droplet spreading on a smooth solid surface[J]. International Journal of Multiphase Flow, 2019, 117: 54. DOI:10.1016/j.ijmultiphaseflow.2019.05.002 |
| [11] |
JU Jiajun, YANG Zhigang, YI Xian, et al. Experimental investigation of the impact and freezing processes of a hot water droplet on an ice surface[J]. Physics of Fluids, 2019, 31: 3. DOI:10.1063/1.5094691 |
| [12] |
姚一娜, 刘呈, 李聪, 等. 液滴撞击超疏水冷表面的反弹/黏附特性对比研究[J]. 中国安全生产科学技术, 2021, 17(1): 32. YAO Yina, LIU Cheng, LI Cong, et al. Comparative study on rebound/adhesion characteristics of droplets impacting superhydrophobic cold surface[J]. Journal of Safety Science and Technology, 2021, 17(1): 32. DOI:10.11731/j.issn.1673-193x.2021.01.005 |
| [13] |
刘炫麟, 王笑珊, 赵殿伟, 等. 液滴撞击超疏水-亲水混合表面的动态行为特性[J]. 南京师范大学学报, 2019, 19(2): 19. LIU Xuanlin, WANG Xiaoshan, ZHAO Dianwei, et al. Dynamic behavioral characteristics of water droplet impacting on superhydrophobic-hydrophilic surface[J]. Journal of Nanjing Normal University, 2019, 19(2): 19. DOI:10.3969/j.issn.1672-1292.2019.02.003 |
| [14] |
LATKA A, STRANDBURG-PESHKIN A, DRISCOLL M M, et al. Creation of prompt and thin-sheet splashing by varying surface roughness or increasing air pressure[J]. Physical Review Letters, 2012, 109: 1. DOI:10.1103/PhysRevLett.109.054501 |
| [15] |
LEE J B, DEROME D, GUYER R, et al. Modeling the maximum spreading of liquid droplets impacting wetting and nonwetting surfaces[J]. Langmuir, 2016, 32: 1299. DOI:10.1021/acs.langmuir.5b04557 |
| [16] |
ALMOHAMMADI H, AMIRFAZLI A. Droplet impact: viscosity and wettability effects on splashing[J]. Journal of Colloid and Interface Science, 2019, 553: 23. DOI:10.1016/j.jcis.2019.05.101 |
| [17] |
GOEDE T C, LAAN N, BRUIN K G, et al. Effect of wetting on drop splashing of Newtonian fluids and blood[J]. Langmuir, 2018, 34: 5164. DOI:10.1021/acs.langmuir.7b03355 |
| [18] |
AYTOUNA M, BARTOLO D, WEGDAM G, et al. Impact dynamics of surfactant laden drops: dynamic surface tension effects[J]. Experiments in Fluids, 2010, 48: 50. DOI:10.1007/s00348-009-0703-9 |
| [19] |
ALLEN R F, FRANCIS R. The role of surface tension in splashing[J]. Journal of Colloid and Interface Science, 1975, 51: 350. DOI:10.1016/0021-9797(75)90126-5 |
| [20] |
THORODDSEN S T, SAKAKOBARA J. Evolution of the fingering pattern of an impacting drop[J]. Physics of Fluids, 1998, 10(6): 1370. DOI:10.1063/1.869661 |
| [21] |
HOLMAN J P. Heattransfer[M]. New York: McGrawHill, 2010: 6.
|
| [22] |
ACOSTA C A, BHALLA A, GUO R. Empirical and numerical determination of the freezing point depression of an unsteady flow in a scraped surface crystallizer[J]. Applied Thermal Engineering, 2020, 179: 1. DOI:10.1016/j.applthermaleng.2020.115734 |
| [23] |
RUITER J, SOTO D, VARANASI K K. Self-peeling of impacting droplets[J]. Nature Physics, 2018, 14: 37. DOI:10.1038/NPHYS4252 |
| [24] |
WILDEMAN S, VISSER C W, SUN C, et al. On the spreading of impacting drops[J]. Journal of Fluid Mechanics, 2016, 805: 646. DOI:10.1017/jfm.2016.584 |
 2022, Vol. 54
2022, Vol. 54


