转子不平衡是旋转机械振动的主要激振源，导致的剧烈振动会降低机器使用寿命和效率，甚至造成安全事故，因此转子的动平衡非常重要。常用的平衡方法有影响系数法和模态平衡法，与影响系数法相比，模态平衡法无需添加试重，但其前提是需要先识别转子不平衡参数和轴承特性参数，包括转子不平衡量的大小和位置信息以及轴承的刚度、阻尼信息。转子不平衡参数和轴承特性参数的辨识方法主要有基于集中不平衡模型和分布不平衡模型两大类。基于集中不平衡模型的参数辨识方法认为不平衡质量存在于转子的某几个平面上，在已知轴承特性参数的基础上辨识转子的集中不平衡参数^[1-6]。通常，轴承特性参数是未知的，对此有学者提出了轴承特性参数和集中不平衡参数同时辨识的方法，郑钢铁^[7]和毕世华等^[8]基于有限元模型，以实测轴承处振动响应辨识转子集中不平衡参数和轴承特性参数；姚伟^[9]提出了微调转速四测点频域融合辨识方法，实现了对滑动轴承-转子系统、滚动轴承-转子系统的刚度阻尼系数和集中不平衡参数的同时辨识；Tiwari等^[10]采用有限元子结构法同时辨识轴承特性参数和集中不平衡参数。针对转子任意位置都可能存在不平衡的情况，Lee等^[11]首次提出了转子“连续不平衡”的概念，认为转子的不平衡质量是任意分布的，并用傅里叶级数表征；随后Yang等^[12]提出采用多项式曲线表征分布的不平衡质量，并结合有限元法通过轴承处振动响应完成了多项式曲线系数的辨识；Deepthikumar等^[13]完成了转子分布不平衡参数的辨识和一阶模态动平衡，并通过实验进行了验证。但上述方法只能辨识分布不平衡参数，无法辨识轴承特性参数。后来Lee等^[14]将傅里叶级数表征的分布不平衡与传递矩阵法结合，完成转子分布不平衡参数和轴承特性参数的分别辨识，但此方法需要获取轴的各段连接处及圆盘处的振动数据，实际实施比较困难。

针对上述问题，本文引入转子集中不平衡参数和轴承特性参数同时辨识的思想，采用有限元法建立转子/轴承子结构运动微分方程，以多项式曲线表征转子的分布不平衡，通过虚功原理将连续的广义不平衡力转化为节点处集中的广义不平衡力；把子结构运动微分方程转换至频域，建立轴承特性参数和多项式曲线系数的同时辨识方程，根据轴承处振动响应即可同时辨识转子分布不平衡参数与轴承特性参数。以一转子轴承系统为例进行仿真和实验，验证了该参数辨识方法的有效性。

1 转子/轴承子结构运动微分方程

以Timoshenko梁单元、点单元和经典轴承单元分别模拟转轴、圆盘和轴承。其中，转轴和圆盘组成转子子结构，所有轴承组成轴承子结构，采用有限元法建立转子/轴承子结构运动微分方程。

对于转轴，采用如图 1所示的两节点Timoshenko梁单元等效，每个节点考虑沿X和Y方向的平移自由度u、v和绕X和Y轴的旋转自由度θ_x、θ_y等4个自由度。

根据经典梁单元理论建立轴单元运动微分方程，将所有轴单元微分方程组装得到转轴的运动微分方程^[15]为

$ \boldsymbol{M}_{\mathrm{a}} \ddot{q}_{\mathrm{a}}-\varOmega \boldsymbol{G}_{\mathrm{a}} \dot{\boldsymbol{q}}_{\mathrm{a}}+\boldsymbol{K}_{\mathrm{a}} \boldsymbol{q}_{\mathrm{a}}=\boldsymbol{f}_{\mathrm{a}} $

(1)

式中：M、G和K分别为质量阵、陀螺阵和刚度阵，下同；下标a表示转轴，Ω为转子角速度；q={u₁  v₁  θ_x1  θ_y1 … u_n+1  v_n+1 θ_x(n+1)  θ_y(n+1))^T，f={f_x1  f_y1   M_x1  M_y1… f_x(n+1)  f_y(n+1)   M_x(n+1)   M_y(n+1)}^T分别为节点处广义位移和广义不平衡力向量，n为轴单元数。

对于圆盘单元，以具有4个自由度的点单元等效，其运动微分方程为

$ \boldsymbol{M}_{\mathrm{d}} \ddot{\boldsymbol{q}}_{\mathrm{d}}-\varOmega \boldsymbol{G}_{\mathrm{d}} \dot{\boldsymbol{q}}_{\mathrm{d}}=\boldsymbol{f}_{\mathrm{d}} $

(2)

式中下标d表示圆盘，当不考虑圆盘偏心时f_d=0。

对于转子子结构，其运动微分方程由式(1)和式(2)组合得到

$ \boldsymbol{M}_{\mathrm{R}} \ddot{\boldsymbol{q}}_{\mathrm{R}}-\varOmega \boldsymbol{G}_{\mathrm{R}} \dot{\boldsymbol{q}}_{\mathrm{R}}+\boldsymbol{K}_{\mathrm{R}} \boldsymbol{q}_{\mathrm{R}}=\boldsymbol{f}_{\mathrm{R}} $

(3)

式中f_R为转子的广义不平衡力，下标R代表转子子结构。

对于系统中的轴承，以具有4个刚度系数和4个阻尼系数的经典模型等效，建立轴承单元的运动微分方程。将所有轴承单元运动微分方程组合，得到轴承子结构运动微分方程：

$ \boldsymbol{C}_{\mathrm{B}} \dot{\boldsymbol{q}}_{\mathrm{B}}+\boldsymbol{K}_{\mathrm{B}} \boldsymbol{q}_{\mathrm{B}}=\boldsymbol{f}_{\mathrm{B}} $

(4)

式中：$\boldsymbol{C}_{\mathrm{B}}={diag}\left(\boldsymbol{C}_{\mathrm{b}}^{1} \cdots \boldsymbol{C}_{\mathrm{b}}^{p}\right), \boldsymbol{K}_{\mathrm{B}}={diag}\left(\boldsymbol{K}_{\mathrm{b}}^{1} \cdots \boldsymbol{K}_{\mathrm{b}}^{p}\right)$；$\boldsymbol{C}_{\mathrm{b}}^{p}=\left[\begin{array}{cc}c_{x x}^{p} & c_{x y}^{p} \\ c_{y x}^{p} & c_{y y}^{p}\end{array}\right], \boldsymbol{K}_{\mathrm{b}}^{p}=\left[\begin{array}{cc}k_{x x}^{p} & k_{x y}^{p} \\ k_{y x}^{p} & k_{y y}^{p}\end{array}\right]$为轴承单元的阻尼阵和刚度阵，下标b和B代表轴承单元和轴承子结构，p为轴承数。

通过有限元法建立单元运动微分方程，将其组合成转子/轴承子结构的运动微分方程，用于建立轴承处振动响应与分布不平衡参数和轴承特性参数的关系。

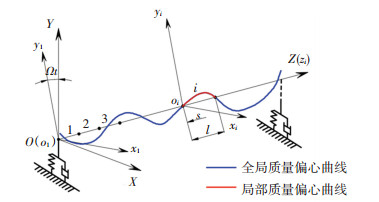
2 转子分布不平衡力向节点集中力的转换

以λ次多项式表征转子沿轴向连续分布的不平衡质量，称为全局质量偏心曲线，如图 2所示，其在全局坐标系{O; XYZ}中的XOZ和YOZ平面表达为

$ X(Z)=\sum\limits_{m=0}^{\lambda} A_{m} Z^{m}, \quad Y(Z)=\sum\limits_{m=0}^{\lambda} B_{m} Z^{m} $

(5)

式中A_m和B_m分别为XOZ和YOZ平面的偏心曲线系数。

考虑到连续分布的广义不平衡力难以确定，将全局质量偏心曲线按轴单元划分，离散为局部质量偏心曲线，以便通过虚功原理将轴单元分布的广义不平衡力转换为节点处集中的广义不平衡力。局部质量偏心曲线在各单元局部坐标系{o_i; x_iy_iz_i}(随转子以角速度Ω旋转)中的x_io_iz_i和y_io_iz_i平面表达为

$ x_{i}(s)=\sum\limits_{m=0}^{\lambda} a_{m i}\left(\frac{s}{l}\right)^{m}, \quad y_{i}(s)=\sum\limits_{m=0}^{\lambda} b_{m i}\left(\frac{s}{l}\right)^{m} $

(6)

式中：i代表第i段轴单元，a_mi和b_mi为x_io_iz_i和y_io_iz_i平面的偏心曲线系数，l表示轴单元长度，s为轴单元中任意一点到该单元局部坐标系原点的距离。

基于局部质量偏心曲线，利用虚功原理将轴单元连续分布的不平衡力转换为该单元节点的集中不平衡力。当轴单元具有分布的偏心距x_i(s)和y_i(s)，微元不平衡力在X和Y轴上的投影为

$ \mathrm{d} \boldsymbol{f}_{i}=\gamma \varOmega^{2}\left(\left\{\begin{array}{c} -y_{i}(s) \\ x_{i}(s) \\ 0 \\ 0 \end{array}\right\} \sin \varOmega t+\left\{\begin{array}{c} x_{i}(s) \\ y_{i}(s) \\ 0 \\ 0 \end{array}\right\} \cos \varOmega t\right) \mathrm{d} s $

(7)

式中γ为对应轴单元单位长度的质量。广义不平衡力f_i在虚位移δq_i上的虚功为

$ \begin{aligned} \delta \boldsymbol{q}_{i}^{\mathrm{T}} \boldsymbol{f}_{i}=& \int_{0}^{l} \gamma \varOmega^{2}\left(x_{i}(s) \cos \varOmega t-y_{i}(s) \sin \varOmega t\right)\left(N_{v} \delta q_{i}\right)^{\mathrm{T}} \mathrm{d} s+\\ & \int_{0}^{l} \gamma \varOmega^{2}\left(x_{i}(s) \sin \varOmega t+y_{i}(s) \cos \varOmega t\right)\left(\boldsymbol{N}_{w} \delta \boldsymbol{q}_{i}\right)^{\mathrm{T}} \mathrm{d} s=\\ & \delta \boldsymbol{q}_{i}^{\mathrm{T}} \int_{0}^{l} \gamma \varOmega^{2}\left(x_{i}(s) \cos \varOmega t-y_{i}(s) \sin \varOmega t\right) \boldsymbol{N}_{v}^{\mathrm{T}} \mathrm{d} s+\\ & \delta \boldsymbol{q}_{i}^{\mathrm{T}} \int_{0}^{l} \gamma \varOmega^{2}\left(x_{i}(s) \sin \varOmega t+y_{i}(s) \cos \varOmega t\right) \boldsymbol{N}_{w}^{\mathrm{T}} \mathrm{d} s \end{aligned} $

(8)

将式(8)化简得

$ \begin{aligned} \boldsymbol{f}_{i}=& \int_{0}^{l} \gamma \varOmega^{2} \boldsymbol{\varPsi}^{T}\left(\left\{\begin{array}{c} -y_{i}(s) \\ x_{i}(s) \end{array}\right\} \sin \varOmega t+\left\{\begin{array}{l} x_{i}(s) \\ y_{i}(s) \end{array}\right\} \cos \varOmega t\right) \mathrm{d} s=\\ & \boldsymbol{f}_{\mathrm{s} i} \sin \varOmega t+\boldsymbol{f}_{\mathrm{c} i} \cos \varOmega t \end{aligned} $

(9)

式中：${\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{T}}}=\left\{\begin{array}{l}\boldsymbol{N}_{v} \\ \boldsymbol{N}_{w}\end{array}\right\}^{\mathrm{T}}$为Timoshenko梁单元形函数^[15]; f_si和f_ci为轴单元广义不平衡力的正弦项和余弦项分量系数，${\mathit{\boldsymbol{f}}_{{\rm{s}}\mathit{i}}} = {\mathit{\Omega }^2}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{D}}_{{\rm{s}}\mathit{i}}}\left\{ {\begin{array}{*{20}{l}} {{\varphi _{\lambda ix}}}\\ {{\varphi _{\lambda iy}}} \end{array}} \right\}, {\mathit{\boldsymbol{f}}_{{\rm{c}}i}} = {\mathit{\Omega }^2}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{D}}_{{\rm{c}}i}}\left\{ {\begin{array}{*{20}{l}} {{\varphi _{\lambda ix}}}\\ {{\varphi _{\lambda iy}}} \end{array}} \right\}$; QD_si和QD_ci为不平衡力正余弦分量系数与该单元偏心曲线系数之间的关系矩阵; φ_λix和φ_λiy为局部偏心曲线系数组成的向量(具体形式将在下面给出)。

根据局部和全局质量偏心曲线在节点处的值与(λ－1)/2阶导数值相同^[12]，局部与全局质量偏心曲线系数的关系为

$ \boldsymbol{\varphi}_{\lambda}=\boldsymbol{T \varPhi}_{\lambda} $

(10)

式中: φ_λ为所有局部质量偏心曲线系数构成的向量, Φ_λ为全局质量偏心曲线系数构成的向量，且$\boldsymbol{\varphi}_{\lambda}=\left\{\boldsymbol{\varphi}_{\lambda 1 x} \quad \boldsymbol{\varphi}_{\lambda 1 y} \cdots \boldsymbol{\varphi}_{\lambda n x} \quad \boldsymbol{\varphi}_{\lambda n y}\right\}^{\mathrm{T}}, \boldsymbol{\varphi}_{\lambda n x}=\left\{a_{\lambda n} \cdots\right.$ $\left.a_{1 n} \quad a_{0 n}\right\}, \quad \boldsymbol{\varphi}_{\lambda n y}=\left\{b_{\lambda n} \cdots b_{1 n} b_{0 n}\right\}, \quad \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\lambda}=$ $\left\{\begin{array}{lllll}A_{\lambda} \cdots A_{1} & A_{0} & B_{\lambda} \cdots & B_{1} & B_{0}\end{array}\right\}^{\mathrm{T}}$, T为局部与全局质量偏心曲线系数之间的关系矩阵。

将式(9)推广至所有的轴单元即可将全局的分布不平衡力转换为节点的集中不平衡力，并将式(10)代入式(9)(去下标i)得

$ \boldsymbol{f}_{\mathrm{s}}=\varOmega^{2} \boldsymbol{Q D}_{\mathrm{s}} \boldsymbol{T \varPhi}_{\lambda}, \quad \boldsymbol{f}_{\mathrm{c}}=\varOmega^{2} \boldsymbol{Q D}_{c} \boldsymbol{T \varPhi}_{\lambda} $

(11)

3 偏心曲线系数和轴承参数同时辨识方法 3.1 偏心曲线系数和轴承特性参数同时辨识方程

基于前面建立的转子/轴承子结构运动微分方程和节点集中不平衡力与全局偏心曲线系数的关系，引入转子集中不平衡参数和轴承特性参数同时辨识思想，在频域中建立全局偏心曲线系数和轴承特性参数与轴承处振动响应的关系，并推导出同时辨识方程。

广义位移和不平衡力在频域中可表示为：

$ \boldsymbol{q}=\boldsymbol{Q} \mathrm{e}^{\mathrm{j} \varOmega t}, \boldsymbol{f}=\boldsymbol{F} \mathrm{e}^{\mathrm{j} \varOmega t} $

(12)

式中：Q和F分别为广义位移和广义力向量，包含幅值和相位。

转子/轴承子结构运动微分方程在频域中表达为

$ \left\{\begin{array}{l} \boldsymbol{H}_{\mathrm{R}} \boldsymbol{Q}_{\mathrm{R}}=\boldsymbol{F}_{\mathrm{R}}=\boldsymbol{f}_{\mathrm{c}}-\mathrm{j} \boldsymbol{f}_{\mathrm{s}}=\varOmega^{2} \boldsymbol{Q} \boldsymbol{D}_{\mathrm{cs}} \boldsymbol{T} \boldsymbol{\varPhi}_{\lambda}, \\ \boldsymbol{H}_{\mathrm{B}} \boldsymbol{Q}_{\mathrm{B}}=F_{\mathrm{B}} \\ \boldsymbol{H}_{\mathrm{R}}=\boldsymbol{K}_{\mathrm{R}}-\varOmega^{2} \boldsymbol{M}_{\mathrm{R}}-\mathrm{j} \varOmega^{2} \boldsymbol{G}_{\mathrm{R}}, \\ \boldsymbol{H}_{\mathrm{B}}=\boldsymbol{K}_{\mathrm{B}}+\mathrm{j} \varOmega \boldsymbol{C}_{\mathrm{B}} \end{array}\right. $

(13)

式中：QD_cs=QD_c－jQD_s，H为广义刚度阵，下同。

为实现以轴承处振动响应同时辨识不平衡参数和轴承特性参数，首先基于子结构法将轴承处节点的X、Y向平移自由度记为连接自由度J，其余为内部自由度I，然后将内部自由度振动响应用连接自由度振动响应等量替换，构造同时辨识方程。

根据连接自由度和内部自由度的划分，转子/轴承子结构在频域中运动方程可表达为：

$ \left\{\begin{array}{l} \left[\begin{array}{ll} \boldsymbol{H}_{\mathrm{R}, \mathrm{II}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{IJ}} \\ \boldsymbol{H}_{\mathrm{R}, \mathrm{JI}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{JJ}} \end{array}\right]\left\{\begin{array}{l} \boldsymbol{Q}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{Q}_{\mathrm{R}, \mathrm{J}} \end{array}\right\}=\left\{\begin{array}{c} \boldsymbol{F}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{F}_{\mathrm{R}, \mathrm{J}} \end{array}\right\}, \\ {\left[\begin{array}{cc} \boldsymbol{H}_{\mathrm{B}, \mathrm{JJ}} & \boldsymbol{H}_{\mathrm{B}, \mathrm{JI}} \\ \boldsymbol{H}_{\mathrm{B}, \mathrm{IJ}} & \boldsymbol{H}_{\mathrm{B}, \mathrm{II}} \end{array}\right]\left\{\begin{array}{c} \boldsymbol{Q}_{\mathrm{B}, \mathrm{J}} \\ \boldsymbol{Q}_{\mathrm{B}, \mathrm{I}} \end{array}\right\}=\left\{\begin{array}{c} \boldsymbol{F}_{\mathrm{B}, \mathrm{J}} \\ \bf{0} \end{array}\right\}} \end{array}\right. $

(14)

式中：Q_{R, J}=Q_{B, J}, F_{R, I}=Ω²QD_csITΦ_λ, F_{R, J}=－F_{B, J}+F_J=－F_{B, J}+QD_csJTΦ_λ, F_{R, I}和F_{R, J}分别为内部自由度与连接自由度处的集中不平衡力，QD_csI和QD_csJ分别为QD_cs中内部自由度与连接自由度对应的行构成的矩阵。

将式(14)中两个运动方程组合：

$ \left[\begin{array}{ccc} \boldsymbol{H}_{\mathrm{R}, \mathrm{II}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{IJ}} & 0 \\ \boldsymbol{H}_{\mathrm{R}, \mathrm{JI}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{JJ}}+\boldsymbol{H}_{\mathrm{B}, \mathrm{JJ}} & \boldsymbol{H}_{\mathrm{B}, \mathrm{JI}} \\ 0 & \boldsymbol{H}_{\mathrm{B}, \mathrm{IJ}} & \boldsymbol{H}_{\mathrm{B}, \mathrm{II}} \end{array}\right]\left\{\begin{array}{l} \boldsymbol{Q}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{Q}_{\mathrm{R}, \mathrm{J}} \\ \boldsymbol{Q}_{\mathrm{B}, \mathrm{I}} \end{array}\right\}=\left\{\begin{array}{l} \boldsymbol{F}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{F}_{\mathrm{J}} \\ 0 \end{array}\right\} $

(15)

忽略轴承内部自由度，则式(15)缩减为

$ \left[\begin{array}{cc} \boldsymbol{H}_{\mathrm{R}, \mathrm{II}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{IJ}} \\ \boldsymbol{H}_{\mathrm{R}, \mathrm{JI}} & \boldsymbol{H}_{\mathrm{R}, \mathrm{JJ}}+\boldsymbol{H}_{\mathrm{B}, \mathrm{JJ}} \end{array}\right]\left\{\begin{array}{l} \boldsymbol{Q}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{Q}_{\mathrm{R}, \mathrm{J}} \end{array}\right\}=\left\{\begin{array}{l} \boldsymbol{F}_{\mathrm{R}, \mathrm{I}} \\ \boldsymbol{F}_{\mathrm{J}} \end{array}\right\} $

(16)

将式(16)展开，Q_{R, I}用Q_{R, J}等量替换，整理得到轴承特性参数和全局质量偏心曲线系数的同时辨识方程：

$ \boldsymbol{U} \boldsymbol{\beta}+\boldsymbol{V} \boldsymbol{\varPhi}_{\lambda}=\boldsymbol{P} $

(17)

式中：$ \boldsymbol{P}=\left(\boldsymbol{H}_{\mathrm{R}, \mathrm{JI}} \boldsymbol{H}_{\mathrm{R}, \mathrm{II}}^{-1} \boldsymbol{H}_{\mathrm{R}, \mathrm{JJ}}-\boldsymbol{H}_{\mathrm{R}, \mathrm{JJ}}\right) \boldsymbol{Q}_{\mathrm{R}, \mathrm{J}}$

$ \boldsymbol{V}=\varOmega^{2}\left(\boldsymbol{H}_{\mathrm{R}, \mathrm{JI}} \boldsymbol{H}_{\mathrm{R}, \mathrm{II}}^{-1} \boldsymbol{Q} \boldsymbol{D}_{\mathrm{csI}}-\boldsymbol{Q} \boldsymbol{D}_{\mathrm{csJ}}\right) \boldsymbol{T} $

$ \boldsymbol{\beta}=\left\{\boldsymbol{\beta}_{k} \quad \boldsymbol{\beta}_{c}\right\}^{\mathrm{T}} $

$ \boldsymbol{\beta}_{k}=\left\{\begin{array}{llllllll} k_{x x}^{1} & k_{x y}^{1} & k_{y x}^{1} & k_{y y}^{1} & k_{x x}^{2} & k_{x y}^{2} & k_{y x}^{2} & k_{y y}^{2} \end{array}\right\}^{\mathrm{T}} $

$ \boldsymbol{\beta}_{c}=\left\{\begin{array}{llllllll} c_{x x}^{1} & c_{x y}^{1} & c_{y x}^{1} & c_{y y}^{1} & c_{x x}^{2} & c_{x y}^{2} & c_{y x}^{2} & c_{y y}^{2} \end{array}\right\}^{\mathrm{T}} $

$ \boldsymbol{U}=\left[\begin{array}{cccc} \boldsymbol{U}_{k 1} & 0 & \boldsymbol{U}_{c 2} & 0 \\ 0 & \boldsymbol{U}_{k 2} & 0 & \boldsymbol{U}_{c 2} \end{array}\right] $

$ \boldsymbol{U}_{k 1}=\left[\begin{array}{cccc} u_{1 \mathrm{b}} & v_{1 \mathrm{b}} & 0 & 0 \\ 0 & 0 & u_{1 \mathrm{b}} & v_{1 \mathrm{b}} \end{array}\right] $

$ \boldsymbol{U}_{k 2}=\left[\begin{array}{cccc} u_{2 \mathrm{b}} & v_{2 \mathrm{b}} & 0 & 0 \\ 0 & 0 & u_{2 \mathrm{b}} & v_{2 \mathrm{b}} \end{array}\right] $

$ \boldsymbol{U}_{c 1}=\left[\begin{array}{cccc} \mathrm{j} \varOmega u_{1 \mathrm{b}} & \mathrm{j} \varOmega v_{1 \mathrm{b}} & 0 & 0 \\ 0 & 0 & \mathrm{j} \varOmega u_{1 \mathrm{b}} & \mathrm{j} \varOmega v_{1 \mathrm{b}} \end{array}\right] $

$ \boldsymbol{U}_{c 2}=\left[\begin{array}{cccc} \mathrm{j} \varOmega u_{2 \mathrm{b}} & \mathrm{j} \varOmega v_{2 \mathrm{b}} & 0 & 0 \\ 0 & 0 & \mathrm{j} \varOmega u_{2 \mathrm{b}} & \mathrm{j} \varOmega v_{2 \mathrm{b}} \end{array}\right] $

根据建立的辨识方程，只需测量轴承处振动响应，即可对全局质量偏心曲线系数及轴承特性参数同时辨识。当系统中存在多个轴承时，式(17)中的β和U需进行相应改变。假定轴承特性参数不随转速变化，为保证式(17)有解，可通过增加转速数来增加方程数。由于偏心曲线系数和轴承特性参数数量级相差较大导致方程的病态问题，可通过共轭梯度法结合列处理进行求解。

3.2 偏心曲线系数和轴承特性参数同时辨识流程

偏心曲线系数与轴承特性参数同时辨识流程如图 3所示。

基于辨识结果，可采用模态平衡方法将转子连续的分布不平衡质量分解至各阶模态后逐阶平衡。以第i阶为例，其平衡配重大小和相位可由下式计算^[17]：

$ \left\{\begin{array}{l} P_{x} m(c) \varGamma_{x i}(c)=-\int_{0}^{L} m^{2}(Z) X(Z) \varGamma_{x i}(Z) \mathrm{d} Z, \\ P_{y} m(c) \varGamma_{y i}(c)=-\int_{0}^{L} m^{2}(Z) Y(Z) \varGamma_{y i}(Z) \mathrm{d} Z \\ P=\sqrt{P_{x}{}^{2}+P_{y}{}^{2}}, \alpha=\tan ^{-1}\left(P_{y} / P_{x}\right) \end{array}\right. $

(18)

式中：L为转子长度，m(Z)为转子沿轴向质量分布函数，P_x和P_y分别为位置c处在XOZ和YOZ平面配重的大小，Γ_xi和Γ_yi分别为XOZ和YOZ平面第i阶振型函数，P为位置c处总配重大小，α为位置c处配重相位。

4 参数辨识仿真与实验

首先分析转子偏心曲线阶次对参数辨识精度的影响。以一转子轴承系统为例(图 4所示)，给定轴承特性参数与偏心曲线系数，模拟不同转速下轴承处的不平衡响应，然后采用本文提出的参数辨识方法辨识转子分布不平衡参数和轴承特性参数，比较相同振动响应下不同偏心曲线阶次的辨识效果。

给定5次多项式描述转子在XOZ、YOZ平面的全局质量偏心曲线：

$ \left\{\begin{array}{l} X(Z)=0.000\ 89 Z^{5}-0.000\ 88 Z^{4}-0.004\ 24 Z^{3}+0.004\ 26 Z^{2}+0.001\ 88 Z-0.000\ 57 \\ Y(Z)=0.001\ 54 Z^{5}+0.001\ 14 Z^{4}-0.008\ 04 Z^{3}+0.006\ 53 Z^{2}+0.004\ 51 Z-0.001\ 11 \end{array}\right. $

(19)

在不考虑陀螺效应的影响的情况下，结合式(3)及式(4)在MATLAB中编程计算轴承在2 800、2 700… …2 000 r/min下的振动响应。以此振动响应分别辨识3次、5次、7次偏心曲线系数及对应阶次下轴承特性参数。随机选取50个点，以辨识得到曲线与给定偏心曲线(式(19))纵坐标的平均误差来判断辨识出的偏心曲线与给定偏心曲线的相似度，辨识结果如表 1所示。结果表明：偏心曲线阶次的选取对参数辨识结果影响较小，但是对于高次的偏心曲线需要通过增加选定转速数量以保证其辨识精度。

为验证该辨识方法的有效性，进行了参数辨识实验。转子实验台如图 5所示。该实验台所用转子与图 4所示转子相同。采用B & K4506型三向加速度传感器测量左右轴承处不平衡响应的振幅；采用转速传感器测量左右轴承处不平衡响应的相位，通过PULSE数据采集器将测量数据传输至计算机。

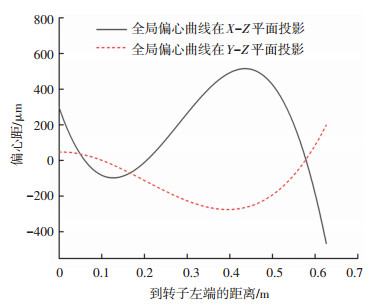
由于病态方程对数据的精确性要求较高，为保证辨识结果的准确性, 需要尽可能降低由于单次测量导致的随机误差。因此，以2 502、2 599、2 702、2 805 r/min下多次测量平均后的轴承处不平衡响应(表 2所示)进行参数辨识。全局质量偏心曲线和轴承特性参数辨识结果如式(20)(图 6)和表 3所示。

$ \left\{\begin{array}{l} X(Z)=-0.041\ 504 Z^{3}+0.035\ 030 Z^{2}-0.006\ 882 Z+0.000\ 296 \\ Y(Z)=0.010\ 978 Z^{3}-0.006\ 631 Z^{2}+0.000\ 091 Z+0.000\ 047 \end{array}\right. $

(20)

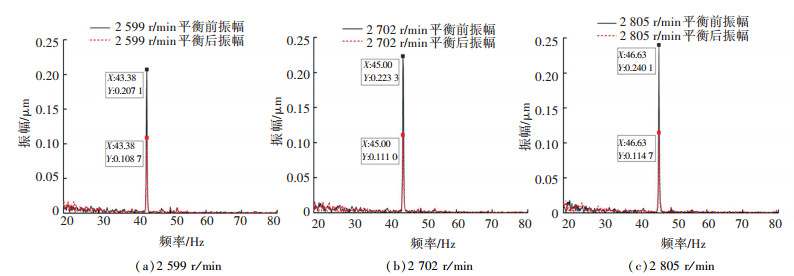
基于上述参数辨识结果，根据式(18)计算该转子轴承系统在圆盘处添加的一阶平衡配重的质径积为4.442 9 e-4 kg·m，相位为147.301°。动平衡后轴承处振动明显降低，在2 599、2 702和2 805 r/min转速下左/右轴承y方向的平衡效果如图 7和8所示，平衡后左轴承y方向的降振幅度在50%左右；右轴承y方向的降振幅度在55%左右，验证了该参数辨识方法的有效性。

5 结论

1) 本文采用有限元方法建立了系统的运动微分方程，考虑转子存在连续分布的不平衡质量并用偏心曲线表征，同时将转子集中不平衡参数和轴承特性参数同时辨识思想发展到具有分布不平衡质量的转子轴承系统中，推导出分布不平衡参数(偏心曲线系数)和轴承特性参数同时辨识方程。

2) 以一转子轴承系统为例进行分布不平衡参数和轴承特性参数同时辨识的仿真，讨论了偏心曲线阶次对参数辨识结果的影响，仿真结果表明偏心曲线阶次的选择对辨识结果影响较小。

3) 搭建转子轴承实验台，采用本文提出的方法进行现场参数辨识实验，基于辨识结果进行了动平衡。一阶模态动平衡后左、右轴承处y方向振幅分别降低约50%、55%，验证了本文提出的辨识方法及其在模态动平衡中的有效性。