机器人的自动化分拣大大提高了生产力,在零件装配、搬运码垛以及物流分拣等领域中具有广泛的应用前景。然而,在一些复杂场景中目标任意堆放、相互遮挡等问题,给机器人的自动化分拣带来了巨大的挑战,其中获取目标的6D位姿是机器人成功分拣的关键。目前,已经有许多学者针对目标位姿估计研究提出了可行的方法。Rad等[1]基于卷积神经网络的方法对图像中的目标进行定位和分割,以2D投影点预测目标的位姿,但该方法对旋转对称目标效果较差。Hu等[2]引入一个分割驱动的位姿估计框架,以目标可见部分的关键点预测整体位姿,不足之处在于对多同类物体的情况表现不好。Pavlakos等[3]利用卷积神经网络从单一RGB图像中预测一组关键点,结合可变形状模型估计目标的姿态,无法应对目标存在遮挡的情况。在2D-3D对应点匹配的基础上,为了提高搜索效率,基于投票思想产生了新的位姿估计方法。Drost等[4]提出了将点对特征PPF(Point pair features)作为模型的整体描述,对参数空间投票求解出目标位姿。Wang等[5]提出了一个端到端的网络框架DenseFusion,将RGB数据和点云数据融合估计目标姿态。Peng等[6]提出采用PVNet(Pixel-wise voting network)对投影的2D关键点位置进行投票,然后转换为PnP(Perspective-n-point)问题来估算位姿[7]。然而2D关键点的预测依赖于强纹理特征,对于弱纹理目标的效果较差,通常采用CAD模型配准的方式解决此类问题。Hinterstoisser等[8]提出了基于图像梯度信息和点云法向特征的模板匹配方法来实时获取目标位姿,对于相互重叠等复杂情况下的物体位姿估计仍存在不足。Mellado等[9]和Yang等[10]将目标点云与模型点云进行配准对齐获取目标位姿,在含有噪声情况下具有一定的鲁棒性,但是运行效率较低,无法达到实时估计。Kehl等[11]基于扩展的SSD范式从RGB图像中检测三维模型实例以估计目标6D位姿,该方法可以实时获取目标位姿,但对目标和模型之间的颜色偏差比较敏感。
现有研究中基于CAD模型配准的方式获取目标位姿存在着耗时长、精度低以及色差要求等问题。针对上述问题,本文先通过点云分割的方式获取单个目标的点云数据进行处理,提取3D特征描述子进行识别,避免了颜色偏差的干扰;融合截断最小二乘-半定松弛算法和迭代最近点算法建立目标6D位姿估计模型,在运行效率和精度上均具有一定优势,并完成机器人的无序分拣实验。
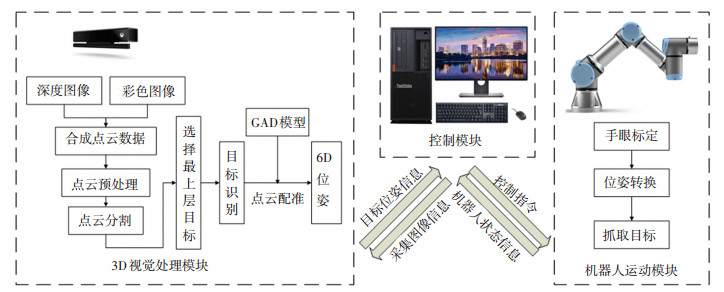
1 系统框架针对多目标散乱堆叠情况下地机器人分拣作业,提出了分拣系统框架,如图 1所示。
|
图 1 堆叠散乱目标的无序分拣系统 Fig. 1 Unordered picking system for stacked cluttered objects |
系统包括3D视觉处理模块、控制模块以及机器人运动模块3个部分,其中3D视觉处理模块是系统的核心部分。3D视觉处理模块主要实现场景点云采集、目标分割与识别以及目标6D位姿估计,控制模块将目标的6D位姿信息与机器人手眼标定结果进行位姿转换,获取目标在机器人基坐标系下的6D位姿,最后由机器人运动模块完成目标的抓取动作。
2 3D视觉处理模块设计 2.1 点云预处理针对目标堆叠的特性,为便于对单个目标进行处理,先从场景点云中提取出堆叠目标点云,并进行点云分割,得到分离的各个目标点云。
场景点云为深度相机采集彩色图像和深度图像进行融合得到,如图 2(a)所示为深度相机获取场景点云的一个实例,对场景点云进行预处理,过滤掉堆叠目标周围的点云,再拟合实验平台平面的点云并去除,得到如图 2(b)所示的堆叠目标点云。

|
图 2 点云预处理实例 Fig. 2 Example of point cloud preprocessing |
由于目标之间相互堆叠,处于下层的目标往往会被遮挡。对于该类目标,一方面机械臂执行器很难到达抓取点位置,即使抓取到目标点,也会在运动中带动上层目标,很可能导致目标抓飞。同时考虑到尽量避免抓取目标周边环境的干扰,故确定每一轮抓取目标是从上至下进行的。因此首先采用局部凸性连接方法对堆叠目标点云进行分割[12-13],该算法可以无监督地将堆叠散乱的目标分割成一个个独立的点云子集,虽然被遮挡的目标分割成了多个部分,但最上面一层的目标是完整的。图 3为目标点云分割的一个实例,其中不同颜色的点云代表着分割出的各个目标。

|
图 3 点云分割实例 Fig. 3 Example of point cloud segmentation |
结合实际点云分割的情况,上层目标相对下层目标距离相机的距离更近,该距离可以衡量为目标点云质心到深度相机坐标系原点的距离;此外由于上层目标没有被其他目标所遮挡,其点云也会相对完整,因此点云中点的数量比下层目标多。综合以上两个因素,为了衡量分割出的各个目标之间的抓取优先级,定义了抓取分数为
| $ G_{\mathrm{o}}=\sqrt{w_{1}(1 / Z)^{2}+w_{2}\left(N / N_{\mathrm{t}}\right)^{2}} $ | (1) |
式中:w1和w2分别为点云质心位置和点云数量的权重系数, Z表示点云质心到深度相机坐标系原点的距离, N表示点云中点的数量, Nt是一个常数。因为对于分拣而言点云质心位置更为重要,所以分别设置权重系数w1=0.8和w2=0.2。
根据抓取分数从图 3中筛选出候选抓取目标,其中深紫色、浅紫色和棕色点云分别代表抓取分数最高、次高和第3高的目标。
2.3 目标识别不同形状目标进行抓取时的位姿各不相同,目标识别的目的在于找到与待抓取目标点云所匹配的模型点云,以此获取其6D位姿。针对目标已知的CAD模型,设计了一种基于匹配相似度函数的目标识别方法。
模型点云是通过建模软件生成CAD模型后,采样其表面的点形成,并经过体素滤波的方式减少点的数量以提高点云识别过程的运行效率。从目标点云和各个模型点云中提取SIFT3D(3D Scale Invariant Feature Transform)关键点[14],根据这些关键点计算FPFH(Fast Point Feature Histograms)特征[15]。FPFH特征是基于查询点与其近邻点之间的空间差异形成的一个多维直方图对点的近邻进行几何描述。直方图提供的信息对于点云具有平移旋转不变性,对采样密度和噪声点具有稳健性,因此一定程度上可以描述点云的局部特征,其计算公式为
| $ F\left(p_{q}\right)=S\left(p_{q}\right)+\frac{1}{k} \sum\limits_{i=1}^{k} \frac{1}{\omega_{k}} \cdot S\left(p_{k}\right) $ | (2) |
式中pq为提取出的一个关键点,pk为pq的近邻点,k为近邻点的数目,wk为距离权重,S(·)表示只计算查询点与近邻点之间的特征元素。
对每一个关键点与其近邻点计算FPFH特征,将目标点云的FPFH特征与各个模型点云的FPFH特征进行匹配,根据每一对目标与模型的特征匹配点对数量设计了匹配相似度函数来衡量目标与模型的匹配程度,其定义为
| $ M=\underset{i}{\operatorname{argmax}}\left(c_{i} / \sum\limits_{i=1}^{t} c_{i}\right) $ | (3) |
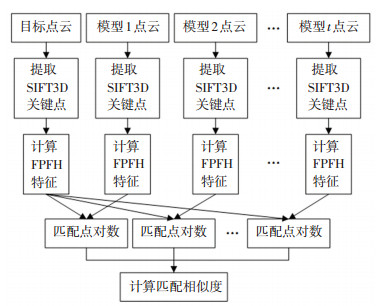
式中: ci为目标与第i个模型的匹配点对数量,t为模型的数目,M所对应的模型为目标识别的结果。目标识别方法的具体流程如图 4所示。
|
图 4 目标识别流程 Fig. 4 Workflow of object recognition |
精确的目标6D位姿估计是保证机械臂准确抓取目标的重要前提。针对目标点云和模型点云重合率低的问题,融合截断最小二乘-半定松弛算法TEASER(Truncated least squares Estimation And SEmidefinite Relaxation)[16]和迭代最近点算法ICP(Iterative Closest Point)[17]解决点云配准的问题,实现目标在机器人基坐标系下的6D位姿估计。
TEASER算法用于解决存在大量离群点对应的情况下两组3D点云的配准,基于模板匹配的原理来确定待配准的两个点云之间的刚体变换矩阵。对于输入的目标点云A= {ai}i=1N和模型点云B= {bi}i=1N,且ai, bi∈ R3。假定噪声未知但有界,构造截断最小二乘代价函数进行配准,其函数形式为
| $ \min \limits_{\boldsymbol{R} \in {SO(3)}, \boldsymbol{t} \in {\bf{R}}^{3}} \sum\limits_{i=1}^{N} \frac{1}{\beta_{i}^{2}}\left\|\boldsymbol{b}_{i}-\boldsymbol{R} \boldsymbol{a}_{i}-\boldsymbol{t}\right\|^{2} $ | (4) |
式中: βi为给定的噪声边界,R为待求的旋转变换,t为待求的平移变换。
穷举搜索式(4)全局最优解的时间复杂度为指数时间O(2N),为了提高算法的运行效率,对问题解耦形式化,转换问题为旋转和平移不变量的测量。旋转不变量的估计为
| $ \hat{\boldsymbol{R}}=\underset{\boldsymbol{R} \in S O(3)}{\operatorname{argmin}} \sum\limits_{k=1}^{N} \min \frac{\left\|\overline{\boldsymbol{b}}_{k}-\boldsymbol{R} \overline{\boldsymbol{a}}_{k}\right\|^{2}}{\delta_{k}^{2}} $ | (5) |
式中: δk为噪声边界,
根据估计出的旋转不变量,再对平移不变量进行估计:
| $ \hat{t}_{j}=\underset {t_{j}} {\arg \min}\sum\limits_{i=1}^{N} \min \frac{\left(t_{j}-\left[\boldsymbol{b}_{i}-\hat{\boldsymbol{R}} \boldsymbol{a}_{i}\right]_{j}\right)^{2}}{\beta_{i}^{2}}(j=1,2,3) $ | (6) |
式中βi为噪声边界,[·]j表示向量的第j个分量,
TEASER算法可以快速获取目标点云和模型点云之间的位姿转换关系,但转换精度不高。为了得到更精确的位姿转换关系,基于ICP算法进行局部位姿修正。将估计出的旋转和平移不变量作为ICP算法的初始估计位姿,使式(7)中的目标函数取得最小值。
| $ \boldsymbol{E}\left(\boldsymbol{R}^{*}, \boldsymbol{t}^{*}\right) =\frac{1}{n} \sum\limits_{i=1}^{n}\left\|\boldsymbol{b}_{i}-\left(\hat{\boldsymbol{R}}{\boldsymbol{a}_{i}}+\hat{\boldsymbol{t}}\right)\right\|^{2} $ | (7) |
| $ \hat{\boldsymbol{t}} =\left[\begin{array}{lll} \hat{t}_{1} & \hat{t}_{2} & \hat{t}_{3} \end{array}\right]^{\mathrm{T}} $ | (8) |
式中: n为目标点云与模型点云匹配点对数量,R*为所求的旋转变换,t*为所求的平移变换,二者组合成4×4齐次变换矩阵
| $ \boldsymbol{T}^{*}=\left[\begin{array}{cc} \boldsymbol{R}^{*} & \boldsymbol{t}^{*} \\ 0 & 1 \end{array}\right]_{4 \times 4} $ | (9) |
通过手眼标定,获取相机坐标系与机器人基坐标系之间的转换关系,其结果表示为
| $ \boldsymbol{T}_{c}=\left[\begin{array}{cc} \boldsymbol{R}_{\mathrm{c}} & \boldsymbol{t}_{\mathrm{c}} \\ 0 & 1 \end{array}\right]_{4 \times 4} $ | (10) |
目标在机器人基坐标系下的6D位姿估计Hp表示为
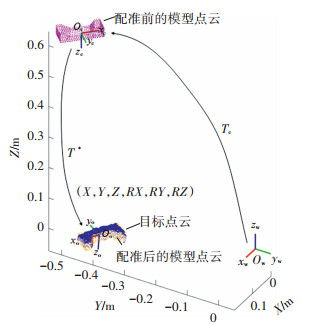
| $ \boldsymbol{H}_{\mathrm{p}}=\boldsymbol{T}_{\mathrm{c}} \times \boldsymbol{T}^{*}=\left[\begin{array}{cc} \widetilde{\boldsymbol{R}} & \tilde{\boldsymbol{t}} \\ 0 & 0 \end{array}\right]_{4 \times 4} $ | (11) |
|
图 5 目标6D位姿估计过程 Fig. 5 Process of object 6D pose estimation |
实验中测试的对象采用凹型块(长125 mm、宽50 mm、高30 mm)、圆柱(直径50 mm、高125 mm) 以及四棱柱(长100 mm、宽50 mm、高50 mm)3类目标组成。将12个目标(凹型块8个,圆柱2个以及四棱柱2个)随意散乱堆叠在实验平台上,采集点云数据提取堆叠目标点云并分割,获取如图 6所示的目标点云分割结果。从图 6的分割点云中选取序号为1、2、3、4、5和6的6个目标进行6D位姿估计实验,根据2.4节介绍的方法将这6个目标分别与对应的模型点云配准,获取各个目标在机器人基坐标系下的6D位姿。为了评估文中6D位姿估计方法的性能,与现有流行的3种方法(基于RANSAC算法[18],基于NDT算法[19],以及基于3DSC算法[20])进行比较。

|
图 6 目标点云分割结果 Fig. 6 Point cloud segmentation results of objects |
为了定量衡量实验结果的精度,定义了均方根距离误差De和均方根角度误差Ne两个评价指标对结果进行分析
| $ D_{\mathrm{e}}=\sqrt{\left(\sum\limits_{i=1}^{m}\left(\boldsymbol{X}_{p i}-\boldsymbol{X}_{q i}\right)^{2}\right) / m} $ | (12) |
| $ N_{\mathrm{e}}=\sqrt{\left(\sum\limits_{i=1}^{m}\left(\cos ^{-1}\left(\frac{\boldsymbol{n}_{p i} \cdot \boldsymbol{n}_{q i}}{\left|\boldsymbol{n}_{p i}\right|\left|\boldsymbol{n}_{q i}\right|}\right)\right)^{2}\right) / m} $ | (13) |
式中m表示目标点云和模型点云配准后匹配点对的数量,Xpi和Xqi分别表示目标点云和模型点云配准后对应点的空间三维坐标值,npi和nqi分别表示目标点云和模型点云配准后对应点的法向量。因此评价指标De和Ne分别衡量的是目标点云中所有的点通过估计出的6D位姿变换后与模型点云中的对应点的距离和法向量夹角的平均值,这两个指标的值越小,则目标点云与模型点云的匹配程度越高,即6D位姿估计越准确。
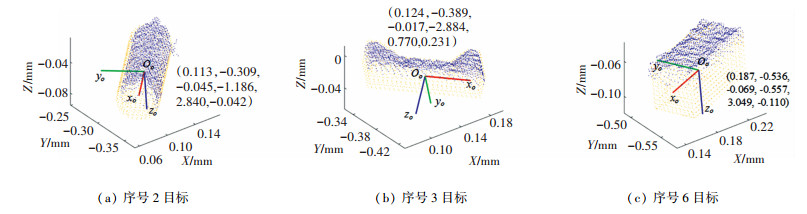
序号为2、3、6目标在机器人基坐标系下的6D位姿估计结果如图 7所示。统计文中算法和另外3种算法的位姿估计误差和平均运行时间,计算出的De和Ne如表 1所示,平均运行时间Ta如表 2所示。
|
图 7 3个目标的6D位姿估计结果 Fig. 7 6D pose estimation results of three objects |
| 表 1 不同方法的位姿估计误差对比 Tab. 1 Comparison of pose estimation accuracy of different methods |
| 表 2 不同方法的平均运行时间对比 Tab. 2 Comparison of average running time of different methods |
从表 1结果可以看出,对于不同目标的6D位姿估计,文中算法的De在3.3 mm之内,Ne在5.6°之内,误差在无序分拣系统允许的范围之内。与其他3种方法相比,本文方法的位姿估计误差都是最小的,说明本文6D位姿估计方法具有较高的精度和鲁棒性。序号2和5目标的De比较大,这是由于这两个目标表面为曲面,而测试的目标均由3D打印零件组成,其表面纹路凹凸不平,因此采集的点云数据与CAD模型有较大误差,导致点云配准的误差较大。从表 2可以看出,本文方法的平均运行时间为0.23 s,在这几种方法中耗时最短,可以满足系统分拣的实时性要求。
3.2 机器人无序分拣实验搭建了无序分拣系统,在实际场景中,用机器人分拣堆叠散乱的目标。整个分拣系统主要由Kinect V2深度相机、UR3e机器人、机器人控制器、真空吸盘、真空泵以及工控机组成。
实验以3.1节中的实验对象作为分拣对象,其中凹型块和四棱柱零件的抓取位置为平面,而圆柱零件的抓取位置为曲面。系统抓取目标后,将目标放置到对应的位置释放后,机械臂返回到初始位置,等待下一个目标的抓取。重复上述步骤,直至将工作台上的目标全部分拣完成。然后再次随机散乱放置零件在实验台上,重复完成5组实验,统计5组实验中目标的分拣结果来评估分拣系统的性能。
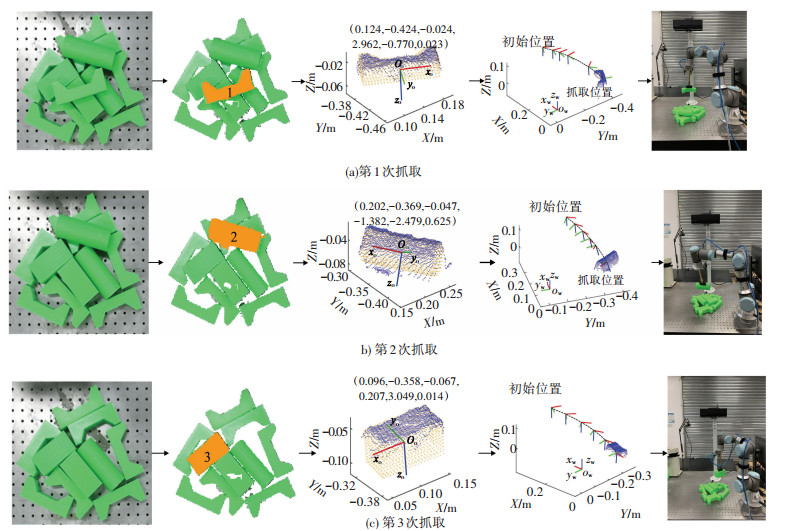
图 8为无序分拣系统在第1组实验过程中前3个目标的抓取过程图。图 8(a)为第一个目标(序号1)抓取,抓取完并放置目标后,机械臂返回初始位置,进行下一个目标的抓取。从图 8可以看出,前3个目标(序号1、2、3)都被顺利分拣出来,证明该系统可以应用于堆叠目标的分拣场景中。
|
图 8 无序分拣系统工作过程图(从左至右依次为:堆叠目标图片、最上层目标筛选、目标6D位姿估计、机器人抓取运动轨迹以及目标实际抓取图) Fig. 8 Working process of unordered picking system (from left to right: stacked objects, uppermost object selection, object 6D pose estimation, robot picking trajectory, actual object picking) |
为了定量评价该分拣系统的性能,从抓取成功率和抓取时间两个方面进行评估。抓取成功率Gp的定义为
| $ G_{\mathrm{p}}=n_{\mathrm{s}} / n_{\mathrm{g}} \times 100 \% $ | (14) |
式中ng为每组实验中总的抓取目标次数,ns表示每组实验中正确分拣目标的次数,正确分拣目标表示成功将目标抓取并放置到特定区域中。
系统的抓取时间Tg的定义为
| $ T_{\mathrm{g}}=T_{1}+T_{2} $ | (15) |
式中T1为从采集点云数据到估计目标6D位姿所花费的时间,T2为机器人从抓取目标到放置目标并返回抓取起始点所花费的时间。因此,Tg衡量的是分拣系统工作一个周期所需要的时间。
对5组实验数据进行统计分析,每组实验的抓取成功率如表 3所示。从表 3可以看出,两组实验的抓取成功率达到100%,3组实验的抓取成功率为91.76%。实验中抓取失败的对象主要是圆柱体,原因在于圆柱的抓取位置为曲面,只有当椭圆吸盘长轴方向与圆柱体表面完全贴合,才会抓取成功,因此对圆柱体位姿精度要求较高,误差较大时容易导致抓取失败。表 4从时间性能上对分拣系统进行分析,不同分拣对象的平均抓取时间在14 s以内,其中视觉处理的时间在3 s以内,远小于机械臂运动的时间,可以保证机器人分拣过程的实时性要求。
| 表 3 5组实验的抓取成功率 Tab. 3 Object grasping success rates of five groups of experiments |
| 表 4 不同分拣对象的平均抓取时间 Tab. 4 Average grasping time for different objects |
针对堆叠散乱目标的无序分拣系统,开展了目标的点云识别与位姿估计研究,根据目标的6D位姿完成机器人的自动化抓取,主要结论如下:
1) 提出了抓取分数来判断堆叠目标中的最上层目标,保证系统可以从上至下进行抓取目标,避免出现抓飞的情况。
2) 提出了基于匹配相似度函数的目标识别方法,并融合TEASER算法和ICP算法实现精确的目标6D位姿估计
3) 在自采数据上进行实验验证,本文方法均方根距离误差<3.3 mm,均方根角度误差 < 5.6°,与现有普遍采用的3种方法相比具有更高的位姿估计精度;在实际堆叠散乱目标的场景下进行分拣实验,结果表明搭建的系统可以实现目标的无序分拣。
该系统适用于多个目标尺寸相近情形下的无序分拣,其性能可以适应实际生产需要。
| [1] |
RAD M, LEPETIT V. BB8: a scalable, accurate, robust to partial occlusion method for predicting the 3D poses of challenging objects without using depth[C]// IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017: 3848. DOI: 10.1109/ICCV.2017.413
|
| [2] |
HU Yinlin, HUGONOT J, FUA P, et al. Segmentation-driven 6D object pose estimation[C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2020: 3380. DOI: 10.1109/CVPR.2019.00350
|
| [3] |
PAVLAKOS G, ZHOU Xiaowei, CHAN A, et al. 6-DoF object pose from semantic keypoints[C]// IEEE International Conference on Robotics and Automation (ICRA). Singapore: IEEE, 2017: 2011. DOI: 10.1109/ICRA.2017.7989233
|
| [4] |
DROST B, ILIC S. 3D object detection and localization using multimodal point pair features[C]// Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission. Zurich: IEEE, 2012: 9. DOI: 10.1109/3DIMPVT.2012.53
|
| [5] |
WANG Chen, XU Danfei, ZHU Yuke, et al. DenseFusion: 6D object pose estimation by iterative dense fusion[C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019: 3338. DOI: 10.1109/CVPR.2019.00346
|
| [6] |
PENG Sida, LIU Yuan, HUANG Qixing, et al. PVNet: pixel-wise voting network for 6DoF pose estimation[C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019: 4556. DOI: 10.1109/TPAMI.2020.3047388
|
| [7] |
LEPETIT V, MORENO F, FUA P. EPnP: an accurate O(n) solution to the PnP problem[J]. International Journal of Computer Vision, 2009, 81(2): 155. DOI:10.1007/s11263-008-0152-6 |
| [8] |
HINTERSTOISSER S, HOLZER S, CAGNIART C, et al. Multimodal templates for real-time detection of texture-less objects in heavily cluttered scenes[C]// International Conference on Computer Vision. Barcelona: IEEE, 2011: 858. DOI: 10.1109/ICCV.2011.6126326
|
| [9] |
MELLADO N, AIGER D, MITRA N J. Super 4PCS fast global pointcloud registration via smart indexing[J]. Computer Graphics Forum, 2014, 33(5): 205. DOI:10.1111/cgf.12446 |
| [10] |
YANG Jiaolong, LI Hongdong, CAMPBELL D, et al. Go-ICP: a globally optimal solution to 3D ICP point-set registration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2241. DOI:10.1109/TPAMI.2015.2513405 |
| [11] |
KEHL W, MANHARDT F, TOMBARI F, et al. SSD-6D: making RGB-based 3D detection and 6D pose estimation great again[C]// IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017: 1530. DOI: 10.1109/ICCV.2017.169
|
| [12] |
PAPON J, ABRAMOV A, SCHOELER M, et al. Voxel cloud connectivity segmentation-supervoxels for point clouds[C]// IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013: 2027. DOI: 10.1109/CVPR.2013.264
|
| [13] |
STEIN S, SCHOELER M, PAPON J, et al. Object partitioning using local convexity[C]// IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 304. DOI: 10.1109/CVPR.2014.46
|
| [14] |
SCOVANNER P, ALI S, SHAH M. A 3-dimensional sift descriptor and its application to action recognition[C]// Proceedings of the 15th ACM international conference on Multimedia. New York: Association for Computing Machinery, 2007: 357. DOI: 10.1145/1291233.1291311
|
| [15] |
RUSU R, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration[C]// IEEE International Conference on Robotics and Automation. Kobe: IEEE, 2009: 3212. DOI: 10.1109/ROBOT.2009.5152473
|
| [16] |
YANG Heng, SHI Jingnan, CARLONE L. TEASER: fast and certifiable point cloud registration[J]. IEEE Transactions on Robotics, 2021, 37(2): 314. DOI:10.1109/TRO.2020.3033695 |
| [17] |
BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1992, 14(2): 239. DOI:10.1109/34.121791 |
| [18] |
BUCH A, KRAFT D, KAMARAINEN J, et al. Pose estimation using local structure-specific shape and appearance context[C]// IEEE International Conference on Robotics and Automation. Karlsruhe: IEEE, 2013: 2080. DOI: 10.1109/ICRA.2013.6630856
|
| [19] |
DAS A, WASHLANDER S. Scan registration using segmented region growing NDT[J]. The International Journal of Robotics Research, 2014, 33(13): 1645. DOI:10.1177/0278364914539404 |
| [20] |
TOMBARI F, SALTI S, STEFANO L. Unique shape context for 3D data description[C]// Proceedings of the ACM Workshop on 3D Object Retrieval. New York: Association for Computing Machinery, 2010: 57. DOI: 10.1145/1877808.1877821
|
 2022, Vol. 54
2022, Vol. 54


