2. 北京首创股份有限公司,北京 100044;
3. 哈尔滨凯纳科技股份有限公司,哈尔滨 150028
2. Beijing Capital Co., Ltd., Beijing 100044, China;
3. Harbin Corner Science & Technology Inc., Harbin 150028, China
需水量预测[1-3]主要包括长期预测、中期预测和短期预测,分别用于供水规划、决策支持、运营管理[4-5]。其中,短期需水量波动性大,具有很强的随机性,且易受多种因素影响(天气、人口、地理位置、商业活动、工业生产、水价等),预测难度最大。对短期需水量预测问题进行研究,不仅有利于供水管网科学化管理, 保障龙头水水质,实现降低漏损、节能降耗、减少水资源及能源浪费的目标,还能为复杂不稳定系统的预测问题提供新的范式[6]。
早期的需水量预测主要采用线性回归和时间序列分析的方法,但由于短期需水量的非线性和非平稳性,线性回归和本质上捕捉线性关系的时间序列分析等方法受到限制,不能准确地模拟出需水量的随机性波动[7-8]。近年来,随着建模技术的发展,更为复杂的机器学习模型在需水量预测领域得到了广泛的应用,为需水量预测带来新的机遇[9]。其中,以人工神经网络(artificial neural network, ANN)、支持向量机(support vector machine, SVM)和以它们为基础的变种模型研究最多[10-13],也取得较好的成果。ANN和SVM常用作基准模型,来评价各类需水量预测模型的性能[7]。此外,基于决策树的机器学习模型由于易于理解和实现,且效果良好,也逐渐应用于需水量预测领域[14-15]。LightGBM(light gradient boosting machine)是微软公司提出的基于梯度提升决策树的算法[16],在继承了梯度提升决策树类算法高精度的同时还具有较高的计算效率,已在很多领域得到应用[17-18],但在短期需水量预测领域的性能尚未得到验证。
除了对预测模型进行改进,数据的预处理环节也对提高需水量预测的准确性至关重要。短期需水量数据不仅波动性大,呈现非线性、非平稳性的特点,还容易受到短期异常事件的影响,包括通讯传输异常和用水设备或行为异常等[19]。基于这些异常数据进行建模会影响需水量预测的准确性,在使用小时计量小区(district metered area,DMA)数据进行建模时,现象尤为明显。因此,对短期需水量数据进行异常值预处理具有重要意义。本文采用局部离群因子(local outlier factor,LOF)异常值识别方法,并将其与LightGBM结合,提出LOF+LightGBM组合模型,改善需水量预测模型性能。
1 研究方法 1.1 异常值检测算法LOF原理异常值通常具备远离正常数据的趋势,因此,通过基于距离或密度的方式能有效地检测异常值。LOF是基于密度的无监督异常值检测算法,通过观测数据分布的密度给出数据点得分,作为判断该点是否为异常值的依据[20]。假设Nk(O)为点O的第k距离邻域,即Nk(O)为点O的第k距离以内的所有点,包括第k距离点。对于点O,其局部可达密度ρk(O)可以表示为
| $ {\rho _k}(O) = \frac{1}{{\frac{{\sum\nolimits_{P \in {N_k}(O)} {{d_k}} (O, P)}}{{\left| {{N_k}(O)} \right|}}}} $ | (1) |
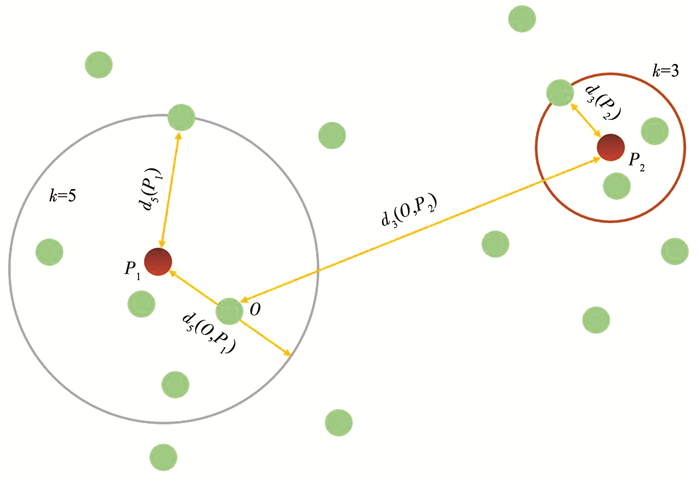
式中:|Nk(O)|为点O第k距离邻域点的个数;dk(O, P)为点P到点O的可达距离,取P点的第k距离dk(P)和P点到O点的实际距离中的最大值,如图 1所示。通过局部可达密度计算点P的局部离群因子,表示为
| $ {F_k}(O) = \frac{{\sum\nolimits_{P \in {N_k}(O)} {\frac{{{\rho _k}(P)}}{{{\rho _k}(O)}}} }}{{\left| {{N_k}(O)} \right|}} $ | (2) |
|
图 1 第k距离dk(P)、局部可达距离dk(O, P)示意 Fig. 1 Schematic of kth-distance dk(P) and local reachability density dk(O, P) |
该式表示点O第k距离邻域所有点的局部可达密度与点O局部可达密度的比的平均数。Fk(O)大于1时,越大则说明点O的密度相对其邻域点越小,越有可能是异常点; 当Fk(O)越接近于1,则说明点O与其邻域点的密度相当,可能属于同一簇。
1.2 LightGBM原理LightGBM是基于梯度提升树的算法,具有高精度、高效率、低内存使用的特点。LightGBM的一个重要特性是提供了数据类型的封装,将连续的特征存储到离散的箱中,在训练过程使用直方图算法,大大提高了模型的训练速度[21]。LightGBM算法进行回归的目标就是通过建立T棵回归树,对数据集D={(x1, y1), (x2, y2),…,(xn, yn)}进行回归。在迭代计算T次后,最终的预测
| $ \hat y_i^{(T)} = \sum\limits_{t = 1}^T {{f_t}} \left( {{x_i}} \right) $ | (3) |
含正则项的模型目标函数为
| $ {L^T} = \sum\limits_{i = 1}^n l \left( {{y_i}, {{\hat y}_i}} \right) + \sum\limits_{t = 1}^T \mathit{\Omega } \left( {{f_t}} \right) $ | (4) |
| $ \mathit{\Omega }(f) = \gamma N + \frac{1}{2}\lambda {\left\| w \right\|^2} $ | (5) |
式中:Ω为模型的正则项,N为树中叶子节点数,w为叶子节点权重,γ、λ为正则化系数。在每次迭代过程中向损失函数负梯度方向移动,使损失函数尽可能小,得到一棵较优树。
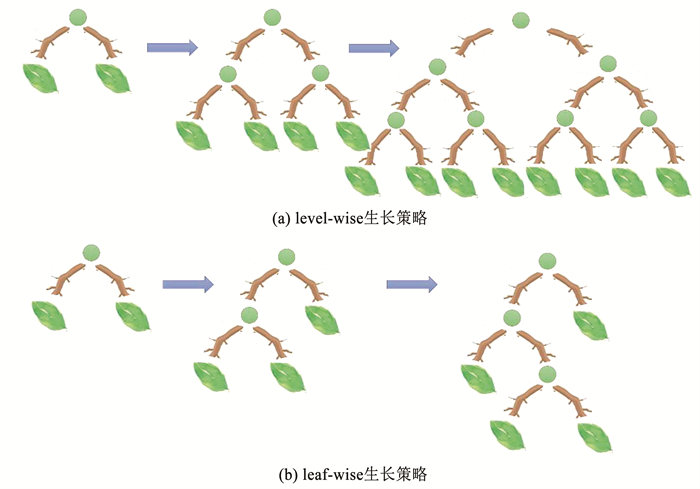
除了采用直方图算法,LightGBM还具有两个重要的特点:一是结合了基于梯度的单侧采样算法,在数据和精度之间取得了良好的平衡,注意力更多地放在梯度较大的样本上,只采用一部分小梯度样本;二是LightGBM树的生长采用leaf-wise策略,而非大多数梯度提升决策树的level-wise按层生长的策略。leaf-wise策略选择信息增益最大的叶进行生长,这意味着每层叶子的数量不总是相同的,如图 2所示,leaf-wise的树生长策略有助于减少训练量。总的来说,LightGBM有高效率、高精度、具备处理许多非线性关系问题的强大能力。因此,LightGBM在回归预测领域中具有广阔的应用前景。
|
图 2 决策树生长策略示意 Fig. 2 Schematic of growth strategy for decision tree |
使用江浙沪地区某市的真实DMA小时需水量数据分析提出的LOF+LightGBM模型的预测性能,包括不同规模的3个DMA居民住宅小区小时需水量数据,小区内包含少量商铺用水户。3个小区具有相差较大的需水量变化曲线(如图 3、4),DMA1需水量曲线波动大,高峰需水量与夜间需水量差别明显; 而DMA3需水量曲线波动小,每小时需水量分布密集;DMA2则在两者之间。3个小区能够代表不同的居民住宅小区的用水特点,验证提出组合模型的普适性。DMA1数据集包含2016年4月23日—2016年7月1日的小时需水量数据,DMA2数据集包含2016年1月5日—2016年3月14日的小时需水量数据,DMA3数据集包含2016年5月14日—2016年7月22日的小时需水量数据。对于每个DMA,80%的数据用于训练模型,剩余20%的数据作为测试集来评价提出模型性能及探究异常值处理对于需水量预测的影响。各DMA小区需水量数据基本特征如表 1所示。DMA1与DMA3最小需水量均为0,但通常情况下,居民小区用水户基数较大,且存在背景暗漏,出现小时需水量为0的可能性较低,更有可能是通讯信号干扰导致的数据丢失,或者是爆管、检修等异常行为造成停水。3/4分位数与平均值比较接近,而需水量最大值与3/4分位数的差距悬殊,尤其是DMA1与DMA3,如DMA1的需水量3/4分位数为20.879 m3/h,而最大需水量高达123.844 m3/h。这很有可能是由通讯信号干扰、机械振动等导致的数据异常。由此可见,实际工程中异常值问题十分普遍,且异常值与正常值相差较大,对实际工程中需水量进行预测前进行异常值处理是十分必要的。
|
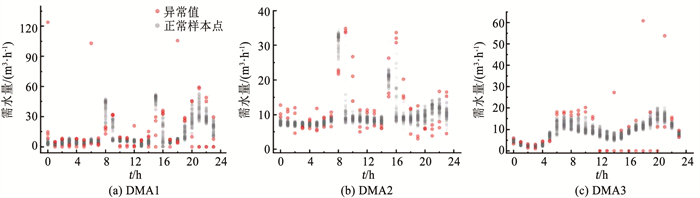
图 3 LOF异常值识别结果 Fig. 3 Results of abnormal detection by LOF |
|
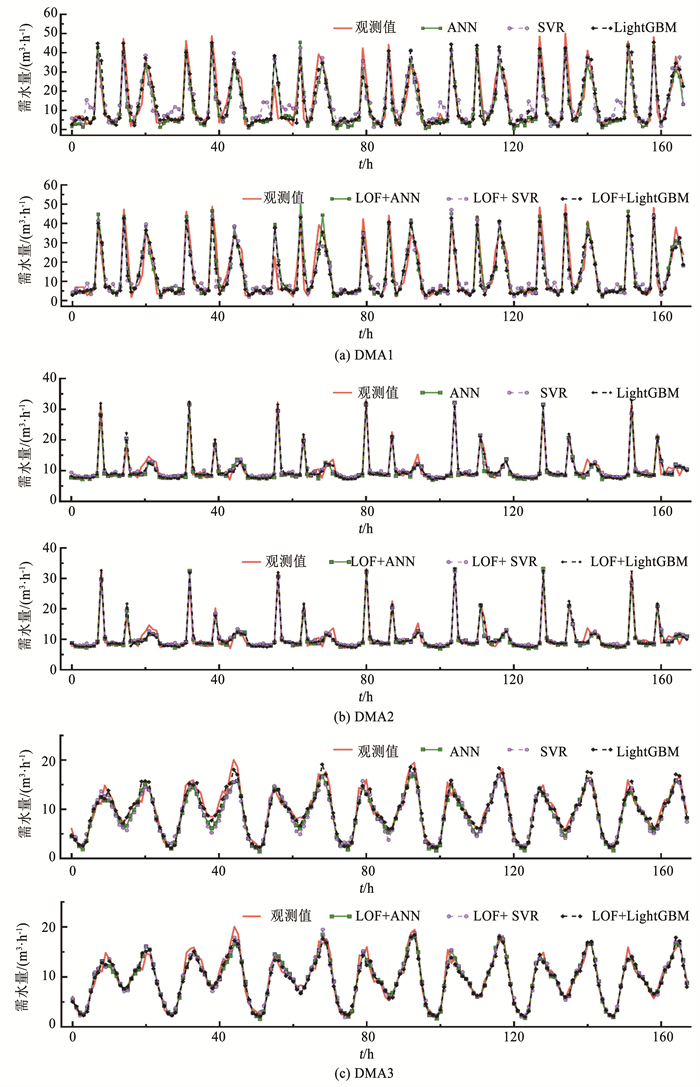
图 4 观测值与各预测模型预测值曲线 Fig. 4 Curve of observed values and predicted results of forecasting models |
| 表 1 DMA小区需水量数据基本特征 Tab. 1 Basic characteristics of water demand datasets for three DMAs |
通过对模型的输入特征进行选择,保留强相关特征,筛出相关性弱的特征,有利于提高预测准确性,减少建模时间。可作为需水量预测模型的输入特征包括历史需水量数据、温度、降雨量、经济等[6]。对于水务企业,降雨量等气候信息较难获得,且以往研究表明,使用历史需水量作为输入足以建立准确的需水量预测模型[22],故采用历史需水量数据作为组合模型的输入。
参考Guo等[23]的特征输入方案,考虑短期需水量的周期性,将需水量输入特征分为3段,包括周周期相关特征、日周期相关特征和近期特征。周周期特征考虑预测时间一周前x(t-24×7)及其附近的需水量特征{x(t-24×7-i), …, x(t-24×7), …, x(t-24×7+i)},日周期特征考虑预测时间1 d前x(t-24)及其附近的需水量特征{x(t-24-j), …, x(t-24), …, x(t-24+j)},近期特征考虑预测时间x(t)前一段时间的需水量特征{x(t-k), …, x(t-1)},取i=j=k=10,具体见表 2。将周周期特征、日周期特征和近期特征数据作为输入,使用LightGBM对特征重要性进行排序,对于每个DMA选择重要性前10特征进行后续需水量预测模型的建模,用来预测t时刻的需水量,特征选择结果如表 2所示。特征重要性前10的特征中周周期特征最少,说明较远的数据对当前需水量的影响较小。而x(t-24×7),x(t-24)始终在重要性前10中,进一步验证了需水量的强周期性。
| 表 2 模型特征选择范围和结果 Tab. 2 Range and results of feature selection |
通过构建LOF+LightGBM组合模型进行需水量预测,包括异常值识别及校正步骤和需水量预测步骤。具体如下:
1) 在异常值识别及校正步骤中,首先将需水量数据按小时分为24个子集,分别对每个子集构建LOF模型并识别每个子集中的异常值。使用每小时需水量的平均值校正当前小时子集中的异常值,之后将子集重新合并为一个数据集以供后续需水量预测。
2) 在需水量预测步骤中,使用异常值校正后的需水量数据训练LightGBM模型,先将需水量数据归一化到0和1之间,输入为经特征选择后的特征,输出为预测的需水量。最后, 对测试集的需水量进行预测并评价模型性能。为了客观评价所提出的模型,在需水量预测步骤中引入常用作基准模型的ANN和SVM中用于回归的支持向量回归模型(support vector regression,SVR)参与组合模型的构建与性能评价,其输入与LightGBM模型相同。有关ANN和SVR的算法原理见Herrera[4]、Adamowski[24]、Bougadis等[25]的描述。
2.3.2 模型超参数调优超参数的选择决定了模型的性能,对于LOF,有两个超参数需要进行优化,即数据中异常点的比例和样本点的邻域点数。由于LOF为非监督学习算法,数据集中异常点的比例未知,需要先通过试错法确定各个DMA小区需水量数据中的异常点比例,再对样本点的邻域点数进行超参数调优,其中异常点的比例分别尝试0.01、0.02、…、0.10,样本点的邻域点数分别尝试10、20、30、40、50、60。
需水量预测模型通过5折交叉验证及网格搜索进行超参数调优。对于ANN,采用3层前馈神经网络进行需水量预测,其具有1个隐藏层,通过误差反向传播的方式确定神经网络中的权重和偏置等。该神经网络模型需要对隐藏层节点数和初始学习率进行超参数调节。分别设置隐藏层节点数为2、5、7、10、20、30、40、50、60、70、80和初始学习率为0.000 1、0.001、0.005、0.01、0.05、0.1进行网格搜索调参,即在66个超参数组合中寻优。
SVR模型选择径向基函数作为核函数,有两个重要的超参数C和gamma需要优化。C是正则化超参数,可以调整预测误差和模型复杂度的权重,gamma是径向基函数的核系数。本研究尝试了超参数C的e-2、e-1、e0、e1、e2、e3、e4、e5取值,超参数gamma的e-4、e-3、e-2、e-1、e0、e1取值,即SVR模型尝试了超参数的48种不同组合。
控制LightGBM模型的超参数较多,分步通过网格搜索进行超参数的优化。
1) 首先对Max_depth树模型最大学习深度和Num_leaves构成每棵树叶子的数量进行超参数优化,Max_depth分别取3、4、5、6,Num_leaves不宜设置过大,过大可能造成过拟合,故分别取5、15、25、35、45,总共20个组合。
2) 随后对Min_data_in_leaf一片叶子中最小数据量和Max_bin箱的最大数量进行优化,Min_data_in_leaf用于控制过拟合,分别取1、11、21、…、101,Max_bin分别取5、15、25、…、255,进行网格搜索调参。
3) 再对Feature_fraction每次迭代过程随机选择特征占特征总数比、Bagging_fraction选择的数据占总数据量的比和Bagging_freq子采样频率进行网格搜索超参数优化,Feature_fraction分别取0.6、0.7、0.8、0.9、1.0,Bagging_fraction分别取0.6、0.7、0.8、0.9、1.0,Bagging_freq分别取0、10、20、…、80。
4) 最后,对Lambda_l1和Lambda_l2正则化相关超参数进行优化,Lambda_l1分别取0.000 01、0.001、0.1、0、0.3、0.5、0.7、0.9、1.0,Lambda_l2分别取0.000 01、0.001、0.1、0、0.3、0.5、0.7、0.9、1.0。其他超参数如Boosting_type估计器的类型选择默认的gbdt,为保证精度学习率选择较低的0.01,n_estimators估计器数量选择1 000棵树。
2.4 模型性能评估指标为了评估预测模型的性能,使用两个绝对误差评价指标和一个无量纲评价指标衡量预测值和实际值之间的误差。绝对误差评价指标为均方根误差(root-mean-square error,ERMS)和平均绝对误差(mean absolute error,EMA)。无量纲评价指标为纳什效率系数(nash-sutcliffe model efficiency coefficient,ENS),常用于验证水文和环境相关模型的准确性,具体表达如下:
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{Q_i} - Q_i^{\rm{f}}} \right)}^2}} } $ | (6) |
| $ {E_{{\rm{MA}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{Q_i} - Q_i^{\rm{f}}} \right|} $ | (7) |
| $ {E_{{\rm{NS}}}} = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left( {{Q_i} - Q_i^{\rm{f}}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\left( {{Q_i} - {{\bar Q}_i}} \right)}^2}} }} $ | (8) |
式中:Qi为观测需水量,Qif为预测需水量,Qi为观测需水量的平均值。EMA和ERMS均能衡量预测值和观测值之间的差别,ERMS更注重误差较大的点,而EMA对所有点的误差是平等对待的。ENS将预测值和观测值之间的误差与需水量平均值和观测值之间的差别进行比较,以此作为判断模型准确性的标准,ENS越接近1模型越准确。
3 结果与讨论 3.1 LOF模型异常值识别效果分析通过对3个DMA需水量数据进行异常值识别,探索LOF模型的有效性,异常值识别结果如图 3所示。不同DMA需水量数据及其异常值的分布呈现明显的差异性,LOF均能较好地识别出需水量异常值。对于DMA1、DMA2(图 3(a)、(b)),每小时需水量数据分布较为分散,增加了异常值识别的难度,尤其是DMA2,为避免将正常需水量误识别为异常值,仅将部分远离集中数据的点识别为异常点,保留了部分接近集中数据的离散需水量点,为需水量预测模型提供尽可能多的数据信息。对于DMA3(图 3(c)),每小时数据分布集中,异常数据和正常数据能较好地区分开,LOF能够很好地识别出离群异常值和丢失数据,为需水量预测模型提供较高质量的数据集。
3.2 LOF+LightGBM模型预测性能分析为探究LOF模型、LightGBM模型及其组合模型LOF+LightGBM的性能,分别设置3个对比组进行实验,第1组为ANN与LOF+ANN、SVR与LOF+SVR、LightGBM与LOF+LightGBM;第2组为ANN、SVR与LightGBM;第3组为LOF+LightGBM与ANN、SVR、LightGBM、LOF+ANN、LOF+SVR。各模型预测性能评价结果如表 3所示。为直观观察各模型的预测结果,绘制各模型预测值和观测值曲线,如图 4所示。
| 表 3 各预测模型性能评价 Tab. 3 Performance indicators of forecasting models |
在不同DMA的需水量数据分布下,基于LOF+预测模型的组合模型性能均得到了提升(表 3),预测模型ERMS平均降低了10%,DMA3的ANN模型ERMS为1.321 m3/h,LOF+ANN模型的ERMS为1.055 m3/h,降低了近20%。通过对比DMA1(图 4(a))、DMA2(图 4(b))、DMA3(图 4(c))的预测模型和LOF+预测模型预测曲线可知,LOF+预测模型的需水量曲线明显更贴合观测曲线,尤其DMA1和DMA3中需水量较低时的预测性能改善更为明显。结果表明,经过LOF进行异常值识别和校正后的数据集利于提升后续预测模型的准确性,这可能是因为在模型进行训练的过程中会尽可能减少模型计算值和训练数据之间的误差,异常值的存在,尤其是需水量数据波动大、存在极端异常值的情况下,训练模型偏离正常值,模型的准确性降低,而异常值校正后的数据集排除了异常数据的干扰,达到提升模型性能的目的。
由第2对比组ANN、SVR与LightGBM的模型性能结果(表 3)可知,LightGBM具有强大的预测性能,对于所有DMA的需水量预测结果,LightGBM始终呈现最佳性能,不同数据集上的EMA比ANN和SVR平均降低了24.7%,DMA1中LightGBM的EMA相较SVR降低了41.8%,验证了LightGBM在需水量预测领域的高精度和可行性。
而提出的组合模型LOF+LightGBM相较其他3个预测模型(ANN、SVR、LightGBM)和两个组合模型(LOF+ANN、LOF+SVR),具有明显的预测优势,在绝大多数情况下均优于其他模型的预测性能。如表 3可知,DMA2、DMA3中LOF+LightGBM的ENS分别为0.951、0.942,预测精度高。DMA1由于需水量的波动性大(图 4(a)),预测难度最大,ANN、SVR、LOF+ANN、LOF+SVR均不能很好地捕捉到峰值的需水量,在需水量较低时,预测曲线也偏离观测值较大,LOF+LightGBM不仅在峰值时最贴近观测曲线,且在需水量较低时,也能捕捉到相对较小的需水量波动,预测精度较高。
通过计算时间对模型训练和预测的速度进行量化,结果见图 5。所有模型使用Python 3.6.9,计算机CPU为AMD Ryzen5 3600。由图 5可知,基于LightGBM的模型所使用的计算时间相比ANN和SVR模型长。这可能是研究中为了保障预测的精度,选取较低的学习率和较大的树的数目,使得预测时间变长。整体上LOF+预测模型的计算时间更短。总的来说,所有模型的计算时间均小于0.7 s,计算效率高。

|
图 5 各模型计算时间 Fig. 5 Computational time of models |
为了改善短期需水量预测模型的性能,提出了LOF异常值识别模型和高精度、高效率的LightGBM预测模型相结合的组合模型LOF+LightGBM。模型采用经过特征选择的周周期、日周期和近期相关需水量特征作为输入,使用江浙沪某市3个不同需水量分布的DMA数据实例,进行需水量预测模型性能测试,主要结论如下:
1) 日周期和近期相关需水量数据对预测模型的影响较大,周周期相关数据的影响相对较小,x(t-24×7),x(t-24)对预测模型的重要性始终排在前10,验证了需水量的强周期性。
2) 异常值处理有利于提高预测模型的准确性,基于LOF的预测模型ERMS平均降低了10%。LightGBM预测模型在不同数据集上均表现出高精度,其EMA比ANN和SVR平均降低了24.7%。
3) LOF+LightGBM相比其他模型具有明显的优势,能较好地预测出需水量波动。无论是LOF模型、LightGBM模型还是LOF+LightGBM模型,均有利于提升需水量预测模型的预测准确性。
在今后的研究中,可以在识别异常值的基础上,对异常值的产生进行归因,有利于进行管网漏损检测和事故预警。
| [1] |
蔡剑英, 王烜, 蔡宴朋. 基于无偏灰色-马尔科夫链模型的北京市水资源需求预测研究[J]. 三峡生态环境监测, 2022, 1. CAI Jianying, WANG Xuan, CAI Yanpeng. The prediction of water resource demands in Beijing city based on unbiased grey Markov chain model[J]. Ecology and Environmental Monitoring of Three Gorges, 2022, 1. |
| [2] |
吕良华, 姜蓓蕾, 耿雷华, 等. 不同发展情景下雄安新区用水强度及需水量预测[J]. 水利水运工程学报, 2021(1): 18. LV Lianghua, JIANG Beilei, GENG Leihua, et al. Water use intensity and water demand prediction of Xiongan New Area under different development scenarios[J]. Hydro-Science and Engineering, 2021(1): 18. DOI:10.12170/2020040100 |
| [3] |
刘书明, 吴雪, 欧阳乐岩. 不确定节点水量下水质监测点优化选址方法[J]. 环境科学, 2013, 34(8): 3108. LIU Shuming, WU Xue, OUYANG Leyan. Method for optimal sensor placement in water distribution systems with nodal demand uncertainties[J]. Environmental Science, 2013, 34(8): 3108. DOI:10.13227/j.hjkx.2013.08.009 |
| [4] |
HERRERA M, TORGO L, IZQUIERDO J, et al. Predictive models for forecasting hourly urban water demand[J]. Journal of Hydrology, 2010, 387(1): 141. DOI:10.1016/j.jhydrol.2010.04.005 |
| [5] |
JAIN A, VARSHNEY A K, JOSHI U C. Short-term water demand forecast modelling at ⅡT Kanpur using artificial neural networks[J]. Water Resources Management, 2001, 15(5): 299. DOI:10.1023/A:1014415503476 |
| [6] |
TIAN D, MARTINEZ C J, ASEFA T. Improving short-term urban water demand forecasts with reforecast analog ensembles[J]. Journal of Water Resources Planning and Management, 2016, 142(6). DOI:10.1061/(ASCE)WR.1943-5452.0000632 |
| [7] |
韩宏泉, 吴珊, 侯本伟. 采用核极限学习机的短期需水量预测模型[J]. 哈尔滨工业大学学报, 2022, 54(2): 8. HAN Hongquan, WU Shan, HOU Benwei. Short-term water demand prediction model using the kernel-based extreme learning machine[J]. Journal of Harbin Institute of Technology, 2022, 54(2): 8. DOI:10.11918/202012021 |
| [8] |
辛珂. 基于GA-ELM的城市短期需水预测与误差修正方法研究[D]. 邯郸: 河北工程大学, 2020 XIN Ke. The Research on urban short-term water demand prediction and error correction method based on GA-ELM[D]. Handan: Hebei University of Engineering, 2020 |
| [9] |
董云程, 周明, 杜坤, 等. 城市需水量预测方法与模型综述[J]. 软件导刊, 2019, 18(12): 1. DONG Yuncheng, ZHOU Ming, DU Kun, et al. Review of urban water demand forecasting methods and models[J]. Software Guide, 2019, 18(12): 1. DOI:10.11907/rjdk.192178 |
| [10] |
GHIASSI M, ZIMBRA D K, SAIDANE H. Urban water demand forecasting with a dynamic artificial neural network model[J]. Journal of Water Resources Planning and Management-Asce, 2008, 134(2): 138. DOI:10.1061/(ASCE)0733-9496(2008)134:2(138) |
| [11] |
单义明, 杨侃. 基于灰色关联度分析的山西省PSO-SVR需水量预测模型[J]. 水电能源科学, 2021, 39(2): 18. SHAN Yiming, YANG Kan. Forecasting model of PSO-SVR water requirement in Shanxi Province based on grey correlation analysis[J]. Water Resources and Power, 2021, 39(2): 18. |
| [12] |
李慧敏, 刘欣欣, 安笑洁. 基于LASSO-SVMR模型城市生活需水量的预测[J]. 长江技术经济, 2019, 3(增刊1): 138. LI Huimin, LIU Xinxin, AN Xiaojie. Forecast of urban domestic water demand based on LASSO-SVMR model[J]. Technology and Economy of Changjiang, 2019, 3(S1): 138. DOI:10.19679/j.cnki.cjjsjj.2019.0538 |
| [13] |
吴珊, 宋凌硕, 侯本伟, 等. 基于Bayesian-LSSVM和残差修正的用户短期需水量预测[J]. 哈尔滨工业大学学报, 2019, 51(8): 88. WU Shan, SONG Lingshuo, HOU Benwei, et al. Short-term water demand forecast based on Bayesian least squares support vector machine and residual correction[J]. Journal of Harbin Institute of Technology, 2019, 51(8): 88. DOI:10.11918/j.issn.0367-6234.201807113 |
| [14] |
VIJAI P, SIVAKUMAR B P. Performance comparison of techniques for water demand forecasting[J]. Procedia Computer Science, 2018, 143: 258. DOI:10.1016/j.procs.2018.10.394 |
| [15] |
XENOCHRISTOU M, KAPELAN Z. An ensemble stacked model with bias correction for improved water demand forecasting[J]. Urban Water Journal, 2020, 17(3): 212. DOI:10.1080/1573062X.2020.1758164 |
| [16] |
KE G, MENG Q, FINLEY T, et al. LightGBM: a highly efficient gradient boosting decision tree[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17). New York: Curran Associates Inc, Red Hook, 2018: 3149
|
| [17] |
MA X, SHA J, WANG D, et al. Study on a prediction of P2P network loan default based on the machine learning LightGBM and XGboost algorithms according to different high dimensional data cleaning[J]. Electronic Commerce Research and Applications, 2018, 31: 24. DOI:10.1016/j.elerap.2018.08.002 |
| [18] |
JU Y, SUN G, CHEN Q, et al. A model combining convolutional neural network and LightGBM algorithm for ultra-short-term wind power forecasting[J]. IEEE Access, 2019, 7: 28309. DOI:10.1109/ACCESS.2019.2901920 |
| [19] |
SEOK J, KIM J, LEE J, et al. Abnormal data refinement and error percentage correction methods for effective short-term hourly water demand forecasting[J]. International Journal of Control Automation and Systems, 2014, 12(6): 1245. DOI:10.1007/s12555-014-0001-z |
| [20] |
BREUNIG M, KRIEGEL H, NG R, et al. LOF: identifying density-based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data (SIGMOD'00). New York: Association for Computing Machinery, 2000: 93. DOI: 10.1145/342009.335388
|
| [21] |
ZHANG D, GONG Y. The comparison of lightGBM and XGboost coupling factor analysis and prediagnosis of acute liver failure[J]. IEEE Access, 2020, 8: 220990. DOI:10.1109/access.2020.3042848 |
| [22] |
BAKKER M, VREEBURG J H G, VAN SCHAGEN K M, et al. A fully adaptive forecasting model for short-term drinking water demand[J]. Environmental Modelling & Software, 2013, 48: 141. DOI:10.1016/j.envsoft.2013.06.012 |
| [23] |
GUO G, LIU S, WU Y, et al. Short-term water demand forecast based on deep learning method[J]. Journal of Water Resources Planning and Management, 2018, 144(12). DOI:10.1061/(ASCE)WR.1943-5452.0000992 |
| [24] |
ADAMOWSKI J, CHAN H F, PRASHER S O, et al. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada[J]. Water Resources Research, 2012, 48(1). DOI:10.1029/2010WR009945 |
| [25] |
BOUGADIS J, ADAMOWSKI K, DIDUCH R. Short-term municipal water demand forecasting[J]. Hydrological Processes, 2005, 19(1): 137. DOI:10.1002/hyp.5763 |
 2022, Vol. 54
2022, Vol. 54


