2. 武汉众智鸿图科技有限公司,武汉 430223
2. HopeTop Technology Co., Ltd., Wuhan 430223, China
以工业污染和生活有机物污染为代表的城市水质污染问题长期影响着中国城市供水安全。在供水管网中布设一系列监测点,是实现水质管控的基本手段。如何以较低的布设成本获得较高的监测性能,在管网中合理布设水质监测点位,是业界关注的重点问题。针对此类问题,Kessler等[1]最早提出了一种基于“服务水平q”的水质监测点布设方法,使用水力模型进行污染模拟并求解水质监测点组合,使其能够监测到尽可能多的污染事件。覆盖水量的水质监测方法也是常用方法,该方法使用流量来表征静态工况下管网的水质状况[2-4]。
考虑到仅使用水力模拟的方法难以平衡水质监测的性能和效率,后续研究开始使用多目标规划的方法进行水质监测点布局优化。Watson等[5]综合考虑了污染事件的时间、管网排出污染水体积、污染总人口、无法监测的污染事件总数以及被污染管道总长度5个目标进行求解,通过分析它们之间的相关性,发现布设水质监测点时如果仅考虑单目标有很大的风险,应该同时考虑多个优化目标。Carr等[6]构建最少污染人口和最小污染管段比例的双目标函数,提出双重线性化的方法,缩短了模拟时间。此外,最少已受污染输水量和最少已受影响人口也是常见的目标函数[7-8],也有研究专注于提高监测到的严重污染事件的比例[9-10]。
上述优化方法仍然缺少布设成本和计算复杂度等约束,所得解集的经济性和实用性不强。Berry等[11]在构建优化模型时增加了成本约束,解得监测点总数并非固定数量,而是通过计算优化得出。Ostfeld等[12]进一步改进,综合考虑节点用水量、监测设备的灵敏性等不确定性来优化水质监测点,结果表明,随着监测点数量增加,监测性能提升幅度有限。Huang等[13]构建了最大化监测污染事件比例、监测污染事件的最小化时间以及受影响的人口数最少3个目标,使用遗传算法求出监测点的帕累托解集,认为管网规模较为复杂时,可仅使用主干管段代替整个管网,从而减少计算时间。
然而,随着管网规模的扩大,多目标优化方法的计算耗时也会迅速增长。为了减少优化过程的计算量,提高优化效率,Propato等[14-15]提出了统一的多目标布局优化公式,简化了多目标函数运算。Dorini等[16]采用“交叉熵”法,改进了水质模拟软件,在计算机内存中读取和计算水力数据,节省了计算时间。Berry等[17]合并了受到污染的节点和污染工况,对管网进行了简化。Preis等[18-19]提出在污染事件模拟时仅选取若干重要节点进行实验,一定程度上可以缩小模拟过程的计算量。
既往研究在小规模管网的水质监测点布局优化中取得了较好的效果,但是管网的连接复杂度随其规模增大会呈现几何式增长,将传统的水质监测点布局优化方法直接应用于大规模管网可能会引起计算量激增,难以迭代出优质解集。为了弥补这一不足,本文聚焦于大规模管网的监测点布局优化问题,设计基于复杂网络和水力特征指标的节点筛选模型以及基于节点空间相似性的遗传算法演化策略,提出一种适用于大规模供水管网的水质监测点布局优化方法,解决计算效率和解集质量低的问题。
1 监测点布局求解框架水质监测点布局求解框架由污染事件模拟、优化目标设定、优化目标计算和遗传算法迭代求解4个部分组成。污染事件模拟是通过实验模拟的方法,记录某一节点上发生污染事件时其他节点受该事件影响的过程。使用EPANET等水力计算工具,模拟污染物注入后水质随时间的变化。由于节点污染事件互相独立,采用多进程技术并行模拟多个污染事件以提高效率。为了聚焦基于水力的污染扩散物理模型,发现污染物随水流扩散的规律,依照污染事件监测研究的常规做法[20-21],假定污染物是一种可随管道输送、不在管网中发生反应也不随时间衰减的“保守态”有害物质。恐怖袭击或恶意破坏等蓄意污染注入事件中,破坏者常使用毒性强、不易发生反应也不易消解变质的物质,以实现破坏效果最大化。“保守态”有害物质假设不仅有助于简化计算,也符合上述蓄意污染注入情境。针对日常运营中可能出现的常规污染物,则需要在水质模拟阶段根据不同污染物的物理化学特性,添加相应的扩散衰减系数。
为保证水质监测点布局的响应速度和污染事件覆盖能力,设定污染事件监测时间最小化和污染事件监测覆盖比例最大化,作为突发污染情况下的水质监测点优化目标,具体如下:
| $ \min {f_1} = \frac{1}{P}\sum\limits_{i = 1}^P {{t_i}} $ | (1) |
| $ \max {f_2} = \frac{1}{P}\sum\limits_{i = 1}^P {{x_i}} $ | (2) |
| $ 1 \le \sum\limits_{k = 1}^P {{y_{ik}}} $ | (3) |
| $ {x_i}, {y_{ik}} \in \{ 0, 1\} , i \in \{ 1, 2, \cdots , P\} , k \in \left\{ {1, 2, \cdots , {N_{\rm{s}}}} \right\} $ | (4) |
式中:P为污染事件总数;ti为污染事件i被监测的最短用时;xi为二进制数,若污染事件i被监测到,xi为1,否则为0;yik为二进制数,若监测点k能在模拟时间内发现污染事件i,yik为1,否则为0;NS为需要布设的水质监测点总数。目标函数f1表示在水质模拟时间内,水质监测点布局监测到各个污染事件的平均时间最短;目标函数f2表示水质监测点布局能够覆盖到污染事件的比例最大。污染事件i能够被监测到的条件是该事件影响到的节点中必须布设至少一个水质监测点,且污染物浓度触及监测阈值所需时间不超过模拟时间。
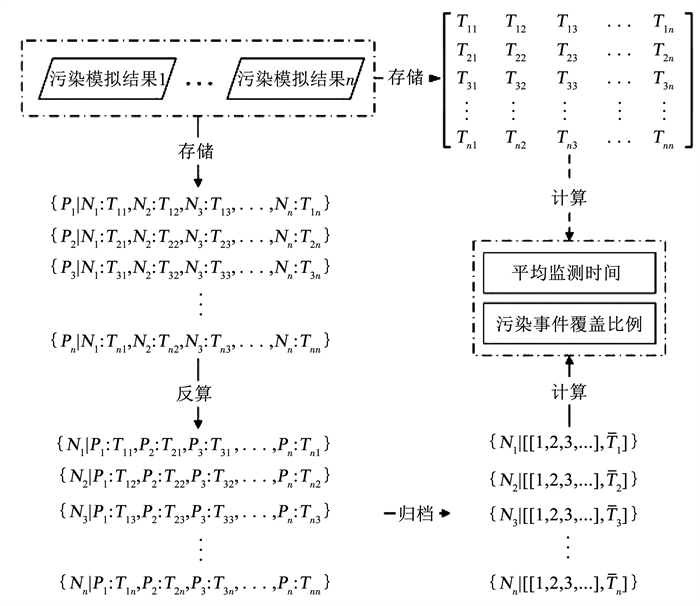
优化目标计算是将某一水质监测点布局代入目标函数并解得函数值的过程,可以反映该布局的性能。以数据存储的字典结构建立时间矩阵,存储发生污染节点、受到影响节点以及其首次受到影响的时间等信息。由该矩阵可以反推出某一受污染节点可能由哪些污染事件引起,即在该节点布设传感器可以监测到哪些污染事件。将反推结果进行数据归档后,即可计算优化目标值。计算流程见图 1,其中Pi为发生污染的节点,Ni为受到污染事件影响的节点,Tij为节点首次受到污染的时间。
|
图 1 优化目标计算流程 Fig. 1 Calculation process of optimization target |
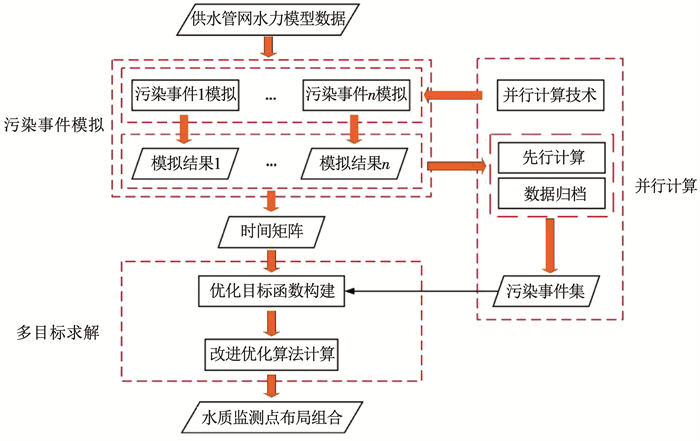
求解水质监测点布局时,将初始化的水质监测点布局代入基于经典NSGA2算法[22]的改进遗传算法进行迭代,待收敛后得到最终布局结果。该算法设计了基于空间相似性的定向变异和交叉算子,以提高迭代寻优性能、降低计算复杂度。总体求解框架见图 2。
|
图 2 水质监测点布局求解框架 Fig. 2 Solution framework of water quality monitoring points layout |
筛选管网中最重要的节点进行污染模拟,可以在降低计算复杂度的同时保证污染事件的覆盖比例。研究表明,复杂网络指标值或水力指标值较高的节点可靠性更弱,遭受突发破损和污染事故的概率更大[23],因此,选择此类节点进行污染事件模拟和水质监测点布设更加有效。节点筛选分别采用两种策略:一是复杂网络节点重要性指标评价,二是耦合水力特征的节点污染概率综合评价。
复杂网络理论中常用的节点重要性指标包括:度中心性(degree centrality,DC)、介数中心性(betweenness centrality,BC)、接近中心性(closeness centrality,CC)、特征向量中心性(eigenvector centrality,EC)、HITS(hyperlink-induced topic search)以及PageRank值。分别按照以上6个指标对所有节点重要性排序,选取位于前列的若干节点,可得到6组基于复杂网络重要性指标的节点筛选结果。
综合评价管网节点的多种水力特征,可以衡量节点受到污染的概率,筛选污染风险高的节点。选取5个水力指标:1)节点需水量改变(NDC),反映24 h内节点用水量变化;2)节点内压力极差(NPR),反映24 h内节点压力的变化;3)节点连接管道的平均管径(NAD),反映节点的水流量;4)节点连接管道的管径极差(NDD),反映节点的稳定性;5)节点的度(NDR),表示节点连接其他节点的数量。其中,指标NDC、NPR可以运用EPANET等水力模拟计算工具获得。综合权衡运算量和节点筛选效果,将水力模拟步长设置为1 h,计算分小时水力指标,即可得到24 h内需水量和压力变化量。
为了将上述水力特征集成到一个综合评价指标体系中,使用归一化数学变换消除由各指标原始量纲不同引起的数量级差异。根据各指标的数值分布规律差异,设定综合评价权重。某一指标数值分布的离散程度越大,其对综合评价的影响也越大。因此,根据各个指标的信息熵值衡量其离散程度,再采用熵值法[24]根据各指标数据的离散程度确定其权重系数。
最后构建综合评价的数学模型,采用线性集结方式构建节点筛选模型,对各个指标加权求和,得到综合评价值:
| $ y = \sum\limits_{i = 1}^5 {{w_i}} {x_i} $ | (5) |
式中:wi(i=1、2、3、4、5,分别表示NDC、NPR、NAD、NDD、NDR)为综合评价指标权重,xi为各水力指标值。
按照耦合水力特征的综合评价模型对所有节点进行排序,选取位于前列的若干节点,可得到1组筛选结果。
3 基于空间相似性的遗传迭代水质监测点布局优化使用遗传算法进行迭代。遗传过程中基因代表监测点,个体代表监测点组合,一个种群包含多个个体。个体上的基因可以进行单点变异,产生一个新基因并替换原基因。不同个体间还可以交叉、交换基因。遗传算法可以在多次迭代中寻求最优解。
经典NSGA2算法采用随机变异和交叉的方法[22],种群的进化方向不确定,因而收敛速度慢,解集质量差。考虑到供水管网中距离相近节点的水力特征和复杂网络特征相似性高,且功能接近,使用空间位置与监测污染事件的重复比例共同定义管网节点i与j的相似性。根据空间相似性的概念为遗传过程的变异和交叉指定方向,有助于加快收敛速度,提高解集质量。节点间空间相似性定义如下:
| $ {S_{ij}} = \left( {{O_{ij}}, {P_{ij}}} \right) $ | (6) |
| $ {O_{ij}} = \frac{{N{L_{ij}}}}{{\sum\limits_{k = 1}^n {{L_{ik}}} }} $ | (7) |
式中:Sij为节点i与节点j的空间相似性;n为管网总节点数;Lij为节点i与j的距离;Oij为节点i与j的距离相似性,根据节点i到其他节点k的平均距离与节点i到j的距离之比定义,当节点i与j的距离小于平均距离时,Oij为1,否则为0;Pij为节点i与j的监测性能相似性,根据节点i与j监测事件的重复比例定义,重复比例超过50%时,Pij为1,否则为0。Oij和Pij均为1时,节点间空间相似性Sij高;Oij和Pij均为0时,节点间空间相似性Sij低;其他情况节点间空间相似性Sij一般。
经典NSGA2算法采用固定概率随机交叉个体对[22],未考虑个体间相似性和差异性,可能会导致父代个体中的良好基因无法遗传到子代,从而减慢收敛速度。为了保留种群中的优势个体,可以根据供水管网中节点的空间特性,将节点的空间相似性应用于交叉算子。两个体A与B之间的空间相似性S定义为
| $ S(A, B) = \frac{l}{n} $ | (8) |
式中:l为两个个体共同包含的空间相似性高的节点数量,n为种群中节点总数。设定种群个体的相似性阈值P为0.5,当两个个体的相似性S < P时进行单点交叉,互换基因片段。
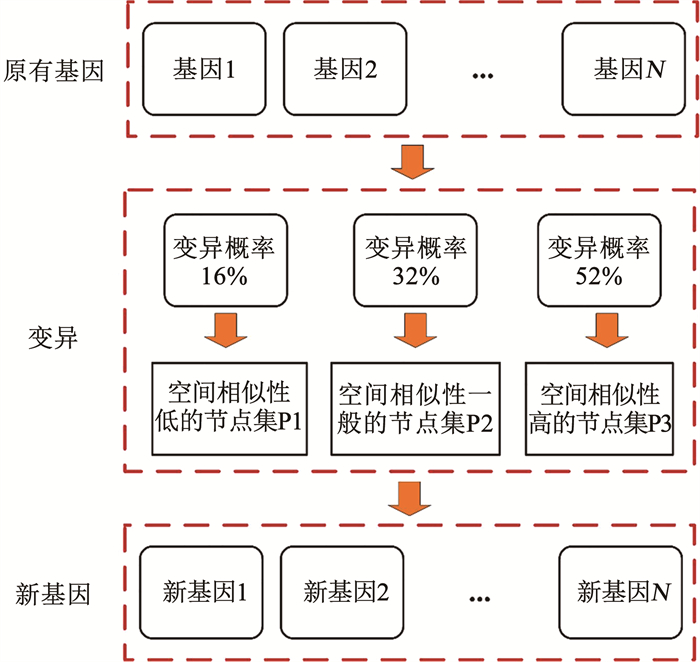
变异算子的流程见图 3。变异过程包括:1)依据固定的变异概率判断个体内的基因是否变异;2)若基因变异,为与当前节点空间相似性低、一般、高的3个节点集P1、P2、P3分别赋予16%、32%、52%的选择概率(近似比1∶ 2∶ 3,总和100%),依概率从3个节点集中选取新基因替换原基因;3)若选取的节点基因与当前个体中已包含的节点重复,则重复步骤2)的操作,直至变异完成。

|
图 3 改进的交叉算子 Fig. 3 Improved crossover operator |
基于空间相似性的变异算子以节点间空间相似性为基础,当个体变异时,根据空间相似性选择方向,以保证优良基因遗传给子代的概率更大。按照1∶ 2∶ 3的权重为节点空间相似性低、一般、高的变异方向赋予选择概率,约束着变异向空间相似性高的方向进行。变异算子的流程见图 4。
|
图 4 改进的变异算子 Fig. 4 Improved mutation operator |
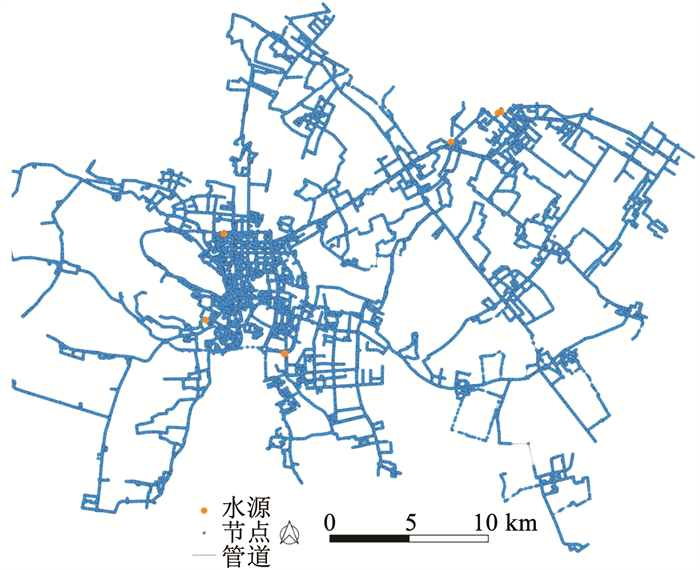
选取中国华东CS市管网为实验数据,该管网包括10个水源、53 166个节点和60 811个管段,管段总长约1 595.52 km,见图 5。
|
图 5 中国华东CS市供水管网 Fig. 5 Water supply network in CS City, East China |
实验以单节点污染注入方式模拟所有节点上的污染事件。考虑到污染物监测过程的灵敏度,从污染跟踪和应急处置的实际需要出发,将水质模拟步长和报告的间隔设置为10 min,模拟时长为24 h。此时水质模拟计算考虑的是10 min间隔下水力状况的变化,比注入节点筛选阶段更为精细。污染物注入方式为以500 g/min的固定速率注入,在整个模拟过程中持续注入。假定水质监测点在模拟期间保持正常工况,一旦污染物浓度超过设定阈值,能够立即报告。污染物监测最低阈值为0.01 mg/L。
模拟节点的筛选,分别按照前文提出的复杂网络节点重要性指标以及耦合水力特征的节点污染概率综合评价方法两种策略进行。
按照复杂网络节点重要性指标筛选策略,分别对节点按度中心性(DC)、介数中心性(BC)、接近中心性(CC)、特征向量中心性(EC)、HITS和PageRank值等复杂网络节点重要性指标排序,筛选出6组规模为3 000的重要性强的节点作为实验数据,见表 1。
| 表 1 各重要性指标下的管网节点重要性排序 Tab. 1 Importance ranking of network nodes under each importance index |
按照耦合水力特征的多指标综合评价方法,计算各个节点的需水量改变(NDC)、压力极差(NPR)、连接管道的平均管径(NAD)、连接管道的管径极差(NDD)、节点的度(NDR),部分节点的水力指标见表 2。用熵值法求解得到5个指标的权重系数,见表 3。
| 表 2 部分节点的水力指标 Tab. 2 Hydraulic index values of some nodes |
| 表 3 水力指标权重系数 Tab. 3 Weight coefficient of hydraulic indexes |
由式(5)提出的节点筛选模型,耦合水力特征的节点污染概率模型即为
| $ y = 0.154{x_1} + 0.02{x_2} + 0.05{x_3} + 0.835{x_4} + 0.04{x_5} $ | (9) |
根据此污染概率模型计算得到各节点的多指标综合评价值,筛选得到1组规模为3 000的污染概率较高节点组合作为实验数据。
既往针对小规模实验型管网的水质监测点布局研究,常随机选取污染注入节点,因此,实验针对等概率节点筛选策略,增设一组规模为3 000的节点组合作为对比,以评估本文节点筛选策略是否更具优势。
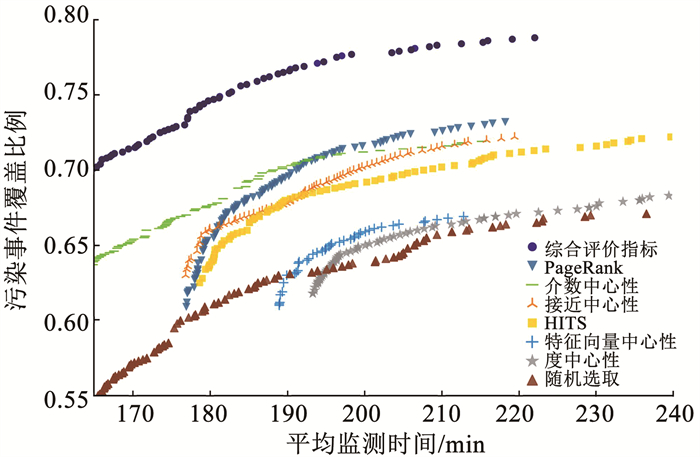
对以上8组筛选节点,根据全节点上的污染模拟结果构建各自的污染事件数据集,采用水质监测点布局求解框架,分别使用基于空间相似性改进交叉和变异算子的遗传算法迭代求解。设定种群规模为3 000,交叉概率为0.9,变异概率为0.1,经过1 000次迭代得到监测点解集,反映解集性能的帕累托前沿分布见图 6。图例中综合评价指标代表耦合水力特征的污染概率筛选模型,度中心性、介数中心性、接近中心性、特征向量中心性、HITS和PageRank代表相应的复杂网络节点重要性筛选策略,随机选取则代表等概率筛选策略。
|
图 6 不同节点筛选策略下的帕累托解集 Fig. 6 Pareto solution sets based on different nodes election strategies |
结果表明,耦合水力特征的综合评价和复杂网络节点重要性指标筛选出的水质监测点布局解集,均比随机选取的节点解集性能更好,即在相同的平均监测时间下能够覆盖更多的污染事件,其中,耦合水力特征的综合评价方法效果最好。在8种节点筛选策略中,随机选取策略寻优性能最差,不适合在大规模供水管网中求解水质监测点布局。
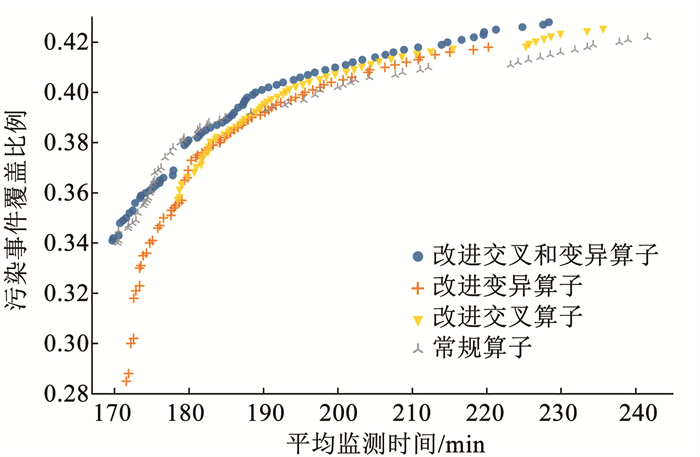
为验证遗传算子的改进效果,分别使用改进交叉和变异算子、仅改进交叉算子、仅改进变异算子和常规算子进行迭代。随机选取200个节点布置水质监测点,交叉概率为0.9,变异概率为0.1,经过500次迭代,4种遗传算子的解集性能见图 7。可以看出,本文提出的改进的交叉和变异算子迭代产生的水质监测点布局组合具有更好的监测性能,且具有更高的寻优效率。
|
图 7 改进算子与常规算子的水质监测点解集比较 Fig. 7 Comparison of solution sets of water quality monitoring points between improved operators and conventional operators |
以最小污染事件监测时间和最大污染事件监测比例为优化目标,提出了一种面向大规模供水管网水质监测点布局的遗传优化求解框架。针对大规模供水管网节点数量众多、水质模拟耗时长且解集质量低等问题,引入基于复杂网络节点重要性和耦合水力特征综合评价的节点筛选模型,选择具有代表性的重要节点进行水质模拟,有效提高了大规模供水管网中水质模拟的效率。针对优化算法在大规模管网选取监测点数量较多情况下寻优效率低下的问题,基于节点的空间相似性改进了交叉和变异遗传算子,避免了优化过程的过早收敛。实验证明,采用节点筛选模型和改进的遗传算子,不仅显著提高了计算效率,还能获得性能明显更优的解集。本文提出的监测点布局优化方法,兼顾水质监测性能和监测点布设成本,在水质监测点总数既定的前提下,能有效提升突发污染事件的监测性能。
| [1] |
KESSLER A, OSFFELD A, SINAI G. Detecting accidental contaminations in municipal water networks[J]. Journal of Water Resources Planning and Management, 1998, 124(4): 192. DOI:10.1061/(ASCE)0733-9496(1998)124:4(192) |
| [2] |
黄善钦, 王圃, 王峰青, 等. 基于覆盖水量的水质监测点选址模型改进及应用[J]. 中国给水排水, 2020, 36(11): 46. HUANG Shanqin, WANG Pu, WANG Fengqing, et al. Modification and application of water quality monitoring points location model based on demand coverage[J]. China Water and Wastewater, 2020, 36(11): 46. |
| [3] |
李龙云, 李树平, 张春杰, 等. 配水系统中水质监测点的优化布置[J]. 供水技术, 2008, 2(3): 47. LI Longyun, LI Shuping, ZHANG Chunjie, et al. Optimized locations of water quality monitoring sites in water distribution system[J]. Water Technology, 2008, 2(3): 47. |
| [4] |
LEE B H, DEININGER R A. Optimal locations of monitoring stations in water distribution system[J]. Journal of Environmental Engineering, 1992, 118(1): 4. DOI:10.1061/(ASCE)0733-9372(1992)118:1(4) |
| [5] |
WATSON J P, GREENBERG H J, HART W E. A multiple-objective analysis of sensor placement optimization in water networks[C]//World Water and Environmental Resources Congress. Salt Lake City: American Society of Civil Engineers, 2004. DOI: 10.1061/40737(2004)456
|
| [6] |
CARR R D, GREENBERG H J, HART W E, et al. Addressing modeling uncertainties in sensor placement for community water systems[C]//World Water and Environmental Resources Congress. Salt Lake City: American Society of Civil Engineers, 2004. DOI: 10.1061/40737(2004)457
|
| [7] |
GUIDORZI M, FRANCHINI M, ALVISI S. A multi-objective approach for detecting and responding to accidental and intentional contamination events in water distribution systems[J]. Urban Water Journal, 2009, 6(2): 115. DOI:10.1080/15730620802566836 |
| [8] |
ARAL M M, GUAN J B, MASLIA M L. Optimal design of sensor placement in water distribution networks[J]. Journal of Water Resources Planning and Management, 2010, 136(1): 5. DOI:10.1061/(ASCE)WR.1943-5452.0000001 |
| [9] |
KRAUSE A, GUESTRIN C. Robust sensor placement for detecting adversarial contaminations in water distribution systems[C]//World Environmental and Water Resources Congress. Kansas City: American Society of Civil Engineers, 2009. DOI: 10.1061/41036(342)45
|
| [10] |
WATSON J P, MURRAY R, HART W E. Formulation and optimization of robust sensor placement problems for drinking water contamination warning systems[J]. Journal of Infrastructure Systems, 2009, 15(4): 330. DOI:10.1061/(ASCE)1076-0342(2009)15:4(330) |
| [11] |
BERRY J, FLEISCHER L, HART W, et al. Sensor placement in municipal water networks[J]. Journal of Water Resources Planning and Management, 2005, 131(3): 237. DOI:10.1061/(ASCE)0733-9496(2005)131:3(237) |
| [12] |
OSTFELD A, SALOMONS E. Securing water distribution systems using online contamination monitoring[J]. Journal of Water Resources Planning and Management, 2005, 131(5): 402. DOI:10.1061/(ASCE)0733-9496(2005)131:5(402) |
| [13] |
HUANG J J, MCBEAN E A, JAMES W. Multi-objective optimization for monitoring sensor placement in water distribution systems[C]//8th Annual Water Distribution Systems Analysis Symposium. Cincinnati: American Society of Civil Engineers, 2006. DOI: 10.1061/40941(247)113
|
| [14] |
PROPATO M, PILLER O, UBER J G. A sensor location model to detect contaminations in water distribution networks[C]//World Water and Environmental Resources Congress. Anchorage: American Society of Civil Engineers, 2005: 1. DOI: 10.1061/40792(173)45
|
| [15] |
PROPATO M. Contamination warning in water networks: general mixed integer linear models for sensor location design[J]. Journal of Water Resources Planning and Management, 2006, 132(4): 225. DOI:10.1061/(ASCE)0733-9496(2006)132:4(225) |
| [16] |
DORINI G, JONKERGOUW P, KAPELAN Z, et al. An efficient algorithm for sensor placement in water distribution systems[C]//8th Annual Water Distribution Systems Analysis Symposium. Cincinnati: American Society of Civil Engineers, 2006. DOI: 10.1061/40976(316)510
|
| [17] |
BERRY J W, CARR R D, HART W E, et al. Scalable water network sensor placement via aggregation[C]//World Environmental and Water Resources Congress. Tampa: American Society of Civil Engineers, 2007. DOI: 10.1061/40927(243)465
|
| [18] |
PREIS A, OSTFELD A. Optimal sensors layout for contamination source identification in water distribution systems[C]//8th Annual Water Distribution Systems Analysis Symposium. Cincinnati: American Society of Civil Engineers, 2006. DOI: 10.1061/40941(247)127
|
| [19] |
PREIS A, OSTFELD A. Efficient contamination events sampling for sensors layout design[C]//World Environmental and Water Resources Congress. Tampa: American Society of Civil Engineers, 2007. DOI: 10.1061/40927(243)462
|
| [20] |
ZENG D, GU L, LIAN L, et al. Oncost-efficient sensor placement for contaminant detection in water distribution systems[J]. IEEE Transactions on Industrial Informatics, 2016, 12(6): 2177. DOI:10.1109/TⅡ.2016.2569413 |
| [21] |
BANIK B K, ALFONSO L, TORRES A S, et al. Optimal placement of water quality monitoring stations in sewer systems: an information theory approach[J]. Procedia Engineering, 2015, 119: 1308. DOI:10.1016/j.proeng.2015.08.956 |
| [22] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182. DOI:10.1109/4235.996017 |
| [23] |
徐得潜, 赵娟. 供水管网节点可靠性评估方法研究[J]. 工程与建设, 2015(3): 289. XU Deqian, ZHAO Juan. Research on reliability evaluation method of water supply pipeline network nodes[J]. Engineering and Construction, 2015(3): 289. |
| [24] |
郭显光. 熵值法及其在综合评价中的应用[J]. 财贸研究, 1994(6): 58. GUO Xianguang. Entropy value method and its application in comprehensive evaluation[J]. Finance Research, 1994(6): 58. |
 2022, Vol. 54
2022, Vol. 54


