2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
圆孔扩张理论主要研究圆孔扩张或收缩所引起的应力场和位移场的变化,广泛应用于静力触探试验(CPT)和旁压试验(PMT)结果的解释[1-2]、静压桩的沉桩效应分析[3-4]和隧道围岩压力的计算[5]等。在过去的几十年里,圆孔扩张理论所涉及的土体模型从早期的理想弹塑性模型逐渐发展到临界状态模型。目前,不少学者将研究聚焦于土体各向异性[6-7]、三维强度[8]和不同原位应力[9]对圆孔扩张过程中土体力学行为的影响。然而,上述解答大多是针对两相的饱和土提出的,饱和土在圆孔扩张过程中饱和度没有变化,仅具有力学响应。而对于非饱和土来说,扩张响应还需充分考虑其水力耦合特性。
目前,部分学者对非饱和土中圆孔扩张问题进行了研究。Russell等[10-11]在研究中引入基质吸力,分别假定土体屈服后服从边界面模型和修正剑桥模型,采用相似求解技术给出有限径向范围内非饱和土中圆孔扩张问题的解答。Yang等[12-13]进一步拓展了排水条件和边界条件,分别研究了水力滞后和边界效应的影响。张亚国等[14]考虑吸力效应的影响,采用单应力状态变量法将Chen等[15]的饱和土排水精确解拓展至非饱和土中。为了更好地模拟非饱和土的水力耦合特性,Chen等[16-17]采用Sun[18]提出的非饱和土临界状态模型(UCSM),引入孔隙比相关的土水特征曲线(SWCC),分别提出了不同排水条件下非饱和土柱孔扩张和球孔扩张的精确解答。Yang等[19]考虑了非饱和土的超固结特性,在水力耦合特性的基础上,建立了超固结非饱和土柱孔扩张的弹塑性半解析解。
Sun[20]的非饱和土三轴试验和王永洪等[21]的非饱和土桩土界面剪切试验均表明,饱和度对非饱和土的应力- 应变特性和强度具有重要影响。因此,在求解非饱和土圆孔扩张问题时须充分考虑其饱和度响应。上述解答[16-17, 19]均假定饱和度随孔隙比呈线性负相关,但事实上,非饱和土常吸力压缩过程中,饱和度随着孔隙比减小既有可能增加,也有可能减小。Gallipoli[22]通过非饱和土的常吸力压缩试验观察到饱和度随着孔隙比的减小而增大。Sun等[20]的非饱和珍珠黏土三轴试验和李涛等[23]的非饱和土水- 力耦合本构也得出了相同的结果。然而,Koliji等[24]发现在粉质黏土的常吸力加载过程中,土体的饱和度减小。Romero等[25-26]也均在固结试验中观测到了饱和度减小的趋势。基于上述试验结果,Pash等[27]提出了非饱和土常吸力加载路径下饱和度随孔隙比变化的模型,并讨论了该模型预测饱和度变化的能力。该模型可根据有效应力参数增量ψ与饱和度Sr的大小关系,将土体受力过程中饱和度随孔隙比的变化定义为负/正相关关系,因此,其能够更好地预测非饱和土受力过程中饱和度增大或减小的趋势。
此外,之前的解答大多采用双应力状态变量来描述非饱和土的水力行为。而单应力状态变量形式简单,对试验条件要求较低[28],又与传统土力学中有效应力的表达式相协调,更便于指导工程实践。同时,许多研究都假设非饱和土CPT过程中基质吸力保持不变[29-31],即为排水条件。因此,采用有效应力这一单一状态变量,结合非饱和土临界状态模型[18]和Pash等[27]提出的常吸力下非饱和土饱和度随孔隙比非线性变化模型,推导非饱和土中排水条件下柱孔扩张问题的精确半解析解。与Chen等[16]采用的方法相比,本文采用的本构关系能够较为全面地模拟非饱和土柱孔扩张过程中的水力行为。所提出的解答可为非饱和土中柱孔扩张问题提供一个通用的分析框架,也为分析非饱和土中沉桩效应、CPT等提供参考。
1 力学模型如图 1所示,柱孔在一定范围内受初始水平地应力σh0和竖直地应力σv0作用,当内部压力由σh0增大到σa,孔径从a0扩张到a,孔周一定范围内土体任一点从r0移动至r位置,形成一个半径为rp的塑性区,塑性区外为弹性区。规定应力以压为正,应变以体积收缩为正。
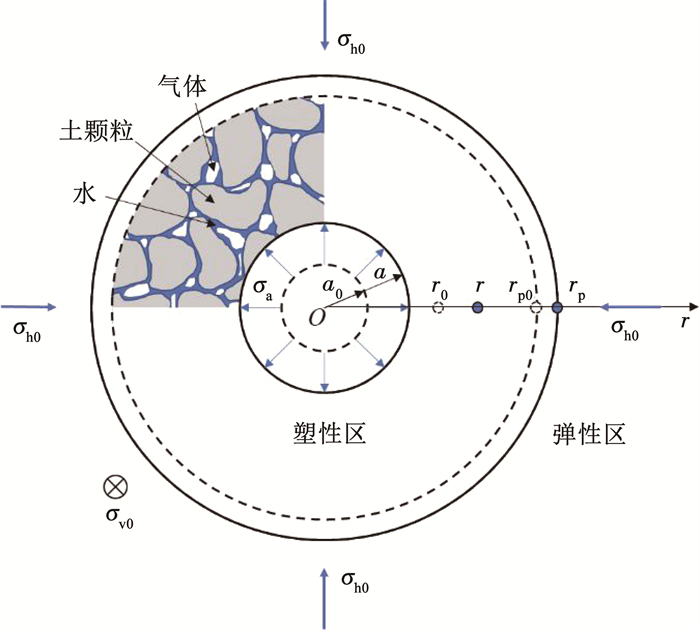
|
图 1 非饱和土柱孔扩张模型 Fig. 1 Model of cylindrical cavity expansion in unsaturated soil |
在极坐标系内,柱孔周围的弹性区和塑性区内任一土单元的位置可表示为(r、θ、z),其有效应力分量可表示为σ′r、σ′θ、σ′z。排水条件下非饱和土中柱孔周围土单元的平衡微分方程可表示为
| $ \frac{{{\rm{d}}\sigma _r^\prime }}{{{\rm{d}}r}} + \frac{{\sigma _r^\prime - \sigma _\theta ^\prime }}{r} = 0 $ | (1) |
Bishop等[32]建议非饱和土有效应力表达式为
| $ \sigma ' = {\sigma _{\rm{n}}} + \chi s $ | (2) |
式中:σn为净应力,等于总应力减去孔隙气压力(假设孔隙气与大气相通,可视为0);χ为有效应力参数,表示吸力对有效应力的贡献;s为吸力,等于孔隙气压力ua与孔隙水压力uw的差值,即ua-uw。
2 本构模型 2.1 屈服面及硬化准则UCSM在p′-q平面上的屈服面是一个椭圆,如图 2所示。随着扩孔压力逐渐增大,孔壁及周围土体依次从弹性状态发生屈服,进入塑性状态。假设土体服从相关联的流动法则,屈服函数(f)和塑性势函数(g)可采用以下形式:
| $ f = g = {q^2} + {M^2}p'\left( {p' - p_{\rm{y}}^\prime } \right) = 0 $ | (3) |
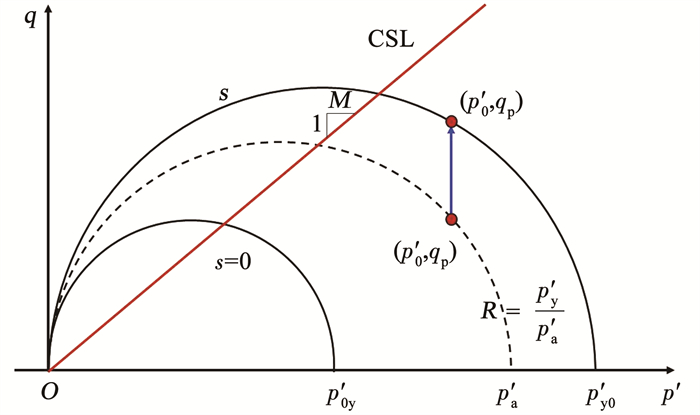
|
图 2 p′-q平面常吸力下屈服曲线 Fig. 2 Yield curve under constant suction in p′-q plane |
式中:M为p′-q平面上临界状态线(CSL)的斜率; p′=(σ′r+σ′θ+σ′z)/3为平均有效应力; q=
| $ p_{\rm{y}}^\prime = p_{\rm{n}}^\prime {\left( {\frac{{p_{0{\rm{y}}}^\prime }}{{p_{\rm{n}}^\prime }}} \right)^{\frac{{\lambda (0) - \kappa }}{{\lambda (s) - \kappa }}}} $ | (4) |
| $ \lambda (s) = \lambda (0)\left[ {(1 - c){e^{ - bs}} + c} \right] $ | (5) |
式中:λ(0)和λ(s)分别为饱和土和非饱和土(基质吸力为s)在e-lnp′平面上正常压缩线(NCL)的斜率;p′n为参考应力;b和c为材料参数,可分别取0.65和0.125[18];κ为υ-p′平面内非饱和土加载-再加载线的斜率。
2.2 水力耦合条件在小应变和土颗粒不可压缩的假设下,饱和度Sr的变化可归因于孔隙水体积应变量(dεw=-dVw/V,Vw和V为水的体积和总体积)和总体积应变量(dευ=-dV/V=-dVυ/V=-de/(1+e),Vυ为孔隙的体积,e为孔隙比),即
| $ {\rm{d}}{S_{\rm{r}}} = - \frac{{{\rm{d}}{\varepsilon _{\rm{w}}} - {S_{\rm{r}}}{\rm{d}}{\varepsilon _v}}}{n} $ | (6) |
式中n=e/(1+e)为孔隙率。常吸力加载条件下,水的体积应变率与总体积应变率有关[33],即
| $ {\rm{d}}{\varepsilon _{\rm{w}}} = \psi {\rm{d}}{\varepsilon _v} $ | (7) |
式中ψ为有效应力参数增量。联立式(6)和(7),饱和度随孔隙比的变化可表示为
| $ {\rm{d}}{S_{\rm{r}}} = \left( {\psi - {S_{\rm{r}}}} \right)\frac{{{\rm{d}}e}}{e} $ | (8) |
ψ计算如下:
| $ \psi = \frac{{\partial (\chi s)}}{{\partial s}} = \left( {1 + \frac{{\partial \ln \chi }}{{\partial \ln s}}} \right)\chi $ | (9) |
有效应力参数χ对于饱和土和干土其值分别为1和0;对于非饱和土,χ可表示为[10, 34]
| $ \chi = \left\{ {\begin{array}{*{20}{l}} {1, \frac{s}{{{s_{\rm{e}}}}} \le 1}\\ {{{\left( {\frac{s}{{{s_{\rm{e}}}}}} \right)}^{ - \mathit{\Omega }}}, 1 < \frac{s}{{{s_{\rm{e}}}}}} \end{array}} \right. $ | (10) |
式中:Ω为材料参数,最佳拟合值为0.55。se为饱和状态与非饱和状态转换所对应的吸力值,对于沿主干路径饱和度降低的土体,se等于进气值(sae);对于沿主湿路径饱和度升高的土体,se等于排气值(sex),如图 3所示。se取进气值sae。
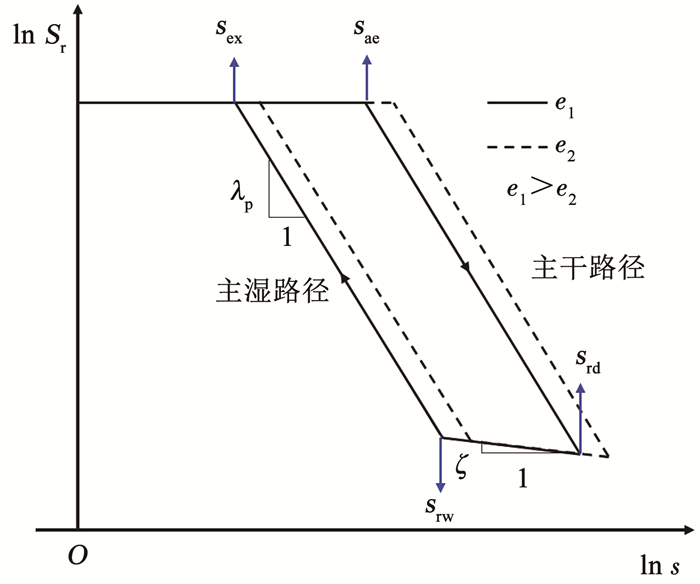
|
图 3 考虑水力滞后和孔隙比变化影响的SWCC Fig. 3 SWCC considering hydraulic hysteresis and effect of change in void ratio |
联立式(8)~(10),可将饱和度增量表示为
| $ {\rm{d}}{S_{\rm{r}}} = \left[ {(1 + \zeta )\chi - {S_{\rm{r}}}} \right]\frac{{{\rm{d}}e}}{e} $ | (11) |
式中
| $ \zeta = \left\{ {\begin{array}{*{20}{l}} {0, \frac{s}{{{s_{\rm{e}}}}} \le 1}\\ { - \mathit{\Omega }, 1 < \frac{s}{{{s_{\rm{e}}}}}} \end{array}} \right. $ | (12) |
为了利用上式预测土体受力过程中饱和度的变化,有必要考虑SWCC参数的演化,即进气值se、孔径分布指数λp随孔隙比的变化。采用Pasha等[35]提出的模型,考虑孔隙比变化的SWCC参数可表示为(更新参数均用*表示)
| $ s_{\rm{e}}^* = {s_{\rm{e}}}\left[ {1 - \frac{\mathit{\Omega }}{{\left( {1 - {S_{{\rm{res}}}}} \right){\lambda _{\rm{p}}}}}\frac{{{\rm{d}}e}}{e}} \right] $ | (13) |
| $ \lambda _{\rm{p}}^ * = {\lambda _{\rm{p}}}\left\{ {1 - \frac{{3\left[ {\left( {1 - \mathit{\Omega }} \right)\left( {{2^{1 - \mathit{\Omega /}{\lambda _{\rm{p}}}}} - 1} \right) - {S_{{\rm{res}}}}} \right]}}{{2\left( {1 - {S_{{\rm{res}}}}} \right)}}\frac{{{\rm{d}}e}}{e}} \right\} $ | (14) |
式中Sres为残余饱和度,取0.1[27]。
3 扩张响应 3.1 弹性区在弹性区(r>rp),假设土体符合胡克定律和小应变理论,则弹性区应变张量以增量形式表示为
| $ {\rm{D}}\varepsilon _{ij}^{\rm{e}} = \frac{{1 + \mu }}{E}{\rm{D}}\sigma _{ij}^\prime - \frac{\mu }{E}{\delta _{ij}}{\rm{D}}\sigma _{ij}^\prime $ | (15) |
式中:Dεije、Dσ′ij分别为弹性应变和平均有效应力增量;μ为泊松比;E为弹性模量,可表示为平均有效应力p′和比体积υ的函数,即
| $ E = \frac{{3(1 - 2\mu )vp'}}{\kappa } $ | (16) |
另外,在弹性区,弹性模量E和剪切模量G保持不变,分别等于其初始值。弹性区内任意点的应力分布可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\sigma _r^\prime = \sigma _{{\rm{h}}0}^\prime + \left( {\sigma _{{\rm{rp}}}^\prime - \sigma _{{\rm{h}}0}^\prime } \right){{\left( {\frac{{{r_{\rm{p}}}}}{r}} \right)}^2}}\\ {\sigma _\theta ^\prime = \sigma _{{\rm{h}}0}^\prime - \left( {\sigma _{{\rm{rp}}}^\prime - \sigma _{{\rm{h}}0}^\prime } \right){{\left( {\frac{{{r_{\rm{p}}}}}{r}} \right)}^2}}\\ {\sigma _{\rm{v}}^\prime = \sigma _{{\rm{v}}0}^\prime } \end{array}} \right. $ | (17) |
式中σ′rp为弹塑性边界处的径向有效应力。
由式(17)可以看出,弹性区平均有效应力p′在扩张过程中保持不变,即
| $ {\rm{D}}p' = 0 $ | (18) |
因此,在柱孔扩张过程中,体积应变增量在弹性区等于0,即
| $ {\rm{d}}\varepsilon _v^{\rm{e}} = \frac{{\kappa {\rm{d}}p'}}{{(1 + e)p'}} = 0 $ | (19) |
塑性区内的3个总主应变增量Dεr、Dεθ和Dεz可以分解为弹性分量和塑性分量,即
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{D}}{\varepsilon _r} = {\rm{D}}\varepsilon _r^{\rm{e}} + {\rm{D}}\varepsilon _r^{\rm{p}}}\\ {{\rm{D}}{\varepsilon _\theta } = {\rm{D}}\varepsilon _\theta ^{\rm{e}} + {\rm{D}}\varepsilon _\theta ^{\rm{p}}}\\ {{\rm{D}}{\varepsilon _z} = {\rm{D}}\varepsilon _z^{\rm{e}} + {\rm{D}}\varepsilon _z^{\rm{p}}} \end{array}} \right. $ | (20) |
式中:Dεre、Dεθe和Dεze为3个主弹性应变增量,可由式(15)计算;Dεrp、Dεθp和Dεzp为3个主塑性应变增量。根据相关联的流动准则,任意一点土体的塑性应变增量为
| $ {\rm{D}}\mathit{\varepsilon }_{ij}^{\rm{p}} = \mathit{\Lambda }\frac{{\partial f}}{{\partial {\sigma _{ij}}}} $ | (21) |
式中:Dεijp为塑性应变增量,Λ为一个塑性乘子。
由于Dp′y是s和p′0y的函数,在排水条件下,s为常数,即Ds=0,屈服函数f的全微分可表示为
| $ {\rm{D}}f = \frac{{\partial f}}{{\partial p'}}{\rm{D}}p' + \frac{{\partial f}}{{\partial q}}{\rm{D}}q + \frac{{\partial f}}{{\partial p_{\rm{y}}^\prime }}\frac{{\partial p_{\rm{y}}^\prime }}{{\partial p_{0{\rm{y}}}^\prime }}{\rm{D}}p_{0{\rm{y}}}^\prime = 0 $ | (22) |
根据硬化准则,可得
| $ {\rm{D}}p_{0{\rm{y}}}^\prime = \frac{{(1 + e)p_{0{\rm{y}}}^\prime }}{{\lambda (0) - \kappa }}\mathit{\Lambda }\frac{{\partial f}}{{\partial p'}} $ | (23) |
联立式(22)和(23),可得
| $ {\rm{\Lambda }} = - \frac{{\frac{{\partial f}}{{\partial p'}}{\rm{D}}p' + \frac{{\partial f}}{{\partial q}}{\rm{D}}q}}{{\frac{{\partial f}}{{\partial p'}}\frac{{\partial f}}{{\partial p_{\rm{y}}^\prime }}\frac{{\partial p_{\rm{y}}^\prime }}{{\partial p_{0{\rm{y}}}^\prime }}\frac{{(1 + e)p_{0{\rm{y}}}^\prime }}{{\lambda (0) - \kappa }}}} $ | (24) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial f}}{{\partial p'}} = {M^2}\left( {2p' - p_{\rm{y}}^\prime } \right)}\\ {\frac{{\partial f}}{{\partial q}} = 2q}\\ {\frac{{\partial f}}{{\partial p_{\rm{y}}^\prime }} = - {M^2}p'}\\ {\frac{{\partial p_{\rm{y}}^\prime }}{{\partial p_{0{\rm{y}}}^\prime }} = \frac{{\lambda (0) - \kappa }}{{\lambda (s) - \kappa }}{{\left( {\frac{{p_{0{\rm{y}}}^\prime }}{{p_{\rm{n}}^\prime }}} \right)}^{\frac{{\lambda (0) - \lambda (s)}}{{\lambda (s) - \kappa }}}}} \end{array}} \right. $ | (25) |
联立式(3)和(21),主塑性应变增量可用矩阵形式表示为
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{D}}\varepsilon _r^{\rm{p}}}\\ {{\rm{D}}\varepsilon _\theta ^{\rm{p}}}\\ {{\rm{D}}\varepsilon _z^{\rm{p}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {ya_r^2}&{y{a_r}{a_\theta }}&{y{a_r}{a_z}}\\ {y{a_\theta }{a_r}}&{ya_\theta ^2}&{y{a_\theta }{a_z}}\\ {y{a_z}{a_r}}&{y{a_z}{a_\theta }}&{ya_z^2} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{D}}\sigma _r^\prime }\\ {{\rm{D}}\sigma _\theta ^\prime }\\ {{\rm{D}}\sigma _z^\prime } \end{array}} \right] $ | (26) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {y = \frac{{\lambda (s) - \kappa }}{{{M^4}p'\left( {2p' - {p_{\rm{y}}}} \right)(1 + e)p_{0{\rm{y}}}^\prime }}{{\left( {\frac{{p_{\rm{n}}^\prime }}{{p_{0{\rm{y}}}^\prime }}} \right)}^{\frac{{\lambda (0) - \lambda (s)}}{{\lambda (s) - \kappa }}}}}\\ {{a_r} = \frac{{\partial f}}{{\partial \sigma _r^\prime }} = \frac{{{M^2}\left( {2p' - p_{\rm{y}}^\prime } \right)}}{3} + 3\left( {\sigma _r^\prime - p'} \right)}\\ {{a_\theta } = \frac{{\partial f}}{{\partial \sigma _\theta ^\prime }} = \frac{{{M^2}\left( {2p' - p_{\rm{y}}^\prime } \right)}}{3} + 3\left( {\sigma _\theta ^\prime - p'} \right)}\\ {{a_z} = \frac{{\partial f}}{{\partial \sigma _z^\prime }} = \frac{{{M^2}\left( {2p' - p_{\rm{y}}^\prime } \right)}}{3} + 3\left( {\sigma _z^\prime - p'} \right)} \end{array}} \right. $ | (27) |
联立式(11)、(15)、(20)和(26),并转置,该问题的弹塑性本构关系用拉格朗日形式表示为
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{D}}\sigma _r^\prime }\\ {{\rm{D}}\sigma _\theta ^\prime }\\ {{\rm{D}}\sigma _z^\prime }\\ {{\rm{D}}e} \end{array}} \right] = \frac{1}{\mathit{\Delta }}\left[ {\begin{array}{*{20}{c}} {{b_{rr}}}&{{b_{r\theta }}}&{{b_{rz}}}&0\\ {{b_{\theta r}}}&{{b_{\theta \theta }}}&{{b_{\theta z}}}&0\\ {{b_{zr}}}&{{b_{z\theta }}}&{{b_{zz}}}&0\\ 0&0&0&{\frac{{\mathit{\Delta }e}}{{(1 + \zeta )\chi - {S_{\rm{r}}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\rm{D}}{\varepsilon _r}}\\ {{\rm{D}}{\varepsilon _\theta }}\\ {{\rm{D}}{\varepsilon _z}}\\ {{\rm{D}}{S_{\rm{r}}}} \end{array}} \right] $ | (28) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\rm{\Delta }} = (1 + \mu )\left[ {(1 - \mu )Ey\left( {a_r^2 + a_\theta ^2 + a_z^2} \right) + } \right.\\ \left. {\;\;\;\;\;\;2\mu Ey\left( {{a_r}{a_\theta } + {a_r}{a_z} + {a_\theta }{a_z}} \right) + 1 - \mu - 2{\mu ^2}} \right] \end{array}\\ {{b_r} = E\left[ {Ey\left( {a_\theta ^2 + 2\mu {a_\theta }{a_z} + a_z^2} \right) + 1 - {\mu ^2}} \right]}\\ {{b_{\theta \theta }} = E\left[ {Ey\left( {a_r^2 + 2\mu {a_r}{a_z} + a_z^2} \right) + 1 - {\mu ^2}} \right]}\\ {{b_{zz}} = E\left[ {Ey\left( {a_r^2 + 2\mu {a_r}{a_\theta } + a_\theta ^2} \right) + 1 - {\mu ^2}} \right]}\\ {{b_{r\theta }} = {b_{\theta r}} = E\left[ {\mu + {\mu ^2} + Ey\left( {\mu a_z^2 - {a_r}{a_\theta } - \mu {a_r}{a_z} - \mu {a_\theta }{a_z}} \right)} \right]}\\ {{b_{rz}} = {b_{zr}} = E\left[ {\mu + {\mu ^2} + Ey\left( {\mu a_\theta ^2 - {a_r}{a_z} - \mu {a_r}{a_\theta } - \mu {a_\theta }{a_z}} \right)} \right]}\\ {{b_{\theta z}} = {b_{z\theta }} = E\left[ {\mu + {\mu ^2} + Ey\left( {\mu a_r^2 - {a_\theta }{a_z} - \mu {a_r}{a_\theta } - \mu {a_r}{a_z}} \right)} \right]} \end{array}} \right. $ | (29) |
上述方程中存在σ′r、σ′θ、σ′z、e和Sr5个未知数,未能直接求解,需要引入平衡微分方程(式(1))联立求解。但平衡方程用欧拉形式表示,而本构矩阵用拉格朗日形式表示,因此,需要引入Chen等[15]提出的辅助变量ξ,将欧拉系转化到拉格朗日系下。ξ可表示为
| $ \xi = \frac{{{u_{\rm{r}}}}}{r} = \frac{{r - {r_0}}}{r} $ | (30) |
式中ur为径向位移。
对于柱孔扩张问题,其竖向应变Dεz=0,因此,体应变增量Dεv=Dεθ+Dεr;利用辅助变量,根据对数应变的定义,应变分量可表示为
| $ {\rm{D}}{\varepsilon _\theta } = - \frac{{{\rm{D}}r}}{r} = - \frac{{{\rm{D}}\xi }}{{1 - \xi }} $ | (31) |
| $ {\rm{D}}{\varepsilon _r} = {\rm{D}}{\varepsilon _v} - {\rm{D}}{\varepsilon _\theta } = - \frac{{{\rm{D}}e}}{{1 + e}} + \frac{{{\rm{D}}\xi }}{{1 - \xi }} $ | (32) |
将辅助变量代入平衡方程,平衡方程可以用拉格朗日形式表示为
| $ \frac{{{\rm{D}}\sigma _r^\prime }}{{{\rm{D}}\xi }}\frac{1}{r}\left[ {1 - \xi - \frac{{1 + {e_0}}}{{(1 + e)(1 - \xi )}}} \right] + \frac{{\sigma _r^\prime - \sigma _\theta ^\prime }}{r} = 0 $ | (33) |
将式(31)和(32)代入式(28)并联立式(33),可组成求解排水条件下非饱和土中柱孔扩张问题的方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{D}}e}}{{{\rm{D}}\xi }} = \left[ {{b_{rr}} - {b_{r\theta }} + {\rm{\Delta }}\left( {\sigma _r^\prime - \sigma _\theta ^\prime } \right)} \right]\frac{{1 + e}}{{(1 - \xi ){b_{rr}}}}}\\ {\frac{{{\rm{D}}\sigma _r^\prime }}{{{\rm{D}}\xi }} = \frac{{{b_{rr}} - {b_{r\theta }}}}{{{\rm{\Delta }}(1 - \xi )}} - \frac{{{b_{rr}}}}{{{\rm{\Delta }}(1 + e)}}\frac{{{\rm{D}}e}}{{{\rm{D}}\xi }}}\\ {\frac{{{\rm{D}}\sigma _\theta ^\prime }}{{{\rm{D}}\xi }} = \frac{{{b_{\theta r}} - {b_{\theta \theta }}}}{{{\rm{\Delta }}(1 - \xi )}} - \frac{{{b_{\theta r}}}}{{{\rm{\Delta }}(1 + e)}}\frac{{{\rm{D}}e}}{{{\rm{D}}\xi }}}\\ {\frac{{{\rm{D}}\sigma _z^\prime }}{{{\rm{D}}\xi }} = \frac{{{b_{zz}} - {b_{z\theta }}}}{{{\rm{\Delta }}(1 - \xi )}} - \frac{{{b_{zr}}}}{{{\rm{\Delta }}(1 + e)}}\frac{{{\rm{D}}e}}{{{\rm{D}}\xi }}}\\ {\frac{{{\rm{D}}{S_{\rm{r}}}}}{{{\rm{D}}\xi }} = \frac{{(1 + \zeta )\chi - {S_{\rm{r}}}}}{e}\frac{{{\rm{D}}e}}{{{\rm{D}}\xi }}} \end{array}} \right. $ | (34) |
根据连续性条件,在弹塑性交界面应保持弹性区的性质:平均应力保持不变,即Δp′=0。因此,在弹塑性交界面(r=rp)的平均有效应力等于初始值,即
| $ p'\left( {{\xi _{\rm{p}}}} \right) = p_0^\prime $ | (35) |
将上式代入屈服函数式(3),并考虑非饱和土先期固结压力的影响,如图 2所示,可将弹塑性交界面的偏应力表示为
| $ q\left( {{\xi _{\rm{p}}}} \right) = Mp_0^\prime \sqrt {R\left[ {1 + \frac{1}{{{M^2}}}{{\left( {\frac{{{q_0}}}{{p_0^\prime }}} \right)}^2}} \right] - 1} $ | (36) |
式中:R=p′y0/p′a为非饱和土的各向同性固结比,p′y0为最大各向同性平均预固结应力,p′a为初始屈服线与横轴相交处的平均有效应力,如图 2所示。
根据式(17),弹塑性交界处有效应力为
| $ \left\{ {\begin{array}{*{20}{l}} {\sigma _r^\prime \left( {{\xi _{\rm{p}}}} \right) = \sigma _{{\rm{h}}0}^\prime + \frac{{\sqrt 3 }}{3}\sqrt {q{{\left( {{\xi _{\rm{p}}}} \right)}^2} - {{\left( {\sigma _{{\rm{h}}0}^\prime - \sigma _{{\rm{v}}0}^\prime } \right)}^2}} }\\ {\sigma _\theta ^\prime \left( {{\xi _{\rm{p}}}} \right) = \sigma _{{\rm{h}}0}^\prime - \frac{{\sqrt 3 }}{3}\sqrt {q{{\left( {{\xi _{\rm{p}}}} \right)}^2} - {{\left( {\sigma _{{\rm{h}}0}^\prime - \sigma _{{\rm{v}}0}^\prime } \right)}^2}} }\\ {\sigma _z^\prime \left( {{\xi _{\rm{p}}}} \right) = \sigma _{{\rm{v}}0}^\prime } \end{array}} \right. $ | (37) |
从弹性解和连续性条件可知,弹塑性交界面处土体孔隙比e(ξp)和饱和度Sr(ξp)分别等于初始值,即
| $ e\left( {{\xi _{\rm{p}}}} \right) = {e_0} $ | (38) |
| $ {S_{\rm{r}}}\left( {{\xi _{\rm{p}}}} \right) = {S_{{\rm{r}}0}} $ | (39) |
另外,辅助变量ξp的初始值可表示为
| $ {\xi _0} = {\xi _{\rm{p}}} = \frac{{{u_{\rm{r}}}\left( {{\xi _{\rm{p}}}} \right)}}{{r\left( {{\xi _{\rm{p}}}} \right)}} = \frac{{{\sigma _{\rm{r}}}\left( {{\xi _{\rm{p}}}} \right) - {\sigma _{{\rm{h}}0}}}}{{2{G_0}}} $ | (40) |
至此,弹塑性交界面处的基本未知量都已确定,所有控制方程都表示为辅助变量ξ的函数。因此,方程求解后需将辅助变量ξ与径向坐标r进行转换:
| $ \frac{r}{a} = \exp \left\{ {\int_{{\xi _{\rm{a}}}}^\xi {\frac{{{\rm{d}}\xi }}{{1 - \xi - \left( {1 + {e_0}} \right)/[(1 + e)(1 - \xi )]}}} } \right\} $ | (41) |
本节中,将基质吸力和超固结比对柱孔扩张的响应特性进行了研究,以探究扩张过程中柱孔周围应力的分布和饱和度的变化等,所选参数如表 1所示。
| 表 1 土体参数取值 Tab. 1 Soil parameters for example analyses |
当土体呈饱和状态时,土体吸力为0。因此,为了验证本文所提出的解答,可假设基质吸力s=0,χ=1,使本文解答退化至饱和土情况,并与Chen等[15]提出的饱和土柱孔扩张排水解进行对比,其中初始比体积υ0取值与文献[15]相同。图 4(a)为柱孔扩张过程中不同超固结比下的扩孔压力曲线对比,图 4(b)~(d)分别为a/a0=2时柱孔周围土体应力及比体积的径向变化及应力路径在p′-q和p′-υ平面上投影的对比。可以看出,当吸力等于0时,本文解答与文献[15]的饱和土柱孔扩张解答基本相同,证明本文解对于排水情况的求解是有效的。同时,由4(a)可知,随着孔径的增大,扩孔压力先快速增大,当柱孔扩大至约2倍初始孔径时,扩孔压力增速放缓,并逐渐趋于恒定值。因此,取2倍初始孔径(a/a0=2)为当前柱孔扩张状态进行分析。
4.2 敏感性分析图 5为不同基质吸力和超固结比条件下的扩张- 压力曲线。可以看出,当a/a0 < 2时,扩张压力显著增长;之后,扩孔压力随着孔径的增大缓慢增大,最终接近定值。同时,随着吸力和超固结比增大,扩孔压力明显增大,表明吸力和超固结比对扩孔压力具有显著影响。这可能是由于吸力和先期固结压力分别对非饱和土的平均有效应力和屈服应力具有增强作用,从而有效增强土体的强度。
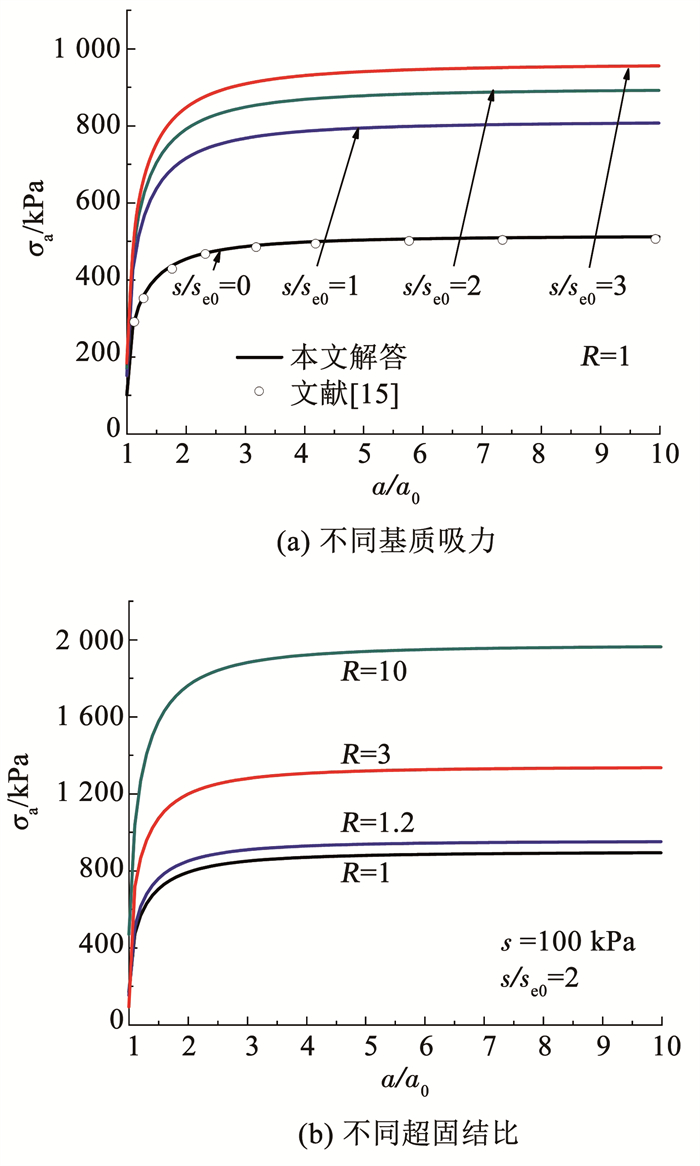
|
图 5 扩张- 压力曲线 Fig. 5 Expansion-pressure curves |
图 6探究了a/a0=2时非饱和土中不同超固结比下基质吸力对扩孔压力的影响(初始地应力取值与R=1时相同)。可以看出,当吸力较小(s/se0 < 1) 时,扩孔压力随着吸力的增长较快;吸力值进一步增大到s/se0>1时,扩孔压力的增长放缓,扩孔压力斜率发生突变,即吸力对扩孔压力的增强作用降低。由Bishop的非饱和土有效应力原理可知,这是吸力对土体有效应力的贡献(有效应力参数)随着吸力的增大而降低导致的。
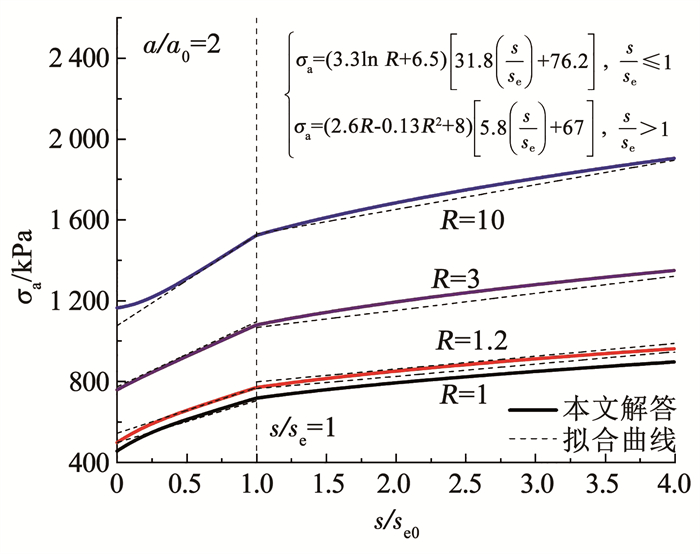
|
图 6 不同超固结比下扩孔压力随基质吸力的变化 Fig. 6 Expanding pressure curves with matric suction under different over-consolidation ratios |
同时,柱孔周围土体的应力- 应变响应(见图 5、6)常被用于解释原位试验,如静力触探试验(CPT)和旁压试验(PMT)。在大应变的假设下,孔壁处的应力σa接近一个极限值,该现象可用来解释CPT的锥尖阻力和PMT的扩孔压力。值得注意的是,σa随着基质吸力的增大而增大,且重超固结土的扩孔压力明显大于正常固结土,即吸力和超固结比能够显著增加原位试验圆孔扩张所需的压力。因此,非饱和土的原位试验过程中,如果不能正确地考虑吸力对孔壁极限压力的影响,易将吸力对极限压力的贡献误当作土体自身强度的贡献,从而导致土体强度参数的过高估计。为了加强理论分析,建立了扩孔压力与吸力、超固结比间的拟合公式。由于扩孔压力曲线与吸力基本呈线性关系,但在进气值处分段,将扩孔压力曲线在进气值处分段进行线性拟合,如式(42)所示,拟合曲线的相关系数r2∈[0.994 2, 0.999 7]。
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{a}}} = (3.3\ln R + 6.5)\left[ {31.8\left( {\frac{s}{{{s_{\rm{e}}}}}} \right) + 76.2} \right], \frac{s}{{{s_{\rm{e}}}}} \le 1}\\ {{\sigma _{\rm{a}}} = \left( {2.6R - 0.13{R^2} + 8} \right)\left[ {5.8\left( {\frac{s}{{{s_{\rm{e}}}}}} \right) + 67} \right], \frac{s}{{{s_{\rm{e}}}}} > 1} \end{array}} \right. $ | (42) |
图 7给出了a/a0=2时,常吸力(s/se0=2)和无吸力状态下,不同超固结比柱孔周围径向应力σ′r、切向应力σ′θ、竖向应力σ′z和比体积υ沿归一化半径方向的分布曲线。结果显示,无论原位应力状态如何,扩张后σ′r和σ′θ分别成为大主应力和小主应力,且σ′r和σ′z在孔壁附近随着径向距离增加显著降低,这意味着孔壁处土体仍未达到临界状态。此外,可以看出,超固结比增大,孔壁处应力和比体积增大,柱孔周围塑性区减小,弹性区增大。这可能是超固结比增强了土的屈服应力,使土体的屈服面增大的结果。
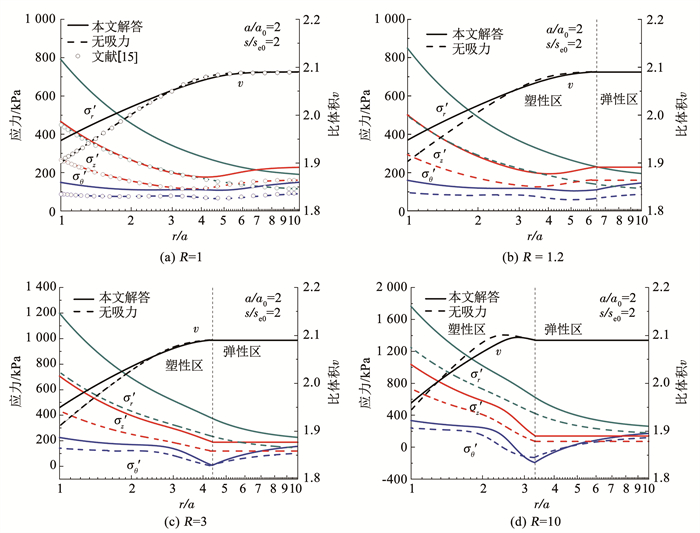
|
图 7 孔周土体应力及比体积的径向变化 Fig. 7 Distribution of stress components and specific volume around cavity along radial distance |
为了更直观地展现孔壁处土体应力路径,将其在p′-q平面上投影,如图 8所示,图中O点、Y点、C点分别对应初始应力点、屈服应力点和当前临界应力点。可以看出,非饱和土与饱和土的应力路径相似。正常固结土(R=1)和轻超固结土(R=1.2)的应力路径偏离初始屈服曲线,向右直接逼近CSL,在整个扩张过程中经历应变硬化。而中超固结土(R=3)和重超固结土(R=10)的应力路径跨越CSL垂直移动到初始屈服面,而后向右逼近CSL,表明其在弹性阶段平均有效应力保持不变,先发生应变软化然后发生应变硬化。
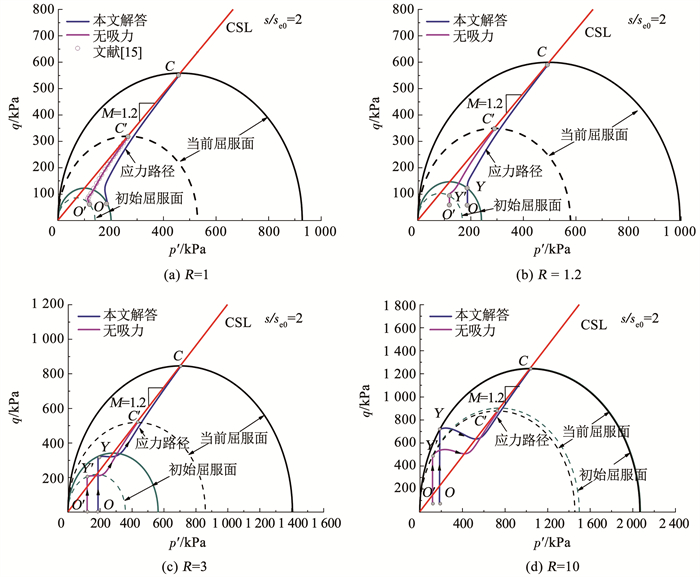
|
图 8 p′-q平面内应力路径 Fig. 8 Stress path in p′-q plane |
上述现象也能通过应力路径在p′-υ平面上投影看出,如图 9绘制了a/a0=2时不同超固结比下吸力的大小对应力路径的影响曲线,柱孔的扩张和收缩可以通过比体积υ的增大和减小来反映。弹性区的p′和υ均为常数,其应力路径为初始值对应的一个点。而塑性区,由图 8(a)和9(a)可知,正常固结土在扩张初始阶段,p′有所减小,这是加载初始阶段竖向有效应力σ′z减小为中主应力导致的。同时,当土体超固结比较小时,随着p′增大,υ快速减小;而适度固结土(R =3),υ先缓慢减小,而后快速减小到CSL;对于重超固结土(R=10),υ随着p′的增大先增大后减小。因此,柱孔扩张过程中,超固结比较小的土体屈服面始终扩张,而重超固结土的屈服面先收缩,然后在排水过程中扩张。同时可以注意到,重超固结土比体积在塑性区随着p′的增大呈先增大后减小的变化趋势,说明扩张挤土过程中出现了剪胀现象。
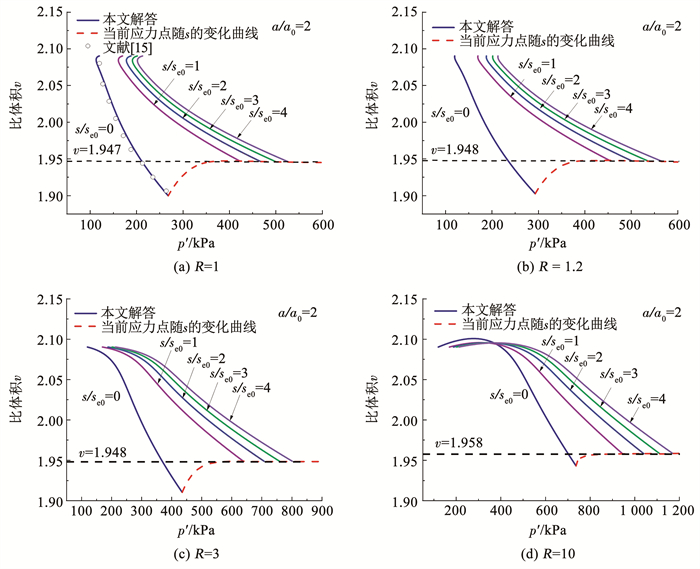
|
图 9 不同吸力下p′-υ平面内应力路径 Fig. 9 Stress path in p′-υ plane under different suctions |
另外,对比不同基质吸力下的应力路径可知,随着吸力的增大,柱孔扩张到相同程度所需的平均有效应力p′越大,土体达到临界状态时所对应的p′和υ也越大,即土体的CSL应该是向右移动了,这一现象也能通过图 7看出。本解答预测的主应力高于无吸力时的主应力,比体积的变化量小于无吸力时的比体积变化量,这可能是土体出现了吸力硬化现象导致的。另外,值得注意的是,当s较小时,对υ的影响很大,当超过某一范围(s/se0≥1),对υ的影响降低,比体积υ基本稳定在1.95,即吸力硬化的效果随着吸力的增大而趋于稳定。
为了展现常吸力柱孔扩张过程中饱和度的非线性响应,图 10绘制了不同基质吸力和超固结比下孔壁处饱和度Sr随孔径的变化曲线。值得注意的是,非饱和土柱孔扩张过程中,保持吸力不变时,饱和度会发生变化。由图 10(a)可知,当s/se0 < 1.5时,孔壁处饱和度随着孔径的增大而减小,且基质吸力越大,饱和度的变化范围越小;吸力继续增大,孔壁处饱和度曲线呈现先增大后减小的趋势;当吸力增大到s/se0>2.5时,饱和度随着孔径的增大而增大。由图 10(b)可知,吸力较低的土体(s/se0=1),超固结比越大,饱和度的变化范围越小;吸力较高时(s/se0=2),超固结比对饱和度大小的影响较小,但会影响饱和度峰值所对应的孔径大小。所有的饱和度变化曲线都表明a/a0 < 2时,扩孔程度对孔壁处饱和度的影响显著,之后饱和度趋于恒定值。
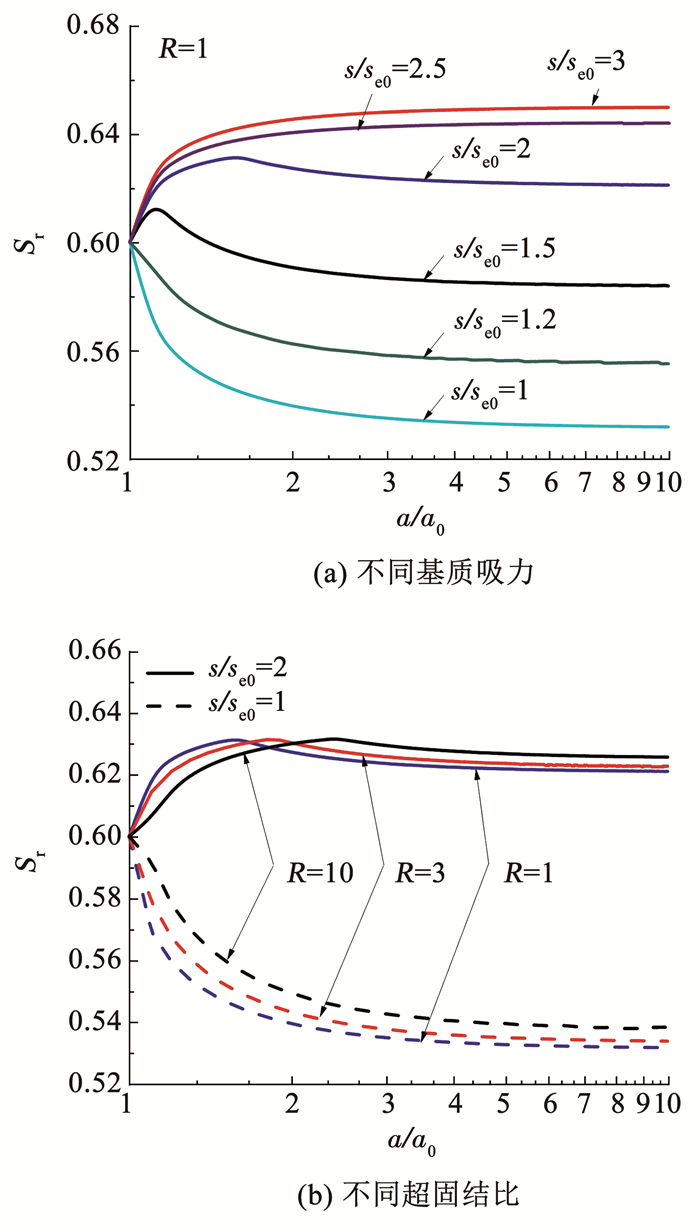
|
图 10 孔壁处饱和度随孔径的变化 Fig. 10 Curve of degree of saturation at cavity wall with cavity radius |
为了进一步探究扩孔过程中饱和度的变化,绘制了a/a0=2时正常固结土孔周饱和度径向分布曲线,如图 11所示。所有吸力值的饱和度变化曲线在径向位置r/a=6时,近似收敛到饱和度初值,因此,可认为孔周土体饱和度的影响范围为6倍孔径。从无限远处到孔壁处,当s/se0≤1时,土体饱和度不断减小;s增大到s/se0>1时,土体饱和度增长显著,且吸力越大饱和度增长越快,之后饱和度曲线会发生明显偏转,表明孔周一定范围内土体孔隙水排出且饱和度降低,此外,吸力越大曲线偏转位置越靠近孔壁。当s/se0=1.6时,孔壁处饱和度等于初始饱和度;当s/se0>2.5时,几乎呈现饱和度不断增大的趋势。这可能是由于吸力较低时,土体保水性较差,孔隙水顺利排出,此时土体饱和度主要受含水率控制,表现为扩孔过程中饱和度降低;吸力较高的土体保水性较强,远离孔壁处土体排水过程受到阻碍,土体饱和度变化主要受孔隙比变化的影响,饱和度随着孔隙比的减小而增大。而饱和度曲线发生偏转的现象可用式(8)~(10)和图 3来解释,由于在柱孔扩张过程中孔隙比减小,SWCC向右移动,相应的进气值se增大,进而影响有效应力参数的取值。当有效应力参数取值为1,即吸力对有效应力的贡献达到最大时,非饱和土气- 水界面与固体颗粒的接触角最小,排水通道连通,利于孔隙水排出,含水率降低,因此,饱和度减小,表现为饱和度曲线的偏转。而随着吸力取值增大,吸力对有效应力的贡献减小,不易排水通道连通,进而影响孔隙水的排出。因此,孔周一定范围内土体表现为吸力越大,饱和度曲线偏转点越靠近孔壁,直至无偏转点,饱和度不断增大。进一步由式(9)可知,如果取有效应力参数等于饱和度,此时ψ恒小于Sr,饱和度变化与孔隙比变化恒负相关,则圆孔在常吸力作用下扩张时,饱和度总是增大。因此,本文的解答也能很好地解释此前解答[16-17, 19]中饱和度随着扩孔半径增大不断增大的现象。这充分表明了本文解答模拟非饱和土圆孔扩张过程中水力耦合特性的先进性。
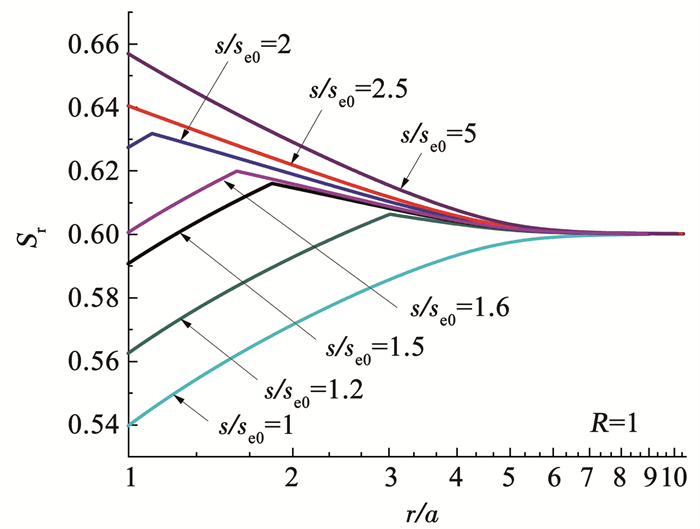
|
图 11 不同吸力下孔周土体饱和度径向分布 Fig. 11 Distribution of degree of saturation around cavity under different suctions |
结合非饱和临界状态模型并考虑非饱和土常吸力压缩过程中饱和度与孔隙比非线性相关的可能性,引入辅助变量,推导了非饱和土中排水柱孔扩张问题的精确半解析解。通过参数敏感性分析,得到以下结论:
1) 吸力对非饱和土扩张响应有显著影响,土体表现出吸力硬化特性。由于吸力的存在,柱孔周围应力、扩孔压力增大,而比体积降幅减小;吸力硬化的效果随着吸力的增大而趋于稳定。
2) 孔壁处饱和度在常吸力扩张过程中变化显著,当吸力较低时(s/se < 1.6),孔壁处饱和度较初始饱和度降低;且超固结比越大,饱和度变化范围越小。当吸力较高时(s/se>1.6),孔壁处饱和度高于初始饱和度;且吸力越高,孔壁处饱和度越高,而超固结比对饱和度的影响减弱。
3) 当吸力较低时,柱孔周围土体饱和度减小,饱和度变化主要受含水量变化的影响;当吸力较高时,柱孔周围土体饱和度升高,饱和度变化主要受孔隙比变化的影响。
| [1] |
MO Pinqiang, MARSHALL A M, YU Haisui. Interpretation of cone penetration test data in layered soils using cavity expansion analysis[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(1): 04016084. DOI:10.1061/(ASCE)GT.1943-5606.0001577 |
| [2] |
RUSSELL A R, KHALILI N. On the problem of cavity expansion in unsaturated soils[J]. Computational Mechanics, 2006, 37(4): 311. DOI:10.1007/s00466-005-0672-7 |
| [3] |
LI Lin, CHEN Shengli, ZHANG Zhongjie. Practical analytical approach for estimating long-term and set-up shaft resistance of prebored piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(10): 11. DOI:10.1061/(ASCE)GT.1943-5606.0002354 |
| [4] |
LI Lin, CHEN Shengli, ZHANG Zhongjie. A numerical study on installation effects and long-term shaft resistance of pre-bored piles in cohesive soils[J]. Transportation Research Record: Journal of the Transportation Research Board, 2019, 2673(3): 494. DOI:10.1177/0361198119835505 |
| [5] |
ZOU Jinfeng, YANG Tao, LING Wang, et al. A numerical stepwise approach for cavity expansion problem in strain-softening rock or soil mass[J]. Geomechanics and Engineering, 2019, 18(3): 225. DOI:10.12989/gae.2019.18.3.225 |
| [6] |
LIU Kai, CHEN Shengli. Analysis of cylindrical cavity expansion in anisotropic critical state soils under drained conditions[J]. Canadian Geotechnical Journal, 2019, 56(5): 675. DOI:10.1139/cgj-2018-0025 |
| [7] |
李林, 李镜培, 龚卫兵, 等. K0固结天然饱和黏土中柱孔扩张弹塑性解[J]. 哈尔滨工业大学学报, 2017, 49(6): 90. LI Lin, LI Jingpei, GONG Weibing, et al. Elasto-plastic solution to expansion of a cylindrical cavity in K0-consolidated natural saturated clay[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 90. DOI:10.11918/j.issn.0367-6234.201602038 |
| [8] |
YANG Changyi, CHEN Haohua, LI Jingpei. Drained cylindrical cavity expansion analysis in anisotropic soils considering 3D strength[J]. Geotechnique Letters, 2020, 10(2): 346. DOI:10.1680/jgele.19.00043 |
| [9] |
ZHUANG Peizi, YU Haisui. A unified analytical solution for elastic-plastic stress analysis of a cylindrical cavity in Mohr-Coulomb materials under biaxial in situ stresses[J]. Geotechnique, 2019, 69(4): 369. DOI:10.1016/j.tust.2021.104277 |
| [10] |
RUSSELL A R, KHALILI N. A unified bounding surface plasticity model for unsaturated soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(3): 181. DOI:10.1002/nag.475 |
| [11] |
RUSSELL A R, KHALILI N. On the problem of cavity expansion in unsaturated soils[J]. Computational Mechanics, 2006, 37(4): 311. DOI:10.1007/s00466-005-0672-7 |
| [12] |
YANG Hongwei, RUSSELL A R. Cavity expansion in unsaturated soils exhibiting hydraulic hysteresis considering three drainage conditions[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(18): 1975. DOI:10.1002/nag.2379 |
| [13] |
CHENG Yan, YANG Hongwei, SUN Dean. Cavity expansion in unsaturated soils of finite radial extent[J]. Computers and Geotechnics, 2018, 102: 216. DOI:10.1016/j.compgeo.2018.06.013 |
| [14] |
张亚国, 翟张辉, 梁发云, 等. 非饱和土中圆柱孔扩张问题不排水解答及吸力影响效应分析[J]. 岩土工程学报, 2021, 43(4): 734. ZHANG Yangguo, ZHAI Zhanghui, LIANG Fayun, et al. Solution of cylindrical cavity expansion in unsaturated soil under undrained conditions incorporating suction effects analysis[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(4): 734. DOI:10.11779/CJGE202104016 |
| [15] |
CHEN Shengli, ABOUSLEIMAN Y N. Exact drained solution for cylindrical cavity expansion in modified cam clay soil[J]. Geotechnique, 2013, 63(6): 510. DOI:10.1680/geot.11.P.088 |
| [16] |
CHEN Haohua, LI Lin, LI Jingpei, et al. Elastoplastic solutions for cylindrical cavity expansion in unsaturated soils[J]. Computers and Geotechnics, 2020, 123: 103569. DOI:10.1016/j.compgeo.2020.103569 |
| [17] |
TANG Jianhua, WANG Hui, LI Jingpei. A semi-analytical solution to spherical cavity expansion in unsaturated soils[J]. Geomechanics and Engineering, 2021, 25(4): 283. DOI:10.12989/gae.2021.25.4.283 |
| [18] |
SUN De'an, SHENG Daichao, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007, 39(3): 212. DOI:10.1016/j.mechmat.2006.05.002 |
| [19] |
YANG Changyi, LI Jingpei, LI Lin, et al. Expansion responses of a cylindrical cavity in overconsolidated unsaturated soils: a semi-analytical elastoplastic solution[J]. Computers and Geotechnics, 2021, 130. DOI:10.1016/j.compgeo.2020.103922 |
| [20] |
SUN Dean, SUN Wenjing, LI Xiang. Effect of degree of saturation on mechanical behaviour of unsaturated soils and its elastoplastic simulation[J]. Computers and Geotechnics, 2010, 37(5): 678. DOI:10.1016/j.compgeo.2010.04.006 |
| [21] |
王永洪, 张明义, 刘俊伟, 等. 基于非饱和黏性土桩土界面剪切特性试验研究[J]. 地下空间与工程学报, 2019, 15(5): 1465. WANG Yonghong, ZHANG Mingyi, LIU Junwei, et al. Experimental research on shear characteristics of pile-soil interface in unsaturated clayey soil[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(5): 1465. |
| [22] |
GALLIPOLI D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio[J]. Geotechnique, 2012, 62(7): 605. |
| [23] |
李涛, 李潇旋, 彭丽云. 常吸力下非饱和土水-力耦合循环塑性的模拟[J]. 哈尔滨工业大学学报, 2021, 53(5): 104. LI Tao, LI Xiaoxuan, PENG Liyun. Simulation of hydro-mechanical coupling cyclic plasticity of unsaturated soils under constant suction condition[J]. Journal of Harbin Institute of Technology, 2021, 53(5): 104. DOI:10.11918/201907209 |
| [24] |
KOLIJI A, LALOUI L, VULLIET L. Constitutive modeling of unsaturated aggregated soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(17): 1846. DOI:10.1002/nag.888 |
| [25] |
ROMERO E, DELLA V G, JOMMI C. An insight into the water retention properties of compacted clayey soils[J]. Geotechnique, 2011, 61(4): 313. DOI:10.1680/geot.2011.61.4.313 |
| [26] |
BURTON G J, SHENG Daichao, AIREY D. Experimental study on volumetric behaviour of Maryland clay and the role of degree of saturation[J]. Canadian Geotechnical Journal, 2014, 51(12): 1449. DOI:10.1139/cgj-2013-0332 |
| [27] |
PASHA A Y, KHOSHGHALB A, KHALILI N. Can degree of saturation decrease during constant suction compression of an unsaturated soil?[J]. Computers and Geotechnics, 2019, 106: 199. DOI:10.1016/j.compgeo.2018.10.015 |
| [28] |
赵成刚, 蔡国庆. 非饱和土广义有效应力原理[J]. 岩土力学, 2009, 30(11): 3232. ZHAO Chenggang, CAI Guoqing. Principle of generalized effective stress for unsaturated soils[J]. Rock and Soil Mechanics, 2009, 30(11): 3232. DOI:10.16285/j.rsm.2009.11.026 |
| [29] |
POURNAGHIAZAR M, RUSSELL A R, KHALILI N. The cone penetration test in unsaturated sands[J]. Geotechnique, 2013, 63(14): 1209. DOI:10.1680/geot.12.P.083 |
| [30] |
YANG Hongwei, RUSSELL A R. Cone penetration tests in unsaturated silty sands[J]. Canadian Geotechnical Journal, 2016, 53(3): 431. DOI:10.1139/cgj-2015-0142 |
| [31] |
MILLER G A, TAN N K, COLLINS R W, et al. Cone penetration testing in unsaturated soils[J]. Transportation Geotechnics, 2018, 17: 85. DOI:10.1016/j.trgeo.2018.09.008 |
| [32] |
BISHOP A W. The principle of effective stress[J]. Teknisk Ukeblad, 1959, 39: 859. |
| [33] |
KHALILI N, HABTE M A, ZARGARBASHI S. A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses[J]. Computers and Geotechnics, 2008, 35(6): 872. DOI:10.1016/j.compgeo.2008.08.003 |
| [34] |
KHALILI N, ZARGARBASHI S. Influence of hydraulic hysteresis on effective stress in unsaturated soils[J]. Geotechnique, 2010, 60(9): 729. DOI:10.1680/geot.09.T.009 |
| [35] |
PASHA A Y, KHOSHGHALB A, KHALILI N. Hysteretic model for the evolution of water retention curve with void ratio[J]. Journal of Engineering Mechanics, 2017, 143(7): 0401703. DOI:10.1061/(asce)em.1943-7889.0001238 |
 2022, Vol. 54
2022, Vol. 54