2. 山东理工大学 建筑工程学院,山东 淄博 255000
2. School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255000, Shandong, China
对路堤进行加筋能提高路堤的承载力,并增加路堤的稳定性,因此,加筋法被广泛应用到高速公路的路基处理中[1]。近年来,为了节约土地资源,中国一些高速公路的建设开始采用低路堤的设计方案,静载与运动荷载作用下加筋低路堤动力响应问题一直受到学者们的关注,许多学者运用双梁模型研究该问题。Zhao等[2]通过与有限元结果的对比,验证了双梁模型的合理性;Zhang等[3]基于双梁模型,给出了加筋低路堤受静载作用下的半解析解;Wu等[4-5]推导出两端简支情况下双梁模型受运动简谐荷载作用下的级数解;Hussein等[6-7]推导出了无限长双梁模型在运动荷载作用下的解析解。以上研究均将路堤填土及地基土假设成Winkler模型,但是Winkler模型过于简化,当路堤填土层或地基土层较厚时,采用黏弹性Winkler模型会产生较大误差[8],同时,在分析动力响应的问题时,由于忽略了土体的惯性力和剪切作用,黏弹性Winkler模型的结果与有限元的结果相差较大[9]。
由于黏弹性Winkler模型的不足,许多学者基于弹性连续介质模型对土体进行了研究。左迎辉等[10]求出了移动荷载作用下Gibson地基的动力响应;Yan等[11]基于层状弹性介质模型,给出了道路结构受移动荷载作用下的谱元解;刘飞禹等[12-14]对匀速荷载作用下加筋道路体系的动力响应问题进行了系统研究。这些研究仅考虑层间完全连续条件,且都是将车载假设成匀速移动荷载,实际上,车辆在行驶过程中存在大量的变速情况[15-16],如启动、刹车、超车等,将车载假设成变速荷载更为合理。Beskou和Muho等[17-18]分别利用Duhamel积分和Laplace变换的方法求出了变速荷载作用下地基上梁的动力响应,但是该研究中均假设初始条件为梁的挠度及其对时间的一阶偏导为0,这与真实情况不符。而有关变速荷载作用下加筋低路堤动力响应的研究还未见报道。
本文将车载假设成均布变速线荷载,将加筋低路堤视为层状各向同性弹性体,在荷载运动方向上无限长,筋材层与路堤填土层以及地基土层间采用Goodman模型[19]模拟非完全连续条件。利用Garlerkin法推导出Fourier变换域内变速荷载作用下加筋低路堤动力响应的控制方程。提出了一种模态叠加法和Duhamel积分相结合的方法,得出了变速荷载作用下加筋低路堤动力响应的数值解。利用数值结果,分析了层间接触条件、荷载加速度、路堤高度和筋材刚度对加筋低路堤动力响应的影响。
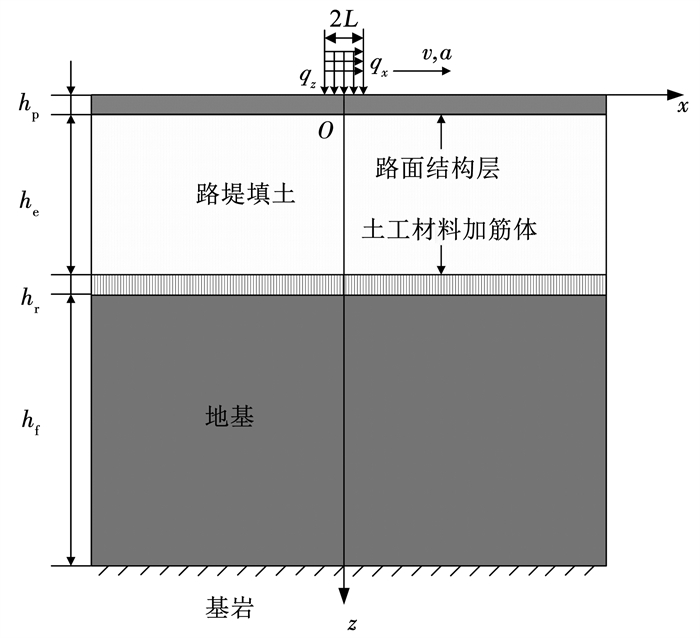
1 控制方程及求解已有研究[7, 9-11]均将土体假设成弹性模型,并基于平面应变假设分析道路结构的动力响应,本文在这些研究的基础上,提出如图 1所示的加筋低路堤计算模型示意,假设加筋低路堤系统从上至下依次分为路面结构层、路堤填土层、筋材、地基层和基岩。假设荷载分布宽度为2L,竖向荷载和水平向荷载大小为qz和qx,荷载以初速度v和加速度a沿x轴正向作匀变速运动。Sun等[20]的实验结果表明,将道路结构假设成层状弹性体是合理的,因此,直接将加筋路堤系统假设成层状弹性体,且每一层拥有不同的弹性参数:弹性模量E、泊松比ν、拉梅常数λ和G、厚度h、密度ρ。用不同下标表示各层的参数,路面结构层的下标是p,路堤填土层的下标是e,筋材的下标是r,地基土的下标是f。由于本文针对加筋低路堤进行研究,路堤填土高度取小于等于3 m,即he≤3 m。假设路面结构层与路堤填土层间完全连续,采用Goodman模型模拟筋材与路堤填土和地基土之间的非完全连续状态,即
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{\tau _{zx}}} \right)_{\rm{r}}^{{\rm{up }}} = - \left( {{k_{\rm{h}}}} \right)_{\rm{r}}^{{\rm{up }}}\left( {u_{\rm{r}}^{{\rm{up}}} - u_{\rm{e}}^{{\rm{bottom }}}} \right)}\\ {\left( {{\tau _{zx}}} \right)_{\rm{r}}^{{\rm{bottom }}} = \left( {{k_{\rm{h}}}} \right)_{\rm{r}}^{{\rm{bottom }}}\left( {u_{\rm{r}}^{{\rm{bottom }}} - u_{\rm{f}}^{{\rm{up }}}} \right)} \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{\sigma _z}} \right)_{\rm{r}}^{{\rm{up }}} = - \left( {{k_{\rm{v}}}} \right)_{\rm{r}}^{{\rm{up }}}\left( {w_{\rm{r}}^{{\rm{up }}} - w_{\rm{e}}^{{\rm{bottom }}}} \right)}\\ {\left( {{\sigma _z}} \right)_{\rm{r}}^{{\rm{bottom }}} = \left( {{k_{\rm{v}}}} \right)_{\rm{r}}^{{\rm{bottom }}}\left( {w_{\rm{r}}^{{\rm{bottom }}} - w_{\rm{f}}^{{\rm{up }}}} \right)} \end{array}} \right. $ | (2) |
|
图 1 移动荷载作用下加筋低路堤示意 Fig. 1 Schematic of low height reinforced embankment under moving load with variable velocity |
式中:上标up表示该层的上表面,上标bottom表示该层的下表面,(kh)rup和(kh)rbottom分别表示筋材的上下表面x方向上的接触刚度系数,(kv)rup和(kv)rbottom则表示筋材上下表面z方向上的接触刚度系数。不难看出,当接触刚度系数为0时,层间为完全滑动状态;当接触刚度系数趋近于无穷大时,层间为完全连续状态;当接触刚度系数为有限值时,层间为非完全连续状态。
根据平面应变假设,二维直角坐标系下弹性体Navier控制方程为
| $ \left\{ {\begin{array}{*{20}{l}} {(\lambda + 2G)\frac{{{\partial ^2}u}}{{\partial {x^2}}} + G\frac{{{\partial ^2}u}}{{\partial {z^2}}} + (\lambda + G)\frac{{{\partial ^2}w}}{{\partial x\partial z}} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}}}\\ {(\lambda + 2G)\frac{{{\partial ^2}w}}{{\partial {z^2}}} + G\frac{{{\partial ^2}w}}{{\partial {x^2}}} + (\lambda + G)\frac{{{\partial ^2}u}}{{\partial x\partial z}} = \rho \frac{{{\partial ^2}w}}{{\partial {t^2}}}} \end{array}} \right. $ | (3) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to \infty } \frac{{{\partial ^n}u}}{{\partial {x^n}}} = \mathop {\lim }\limits_{x \to \infty } \frac{{{\partial ^n}w}}{{\partial {x^n}}} = 0, n = 0, 1, 2, 3}\\ {{{\left. u \right|}_{z = {h_{\rm{p}}} + {h_{\rm{e}}} + {h_{\rm{r}}} + {h_{\rm{f}}}}} = {{\left. w \right|}_{z = {h_{\rm{p}}} + {h_{\rm{e}}} + {h_{\rm{r}}} + {h_{\rm{f}}}}} = 0} \end{array}} \right. $ | (4) |
定义x对变换域上β的Fourier变换及其逆变换为
| $ \left\{ {\begin{array}{*{20}{l}} {\bar u(\beta , z, t) = \int_{ - \infty }^{ + \infty } u (x, z, t){{\rm{e}}^{ - {\rm{i}}\beta x}}{\rm{d}}x}\\ {u(x, z, t) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } - \bar u(\beta , z, t){{\rm{e}}^{{\rm{i}}\beta x}}{\rm{d}}\beta }\\ {\bar w(\beta , z, t) = \int_{ - \infty }^{ + \infty } w (x, z, t){{\rm{e}}^{ - {\rm{i}}\beta x}}{\rm{d}}x}\\ {w(x, z, t) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {\bar w} (\beta , z, t){{\rm{e}}^{{\rm{i}}\beta x}}{\rm{d}}\beta } \end{array}} \right. $ | (5) |
对式(3)中的x进行Fourier变换,可得
| $ \left\{ {\begin{array}{*{20}{l}} {{f_1} = - (\lambda + 2G){\beta ^2}\bar u + G\frac{{{\partial ^2}\bar u}}{{\partial {z^2}}} + {\rm{i}}\beta (\lambda + G)\frac{{\partial \bar w}}{{\partial z}} - \rho \frac{{{\partial ^2}\bar u}}{{\partial {t^2}}} = 0}\\ {{f_2} = (\lambda + 2G)\frac{{{\partial ^2}\bar w}}{{\partial {z^2}}} - G{\beta ^2}\bar w + {\rm{i}}\beta (\lambda + G)\frac{{\partial \bar u}}{{\partial z}} - \rho \frac{{{\partial ^2}\bar w}}{{\partial {t^2}}} = 0} \end{array}} \right. $ | (6) |
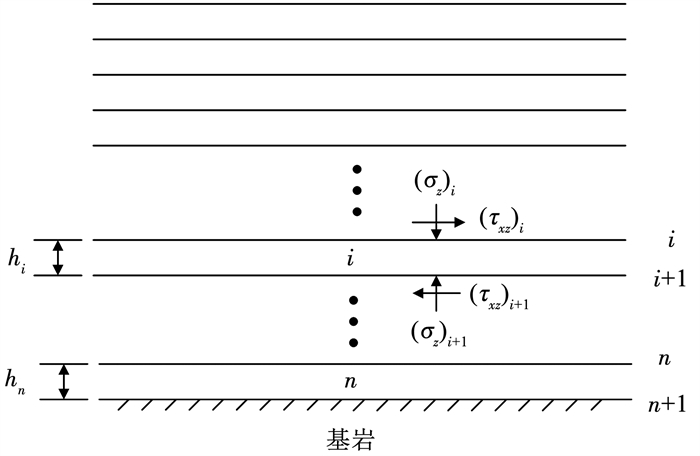
将加筋路堤沿厚度方向分层,如图 2所示。假设总共有n层,且每一层的位移呈线性变化,即
| $ \left\{ {\begin{array}{*{20}{l}} {u = {N_1}{u_i} + {N_2}{u_{i + 1}}}\\ {w = {N_1}{w_i} + {N_2}{w_{i + 1}}} \end{array}} \right. $ | (7) |
|
图 2 加筋路堤分层示意 Fig. 2 Layered reinforced embankment |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{N_i} = \frac{{{z_{i + 1}} - z}}{{{z_{i + 1}} - {z_i}}}}\\ {{N_{i + 1}} = \frac{{z - {z_i}}}{{{z_{i + 1}} - {z_i}}}} \end{array}} \right. $ | (8) |
根据Garlerkin法,有
| $ \int_0^{{h_i}} {{f_i}} {N_j}{\rm{d}}z = 0, i = 1, 2;j = 1, 2 $ | (9) |
假设每一层位移向量χi=[ui, -wi, ui+1, -wi+1]T,整体位移向量χ=[ui, -wi, …, un, -wn]T,则χi=[ui, -wi, ui+1, -wi+1]T,χ =[ui, -wi, …, un, -wn]T。利用上式得到第i层的计算结果为
| $ {\mathit{\boldsymbol{\bar M}}_i}{(\beta )_{4 \times 4}}\frac{{{{\rm{d}}^2}{{\mathit{\boldsymbol{\bar \chi }}}_i}(\beta , t)}}{{{\rm{d}}{t^2}}} + {\mathit{\boldsymbol{\bar K}}_i}{(\beta )_{4 \times 4}}{\mathit{\boldsymbol{\bar \chi }}_i}(\beta , t) = {\mathit{\boldsymbol{\bar F}}_i}(\beta , t) $ | (10) |
矩阵Mi和Ki的元素见附录。将各层按照文献[20]中的方式组装,即可得到加筋路堤系统在积分域上的动力响应控制方程:
| $ \begin{array}{c} \mathit{\boldsymbol{\bar M}}{(\beta )_{(2n + 4) \times (2n + 4)}}\frac{{{{\rm{d}}^2}\mathit{\boldsymbol{\bar \chi }}(\beta , t)}}{{{\rm{d}}{t^2}}} + \\ \mathit{\boldsymbol{\bar K}}{(\beta )_{(2n + 4) \times (2n + 4)}}\mathit{\boldsymbol{\bar \chi }}(\beta , t) = \mathit{\boldsymbol{\bar F}}(\beta , t) \end{array} $ | (11) |
其中
| $ \mathit{\boldsymbol{\bar F}} = {\left[ {{q_x}, {q_z}, 0, \cdots , 0} \right]^{\rm{T}}}\frac{{2\sin (\beta L)}}{\beta }{{\rm{e}}^{ - {\rm{i}}\beta \left( {tt + 0.5a{t^2}} \right)}} $ | (12) |
式(11)中矩阵M和K均为对称矩阵,可以通过模态叠加法[21]求解。定义式(11)的特征值矩阵及其对应模态组成的矩阵分别为ω和ϕ,同时,定义主质量矩阵和主刚度矩阵分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_{\rm{d}}} = {{\mathit{\boldsymbol{\phi}}} ^{\rm{T}}}\mathit{\boldsymbol{\bar M}}{\mathit{\boldsymbol{\phi}}} = {\rm{diag}}\left( {{\mathit{M}_{{\rm{d}}1}}, {\mathit{M}_{{\rm{d}}2}}, \cdots , {\mathit{M}_{{\rm{d}}(2n + 4)}}} \right)}\\ {{\mathit{\boldsymbol{K}}_{\rm{d}}} = {{\mathit{\boldsymbol{\phi}}} ^{\rm{T}}}\mathit{\boldsymbol{\bar K}}{\mathit{\boldsymbol{\phi}}} = {\rm{diag}}\left( {{K_{{\rm{d}}1}}, {K_{{\rm{d}}2}}, \cdots , {K_{{\rm{d}}(2n + 4)}}} \right)} \end{array}} \right. $ | (13) |
定义广义位移和广义应力为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\bar \chi }}}_{\rm{d}}} = {{\mathit{\boldsymbol{\phi}}} ^{ - 1}}\mathit{\boldsymbol{\bar \chi }}}\\ {{{\mathit{\boldsymbol{\bar F}}}_{\rm{d}}} = {{\mathit{\boldsymbol{\phi}}} ^{\rm{T}}}\mathit{\boldsymbol{\bar F}}} \end{array}} \right. $ | (14) |
则式(11)可以写成
| $ {\mathit{\boldsymbol{M}}_{\rm{d}}}\frac{{{{\rm{d}}^2}{{\mathit{\boldsymbol{\bar \chi }}}_{\rm{d}}}}}{{{\rm{d}}{t^2}}} + {\mathit{\boldsymbol{K}}_{\rm{d}}}{\mathit{\boldsymbol{\bar \chi }}_{\rm{d}}} = {\mathit{\boldsymbol{\bar F}}_{\rm{d}}} $ | (15) |
该方程为完全解耦的方程组,即可以写成
| $ {M_{{\rm{d}}i}}\frac{{{{\rm{d}}^2}{{\bar \chi }_{{\rm{d}}i}}}}{{{\rm{d}}{t^2}}} + {K_{{\rm{d}}i}}{\bar \chi _{{\rm{d}}i}} = {\bar F_{{\rm{d}}i}}, i = 1, 2, \cdots , 2n + 4 $ | (16) |
该方程组可以看成多个单自由度系统的受迫振动,它的解是对应的齐次方程满足初始条件的通解和满足零初始条件的特解之和。采用匀速荷载作用下加筋路堤动位移稳态响应作为初始条件[22],当荷载以初速度v匀速运动时,式(12)简化为
| $ \mathit{\boldsymbol{\bar F}} = {\left[ {{q_x}, {q_z}, 0, \cdots , 0} \right]^{\rm{T}}}\frac{{2\sin (\beta L)}}{\beta }{{\rm{e}}^{ - {\rm{i}}\beta ut}} $ | (17) |
此时式(11)存在稳态解,可以写成如下形式[21]
| $ \begin{array}{l} \mathit{\boldsymbol{\bar \chi }}(\beta , t) = {\left[ {\mathit{\boldsymbol{\bar K}}(\beta ) - {\beta ^2}{v^2}\mathit{\boldsymbol{\bar M}}(\beta )} \right]^{ - 1}} \cdot \\ {\left[ {{q_x}, {q_z}, 0, \cdots , 0} \right]^{\rm{T}}}\frac{{2\sin (\beta L)}}{\beta }{{\rm{e}}^{ - {\rm{i}}\beta vt}} \end{array} $ | (18) |
结合式(14),可得广义位移的初始值为
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\mathit{\boldsymbol{\bar \chi }}}_{\rm{d}}}(\beta , 0) = {{\mathit{\boldsymbol{\phi}}} ^{ - 1}}\mathit{\boldsymbol{\bar \chi }}(\beta , 0) = \frac{{2\sin (\beta L)}}{\beta } \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\phi}}} ^{ - 1}}{\left[ {\mathit{\boldsymbol{\bar K}}(\beta ) - {\beta ^2}{v^2}\mathit{\boldsymbol{\bar M}}(\beta )} \right]^{ - 1}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {{q_x}, {q_z}, 0, \cdots , 0} \right]^{\rm{T}}} \end{array}\\ \begin{array}{l} \frac{{{\rm{d}}{{\mathit{\boldsymbol{\bar \chi }}}_{\rm{d}}}(\beta , 0)}}{{{\rm{d}}t}} = {{\mathit{\boldsymbol{\phi}}} ^{ - 1}}\frac{{{\rm{d}}\mathit{\boldsymbol{\bar \chi }}(\beta , 0)}}{{{\rm{d}}t}} = - 2{\rm{i}}v\sin (\beta L) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\phi}}} ^{ - 1}}{\left[ {\mathit{\boldsymbol{\bar K}}(\beta ) - {\beta ^2}{v^2}\mathit{\boldsymbol{\bar M}}(\beta )} \right]^{ - 1}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {{q_x}, {q_z}, 0, \cdots , 0} \right]^{\rm{T}}} \end{array} \end{array}} \right. $ | (19) |
利用式(19)所得到的初始值求解式(16),可以求出荷载以初速度v、加速度a作匀变速运动时式(16)中广义位移在任意时刻的通解
| $ \begin{array}{l} {\left( {{{\bar \chi }_{{\rm{d}}i}}} \right)_{通解}}(\beta , t) = {{\bar \chi }_{{\rm{d}}i}}(\beta , 0)\cos \left( {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{{{M_{{\rm{d}}i}}}}{{{K_{{\rm{d}}i}}}}} \frac{{{\rm{d}}{{\bar \chi }_{{\rm{d}}i}}(\beta , 0)}}{{{\rm{d}}t}}\sin \left( {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} t} \right) \end{array} $ | (20) |
再利用Duhamel积分,可以得到广义位移在任意时刻的特解为
| $ {\left( {{{\bar \chi }_{{\rm{d}}\mathit{i}}}} \right)_{特解}}(\beta , t) = \frac{1}{{\sqrt {{M_{{\rm{d}}\mathit{i}}}{K_{{\rm{d}}i}}} }}\int_0^t{F_{{\rm{d}}i}}(\tau )\sin \left[ {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} (t - \tau )} \right]{\rm{d}}\tau $ | (21) |
结合式(20)和(21),可以得到广义位移在任意时刻的表达式为
| $ \begin{array}{l} {{\bar \chi }_{{\rm{d}}i}}(\beta , t) = {\left( {{{\bar \chi }_{{\rm{d}}i}}} \right)_{通解}}(\beta , t) + {\left( {{{\bar \chi }_{{\rm{d}}i}}} \right)_{特解}}(\beta , t) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\bar \chi }_{{\rm{d}}i}}(\beta , 0)\cos \left( {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{{{M_{{\rm{d}}i}}}}{{{K_{{\rm{d}}i}}}}} \frac{{{\rm{d}}{{\bar \chi }_{{\rm{d}}i}}(\beta , 0)}}{{{\rm{d}}t}}\sin \left( {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\sqrt {{M_{{\rm{d}}i}}{K_{{\rm{d}}i}}} }}\int_0^t{F_{{\rm{d}}i}}(\tau )\sin \left[ {\sqrt {\frac{{{K_{{\rm{d}}i}}}}{{{M_{{\rm{d}}i}}}}} (t - \tau )} \right]{\rm{d}}\tau \end{array} $ | (22) |
其中,i=1, 2, …, 2n+4。结合式(14),并采用Fourier逆变换,可以求出变速荷载作用下加筋路堤系统的动位移响应。再通过弹性力学几何方程和本构方程求出动应力响应。
2 数值验证采用两个算例验证本文方法的正确性。文献[10]给出了匀速荷载作用下有限弹性层竖向位移沿深度的分布,弹性层的计算参数为:剪切模量G=100 MPa,泊松比ν=0.45,厚度h=5 m,荷载qz=400 kPa,分布宽度2L=4 m,速度v=20 m/s。本文计算结果和文献[10]的结果如图 3所示,结果吻合很好。
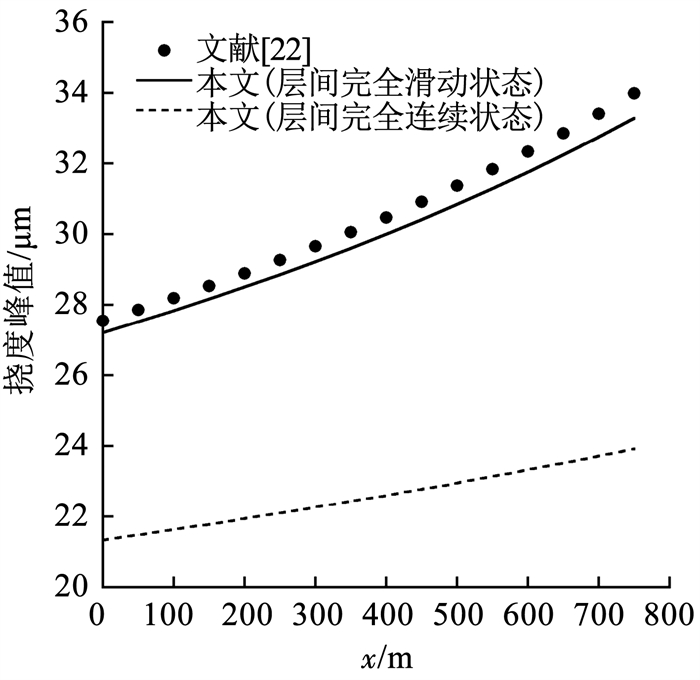
文献[22]给出了幅值qz=3 333 Pa、分布宽度2L=0.3 m的荷载从原点开始以初速度v=0、加速度a=3 m/s2运动的过程中,弹性地基上梁不同位置的动挠度峰值。本文将路面梁模拟为路面弹性层,其弹性模量Ep=3 100 MPa,厚度hp=0.3 m,假设路面弹性层的泊松比νp=0.49[2],用以模拟文献[22]中的路面梁;地基的弹性模量Ef=26.9 MPa,泊松比νf=0.3,厚度hf=3 m,约束地基的水平向位移为0, 只将地基分为一层,并假设路面层和地基层处于完全滑动状态,则本文计算的模型和文献[22]中的模型一致。本文计算的结果和文献[22]的结果如图 4所示。可以看出,层间完全滑动状态下本文的结果和文献[22]的结果几乎一致,仅有1.5%的误差,这是路面模型差异导致的。层间完全连续状态下的结果小于层间完全滑动状态下的结果,这个规律和文献[11]一致。从这两个算例可以看出,本文的方法正确可行。
3 数值分析已有文献大多将车载假设为匀速荷载作分析,且并未考虑水平向荷载的影响。本文将考虑荷载的变速,并考虑变速过程中荷载对路面表面产生的切向应力。根据JTG D50—2017《公路沥青路面设计规范》以及文献[3, 7],选取的参数见表 1。
| 表 1 加筋低路堤数值分析中的参数 Tab. 1 Parameters in numerical analysis of low height reinforced embankment |
引入反应地基土阻尼的因子ηf=0.1[12],则地基土的弹性常数可以写成
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _{\rm{f}}} = \frac{{{E_{\rm{f}}}\left( {1 + {\rm{i}}{\eta _{\rm{f}}}} \right){\nu _{\rm{f}}}}}{{\left( {1 + {\nu _{\rm{f}}}} \right)\left( {1 - 2{\nu _{\rm{f}}}} \right)}}}\\ {{G_{\rm{f}}} = \frac{{{E_{\rm{f}}}\left( {1 + {\rm{i}}{\eta _{\rm{f}}}} \right)}}{{2\left( {1 + {\nu _{\rm{f}}}} \right)}}} \end{array}} \right. $ | (23) |
根据文献[19],荷载分布宽度2L=0.24 m,根据标准轴载BZZ-100进行换算,可得竖向荷载qz=0.42 MN/m,初始中心位置为原点,沿x轴正方向以初速度v和加速度a作匀变速运动,由理论力学不难推出荷载对路面产生的切应力为
| $ {q_x} = \frac{{2L{q_z}a}}{{g2L}} = {q_z}\frac{a}{g} $ | (24) |
其中,a和g分别表示车辆的加速度和重力加速度,g=9.8 m/s2。本文计算时选取的初速度和加速度范围分别为v≤60 m/s和-3 m/s2≤a≤3 m/s2[22]。
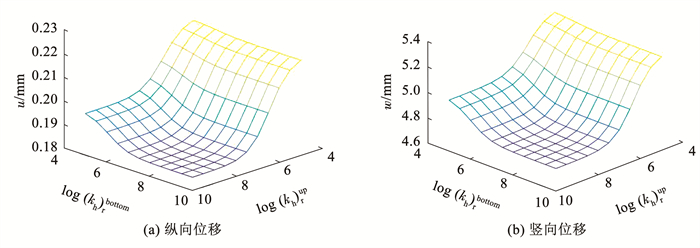
3.1 接触刚度系数对动力响应的影响图 5和6表示荷载以初速度v=20 m/s和不同的加速度从x=0运动至x=50 m时,在不同的接触刚度系数(kh)rup和(kh)rbottom条件下,路面结构层底部的最大位移。可以看出,对于荷载匀速运动的情况,当接触刚度系数(kh)rup,(kh)rbottom≥108时,位移的计算结果趋于稳定,说明此时层间为完全连续状态。随着接触刚度系数的降低,位移逐渐增加,当(kh)rup,(kh)rbottom≤105时, 位移同样趋于稳定,此时层间为完全滑动状态。在荷载匀速运动时,完全滑动状态下路面结构层底部纵向位移和竖向位移分别为完全连续状态下的1.19倍和1.12倍。在加速度为2 m/s2时,完全滑动状态下路面结构层底部纵向位移和竖向位移分别为完全连续状态下的10.83倍和1.13倍,说明筋材上下表面的层间接触状态对加筋路堤的变形影响很大,且变速状态下这种影响更加明显,同时, (kh)rup的影响比(kh)rbottom更大。由上述分析可知,层间接触状态对路面结构层底部的位移影响显著,在荷载变速时的影响更大,因此,在道路设计中,应对层间接触状态予以充分考虑,当层间接触状态不良时,会造成路面结构层底部纵向位移与竖向位移的增加,从而加重路面结构的疲劳[19],因此,应尽量使筋材上下表面处于完全连续状态。
|
图 5 荷载匀速时不同接触刚度系数下路面结构层底部动力响应 Fig. 5 Dynamic response at bottom of pavement with different contact stiffness under uniform moving load |

|
图 6 荷载变速时不同接触刚度系数下路面结构层底部动力响应 Fig. 6 Dynamic response at bottom of pavement with different contact stiffness under moving load with variable velocity |
图 7显示层间完全连续条件下,荷载以不同的初速度v和加速度a运动至x=50 m时,路面结构层底部的位移峰值。可以看出,纵向位移峰值和竖向位移峰值与加速度、初速度均呈正相关关系。纵向位移u受加速度影响较速度影响更大,且加速情况下纵向位移峰值比减速情况下位移峰值更大;相比最小竖向位移,本文计算的最大竖向位移增加了12.4%。竖向位移w受加速度的影响程度与初速度有关,当初速度为v=17.5 m/s时,a从-3 m/s2变化至3 m/s2时,位移峰值增幅为4.7%;而当初速度为32.5 m/s时,位移峰值增幅为5.8%,说明初速度越大,加速度对竖向位移峰值的影响越大,且加速的影响比减速的影响更大。

|
图 7 不同加速度条件下路面结构层底部动位移峰值 Fig. 7 Dynamic peak deflection at bottom of pavement under different acceleration conditions |
图 8和9为荷载以初速度v=30 m/s和不同的加速度运动至x=200 m时,路面结构层底部和地基土表面的应力分布(中心点x=200 m)。可以看出,当荷载的加速度为0时,切应力分布关于中心点反对称,竖向应力分布相对于中心轴左右对称;当荷载的加速度不为0时,应力分布关于中心点非对称,且随着荷载加速度的增加,应力峰值逐渐增加。对于剪切应力τxz,峰值出现的位置逐渐由中心点负方向移动至正方向,路面结构层底部和地基表面剪切应力的最大增幅分别可达29.4%和22.7%;对于正应力σz,最大压应力始终位于中心点,且随着加速度的增加,应力幅值逐渐增加,路面结构层底部和地基表面正应力的最大增幅分别为4.9%和4.4%。由此可见,加速度对路面结构层底部和地基表面的应力有很大影响,对剪应力影响更大,应予以充分考虑。

|
图 8 不同加速度条件下路面结构层底部应力分布 Fig. 8 Stress distribution on bottom of pavement under different acceleration conditions |

|
图 9 不同加速度条件下地基表面应力分布 Fig. 9 Stress distribution on foundation surface under different acceleration conditions |
图 10给出了荷载以相同的速度v=30 m/s和不同的加速度从初始位置运动至x=200 m的过程中,x=200 m正下方的路面结构层底部和地基表面动应力路径图。可以看出,路面结构层底部的动应力路径形状和地基表面的动应力路径形状不同。随着加速度的增加,路面结构层底部的动应力路径的大小增加,而地基表面的动应力路径不仅大小增加,也朝顺时针旋转。加速情况下地基表面的动应力路径明显大于匀速情况和减速情况。综上,加速荷载相较匀速荷载更容易导致地基土的不均匀沉降[23],应在道路设计时充分考虑加速度对道路沉降的影响。
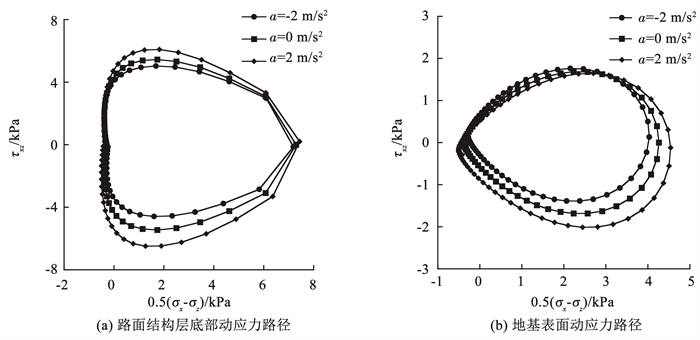
|
图 10 不同加速度条件下加筋低路堤动应力路径 Fig. 10 Dynamic stress paths of low height reinforced embankment under different acceleration conditions |
为方便分析应力在加筋低路堤内的应力传递规律,定义剪应力比τ为地基表面最大剪应力与路堤填土表面最大剪应力之比,定义正应力比σ为地基表面最大正应力与路堤填土表面最大正应力之比,即
| $ \left\{ {\begin{array}{*{20}{l}} {\tau = \frac{{\max \left( {{{\left. {{\tau _{xz}}} \right|}_{z = {h_{\rm{p}}} + {h_{\rm{e}}} + {h_{\rm{r}}}}}} \right)}}{{\max \left( {{{\left. {{\tau _{xz}}} \right|}_{z = {h_{\rm{p}}}}}} \right)}}}\\ {\sigma = \frac{{\max \left( {{{\left. {{\sigma _z}} \right|}_{z = {h_{\rm{p}}} + {h_{\rm{e}}} + {h_{\rm{r}}}}}} \right)}}{{\max \left( {{{\left. {{\sigma _z}} \right|}_{z = {h_{\rm{p}}}}}} \right)}}} \end{array}} \right. $ | (25) |
图 11显示荷载以初速度v=30 m/s和不同的加速度运动至x=200 m时,不同路堤高度下的剪应力比和正应力比。可以看出,随着路堤高度的减小,剪应力比和正应力比均增大,说明在低路堤的情况下,应力在路堤中的衰减较小。随着加速度的增加,正应力比逐渐增加,剪应力比先减小,后趋于稳定,这说明加速度对于正应力和剪应力在加筋低路堤中的衰减有一定的影响。

|
图 11 不同加速度条件下的应力比 Fig. 11 Stress ratio under different acceleration conditions |
图 12显示荷载以初速度v=30 m/s和加速度a=2 m/s2运动至x=200 m时,不同路堤高度、筋材刚度条件下的剪应力比和正应力比。可以看出,当筋材刚度一定时,随着路堤高度的增加,剪应力比和正应力比均减少,正应力比下降的幅度要大于剪应力比;随着筋材刚度的增加,剪应力比先增加后下降,正应力比一直下降,且都逐渐趋于稳定。对于加筋低路堤的情况,应力在路堤中的衰减较少,仍有很大一部分应力传递至地基表面。增大筋材刚度能有效增加应力的衰减,减少地基表面的应力。当路堤高度为1.5 m时,筋材刚度从10 MPa增加到290 MPa, 剪应力比减小47.9%,正应力比减小29%;当路堤高度为3 m时,剪应力比减小34.9%,正应力比减小20.6%。这说明增加筋材刚度可以导致加筋低路堤中应力的衰减,且这种影响随着路堤高度的减小而增加。因此,在加筋低路堤中,采用刚度较大的加筋材料,可有效减少传递至地基土表面的应力。
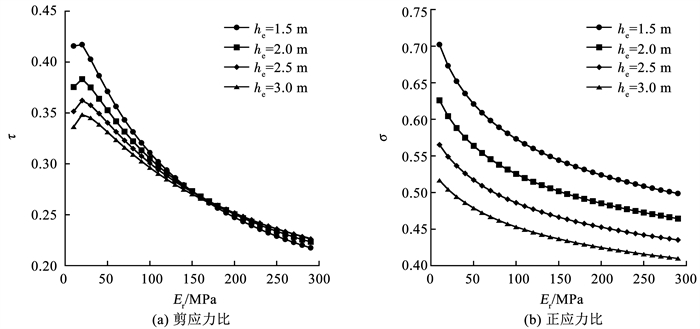
|
图 12 不同路堤高度、筋材刚度条件下的应力比 Fig. 12 Stress ratio under different embankment height and reinforcement stiffness conditions |
提出一种模态叠加法、Duhamel积分和Fourier逆变换相结合的方法,得到了加筋低路堤在变速荷载作用下动应力和动位移的数值解,通过与已有文献的计算结果对比,验证了本文方法的正确性,通过对加筋低路堤进行参数分析,得出了以下结论:
1) 筋材上下表面的接触刚度对加筋低路堤路面结构层底部的位移影响显著,尤其是对纵向位移的影响更明显,在荷载变速时这种影响更大。因此,在加筋低路堤的设计中,应尽量使筋材上下表面处于完全连续状态,以防止路面结构层过大的变形,减少路面结构的疲劳。
2) 相较减速荷载和匀速荷载,加速荷载会引起更大的位移响应和更大的应力峰值,而且路面结构层底部和地基表面的动应力路径更大,这主要是由速度的增加以及荷载变速时产生的水平应力导致。因此,在工程中应当充分考虑荷载变速的影响,尤其是加速荷载的影响。
3) 加速度对于正应力和剪应力在加筋路堤中的衰减有一定的影响。随着加速度的增加,正应力比逐渐增加,剪应力比先减小,后趋于稳定。说明荷载在加速过程中,应力在加筋低路堤中的衰减有所减小。
4) 对于加筋低路堤的情况,由于路堤高度较低,应力在路堤中的衰减较少,仍有很大一部分应力传递至地基表面。增加筋材刚度可以增加应力在加筋低路堤中的衰减,减小传递至地基表面的应力,且这种影响随着路堤高度的减小而增加。因此,应该在加筋低路堤中采用刚度较大的筋材,减少传递至地基土表面的应力,从而减小荷载变速对加筋低路堤的影响。
后续研究可以考虑车辆由于路面不平整度产生的附加动荷载和变速过程中前后轮对地面压力变化产生的影响,完善交通荷载作用下加筋低路堤的动力响应研究。
附录矩阵Mi、Ki为对称矩阵,Ki的元素为
对于Goodman层间接触情况,Ki为
| $ \begin{array}{c} {{\mathit{\boldsymbol{\bar K}}}_{i12}} = {{\mathit{\boldsymbol{\bar K}}}_{i14}} = {{\mathit{\boldsymbol{\bar K}}}_{i23}} = {{\mathit{\boldsymbol{\bar K}}}_{i34}} = 0, {{\mathit{\boldsymbol{\bar K}}}_{i13}} = - {k_{\rm{h}}}\\ {{\mathit{\boldsymbol{\bar K}}}_{i24}} = - {k_{\rm{v}}}, {{\mathit{\boldsymbol{\bar K}}}_{i11}} = {{\mathit{\boldsymbol{\bar K}}}_{i33}} = {k_{\rm{h}}}, {{\mathit{\boldsymbol{\bar K}}}_{i22}} = {{\mathit{\boldsymbol{\bar K}}}_{i44}} = {k_{\rm{v}}} \end{array} $ |
Mi的元素为
| $ \begin{array}{c} {{\mathit{\boldsymbol{\bar M}}}_{i13}} = {{\mathit{\boldsymbol{\bar M}}}_{i14}} = {{\mathit{\boldsymbol{\bar M}}}_{i23}} = {{\mathit{\boldsymbol{\bar M}}}_{i24}} = 0\\ {{\mathit{\boldsymbol{\bar M}}}_{i11}} = {{\mathit{\boldsymbol{\bar M}}}_{i22}} = {{\mathit{\boldsymbol{\bar M}}}_{i33}} = {{\mathit{\boldsymbol{\bar M}}}_{i44}} = \frac{{\rho \left( {{z_{i + 1}} - {z_i}} \right)}}{3}\\ {{\mathit{\boldsymbol{\bar M}}}_{i12}} = {{\mathit{\boldsymbol{\bar M}}}_{i34}} = \frac{{\rho \left( {{z_{i + 1}} - {z_i}} \right)}}{6} \end{array} $ |
| [1] |
张军, 郑俊杰, 马强, 等. 路桥过渡段路堤加筋现场试验和数值模拟分析[J]. 华中科技大学学报(自然科学版), 2011, 39(9): 87. ZHANG Jun, ZHENG Junjie, MA Qiang, et al. Experimental and numerical simulation analysis on geosynthetic reinforcement embankment at bridge approaches[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(9): 87. DOI:10.13245/j.hust.2011.09.020 |
| [2] |
ZHAO Linshuang, ZHOU Wanhuan, FATAHI B, et al. A dual beam model for geosynthetic-reinforced granular fill on an elastic foundation[J]. Applied Mathematical Modelling, 2016, 40(21/22): 9254. DOI:10.1016/j.apm.2016.06.003 |
| [3] |
ZHANG Ling, OU Qiang, ZHAO Minghua. Double-beam model to analyze the performance of a pavement structure on geocell-reinforced embankment[J]. Journal of Engineering Mechanics, 2018, 144(8): 06018002. DOI:10.1061/(ASCE)EM.1943-7889.0001453 |
| [4] |
WU Yongxin, GAO Yufeng. Analytical solutions for simply supported viscously damped double-beam system under moving harmonic loads[J]. Journal of Engineering Mechanics, 2015, 141(7): 04015004. DOI:10.1061/(ASCE)EM.1943-7889.0000900 |
| [5] |
WU Yongxin, GAO Yufeng. Dynamic response of a simply supported viscously damped double-beam system under the moving oscillator[J]. Journal of Sound and Vibration, 2016, 384: 1. DOI:10.1016/j.jsv.2016.08.022 |
| [6] |
HUSSEIN M F M, HUNT H E M. Modelling of floating-slab tracks with continuous slabs under oscillating moving loads[J]. Journal of Sound and Vibration, 2006, 297(1/2): 37. DOI:10.1016/j.jsv.2006.03.026 |
| [7] |
ZHANG Ling, OU Qiang, ZHOU Shuai. Analytical study of the dynamic response of a double-beam model for a geosynthetic-reinforced embankment under traffic loads[J]. Computers and Geotechnics, 2020, 118: 103330. DOI:10.1016/j.compgeo.2019.103330 |
| [8] |
高广运, 邱畅, 王贻荪. 改进的双参数层状地基模型[J]. 岩土力学, 2013, 24(2): 159. GAO Guangyun, QIU Chang, WANG Yisun. An improved two-parameter layer model[J]. Rock and Soil Mechanics, 2013, 24(2): 159. DOI:10.16285/j.rsm.2003.02.004 |
| [9] |
黄强, 黄宏伟, 张冬梅, 等. 移动简谐荷载作用下Kerr地基梁的稳态响应研究[J]. 振动与冲击, 2018, 37(1): 14. HUANG Qiang, HUANG Hongwei, ZHANG Dongmei. Steady-state response of an infinite Euler-Bernoulli beam on Kerr foundation subjected to a moving oscillating load[J]. Journal of Vibration and Shock, 2018, 37(1): 14. DOI:10.13465/j.cnki.jvs.2018.01.003 |
| [10] |
左迎辉, 徐长节, 蔡袁强. 移动荷载下下卧基岩Gibson地基的动力响应[J]. 振动工程学报, 2005, 18(3): 351. ZUO Yinghui, XU Changjie, CAI Yuanqiang. Dynamic analysis of Gibson soil medium on bedrock under moving load[J]. Journal of Vibration Engineering, 2005, 18(3): 351. |
| [11] |
YAN Kezhen, SHI Tingwei, YOU Lingyun, et al. Spectral element method for dynamic response of multilayered half medium subjected to harmonic moving load[J]. International Journal of Geomechanics, 2018, 18(12): 04018161-1. DOI:10.1061/(ASCE)GM.1943-5622.0001305 |
| [12] |
刘飞禹, 赵国兴, 蔡袁强, 等. 移动荷载下加筋道路系统的动力响应[J]. 浙江大学学报(工学版), 2007, 41(1): 57. LIU Feiyu, ZHAO Guoxing, CAI Yuanqiang, et al. Dynamic response of reinforced pavements systems subjected to moving loads[J]. Journal of Zhejiang University(Engineering Science), 2007, 41(1): 57. DOI:10.1007/s11747-006-0011-3 |
| [13] |
刘飞禹, 蔡袁强, 余炜, 等. 移动荷载下无面层加筋路基的动力响应[J]. 哈尔滨工业大学学报, 2009, 41(2): 145. LIU Feiyu, ZHAO Guoxing, YU Wei, et al. Dynamic response of reinforced unpaved subgrade subjected to moving loads[J]. Journal of Harbin Institute of Technology, 2009, 41(2): 145. |
| [14] |
刘飞禹, 杨凤云. 移动荷载作用下加筋路堤和轨道系统的三维动力响应[J]. 土木建筑与环境工程, 2013, 35(4): 101. LIU Feiyu, YANG Fengyun. 3-D dynamic response of reinforced embankment and track system subjected to mocing traffic load[J]. Journal of Civil Architectural and Environmental Engineering, 2013, 35(4): 101. DOI:10.1109/CLEOE-EQEC.2009.5194697 |
| [15] |
LIN J, NIEMEIER D A. An exploratory analysis comparing a stochastic driving cycle to California's regulatory cycle[J]. Atmospheric Environment, 2002, 36(38): 5759. DOI:10.1016/S1352-2310(02)00695-7 |
| [16] |
KNEZ M, MUNEER T, JEREB B, et al. The estimation of a driving cycle for Celje and a comparison to other European cities[J]. Sustainable Cities and Society, 2014, 11: 56. DOI:10.1016/j.scs.2013.11.010 |
| [17] |
BESKOU N D, MUHO E V. Dynamic response of a finite beam resting on a Winkler foundation to a load moving on its surface with variable speed[J]. Soil Dynamics and Earthquake Engineering, 2018, 109: 222. DOI:10.1016/j.soildyn.2018.02.033 |
| [18] |
MUHO E V, BESKOU N D. Dynamic response of an infinite beam resting on a Winkler foundation to a load moving on its surface with variable speed[J]. Soil Dynamics and Earthquake Engineering, 2018, 109: 150. DOI:10.1016/j.soildyn.2018.02.034 |
| [19] |
马宪永, 全蔚闻, 董泽蛟. 横观各向同性黏弹性沥青路面动力响应解析解[J]. 中国公路学报, 2020, 33(10): 135. MA Xianyong, QUAN Weiwen, DONG Zejiao. Analytical solution for dynamic response of transversely isotropic viscoelastic asphalt pavement[J]. China Journal of Highway and Transport, 2020, 33(10): 135. |
| [20] |
SUN Zhaojie, KASBERGEN C, SKARPAS A, et al. Dynamic analysis of layered systems under a moving harmonic rectangular load based on the spectral element method[J]. International Journal of Solids and Structures, 2019, 180: 45. DOI:10.1016/j.ijsolstr.2019.06.022 |
| [21] |
刘延柱, 陈文良, 陈立群. 振动力学[M]. 2版. 北京: 高等教育出版社, 2011. LIU Yanzhu, CHEN Wenliang, CHEN Liqun. Mechanics of vibrations[M]. 2nd ed. Beijing: Higher Education Press, 2011. |
| [22] |
方昊, 刘洋, 郑俊杰. 匀变速荷载作用下Vlazov地基上梁的动力响应分析[J]. 哈尔滨工程大学学报, 2021, 42(7): 946. FANG Hao, LIU Yang, ZHENG Junjie. Dynamic response analysis of a beam resting on the Vlazov foundation under loads moving with uniform velocity[J]. Journal of Harbin Engineering University, 2021, 42(7): 946. |
| [23] |
凌道盛, 张凡, 赵云, 等. 飞机荷载作用下非均匀道基动力响应分析[J]. 土木工程学报, 2017, 50(2): 97. LING Daosheng, ZHANG Fan, ZHAO Yun, et al. Dynamic responses analysis of inhomogeneous subgrade subjected to moving aircraft loads[J]. China Civil Engineering Journal, 2017, 50(2): 97. |
 2022, Vol. 54
2022, Vol. 54