2. 广西防灾减灾与工程安全重点实验室(广西大学),南宁 530004;
3. 广东省海洋土木工程重点实验室,广东 珠海 519082;
4. 浙江大学 滨海和城市岩土工程研究中心,杭州 310058
2. Guangxi Key Laboratory of Disaster Prevention and Structural Safety (Guangxi University), Nanning 530004, China;
3. Key Laboratory of Marine Civil Engineering in Guangdong Province, Zhuhai 519082, Guangdong, China;
4. Research Center of Costal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
随着中国沿海城市的蓬勃发展以及岛礁建设的快速推进,基础设施建设逐渐向沿海和海上扩张,填海造陆工程方兴未艾。然而这种吹填土具有天然含水率高、压缩性大、渗透性差的特点,在自重作用下会产生明显的固结沉降。桩基础因其对地层的广泛适应性而被大量用于滨海和吹填场地的基础工程建设,由于场地固结沉降产生的桩侧负摩阻力已经成为新吹填场地桩基施工的关键问题之一[1]。
桩侧负摩阻力来源于土体固结效应产生的地基沉降,因而,研究负摩阻力对桩基受力和变形特性的影响依赖于精确固结理论的选取。自1925年Terzaghi[2]提出土体一维固结理论以来,国内外学者从荷载形式、土体本构关系、边界条件等方面不断对其进行发展完善。但是在这些固结理论中,土体固结的排水边界被假设为完全透水,这使得在开始考虑土体固结的瞬间,孔压边界由传统排水边界突变为零,造成了边界处孔压在时间上的不连续。为了考虑排水边界渗透特性对边界孔压的影响,Gray[3]最早提出了半透水边界条件。基于此边界条件,学者们给出不同工况下的固结解答[4-8]。然而,基于半透水边界得到的解答都是形式复杂的数值解,工程应用性较差。为此,梅国雄等[9]提出了一种连续排水边界,既有效解决了传统Terzaghi排水边界的不连续问题,还能得到形式简单的解析解答。之后,许多学者将连续边界条件推广应用到非线性土体[10]、成层土体[11]、城市固废[12]等工况中,并对该边界条件的合理性和适用性进行了验证和分析。综上,固结理论对认识土体固结效应、解析土体固结沉降具有重要意义,但是这些理论仅以土体为研究对象,无法模拟固结效应下结构-土的相互作用。虽然Randolph等[13]早在1979年就给出了桩基打入后由固结效应导致的桩侧摩阻力分布解析解,但是该解只能对侧摩阻力的分布进行模拟,无法预测桩-土的耦合变形和桩顶的沉降。为了预测固结效应下桩基的变形特性,必须引入桩土相互作用模型进行模拟。
桩-土界面负摩阻力的精确模拟依赖于桩土系统平衡方程的求解精度,目前严格考虑土体固结效应的桩土耦合变形连续理论解析解仍未实现。比较有代表性的严格理论解有:Poulos等[14]基于Mindlin解在不考虑桩身自身变形的情况下,给出了均匀介质中桩-土耦合变形解析解;Randolph等[15]进一步给出了考虑桩身自身变形的数值解;王奎华等[16]基于虚土桩模型及理想弹塑性荷载传递法给出了桩身轴力及桩侧摩阻力的计算方法;Zhang等[17-18]将连续理论发展到成层地基中,并引入虚土桩模型统一了摩擦桩和端承桩的计算。但是上述理论的计算过于复杂,且同时考虑固结变形时必须进行数值求解,不利于工程人员学习掌握。荷载传递法将桩土的相互作用简化为线性或者非线性弹簧,求解简单可靠,并且能有效处理非线性问题,受到工程人员的青睐[19-22]。在求解固结引发的桩侧负摩阻力及不同荷载下的桩顶沉降问题中,荷载传递法已有较好的应用案例。例如,赵明华等[23-24]先后基于双折线模型和双曲线模型,结合Gibson地基理论,建立了桩侧负摩阻力计算方法,发现堆载对桩侧摩阻力具有显著影响,堆载越大,负摩阻力越大。杨怡青[25]建立了考虑固结效应的双层地基沉降数学模型,并结合双折线荷载传递函数建立了沉降与桩侧负摩阻力的关系,进一步研究了桩顶荷载和固结时间对负摩阻力分布的影响,发现桩顶荷载大小和固结时间长短对侧摩阻力中性点的位置影响是相反的。然而上述模型建立在传统Terzaghi固结边界条件下,仍然没有解决初始时刻孔压边界的矛盾。虽然模型或现场试验[26-30]和数值模拟[31]在一定程度上能够严格模拟真实的固结-沉降-负摩阻力分布特性,但是都操作复杂,不具有对工程问题普适性的特点。因此,建立连续排水边界条件下的桩土系统固结沉降-负摩阻力全过程理论将为解决新近吹填场地的桩基工程问题提供极大便利。
本研究基于连续排水边界条件,并考虑吹填土的自重固结,求解双层地基的一维固结解析解。将固结引起的沉降耦合进桩基荷载传递模型中,建立考虑新近吹填场地吹填土自重固结的桩-土耦合变形模型。通过与试验结果的对比,验证本文解答的合理性。最后,通过详细的参数分析探究考虑新近吹填土体固结效应的桩基变形特性。
1 数学模型与基本假设 1.1 模型描述在均质地基上开展吹填工程,由于原状土与吹填土的物理力学性质差异较大,可将整个土体视为双层地基土。如图 1所示,上层土为吹填土,有效重度为γ′,下层土为原状土,厚度分别为h1和h2,渗透系数分别为kv1和kv2,固结系数分别为Cv1和Cv2,压缩模量分别为Es1和Es2。在该双层地基中,假设原状土已完成自重固结。吹填完成后,原状土和吹填土在吹填土重力作用下发生固结,固结时间因子为Tv=Cv1t/H2,其中, H为双层地基总厚度。假设在土体固结一段时间后打桩,桩长为H,桩径为D,桩身截面积为A,桩身弹性模量为E。
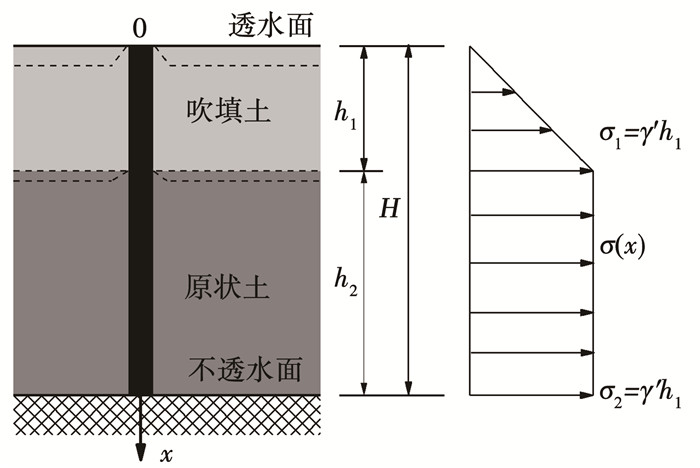
|
图 1 双层地基分析模型 Fig. 1 Analysis model of double-layer foundation |
作以下基本假设:
1) 土体初始自重应力沿深度线性分布(如图 2所示)。
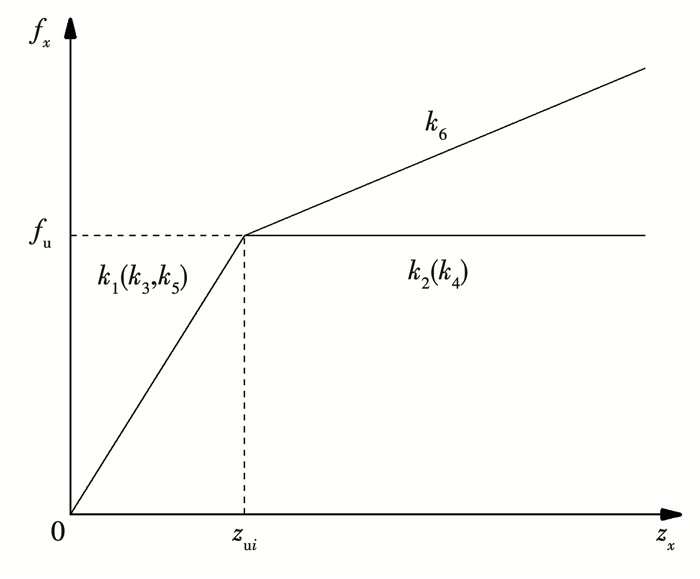
|
图 2 荷载传递模型 Fig. 2 Load transfer model |
2) 土层顶面连续排水,底面不透水。
3) 在土层顶面施加瞬时外荷载。
4) 如图 2所示,桩侧土采用理想弹塑性模型,桩端土采用双折线模型。fx(kN/mm)为单位厚度土所提供的摩阻力, zx为深度x处桩土相对位移, fu(kN)为桩侧土弹性阶段摩擦阻力极限值, zui为桩周土的弹性极限变形, k1、k3和k2、k4分别为弹性阶段和塑性阶段的刚度系数, k5、k6为桩端土体反力系数。
5) 其假定与Terzaghi一维固结假定相同。
2 解析方法 2.1 一维固结解答基于以上假设,土体的固结微分方程为
| $ \frac{{\partial {w_i}}}{{\partial t}} = {C_{{\rm{v}}i}}\frac{{{\partial ^2}{w_i}}}{{\partial {x^2}}}, i = 1, 2 $ | (1) |
式中:wi为第i层土内的超孔隙水压力,t为固结时间。
土层顶面为连续排水边界条件[9]
| $ {w_1}(0, t) = {q_0}{{\rm{e}}^{ - \frac{{{C_{{\rm{vl}}}}}}{{{H^2}t}}}} $ | (2) |
式中:r为土体界面参数,可通过试验模拟或工程实测反演得出;q0为施加在土体表面的瞬时荷载。
底面为不透水边界
| $ {\left. {\frac{{\partial {w_2}}}{{\partial z}}} \right|_{x = H}} = 0 $ | (3) |
孔压连续条件
| $ {\left. {{w_1}} \right|_{x = {h_1}}} = {\left. {{w_2}} \right|_{x = {h_1}}} $ | (4) |
流量连续条件
| $ {\left. {{k_{{\rm{v}}1}}\frac{{\partial {w_1}}}{{\partial z}}} \right|_{x = {h_1}}} = {\left. {{k_{{\rm{v}}2}}\frac{{\partial {w_2}}}{{\partial z}}} \right|_{x = {h_1}}} $ | (5) |
初始条件为
| $ {w_i}(x, 0) = {q_0} + \sigma (x) $ | (6) |
定义无量纲参数
| $ a = \frac{{{k_{{\rm{v}}2}}}}{{{k_{{\rm{v}}1}}}}, b = \frac{{{m_{{\rm{v}}2}}}}{{{m_{{\rm{v}}1}}}} = \frac{{{E_{{\rm{s}}1}}}}{{{E_{{\rm{s}}2}}}}, c = \frac{{{h_2}}}{{{h_1}}} $ | (7) |
参照谢康和等[31]的求解方法,结合边界条件和初始条件,可求得本研究的孔压解答为
| $ {w_1} = \sum\limits_{m = 1}^\infty {\sin } \left( {{\lambda _m}\frac{x}{{{h_1}}}} \right){e_{{T_{\rm{v}}}}} + {q_0}{{\rm{e}}^{ - \frac{{{C_{{\rm{v}}1}}}}{{H{2^2}}}}} $ | (8) |
| $ {w_2} = \sum\limits_{m = 1}^\infty {\frac{{\sin\;{\lambda _m}}}{{\cos \left( {\mu c{\lambda _m}} \right)}}} \cos \left( {\mu {\lambda _m}\frac{{H - x}}{{{h_1}}}} \right){e_{{T_{\rm{v}}}}} + {q_0}{{\rm{e}}^{ - \frac{{{C_{{\rm{v}}1}}}}{{H{2^2}}}t}} $ | (9) |
其中λm为超越方程
| $ \mu = \sqrt {\frac{{{C_{{\rm{v}}1}}}}{{{C_{{\rm{v}}2}}}}} = \sqrt {\frac{b}{a}} $ | (10) |
| $ {e_{{T_{\rm{v}}}}} = {B_m}{{\rm{e}}^{ - \lambda _m^2{T_{\rm{v}}}}} + {C_m}\frac{{r{q_0}}}{{\lambda _m^2 - r}}\left( {{{\rm{e}}^{ - r{T_{\rm{v}}}}} - {{\rm{e}}^{ - \lambda _m^2{T_{\rm{v}}}}}} \right) $ | (11) |
| $ {C_m} = \frac{2}{{{\lambda _m}\left( {1 + bcA_m^2} \right)}} $ | (12) |
| $ {B_m} = \frac{{2{h_1}{\gamma ^\prime }\sin\;{\lambda _m}}}{{\lambda _m^2\left( {1 + bcA_m^2} \right)}} $ | (13) |
| $ {A_m} = \frac{{\sin\;{\lambda _m}}}{{\cos \left( {\mu c{\lambda _m}} \right)}} $ | (14) |
基于求得的孔压解答,t时刻第i层土深度x处桩侧土的沉降变形vix可表示为
| $ \begin{array}{l} {v_{1x}}(x, t) = \frac{1}{{{E_{{\rm{s}}1}}}}\left\{ {\left[ {\int_x^{{h_1}} {\left( {{\gamma ^\prime }\tau + {q_0} - {w_1}} \right)} {\rm{d}}\tau } \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{E_{{\rm{s}}1}}}}{{{E_{{\rm{s}}2}}}}\left[ {\int_{{h_1}}^H {\left( {{\gamma ^\prime }{h_1} + {q_0} - {w_2}} \right)} {\rm{d}}\tau } \right]} \right\} \end{array} $ | (15) |
| $ {v_{2x}}(x, t) = \frac{1}{{{E_{{\rm{s}}2}}}}\int_x^H {\left( {{\gamma ^\prime }{h_1} + {q_0} - {w_2}} \right)} {\rm{d}}\tau $ | (16) |
任意深度x处取一桩体微元,根据微元段的桩土间平衡条件可得
| $ \frac{\mathrm{d} N_{x}}{\mathrm{~d} x}=-f_{x} $ | (17) |
式中Nx为桩身轴力。
由桩的本构方程可得桩身压缩量
| $ \mathrm{d} u_{x}=-\frac{N_{x} \mathrm{~d} x}{E A} $ | (18) |
式中ux为桩在深度x处的桩身压缩量。
将式(17)代入(18)得
| $ E A \frac{\mathrm{d}^{2} u_{x}}{\mathrm{~d} x^{2}}=f_{x} $ | (19) |
其中,桩身压缩量为土体沉降量与桩土相对位移之差,即
| $ z_{i x}=u_{x}-v_{i x} $ | (20) |
式中zix为第i层土内的桩土相对位移。
将式(20)代入式(19)可得
| $ \frac{{{{\rm{d}}^2}{z_{ix}}}}{{{\rm{d}}{x^2}}} + \frac{{{{\rm{d}}^2}{v_{ix}}}}{{{\rm{d}}{x^2}}} = \frac{{{f_x}}}{{EA}} $ | (21) |
当桩侧土和桩端土相对位移均小于弹性位移极限值时,土体处于弹性状态,在桩体上任意深度x处取一单元体,该单元体受到的桩侧摩阻力为
| $ f_{x}= \begin{cases}k_{1} z_{1 x}, & 0<x \leqslant h_{1} \\ k_{3} z_{2 x}, & h_{1}<x \leqslant H\end{cases} $ | (22) |
此时,桩身以及桩周土满足以下条件:
1) 桩顶边界条件
| $ {N_{1x}}{\left| {_{x = 0} = - EA\frac{{{\rm{d}}{u_x}}}{{{\rm{d}}x}}} \right|_{x = 0}} = P $ | (23) |
其中P为桩顶瞬时施加荷载。
2) 桩端边界条件
| $ {N_{2x}}{\left| {_{x = H} = - EA\frac{{{\rm{d}}{u_x}}}{{{\rm{d}}x}}} \right|_{x = H}} = {k_5}{z_{2x}} $ | (24) |
3) 桩身的层间连续性条件
| $ {\left. {{u_1}} \right|_{x = {h_1}}} = {\left. {{u_2}} \right|_{x = {h_1}}} $ | (25) |
| $ {\left. {EA\frac{{{\rm{d}}{u_1}}}{{{\rm{d}}x}}} \right|_{x = {h_1}}} = {\left. {EA\frac{{{\rm{d}}{u_2}}}{{{\rm{d}}x}}} \right|_{x = {h_1}}} $ | (26) |
令
| $ {\alpha _1} = \sqrt {\frac{{{k_1}}}{{EA}}} , {\alpha _3} = \sqrt {\frac{{{k_3}}}{{EA}}} , {\alpha _5} = \sqrt {\frac{{{k_5}}}{{EA}}} $ | (27) |
将上文求得的土体沉降解答(式(15)和(16))和桩侧摩阻力(式(22))代入式(21)可得
| $ \frac{{{{\rm{d}}^2}{z_{1x}}}}{{{\rm{d}}{x^2}}} - \alpha _1^2{z_x} = \frac{1}{{{E_{{\rm{s}}1}}}}\left[ {{\gamma ^\prime } - \sum\limits_{m = 1}^\infty {\frac{{{\lambda _m}}}{{{h_1}}}} \cos \left( {\frac{{{\lambda _m}x}}{{{h_1}}}} \right){e_{{T_{\rm{v}}}}}} \right] $ | (28) |
| $ \begin{aligned} \frac{\mathrm{d}^{2} z_{2 x}}{\mathrm{~d} x^{2}}-\alpha_{3}^{2} z_{x}=&-\frac{1}{E_{\mathrm{s} 2}} \sum\limits_{m=1}^{\infty}\left\{\frac{\mu \lambda_{m}}{h_{1}} \frac{\sin\;\lambda_{m}}{\cos \left(\mu c \lambda_{m}\right)} \times\right.\\ &\left.\sin \left[\frac{\mu \lambda_{m}}{h_{1}}(H-x)\right] e_{T_{v}}\right\} \end{aligned} $ | (29) |
解二阶非齐次微分方程(21)可得
| $ \begin{aligned} z_{1 x}=& c_{3} \sinh \left(\alpha_{1} x\right)+c_{4} \cosh \left(\alpha_{1} x\right)+\\ & \sum\limits_{m=1}^{\infty} c_{1 m} \cos \frac{\lambda_{m} x}{h_{1}}-\frac{\gamma^{\prime}}{E_{\mathrm{s} 1} \alpha_{1}^{2}}, 0<x \leqslant h_{1} \end{aligned} $ | (30) |
| $ \begin{aligned} z_{2 x}=& c_{7} \sinh \left(\alpha_{3} x\right)+c_{8} \cosh \left(\alpha_{3} x\right)+\\ & \sum\limits_{m=1}^{\infty}\left(c_{5 m} \cos \frac{\mu \lambda_{m} x}{h_{1}}+c_{6 m} \sin \frac{\mu \lambda_{m} x}{h_{1}}\right), h_{1}<x \leqslant H \end{aligned} $ | (31) |
其中,各待定系数可由代入边界条件(式(23)~(26))确定为
| $ {c_{1m}} = \frac{{{\lambda _m}{e_{{T_{\rm{v}}}}}}}{{{E_{{\rm{s}}1}}{h_1}\left[ {{{\left( {{\lambda _m}/{h_1}} \right)}^2} + \alpha _1^2} \right]}} $ | (32) |
| $ {c_{5m}} = \frac{{{A_m}{e_{{T_v}}}\mu {\lambda _m}\sin \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _3^2} \right]}} $ | (33) |
| $ {c_{6m}} = - \frac{{{A_m}{e_{{T_v}}}\mu {\lambda _m}\cos \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _3^2} \right]}} $ | (34) |
| $ {c_3} = - \frac{P}{{EA{\alpha _1}}} + \frac{{{e_{{T_{{\rm{v}}1}}}}}}{{{E_{{\rm{s}}1}}{\alpha _1}}} $ | (35) |
| $ \begin{aligned} c_{4}=& \frac{1}{\cosh \left(\alpha_{1} h_{1}\right)}\left[c_{7} \sinh \left(\alpha_{3} h_{1}\right)+c_{8} \cosh \left(\alpha_{3} h_{1}\right)+\right.\\ &\left.d+\frac{\gamma^{\prime}}{E_{\mathrm{s} 1} \alpha_{1}^{2}}-c_{3} \sinh \left(\alpha_{1} h_{1}\right)\right] \end{aligned} $ | (36) |
| $ c_{7}=\frac{g-e-c_{8} A}{B} $ | (37) |
| $ \begin{aligned} c_{8}=& \frac{B}{C A-W B}\left\{\alpha_{1} c_{3} \cosh \left(\alpha_{1} h_{1}\right)-i+n+\right.\\ & \alpha_{1} \tanh \left(\alpha_{1} h_{1}\right)\left[d+\gamma^{\prime} / E_{\mathrm{s} 1} \alpha_{1}^{2}-\right.\\ &\left.\left.c_{3} \sinh \left(\alpha_{1} h_{1}\right)\right]+(g-e) C / B\right\} \end{aligned} $ | (38) |
其中
| $ d = \sum\limits_{m = 1}^\infty {\left[ {{c_{5m}}\cos \left( {\mu {\lambda _m}} \right) + {c_{6m}}\sin \left( {\mu {\lambda _m}} \right) - {c_{1m}}\cos\;{\lambda _m}} \right]} $ | (39) |
| $ \begin{array}{l} e = \sum\limits_{m = 1}^\infty {\left[ {\left( {\alpha _5^2{c_{6m}} - \frac{{\mu {\lambda _m}}}{{{h_1}}}{c_{5m}}} \right)\sin \left( {\frac{{\mu {\lambda _m}H}}{{{h_1}}}} \right) + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\left( {\frac{{\mu {\lambda _m}{c_{6m}}}}{{{h_1}}} + \alpha _5^2{c_{5m}}} \right)\cos \left( {\frac{{\mu {\lambda _m}H}}{{{h_1}}}} \right)} \right] \end{array} $ | (40) |
| $ g = - \sum\limits_{m = 1}^\infty {\frac{{{e_{{T_v}}}{A_m}}}{{{E_{{\rm{s}}2}}}}} + \frac{{{\gamma ^\prime }{h_1} + {e_{{T_{{\rm{v}}1}}}}}}{{{E_{{\rm{s}}2}}}} $ | (41) |
| $ n = \left( {\frac{1}{{{E_{{\rm{s}}1}}}} - \frac{1}{{{E_{{\rm{s}}2}}}}} \right)\left( {{e_{{T_{\rm{v}}}}}\sin\;{\lambda _m} - {\gamma ^\prime }{h_1} - {e_{{T_{{\rm{v}}1}}}}} \right) $ | (42) |
| $ \begin{array}{l} i = \sum\limits_{m = 1}^\infty {\frac{{{\lambda _m}}}{{{h_1}}}} \left[ {\mu {c_{6m}}\cos \left( {\mu {\lambda _m}} \right) - } \right.\\ \;\;\;\;\;\left. {\mu {c_{5m}}\sin \left( {\mu {\lambda _m}} \right) + {c_{1m}}\sin\;{\lambda _m}} \right] \end{array} $ | (43) |
| $ A = {\alpha _3}\sinh \left( {{\alpha _3}H} \right) + \alpha _5^2\cosh \left( {{\alpha _3}H} \right) $ | (44) |
| $ B = {\alpha _3}\cosh \left( {{\alpha _3}H} \right) + \alpha _5^2\sinh \left( {{\alpha _3}H} \right) $ | (45) |
| $ C = {\alpha _1}\tanh \left( {{\alpha _1}{h_1}} \right)\sinh \left( {{\alpha _3}{h_1}} \right) - {\alpha _3}\cosh \left( {{\alpha _3}{h_1}} \right) $ | (46) |
| $ W = {\alpha _1}\tanh \left( {{\alpha _1}{h_1}} \right)\cosh \left( {{\alpha _3}{h_1}} \right) - {\alpha _3}\sinh \left( {{\alpha _3}{h_1}} \right) $ | (47) |
| $ {e_{{T_{{\rm{v}}1}}}} = {q_0} - {q_0}{{\rm{e}}^{ - r{T_v}}} $ | (48) |
当桩土相对位移较大时,桩周土由浅至深逐渐进入塑性状态,但此时桩端土体仍处于弹性阶段,将该阶段定义为过渡阶段。设发生塑性变形的深度范围为h(h1 < h < H),处于弹性塑性硬化阶段的范围为0 < x≤h1,处于弹性阶段的范围为h1 < x≤H。
此时,桩侧摩阻力的模型为
| $ {f_x} = \left\{ {\begin{array}{*{20}{l}} {{k_2}\left( {{z_{1x}} - {z_{{\rm{u}}1}}} \right) + {k_1}{z_{{\rm{u}}1}} = {k_1}{z_{{\rm{u}}1}}, 0 < x \le {h_1}}\\ {{k_4}\left( {{z_{2x}} - {z_{{\rm{u}}2}}} \right) + {k_3}{z_{{\rm{u}}2}} = {k_3}{z_{{\rm{u}}2}}, {h_1} < x \le h}\\ {{k_3}{z_{2x}}, h < x \le H} \end{array}} \right. $ | (49) |
其中,根据文献[18], 土体的极限侧摩阻力可通过式(50)[32]确定,其对应的土体极限位移可由后处理得到。例如,对于直径为0.7~1.1 m钻孔灌注桩,zu1和zu2的取值为5~25 mm。
| $ \tau_{\mathrm{su}}=K_{0}\left(\frac{K}{K_{0}}\right) \tan \left[\varphi^{\prime}\left(\frac{\delta}{\varphi^{\prime}}\right)\right] \sigma_{\mathrm{v}}^{\prime} $ | (50) |
式中:δ/φ′的取值为0.8~1.0,K/K0对于嵌岩桩取为0.7~1.2,对于摩擦桩取为1.0~2.0。
桩周土的层间连续性条件:
| $ {\left. {{u_{2x}}} \right|_{x = {h^ - }}} = {\left. {{u_{2x}}} \right|_{x = {h^ + }}} $ | (51) |
| $ {\left. {EA\frac{{{\rm{d}}{u_{2x}}}}{{{\rm{d}}x}}} \right|_{x = {h^ - }}} = {\left. {EA\frac{{{\rm{d}}{u_{2x}}}}{{{\rm{d}}x}}} \right|_{x = {h^ + }}} $ | (52) |
将式(48)代入式(21)中求解可得
| $ z_{1 x}=\sum\limits_{m=1}^{\infty} c_{10 m} \cos \left(\frac{\lambda_{m} x}{h_{1}}\right)+c_{12} x+c_{13} x^{2} $ | (53) |
| $ \begin{aligned} z_{2 x}=& \sum\limits_{m=1}^{\infty}\left[c_{15 m} \cos \left(\frac{\mu \lambda_{m} x}{h_{1}}\right)+c_{16 m} \sin \left(\frac{\mu \lambda_{m} x}{h_{1}}\right)\right]+\\ & c_{17} x+c_{18} x^{2} \end{aligned} $ | (54) |
| $ \begin{aligned} z_{2 x}=& c_{21} \sinh \left(\alpha_{3} x\right)+c_{22} \cosh \left(\alpha_{3} x\right)+\\ & \sum\limits_{m=1}^{\infty}\left[c_{19 m} \cos \left(\frac{\mu \lambda_{m} x}{h_{1}}\right)+c_{20 m} \sin \left(\frac{\mu \lambda_{m} x}{h_{1}}\right)\right] \end{aligned} $ | (55) |
其中,根据层间连续性条件和边界条件可得
| $ {c_{10m}} = \frac{{{\lambda _m}{e_{{T_{\rm{v}}}}}}}{{{E_{{\rm{s}}1}}{h_1}\left( {\lambda _m^2/h_1^2 + \alpha _2^2} \right)}} $ | (56) |
| $ {c_{15m}} = \frac{{{A_m}\mu {\lambda _m}{e_{{T_v}}}\sin \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _4^2} \right]}} $ | (57) |
| $ {c_{16m}} = - \frac{{{A_m}\mu {\lambda _m}{e_{{T_v}}}\cos \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _4^2} \right]}} $ | (58) |
| $ {c_{19m}} = \frac{{{A_m}\mu {\lambda _m}{e_{{T_{\rm{v}}}}}\sin \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _3^2} \right]}} $ | (59) |
| $ {c_{20m}} = - \frac{{\mu {\lambda _m}{e_{{T_{\rm{v}}}}}{A_m}\cos \left( {\mu {\lambda _m}H/{h_1}} \right)}}{{{E_{{\rm{s}}2}}{h_1}\left[ {{{\left( {\mu {\lambda _m}/{h_1}} \right)}^2} + \alpha _3^2} \right]}} $ | (60) |
| $ {c_{12}} = \frac{{{e_{{T_{{\rm{v}}1}}}}}}{{{E_{{\rm{s}}1}}}} - \frac{P}{{EA}} $ | (61) |
| $ {c_{13}} = \frac{{{c_{17}}{h_1} + {c_{18}}h_1^2 + {d_1} - {c_{12}}{h_1}}}{{h_1^2}} $ | (62) |
| $ {c_{17}} = \frac{{{c_{21}}\sinh \left( {{\alpha _3}h} \right) + {c_{22}}\cosh \left( {{\alpha _3}h} \right) + m - {c_{18}}{h^2}}}{h} $ | (63) |
| $ {c_{18}} = \frac{{{c_{12}} + 2{c_{13}}{h_1} + {i_1} - n - {c_{17}}}}{{2{h_1}}} $ | (64) |
| $ {c_{21}} = \frac{{g + {e_1} - {c_{22}}A}}{B} $ | (65) |
| $ {c_{22}} = \frac{{{i_1} - {c_{12}} - n - {m_1} + {c_{21}}{A^{\prime \prime }} + 2m/h + 2{d_1}/{h_1}}}{{{C^\prime }}} $ | (66) |
式中
| $ d_{1}=\sum\limits_{m=1}^{\infty} c_{15 m} \cos \left(\mu \lambda_{m}\right)+c_{16 m} \sin \left(\mu \lambda_{m}\right)-c_{10 m} \cos \lambda_{m} $ | (67) |
| $ \begin{aligned} m=& \sum\limits_{m=1}^{\infty}\left[\left(c_{19 m}-c_{15 m}\right) \cos \left(\mu \lambda_{m} h / h_{1}\right)+\right.\\ &\left.\left(c_{20 m}-c_{16 m}\right) \sin \left(\mu \lambda_{m} h / h_{1}\right)\right] \end{aligned} $ | (68) |
| $ \begin{aligned} i_{1}=& \sum\limits_{m=1}^{\infty} \frac{\lambda_{m}}{h_{1}}\left[-\mu c_{16 m} \cos \left(\mu \lambda_{m}\right)+\right.\\ &\left.\mu c_{15 m} \sin \left(\mu \lambda_{m}\right)-c_{10 m} \cos \lambda_{m}\right] \end{aligned} $ | (69) |
| $ \begin{aligned} m_{1}=& \sum\limits_{m=1}^{\infty} \frac{\mu \lambda_{m}}{h_{1}}\left[\left(c_{19 m}-c_{15 m}\right) \sin \left(\mu \lambda_{m} h / h_{1}\right)+\right.\\ &\left.\left(c_{20 m}-c_{16 m}\right) \cos \left(\mu \lambda_{m} h / h_{1}\right)\right] \end{aligned} $ | (70) |
| $ \begin{aligned} e_{1}=& \sum\limits_{m=1}^{\infty}\left[\left(\mu \lambda_{m} / h_{1} c_{19 m}-\alpha_{5}^{2} c_{20 m}\right) \sin \left(\mu \lambda_{m} H / h_{1}\right)-\right.\\ &\left.\left(c_{20 m} \mu \lambda_{m} / h_{1}+c_{19 m} \alpha_{5}^{2}\right) \cos \left(\mu \lambda_{m} H / h_{1}\right)\right] \end{aligned} $ | (71) |
| $ {A^{\prime \prime }} = 2\sinh \left( {{\alpha _3}h} \right)/h - {\alpha _3}\cosh \left( {{\alpha _3}h} \right) $ | (72) |
| $ {C^\prime } = {\alpha _3}\sinh \left( {{\alpha _3}h} \right) - 2\cosh \left( {{\alpha _3}h} \right)/h $ | (73) |
在桩周土变形进入塑性阶段后,桩侧土体仅短暂处于弹性阶段,随后很快进入塑性阶段。此时,桩端土和桩周土均处于硬化阶段。
下桩侧摩阻力的模型为
| $ f_{x}= \begin{cases}k_{2}\left(z_{1 x}-z_{\mathrm{u} 1}\right)+k_{1} z_{\mathrm{u} 1}=k_{1} z_{\mathrm{u} 1}, & 0<x \leqslant h_{1} \\ k_{4}\left(z_{2 x}-z_{\mathrm{u} 2}\right)+k_{3} z_{\mathrm{u} 2}=k_{3} z_{\mathrm{u} 2}, & h_{1}<x \leqslant H\end{cases} $ | (74) |
桩端处的边界条件
| $ {N_{2x}}{\left| {_{x = H} = - EA\frac{{{\rm{d}}{u_{2x}}}}{{{\rm{d}}x}}} \right|_{x = H}} = {k_5}{z_{{\rm{u}}2}} + {\left. {{k_6}\left( {{z_{2x}} - {z_{{\rm{u}}2}}} \right)} \right|_{x = H}} $ | (75) |
同理,可得塑性阶段桩土相对位移的解答为
| $ \begin{gathered} z_{1 x}=c_{23} x+c_{24} x^{2}+ \\ \sum\limits_{m=1}^{\infty} c_{10 m} \cos \frac{\lambda_{m} x}{h_{1}} \end{gathered} $ | (76) |
| $ \begin{aligned} z_{2 x}=& c_{25} x+c_{26} x^{2}+\\ & \sum\limits_{m=1}^{\infty}\left(c_{15 m} \cos \frac{\mu \lambda_{m} x}{h_{1}}+c_{16 m} \sin \frac{\mu \lambda_{m} x}{h_{1}}\right) \end{aligned} $ | (77) |
其中
| $ c_{23}=\frac{e_{T_{\mathrm{v} 1}}}{E_{\mathrm{s} 1}}-\frac{P}{E A} $ | (78) |
| $ c_{24}=\frac{c_{25} h_{1}+c_{26} h_{1}^{2}+d_{1}-c_{23} h_{1}}{h_{1}^{2}} $ | (79) |
| $ c_{25}=\frac{g+e_{2}-\left(\alpha_{5}^{2}-\alpha_{6}^{2}\right) z_{\mathrm{u} 2}-c_{26}\left(2 H+\alpha_{6}^{2} H^{2}\right)}{\alpha_{6}^{2} H+1} $ | (80) |
| $ \begin{aligned} c_{26}=&\left(\alpha_{6}^{2} H+1\right)\left(c_{23}-i_{1}+n-d_{1}\right) /\left(2 H+\alpha_{6}^{2} H^{2}\right)-\\ & {\left[g+e_{2}-\left(\alpha_{5}^{2}-\alpha_{6}^{2}\right) z_{\mathrm{u} 2}\right] /\left(2 H+\alpha_{6}^{2} H^{2}\right) } \end{aligned} $ | (81) |
| $ \begin{aligned} e_{2}=& \sum\limits_{m=1}^{\infty}\left[\left(\frac{\mu \lambda_{m}}{h_{1}} c_{15 m}-\alpha_{6}^{2} c_{16 m}\right) \sin \left(\frac{\mu \lambda_{m} H}{h_{1}}\right)+\right.\\ &\left.\left(-\frac{\mu \lambda_{m}}{h_{1}} c_{16 m}-\alpha_{6}^{2} c_{15 m}\right) \cos \left(\frac{\mu \lambda_{m} H}{h_{1}}\right)\right] \end{aligned} $ | (82) |
| $ \alpha_{6}=\sqrt{\frac{k_{6}}{E A}} $ | (83) |
基于求得的桩土相对位移,桩身轴力可表示为
| $ N_{i x}=-E A \frac{\mathrm{d} u_{i x}}{\mathrm{~d} x}=-E A\left(\frac{\mathrm{d} z_{i}}{\mathrm{~d} x}+\frac{\mathrm{d} v_{i x}}{\mathrm{~d} x}\right) $ | (84) |
为验证本研究解答的合理性,将求解结果与律文田等[30]报道的试验结果进行对比。根据文献[30]的数据,上层吹填土在填土完成后,原天然土视作均匀土层,厚度为h2=39.26 m,桩周土体参数取值如表 1所示。
| 表 1 桩周土体参数 Tab. 1 Parameters of soil around piles |
参考既有文献报道[15],压缩模量和土层的刚度系数(弹性阶段)公式为
| $ k_{i}=\frac{\pi E_{s i}}{\left(1+v_{i}\right) \ln \left(r_{m} / r_{1}\right)} $ | (85) |
式中: υi为第i层土体的泊松比,ln(rm/r1)根据Randolph等[15]的建议取4。因此,k1和k3分别取3.187和9.610。取桩身长度为44.3 m,弹性模量为30 GPa,半径为0.5 m。
由图 3、4可知,基于本研究解答得到的桩身轴力和侧摩阻力与试验结果较为吻合,验证了本研究解答的合理性。同时,可以认为本研究提出的双层地基模型适用于新吹填场地的模拟。

|
图 3 轴力的计算值与试验值对比 Fig. 3 Comparison between calculated and experimental values of axial force |
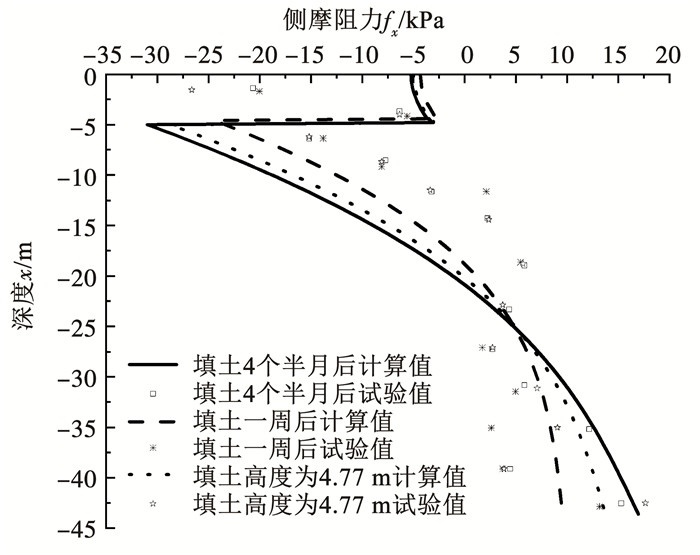
|
图 4 侧摩阻力的计算值与试验值对比 Fig. 4 Comparison between calculated and experimental values of skin friction |
基于对比验证中桩土数据参数进行分析,选取填土高度为4.05 m。
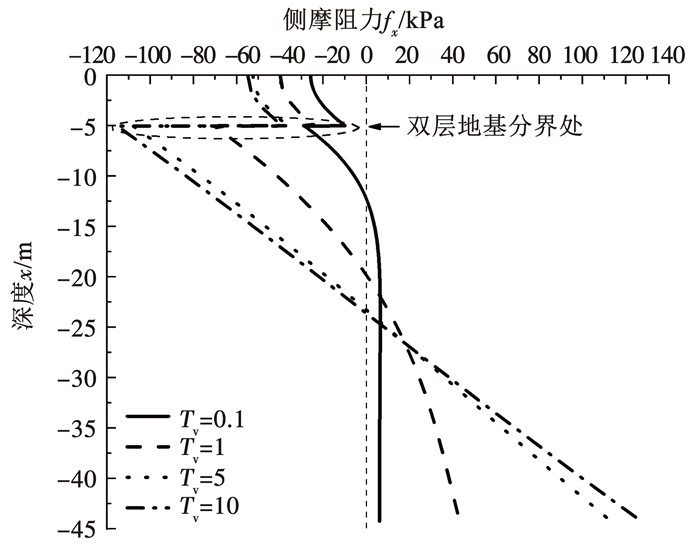
4.1 桩周土不同时间因子下打桩对桩基受力的影响保持其他因素不变,改变固结的时间因子,对应时间因子下的轴力和负摩阻力见图 5、6,其中,固结时间因子代表固结时间的长短。如图 5所示,随着固结时间的增加,桩的最大轴力增大,最大轴力位置下移,但随着固结时间的增加,固结时间的改变对轴力的影响逐渐减小。图 6展示了固结时间因子对桩侧摩阻力的影响,可以看出,桩侧摩阻力中性点的位置变化与最大轴力位置变化一致,都逐渐下移。而最大负摩阻力会随着时间的增加而增加,但增量越来越小。
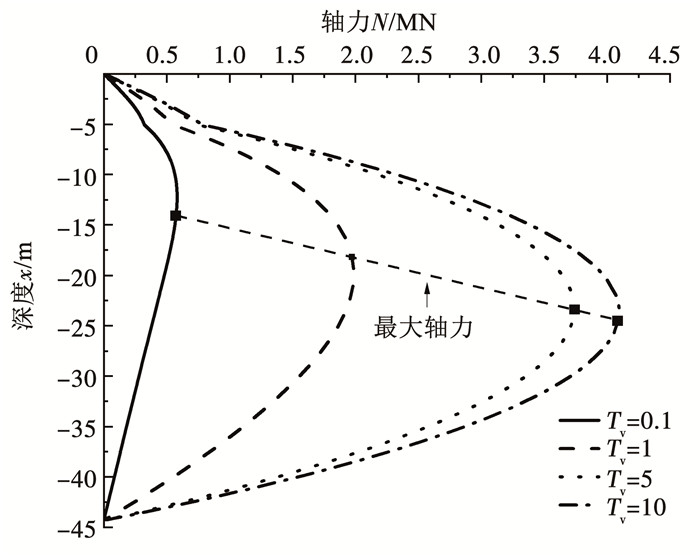
|
图 5 时间因子对轴力的影响 Fig. 5 Influence of time factor on axial force |
|
图 6 时间因子对侧摩阻力的影响 Fig. 6 Influence of time factor on skin friction |
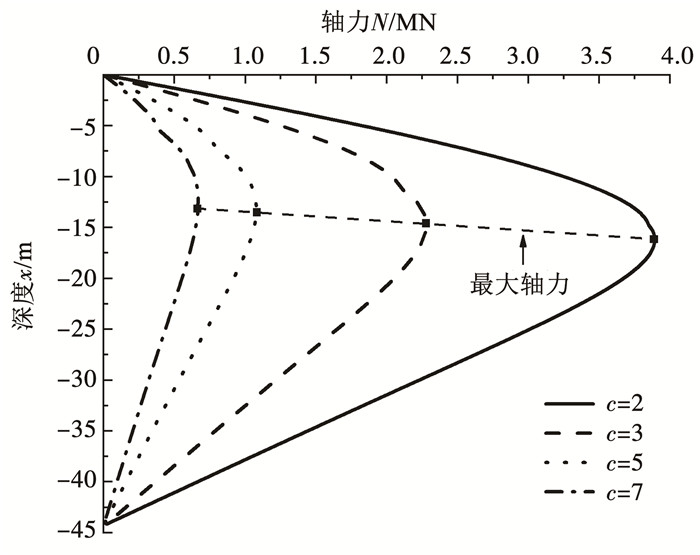
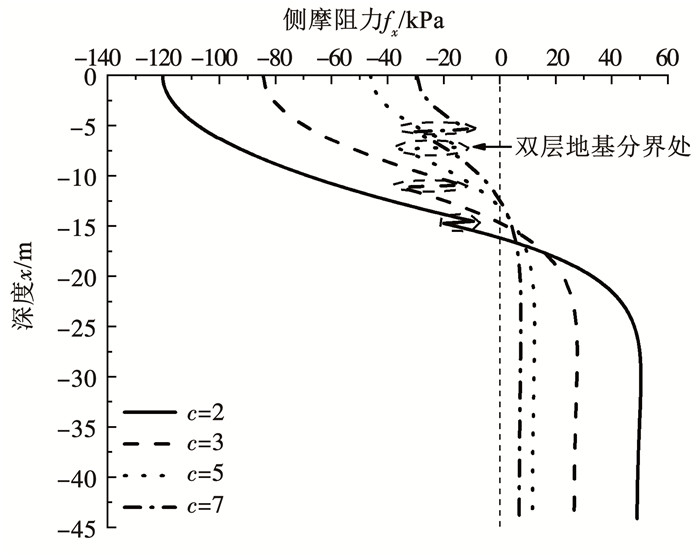
吹填的厚度对桩基的负摩阻力分布影响极大,为研究吹填土和原状土厚度对桩基轴力和侧摩阻力的影响,在其他因素不变的情况下,改变双层地基的厚度比c(下层土层厚度与上层土层厚度的比值),对比分析轴力和负摩阻力的变化。如图 7所示,随着厚度比的减小,桩的最大轴力增大,最大轴力位置下移。由图 8可知,桩侧摩阻力中性点的位置变化与最大轴力位置变化一致,都逐渐下移,但最大负摩阻力随厚度比的减小而增大。
|
图 7 双层地基厚度比对轴力的影响 Fig. 7 Influence of thickness ratio of double-layer foundation on axial force |
|
图 8 双层地基厚度比对侧摩阻力的影响 Fig. 8 Influence of thickness ratio of double-layer foundation on skin friction |
为研究桩顶受到的常荷载对桩身受力变形的影响,保持其他参数不变,采用不同的桩顶应力边界条件模拟不同外荷载下的桩基工作情况。对应工况下桩身轴力和侧摩阻力分布曲线如图 9、10所示。

|
图 9 桩顶荷载对轴力的影响 Fig. 9 Influence of pile head load on axial force |

|
图 10 桩顶荷载对侧摩阻力的影响 Fig. 10 Influence of pile head loadon skin friction |
图 9中的黑色直线表示不同桩顶荷载下桩身最大轴力的位置。可以看出,随着荷载的增大,桩的最大轴力增大,最大轴力位置上移。由图 10可知,侧摩阻力中性点的位置变化与最大轴力位置变化一致,都逐渐上移,而摩阻力会向正向移动。
4.4 桩径对桩基受力的影响为研究桩径对桩身受力的影响,在其他参数不变的条件下,同时保证桩的截面面积不变(建造材料相当)改变桩基直径,分析对应桩径下的轴力和负摩阻力分布情况。
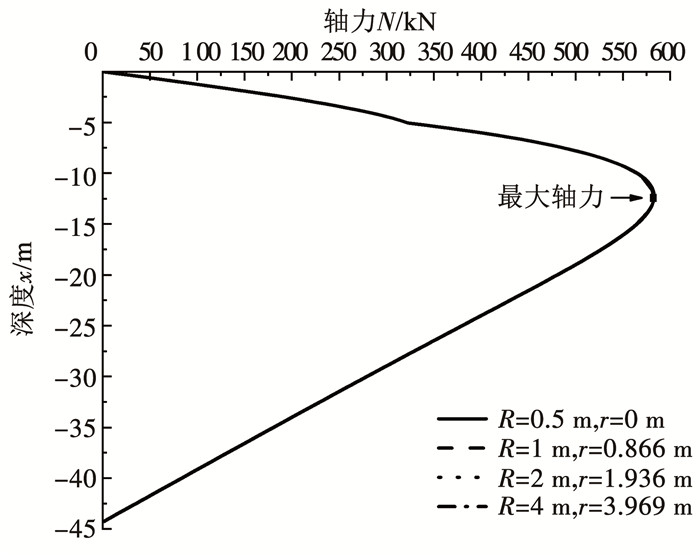
如图 11所示,随着桩径的增大,桩的最大轴力不变,且最大轴力位置并不会改变。如图 12所示,桩侧摩阻力中性点的位置变化与最大轴力位置变化一致,都不会改变,而最大负摩阻力随桩径的增大而增大。因此,面积不变的情况下,增大管桩外径,并不会改变桩侧摩阻力中性点的位置,并且轴力的大小完全不变,但是会减小侧摩阻力。
|
图 11 桩径对轴力的影响 Fig. 11 Influence of pile diameter on axial force |
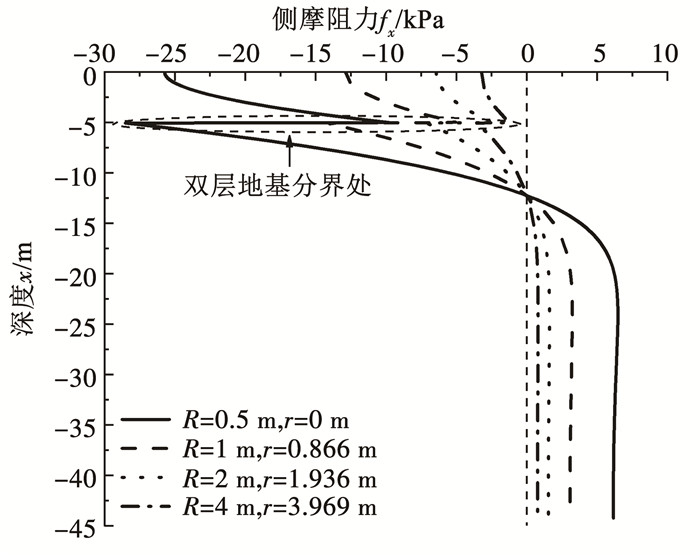
|
图 12 桩径对侧摩阻力的影响 Fig. 12 Influence of pile diameter on skin friction |
基于连续排水边界条件,建立了考虑吹填土及下卧地基土在吹填土自重作用下固结沉降的桩土相互作用模型,求解了桩侧摩阻力、桩身轴力随时间和深度变化的解析解,并将本文解析解与已有文献中的试验数据进行了对比,验证了本文解析解的合理性。通过在顶层和底层土体之间添加孔压和渗透速率连续的成层土体,本文的理论解可扩展到成层地基问题中去,这一问题将在之后的工作中展现。本文的主要结论有:
1) 固结时间对桩的侧摩阻力有影响,随着时间的增加,侧摩阻力逐渐增大,但随着时间的增加,对侧摩阻力和轴力的影响越来越小,因此,实际工程中在时间因子达到5时进行施工,可以结合土体高度和固结系数求出最佳施工时间(t=TvH2/Cv)。
2) 较大的双层地基厚度比和桩顶荷载是减小负摩阻力的有利因素。双层地基厚度比越大,侧摩阻力越小,桩侧摩阻力中性点位置越浅;桩顶荷载越大,负摩阻力越小,桩侧摩阻力中性点的位置越浅。
3) 在截面面积不变的情况下,增大管桩外径,并不会改变中性点的位置,并且轴力的大小完全不变,但是会减小侧摩阻力,故工程中可以通过增大桩径提高桩基的承载力。
| [1] |
韩会令, 刘振旺, 李国杰. 滨海吹填造陆地区岩土工程勘察问题分析与评价[J]. 土工基础, 2014, 28(3): 106. HAN Huiling, LIU Zhenwang, LI Guojie. Geotechnical considerations in near shore land reclamation by hydraulic fill[J]. Soil Engineering and Foundation, 2014, 28(3): 106. |
| [2] |
TERZAGHI K. Erdbaumechanik auf bodenphysikalischer grundlage[M]. Vienna: Leipzig Deuticke, 1925: 175.
|
| [3] |
GRAY H. Simultaneous consolidation of contiguous layers of unlike compressible soils[J]. Transactions of the American Society of Civil Engineering, 1945, 37(4): 426. |
| [4] |
SCHIFFMAN R L, STEIN J R. One-dimensional consolidation of layered systems[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(4): 1499. DOI:10.1061/JSFEAQ.0001453 |
| [5] |
LEE P K K, XIE K H, CHEUNG Y K. A study on one-dimensional consolidation of layered systems[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 1992, 16(11): 815. DOI:10.1002/nag.1610161104 |
| [6] |
XIE Kanghe, XIE Xinyu, GAO Xiang. Theory of one dimensional consolidation of two-layered soil with partially drained boundaries[J]. Computers and Geotechnics, 1999, 24(4): 265. DOI:10.1016/S0266-352X(99)00012-9 |
| [7] |
CHEN Renpeng. One-dimensional nonlinear consolidation of multi-layered soil by differential quadrature method[J]. Computers and Geotechnics, 2005, 32(5): 358. DOI:10.1016/j.compgeo.2005.05.003 |
| [8] |
ZOU Shengfeng, LI Jinzhu, XIE Xinyu. A semi-analytical solution for one-dimensional elasto-viscoplastic consolidation of layered soft clay[J]. Applied Clay Science, 2018, 153: 9. DOI:10.1016/j.clay.2017.11.042 |
| [9] |
梅国雄, 夏君, 梅岭. 基于不对称连续排水边界的太沙基一维固结方程及其解答[J]. 岩土工程学报, 2011, 33(1): 28. MEI Guoxiong, XIA Jun, MEI Ling. Terzaghi's one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 28. |
| [10] |
宗梦繁, 吴文兵, 梅国雄, 等. 连续排水边界条件下土体一维非线性固结解析解[J]. 岩石力学与工程学报, 2018, 37(12): 2829. ZONG Mengfan, WU Wenbing, MEI Guoxiong, et al. An analytical solution for one-dimensional nonlinear consolidation of soils with continuous boundary[J]. Chinese Journal of Mechanics and Engineering, 2018, 37(12): 2829. DOI:10.13722/j.cnki.jrme.2018.0602 |
| [11] |
YANG Xiaoyan, ZONG Mengfan, TIAN Yi, et al. One-dimensional consolidation of layered soils under ramp load based on continuous drainage boundary[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2021, 45(6): 738. DOI:10.1002/nag.3176 |
| [12] |
李称, 吴文兵, 梅国雄, 等. 不同排水条件下城市固废一维降解固结解析解[J]. 岩土力学, 2019, 40(8): 3071. LI Chen, WU Wenbing, MEI Guoxiong, et al. Analytical solution for 1D degradation-consolidation of municipal solid waste under different drainage conditions[J]. Engineering Mechanics, 2019, 40(8): 3071. DOI:10.16285/j.rsm.2018.0936 |
| [13] |
RANDOLPH M F, WROTH C P. Analytical solution for the consolidation around a driven pile[J]. Journal of the Geotechnical Engineering Division, 1979, 3(3): 217. DOI:10.1002/nag.1610030302 |
| [14] |
POULOS H G, DAVIS E H. The settlement behaviour of single axially loaded incompressible piles and piers[J]. Géotechnique, 1968, 18(3): 351. DOI:10.1680/geot.1968.18.3.351 |
| [15] |
RANDOLPH M F, WORTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of the Geotechnical Engineering Division, 1978, 104(12): 1465. DOI:10.1061/AJGEB6.0000729 |
| [16] |
王奎华, 吕述晖, 吴文兵, 等. 层状地基中基于虚土桩模型的单桩沉降计算方法[J]. 工程力学, 2013, 30(7): 75. WANG Kuihua, LV Shuhui, WU Wenbing, et al. A new calculation method for the settlement of single pile based on virtual soil-pile model in layered soils[J]. Engineering Mechanics, 2013, 30(7): 75. DOI:10.6052/j.issn.1000-4750.2012.03.0171 |
| [17] |
ZHANG Yunpeng, WU Wenbing, JIANG Guosheng, et al. A new approach for estimating the vertical elastic settlement of a single pile based on the fictitious soil pile model[J]. Computers and Geotechnics, 2021, 134: 104100. DOI:10.1016/j.compgeo.2021.104100 |
| [18] |
ZHANG Y P, ZHANG H K, EL NAGGAR M H, et al. A novel soil-pile interaction model for vertical pile settlement prediction[J]. Applied Mathematical Modelling, 2021, 99: 478. DOI:10.1016/j.apm.2021.07.004 |
| [19] |
NI Pengpeng, SONG Linhui, MEI Guoxiong, et al. Generalized nonlinear softening load-transfer model for axially loaded piles[J]. International Journal of Geomechanics, 2017, 17(8): 04017019. DOI:10.1061/(asce)gm.1943-5622.0000899 |
| [20] |
ZHANG Qianqing, ZHANG Zhongmiao. A simplified nonlinear approach for single pile settlement analysis[J]. Canadian Geotechnical Journal, 2012, 49(11): 1256. DOI:10.1139/t11-110 |
| [21] |
曹汉志. 桩的轴向荷载传递及荷载-沉降曲线的数值计算方法[J]. 岩土工程学报, 1986, 8(6): 37. CAO Hanzhi. Numerical calculation method of axial load transfer and load settlement curve of pile[J]. Chinese Journal of Geotechnical Engineering, 1986, 8(6): 37. |
| [22] |
周国林. 单桩负摩阻力传递机理分析[J]. 岩土力学, 1991, 12(3): 35. ZHOU Guolin. Analysis of negative skin friction transfer mechanism of single pile[J]. Rock and Soil Mechanics, 1991, 12(3): 35. DOI:10.16285/j.rsm.1991.03.004 |
| [23] |
赵明华, 贺炜, 曹文贵. 基桩负摩阻力计算方法初探[J]. 岩土力学, 2004, 25(9): 1442. ZHAO Minghua, HE Wei, CAO Wengui. Study on calculation of negative skin friction resistance on piles[J]. Rock and Soil Mechanics, 2004, 25(9): 1442. DOI:10.16285/j.rsm.2004.09.020 |
| [24] |
赵明华, 胡倩, 杨超炜, 等. 考虑地基土非线性固结的桩侧负摩阻力计算方法研究[J]. 岩土工程学报, 2016, 38(8): 1417. ZHAO Minghua, HU Qian, YANG Chaowei, et al. Negative skin friction of piles considering nonlinear consolidation of soil[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1417. DOI:10.11779/CJGE201608008 |
| [25] |
杨怡青. 自重固结影响下吹填土中桩基负摩阻力及承载力分析[D]. 镇江: 江苏大学, 2020 YANG Yiqing. The analysis for the negative frictional force and bearing capacity of pile foundations in a dredging site with consideration of self-weight consolidation[D]. Zhenjiang: Jiangsu University, 2020 |
| [26] |
马时冬. 桩身负摩阻力的现场测试与研究[J]. 岩土力学, 1997, 18(1): 8. MA Shidong. Field test and research on negative skin friction of piles[J]. Rock and Soil Mechanics, 1997, 18(1): 8. DOI:10.16285/j.rsm.1997.01.00 |
| [27] |
夏力农, 雷鸣, 聂重军. 桩顶荷载对负摩阻力性状影响的现场试验[J]. 岩土力学, 2009, 30(3): 664. XIA Linong, LEI Ning, NIE Chongjun. Field test of influence of load at pile top on negative skin friction behaviors[J]. Rock and Soil Mechanics, 2009, 30(3): 664. DOI:10.16285/j.rsm.2009.03.045 |
| [28] |
黄挺, 龚维明, 戴国亮, 等. 桩基负摩阻力时间效应试验研究[J]. 岩土力学, 2013(10): 108. HUANG Ting, GONG Weiming, DAI Guoliang, et al. Experimental study of time effect of negative skin friction on pile[J]. Rock and Soil Mechanics, 2013(10): 108. DOI:10.16285/j.rsm.2013.10.039 |
| [29] |
马学宁, 付江, 王军, 等. 不同堆载形式对群桩负摩阻力的影响[J]. 岩土力学, 2018, 39(10): 33. MA Xuening, FU Jiang, WANG Jun, et al. Effect of different surcharge loading forms on negative skin friction of pile groups[J]. Rock and Soil Mechanics, 2018, 39(10): 33. DOI:10.16285/j.rsm.2017.2134 |
| [30] |
律文田, 冷伍明, 王永和. 软土地区桥台桩基负摩阻力试验研究[J]. 岩土工程学报, 2005, 27(6): 24. LV Wentian, LENG Wuming, WANG Yonghe. Experimental study on negative skin friction of abutment pile foundation in soft soil area[J]. Journal of Geotechnical Engineering, 2005, 27(6): 24. DOI:10.3321/j.issn:1000-4548.2005.06.007 |
| [31] |
夏力农, 杨秀竹. 桩顶荷载影响负摩阻力的现场试验与数值模拟[J]. 铁道科学与工程学报, 2008, 5(5): 46. XIA Linong, YANG Xiuzhu. Field tests and numerical simulation of working load influences on negative skin friction behaviors of piles[J]. Journal of Railway Science and Engineering, 2008, 5(5): 46. DOI:10.19713/j.cnki.43-1423/u.2008.05.010 |
| [32] |
谢康和. 双层地基一维固结理论与应用[J]. 岩土工程学报, 1994, 16(5): 24. XIE Kanghe. One dimensional consolidation theory and application of double layered foundation[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24. DOI:10.3321/j.issn:1000-4548.1994.05.004 |
| [33] |
KULHAWY F H. Limiting tip and side resistance: fact or fallacy?[C]// Proceeding of Symposium on Analysis and Design of Pile Foundations. San Francisco: American Society of Civil Engineers, 1984: 80. DOI: 10.1016/0148-9062(86)91224-6
|
 2022, Vol. 54
2022, Vol. 54


