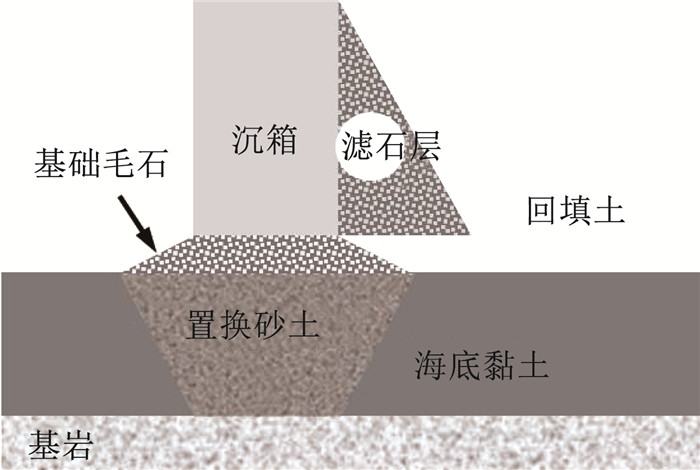
重力式沉箱结构广泛应用于港口码头和挡墙岸壁。港口码头常处于河流冲积区域,地基土软弱,常需对沉箱基础进行置换和回填处理,常用材料有砂土、碎石土等。图 1为典型的沉箱结构示意,沉箱底部和墙后一定范围内的海底黏土需置换为强度较高的砂土或碎石土等以满足承载力和正常工作要求。由于地下水位较高,在波浪或地震荷载作用下,基底和墙后置换砂土的动力液化可能导致沉箱码头出现倾斜、向海侧移动、沉降等灾害[1]。
|
图 1 沉箱码头示意 Fig. 1 Diagram of caisson wharf |
Taiyab等[2]研究了动力作用下沉箱码头结构与土的相互作用,并分析了置换区和回填区土体密实度对沉箱结构抗震能力的影响,发现沉箱趾部地基土体的致密化能显著减轻沉箱码头的位移响应。Alyami等[3]探究了渗透系数对沉箱码头结构孔隙水压力的影响以及回填土和地基土的相对密实度对沉箱码头抵抗地震残余变形的影响。Dakoulas等[4]研究了沉箱码头在地震荷载作用下侧向位移、塑性应变和孔隙水压力的演化规律,发现了沉箱码头惯性力、墙后土压力和孔隙水压力之间复杂的相互作用。王丽艳等[5]详细讨论了地震动水平、结构宽高比等因素对液化地基中沉箱码头残余变形的影响规律。佟彬等[6]分析了振冲加密优化设计对沉箱码头液化灾害的减弱作用。
上述基于有限元方法的沉箱码头地震响应研究对工程领域沉箱结构减灾设计具有重要指导作用。但对于存在较大变形的情况,传统有限元方法可能由于网格畸变出现分析中断、精度丧失等问题而不能正确反映结构的动力响应过程。对于重力式沉箱码头,在置换区和回填区土体密实度较小的情况下,严重的液化变形可能导致网格畸变从而引起分析中断。基于此,开发了一种解耦合任意拉格朗日欧拉方法(ALE方法)解决强震作用下沉箱码头大变形导致的网格畸变、分析中断、精度丧失等问题,并将其用于沉箱码头的液化减灾措施评价。
1 控制方程及ALE方法简介 1.1 饱和砂土控制方程基于水土二相混合理论,将土骨架位移u和孔隙水压力p作为变量,Uzuoka[7]建立了u-p形式的饱和砂土场方程式:
| $ \begin{gathered} \rho \boldsymbol{\ddot{u}}^{\mathrm{s}}=\nabla \boldsymbol{\sigma}+\rho \boldsymbol{b} \\ \rho^{1} \operatorname{tr}\left(\ddot{\boldsymbol{\varepsilon}}^{\mathrm{s}}\right)-\nabla^{2} \boldsymbol{p}_{\mathrm{d}}-\frac{\gamma^{1}}{k}\left(\frac{1}{n} \operatorname{tr}\left(\ddot{\boldsymbol{\varepsilon}}^{\mathrm{s}}\right)-\frac{1}{K^{\mathrm{l}}} \dot{p_{\mathrm{d}}}\right)=\bf{0} \end{gathered} $ | (1) |
式中:ρ为二相混合体密度;
采用虚位移原理对式(1)进行空间离散,其中超孔隙水压力二阶梯度项采用有限差分法进行空间离散[8],得到FEM-FDM耦合的二相混合体空间离散方程,即
| $ \begin{aligned} &{[\boldsymbol{M}]\left\{{ }^{t+\Delta t} \ddot{\boldsymbol{U}}\right\}+[\boldsymbol{C}]\left\{{ }^{t+\Delta t} \dot{\boldsymbol{U}}\right\}+[\boldsymbol{K}]\{\Delta \boldsymbol{U}\}+} \\ &{\left[\boldsymbol{K}_{\mathrm{V}}\right]\left\{{ }^{t+\Delta t} p_{\mathrm{E}}\right\}=\{\boldsymbol{F}\}} \\ &\rho^{1}\left[\boldsymbol{K}_{\mathrm{V}}\right]^{\mathrm{T}}\left\{{ }^{t+\Delta t} \boldsymbol{U}\right\}-\frac{\gamma^{1}}{k}\left[\boldsymbol{K}_{\mathrm{V}}\right]^{\mathrm{T}}\left\{{ }^{t+\Delta t} \dot{\boldsymbol{U}}\right\}+[\boldsymbol{a}]\left\{{ }^{t+\Delta t} p_{\mathrm{E}}\right\}- \\ &{[\boldsymbol{A}]\left\{{ }^{t+\Delta t} p_{\mathrm{E}}\right\}=\bf{0}} \end{aligned} $ | (2) |
式中:[M]为质量矩阵;[K]为刚度矩阵;[KV]为耦合矩阵;ΔU为固相位移增量;
Donea等[10]结合拉格朗日方法和欧拉方法的优点,发展了一种任意拉格朗日欧拉方法(Arbitrary Lagrangian Eulerian Method)用以解决流体力学问题,此后该方法被众多研究者引入固体力学的非线性问题研究中。
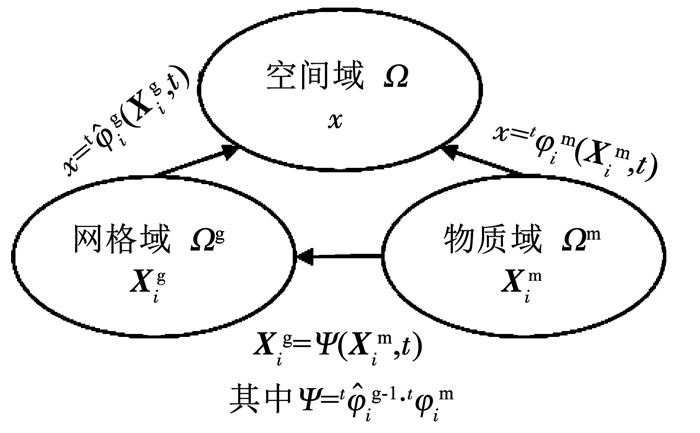
ALE方法中,在计算空间上定义了物质域和网格域(计算参考域),分别由一系列物质点Xm和网格点Xg组成,由此将物质点运动和网格的变形分离。令x=tφim(Xim, t)和
|
图 2 物质域、网格域、空间域之间的映射关系 Fig. 2 Mapping relationship among material domain, grid domain, and spatial domain |
ALE方法中,场方程式的建立和离散基于计算参考域,任意时刻t,式(1)的各变量为当前时刻网格域对应的值,而变量的更新基于材料的物质域。网格域和物质域的变量映射关系可由对流方程[11]表示
| $ { }^{t} \dot{f}^{\mathrm{m}}={ }^{t} \dot{f}^{\mathrm{g}}+{ }^{t} \boldsymbol{c} \cdot \frac{\partial^{t} f}{\partial^{t} x} $ | (3) |
式中:tc=(tvm-tvg)为物质点和网格点的对流速度,
| $ \begin{aligned} &{[\boldsymbol{M}]\left\{{ }^{t+\Delta t} \dot{\boldsymbol{U}}^{\mathrm{m}}\right\}+\left[\boldsymbol{C}^{1}+\boldsymbol{C}^{2}\right]\left\{{ }^{t+\Delta t} \dot{\boldsymbol{U}}^{\mathrm{m}}\right\}-\left[\boldsymbol{C}^{2}\right]\left\{{ }^{t+\Delta t} \dot{\boldsymbol{U}}^{\mathrm{g}}\right\}+} \\ &{\left[\boldsymbol{K}+\boldsymbol{K}^{1}\right]\left\{\Delta \boldsymbol{U}^{\mathrm{m}}\right\}-\left[\boldsymbol{K}^{1}\right]\left\{\Delta \boldsymbol{U}^{\mathrm{g}}\right\}=\{\boldsymbol{F}\}} \end{aligned} $ | (4) |
式中:C1、C2和K1均为完全耦合ALE方法中与对流项相关的矩阵,具体形式见文献[11],右上标m表示物质,g表示网格,其余各矩阵的含义均与式(2)相同。式(4)未考虑黏滞阻尼,如考虑可参考式(2)引入阻尼项。
式(4)中存在物质点和网格点两组未知量,无法得到系统的唯一解,因此,需要引入反映物质点和网格点运动关系的补充方程,通常表达如下[12]:
| $ \boldsymbol{u}^{\mathrm{g}}=\boldsymbol{\alpha}+\boldsymbol{B} \boldsymbol{u}^{\mathrm{m}} $ | (5) |
式中α和B 为反映物质点和网格点相对运动的矢量和矩阵,在耦合的ALE方法中,可依据事先指定的网格运动方法和边界限制条件确定其具体形式[12]。当α= 0,B=I时,ALE方法退化为更新拉格朗日方法;当α= 0,B= 0时,ALE方法退化为欧拉方法。
耦合的ALE方法需事先指定物质点和网格点的运动关系,而预先指定的运动关系往往比较简单,如超限映射法等。对于结构形式复杂或变形较大的情况,相对简单的物质点和网格点运动关系可能限制ALE方法解决大变形问题的能力。因此在实践中,解耦合的ALE方法更为普遍。该方法基于算子分离技术将一个完整的ALE分析步分解为:1) 一个忽略网格和物质相对运动的拉格朗日分析步,即传统更新拉格朗日方法;2) 跟随一个将场变量在物质域和网格域之间传递的欧拉分析步。在拉格朗日分析步,网格随物质点变形;在欧拉分析步利用网格优化算法对计算域变形网格进行调整,并借助变量传递算法将场变量从物质域传递到调整后的网格域,详细实现过程可参考文献[13]。本文基于有限变形理论和既有更新拉格朗日程序,利用算子分离技术,在每一个拉格朗日分析步后增加一个欧拉分析步,将其扩展为解耦的ALE分析步,发展了一种解耦合ALE有限元程序[13]并将其用于重力式沉箱码头的动力液化及减灾措施分析。
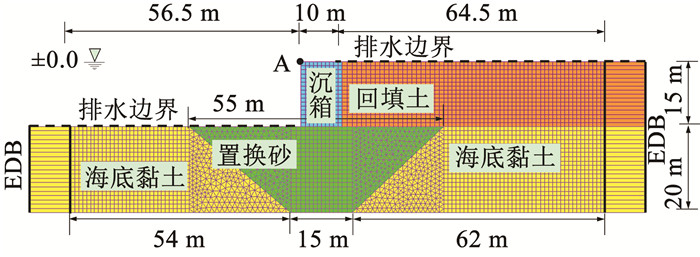
2 数值模型 2.1 模型简介如图 3所示,沉箱模型位于深厚海底黏土层上,沉箱底部用砂土置换海底黏土以提高地基承载力,墙后回填砂土以满足码头正常工作。模型底部完全固定,两侧边界限制水平位移,顶部为可自由排水边界(粗虚线),底部和两侧边界为不排水边界。此外,在模型两侧设置宽高比较大(>100)的单元,并绑定两侧边界单元上同一水平高度处节点的水平自由度模拟自由场边界[14],相关研究[15-16]也表明这种等位移边界条件可以消除边界效应的影响,在砂土动力液化分析中具有良好的效果。
|
图 3 沉箱结构及其有限元网格 Fig. 3 Caisson structure and its finite element mesh |
采用Oka等[17]基于非线性移动硬化准则提出的一种循环弹塑性模型模拟饱和砂土。该模型通过引入超固结边界面模拟超固结状态下砂土的剪胀特性,同时考虑了初始各向异性的衰退特性从而能够描述各项异性固结。模型中各部分土体的参数如表 1所示,剪胀参数(D0,n)以调整抗液化强度线的斜率,参考应变(γrefp,γrefe)用来控制应力比超过相转换线后的应变快速增长。由于黏土具有黏聚力且不会因液化迅速软化,将黏土参数中的参考剪应变γrefp和γrefe均设定为一个较大的值,使得黏土刚度随着剪应变的累积而逐渐衰减,但又不像砂土一样在达到相变比后急剧减小[14]。此外,对于液化后的砂土,考虑本构模型中剪切模量的应力依赖,引入相应的液化机制,使液化土体表现出类似于牛顿黏性流体的特征。为反映地震作用下最不利的状况,置换砂和回填土均为松砂,沉箱结构赋予较大的弹性模量和泊松比模拟刚体。
| 表 1 土体参数 Tab. 1 Soil parameters |
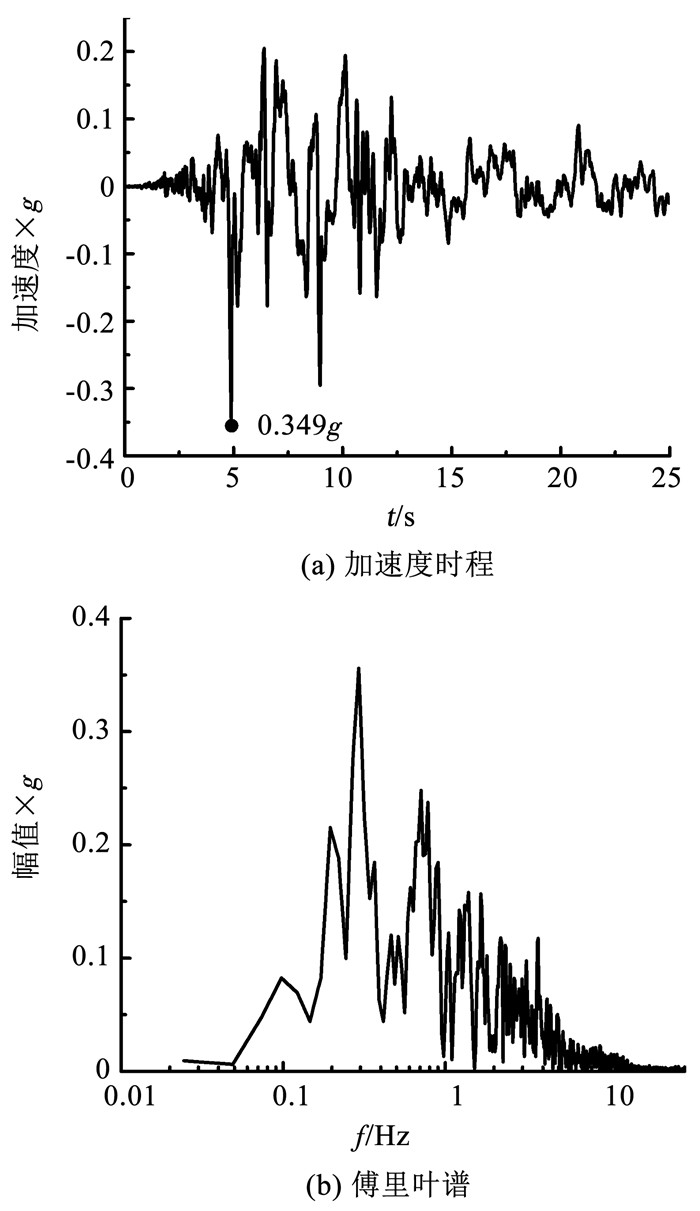
Taiyab等[2]研究表明,相对于高频荷载,重力式码头在低频荷载作用下产生更大的位移。选择1999年土耳其地震记录的Kocaeli波作为输入荷载,其加速度时程曲线和傅里叶谱如图 4所示。该波的峰值加速度为0.349g,作为强震输入时将被调整至0.5g,持时25 s,记录间隔为0.01 s。图 4(b)显示,Kocaeli波的主频小于1 Hz,可以使沉箱码头产生较大的动力响应。
|
图 4 Kocaeli波及其傅里叶谱 Fig. 4 Acceleration and Fourier spectrums of Kocaeli |
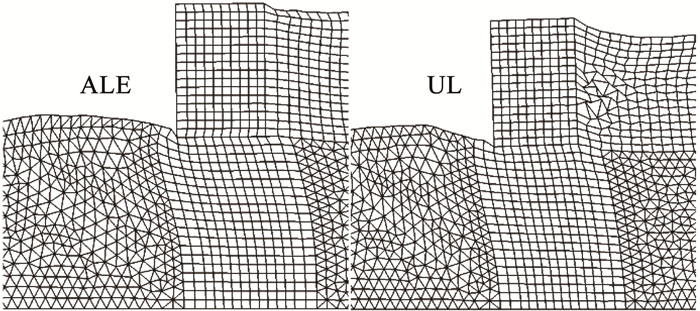
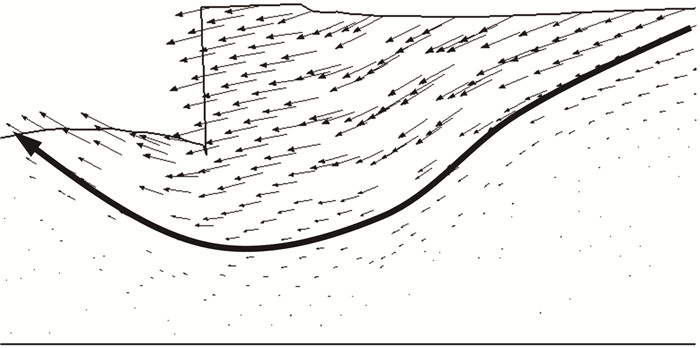
ALE方法能完整反映结构变形并保持网格的整体质量。图 5为使用UL方法和ALE方法计算时,沉箱结构的网格变形,其中,使用UL方法计算时,墙后土体变形较大引起墙后局部网格畸变,导致计算在t=17.9 s时中断。而ALE方法显示,计算完成时整体网格仍处于健康状态。图 5中两种方法的变形网格在沉箱趾部前端区域有明显的隆起,沉箱墙体后背有明显的沉降。ALE方法计算结束时的位移矢量图显示了趾部前端隆起和墙后沉降的原因。如图 6所示,由于置换区和回填区砂土液化,沉箱结构沿着置换区和海底黏土交界面形成弧形的滑动带,最终土体变形在沉箱趾部前端堆积,导致趾部前端隆起,墙体后方沉降。
|
图 5 两种方法变形网格图 Fig. 5 Deformed meshes of UL method and ALE method |
|
图 6 计算结束时位移矢量图(ALE) Fig. 6 Displacement vector graph at the end of calculation (ALE) |
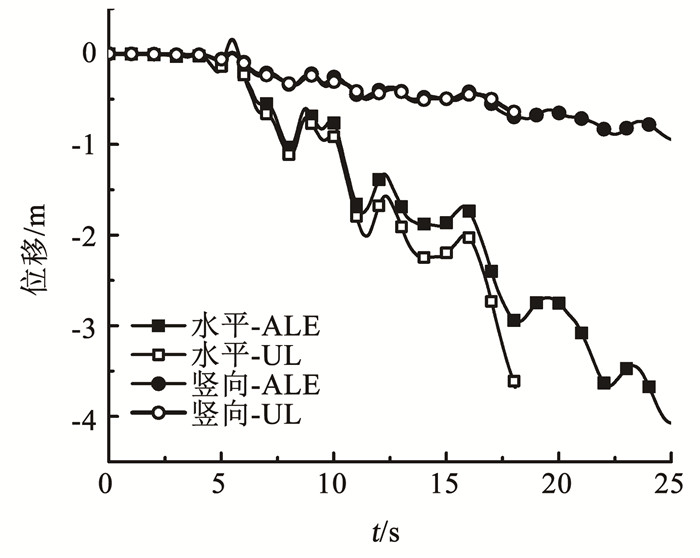
ALE方法能反映最终的结构位移。图 7为沉箱顶点(图 3A点)使用UL方法和ALE方法的水平和竖向位移时程曲线。可以看出,在地震波加载的前10 s, 两种方法计算的沉箱顶点位移基本保持一致。此后,两种方法的计算结果出现偏差,水平位移比竖向位移偏差较大,直到UL方法由于网格畸变中断。UL方法计算中断时,由于地震波振动仍在持续,沉箱顶点位移无收敛趋势,无法正确反映最终的位移响应,而ALE方法计算结束时的沉箱顶点水平位移达4.1 m,比UL方法中断时大11%。
|
图 7 两种方法对应沉箱顶点位移 Fig. 7 Displacement of caisson apex under UL method and ALE method |
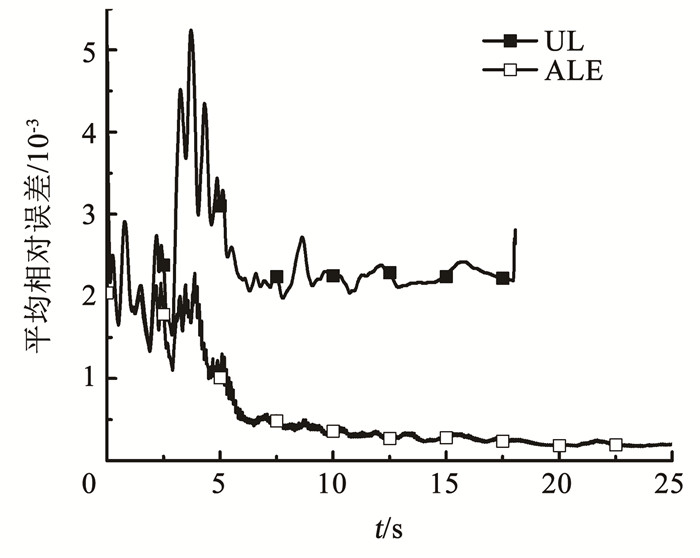
ALE方法能提供相对误差较小的数值解。为表征两种方法的精度,引入基于单元应变的平均相对误差[18]评估计算过程中的整体误差。图 8为两种方法的平均相对误差曲线。两种方法计算的平均相对误差的发展趋势与地震波的波动情况基本一致。在加载初期,荷载和变形很小,相对误差的波动较小。在3~6 s时经历地震荷载的峰值,总体的相对误差不大,导致平均相对误差经历较大的波动,随后出现下降。在8~10 s时,地震波出现一次较大波动,但由于此时总体误差较大,平均相对误差出现小幅增大,但未出现加载前期的剧烈波动。此外,ALE方法的平均相对误差除在加载初期和UL方法相比差别不大之外,总体上远低于UL方法的平均相对误差。
|
图 8 两种方法对应平均相对误差 Fig. 8 Average relative error under UL method and ALE method |
在回填区和置换区为松砂的情况,强震作用下的沉箱趾部前端隆起严重,码头墙后方有明显沉降,沉箱顶点位移达4 m,显然不能保证经历地震后的正常工作。沉箱抗液化减灾措施通常有增加置换区和回填区土体的密实度、利用碎石桩加固回填区土体等,本节将利用ALE方法探究置换区和回填区密砂加固在液化减灾中对沉箱码头位移、变形的影响,所用密砂材料参数见表 1。
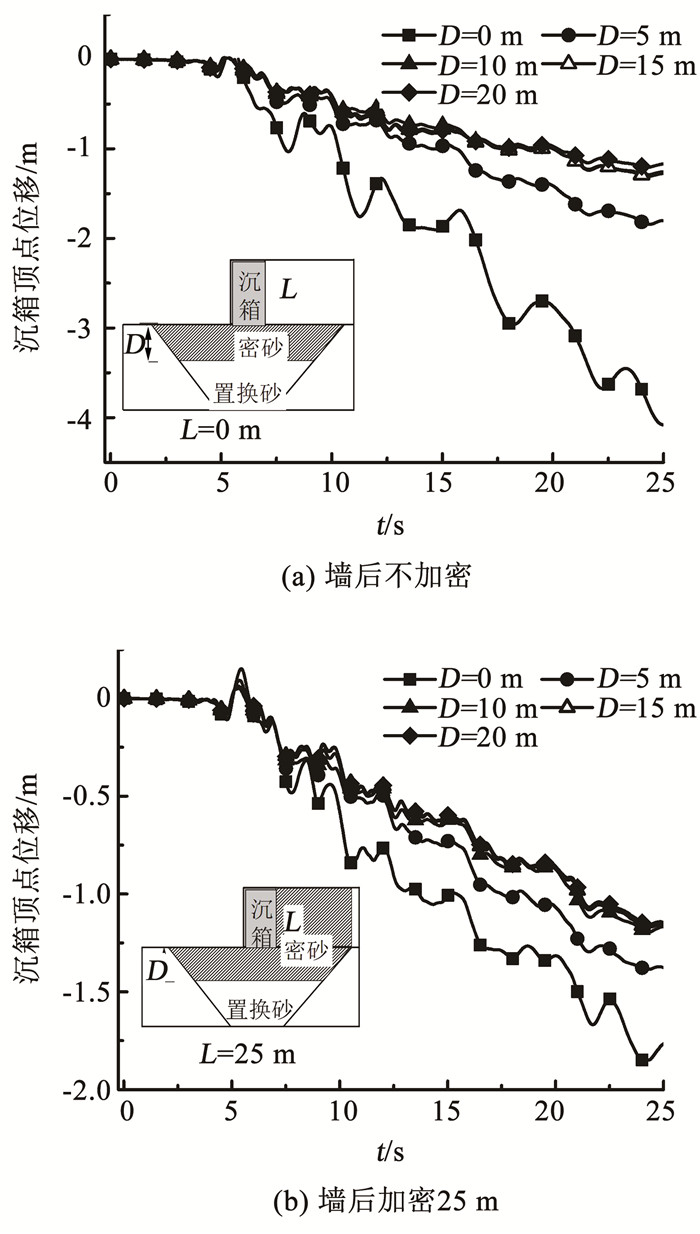
3.2.1 基底置换砂影响分析1) 基底置换砂对沉箱向海侧位移的影响。基底置换砂加密能有效减小沉箱的向海侧位移,但存在有效加密深度。图 9(a)为沉箱结构墙后回填区不加密、置换区加密不同深度时沉箱顶点的位移曲线。可以看出,置换区加密能有效地减小和改变沉箱的位移响应。在置换区加密深度D=0时,沉箱的位移响应在5 s以后变化剧烈,且增长速度较快,加载结束时位移达4.1 m。当D=5 m时,沉箱的位移响应明显发生改变,位移增长缓慢,加载结束时位移为1.8 m。当D增大至10 m时,沉箱的位移增长进一步放缓,加载结束时位移减小至1.26 m。D=15和20 m时,位移增长与D=10 m时差别很小。以上分析表明,当D≥10 m时,置换区加密深度对于沉箱位移发展的影响很小。图 9(b)为沉箱墙后存在25 m宽的回填加密区时,置换区不同加密深度对应的沉箱顶点位移。可以看出,回填加密区的存在不影响置换区加密深度增加对沉箱位移影响的规律,在D≥10 m时,置换加密区的增大对位移发展影响很小。图 9表明,置换区加密能显著改变沉箱位移的发展趋势,但存在有效加密深度,超过此深度,置换区加密深度的增加对沉箱位移的减弱作用影响很小。
|
图 9 沉箱顶点位移时程曲线 Fig. 9 Displacement time history curves of caisson apex |
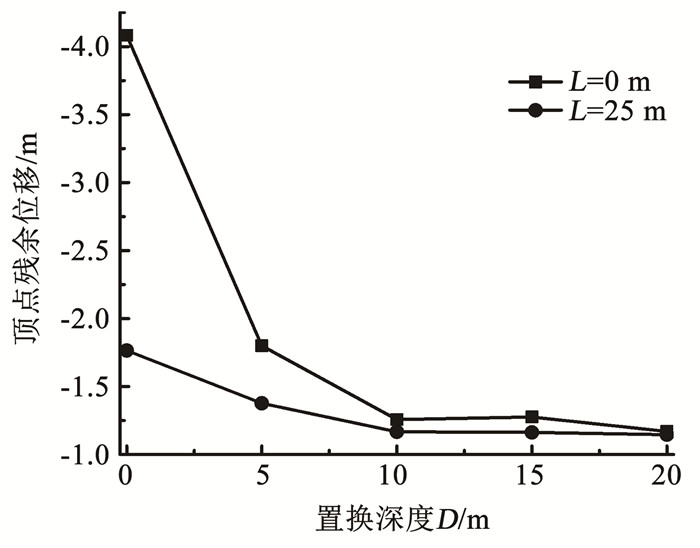
图 10为沉箱顶点的残余位移。可以看出,在D≥10 m时,置换加密深度增加对残余位移的影响很小,此时墙后回填加密区的存在对于残余位移的影响很小。当D < 10 m时,置换加密深度增加使沉箱顶点残余位移迅速减小,此时墙后回填区加密能进一步减小残余位移。以上表明,在置换加密深度达到临界深度前,回填区加密能增强沉箱码头抗震液化变形能力,当置换加密区深度超过临界值,墙后回填区加密对于沉箱码头的位移增长无明显抑制作用。
|
图 10 沉箱顶点残余位移 Fig. 10 Residual displacement of caisson apex |
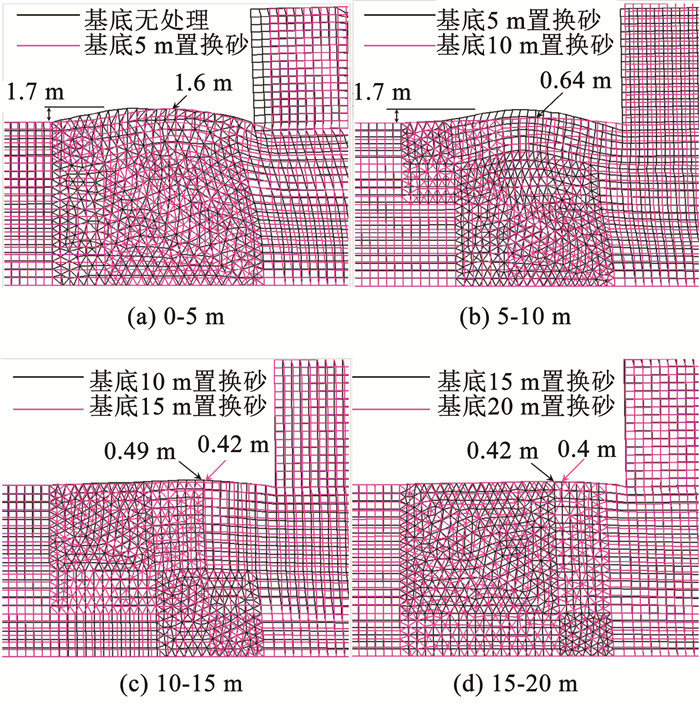
2) 基底置换砂对基础隆起的影响。基底置换区加密对沉箱趾部前端隆起有明显抑制作用。图 11为基底置换砂加密条件下,加载结束时网格的最终变形。图 11(a)显示加载结束,置换区不加密或加密深度不足时,沉箱趾部前端均有明显的隆起现象,最大隆起量达1.7和1.6 m,但基底加密的情况下沉箱的位移显著小于不加密情况。图 11(b)表明, 置换区深度增加至10 m时,沉箱趾部前端的隆起现象得到了明显的抑制,并且沉箱的位移进一步减小。图 11(c)和(d)显示,基底置换区加密深度从10 m增加到20 m,趾部前端最大隆起量仅从0.49 m减小至0.4 m,表明基底置换区加密深度在超过临界有效深度后(>10 m),继续增加对趾部前端隆起和沉箱位移的改善作用不明显。综上表明,基底置换区加密至临界有效深度前,对沉箱趾部前端和沉箱位移有明显的抑制作用,此后继续增加置换深度对隆起和位移的改善作用有限。
|
图 11 基底置换区加密深度对基底隆起的影响 Fig. 11 Influence of densification range of replacement region on the uplift of the front of the caisson toe |
1) 回填区对沉箱向海侧位移的影响。置换区不加密时,回填区加密能减小沉箱结构的位移,但存在有效加密范围;置换区加密时,回填区加密对沉箱结构的位移影响较小。图 12(a)为基底置换砂土不加密时,回填区不同加密宽度对应的沉箱顶点位移。可以看出,在置换区不加密情况下,回填区加密宽度≤25 m时,回填区加密宽度的增加对沉箱顶点位移影响较大,沉箱位移时程曲线差异明显,加密宽度越大,位移越小;回填区宽度≥40 m时,沉箱顶点位移时程曲线几乎重合。这表明沉箱背后回填区也存在临界加密宽度,超过此宽度,回填区的加密对沉箱位移无影响,而临界加密宽度可能与荷载类型、沉箱结构高宽比、场地地基条件等因素有关,实际应用中应根据具体工况确定合理的临界加密宽度。图 12(b)和(c)为基底置换区分别加密5和10 m时,回填区不同加密宽度对应的沉箱顶点位移时程。可以看出,在置换区加密的情况下,不同置换宽度对应的沉箱顶点位移呈现相似的发展趋势,仅在数值上有较小的差别,回填区加密宽度的增加不能明显减小沉箱顶点位移,说明回填区加密对沉箱顶点位移有抑制作用,但不是影响沉箱位移的主要因素。

|
图 12 沉箱顶点位移时程曲线 Fig. 12 Displacement time history curves of caisson apex |
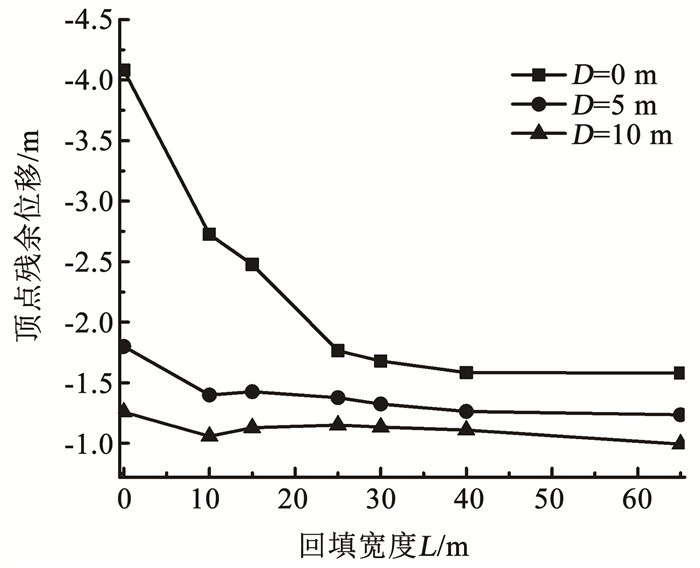
图 13为加载结束时,回填区不同加密宽度对应的沉箱顶点残余位移。可以看出,在置换区加密深度D=0 m时,随着回填区加密宽度增加,沉箱顶点残余位移有较大幅度的减小。而当D=5和10 m时,回填区加密宽度增加对沉箱顶点残余位移减小幅度很小,这也说明回填区的液化变形不是引起沉箱位移的主要原因。此外,可以发现,不同置换区加密深度下,回填区的临界有效加密宽度基本保持不变,这也说明回填区不是影响沉箱位移的主要原因。
|
图 13 沉箱顶点残余位移 Fig. 13 Residual displacement of caisson apex |
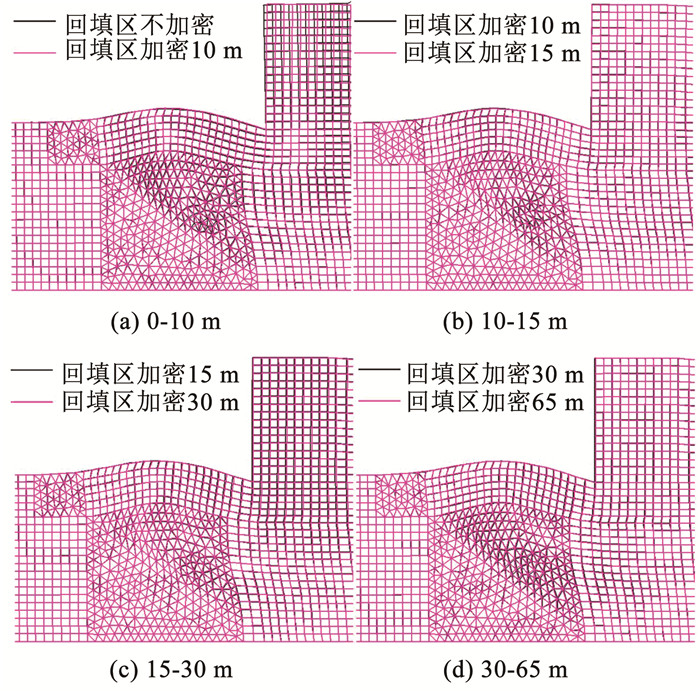
2) 回填区对基础隆起的影响。回填区加密对基础的隆起无影响。图 14为置换区加密深度为5 m时,回填区不同加密宽度对应的网格变形。可以看出,不同加密宽度对应的沉箱趾部前端的隆起形态基本不变,这表明沉箱趾部隆起主要受置换区液化变形影响,与回填区变形无关。此外,观察沉箱变形可以看出,置换区加密情况下,回填区加密对沉箱结构的变形影响很小。
|
图 14 回填区加密宽度对基底隆起的影响 Fig. 14 Influence of densification range of backfill region on the uplift of the front of the caisson toe |
在沉箱结构的液化减灾措施中,碎石桩加固回填区土体也是一种有效的措施[1, 19]。前两节的分析中沉箱结构的置换区和回填区加密都存在一个有效的临界加密范围,超过此范围,增大加密范围对沉箱结构位移响应减小作用基本不变。本节考虑在临界加密范围基础上,加密置换区和回填区土体联合碎石桩加固回填区对沉箱结构抗震性能的影响。
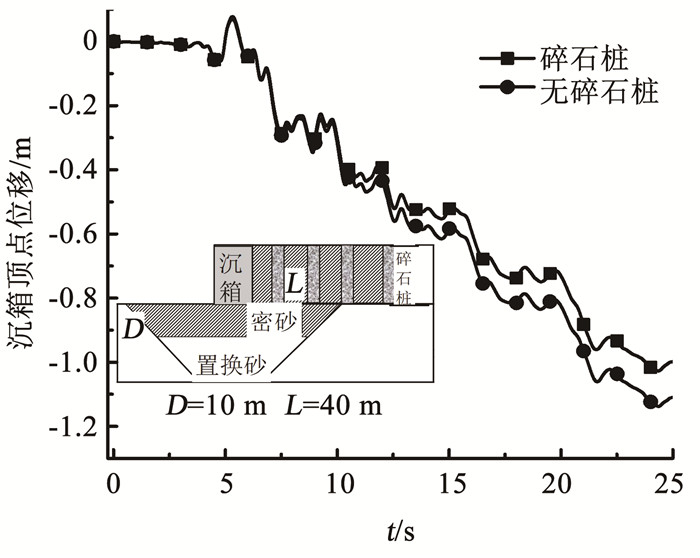
联合碎石桩加固能进一步增强沉箱结构抗震性能。图 15为联合碎石桩加固条件下,沉箱顶点位移时程曲线。可以看出,在加载前10 s左右,两种措施对应的沉箱顶点位移基本一致;随着加载进行和液化区的发展,联合碎石桩加固的条件下,沉箱位移相比无碎石桩的进一步减小,这表明联合碎石桩加固方案能在置换区和回填区临界加密范围的基础上进一步提高沉箱结构的抗震性能。
|
图 15 沉箱顶点位移时程曲线 Fig. 15 Displacement time history curves of caisson apex |
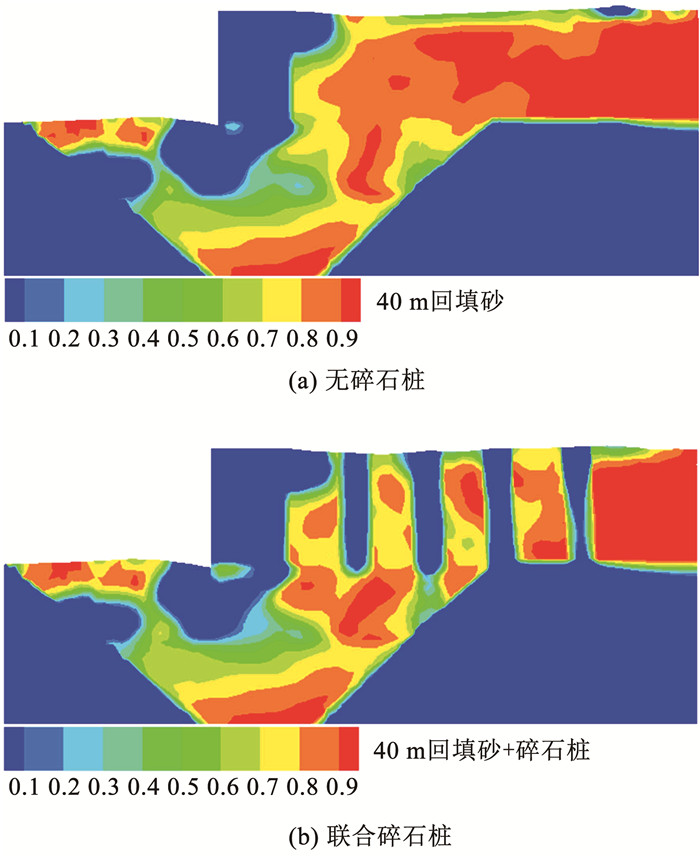
定义单元超孔隙水压力p与初始竖向有效应力σ′v的比值评价土体的液化程度,即超孔隙水压力比。图 16为联合碎石桩加固条件下,加载结束时超孔隙水压力比分布。图 16(a)显示,加载结束时,距离沉箱墙后约40 m的位置,超孔隙水压力比达0.9以上,处于液化状态。在0~40 m内,大部分区域也处于0.8以上的状态,接近液化状态。图 16(b)显示,液化区被阻挡在碎石桩加固范围之外,在碎石桩加固范围内,仅有局部区域孔压在0.8以上,大部分区域超孔隙水压力比相对较低。这是由于碎石桩的渗透系数较大,减小了碎石桩加固区域超孔隙水压力的累积速度,碎石桩的存在提高了沉箱结构抵抗地震液化的潜力。
|
图 16 超孔隙水压力比云图 Fig. 16 Contour of excess pore water pressure ratio |
1) 松砂地基沉箱码头在强震作用下由于液化大变形造成网格畸变而导致UL方法失效,不能完整反映沉箱码头的强震响应;本研究开发的ALE方法能够在保证网格质量的情况下,反映沉箱码头的强震响应过程,并提供精度较高的数值结果。
2) 在松砂地基沉箱码头的抗液化变形措施中,置换区和回填区的加密均存在一个临界的有效加密范围,超过此范围,对于沉箱码头的抗液化变形能力影响不大,与文献[2]的结论一致。而临界有效范围通常与荷载类型、结构高宽比、场地地层条件等因素有关,在实际应用中应根据具体工况加以确定。
3) 沉箱趾部前方的隆起主要受置换区砂土密实度的影响,而与回填区无关,在临界范围内,增加置换区砂土的密实度能显著改善趾部前方的隆起状况。在置换区不加密的情况下,回填区加密能降低沉箱结构的位移;而在置换区加密时,回填区加密处理对沉箱结构的位移影响很小,这也表明置换区土体变形是影响沉箱结构位移的主要原因。这与传统有限元方法结论一致,也表明ALE方法应用于沉箱码头动力液化分析的有效性,可以作为解决砂土动力液化大变形问题的一种有效途径。
4) 碎石桩联合置换区和回填区加密措施能够进一步减小沉箱结构的位移,提高沉箱结构的抗液化潜能。
| [1] |
刘汉龙, 井合进, 一井康二. 大型沉箱式码头岸壁地震反应分析[J]. 岩土工程学报, 1998(2): 26. LIU Hanlong, SUSUMU I, KOJI I. Seismic response analysis of large-size caisson quay wall[J]. Chinese Journal of Geotechnical Engineering, 1998(2): 26. |
| [2] |
TAIYAB A, ALAM J, ABEDIN Z. Dynamic soil-structure interaction of a gravity quay wall and the effect of densification in liquefiable sites[J]. International Journal of Geomechanics, 2014, 14(1): 20. DOI:10.1061/(ASCE)GM.1943-5622.0000278 |
| [3] |
ALYAMI M, ROUAINIA M, WILKINSON S M. Numerical analysis of deformation behaviour of quay walls under earthquake loading[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(3): 525. DOI:10.1016/j.soildyn.2008.06.004 |
| [4] |
DAKOULAS P, GAZETAS G. Insight into seismic earth and water pressures against caisson quay walls[J]. Géotechnique, 2008, 58(2): 95. DOI:10.1680/geot.2008.58.2.95 |
| [5] |
王丽艳, 陈香香, 刘汉龙. 液化地基中沉箱码头墙体地震残余变形的有效动应力研究[J]. 岩土力学, 2011, 32(11): 3361. WANG Liyan, CHEN Xiangxiang, LIU Hanlong. Effective stress study of seismic residual deformations of caisson quay wall in liquefied foundation[J]. Rock and Soil Mechanics, 2011, 32(11): 3361. DOI:10.16285/j.rsm.2011.11.035 |
| [6] |
TONG Bin, SCHAEFER V R. Optimization of vibrocompaction design for liquefaction mitigation of gravity caisson quay walls[J]. International Journal of Geomechanics, 2016, 16(4): 4016005. DOI:10.1061/(ASCE)GM.1943-5622.0000585 |
| [7] |
UZUOKA R. Analytical study on the mechanical behavior and prediction of soil liquefaction and flow[D]. Gifu: Gifu University, 2000
|
| [8] |
OKA F, YASHIMA A, SHIBATA T, et al. FEM-FDM coupled liquefaction analysis of a porous soil using an elasto-plastic model[J]. Applied Scientific Research, 1994, 52(3): 209. DOI:10.1007/BF00853951 |
| [9] |
TSAI C C, PARK D, CHEN C W. Selection of the optimal frequencies of viscous damping formulation in nonlinear time-domain site response analysis[J]. Soil Dynamics and Earthquake Engineering, 2014, 67: 353. DOI:10.1016/j.soildyn.2014.10.026 |
| [10] |
DONEA J, FASIOLI S P, GIULIANI S. Lagrangian and Eulerian finite element techniques for transient fluid structure interaction problems[C]//International Association for Structural Mechanics in Reactor Technology: Therm and Fluid/Struct Dyn Anal. [S. l. ]: [s. n. ], 1977
|
| [11] |
RODRÍGUEZ-FERRAN A, CASADEI F, HUERTA A. ALE stress update for transient and quasistatic processes[J]. International Journal for Numerical Methods in Engineering, 1998, 43(2): 241. |
| [12] |
BAYOUMI H N, GADALA M S. A complete finite element treatment for the fully coupled implicit ALE formulation[J]. Computational Mechanics, 2004, 33(6): 435. DOI:10.1007/s00466-003-0544-y |
| [13] |
LIU Shun, TANG Xiaowei, LI Jing. Extension of ALE method in large deformation analysis of saturated soil under earthquake loading[J]. Computers and Geotechnics, 2021, 133: 104056. DOI:10.1016/J.COMPGEO.2021.104056 |
| [14] |
MATSUO O, SHIMAZU T, UZUOKA R, et al. Numerical analysis of seismic behavior of embankments founded on liquefiable soils[J]. Soils and Foundations, 2000, 40(2): 21. DOI:10.3208/sandf.40.2_21 |
| [15] |
HU Jilei, CHEN Qihua, LIU Huabei. Relationship between earthquake-induced uplift of rectangular underground structures and the excess pore water pressure ratio in saturated sandy soils[J]. Tunnelling and Underground Space Technology, 2018, 79: 35. DOI:10.1016/j.tust.2018.04.039 |
| [16] |
BAO Xiaohua, YE Bin, YE Guanlin, et al. Co-seismic and post-seismic behavior of a wall type breakwater on a natural ground composed of liquefiable layer[J]. Natural Hazards, 2016, 83(3): 1799. DOI:10.1007/s11069-016-2401-2 |
| [17] |
OKA F, YASHIMA A, TATEISHI A, et al. A cyclic elasto-plastic constitutive model for sand considering a plastic-strain dependence of the shear modulus[J]. Géotechnique, 1999, 49(5): 661. DOI:10.1680/geot.1999.49.5.661 |
| [18] |
邵琪. 饱和砂土地震液化的网格自适应数值方法研究[D]. 大连: 大连理工大学, 2014 SHAO Qi. Study onadaptive remeshing numerical methods in seismic liquefaction of saturated sand[D]. Dalian: Dalian University of Technology, 2014 |
| [19] |
刘晓, 唐小微, 栾茂田. 地基液化导致沉箱码头破坏及地基加固方法的非线性数值分析[J]. 防灾减灾工程学报, 2009, 29(5): 518. LIU Xiao, TANG Xiaowei, LUAN Maotian. Nonlinear numerical analysis of caisson quay failure due to soil liquefaction and of soil strengthening method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29(5): 518. DOI:10.3969/j.issn.1672-2132.2009.05.008 |
 2022, Vol. 54
2022, Vol. 54


