2. 河北省地震工程研究中心,河北 唐山 063210;
3. 华北理工大学 建筑工程学院,河北 唐山 063210
2. Earthquake Engineering Research Center of Hebei Province, Tangshan 063210, Hebei, China;
3. College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan 063210, Hebei, China
矿山井塔结构体系一般由井塔和井筒组成。GB 50191—2012[1]第11.2.24条规定:“井塔采用固接于井筒上的井颈基础,抗震计算时,宜计及井塔、井筒和土的相互作用”。然而,工程设计中,往往是将井塔、井筒和地基分别进行考虑,忽略了土与井塔-井筒相互作用对井塔抗震分析的影响,因此,进行土与结构(井塔和井筒)相互作用对井塔抗震分析影响的研究尤为重要。
目前,关于土与井塔-井筒相互作用问题的研究还特别少。王依群等[2]依据波动理论和子结构方法,采用Novak阻抗函数来模拟土-井筒的相互作用,将土-井筒-井塔相互作用的实际受力状态简化为层状土-混凝土井筒-井塔相互作用的结构体系,并以固接于井筒井壁上的井塔(剪力墙结构形式)为例,就第一振型与工程实测数据进行分析对比,结果基本吻合。查晓礼[3]采用ANSYS有限元软件模拟了竖向荷载作用下筏板厚度对井塔-桩筏基础-地基-井壁体系沉降变形、应力变化的影响,结果表明,筏板厚度对桩筏基础的整体沉降变形影响不明显,随着筏板厚度的增加,桩承担的荷载将会减小。
综合国内外研究现状,一方面,仅有极少数学者[4]对土-井筒-井塔体系相互作用的问题进行了研究,并且现有的分析方法中没有直接建立体系时域内的运动方程;另一方面,现有研究并未系统分析不同场地下考虑相互作用对井塔地震反应的影响。基于此,采用理论分析和数值分析两种方法,结合东北某钢筋混凝土剪力墙结构井塔体系,建立了土-井筒-井塔体系在时域内的理论运动方程和数值分析模型,研究了不同场地(Ⅱ、Ⅲ类)下土-井筒-井塔体系的地震反应,评估了土与井塔-井筒相互作用对井塔抗震分析的影响,得出土与井塔-井筒相互作用对井塔地震反应的影响规律,为工程设计提供合理的理论依据和设计建议。
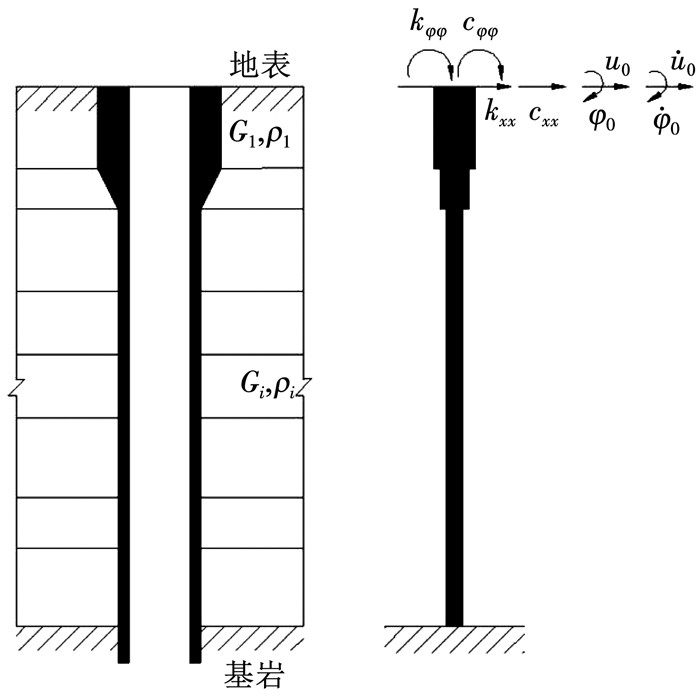
1 土-井筒-井塔体系的理论分析模型井筒采用Winkler[5-6]地基梁模型,井筒构造及简化模型示意见图 1,Gi为第i层地基土的剪切模量,ρi为第i层地基土的密度,kxx、kφφ、cxx和cφφ为井筒顶部运动的阻抗函数,u0、
|
图 1 井筒构造及简化模型示意 Fig. 1 Schematic diagram of well bore and its simplified model |
井塔采用Penzien[8-9]集中质量模型,井塔计算简化模型见图 2,mi为第i层塔的等效质量,ui、

|
图 2 井塔计算简化模型 Fig. 2 Simplified calculation model for shaft tower |
综上,以Winkler地基梁模型和Penzien集中质量模型为基础,采用弹簧和阻尼器模拟土-井筒之间的相互作用,土层采用水平向无限延伸的边界条件,建立考虑土与井塔-井筒相互作用的理论分析模型。
2 体系运动方程的建立根据三维波动理论,对井筒周围的地基土进行运动分析,然后采用传递矩阵法将各个土层内的井筒单元联系起来,求得井筒顶部运动的阻抗函数,再建立土-井筒-井塔体系的运动方程。
2.1 井筒侧土的运动分析在基本假定的基础上,在井筒顶部质点作用水平方向的平动及垂直方向的转动时,根据波动理论,在z位置井筒微元段dz发生单位位移时,井筒侧土产生的横向动反力幅值p(z)[10-12]为
| $ p(z)=\pi G a_{0}^{2} T \mathrm{~d} z=G\left[S_{\mathrm{u} 1}\left(a_{0}, \nu, D\right)+\mathrm{i} S_{\mathrm{u} 2}\left(a_{0}, \nu, D\right)\right] \mathrm{d} z $ | (1) |
式中
| $ \begin{gathered} T=-\frac{4 K_{1}\left(b_{0}^{*}\right) K_{1}\left(a_{0}^{*}\right)+a_{0}^{*} K_{1}\left(b_{0}^{*}\right) K_{0}\left(a_{0}^{*}\right)+b_{0}^{*} K_{0}\left(b_{0}^{*}\right) K_{1}\left(a_{0}^{*}\right)}{b_{0}^{*} K_{0}\left(b_{0}^{*}\right) K_{1}\left(a_{0}^{*}\right)+a_{0}^{*} K_{1}\left(b_{0}^{*}\right) K_{0}\left(a_{0}^{*}\right)+b_{0}^{*} a_{0}^{*} K_{0}\left(b_{0}^{*}\right) K_{1}\left(a_{0}^{*}\right)}, \\ a_{0}^{*}=\frac{a_{0} \mathrm{i}}{\sqrt{1+\mathrm{i} D}}, a_{0}=\frac{r_{0} \omega}{v_{\mathrm{s}}}, v_{\mathrm{s}}=\sqrt{\frac{G}{\rho_{\mathrm{s}}}}, b_{0}^{*}=\frac{1}{\eta_{1}} a_{0}^{*}, \\ \eta_{1}=\sqrt{\frac{2(1-\nu)}{1-2 \nu}}, D=\frac{\lambda_{2}^{*}+2 G_{2}^{*}}{\lambda_{1}^{*}+2 G_{1}^{*}} \end{gathered} $ |
λ1*、G1*、λ2*、G2*均为描述土黏性参数的Lame常数;G为地基土的剪切模量,Pa;i为虚数单位;ρs为土的密度,kg/m3;ω为激振频率,Hz;vs为剪切波的传播速度,m/s;ν为地基土泊松比;r0为圆形井筒半径,m;Su1、Su2分别为土的无量纲复刚度的实部及虚部;K0(z)和K1(z)分别为0阶和1阶第二类修正Bessel函数;D=0.1。
2.2 地基土-井筒体系的总体复刚度地基土参数及井筒截面沿深度是变化的,因此,需要按照地基土的分层及井筒截面的变化情况将井筒划分为若干段(单元),首先将井筒分段,然后在每一个井筒的分段内将土体划分为若干个性质相同的土层,每一个井筒单元水平方向自由振动运动方程为[7]
| $ \begin{gathered} \mu \frac{\partial^{2} u(z, t)}{\partial t^{2}}+c \frac{\partial u(z, t)}{\partial t}+G\left(S_{\mathrm{u} 1}+\mathrm{i} S_{\mathrm{u} 2}\right) u(z, t)+ \\ N_{\mathrm{st}} \frac{\partial^{2} u(z, t)}{\partial z^{2}}+E I \frac{\partial^{4} u(z, t)}{\partial z^{4}}=0 \end{gathered} $ | (2) |
式中:μ为单元长度井筒质量(μ=ρcA),kg;ρc为井筒密度,kg/m3;A为井筒面积,m2;c为井筒等效阻尼系数,N·s/m;Nst为井筒受到的静轴向力,N;EI为井筒弯曲刚度,N·m2。
设u(z, t)=u(z)eiωt,u(z)为井筒元件dz在高度z处的水平位移幅值,代入式(2)可得
| $ u(z)=C_{1} \operatorname{ch} \frac{\lambda}{h} z+C_{2} \operatorname{sh} \frac{\lambda}{h} z+C_{3} \cos \frac{\delta}{h} z+C_{4} \sin \frac{\delta}{h} z $ | (3) |
式中:h为井筒单元长度,m;C1、C2、C3和C4均为待定常数; λ、δ均为考虑井筒轴向静压力Nst时特征方程的特征值:
| $ \lambda, \delta=\frac{\pi}{\sqrt{2}}\left\{\mp \frac{N_{\mathrm{st}}}{N_{\mathrm{E}}}+\sqrt{\left(\frac{N_{\mathrm{st}}}{N_{\mathrm{E}}}\right)^{2}-\frac{4 E I}{N_{\mathrm{E}}^{2}}\left[G S_{\mathrm{u} 1}-\mu \omega^{2}+\mathrm{i}\left(c \omega+G S_{\mathrm{u} 2}\right)\right]}\right\}^{\frac{1}{2}} $ | (4) |
式中
设β=λ/h, η=δ/h,则有λ=βh, δ=ηh。
根据井筒变形与内力之间的关系,截面剪力H(z)=-EIu'''(z),N;截面弯矩M(z)=EIu″(z),N·m;则井筒截面水平位移u(z)、转角φ(z)、剪力H(z)及弯矩M(z)分别为
| $ \left( {\begin{array}{*{20}{l}} {u(z)}\\ {\varphi (z)}\\ {H(z)}\\ {M(z)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathop{\rm ch}\nolimits} \beta z}&{{\mathop{\rm sh}\nolimits} \beta z}&{\cos \eta z}&{\sin \eta z}\\ {\beta {\mathop{\rm sh}\nolimits} \beta z}&{\beta {\mathop{\rm ch}\nolimits} \beta z}&{ - \eta \sin \eta z}&{\eta \cos \eta z}\\ { - EI{\beta ^3}{\mathop{\rm sh}\nolimits} \beta z}&{ - EI{\beta ^3}{\mathop{\rm ch}\nolimits} \beta z}&{ - EI{\eta ^3}\sin \eta z}&{EI{\eta ^3}\cos \eta z}\\ {EI{\beta ^2}{\mathop{\rm ch}\nolimits} \beta z}&{EI{\beta ^2}{\mathop{\rm sh}\nolimits} \beta z}&{ - EI{\eta ^2}\cos \eta z}&{ - EI{\eta ^2}\sin \eta z} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{C_1}}\\ {{C_2}}\\ {{C_3}}\\ {{C_4}} \end{array}} \right) $ | (5) |
对于按土层及井筒分层产生的一个井筒单元i,其长度为hi,上端点(z=0)编号i,对应的位移及内力为[ui, φi, Hi, Mi]T, 下端点(z=hi)编号i+1,对应的位移及内力为[ui+1, φi+1, Hi+1, Mi+1]T,且λ=λi, β=βi, δ=δi, η=ηi,将坐标原点(z=0)取在i-1点,则将z=0、z=hi分别代入式(5),联立消去C1、C2、C3和C4得
| $ \left( {\begin{array}{*{20}{l}} {{u_{i + 1}}}\\ {{\varphi _{i + 1}}}\\ {{H_{i + 1}}}\\ {{M_{i + 1}}} \end{array}} \right) = \left[ {t_i^{\rm{H}}} \right]\left( {\begin{array}{*{20}{l}} {{u_i}}\\ {{\varphi _i}}\\ {{H_i}}\\ {{M_i}} \end{array}} \right) $ | (6) |
式中
| $ \left[ {t_i^{\rm{H}}} \right] = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} \frac{{{\eta _i}{\mathop{\rm ch}\nolimits} {\lambda _i} + \beta _i^2\cos {\delta _i}}}{{\eta _i^2 + \beta _i^2}}\\ \frac{{{\beta _i}\eta _i^2{\mathop{\rm sh}\nolimits} {\lambda _i} - \beta _i^2{\eta _i}\sin {\delta _i}}}{{\eta _i^2 + \beta _i^2}}\\ - \frac{{EI\beta _i^3\eta _i^2{\mathop{\rm sh}\nolimits} {\lambda _i} + EI\beta _i^2\eta _i^3\sin {\delta _i}}}{{\eta _i^2 + \beta _i^2}}\\ \frac{{EI\beta _i^2\eta _i^2{\mathop{\rm ch}\nolimits} {\lambda _i} - EI\beta _i^2\eta _i^2\cos {\delta _i}}}{{\eta _i^2 + \beta _i^2}} \end{array}&\begin{array}{l} \frac{{\eta _i^3{\mathop{\rm sh}\nolimits} {\lambda _i} + \beta _i^3\sin {\delta _i}}}{{{\beta _i}{\eta _i}\left( {\eta _i^2 + \beta _i^2} \right)}}\\ \frac{{\eta _i^2{\mathop{\rm ch}\nolimits} {\lambda _i} + \beta _i^2\cos {\delta _i}}}{{\eta _i^2 + \beta _i^2}}\\ \frac{{EI\beta _i^2\eta _i^2\cos {\delta _i} - EI\beta _i^2\eta _i^2{\mathop{\rm ch}\nolimits} {\lambda _i}}}{{\eta _i^2 + \beta _i^2}}\\ \frac{{EI{\beta _i}\eta _i^2{\mathop{\rm sh}\nolimits} {\lambda _i} - EI\beta _i^2{\eta _i}\sin {\delta _i}}}{{\eta _i^2 + \beta _i^2}} \end{array}&\begin{array}{l} \frac{{{\beta _i}\sin {\delta _i} - {\eta _i}{\mathop{\rm sh}\nolimits} {\lambda _i}}}{{EI{\beta _i}{\eta _i}\left( {\eta _i^2 + \beta _i^2} \right)}}\\ \frac{{\cos {\delta _i} - {\mathop{\rm ch}\nolimits} {\lambda _i}}}{{EI\left( {\eta _i^2 + \beta _i^2} \right)}}\\ \frac{{\beta _i^2{\mathop{\rm ch}\nolimits} {\lambda _i} + \eta _i^2\cos {\delta _i}}}{{\eta _i^2 + \beta _i^2}}\\ - \frac{{{\beta _i}{\mathop{\rm sh}\nolimits} {\lambda _i} + {\eta _i}\sin {\delta _i}}}{{\eta _i^2 + \beta _i^2}} \end{array}&\begin{array}{l} \frac{{{\mathop{\rm ch}\nolimits} {\lambda _i} - \cos {\delta _i}}}{{EI\left( {\eta _i^2 + \beta _i^2} \right)}}\\ \frac{{{\beta _i}{\mathop{\rm sh}\nolimits} {\lambda _i} + {\eta _i}\sin {\delta _i}}}{{EI\left( {\eta _i^2 + \beta _i^2} \right)}}\\ \frac{{\eta _i^3\sin {\delta _i} - \beta _i^3{\mathop{\rm sh}\nolimits} {\lambda _i}}}{{\eta _i^2 + \beta _i^2}}\\ \frac{{\beta _i^2{\mathop{\rm ch}\nolimits} {\lambda _i} + \eta _i^2\cos {\delta _i}}}{{\eta _i^2 + \beta _i^2}} \end{array} \end{array}} \right] $ | (7) |
式(6)中,[tiH]代表了[ui, φi, Hi, Mi]T与[ui+1, φi+1, Hi+1, Mi+1]T之间的传递关系,称为井筒单元hi的传递矩阵。根据式(6),从井筒底部(i=n)开始有如下的递推关系:
| $ \left( {\begin{array}{*{20}{l}} {{u_n}}\\ {{\varphi _n}}\\ {{H_n}}\\ {{M_n}} \end{array}} \right) = \left[ {\begin{array}{*{20}{l}} {t_{n - 1}^{\rm{H}}} \end{array}} \right]\left( {\begin{array}{*{20}{l}} {{u_{n - 1}}}\\ {{\varphi _{n - 1}}}\\ {{H_{n - 1}}}\\ {{M_{n - 1}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{l}} {t_{n - 1}^{\rm{H}}} \end{array}} \right]\left[ {t_{n - 2}^{\rm{H}}} \right]\left( {\begin{array}{*{20}{l}} {{u_{n - 2}}}\\ {{\varphi _{n - 2}}}\\ {{H_{n - 2}}}\\ {{M_{n - 2}}} \end{array}} \right) = \cdots = \left[ {t_{n - 1}^{\rm{H}}} \right]\left[ {t_{n - 2}^{\rm{H}}} \right]\left[ {t_{n - 3}^{\rm{H}}} \right] \cdots \left[ {t_2^{\rm{H}}} \right]\left[ {t_1^{\rm{H}}} \right]\left[ {t_0^{\rm{H}}} \right]\left( {\begin{array}{*{20}{l}} {{u_0}}\\ {{\varphi _0}}\\ {{H_0}}\\ {{M_0}} \end{array}} \right) = \left[ {{T^{\rm{H}}}} \right]\left( {\begin{array}{*{20}{l}} {{u_0}}\\ {{\varphi _0}}\\ {{H_0}}\\ {{M_0}} \end{array}} \right) $ | (8) |
式中:[un, φn, Hn, Mn]T、[u0, φ0, H0, M0]T分别为井筒底端和顶端的水平位移、转角、剪力和弯矩,井筒整体传递函数[TH]=[tn-1H][tn-2H][tn-3H]…[t2H][t1H][t0H] 为从井筒底端到井筒顶端变形与内力的传递关系。
2.3 井筒顶部运动阻抗系数将式(8)写成
| $ \left(\begin{array}{l} u_{n} \\ \varphi_{n} \\ H_{n} \\ M_{n} \end{array}\right)=\left[T^{\mathrm{H}}\right]\left(\begin{array}{l} u_{0} \\ \varphi_{0} \\ H_{0} \\ M_{0} \end{array}\right)=\left[\begin{array}{cc} {\left[T_{11}^{\mathrm{H}}\right]} & {\left[T_{12}^{\mathrm{H}}\right]} \\ {\left[T_{21}^{\mathrm{H}}\right]} & {\left[T_{22}^{\mathrm{H}}\right]} \end{array}\right]\left(\begin{array}{l} u_{0} \\ \varphi_{0} \\ H_{0} \\ M_{0} \end{array}\right) $ | (9) |
将式(9)按分块矩阵式展开,并根据井筒底端边界条件un=0,φn=0,得
| $ \left( {\begin{array}{*{20}{l}} {{H_0}}\\ {{M_0}} \end{array}} \right) = - {\left[ {T_{12}^{\rm{H}}} \right]^{ - 1}}\left[ {T_{11}^{\rm{H}}} \right]\left( {\begin{array}{*{20}{l}} {{u_0}}\\ {{\varphi _0}} \end{array}} \right) $ | (10) |
可得井筒顶部位移与反力关系为
| $ \left(\begin{array}{l} H_{0} \\ M_{0} \end{array}\right)=-\left[K^{\mathrm{H}}\right]_{2 \times 2}\left(\begin{array}{l} u_{0} \\ \varphi_{0} \end{array}\right) $ | (11) |
令
| $ \left[K^{\mathrm{H}}\right]=\left[\begin{array}{ll} K_{\mathrm{HH}} & K_{\mathrm{H} \varphi} \\ K_{\varphi \mathrm{H}} & K_{\varphi \varphi} \end{array}\right] $ | (12) |
式(12)对比式(11)去掉负号是因为井筒顶端内力和外力的方向相反,则井筒顶部运动的阻抗系数kxx、kxφ、kφx、kφφ、cxx、cxφ、cφx和cφφ可按下式计算[13]:
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{xx}} = {\mathop{\rm real}\nolimits} \left( {{K_{{\rm{HH}}}}} \right), {c_{xx}} = 1/\omega \times {\mathop{\rm imag}\nolimits} \left( {{K_{{\rm{HH}}}}} \right)}\\ {{k_{x\varphi }} = {\mathop{\rm real}\nolimits} \left( {{K_{{\rm{H}}\varphi }}} \right), {c_{x\varphi }} = 1/\omega \times {\mathop{\rm imag}\nolimits} \left( {{K_{{\rm{H}}\varphi }}} \right)}\\ {{k_{\varphi x}} = {\mathop{\rm real}\nolimits} \left( {{K_{\varphi {\rm{H}}}}} \right), {c_{\varphi x}} = 1/\omega \times {\mathop{\rm imag}\nolimits} \left( {{K_{\varphi {\rm{H}}}}} \right)}\\ {{k_{\varphi \varphi }} = {\mathop{\rm real}\nolimits} \left( {{K_{\varphi \varphi }}} \right), {c_{\varphi \varphi }} = 1/\omega \times {\mathop{\rm imag}\nolimits} \left( {{K_{\varphi \varphi }}} \right)} \end{array}} \right. $ | (13) |
采用子结构分析方法[14],将上部井塔结构离散简化为多质点体系,考虑土与结构的相互作用时,井塔结构传递下来的底部剪力和倾覆力矩作用在井筒上,在不考虑竖向地震作用时,井筒顶端运动可简化为水平滑移u0和转动φ0来表示[13]。综上,根据结构动力学理论,考虑土-结构相互作用,建立了土-井筒-井塔结构体系在时域内的理论运动方程。
井塔结构各质点的动力平衡简化方程为
| $ \begin{gathered} {[\boldsymbol{M}]\left(\{\ddot{\boldsymbol{u}}\}+\{\boldsymbol{h}\} \ddot{\varphi}_{0}+\left\{\ddot{\boldsymbol{u}}_{0}\right\}+\left\{\ddot{\boldsymbol{u}}_{\mathrm{g}}\right\}\right)+} \\ {[\boldsymbol{C}]\{\dot{\boldsymbol{u}}\}+[\boldsymbol{K}]\{\boldsymbol{u}\}=\{\boldsymbol{0}\}} \end{gathered} $ | (14) |
式中:[M]为井塔的质量矩阵,kg;[K]为井塔的刚度矩阵,N/m;[C]为井塔的阻尼矩阵,N·s/m;{u}为离散后井塔各质点的位移向量,m;
| $ [\mathit{\boldsymbol{K}}] = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - {k_1}}&0&{}&{}&0\\ { - {k_1}}&{{k_1} + {k_2}}&{ - {k_2}}&{}&{}&{}\\ 0&{ - {k_2}}&{{k_2} + {k_3}}&{}&{}&{}\\ {}&{}&{}& \ddots &{}&{}\\ {}&{}&{}&{}&{{k_{n - 2}} + {k_{n - 1}}}&{ - {k_{n - 1}}}\\ 0&{}&{}&{}&{ - {k_{n - 1}}}&{{k_{n - 1}} + {k_n}} \end{array}} \right] $ |
[C]采用Rayleigh阻尼,用[M]和[K]表示为
| $ \begin{gathered} {[\boldsymbol{C}]=a_{1}[\boldsymbol{M}]+a_{2}[\boldsymbol{K}]} \\ \left(\begin{array}{l} a_{1} \\ a_{2} \end{array}\right)=\frac{2 \omega_{i} \omega_{j}}{\omega_{j}^{2}-\omega_{i}^{2}}\left(\begin{array}{cc} \omega_{j} & -\omega_{i} \\ -\frac{1}{\omega_{j}} & \frac{1}{\omega_{i}} \end{array}\right)\left(\begin{array}{l} \zeta_{i} \\ \zeta_{j} \end{array}\right) \end{gathered} $ |
式中:ωi、ωj为第i阶和第j阶振型自振频率,ζi、ζj分别为第i阶和第j阶振型阻尼比。
| $ \begin{aligned} &\{\boldsymbol{u}\}=\left[u_{1}, u_{2}, \cdots, u_{n}\right]^{\mathrm{T}}, \{\dot{\boldsymbol{u}}\}=\left[\dot{u}_{1}, \dot{u}_{2}, \cdots, \dot{u}_{n}\right]^{\mathrm{T}}, \\ &\{\ddot{\boldsymbol{u}}\}=\left[\ddot{u}_{1}, \ddot{u}_{2}, \cdots, \ddot{u}_{n}\right]^{\mathrm{T}}, \{\boldsymbol{h}\}=\left[h_{1}, h_{2}, \cdots, h_{n}\right]^{\mathrm{T}}, \\ &\left\{\ddot{\boldsymbol{u}}_{0}\right\}=\left[\ddot{u}_{0}, \ddot{u}_{0}, \cdots, \ddot{u}_{0}\right]^{\mathrm{T}}, \left\{\ddot{\boldsymbol{u}}_{\mathrm{g}}\right\}=\left[\ddot{u}_{\mathrm{g}}, \ddot{u}_{\mathrm{g}}, \cdots, \ddot{u}_{\mathrm{g}}\right]^{\mathrm{T}} \end{aligned} $ |
井筒顶端质点水平运动方程为
| $ \begin{gathered} \sum\limits_{i=1}^{n} m_{i}\left(\ddot{u}_{i}+h_{i} \ddot{\varphi}_{0}+\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+ \\ m_{0}\left(\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+H_{0}(t)=0 \end{gathered} $ | (15) |
井筒顶端质点摆动的运动方程为
| $ \sum\limits_{i=1}^{n} m_{i} h_{i}\left(\ddot{u}_{i}+h_{i} \ddot{\varphi}_{0}+\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+M_{0}(t)=0 $ | (16) |
| $ \left\{\begin{array}{l} H_{0}(t)=c_{x x} \dot{u}_{0}+c_{\varphi x} \dot{\varphi}_{0}+k_{x x} u_{0}+k_{\varphi x} \varphi_{0} \\ M_{0}(t)=c_{x \varphi} \dot{u}_{0}+c_{\varphi \varphi} \dot{\varphi}_{0}+k_{x \varphi} u_{0}+k_{\varphi \varphi} \varphi_{0} \end{array}\right. $ | (17) |
将式(17)分别代入式(15)和(16)得
| $ \begin{gathered} \sum\limits_{i=1}^{N} m_{i}\left(\ddot{u}_{i}+h_{i} \ddot{\varphi}_{0}+\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+m_{0}\left(\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+ \\ c_{x x} \dot{u}_{0}+c_{\varphi x} \dot{\varphi}_{0}+k_{x x} u_{0}+k_{\varphi x} \varphi_{0}=0 \end{gathered} $ | (18) |
| $ \begin{gathered} \sum\limits_{i=1}^{N} m_{i} h_{i}\left(\ddot{u}_{i}+h_{i} \ddot{\varphi}_{0}+\ddot{u}_{0}+\ddot{u}_{\mathrm{g}}\right)+ \\ c_{x \varphi} \dot{u}_{0}+c_{\varphi \varphi} \dot{\varphi}_{0}+k_{x \varphi} u_{0}+k_{\varphi \varphi} \varphi_{0}=0 \end{gathered} $ | (19) |
联立式(14)、(18)和(19),共有n+2个方程,采用MATLAB语言编制了Runge-Kutta法的求解程序,可解出n+2个未知函数(u1,u2,…,un,u0,φ0)。
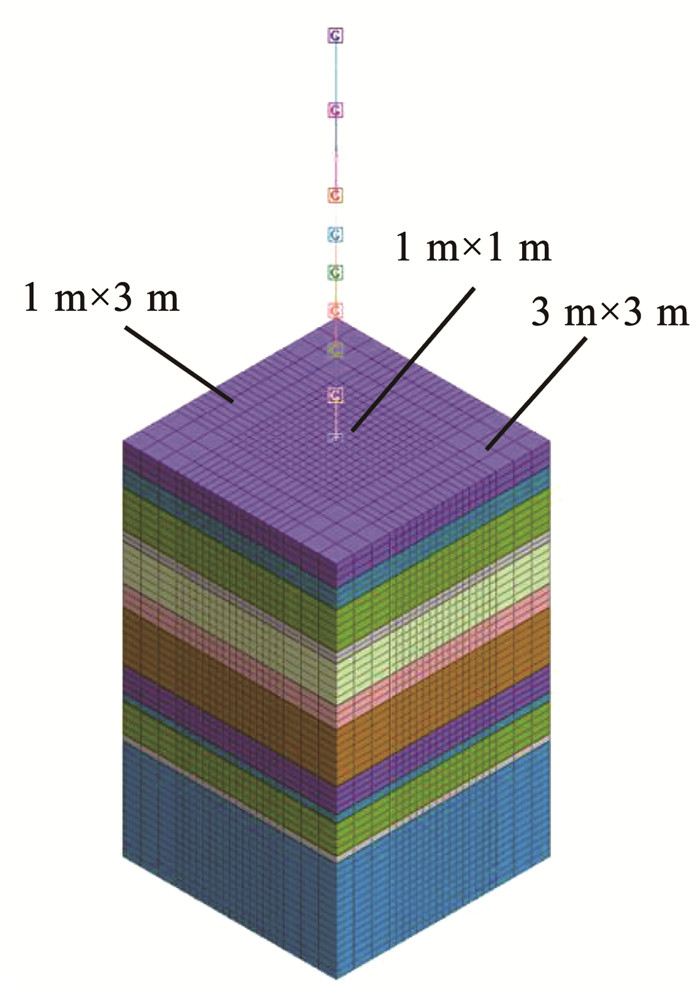
3 体系的数值分析模型数值分析采用有限元软件,土的本构模型为各向同性线弹性模型,土体建模采用三维实体单元,井筒和井塔采用一维梁单元,土-井筒完全耦合,结合三维自由场边界,建立不考虑土-结构相互作用的模型(即纯井塔模型,见图 3(c))、Ⅱ类场地下考虑土与井塔-井筒相互作用的数值分析模型(见图 3)及Ⅲ类场地下考虑土与井塔-井筒相互作用的数值分析模型(见图 4)。图 3中土体尺寸为32 m×32 m×60 m,图 4中土体尺寸为32 m×32 m×54 m,网格尺寸见图中标示,沿土层深度方向网格尺寸控制在1 m左右。

|
图 3 Ⅱ类场地下考虑土与井塔-井筒相互作用的数值分析模型 Fig. 3 Numerical analysis model considering soil-shaft tower-well bore interaction in Ⅱ site |
|
图 4 Ⅲ类场地下考虑土与井塔-井筒相互作用的数值分析模型 Fig. 4 Numerical analysis model considering soil-shaft tower-well bore interaction in Ⅲ site |
为考察不同场地下土-结构相互作用对井塔地震反应分析的影响,以东北某9层钢筋混凝土剪力墙结构井塔(见图 1~4)为工程背景,采用理论分析和数值分析两种方法,各选取3条地震波,分别研究不考虑土-结构相互作用、Ⅱ类场地下考虑土-结构相互作用(模型见图 3)及Ⅲ类场地下考虑土-结构相互作用(模型见图 4)对井塔抗震分析的影响。井塔采用固接于井筒的连接形式,设防烈度为8度,在地表处输入设计基本地震加速度值0.2g。
4.1 地震波选取El Centro、Taft和宁河-天津共3条具有典型代表的地震波,在水平方向单向输入地震动,地震波时间间隔、时长及适合场地条件见表 1,3条地震波反应谱与Ⅱ类场地(第2组)、Ⅲ类场地(第2组)的规范谱对比见图 5。
| 表 1 地震波信息 Tab. 1 Information of seismic waves |

|
图 5 模拟地震波反应谱与规范谱对比 Fig. 5 Comparison of response spectrum of simulated seismic waves with standard spectrum |
本工程选取Ⅱ类和Ⅲ类两类场地的资料,均包括10个土层,每层土的性质是常量,不同土层性质不同,仅考虑土层的线性黏弹性参数,每层土的厚度、埋深、密度、泊松比和动剪切模量见表 2。
| 表 2 场地土参数 Tab. 2 Parameters of site soil |
井筒采用倒锥台式,为钢筋混凝土筒体结构,根据壁厚的不同可以分成3段,每段井筒深度、壁厚、外半径、内半径、截面积和惯性矩等参数详见表 3。
| 表 3 井筒参数 Tab. 3 Parameters of well bore |
井塔为钢筋混凝土剪力墙结构,共9层,采用集中质量模型后可等效为10个质点,质点标高、质点等效质量及井塔每层的等效截面积等参数详见表 4。
| 表 4 井塔参数 Tab. 4 Parameters of shaft tower |
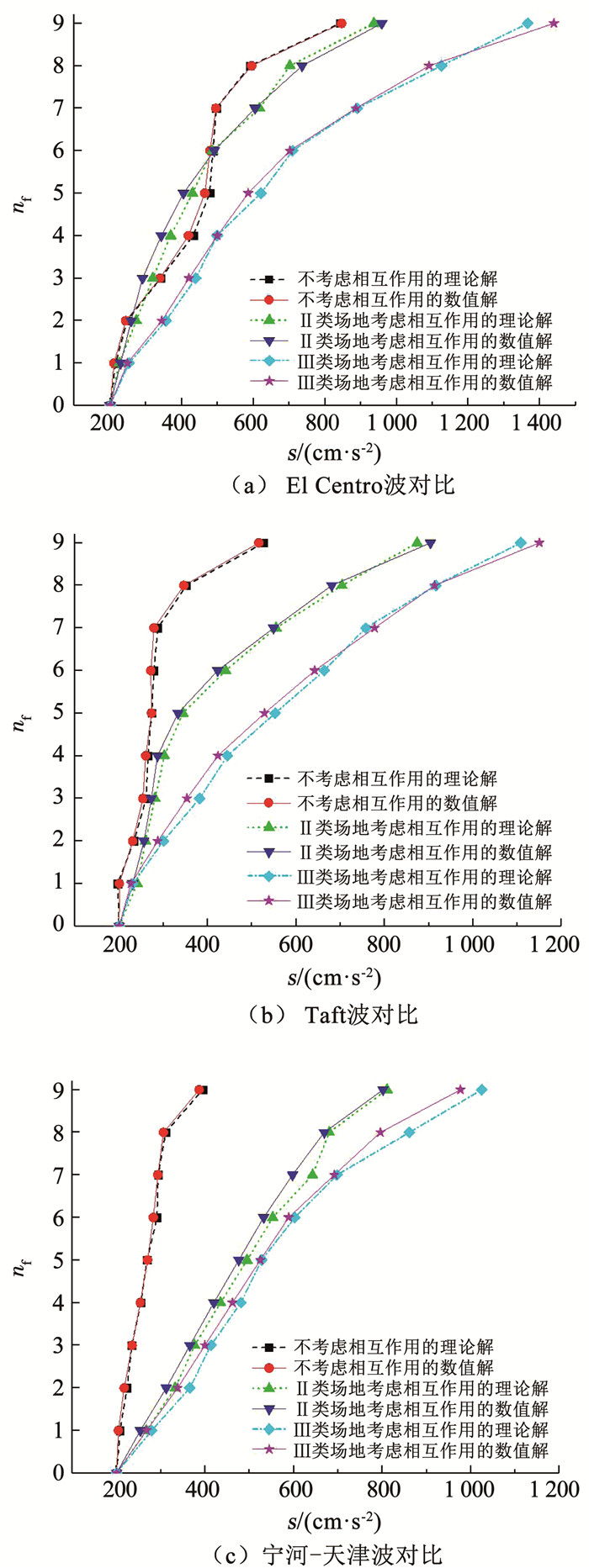
不考虑土-结构相互作用时,表 5及图 6表明,分别输入El Centro、Taft和宁河-天津地震波,理论解与数值解的最大差值分别为第4塔层的3.1%、第7塔层的3.0%和第2塔层的3.0%,3条波中的最大差值为3.1%,差值较小,说明不考虑土-结构相互作用的理论分析模型与数值分析模型吻合较好,为建立不同场地下考虑土-结构相互作用的理论分析模型与数值分析模型打下坚实的基础;Ⅱ类场地下考虑土-结构的相互作用时,分别输入El Centro、Taft和宁河-天津地震波,理论解与数值解的最大差值分别为第3塔层的9.8%、第4塔层的5.3%和第7塔层的7.5%,3条波中的最大差值为9.8%,差值相对较小,表明Ⅱ类场地下考虑土-结构相互作用的理论分析模型与数值分析模型吻合较好;Ⅲ类场地下考虑土-结构相互作用时,分别输入El Centro、Taft和宁河-天津地震波,理论解与数值解的最大差值分别为第5塔层的6.1%、第3塔层的8.2%和第8塔层的8.3%,3条波中的最大差值为8.3%,差值相对较小。综上,建立的理论分析模型与数值分析模型吻合较好,验证了彼此的准确性,为研究场地效应对地震反应的影响奠定了基础。
| 表 5 理论解与数值解的差值 Tab. 5 Difference between theoretical solution and numerical solution |
Ⅱ类场地下考虑土-结构的相互作用时,表 6及图 6表明,输入El Centro波,其塔层加速度与不考虑土-结构相互作用理论解及数值解的最大比值均为第7~8塔层的1.2倍。输入Taft波,其塔层加速度与不考虑土-结构相互作用理论解、数值解的最大比值分别为第8塔层的2.0倍。第7~8塔层的2.0倍。输入宁河-天津波,其塔层加速度与不考虑土-结构相互作用理论解、数值解的最大比值分别为第7~8塔层的2.2倍、第8塔层的2.2倍。Ⅱ类场地下,3条地震波理论解的平均放大系数最大值为第7~8塔层的1.8倍。其数值解的平均放大系数最大值为第8塔层的1.8倍。
| 表 6 地震作用放大系数 Tab. 6 Amplification factors of seismic action |
|
图 6 井塔地震反应分析对比 Fig. 6 Comparison of seismic responses of shaft tower |
Ⅲ类场地下考虑土-结构的相互作用时,表 6及图 6表明,输入El Centro波,其塔层加速度与不考虑土-结构相互作用理论解、数值解的最大比值分别为第8塔层的1.9倍、第7~8塔层的1.8倍。输入Taft波,其塔层加速度与不考虑土-结构相互作用理论解、数值解的最大比值分别为第7~8塔层的2.6倍。第7塔层的2.8倍。输入宁河-天津波,其塔层加速度与不考虑土-结构相互作用理论解、数值解的最大比值分别为第8塔层的2.8倍、第8塔层的2.6倍。Ⅲ类场地下,3条地震波理论解和数值解的平均放大系数最大值均为第8塔层的2.4倍。
Ⅱ、Ⅲ类场地下,3条地震波平均放大系数最大值分别为1.8倍、2.4倍,这主要是因为:1)不同场地对地震动的强度及频谱特性具有不同的影响,土层作为地震波的传播介质,对基岩输入地震动具有低频放大、高频滤波效应,具体表现为接近场地自振频率的地震波分量被保留且充分放大,远离场地自振频率的地震波分量被过滤掉;2)结构的第一及第二阶自振周期分别为0.55 s及0.12 s,与场地的卓越周期较接近(Ⅱ类及Ⅲ类场地分别为0.22 s及0.48 s),尤其是Ⅲ类场地的卓越周期与结构第一阶自振周期接近,会使结构地震响应产生较明显的放大现象。
5 结论1) 理论解与数值解的最大差值为9.8%,总体吻合较好,理论解与数值解互相验证了模型的准确性。
2) 考虑土-结相互作用时,Ⅱ、Ⅲ类场地下3条地震波对应的平均地震动力反应(塔层加速度)分别放大了1.8倍、2.4倍。
3) 建议在工程设计中,Ⅱ、Ⅲ类场地下考虑土-结构相互作用对井塔动力反应放大的影响。
4) 土-结构相互作用对井塔地震动力反应的影响大小与结构自振周期、输入地震波的强度和频谱特性以及场地土的软弱程度等许多因素有关,是一个复杂的课题,有待进行大量且更加深入的研究。
| [1] |
构筑物抗震设计规范: GB 50191—2012[S]. 北京: 中国计划出版社, 2012 Code for seismic design of special structures: GB 50191—2012[S]. Beijing: China Planning Press, 2012 |
| [2] |
王依群, 何玉敖. 考虑土与结构相互作用的井塔抗震分析[J]. 建筑结构学报, 1989, 10(4): 67. WANG Yiqun, HE Yuao. Earthquake analysis of shaft-tower in consideration of soil-structure interaction[J]. Journal of Building Structures, 1989, 10(4): 67. DOI:10.14006/j.jzjgxb.1989.04.009 |
| [3] |
查晓礼. 井塔-桩筏基础-地基-井壁的共同作用机理研究[D]. 西安: 西安科技大学, 2008 ZHA Xiaoli. Study on the mechanism of joint load-bearing of various sections in a mine shaft tower system[D]. Xi'an: Xi'an University of Science and Technology, 2008 |
| [4] |
王依群. 考虑土与结构相互作用的井塔抗震分析[D]. 天津: 天津大学, 1986 WANG Yiqun. Earthquake analysis of shaft-tower in consideration of soil-structure interaction[D]. Tianjin: Tianjin University, 1986 |
| [5] |
申金虎. 桩-土-渡槽结构动力作用数值分析[D]. 郑州: 郑州大学, 2013 SHEN Jinhu. Numerical analysis of pile-soil-aqueduct structure under dynamic loads[D]. Zhengzhou: Zhengzhou University, 2013 |
| [6] |
ANOYATIS G, LEMNITZER A. Dynamic pile impedances for laterally-loaded piles using improved Tajimi and Winkler formulations[J]. Soil Dynamics and Earthquake Engineering, 2017, 92: 279. DOI:10.1016/j.soildyn.2016.09.020 |
| [7] |
NOVAK M. Dynamic stiffness and damping of piles[J]. Canadian Geotechnical Journal, 1974, 11: 574. DOI:10.1139/T74-059 |
| [8] |
赵雅文. 基于集中质量法高桩码头的地震动力响应[D]. 天津: 天津大学, 2015 ZHAO Yawen. Seismic response of high-piled wharf based on lumped mass model[D]. Tianjin: Tianjin University, 2015 |
| [9] |
PENZIEN J, SCHEFFEY C F, PARMELEE R A. Seismic analysis of bridges on long piles[J]. Journal of the Engineering Mechanics Division, 1964, 90(3): 223. DOI:10.1061/JMCEA3.0000489 |
| [10] |
NOGAMI T, NOVAK M. Resistance of soil to a horizontally vibrating pile[J]. Earthquake Engineering and Structural Dynamics, 1977, 5(3): 249. DOI:10.1002/eqe.4290050304 |
| [11] |
孔德森. 桩-土相互作用计算模型及其在桩基结构抗震分析中的应用[D]. 大连: 大连理工大学, 2004 KONG Desen. Study on dynamic computational model of pile-soil interaction and applications in seismic response analysis of pile-supported structures[D]. Dalian: Dalian University of Technology, 2004 |
| [12] |
DING Xuanming, ZHENG Changjie, LIU Hanlong, et al. Resistance of inner soil to the horizontal vibration of pipe piles[J]. Journal of Engineering Mechanics, 2017, 143(11): 1. DOI:10.1061/(ASCE)EM.1943-7889.0001353 |
| [13] |
吴世明. 土动力学[M]. 北京: 中国建筑工业出版社, 2000: 271. WU Shiming. Soil dynamics[M]. Beijing: China Architecture & Building Press, 2000: 271. |
| [14] |
林皋, 栾茂田, 陈怀海. 土-结构相互作用对高层建筑非线性地震反应的影响[J]. 土木工程学报, 1993, 26(4): 1. LIN Gao, LUAN Maotian, CHEN Huaihai. Soil-structure interaction effect on the nonlinear seismic response of high-rise buildings[J]. China Civil Engineering Journal, 1993, 26(4): 1. DOI:10.15951/j.tmgcxb.1993.04.001 |
 2022, Vol. 54
2022, Vol. 54


