2. 生态安全屏障区交通网设施管控及循环修复技术交通运输行业重点实验室(长安大学), 西安 710064;
3. 同济大学 建筑与城市规划学院, 上海 200092
2. Key Laboratory of Transport Industry of Management, Control and Cycle Repair Technology for Traffic Network Facilities in Ecological Security Barrier Area (Chang′an University), Xi'an 710064, China;
3. College of Architecture and Urban Planning, Tongji University, Shanghai 200092, China
快速的居住郊区化与迟缓的就业郊区化[1]使得规划的职住空间与实际通勤网络结构之间的不协调日趋严重。轨道交通成为应对城市职住分离问题的主要通勤方式,其网络结构与职住空间的耦合程度直接影响着城市居民的幸福水平和城市的发展潜能。然而,城市轨道交通与职住空间的发展过程,受居民就业和居住地的自选择性[2-3]、人口特征及土地利用等因素的影响呈现出复杂的交互关系,且影响程度与模式均存在一定的空间异质性。因此,基于城市人流空间的交互视角[4],深入探究职住空间结构形态与轨道交通网络在功能上的协调与耦合关系,是实现轨道交通建设可持续发展,充分发挥城市轨道交通对城市空间结构优化引导作用的理论前提。
现有研究已充分论证了轨道交通发展与城市空间结构形态之间存在相互影响关系[5-6],且这种相互作用体现在不同尺度下的不同因素之间。从站点层面,主要体现在站点周边建成环境对轨道通勤出行的影响[7],轨道交通客流与土地利用的互动关系[8];从网络层面,则体现在轨道交通可达性与土地利用的依赖关系[5]等方面。其中,可达性作为衡量交通出行便捷度的重要指标,是连接城市空间结构与轨道交通系统的关键[5-6]。然而,轨道交通可达性与城市空间结构互动关系的非对称性及其交互影响机制鲜见报道。
在研究轨道交通可达性与城市空间结构互动关系时,主要因素的测度方法和关系模型的构建是决定互动影响关系的关键所在。对职住分布的测度方法,国内外研究提出了职住比[9]、职住平衡指数[10]、职住偏离度指数[11]、职住自足性指数[12]、通勤距离[13]和时间[14]等表征城市职住空间分布的相关指标及计算方法。尤其是,手机信令数据因具有广覆盖、大样本、细粒度等诸多优势而被广泛用于职住空间的相关研究中,使得职住分布的相关指标在时空尺度下更加多样化。对城市轨道交通可达性的量化方法,已有研究提出了平均通达时间[15]、OD最晚可达时间[16]、行程时间[17]等测算指标。如文献[16]提出了末班车开行约束下城市轨道交通路网可达性的计算方法。文献[17]建立了在拥挤条件下考虑动态行程时间的可达性评价模型。然而,现有的基于时间测度的轨道交通可达性计算方法虽然接近现实且可操作性强[18],但仅从供给角度出发,忽视了乘客的实际需求,尤其是轨道交通能够服务的潜在群体。两步移动搜索法(two-step floating catchment area method,2SFCA)可综合考虑设施的供给、居民出行需求和空间阻抗,在公共服务设施的可达性评价中具有广泛的应用[19]。文献[19]基于修正的2SFCA法评估了医疗设施的空间可达性,结果表明不同等级的医疗设施可达性空间分布不均。文献[20]利用2SFCA法分析了城市绿地可达性的空间不平等特征,揭示了不同种族和收入群体之间的绿地可达性差异。关系模型构建方面,近年来多采用以空间计量模型为主的全局回归模型和以地理加权回归模型(geographically weighted regression, GWR)为主的局部回归模型研究交通可达性与城市结构的空间特征和关联效应[5, 21]。文献[5]基于全局空间计量模型和GWR模型探究了公共交通可达性的空间分布特征及其与城市经济活动的空间关联效应。文献[21]采用空间误差模型(spatial error model, SEM)和GWR模型分析了交通可达性对城市房屋价格的空间异质性特征。然而,在实际中职住空间关系通过衍生出的出行需求分布影响轨道交通可达性;反之,轨道交通可达性则通过影响地区综合吸引力改变其职住空间分布形态。职住分布与轨道交通可达性存在双向影响路径的特性,需从双向因果角度[22]出发,构建两者的互动关系模型,探究耦合效应关系。
本文以西安市中心城区为研究范围,基于手机信令数据、轨道交通刷卡数据、城市路网及轨道线网等数据,以空间交互视角开展对职住分布与轨道交通网络的影响关系及耦合效应分析。采用职住自足性指数量化职住空间;基于实际路网距离的高斯2SFCA法测度轨道交通车站空间可达性;构建空间联立方程揭示职住平衡与轨道交通可达性两者的空间耦合效应,引入局部空间自相关探讨西安市轨道交通网络建设与城市空间发展的协调性与适应性,为轨道交通线网结构的优化及城市空间的合理拓展提供理论依据。
1 研究方法本文首先基于多源数据实现两个关键要素的定量化分析,即采用职住自足性指数测度职住平衡,利用改进的高斯两步移动搜索法计算轨道交通可达性;其次,建立空间联立方程探讨职住平衡与轨道交通可达性的交互影响机制。
1.1 职住平衡量化分析职住自足性指数Cfi,即某一空间单元的人口职住自足度(Dsc, i)与全域空间单元人口职住自足度(Dsc, i)均值的比值[12],可定量测度职住平衡,计算公式为
| $ C f_i=\frac{D_{s c, i}}{\operatorname{Avg}\left(D_{s c, i}\right)} $ | (1) |
式中:Dsc, i为在交通小区i内居住并工作的人与该区域居住人口的比值,即自足度(self-containment degree);Avg(Dsc, i)为所有交通小区自足度的平均值。自足性指数Cfi越高,表明职住越平衡,职住一体化程度越高。
1.2 高斯两步移动搜索法的轨道交通可达性分析利用以高斯函数模拟空间阻抗的2SFCA法分析轨道交通可达性,可同时考虑供需要素,更接近实际情况,具体计算流程如下。
第1步,对于每个轨道交通车站j,搜索所有离车站j距离阈值d0之内的需求点(即移动通信基站)k, 计算出轨道交通车站的供需比Rj:
| $ {R_j} = \frac{{{S_j}}}{{\sum\limits_{k \in \left( {{d_{kj}} \le {d_0}} \right)} {\left[ {{D_k}G\left( {{d_{kj}}, {d_0}} \right)} \right]} }} $ | (2) |
式中:Sj为车站j的供给量,本文取车站高峰小时客流量以反映该车站的吸引能力;dkj为车站j和需求点k的距离;d0为距离阈值,本文采用轨道车站半径3 km的合理交通区[23]作为筛选距离阈值,以考虑轨道交通车站所能吸引的步行或其他交通方式乘客到达范围;Dk为搜索区内需求点k的需求量,即经手机信令数据识别与扩样后的居住人口数。G(dkj, d0)为考虑距离阻抗的高斯方程,计算公式为
| $ G\left(d_{k j}, d_0\right)= \begin{cases}\frac{\mathrm{e}^{-0.5 d_{k j}^2 \cdot d_0^{-2}}-\mathrm{e}^{-0.5}}{1-\mathrm{e}^{-0.5}}, & d_{k j} \leqslant d_0 \\ 0, & d_{k j}>d_0\end{cases} $ | (3) |
第2步,对于每个需求点i,搜索所有离需求点i距离阈值d0之内的车站j,将所有车站的供需比Rj求和即得到需求点i的空间可达性指数Ai,将交通小区m内的所有可达性指数Ai求和,得到交通小区m的空间可达性指数Am:
| $ A_i=\sum\limits_{j \in\left(d_{i j} \leqslant d_0\right)}\left[R_j G\left(d_{k j}, d_0\right)\right] $ | (4) |
| $ A_m=\sum A_i $ | (5) |
式中dij为需求点i到车站j距离。
该可达性量化方法同时考虑了车站的供给、地区的需求及车站吸引度的空间衰减效应,计算结果可表征考虑地理距离衰减的人均轨道交通车站吸引强度,Am越大,轨道交通车站服务的空间可达性越好。
1.3 基于空间联立方程的职住平衡与轨道交通可达性的交互影响机制分析空间联立方程模型即由多个相互联系的单一方程构成的空间计量经济模型。联立方程模型描述经济变量间的双向因果关系,即某一经济变量决定着其他经济变量,反过来又受其他经济变量影响。如城市基础设施与经济发展存在显著的双向促进作用,一方面政府可通过基础设施投资带动经济增长,另一方面在经济增长的同时可进行新的投资[24]。同理,由已有研究可知,职住平衡与轨道交通可达性之间也存在复杂的双向因果关系,仅用单一的计量经济模型无法完整地刻画两者之间的互动关系。因此,本文通过引入空间联立方程[25],一方面揭示职住平衡与轨道交通可达性的空间交互机制和溢出效应;另一方面解释建成环境分别对职住平衡与轨道交通可达性影响作用的空间依赖效应和溢出效应。空间联立方程包括职住平衡方程和轨道交通可达性方程,分别为
| $ \begin{aligned} \ln C f_i=& \alpha_0+\alpha_1 \omega_{i j} \ln C f_i+\alpha_2 \ln A_i+\\ & \alpha_3 \omega_{i j} \ln A_i+\alpha \sum \ln X_i+\varepsilon_i \end{aligned} $ | (6) |
| $ \begin{aligned} \ln A_i=& \beta_0+\beta_1 \omega_{i j} \ln A_i+\beta_2 \ln C f_i+\beta_3 \omega_{i j} \ln C f_i+\\ & \beta \sum \ln Y_i+v_i \end{aligned} $ | (7) |
式中:i、j为交通小区;Cfi、Ai分别为交通小区i的职住自足性指数和轨道交通可达性,即模型的内生变量;Xi、Yi分别为影响职住自足性指数和轨道交通可达性的控制变量(外生变量);ωij为空间权重;α0、β0为常数项;α1、β1分别为邻近交通小区职住平衡和轨道交通可达性的空间溢出系数,分别表征职住平衡和轨道交通可达性的空间溢出程度;α2、β2用于刻画职住平衡和轨道交通可达性之间的内生关系,其值正负分别表示一变量对另一变量的推动或抑制作用,其值大小则表示作用的强度;α3、β3用于刻画职住平衡和轨道交通可达性之间的空间交互效应,前者表征邻近交通小区轨道交通可达性对本地区职住平衡的影响程度,后者表征邻近交通小区职住平衡对本地区轨道交通可达性的程度;ε、v为随机项。本文对解释变量进行对数化处理,减少异方差及变量波动对模型结果的影响。
2 研究数据与变量 2.1 研究区域与数据本文选取西安市中心城区即未央区、新城区、莲湖区、碑林区、灞桥区、雁塔区6个行政区作为研究区域,以800个交通小区(traffic analysis zone,TAZ)作为空间分析单元。采用的数据包括西安市2018年5月份手机信令数据、AFC刷卡数据、轨道交通线网数据、公交站点数据、百度POI数据、研究范围内路网数据(OpenStreetMap,OSM)等。数据满足时空范围一致性要求。
手机信令是由手机用户在发生开关机、通话、收发短信或移动位置等事件时,被通信基站捕获并记录的数据,数据空间分辨率为基站,时间分辨率则可精确到秒。每条手机信令数据包括用户ID、事件类型、时间戳、基站编号、位置区编号等字段,通过信息关联可识别用户一天中的停驻行为。具体识别过程为,界定基站服务范围,对相同位置的信令数据在时间轴上合并,结合时间阈值法构建通信活动与现实活动的映射关系。例如,确定白天工作时段为9:00—18:00,晚上居家时段为19:00—次日早上8:00,且同时满足在某点的持续停驻时间及访问天数这两个关键约束。在综合考虑约束的参数敏感性分析和与西安市第六次全国人口普查数据对比结果的基础上,取在某一地点的持续时间1 h且一个月中在该点满足持续时间要求的天数比例40%作为判断居住地与工作地的识别参数。最后,采用多层扩样模型将手机识别的人口数据扩样为总体人群的数据用于后续相关变量的计算[26]。
AFC刷卡数据主要包括交易日期、类型、车站、线路、金额等字段。本文采用西安市轨道线网2021年1月5日的早高峰时段(07:00—09:00)AFC刷卡数据,计算生成中心城区地铁站点进出站客流量。利用数据爬取技术在百度地图开放平台获取西安市轨道交通线网数据和公交站点数据,得到站点名称和经纬度坐标。在爬取的百度地图POI基础上,对二级行业POI数据进行删减和拆分,重组得到8类用地类型POI,具体为居住用地、公共管理与公共服务设施用地、商业服务业设施用地、工业用地、物流仓储用地、道路与交通设施用地、公用设施用地及绿地与广场用地。
2.2 变量构建在空间联立方程模型中,内生变量受所有变量的相互作用、相互影响;外生变量影响模型中的内生变量,但不受其他变量的影响。本文内生变量为表征职住平衡和轨道交通网络的职住自足性指数和可达性。已有研究[27-29]表明,建成环境通过土地利用多样性、道路设计、交通设施覆盖率影响职住平衡,又决定了轨道交通的可达性。因此,在参考“5D”(density, diversity, design, destination accessibility, and distance to transit)量化方法框架[30-31]的基础上,结合已有研究[5, 28]构建基于建成环境要素的联立方程外生变量。其中,选取TAZ的多样性、设计特征、可达性及公共交通邻近性要素为职住平衡方程的外生变量;选取TAZ的职住空间、设计特征及邻近性要素为轨道交通可达性方程的外生变量,对选取的变量说明如下。
1) 职住平衡方程:①多样性,采用土地利用混合度(X1)进行测度,表征TAZ的土地利用开发强度;②设计,采用快速路密度(X2)、主干路密度(X3)、次干路密度(X4)及支路密度(X5)进行测度,表征TAZ的路网连通性;③可达性,利用改进的高斯两步移动搜索法计算轨道交通可达性(A);④公共交通邻近性,采用公交站点密度(X6)进行测度,表征TAZ的公交可达性。
2) 轨道交通可达性方程:①职住空间,采用职住自足性指数(Cf)进行测度,表征TAZ的职住平衡状况;②设计,采用快速路密度(Y1)、主干路密度(Y2)、次干路密度(Y3)及支路密度(Y4)进行测度,表征TAZ的路网连通性;③邻近性,采用出入口密度(Y5)和交通设施密度(Y6)进行测度,表征TAZ的交通设施覆盖情况。
3 实证结果 3.1 基于高斯两步移动搜索法的轨道交通可达性计算结果 3.1.1 基站到车站距离(dkj)相较于传统的以空间单元集计的距离计算方法,即空间单元几何中心到设施几何中心的直线或路网距离,本文充分利用手机信令数据高空间分辨率的优势,采用基站到轨道交通车站之间的路网距离用于高斯两步移动搜索法的距离筛选,使得计算结果更精确,也更符合居民出行的实际情况。通过Network Analyst模块建立OD成本矩阵,求取研究区域内所有基站到轨道交通车站的真实路网距离。
3.1.2 可达性计算与分析采用高斯两步移动搜索模型求解轨道交通车站的空间可达性的计算过程如图 1所示。以鱼化寨车站为例,第1步计算轨道交通车站供需比,首先确定其3 km路网之内的基站,并计算基站识别出来的居住人口数与高斯距离衰减函数的乘积,求和之后得到鱼化寨车站的潜在服务人群;计算鱼化寨车站的高峰小时客流量与潜在服务人数的比值得到鱼化寨车站的供需比;同理可得研究范围内所有轨道交通车站的供需比。第2步计算基站的可达性,以编号为6351的基站为例,其可达性指数为鱼化寨车站和丈八北路车站的供需比与其距离衰减值的乘积之和。计算每个基站的空间可达性,集计在交通小区上即可求得每个空间单元的可达性值,结果如图 2所示。

|
图 1 高斯两步移动搜索法示意图 Fig. 1 Gaussian-based two-step floating catchment area (2SFCA) method |
|
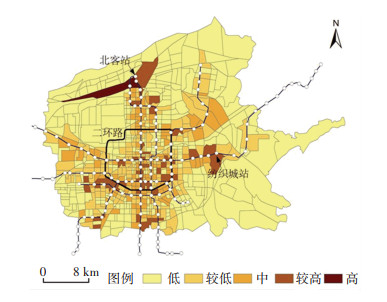
图 2 基于改进高斯2SFCA的可达性计算结果 Fig. 2 Results of accessibility calculation based on improved Gaussian 2SFCA |
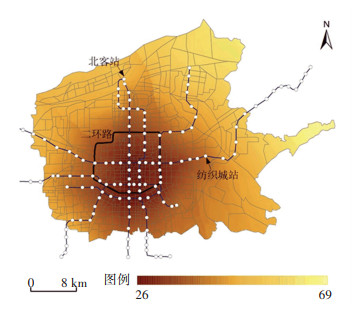
由空间分布来看,传统基于平均通达时间的可达性[15]计算结果(如图 3所示)表明轨道交通可达性呈现城市中心高、郊区低的特征。基于实际路网距离的高斯2SFCA法计算得到的轨道交通可达性呈现空间不均衡性,主要受到线网布局的影响,即轨道沿线区域可达性显著优于其他区域,且主要集中在城市二环区域;同时,还可反映供给能力的影响,即部分大型始发站周边区域轨道交通可达性较高,如北客站、纺织城站等,这些大型始发站站点吸引能力强。
|
图 3 基于平均通达时间的可达性计算结果 Fig. 3 Results of accessibility calculation based on average access time |
根据广义空间自回归三阶段最小二乘法(GS3SLSAR)[32]估计空间联立方程,为了避免多重共线性对模型估计的影响,计算自变量的方差膨胀因子(VIF)[28],所有变量的VIF均小于5,表明自变量之间的多重共线性较弱,可用于后续模型估计。GS3SLSAR的模型估计结果见表 1。结果表明,职住平衡方程和轨道交通可达性方程的调整R2分别为0.724和0.540,拟合优度均较高,验证了模型的有效性。
| 表 1 模型估计结果 Tab. 1 Estimation results |
由表 1可知,在交通分析区尺度下,轨道交通可达性与职住自足性指数的双向影响作用均显著,且都为负向作用。其中职住自足性指数对轨道交通可达性的影响更大,其系数为-3.352,即职住自足性指数每增加1%,轨道交通可达性降低-3.352%。职住平衡和轨道交通可达性存在的这种负向交互效应,一方面因为职住自足性指数的提升提高了居民在本地区寻求就业机会的可能性,削弱了居民对轨道交通的依赖性,弱化了轨道交通的吸引能力,进而降低了本地区的轨道交通可达性;另一方面轨道交通可达性的提升增强了轨道交通吸引能力,使得居民可以通过轨道交通扩大就业搜索空间,以弥补通勤所产生的职住分离,从而导致本地区职住失衡。因此,在实现两者协同发展的实践中,应分别针对城市建成区与拓展区,考虑不同程度的空间影响效应。
就空间溢出效应而言,职住自足性指数和轨道交通可达性具有显著的正向空间溢出效应,分别为0.072和0.033,即邻近地区职住自足性指数和轨道交通可达性增加1%,本地区的自足性指数和轨道交通可达性分别增加0.072%和0.033%。从交互空间溢出效应来看,职住自足性指数对轨道交通可达性的正向溢出效应(0.520)远大于后者对前者的溢出效应(0.005),这表明邻近地区职住自足性指数的提升会促进本地区轨道交通可达性的提高。其原因主要是邻近地区职住自足性指数的提升意味着周边区域整体就业机会的改善,本地区居民在周边区域获得适宜就业岗位的概率增加,需要负担更远的通勤距离,对轨道交通的依赖性有所增强,强化了轨道交通的吸引能力,进而可以提升本地区的轨道交通可达性。
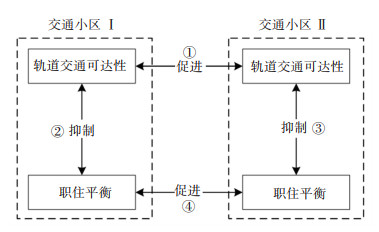
基于上述模型估计结果构建职住平衡与轨道交通可达性的交互影响机制示意图,如图 4所示,以交通小区Ι为例,则交通小区Ⅱ为其邻近地区。邻近地区(小区Ⅱ)轨道交通可达性的提升会通过不同路径(①—②和③—④)反馈于本地区(小区Ι)的职住平衡程度。邻近地区轨道交通可达性的提升会正向作用本地区的轨道交通可达性,进一步影响本地区的职住平衡程度,但邻近地区轨道交通可达性的提升同样也会影响邻近地区职住一体化程度,邻近地区的职住平衡也会影响本地区的职住平衡程度。邻近地区职住平衡程度对本地区轨道交通可达性的影响程度亦同。因此,基于上述两种作用路径的动态博弈关系,对于区域轨道交通的优化与改善,应考虑本区域与近邻区域的综合效应。
|
图 4 职住平衡与轨道交通可达性交互影响机制示意图 Fig. 4 Interaction mechanism between jobs-housing balance and rail transit accessibility |
在职住平衡方程中,土地利用混合度、主干路密度、支路密度及公交站点密度对职住平衡具有显著的正向作用。该结论与已有研究成果相一致,土地利用混合度越高意味着更多的就业岗位,居民在本地区获得就业机会的可能性增大,职住趋于一体化;同样,公交站点、主干路密度和支路密度的增加促进了公交可达性和路网连通性的提升,居民可以在本地区依赖短距离通勤方式获得更多的就业岗位[27-28]。与之相反,快速路密度对职住平衡具有显著的负向作用,这与现有研究结论相一致[29],高等级道路的提升会提高居民的通勤效率,使居民在有限的时间内到达较远的地区,进而加剧本地区的职住失衡。
在轨道交通可达性方程中,出入口密度、交通设施密度、快速路密度、主干路密度及支路密度对轨道交通可达性具有显著的正向作用。这表明丰富的交通设施和良好的路网连通性会显著增加居民获取轨道交通的机会,从而提升轨道交通可达性。
3.4 职住平衡与轨道交通可达性局部空间相关分析全局交互模型验证了职住平衡与轨道交通可达性的互馈作用,但无法揭示局部交通小区职住平衡与轨道交通可达性的空间异质性,为了探究职住平衡与轨道交通可达性的局部空间关联特征,本文借助双变量LISA模型[33],计算全局和局部双变量空间Moran's I系数,计算公式为
| $ I = \frac{{N\sum\limits_{i = 1}^N {\sum\limits_{j \ne i}^N {\left( {{W_{ij}}z_i^{cf}z_j^A} \right)} } }}{{(N - 1)\sum\limits_{i = 1}^N {\sum\limits_{j \ne 1}^N {{W_{ij}}} } }} $ | (8) |
| $ I^{\prime}=z^{C f} \sum\limits_{j=1}^N W_{i j} z_{i j}^A $ | (9) |
式中:I和I′分别为全局和局部双变量Moran's I系数;N为空间单元的个数(本文为交通小区数);Wij为空间权重;ziCf为第i个交通小区的职住自足性指数的标准化值;zjA为第j个交通小区的轨道交通可达性的标准化值。
双变量局部Moran's I系数具体可分为4类:高-高(H-H)聚类、高-低(H-L)聚类、低-高(L-H)聚类和低-低(L-L)聚类。
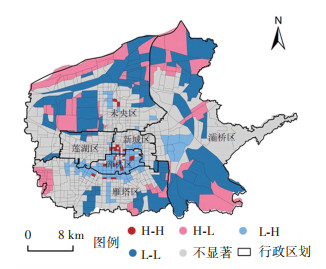
将聚类得到的LISA图进行空间可视化,如图 5所示。西安市主城区职住平衡与轨道交通可达性的全局双变量Moran’I系数为-0.110,即二者之间有较强的负向空间关系。这与空间联立方程组结果一致。由图 5可知:1)职住平衡与轨道交通可达性的H-H聚类区域主要沿轨道交通走廊呈现块状分布,这些区域轨道交通供给充足且职住一体化程度较高,二者匹配性较高;2)职住平衡与轨道交通可达性的H-L聚类区域主要集中在主城区北部(未央区和灞桥区)及城市南部零星区域(灞桥区),这些区域土地利用单一且人口密度不高,导致职住相对平衡,且大部分地区由于轨道交通发展滞后,轨道交通可达性较低,导致职住平衡与轨道交通是呈现出不协调的关系,是未来轨道交通规划与建设应重点关注的区域。由于这些地区大多职住平衡,可以通过轻轨、有轨电车等轻运量交通方式来提高轨道交通可达性,满足区域内城市居民出行需求;3)职住平衡与轨道交通可达性的L-H聚类区域主要集中在主城区的明城墙区域及以南区域,这些区域土地开放强度和人口密度高,职住相对失衡,但区域内轨道交通可达性较高,可以克服居民中长距离通勤所带来的职住分离,根据西安市城市轨道交通第三期建设规划(2019—2024年)方案,未来西安地铁6号线二期工程会贯穿此区域,进一加强站点吸引强度,以克服中心城区职住失衡程度;4)职住平衡与轨道交通可达性的L-L聚类区域主要集中在主城区西北部(未央区)、东北部(灞桥区和未央区)及城市西南部片状区域(灞桥区),西北部主要为汉长安城遗址公园,东北部为未央大学城区域和浐灞公园,西南部为白鹿原地区,这些区域主要为遗址、景区及部分高校,职住一体化程度不高,但轨道交通供给仍存在不足,也是未来轨道交通规划应重点关注的区域。
|
图 5 双变量LISA图 Fig. 5 Bivariate LISA graph |
1) 基于实际路网距离的高斯2SFCA法能够用于评价轨道交通可达性;西安市轨道交通可达性呈现空间不均匀性,轨道交通沿线区域可达性明显优于其他区域;部分大型始发站周边区域轨道交通可达性较高。
2) 职住平衡和轨道交通可达性存在负向空间交互效应,即职住平衡和轨道交通可达性相互抑制;职住平衡和轨道交通可达性均存在正向空间溢出效应,且二者之间存在正向交互空间溢出效应;二者对本地区职住平衡和轨道交通可达性的影响程度存在动态博弈关系。
3) 职住平衡和轨道交通可达性的双变量局部空间自相关分析表明,主城区北部(未灞桥区和未央区)和西南部(灞桥区)聚集了大部分H-L和L-L聚类区域,是未来轨道交通规划与建设应重点关注的区域。
4) 基于多源数据分析了职住平衡和轨道交通可达性的空间交互影响,研究结果可为轨道交通的规划建设及土地利用开发提供理论基础:一方面,通过修建轨道交通可减少部分职住失衡地区的机动车长距离通勤,达到轨道交通出行距离尺度下的职住平衡,实现城市“双碳”目标;另一方面,政府可以通过政策引导实现不同空间尺度的土地集约化利用,以此来弱化区域职住失衡程度,使居民减少对轨道交通的依赖性,从而利用传统的公共交通,优化居民出行结构。
| [1] |
孙铁山. 郊区化进程中的就业分散化及其空间结构演化--以北京都市区为例[J]. 城市规划, 2015, 39(10): 9. SUN Tieshan. Employment decentralization and evolution of employment spatial structure amid suburbanization: an empirical study on Beijing metropolitan area[J]. City Planning Review, 2015, 39(10): 9. |
| [2] |
NASRI A, CARRION C, ZHANG Lei, et al. Using propensity score matching technique to address self-selection in transit-oriented development (TOD) areas[J]. Transportation, 2020, 47(1): 359. DOI:10.1007/s11116-018-9887-2 |
| [3] |
GUAN Xiaodong, WANG Donggen. Residential self-selection in the built environment-travel behavior connection: whose self-selection?[J]. Transportation Research Part D: Transport and Environment, 2019, 67: 16. DOI:10.1016/j.trd.2018.10.015 |
| [4] |
罗桑扎西, 甄峰, 张姗琪. 复杂网络视角下的城市人流空间概念模型与研究框架[J]. 地理研究, 2021, 40(4): 1195. LUO Sangzhaxi, ZHEN Feng, ZHANG Shanqi. A conceptual model and methodological framework for examining urban people flow space based on complex network perspective[J]. Geographical Research, 2021, 40(4): 1195. DOI:10.11821/dlyj020191007 |
| [5] |
朱宇婷, 刘莹, 许奇, 等. 交通可达性与城市经济活动的空间特征分析: 以北京市为例[J]. 交通运输系统工程与信息, 2020, 20(5): 226. ZHU Yuting, LIU Ying, XU Qi, et al. Spatial characteristics analysis of traffic accessibility and city economic activity: a case study of Beijing[J]. Transportation Systems Engineering and Information Technology, 2020, 20(5): 226. DOI:10.16097/j.cnki.1009-6744.2020.05.033 |
| [6] |
KELOBONYE K, MCCARNEY G, XIA Jianhong, et al. Relative accessibility analysis for key land uses: a spatial equity perspective[J]. Journal of Transport Geography, 2019, 75: 82. DOI:10.1016/j.jtrangeo.2019.01.015 |
| [7] |
申犁帆, 王烨, 张纯, 等. 轨道站点合理步行可达范围建成环境与轨道通勤的关系研究--以北京市44个轨道站点为例[J]. 地理学报, 2018, 73(12): 2423. SHEN Lifan, WANG Ye, ZHANG Chun, et al. Relationship between built environment of rational pedestrian catchment areas and URT commuting ridership: evidence from 44 URT stations in Beijing[J]. Acta Geographica Sinica, 2018, 73(12): 2423. DOI:10.11821/dlxb201812011 |
| [8] |
LI Shaoying, LYU Dijiang, HUANG Guanping, et al. Spatially varying impacts of built environment factors on rail transit ridership at station level: a case study in Guangzhou, China[J]. Journal of Transport Geography, 2020, 82: 102631. DOI:10.1016/j.jtrangeo.2019.102631 |
| [9] |
BOUSSAUW K, NEUTENS T, WITLOX F. Relationship between spatial proximity and travel-to-work distance: the effect of the compact city[J]. Region Studies, 2012, 46(6): 687. DOI:10.1080/00343404.2010.522986 |
| [10] |
郑思齐, 徐杨菲, 张晓楠, 等. "职住平衡指数"的构建与空间差异性研究: 以北京市为例[J]. 清华大学学报(自然科学版), 2015, 55(4): 475. ZHENG Siqi, XU Yangfei, ZHANG Xiaonan, et al. Jobs-housing balance index and its spatial variation: a case study in Beijing[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(4): 475. DOI:10.16511/j.cnki.qhdxxb.2015.04.015 |
| [11] |
孙斌栋, 潘鑫, 宁越敏. 上海市就业与居住空间均衡对交通出行的影响分析[J]. 城市规划学刊, 2008(1): 77. SUN Bindong, PAN Xin, NING Yuemin. Analysis on influence of job-housing balance on commute travel in Shanghai[J]. Urban Planning Forum, 2008(1): 77. |
| [12] |
徐卞融, 吴晓. 基于"居住-就业"视角的南京市流动人口职住空间分离量化[J]. 城市规划学刊, 2010(5): 87. XU Bianrong, WU Xiao. Quantitative analysis of the separation of residential and employment space of the floating population in Nanjing[J]. Urban Planning Forum, 2010(5): 87. |
| [13] |
许宁, 尹凌, 胡金星. 从大规模短期规则采样的手机定位数据中识别居民职住地[J]. 武汉大学学报(信息科学版), 2014, 34(6): 750. XU Ning, YIN Ling, HU Jinxing. Identifying home-work locations from short-term, large-scale, and regularly sampled mobile phone tracking data[J]. Geomatics and Information Science of Wuhan University, 2014, 34(6): 750. DOI:10.13203/j.whugis20140085 |
| [14] |
何明卫, 赵胜川, 何民. 个体对通勤时间的态度和偏好视角下的职住空间失调[J]. 交通运输系统工程与信息, 2017, 17(4): 153. HE Mingwei, ZHAO Shengchuan, HE Min. The spatial dissonance of job-housing location: a perspective from individuals' attitudes and preferences toward commuting time[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 153. DOI:10.16097/j.cnki.1009-6744.2017.04.023 |
| [15] |
郭谦, 吴殿廷, 李瑞, 等. 城市轨道交通网络可达性评价方法研究--以北京轨道交通网络为例[J]. 城市发展研究, 2014, 21(4): 59. GUO Qian, WU Dianting, LI Rui, et al. Evaluation of urban rail network accessibility: a case study of Beijing subway[J]. Urban Development Studies, 2014, 21(4): 59. |
| [16] |
郭建媛, 贾利民, 秦勇. 运行计划约束下的动态可达性分析与计算[J]. 交通运输系统工程与信息, 2015, 15(1): 118. GUO Jianyuan, JIA Limin, QIN Yong. Analyzing and computing dynamic accessibility with constraints of schedule[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(1): 118. DOI:10.16097/j.cnki.1009-6744.2015.01.019 |
| [17] |
LI Wei, LUO Qin, ZEPHANIAH S, et al. Evaluating the dynamic accessibility of metro systems in overcrowded conditions[J]. Transportation Research Record: Journal of the Transportation Research Board, 2020, 2674(11): 42. DOI:10.1177/0361198120941845 |
| [18] |
AVIER G. Location, economic potential and daily accessibility: an analysis of the accessibility impact of the high-speed line Madrid-Barcelona-French border[J]. Journal of Transport Geography, 2001, 9(4): 229. DOI:10.1016/S0966-6923(01)00017-5 |
| [19] |
JAMTSHO S, CORNER R, DEWAN A. Spatio-temporal analysis of spatial accessibility to primary health care in Bhutan[J]. ISPRS International of Geo-information, 2015, 4(3): 1584. DOI:10.3390/ijgi4031584 |
| [20] |
LIU Dong, KWAN M P, KAN Z. Analysis of urban green space accessibility and distribution inequity in the city of Chicago[J]. Urban Forestry & Urban Greening, 2021, 59(1): 127029. DOI:10.1016/j.ufug.2021.127029 |
| [21] |
YANG Linchuan, CHAU K W, SZETO W Y, et al. Accessibility to transit, by transit, and property prices: spatially varying relationships[J]. Transportation Research Part D: Transport and Environment, 2020, 85: 102387. DOI:10.1016/j.trd.2020.102387 |
| [22] |
LIU Yansui, YAN Bin, ZHOU Yang. Urbanization, economic growth, and carbon dioxide emissions in China: a panel cointegration and causality analysis[J]. Journal of Geographical Sciences, 2016, 26(2): 131. DOI:10.1007/s11442-016-1259-2 |
| [23] |
王淑伟, 孙立山, 荣建. 北京市轨道站点吸引范围研究[J]. 交通运输系统工程与信息, 2013, 13(3): 183. WANG Shuwei, SUN Lishan, RONG Jian. Catchment area analysis of Beijing transit stations[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(3): 183. DOI:10.16097/j.cnki.1009-6744.2013.03.015 |
| [24] |
储君, 刘一鸣, 林雄斌, 等. 城市市政基础设施投资与经济发展的空间交互影响[J]. 北京大学学报(自然科学版), 2021, 57(2): 291. CHU Jun, LIU Yiming, LIN Xiongbin, et al. Spatial mutual effects between municipal infrastructure investment and economic development[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2021, 57(2): 291. DOI:10.13209/j.0479-8023.2021.015 |
| [25] |
KIM D, MARCOUILLER D W. The role of public lands in local economies of the US Lake States: a spatial simultaneous equation approach[J]. Land Use Policy, 2021, 100: 104883. DOI:10.1016/j.landusepol.2020.104883 |
| [26] |
唐小勇, 周涛, 陆百川, 等. 一种基于手机信令的通勤OD训练方法[J]. 交通运输系统工程与信息, 2016, 16(5): 64. TANG Xiaoyong, ZHOU Tao, LU Baichuan, et al. A commuting OD matrix training method based on mobile phone data[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 64. DOI:10.16097/j.cnki.1009-6744.2016.05.010 |
| [27] |
党云晓, 董冠鹏, 余建辉, 等. 北京土地利用混合度对居民职住分离的影响[J]. 地理学报, 2015, 70(6): 919. DANG Yunxiao, DONG Guanpeng, YU Jianhui, et al. Impact of land-use mixed degree on resident's home-work separation in Beijing[J]. Acta Geographica Sinica, 2015, 70(6): 919. DOI:10.11821/dlxb201506006 |
| [28] |
仝德, 高静, 龚咏喜. 城中村对深圳市职住空间融合的影响--基于手机信令数据的研究[J]. 北京大学学报(自然科学报), 2020, 56(6): 1091. TONG De, GAO Jing, GONG Yongxi. Impact of urban village on job-housing balance in Shenzhen: a study using mobile phone signaling data[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2020, 56(6): 1091. DOI:10.13209/j.0479-8023.2020.069 |
| [29] |
尹春, 孙斌栋, 何舟, 等. 城市建成环境对通勤时耗的影响及规划启示[J]. 城市规划, 2018, 42(8): 83. YIN Chun, SUN Bindong, HE Zhou, et al. Influence of urban built environment on commuting time and its planning implications[J]. City Planning Review, 2018, 42(8): 83. |
| [30] |
CERVERO R, KOCKELMAN K. Traveldemand and the 3Ds: density, diversity, and design[J]. Transportation Research Part D: Transport and Environment, 1997, 2(3): 199. DOI:10.1016/S1361-9209(97)00009-6 |
| [31] |
EWING R, CERVERO R. Travel and thebuilt environment: a synthesis[J]. Transportation Research Record: Journal of the Transportation Research Board, 2001, 1780(1): 87. DOI:10.3141/1780-10 |
| [32] |
KELEJIAN H H, PRUCHA I R. Estimation of simultaneous systems of spatially interrelated cross sectional equations[J]. Journal of Econometrics, 2004, 118(1): 27. DOI:10.1016/S0304-4076(3)00133-7 |
| [33] |
ZHANG Yan, LIU Yanfang, ZHANG Yang, et al. On the spatial relationship between ecosystem services and urbanization: a case study in Wuhan, China[J]. Science of The Total Environment, 2018, 637: 780. DOI:10.1016/j.scitotenv.2018.04.396 |
 2022, Vol. 54
2022, Vol. 54


