2. 湖北省公路工程技术研究中心,武汉 430063;
3. 武汉市政工程设计研究院有限责任公司,武汉 430023
2. Hubei Highway Engineering Research Center, Wuhan 430063, China;
3. Wuhan Municipal Engineering Design & Research Institute Co., Ltd., Wuhan 430023, China
沥青路面在服役周期内直接暴露于自然环境中,承受着温度、湿度等外界因素的共同作用[1-2]。水损害是沥青路面早期最主要的病害之一,其本质是水分以气态或液态的形式引发沥青混合料内的黏附开裂和内聚开裂,并在车辆荷载作用下进一步形成网裂、坑洞、唧浆、辙槽等病害,严重影响了沥青路面的服役性能,缩短了沥青路面的服役寿命[3-5]。现有研究表明,水气在沥青路面中的扩散系数远大于液态水,即水气在沥青路面内部运动的速度更快,在相同时间内携带更多的水分子进入沥青路面内部,说明水气是沥青路面水损害形成更为重要的因素[6-7]。
水气对于沥青路面水损坏的本质是影响沥青与集料的黏附性,造成沥青混合料的黏附开裂与内聚开裂。在道路工程领域,目前针对于水气扩散的研究主要集中于沥青面层材料中,有部分专家学者通过理论分析与试验验证,提出了适用于描述沥青混合料内部水气运动的理论模型,也同时对沥青混合料内部水气扩散的部分影响因素进行了分析[8-10]。然而,现有的水气运动研究集中在沥青面层,对于基层内部水气的运动规律和影响因素研究较少。大量研究证实由于路面覆盖效应,土基的相对湿度总是大于97%,故水气将从土基出发通过基层向上运动,为沥青面层提供水分来源[11-12]。作为中国沥青路面基层的主要形式,半刚性基层在服役时期由于干缩和温缩产生微裂缝,这些微裂缝为半刚性基层中水气运动提供了通道,加剧了水气在半刚性基层中的运动强度[13-14]。基于以上原因,明确服役期半刚性基层中水气运动的一般规律和影响因素,可以分析半刚性基层中微裂缝对水气运动的影响机理,更好地从沥青路面整体角度量化水气扩散对沥青路面水损害的影响程度。
为解决以上问题,本文首先分析了水气扩散的基本原理和理论,并从京港澳高速公路湖北段钻芯获取实际服役的半刚性基层芯样,设计了测量半刚性基层水气扩散系数的试验装置及具体方案,对不同材料厚度和温度条件对半刚性基层内水气扩散的影响进行了研究,得到了材料厚度和温度条件对半刚性基层内水气扩散影响的一般规律,为更好地从水气扩散角度评价沥青路面水损害提供了理论依据。
1 水气扩散原理与理论 1.1 水气扩散原理在沥青路面服役期内,水气从下方进入沥青路面结构层中。而依据沥青路面中水气运动的形式可以分为积聚型水气运动和穿透型水气运动两个阶段[15-16]。对于新修建的沥青路面,其内部相对湿度接近于零,水气从空气和土基中进入,在基层和沥青路面的连接处不断积聚,如图 1(a)所示;对于长期服役的沥青路面而言,沥青路面内部水气趋于动态稳定,主要表现为水气从土基进入基层,穿透沥青面层进入空气,其过程如图 1(b)所示。
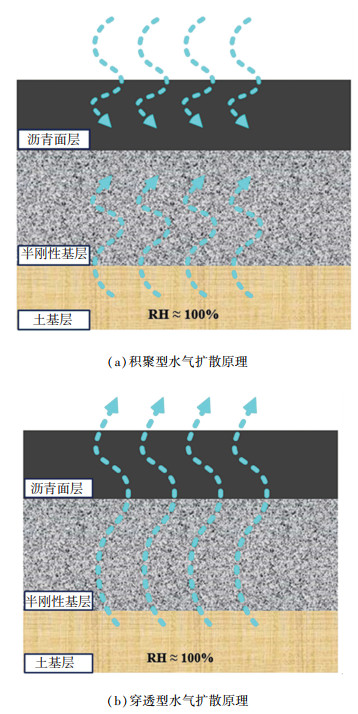
|
图 1 半刚性基层沥青路面水气扩散原理 Fig. 1 Principle of water vapor diffusion in semi-rigid base asphalt pavement |
在已有的研究中发现,在沥青路面中穿透型水气扩散系数是积聚型水气扩散系数的1 000倍以上,穿透型水气扩散运动占据水气运动的主导作用,同时本研究的主要对象为长期服役的半刚性基层材料,故在后续研究中主要对半刚性基层的穿透型水气扩散运动进行研究[17-18]。
1.2 水气扩散理论由于半刚性基层材料为多孔材料,故可以采用菲克定律对半刚性基层中的水气运动进行研究。依据菲克第一定理,在一维状态下单位时间内通过垂直于扩散方向的单位截面积的扩散通量与该截面处的浓度梯度成正比,此时扩散通量与时间无关,其理论模型[19]可以表示为
| $ J=-D \frac{\mathrm{d} C}{\mathrm{~d} y} $ | (1) |
式中:J为扩散通量,kg/(m2·s);D为有效扩散系数,kg/m2;dC/dy为浓度梯度。
同时由扩散通量的定义可知[20]:
| $ J=\frac{1}{A} \frac{\mathrm{d} W_{\mathrm{H}_2 \mathrm{O}}}{\mathrm{d} t} $ | (2) |
式中:A为扩散面积,m2;t为扩散时间,s;dWH2O/dt为水气穿透率,即单位时间内水气穿透过沥青混合料的质量,kg。
联立式(1)和式(2)可以得到水气扩散系数的计算公式为
| $ \begin{aligned} D_{\text {eff }}=&-\frac{1}{A} \frac{\mathrm{d} W_{\mathrm{H}_2 \mathrm{O}}}{\mathrm{d} t}\left(\frac{L}{C_1-C_2}\right)=\\ &-\frac{1}{A} \frac{\mathrm{d} W_{\mathrm{H}_2 0}}{\mathrm{~d} t} \frac{R T}{M_{\mathrm{H}_2 \mathrm{O}}}\left(\frac{L}{P_1-P_2}\right) \end{aligned} $ | (3) |
式中:L为试件厚度,cm;C1、C2为试件两侧的水气体积浓度;P1, P2为试件两侧的水气分压力,Pa;R为通用气体常数,一般取值为8.314 J·mol-1;T为开尔文温度,K;MH2O为水的相对分子质量,一般取值为18.015 g·mol-1。
在式(3)中,水气分压力[21]可以表示为
| $ P=H_{\mathrm{R}} P_{\text {sat }} $ | (4) |
式中:HR为相对湿度;Psat为某温度下水的饱和蒸气压,Pa。
由式(4)可知,当试件两侧的水气体积浓度保持稳定时,在测得某种材料的水气穿透率后,即可以依据式(4)求出某温度条件下试件的水气扩散系数。
此外,由于半刚性基层材料在实际服役环境中上下两侧存在相对湿度差ΔHR,同时也会存在水蒸气浓度差,通过理想气体状态方程转化建立相对湿度差ΔHR与水气体积浓度差ΔC的关系如式(5)所示[22]:
| $ \Delta H_{\mathrm{R}}=H_{\mathrm{R} 1}-H_{\mathrm{R} 2}=\frac{1}{P_0}\left(P_1-P_2\right) $ | (5) |
式中:P0为20 ℃时水的饱和蒸气压,取值为2 338.8 Pa;P1为试件下侧水蒸气分压力,Pa;P2为试件上侧水蒸气分压力,Pa。
水蒸气分压力可以表示为
| $ P=\frac{R T C}{M_{\mathrm{H}_2 0}} $ | (6) |
联立式(5)和式(6)可以得到相对湿度ΔHR有关两侧水气体积浓度差的表达式为
| $ \Delta H_{\mathrm{R}}=\frac{R T}{P_0 M_{\mathrm{H}_2 0}} \cdot \Delta C $ | (7) |
已有研究表明,水气扩散通量J与相对湿度差ΔHR存在线性关系,则经过理论推导可知水气扩散通量与水气体积浓度差也呈线性关系[23]:
| $ J=k \cdot \Delta H_{\mathrm{R}}=k \cdot \frac{R T}{P_0 M_{\mathrm{H}_2 0}} \cdot \Delta C $ | (8) |
当材料厚度可以量化时,式(1)可转化为
| $ J=-D \frac{\mathrm{d} C}{\mathrm{~d} y}=-D \cdot\left(-\frac{\Delta C}{L}\right)=\frac{D}{L} \cdot \Delta C $ | (9) |
联立式(7)和式(9),可得水气扩散系数表达式为
| $ D=k \cdot L \cdot \frac{R T}{P_0 M_{\mathrm{H}_2 \mathrm{O}}} $ | (10) |
从式(10)可知,对水气扩散的穿透过程而言,半刚性基层的水气扩散系数与相对湿度差ΔHR无关,即在各相对湿度差下应为常数,现有针对沥青混合料的研究也证明了这一结论。则为了明确半刚性基层内水气扩散的影响因素,需要对材料厚度和温度两个主要因素进行研究,不需要再进一步考虑相对湿度差的影响。
2 试验方案 2.1 试验材料试验材料来自于京港澳高速公路湖北段的现场芯样,钻芯得到直径为150 mm的现场芯样,经过分层切割及钻芯得到直径为100 mm的半刚性基层芯样,采用切割锯对现场芯样进行分层切割,可以得到不同厚度的半刚性基层试验样品。半刚性基层试验样品的制备过程如图 2所示。

|
图 2 半刚性基层试验样品制备过程 Fig. 2 Preparation process of semi-rigid base course test sample |
为测试得到半刚性基层试验样品的水气扩散系数,本研究设计了相关的试验装置。
采用聚丙烯材质的塑料容器作为盛水装置,因其不吸水,具有良好的密封性能,容积为250 mL,高度50 mm,开口直径为85 mm左右。水气扩散试验装置的制备过程如图 3所示。首先在塑料容器重倒入足量的蒸馏水,并控制每一个塑料容器内的蒸馏水质量保持一致,如图 3(a)所示;在塑料容器边缘涂抹高真空硅脂涂,同时采用足够尺寸的环形硅胶片在容器边缘粘贴保证容器的密封性,如图 3(b)所示;其次,将半刚性基层样品粘贴在塑料容器开口处,如图 3(c)所示;最后采用熔融状态的蜡对塑料容器接缝处进行涂抹密封,进一步保证容器密封性,尽量保证塑料容器内水气只能通过半刚性基层样品进行散失,完成后的试验装置如图 3(d)所示。

|
图 3 组装试验装置的过程 Fig. 3 Process of assembling test device |
同时,为保证试验装置的密封性能,确保在试件称量过程中水气只能从半刚性基层样品穿透至外界环境,本研究也设置了空白对照组,将半刚性基层样品替换为具有密封性的盖子,同样采用蜡进行密封处理,保证试验结果的准确性和科学性。
试验在没有阳光直射的环境下进行,且不考虑风速的影响。待试验开始,称量此时各组试验装置的初始质量,并在24 h后每天对试验装置进行称量,计算得到每天试验装置的质量变化情况,则此时试验装置的变化质量即为试验装置中水气通过半刚性基层样品散失的质量。
2.3 试验方案为探究材料厚度和温度条件对半刚性基层材料水气扩散的影响,试验方案主要针对这两个影响因素进行设计。为确保试验结果的科学性和客观性,每组试验设置3个平行试验样品作为对照组。
2.3.1 不同材料厚度水气扩散试验方案由于实际半刚性基层厚度可达30 cm左右,因此采用与实际厚度相近的半刚性基层样品来进行试验,分别为大约10、20、30、40 mm的厚度。为了与实际环境相适应,试验中控制相对湿度差ΔHR为50%~100%,温度为20 ℃。不同材料厚度的水气扩散试验方案见表 1。
| 表 1 不同材料厚度水气扩散试验方案 Tab. 1 Test plan for water vapor diffusion of different material thicknesses |
在实际服役期的沥青路面结构最高温度可达到50 ℃,但受限于密封材料蜡熔点不高限制,当温度达到40 ℃时蜡就会有软化变形的趋势,会对试验装置的密封能造成影响,因此试验温度选取为10~30 ℃,选取10、20、30 ℃共3个温度进行试验,设置相对湿度差ΔHR为50%~100%。不同温度条件下水气扩散试验方案见表 2。
| 表 2 不同温度条件水气扩散试验方案 Tab. 2 Test plan for water vapor diffusion under different temperature conditions |
以50 d作为一个称量周期,分别整理不同材料厚度水气扩散试验结果和不同温度条件水气扩散试验结果,可得两种因素对水气扩散的影响。
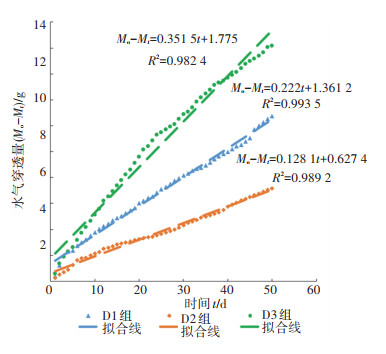
3.1 试件厚度对水气扩散的影响分析计算各组别试件的平均质量变化情况和各组试件质量改变量的平均值,绘制各厚度条件下基层材料的水气穿透量随时间的变化关系,如图 4所示。在得到各材料厚度半刚性基层材料的水气穿透量随时间的变化关系后,则可以依据理论公式计算扩散通量J和扩散系数D。

|
图 4 各组水气穿透量随时间的变化 Fig. 4 Changes in water vapor penetration of each group over time |
依据图 4的试验结果,可以得到各组基层试件水气穿透量随时间的变化斜率,即dWH2O/dt的值,D1组、D2组、D3组和D4组的变化斜率分别为0.222 0、0.193 8、0.141 6和0.106 1。基于此可以计算各组基层材料的扩散通量J和扩散系数D,计算结果见表 3。
| 表 3 不同厚度基层试件质量随时间改变量 Tab. 3 Amount of changes in the quality of specimens with different thicknesses over time |
根据表 3的计算结果,绘制不同材料厚度与扩散通量J和扩散系数D的关系,如图 5所示。
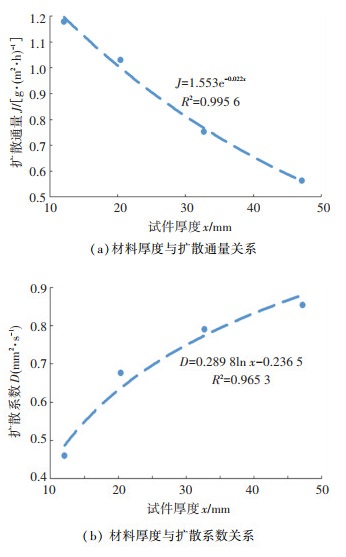
|
图 5 材料厚度与扩散通量和扩散系数关系 Fig. 5 Relationship between material thickness, diffusion flux, and diffusion coefficient |
由图 5可知,扩散系数J和扩散通量D与基层材料厚度x存在着一定的联系,其关系式分别为
| $ J=1.553 \cdot \mathrm{e}^{-0.022 x} $ | (11) |
| $ D=0.2898 \cdot \ln x-0.2365 $ | (12) |
式中x为基层芯样的厚度,mm。
依据式(11)和式(12)可知,扩散通量随着材料厚度增大而减小,二者存在指数函数关系,拟合优度R2为0.995 6;扩散系数随着材料厚度增大而增大,二者存在对数函数关系,拟合优度R2为0.965 3。针对以上试验结果展开分析,试验结果表明扩散通量随材料厚度的增大而减小,这是由于半刚性材料厚度的增大减小了单位时间内水气穿过量而导致的。而水气在半刚性基层的微裂缝通道内部运动,扩散系数随着材料厚度的增大而增大,但由于扩散通量的限制,其增大幅度逐渐减缓。
3.2 温度条件对水气扩散的影响分析计算各组别试件的平均质量变化情况和各组试件质量改变量的平均值,绘制各温度条件下基层材料的水气穿透量随时间的变化关系,如图 6所示。在得到各材料温度半刚性基层材料的水气穿透量随时间的变化关系后,则可以依据理论公式计算扩散通量J和扩散系数D。
|
图 6 各组水气穿透量随时间的变化 Fig. 6 Changes in water vapor penetration of each group over time |
依据图 6的试验结果,可以得到各组基层试件水气穿透量随时间的变化斜率,T1组、T2组和T3组的变化斜率分别为0.128 1、0.222 0和0.351 5。基于此可以计算各组基层材料的扩散通量J和扩散系数D,计算结果见表 4。
| 表 4 不同温度下基层试件质量随时间改变量 Tab. 4 Amount of changes in the quality of specimens under different temperature conditions over time |
根据表 4的计算结果,分别绘制不同温度与扩散通量和扩散系数的关系曲线,如图 7所示。
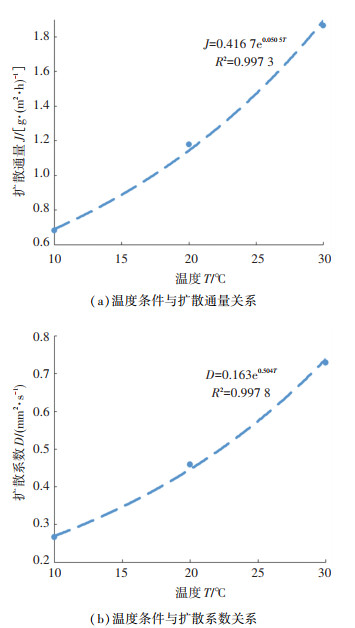
|
图 7 温度条件与扩散通量和扩散系数关系 Fig. 7 Relationship between temperature conditions, diffusion flux, and diffusion coefficient |
由图 7的试验结果可知,扩散系数D和扩散通量J与温度T存在着一定的联系,其关系式分别为
| $ J=0.4167 \cdot \mathrm{e}^{0.050\;5T} $ | (13) |
| $ D=0.163 \cdot \mathrm{e}^{0.050\;4T} $ | (14) |
式中T为温度,℃。
依据式(13)和式(14)可知,扩散通量随着温度增大而增大,二者存在对数函数关系,拟合优度R2为0.993;扩散系数随着温度增大而增大,二者存在对数函数关系,拟合优度R2为0.998。针对以上试验结果展开分析,试验结果表明扩散通量随温度的增大而增大,这是由于温度的增大为水分子提供了能量,提升了水气分子的活跃程度。同时由于水气分子的活跃程度随温度增大而加剧,扩散系数也随之增大,且随着温度增大其变化趋势也随之加剧。通过此结论可以类别得到实际温度下半刚性基层的扩散通量与扩散系数。而本文开展的材料厚度和温度条件这两个影响因素对水气扩散的影响结果可以为沥青路面湿度场的数值模拟提供设计参数,同时为量化水气对沥青路面的水损害影响提供理论依据,具有一定的理论与工程实际价值。
4 结论本文结合沥青路面实际芯样,针对材料厚度和温度条件对半刚性基层内水气扩散的影响开展了研究,得到的主要结论如下:
1) 通过理论推导证明了半刚性基层内水气扩散系数与其两侧的相对湿度差无关,而半刚性基层材料的材料厚度和温度条件与其具有一定的相关性。
2) 材料厚度会影响半刚性基层内的水气运动,水气扩散通量随着材料厚度增大而逐渐减小,且减小趋势逐渐减缓,二者存在指数函数关系,拟合优度R2为0.995 6。而水气扩散系数随着材料厚度增大而增大,且增大趋势逐渐减缓,二者存在对数函数关系,拟合优度R2为0.965 3。这说明材料厚度增大会在一定程度上阻碍半刚性基层内的水气扩散。
3) 温度条件影响半刚性基层内的水气运动,水气扩散通量随着温度增大而增大,且增大趋势逐渐加剧,二者存在对数函数关系,拟合优度R2为0.997 3。而水气扩散系数随着温度增大而增大,且增大趋势逐渐加剧,二者存在对数函数关系,拟合优度R2为0.997 8。这说明温度增大会为水气扩散提供更多的能量,加剧水气在半刚性基层内的扩散。
4) 得到的结论可以类比得到真实服役环境中半刚性基层实际厚度与温度下的水气扩散系数,为沥青路面湿度场的数值模拟提供设计参数,为量化水气对沥青路面的水损害影响提供理论依据。此外,后续研究中将结合车辆荷载进一步分析实际情况下水气的扩散规律。
| [1] |
罗钦, 吴少鹏, 胡锦轩, 等. 沥青路面材料服役寿命全气候模拟技术研究[J]. 交通科技, 2018(1): 121. LUO Qin, WU Shaopeng, HU Jinxuan, et al. Research on full climate simulation technology for service life of asphalt pavement materials[J]. Transportation Science and Technology, 2018(1): 121. DOI:10.3963/j.issn.1671-7570.2018.01.035 |
| [2] |
SALMAN M M, ALWAHAB O. Using phase change material to improve asphalt pavement behavior[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1076(1): 012104. DOI:10.1088/1757-899X/1076/1/012104 |
| [3] |
ZHU X, YE F, CAI Y, et al. Self-healing properties of ferrite-filled open-graded friction course (OGFC) asphalt mixture after moisture damage[J]. Journal of Cleaner Production, 2019, 232(20): 518. |
| [4] |
GAO J, LIU P, WU Y, et al. Moisture damage of asphalt mixture and its evaluation under the long-term soaked duration[J]. International Journal of Pavement Research and Technology, 2021(14): 607. |
| [5] |
WANG W, WANG L, YAN G, et al. Evaluation on moisture sensitivity of asphalt mixture induced by dynamic pore water pressure[J]. International Journal of Pavement Research and Technology, 2020, 489-496: 1. |
| [6] |
LUO R, LIU Z, HUANG T, et al. Water vapor passing through asphalt mixtures under different relative humidity differentials[J]. Construction & Building Materials, 2018, 165: 920. |
| [7] |
黄婷婷. 沥青混合料内部积聚型水气运动机理研究[D]. 武汉: 武汉理工大学, 2018 HUANG Tingting. Investigation on mechanism of water vapor diffusion in asphalt mixtures[D]. Wuhan: Wuhan University of Technology, 2018 |
| [8] |
LUO R, HUANG T. Development of a three-dimensional diffusion model for water vapor diffusing into asphalt mixtures[J]. Construction and Building Materials, 2018, 179: 526. DOI:10.1016/j.conbuildmat.2018.05.076 |
| [9] |
LING M, ZHANG J, FUENTES L, et al. A mechanistic framework for tensile fatigue resistance of asphalt mixtures[J]. International Journal of Fatigue, 2021, 151(6): 106345. |
| [10] |
LUO R, HUANG T. Water vapor diffusion in asphalt mixtures[J]. Journal of Chongqing Jiaotong University (Natural Science), 2016, 35(S1): 49. |
| [11] |
曹长伟. 路基湿度状况及模量调整系数研究[D]. 上海: 同济大学, 2007 CAO Changwei. Research on subgrade humidity and modulus adjustment coefficient[D]. Shanghai: Tongji University, 2007 |
| [12] |
李聪, 邓卫东, 张盛. 考虑非饱和土基质吸力影响的路基回弹模量研究[J]. 公路交通技术, 2008(8): 5. LI Cong, DENG Weidong, ZHANG Sheng. Research on subgrade resilience modulus considering the influence of suction of unsaturated soil matrix[J]. Highway and Transportation Technology, 2008(8): 5. |
| [13] |
权磊, 侯荣国, 田波. 微裂技术在半刚性基层的应用研究[J]. 公路交通科技(应用技术版), 2020, 16(9): 114. QUAN Lei, HOU Rongguo, TIAN Bo. Research on the application of microcracking technology in semi-rigid base[J]. Highway Traffic Technology (Applied Technology Edition), 2020, 16(9): 114. |
| [14] |
王鹏翔. 带裂缝半刚性基层沥青路面力学性能分析[D]. 西安: 长安大学, 2010 WANG Pengxiang. Mechanical performance analysis of asphalt pavement with cracked semi-rigid base course[D]. Xi'an: Chang'an University, 2010 |
| [15] |
罗蓉, 柳子尧, 黄婷婷, 等. 冻融循环对沥青混合料内水气扩散的影响[J]. 中国公路学报, 2018, 31(9): 24. LUO Rong, LIU Ziyao, HUANG Tingting, et al. The influence of freeze-thaw cycle on the diffusion of moisture in asphalt mixture[J]. China Journal of Highway and Transport, 2018, 31(9): 24. |
| [16] |
柳子尧. 沥青混合料穿透型水气扩散影响因素研究[D]. 武汉: 武汉理工大学, 2018 LIU Ziyao. Research on influencing factors of penetrating water vapor diffusion of asphalt mixture[D]. Wuhan: Wuhan University of Technology, 2018 |
| [17] |
HUANG T, LUO R. Investigation of effect of temperature on water vapor diffusing into asphalt mixtures[J]. Construction & Building Materials, 2018, 187: 1204. |
| [18] |
LUO R, TU C. Actual diffusivities and diffusion paths of water vapor in asphalt mixtures[J]. Construction and Building Materials, 2019, 207: 145. DOI:10.1016/j.conbuildmat.2019.02.091 |
| [19] |
CRANK J. The mathematics of diffusion[M]. London: Oxford University Press, 1975.
|
| [20] |
HENON F E, CARBONELL R G, DESIMONE J M. Effect of polymer coating from CO2 on water vapor transport in porous media[J]. The American Institute of Chemical Engineers Journal, 2002, 48(5): 941. DOI:10.1002/aic.690480504 |
| [21] |
SASAKI I, MORIYOSHI A, HACHIYA Y, et al. New test method for moisture permeation in bituminous mixtures[J]. Journal of the Japan Petroleum Institute, 2006, 49(1): 33. DOI:10.1627/jpi.49.33 |
| [22] |
LU N, LIKOS W J. Unsaturated soil mechanics[M]. Hoboken: John Wiley & Sons, Inc., 2004
|
| [23] |
LUO R, HUANG T, ZHANG D, et al. Water vapor diffusion in asphalt mixtures under different relative humidity differentials[J]. Construction and Building Materials, 2017, 136: 126. DOI:10.1016/j.conbuildmat.2017.01.034 |
 2022, Vol. 54
2022, Vol. 54


