2. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090;
3. 山东高速临枣至枣木公路有限公司,山东 枣庄 277101
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China;
3. Shandong Expressway Linzao to Zaomu Highway Co., Ltd., Zaozhuang 277101, Shandong, China
大跨度拱桥跨越能力强、造型美观,是城市公路桥梁中的主要桥型之一[1]。由于该型桥梁的主梁多采用横向跨度很大的钢梁,而吊杆和支撑系统对钢梁的约束往往不足,运营期间该型桥梁常常出现伸缩缝破损、桥面铺装失效和车致动力响应显著等病害[2]。鉴于大跨度拱桥的病害多与车致振动有关,国内外学者采用现场实测及数值分析的方法对该型桥梁的车-桥耦合动力响应进行了广泛研究。文献[3]对一座大跨度异型钢管混凝土拱桥的典型病害进行了调查分析,结果表明伸缩缝及支座病害会导致该型桥梁车致动力响应显著。文献[4]通过试验研究及数值模拟对一座振动响应较大、疲劳开裂现象严重的钢系杆拱桥的病害原因进行了研究,结果表明车致冲击作用增加是导致梁端部构件疲劳损伤的重要原因。文献[5]通过数值分析及现场实测对一座中承式钢拱桥支座与钢梁连接螺栓疲劳开裂的原因进行了研究,研究表明车辆作用下主梁纵向位移引起的轴向力是导致螺栓裂缝和断裂的主要原因。现阶段研究成果表明,车辆荷载对大跨度拱桥梁端各构件的冲击作用显著,易导致梁端构件发生疲劳损伤[6-7];而伸缩缝是该型桥梁梁端最常见的疲劳损伤或失效构件,伸缩缝损伤或失效是造成该型桥梁吊杆应力幅、支座应力幅、钢主梁应力幅变化的重要诱因。
为明晰伸缩缝参数变化对其车致动力响应的影响,国内外学者进行了积极的尝试。文献[8]通过建立的三维车辆模型,采用路面不平整度来模拟伸缩缝损伤,研究了伸缩缝损伤条件下车辆荷载对预应力混凝土箱梁桥桥面板受力的影响,指出伸缩缝的损伤会增加车辆对桥面板和伸缩缝的冲击作用。文献[9]提出了一种基于分布式弹簧-阻尼单元的计算方法来模拟车辆通过伸缩缝时的动力特性,并分析了伸缩缝宽度、车速等参数的变化对车-桥耦合振动的影响。文献[10]提出了一种能够考虑伸缩缝间隙宽度而忽略伸缩缝刚度、阻尼等参数影响的简化力学模型,重点探讨了伸缩缝的缝宽变化对车-桥耦合振动的影响。现阶段研究成果表明,考虑伸缩缝参数影响的车-桥耦合动力响应(车-缝-桥耦合动力响应)参数影响规律分析仍停留在个别参数影响分析阶段,车-缝-桥耦合动力响应分析方法欠缺,考虑伸缩缝参数影响的车桥耦合动力响应参数影响规律尚不明晰。
鉴于此,本文以某大跨度中承式钢管混凝土拱桥为研究对象,结合车辆过缝过程分析和模态综合法提出了一种能够考虑车辆过缝过程的车-桥耦合振动分析方法(简称车-缝-桥耦合振动分析方法),并基于实测数据验证,进而探究了伸缩缝高差、支撑刚度、缝宽等参数变化对车-缝-桥耦合动力响应的参数影响规律。研究成果可作为桥梁车致振动响应规律的补充。
1 车-缝-桥耦合动力响应分析方法 1.1 车-桥耦合动力响应分析模型本文选取中国公路出现频率较高的典型三轴(双后轴)车辆参数作为本文车辆模型的参数,整辆车辆模型包括7个刚体(1个车体,6个车轮)。考虑桥梁车致振动主要包括竖向和横向振动两个方向,可忽略车体及车轮的在行驶方向的自由度以及车体摇头自由度,三轴车模型共16个自由度[11]。桥梁结构动力平衡方程采用模态综合法,当伸缩缝两侧高差较小(小于25 mm)、缝宽较小(不大于80 mm)且车轮与桥梁接触面较大时[12],假定车辆轮胎与桥梁接触位置变形协调,则车-桥耦合运动方程可由下式[13]表示为
| $ \begin{array}{c} {\left[\begin{array}{cc} \boldsymbol{M}_{\mathrm{v}} & \bf{0} \\ \bf{0} & \boldsymbol{M}_{\mathrm{B}} \end{array}\right]\left\{\begin{array}{l} \boldsymbol{X}_{\mathrm{v}} \\ \ddot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right\}+\left[\begin{array}{cc} \boldsymbol{C}_{\mathrm{v}} & \boldsymbol{C}_{\mathrm{vB}} \\ \boldsymbol{C}_{\mathrm{Bv}} & \boldsymbol{C}_{\mathrm{B}}+\boldsymbol{C}_{\mathrm{B}}^{\mathrm{v}} \end{array}\right]\left\{\begin{array}{c} \boldsymbol{X}_{\mathrm{v}} \\ \dot{\boldsymbol{q}}_{\mathrm{B}} \end{array}\right\}+} \\ {\left[\begin{array}{cc} \boldsymbol{K}_{\mathrm{v}} & \boldsymbol{K}_{\mathrm{vB}} \\ \boldsymbol{K}_{\mathrm{Bv}} & \boldsymbol{K}_{\mathrm{B}}+\boldsymbol{K}_{\mathrm{B}}^{\mathrm{v}} \end{array}\right]\left\{\begin{array}{l} \boldsymbol{X}_{\mathrm{v}} \\ \boldsymbol{q}_{\mathrm{B}} \end{array}\right\}=\left\{\begin{array}{l} \boldsymbol{F}_{\mathrm{v}}^{\mathrm{r}} \\ \boldsymbol{F}_{\mathrm{B}}^{\mathrm{rG}} \end{array}\right\}} \end{array} $ | (1) |
式中:MB, CB, KB分别为桥梁的模态质量、阻尼和刚度;FB为车辆与桥梁之间的作用力;v和B分别表示车辆和桥梁,下标Bv、vB表示车桥耦合项,r、G分别表示由不平整度和自重车辆和桥梁之间的作用力。
1.2 车-缝-桥耦合动力响应分析模型1.1节的车桥耦合动力响应分析方法是基于车辆在与桥梁接触点的协调关系建立的,由于伸缩缝间隙的存在,在计算在车致伸缩缝动力响应时,需根据车辆过缝的力学特点,结合车-桥耦合振动方程,推导出车-缝-桥耦合振动方程。
以该桥双缝式模数式伸缩缝为例,在车辆过缝时,伸缩缝各梁的受力与轮胎接触面积有着密切的联系[14-15]。伸缩缝及车轮过缝示意见图 1。图中s0表示伸缩缝宽度,s表示轮胎沿桥梁方向宽度,lc、l0分别表示中横梁、边横梁宽度,L1表示车辆上桥前行驶距离。

|
图 1 模数式伸缩缝及车辆过缝示意图 Fig. 1 Modular expansion joint and its vehicle passing diagram |
假设桥梁受到的总轮载为F,车辆过缝时FBL1、FZL、FBL2分别表示车轮过缝时小桩号侧边横梁、中横梁、大桩号侧边横梁受到的车轮作用力。则各部分的车轮作用力分别表示为
| $ F_{\mathrm{BL} 1}=\beta_{\mathrm{BL} 1} F $ | (2) |
| $ F_{\mathrm{ZL}}=\beta_{\mathrm{ZL}} F $ | (3) |
| $ F_{\mathrm{BL} 2}=\beta_{\mathrm{BL} 2} F $ | (4) |
| $ \beta_{\mathrm{BL} 1}+\beta_{\mathrm{ZL}}+\beta_{\mathrm{BL} 2}=1 $ | (5) |
其中βBL1, βZL, βBL2表示伸缩缝各横梁受力与车轮总作用力的比值(简称等效力分配系数),其与车辆行驶位置,轮胎与伸缩缝横梁接触距离,以及伸缩缝横梁、间隙等参数有关。
伸缩缝各横梁受力与车轮总作用力的比值的具体推导过程及计算公式见文献[16]。将车辆与伸缩缝之间的实际面接触等效为点接触[17],当车胎与伸缩缝边、中横梁同时接触时,等效位移模型如图 2所示。

|
图 2 车辆过缝等效位移 Fig. 2 Equivalent displacement of vehicle passsing joint |
结合本文采用的车辆、伸缩缝模型参数,轮胎接触面的等效位移可表示为
| $ U_{\mathrm{B}}=\gamma U_{\mathrm{BL}}+(1-\gamma) U_{\mathrm{ZL}} $ | (6) |
其中γ表示车轮与边横梁接触长度和车轮与伸缩缝各梁总接触长度之比。
需要指出的是当s≤2s0+lc,车轮可单独作用于伸缩缝中横梁。当前部车轮作用于伸缩缝上,后部车轮会作用于临近桥面或路面。此时,前轮位移与伸缩缝接触面位移等效,可由式(6)计算,后轮与桥梁接触点的位移与车-桥耦合振动方程中一致。以前轴左轮过伸缩缝为例,车胎与伸缩缝接触面(车胎与伸缩缝边横梁、中横梁接触时)的等效竖向位移Zb1、横向位移Yb1分别为
| $ \begin{aligned} Z_{\mathrm{b}}^1=& \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{v}}^n\left(x_{\mathrm{L} 1}\right)=\gamma \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{v}}^n\left(x_{\mathrm{BL.L1}}\right)+\\ &(1-\gamma) \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{v}}^n\left(x_{\mathrm{ZL.} \mathrm{L} 1}\right) \end{aligned} $ | (7) |
| $ \begin{aligned} Y_{\mathrm{b}}{ }^1=& \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{h}}^n\left(x_{\mathrm{L} 1}\right)=\gamma \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{h}}^n\left(x_{\mathrm{BL.} \mathrm{L} 1}\right)+\\ &(1-\gamma) \sum\limits_{n=1}^{N_{\mathrm{b}}} q_n \phi_{\mathrm{h}}^n\left(x_{\mathrm{ZL.L} 1}\right) \end{aligned} $ | (8) |
其中ϕhn(xL1)和ϕvn(xL1)分别表示第n阶振型的水平和竖向分量,qn表示广义模态坐标,xL1表示车轮在桥梁上的位置坐标,xBL.L1表示对应边横梁位置坐标,xZL.L1表示对应中横梁位置坐标。当前轴通过伸缩缝(车胎与伸缩缝边横梁、中横梁接触)、后轴在桥面时,根据上文对车辆过缝时的力学过程分析,利用力分配系数、等效位移,作用于桥梁的第n阶模态力FBn可表示为
| $ \begin{aligned} F_{\mathrm{Bn}}=& {\left[\beta \phi_{\mathrm{h}}^n\left(x_{\mathrm{BL.L} 1}\right) F_{\mathrm{byL}}^1+(1-\beta) \phi_{\mathrm{h}}^n\left(x_{\mathrm{ZL.L1}}\right) F_{\mathrm{byL}}^1+\right.} \\ &\left.\beta \phi_{\mathrm{v}}^n\left(x_{\mathrm{BL.L} 1}\right) F_{\mathrm{bzL}}^1+(1-\beta) \phi_{\mathrm{v}}^n\left(x_{\mathrm{ZL} . \mathrm{L} 1}\right) F_{\mathrm{bzL}}^1\right]+\\ & {\left[\beta \phi_{\mathrm{h}}^n\left(x_{\mathrm{BL} . \mathrm{R} 1}\right) F_{\mathrm{byR}}^1+(1-\beta) \phi_{\mathrm{h}}^n\left(x_{\mathrm{ZL.R} 1}\right) F_{\mathrm{byR}}^1+\right.} \\ &\left.\beta \phi_{\mathrm{v}}^n\left(x_{\mathrm{BL.R} 1}\right) F_{\mathrm{bzR}}^1+(1-\beta) \phi_{\mathrm{v}}^n\left(x_{\mathrm{ZL} . \mathrm{R} 1}\right) F_{\mathrm{bzR}}^1\right]+\\ & \sum\limits_{i=2}^3\left[\phi_{\mathrm{h}}^n\left(x_{i \mathrm{~L}}\right) F_{\mathrm{byL}}^i+\phi_{\mathrm{v}}^n\left(x_{i \mathrm{~L}}\right) F_{\mathrm{bzL}}^i+\right.\\ &\left.\phi_{\mathrm{h}}^n\left(x_{i \mathrm{R}}\right) F_{\mathrm{byR}}^i+\phi_{\mathrm{v}}^n\left(x_{i \mathrm{R}}\right) F_{\mathrm{bzR}}^i\right] \end{aligned} $ | (9) |
由此可以推出边横梁、中横梁受到的横向和纵向模态力,将各式代入桥梁振动方程,从而得到考虑伸缩缝影响的车-桥耦合振动耦合项CvBm, CBvm, KvBm, KBvm, KBvnm, Frv, FBnrG[16]。其中上标m表示考虑伸缩缝参数影响。
至此,可通过前文过程考虑伸缩缝参数对桥梁车致动力响应的影响。
2 车-缝-桥耦合振动分析方法验证 2.1 现场实测对象以一典型的大跨度钢管混凝土中承式拱桥为研究对象,该桥全长260 m,主梁采用宽度为40 m的钢箱梁,长110.8 m,边跨采用预应力混凝土梁与主桥V构固结,混凝土梁总长74.6 m。主梁在西侧和东侧分别采用GQF-MZL80型和GQF-ZLM160型模数式伸缩缝。
为验证车-缝-桥耦合动力响应分析方法,分别对该桥的基本动力特性和主梁动力响应进行了测试。动位移、加速度实测测点布置在主梁梁端截面(Deck-S),1/4跨截面(Deck-Q),1/2跨截面(Deck-M),各实测测点的横向位置为距离截面最外侧3 m处,如图 3所示。

|
图 3 测点布置图 Fig. 3 Layout of measurement points |
采用ANSYS建立本文研究对象的空间有限元模型,主桥钢箱梁采用壳单元Shell181模拟,主拱、副拱(稳定拱)、边跨混凝土箱梁、V构、立柱选用空间梁单元Beam188模拟,并采用等效截面模拟钢管混凝土主拱圈的截面属性;吊杆、系杆均采用空间杆单元Link180来模拟。边横梁与主梁处模拟为活动铰支座,在节点之间加入弹簧-阻尼器单元Combin14单元来实现。伸缩缝各梁采用Beam188模拟,伸缩缝支撑弹簧采用Combin14模拟,最终其有限元模型如图 4所示。图 5给出了典型的桥梁振型、表 1给出了前10阶振型模态信息。需要指出的是主梁是直接承受车辆荷载的构件,且车辆荷载主要引起主梁的竖向动力响应。因此,在实测中仅对主梁关键位置的竖向动力响应进行了测试。由表 1可知,与主梁竖向振型相关的计算结果与实测结果最大误差为2.0%~4.6%,有限元模型能够较准确的描述结构的动力特性,可用于后续动力响应分析。

|
图 4 伸缩缝与桥梁连接处示意图 Fig. 4 Diagram of connection between expansion joint and bridge |

|
图 5 桥梁振型图(主拱主梁对称竖弯) Fig. 5 Typical mode shapes of bridge (symmetric vertical bending of main arch and main beam) |
| 表 1 动力特性计算结果及比较 Tab. 1 Results and comparison of dynamic characteristics |
通过对桥梁各个频段模态进行试算,伸缩缝局部振型主要分布在87~105 Hz频段内。为使得参与计算的振型数量达到精度要求,能够更准确地模拟车-缝-桥之间的耦合作用,选择主梁的主要振型(前50阶振型)以及包含伸缩缝振动的局部振型(局部20阶振型)开展车-缝-桥耦合振动计算。
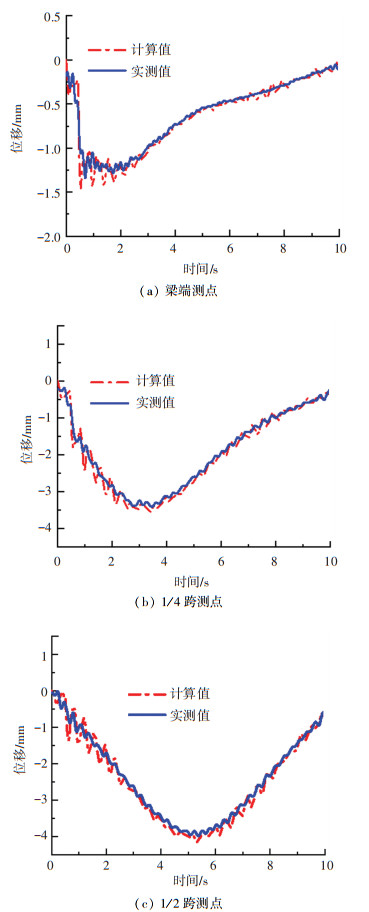
2.3 车-缝-桥耦合振动分析方法验证现场由二轴卡车沿最外侧车道以40 km/h速度行驶,数值模型采用较为接近的二轴车模型来模拟。图 6给出了相同工况下(单车以40 km/h沿最外侧车道行驶)采用本文车-缝-桥耦合动力响应分析方法计算的测点动位移响应和现场实测动位移对比曲线。主梁关键测点的竖向位移峰值对比见表 2。
|
图 6 位移时程曲线对比图 Fig. 6 Comparison of displacement time history curves |
| 表 2 竖向位移峰值实测值与计算值对比 Tab. 2 Comparison of measured and calculated vertical displacement |
由图 6和表 2可知,计算值与实测值拟合较好,实测值与计算值相对误差为4.11%~8.14%,考虑到计算模型中的支座参数、车辆参数等与实际参数存在差异,本文提出的车-缝-桥耦合动力响应计算方法能较为准确地模拟车辆行驶的各个阶段,该方法可用于车-缝-桥耦合动力响应分析。需要指出的是冲击系数受路面不平整度、车辆参数以及桥梁参数等影响十分显著,而单一工况条件下的冲击系数计算与分析是没有实际意义的,因此本文重点探究设定参数条件下桥梁车致冲击系数受伸缩缝参数变化的影响规律。
3 车-缝-桥耦合动力响应分析 3.1 分析工况结合2.3节的相关分析结果,本文的车-缝-桥耦合动力响应分析工况见表 3。
| 表 3 车-缝-桥耦合动力响应分析工况 Tab. 3 Analysis of vehicle-gap-bridge coupling dynamic response |
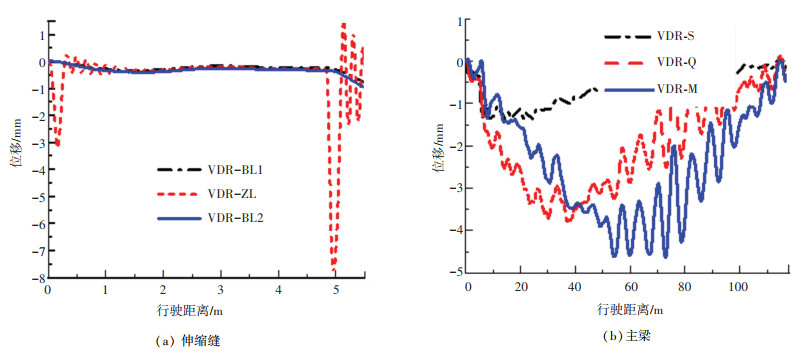
车辆采用与2.1节一致的二轴车,计算数据分析测点包括伸缩缝各梁,主梁梁端截面,1/4跨截面,1/2跨截面、测点布置的位置与2.1节相同。对设计参数、变化参数下各个工况进行车-缝-桥耦合动力响应分析,获得桥梁的动力响应规律。其中VDR-BL1、VDR-BL2、VDR-ZL分别表示伸缩缝边横梁1、边横梁2、中横梁测点位移时程曲线,VDR-S、VDR-Q、VDR-M分别表示主梁端部、1/4跨、1/2跨截面测点位移时程曲线。
3.2 伸缩缝设计参数 3.2.1 车速影响将路面不平整度考虑为“理想”状态,车速参数为10~100 km/h,不同车速下各测点典型的竖向位移时程曲线如图 7所示。

|
图 7 桥梁各测点在不同车速的竖向位移时程曲线 Fig. 7 Vertical displacement time history curves of bridge measurement points under different vehicle speeds |
如图 7所示,随车速变化伸缩缝测点以及主梁梁端测点位移峰值无显著的变化规律,而主梁1/4跨截面、1/2跨截面测点位移峰值随车速增大呈增大趋势。不同车速下各测点冲击系数的变化曲线如图 8所示。需要指出的是,边横梁与主梁梁端之间的连接为刚性连接,边横梁动力响应规律与主梁梁端动力响应的变化规律一致。因此本文并未讨论边横梁测点的动力响应规律。

|
图 8 不同车速下桥梁冲击系数对比图 Fig. 8 Comparison of bridge impact coefficients under different speeds |
如图 8(a)所示,伸缩缝中横梁的冲击系数随车速的增加呈先减小后增大的趋势,并且车速为60~100 km/h时的冲击系数较最小值增幅较大(前轴14.5%~36.8%,后轴7.6%~16.8%)。前轴过缝的冲击系数较后轴过缝的冲击系数大,前轴过缝冲击系数的最大值为1.37,而后轴过缝冲击系数的最大值为1.17。与重车和轻车引起的桥梁冲击系数规律相似,前轴(轴重9.16 t,约为后轴总重轴重25.14 t的1/3)过缝引起的冲击系数更大,但此时伸缩缝的实际受力则比后轴过缝时伸缩缝的受力小。
如图 8(b)所示,主梁各测点的车辆冲击作用相对伸缩缝的车辆冲击作用较小,并随车速呈先上升后趋于平稳的趋势。考虑伸缩缝参数影响后,主梁端部测点冲击系数峰值随车速变化离散性更大,车速为30 km/h时主梁端部测点冲击系数值峰值为1.11;1/4跨截面测点最大冲击系数出现在车速为100 km/h时,最大值为1.07,1/2跨截面测点的冲击系数最大值出现在100 km/h时,最大值为1.02。与梁端测点冲击系数相比,1/4跨截面、1/2跨截面的位移冲击系数逐渐减小,1/4跨、1/2跨截面测点与梁端测点冲击系数值相比分别减小3.51%、8.19%。即考虑伸缩缝参数后车辆对主梁端部伸缩缝附近主梁的冲击作用明显增加。
3.2.2 路面不平整度影响通过上节对车速的参数影响规律分析可知,在较高车速时,车辆的冲击作用较大。因此本文选择车速分别为60、80、100 km/h时,进行路面不平整度参数影响分析。需要指出的是为避免路面不平整度随机生成过程对计算结果的可靠性产生影响,需计算一定数量的路面不平整度样本, 取平均值作为最终结果,本文考虑采用20个路面不平整度样本进行计算[18],且结合桥面的实际工作状况并降低运算量,仅考虑“理想”“很好”,“好”,“一般”4种路面不平度作为车-缝-桥系统模型的输入。限于篇幅,图 9给出了车速为60 km/h时,路面不平度等级为“一般”时各测点典型位移曲线。
|
图 9 典型位移时程曲线 Fig. 9 Typical displacement time history curves |
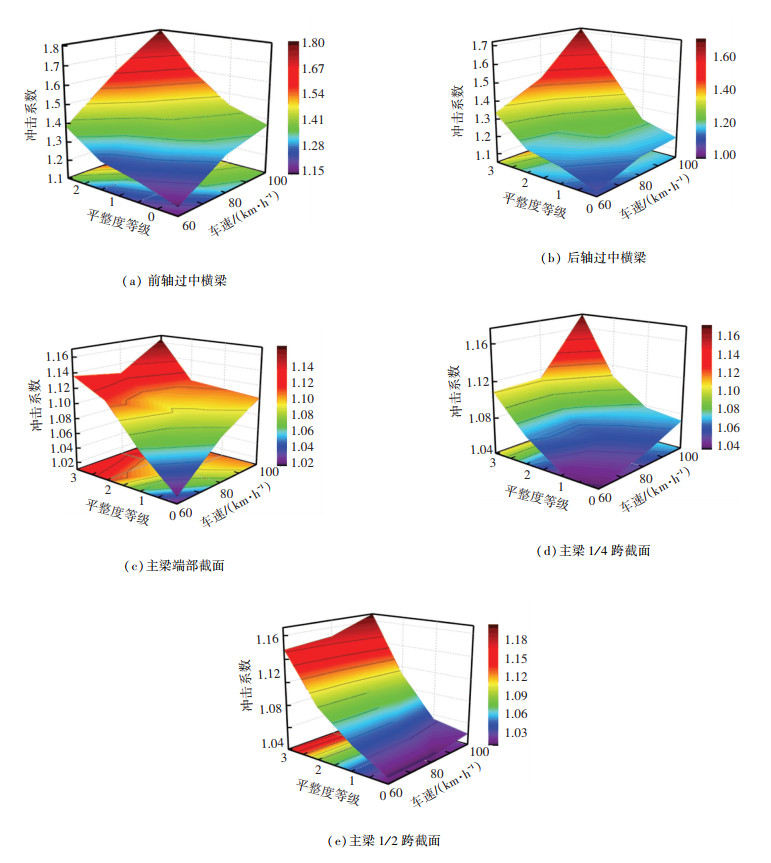
为更直观反映路面不平整度、车速参数对车辆冲击系数的影响,将各测点数据绘制成三维云图,如图 10所示。
|
图 10 冲击系数随车速、路面不平整度的变化规律 Fig. 10 Variation of impact coefficient with vehicle speed and road roughness |
由图 10可知,伸缩缝位置处测点冲击系数随路面不平整度变化显著,在3种路面不平整度下,前轴过缝中横梁冲击系数的增幅分别为5.05%、16.29%、31.97%,最大值为1.805。后轴过缝中横梁的冲击系数的增幅分别为5.31%、26.55%、47.19%,冲击系数最大值为1.719,二者均已超过规范值1.45。主梁冲击系数受路面状况等级影响同样显著,3种路面不平整度情况下,梁端、1/4跨、跨中截面冲击系数较“理想”路面状况冲击系数值的增幅分别为0.32%,0.76%,5.63%;0.59%,3.24%,9.69%;1.19%,8.42%,18.95%。综上,车辆对伸缩缝构件的局部冲击作用要大于主梁的冲击作用,而主梁跨中截面受路面不平度的影响较主梁端部显著。分析原因,路面对车致动力响应的影响是一个累积的过程,不同不平整度条件下车辆在桥梁上行驶的距离越长不平整度对车致动力响应的影响越大。
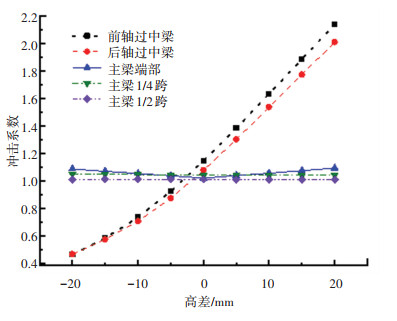
3.3 伸缩缝变化参数 3.3.1 伸缩缝高差影响按照3.1节的分析工况,将伸缩缝支撑刚度和缝宽设定为设计值,仅考虑伸缩缝中横梁高差的变化。采用局部路面不平整度(仅考虑伸缩缝处的不平整度)模拟伸缩缝高差。各测点冲击系数的计算结果对比如图 11所示。
|
图 11 冲击系数随伸缩缝高差变化规律 Fig. 11 Influnence of joint height difference on impact coefficient |
由图 11可知,伸缩缝高差对伸缩缝本身和主梁端部(临近伸缩缝位置)的冲击作用影响较大。伸缩缝测点冲击系数随高差增加而变大,前轴过中横梁的增幅为-59.5%~86.6%。后轴过缝的增幅为-56.6%~86.7%。主梁梁端测点的冲击系数随高差的变化程度呈增大趋势,最大增幅为7.2%。主梁1/4跨截面、1/2跨截面位移峰值受高差影响较小。需要指出的是,在高差达20 mm时,伸缩缝测点位置处冲击系数最大值达2.14,已经远超规范规定值。图 12给出了支座反力变化幅(支座反力变化幅值/零高差支座反力幅值)随高差的变化规律。

|
图 12 支座反力随高差变化规律 Fig. 12 Variation of bearing reaction with height difference |
由图 12可知,随中横梁与边横梁高差绝对值增加(-20~20 mm),支座的应力幅呈增大趋势,增幅为2.1%~9.3%。在伸缩缝高差发生改变后,车辆对支座的冲击作用增大,反复车辆荷载作用下,易导致支座发生疲劳破坏。
3.3.2 伸缩缝支撑刚度影响按照3.1节的分析工况,将伸缩缝高差和缝宽设定为设计值,仅考虑伸缩缝支撑刚度的变化。桥梁各测点冲击系数的变化规律如图 13所示。

|
图 13 不同伸缩缝支撑刚度测点冲击系数 Fig. 13 Impact coefficient of measurement points under different expansion joint support stiffness |
由图 13可知,伸缩缝支撑刚度改变后,伸缩缝中横梁的车辆冲击作用变化显著,随着伸缩缝支撑刚度的削减(-67%),最大增幅为113.2%;而伸缩缝支撑刚度削减对梁端车致冲击系数影响最大,最大增幅为7.0%。
3.3.3 伸缩缝缝宽影响按照3.1节的分析工况,将伸缩缝高差和支撑刚度设定为设计值,仅考虑伸缩缝缝宽的变化。各测点位移峰值及冲击系数见表 4~6。
| 表 4 桥梁各测点在不同缝宽下动力位移峰值 Tab. 4 Peak value of dynamic displacement of each measuring point of the bridge under different joint widths |
| 表 5 桥梁各测点在不同缝宽下静力位移峰值 Tab. 5 Peak value of static displacement at each measuring point of the bridge under different joint widths |
| 表 6 桥梁各测点在不同缝宽下冲击系数 Tab. 6 Impact coefficient of each measuring point of the bridge under different joint widths |
由表 4~6可知,伸缩缝测点位移峰值、冲击系数随伸缩缝缝宽增大而增大。当缝宽为80 mm时,前轴过缝最大伸缩缝车致冲击系数增幅达5%。缝宽参数对主梁各测点位移峰值及冲击系数影响不显著。
4 结论本文以某大跨度中承式钢管混凝土拱桥为研究对象,结合车辆过缝过程分析和模态综合法建立了能够考虑车辆过缝过程的车-桥耦合振动分析方法(简称车-缝-桥耦合振动分析方法),并基于实测验证;进而开展了伸缩缝设计参数条件下和伸缩缝参数典型变化条件下车-缝-桥耦合动力响应分析。主要研究如下结论:
1) 提出的车辆过缝时变接触关系参数化方法可以有效地模拟车辆过缝过程的车轮-缝接触关系,提出的车-缝-桥耦合动力响应分析方法可用于考虑伸缩缝参数对车-桥耦合动力响应分析。
2) 伸缩缝设计参数条件下,伸缩缝中横梁的冲击系数随车速的增加呈先减小后增大的趋势;主梁车致冲击系数随车速增加呈增大趋势,主梁近缝端截面测点的冲击系数更大;路面不平整度越差车致伸缩缝冲击系数越大。
3) 伸缩缝参数变化条件下,中横梁升高会导致车辆对伸缩缝的冲击作用增大,中横梁升高或降低均会增大车辆对梁端、支座冲击作用;伸缩缝支撑刚度降低或缝宽变大会增大车辆对伸缩缝中横梁的冲击作用。但上述参数对主梁1/4跨和1/2跨测点的车致位移响应影响较小。
4) 车辆对临近伸缩缝主梁端部的冲击作用增大可能会造成伸缩缝-支座耦合病害的产生,伸缩缝-支座耦合病害对车-桥耦合动力响应的影响是下一步的工作重点。
| [1] |
CHEN B C, WANG T L. Overview of concrete filled steel tube arch bridges in China[J]. Practice Periodical on Structural Design and Construction, 2009, 14(2): 70. DOI:10.1061/(ASCE)1084-0680(2009)14:2(70) |
| [2] |
OKAMOTO Y, NAKAMURA S, TANAKA H, et al. Study on steel box girder bridges partly stiffened by CFT arch ribs[J]. Journal of Constructional Steel Research, 2012, 70: 28. DOI:10.1016/j.jcsr.2011.08.012 |
| [3] |
侯剑岭, 许维炳, 陈彦江, 等. 大跨度异型钢管混凝土拱桥典型病害分析及支座脱空影响研究[J]. 振动与冲击, 2020, 39(18): 161. HOU Jianling, XU Weibing, CHEN Yanjiang, et al. Typical diseases of long-span concrete filled steel tube arch bridges and the effects of the void of supports[J]. Journal of Vibration and Shock, 2020, 39(18): 161. |
| [4] |
ROEDER C W, MACRAE G, CROCKER P, et al. Dynamic response and fatigue of steel tied arch bridge[J]. Journal of Aerospace Engineering, 2000, 5(1): 14. |
| [5] |
WANG Q, OKUMATSU T, NAKAMURA S, et al. Fatigue failure analysis of cracks near the sole plate of a half-through steel-arch bridge[J]. Journal of Bridge Engineering, 2019, 24(5): 05019004.1-05019004.11. |
| [6] |
付岚岚. 大跨度桥梁伸缩装置的研究[D]. 西安: 长安大学, 2006 FU Lanlan. Research on long-span bridge expansion device[D]. Xi'an: Chang'an University, 2006 |
| [7] |
POURZEYNALI S, HOSSEINNEZHAD A. Reliability analysis of bridge structures for earthquake excitations[J]. Scientia Iranica, 2009, 16(1): 1. |
| [8] |
DENG L, YAN W, ZHU Q. Vehicle impact on the deck slab of concrete box-girder bridges due to damaged expansion joints[J]. Journal of Bridge Engineering, 2016, 21(2): 06015006. DOI:10.1061/(ASCE)BE.1943-5592.0000796 |
| [9] |
丁勇, 俞丹波, 邹毓颖, 等. 车辆-模数式伸缩缝耦合振动与冲击荷载分析[J]. 中国公路学报, 2018, 31(7): 167. DING Yong, YU Danbo, ZOU Yuying, et al. Analysis of impact load and coupling vibration of vehicle and modular bridge expansion joint[J]. China Journal of Highway and Transport, 2018, 31(7): 167. DOI:10.3969/j.issn.1001-7372.2018.07.015 |
| [10] |
GONZALEZ A, CANTERO D, OBRIEN E J. Dynamic increment for shear force due to heavy vehicles crossing a highway bridge[J]. Computers & Structures, 2011, 89(23/24): 2261. |
| [11] |
刘佳锋. 车载下既有损伤公路混凝土简支梁桥动力响应分析[D]. 哈尔滨: 哈尔滨工业大学, 2014 LIU Jiafeng. Analysis of the dynamic response of the existing damaged highway concrete simply supported beam bridge under the vehicle[D]. Harbin: Harbin Institute of Technology, 2014 |
| [12] |
HOU J, XU W, CHEN Y, et al. Typical diseases of a long-span concrete-filled steel tubular arch bridge and their effects on vehicle-induced dynamic response[J]. Frontiers of Structural and Civil Engineering, 2020, 14(4): 867. DOI:10.1007/s11709-020-0649-9 |
| [13] |
LI Y, CAI C S, LIU Y, et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J]. Engineering Structures, 2016, 106: 243. DOI:10.1016/j.engstruct.2015.10.026 |
| [14] |
中华人民共和国交通运输部. 公路桥梁伸缩装置通用技术条件[M]. 北京: 人民交通出版社, 2016. Ministry of Transport of the People's Republic of China. General technical conditions for highway bridge expansion devices[M]. Beijing: China Communications Press, 2016. |
| [15] |
中华人民共和国交通运输部. 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG 3362—2018[S]. 北京: 人民交通出版社, 2018 Ministry of Transport of the People's Republic of China. Speifications for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG 3362—2018[S]. Beijing: China Communications Press, 2018 |
| [16] |
许维炳, 王博, 王瑾, 等. 考虑车辆过缝的车-桥耦合振动分析方法[J]. 东南大学学报(自然科学版), 2022, 52(2): 212. XU Weibing, WANG Bo, WANG Jin, et al. Vehicle-bridge coupled vibration analysis method considering vehicle seam[J]. Journal of Southeast University (Natural Science Edition), 2022, 52(2): 212. |
| [17] |
DENG L, YAN W, ZHU Q. Vehicle impact on the deck slab of concrete box-girder bridges due to damaged expansion Joints[J]. Journal of Bridge Engineering, 2015, 21: 6015006. |
| [18] |
LIU C, HUANG D, WANG T. Analytical dynamic impact study based on correlated road roughness[J]. Computers & Structures, 2002, 80(20/21): 1639. |
 2022, Vol. 54
2022, Vol. 54


