2. 吉林建筑大学 交通科学与工程学院,长春 130118
2. School of Transportation Science and Engineering, Jilin Jianzhu University, Changchun 130118, China
近年中国城市居民的出行需求迅速增长,私家车等出行方式已难以满足居民的出行需求,大力发展城市公共交通成为缓解出行压力的有效方法。因此,针对地铁与常规公交的整体性分析对城市公共交通网络的优化起着重要的作用。
另一方面,作为一门研究网络拓扑结构、网络特性和动力性的学科,复杂网络的发展也为交通网络结构的研究提供了理论基础[1-6]。其中,文献[4]对客流加权的中美航空网络进行分析,证明其边权分布和点权分布均复合幂律分布特征。文献[5]分别以列车流和客流为权重,建立了北京市轨道交通网络模型,其结果证明其车流、客流服从幂律分布,具有明显的无标度网络特征。
目前,由于多层网络的统计特性不如单层网络完善,对复合交通网络的研究多以映射为单层加权网络的方法为主[7-9]。文献[10-12]详细总结了多种多层网络模型、多层网络在不同领域的统计特性计算方法及其动力学研究。然而,单层网络很难体现不同交通方式之间的差异性,因此建立多层交通网络模型是复合交通网络研究的热点。常见的多层交通网络构建思路为逻辑层-物理层,用于研究同一种交通方式不同要素的相互作用关系[13],而物理层-物理层常用于研究多模式的复合交通网络[14-18]。由于不同交通模式之间未必有明确的换乘关系,关于物理层-物理层双层网络的层间连接方法通常为以一个站点为圆心,采用某一确定的、大多数居民可接受的耦合半径R,该站点与半径R内覆盖的异层站点构成层间连边,文献[14]分别采用250 m、500 m和750 m的耦合半径对南京市公交网络的脆弱性进行分析,以两层站点之间的欧氏距离为层间连边权重。文献[15]建立了中国高铁-普铁双层网无权网络模型,研究结果显示其符合小世界特征。文献[16]构建了多层物流网络。文献[17]根据异层站点之间的欧氏距离连接了地铁、公交的单层网络,构建了复合公交网络的space-M模型。文献[18]提出了启发式多层城市网络协同进化模型。然而,因为不同人对于步行换乘距离的接受程度不同,耦合半径覆盖到的点连接强度必然不同,接受距离和居民接受度的关系未必是线性变化的,有待进一步考量。层间连接规则的研究还有必要结合居民出行意愿进一步细化,且在气候变化明显影响出行意愿的严寒城市,采取单一的层间连接方式也并不适用。
关于网络脆弱性和鲁棒性的研究,主要是了解网络节点或者连边失效对网络整体性能的影响以及网络保持功能的能力。相关研究中,文献[19]分析了节点故障和连边故障对地铁-公交双层网络的影响;文献[20]构建了城市轨道交通网络相继故障模型。
针对上述问题,本文以载客能力为连边权重,提出了一种基于出行者换乘意愿的地铁-常规公交双层加权复合网络构建方法,并基于问卷调查对严寒城市不同季节的居民换乘意愿和耦合半径进行了拟合,进而给出了严寒城市地铁-公交复合网络承载力计算方法。最后,以哈尔滨为例建立不同季节下的复合网络,并对其基本统计特性、承载力和鲁棒性进行了分析比对,验证了考虑出行意愿的必要性。
1 基于层间换乘意愿和承载力的双层加权网络构建 1.1 公交与地铁单层网络构建建立基于space-L的单层公交网络GB=(VB, EB, WB)和单层地铁网络GS=(VS, ES, WS)。公交层节点为公交站点,地铁层节点为地铁站点。相邻两站点间有线路依次经过即视为两站点间有连边,其权重为连边的承载力,即这条连边上所有公交或地铁线路每小时可运送的乘客数的总和,网络节点强度和连边权重的总和即可反映节点和连边的承载力。其公交层和地铁层数学模型描述如下(对于公交层,iB、jB均为公交站点,且iB≠jB;对于地铁层iS、jS均为地铁站点,iS≠jS):
| $ A^{\mathrm{B}}=\left|a_{i_{\mathrm{B} }j_{\mathrm{B}}}^{\mathrm{B}}\right| $ | (1) |
| $ a_{i_{\mathrm{B} }j_{\mathrm{B}}}^{\mathrm{B}}=\left\{\begin{array}{l} 1, \text { 存在同条线路依次经过相邻站点 } i_{\mathrm{B}} \text { 和 } j_{\mathrm{B}}\\0, \text { 没有同条线路依次经过相邻站点 } i_{\mathrm{B}} \text { 和 } j_{\mathrm{B}} \end{array}\right. $ | (2) |
| $ W^{\mathrm{B}}=\left|w_{i_{\mathrm{B} }j_\mathrm{B}}^{\mathrm{B}}\right| $ | (3) |
| $ w_{{i_{\rm{B}}}{j_{\rm{B}}}}^{\rm{B}} = a_{{i_{\rm{B}}}{j_{\rm{B}}}}^{\rm{B}}\sum_{n \in {V_{{i_{\rm{B}}}{j_{\rm{B}}}}}} {\frac{{60}}{{h_{{i_{\rm{B}}}{j_{\rm{B}}}}^n}}} {c_{n{\rm{B}}}} $ | (4) |
| $ {A^{\rm{S}}} = \left| {a_{{i_{\rm{S}}}{j_{\rm{S}}}}^{\rm{S}}} \right| $ | (5) |
| $ {a_{{i_{\rm{S}}}{j_{\rm{S}}}}^{\rm{S}}}=\left\{\begin{array}{l} 1, \text { 存在同条线路依次经过相邻站点 } i_{\mathrm{S}} \text { 和 } j_{\mathrm{S}} \\ 0, \text { 没有同条线路依次经过相邻站点 } i_{\mathrm{S}} \text { 和 } j_{\mathrm{S}} \end{array}\right. $ | (6) |
| $ {W^{\rm{S}}} = \left| {w_{{i_{\rm{S}}}{j_{\rm{S}}}}^{\rm{S}}} \right| $ | (7) |
| $ w_{i j}^{\mathrm{S}}=c_{\mathrm{S}} \frac{60}{h_{\mathrm{S}}} \alpha\;a_{i j}^{\mathrm{S}} $ | (8) |
式中:V为节点集,E为连边集合,A为邻接矩阵,W为加权邻接矩阵,EBS为地铁层与公交层的层间连边,cS为单趟地铁的最大载客量,hS为该路线地铁发车间隔,α为i、j之间的地铁线路数,常取0或1;hiBjBn为站点i、j之间第n条公交线路的发车间隔,cnB为第n条线路公交车的最大载客量。
1.2 地铁-公交复合网络构建多层网络的表示方法被定义为space-M,由多个单层网络添加层间连接关系后复合而成,交通领域中常用于描述物理特性相异的多模式交通网络。相对于单层网络,多层网络更贴近于多模式复合交通网络的实际空间特性。建立基于space-M的加权复合网络,其中上层为基于space-L的公交网络GB=(VB, EB, WB),下层为基于space-L的地铁网络GS=(VS, ES, WS)。其层间连接方式表达如下(此时iS为地铁站点, jB为公交站点):
| $ \boldsymbol{G}=\boldsymbol{G}^{\mathrm{\textrm { }}}+\boldsymbol{G}^{\mathrm{B}} $ | (9) |
| $ \boldsymbol{V}=\boldsymbol{V}^{\mathrm{S}}+\boldsymbol{V}^{\mathrm{B}} $ | (10) |
| $ \boldsymbol{E}=\boldsymbol{E}^{\mathrm{B}}+\boldsymbol{E}^{\mathrm{S}}+\boldsymbol{E}^{\mathrm{BS}} $ | (11) |
| $ \boldsymbol{A}=\left[\begin{array}{ll} \boldsymbol{A}^{\mathrm{B}} & \boldsymbol{A}^{\mathrm{BS}} \\ \boldsymbol{A}^{\mathrm{BS}} & \boldsymbol{A}^{\mathrm{S}} \end{array}\right] $ | (12) |
| $ \boldsymbol{W}=\left[\begin{array}{cc} \boldsymbol{W}^{\mathrm{B}} & \boldsymbol{W}^{\mathrm{BS}} \\ \boldsymbol{W}^{\mathrm{BS}} & \boldsymbol{W}^{\mathrm{S}} \end{array}\right] $ | (13) |
| $ {{\boldsymbol{A}}^{{\rm{BS}}}} = \left| {a_{{i_{\rm{S}}}{j_{\rm{B}}}}^{{\rm{BS}}}} \right| $ | (14) |
| $ a_{{i_{\rm{S}}}{j_{\rm{B}}}}^{{\rm{BS}}}=\left\{\begin{array}{l} 1, j_{\mathrm{B}} \text { 是距离 } i_{\mathrm{S}} \text { 最近的异层站点, 且 } i_{\mathrm{S}} \text { 与 } j_{\mathrm{B}} \text { 之间的距离不超过 } R \\ 0, j_{\mathrm{B}} \text { 不是距离 } i_{\mathrm{S}} \text { 最近的异层站点, 或 } i_{\mathrm{S}} \text { 与 } j_{\mathrm{B}} \text { 之间的距离大于 } R \end{array}\right. $ | (15) |
| $ \boldsymbol{W}^{\mathrm{BS}}=\left|w_{i_{\mathrm{S}} j_{\mathrm{B}}}^{\mathrm{BS}}\right| $ | (16) |
| $ {N_{{i_{\rm{S}}}}} = \left\{ {n\mid a_{{i_{\rm{S}}}{j_{\rm{S}}}}^{{\rm{BS}}} = 1, {j_{\rm{S}}} \in {V^{\rm{B}}}} \right\} $ | (17) |
| $ w_{j_{\mathrm{B}}}=\sum\limits_{i_{\mathrm{B}} \in V^{\mathrm{B}}, i_{\mathrm{B}} \neq j_{\mathrm{B}}} w_{i_{\mathrm{B}} j_{\mathrm{B}}} $ | (18) |
| $ w_{j_{\mathrm{S}}}=\sum\limits_{i_{\mathrm{S}} \in V^{\mathrm{S}}, i_{\mathrm{S}} \neq j_{\mathrm{S}}} w_{i_{\mathrm{S}} j_{\mathrm{S}}} $ | (19) |
| $ w_{{i_{\rm{S}}}{j_{\rm{S}}}}^{{\rm{BS}}} = \min \left[ {{\mu _{{i_{\rm{S}}}{j_{\rm{B}}}}}{w_j}, {\mu _{{i_{\rm{S}}}{j_{\rm{B}}}}}{w_{\rm{S}}}\frac{{{\mu _{{i_{\rm{S}}}{j_{\rm{B}}}}}}}{{\sum\limits_{n \in {N_{{i_{\rm{S}}}}}} {{\mu _{n{j_{\rm{B}}}}}} }}} \right] $ | (20) |
式中:G为网络,μij为节点i与j之间的居民换乘意愿系数,R为节点i与j之间的层间耦合半径,aiSjBBS为层间连接关系,WBS为层间连边权重集,wiSjBBS为层间连边权重,wjB为公交单层网络内公交节点jB权重,wjS为地铁单层网络内节点jS权重。
建网过程如图 1所示。

|
图 1 建网流程示意图 Fig. 1 Networking process |
目前研究多模式复合交通网络时,由于不同模式之间没有明确和实质的换乘方式,对换乘站点的识别方式多是以地铁站点为圆心,采取某一确定的、大多数出行者愿意接受的换乘距离作为耦合半径,耦合半径内的公交站点与地铁站点构成换乘关系。如R取500 m时,则以地铁站点为圆心,该地铁站与半径500 m内的公交站点构成换乘关系并有同等强度的层间连边,与超过500 m的公交站点均不构成连接关系。R的取值将直接影响到网络的层间连接关系,进而影响网络的连通特性、承载力和鲁棒性。然而,不同人对R的接受范围不同,耦合半径内不同距离的站点层间连接强度必然不会完全一样。而且,对于不同季节下出行者出行意愿有显著变化的严寒城市,采用某一确定的耦合半径显然不符合实际情况,因此对层间连边规则有必要进一步细化。在此,采用问卷调查法,结合换乘意愿调查结果,确定不同季节耦合半径的变化,拟合出站点距离和换乘意愿系数μij的关系,并对连接强度进行等级划分,进一步细化研究层间连接特性。
本次调查采用问卷星进行问卷设计、发放和收集,调查对象为居住地为哈尔滨等严寒城市、且选择地铁出行的居民。共收集调查问卷264份,有效问卷203份。除冬季以外的其他季节可接受最大步行换乘距离中,最大值为1 470 m,最小值为100 m,均值为707.25 m。调查意愿拟合结果见表 1。
| 表 1 其他季节乘意愿拟合结果 Tab. 1 Fitting results of transfer willingness in other seasons |
由表 1可知,Logistic模型拟合优度最大,拟合效果最好。根据Logistic模型拟合结果,耦合半径R最大取1 380 m(此时μij=0),最小取121 m(此时μij=1),在此范围内地铁站点和公交站点有着强弱不同的换乘意愿,其Logistic拟合曲线如图 2所示。

|
图 2 其他季节换乘意愿的Logistic拟合 Fig. 2 Logistic fitting of transfer willingness in other seasons |
冬季可接受最大步行换乘距离中,最大值为1 357 m,最小值为50 m,均值为480.20 m。冬季换乘意愿拟合结果见表 2。
| 表 2 冬季换乘意愿拟合结果 Tab. 2 Fitting results of transfer willingness in winter |
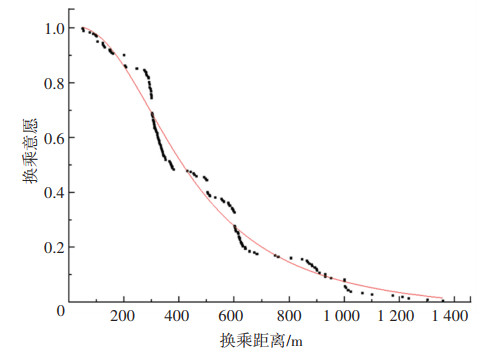
由表 2可知,Logistic模型拟合优度最大,拟合效果最好。根据其Logistic模型拟合结果,冬季、其他季节在μij耦趋于0时R取值相似。因此,为方便分析,冬季耦合半径R最大取1 380 m(此时μij=1×10-5),最小取61 m(此时μij=1),在此范围内地铁站点和公交站点有着强弱不同的换乘意愿,其Logistic模型拟合曲线如图 3所示。
|
图 3 冬季换乘意愿的Logistic拟合 Fig. 3 Logistic fitting of transfer willingness in winter |
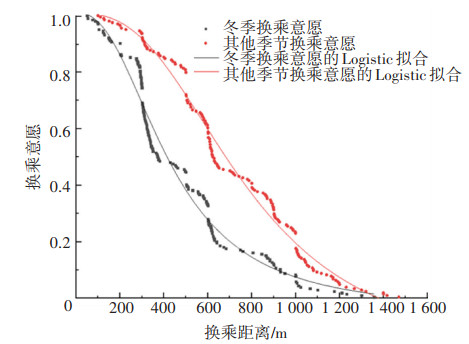
冬季、其他季节的换乘意愿对比如图 4所示。由图 4可知,冬季与其他季节居民换乘意愿有明显的差别,冬季换乘意愿普遍弱于夏季。
|
图 4 冬季与其他季节换乘意愿对比 Fig. 4 Comparison of transfer willingness between winter and other seasons |
网络可被抽象为点集和边集构成的图。定义地铁-公交双层网络的承载力为网络的载客能力,因此,以载客能力为连边赋权的复合网络,其整体网络形态可反映网络承载力的空间分布,可从节点和边两种角度去具体描述整体网络的承载力。
其连边权重的总和为该网络承载力的总和,其连边权重的平均值为网络的平均连边承载力,即
| $ W=\sum\limits_{i \neq j, i . j \in V} w_{i j} $ | (21) |
| $ \bar{W}_E=\frac{W}{n_E} $ | (22) |
式中nE为连边总数。
以节点i为端点的连边数量即为节点的度,反映了该节点在网络中的连通特性。即
| $ k_i=\sum\limits_{j=1}^V a_{i j} $ | (23) |
式中aij为节点i与节点j的连接关系,连接取1,反之取0。
节点i的强度,即以该节点为端点的连边权重总和,反映了该节点在加权网络中的重要性。因此,以载客能力为连边权重的复合网络,其节点的加权度即节点的承载力,其节点的平均强度为节点的平均承载能力:
| $ w_i=\sum\limits_{i \neq j, j \in V} w_{i j} $ | (24) |
| $ \bar{W}_V=\frac{\sum\limits_{i \in V} w_i}{n_V} $ | (25) |
式中nV为节点总数。
2.2 复合网络鲁棒性分析方法复杂网络衡量网络稳定性的指标包括全局网络效能η、最大联通子图相对大小S、网络连通率C等,如式(26) ~ (28)所示。同时,考虑到本文中地铁-公交复合网络的物理意义,可考虑将网络承载力W作为评价指标,其计算方法见式(21)。
| $ \eta=\frac{1}{N(N-1)} \sum\limits_{i \neq j, i . j \in V} \frac{1}{d_{i j}} $ | (26) |
| $ S=\frac{N^{\prime}}{N} $ | (27) |
| $ C=\frac{N_E{ }^{\prime}}{N_E} $ | (28) |
式中:N为节点总数,dij为节点i与j之间的距离(在此指节点i、j之间最短路径经过的连边数),N′指网络遭受攻击后最大连通子图中节点的数量,NE为初始网络连边的总数,NE′为当前网络连边总数。其中,全局网络效能反映了网络信息传输的速度,在交通网络中可反映到达任意站点的便利程度。最大连通子图大小反映了事故对网络结构与大小的影响,网络连通率反映了节点之间的连通程度。
常见的复杂网络攻击策略按攻击对象分类,有点攻击、边攻击两种。节点攻击对应交通网络中事故造成的站点设施损毁或服务中断,连边攻击则视为站间段发生事故而运输中断。节点失效后,以失效节点为端点的连边均失效,其余节点或边正常运行;连边失效仅去除当前连边,不影响其他节点或边。按删除策略有考虑一般情况的随机攻击和考虑最差情况的蓄意攻击。随机攻击即每次随机移除一个或一组节点、连边,生成新的网络后输出全局网络效能、网络承载力等攻击指标。由于单轮的随机攻击结果具有随机性,需要进行多轮攻击后取平均值,为简化计算每次攻击,可去除指定数量的节点。蓄意攻击即按照一定的规则移除网络中的节点或边,而后输出网络的评价指标。
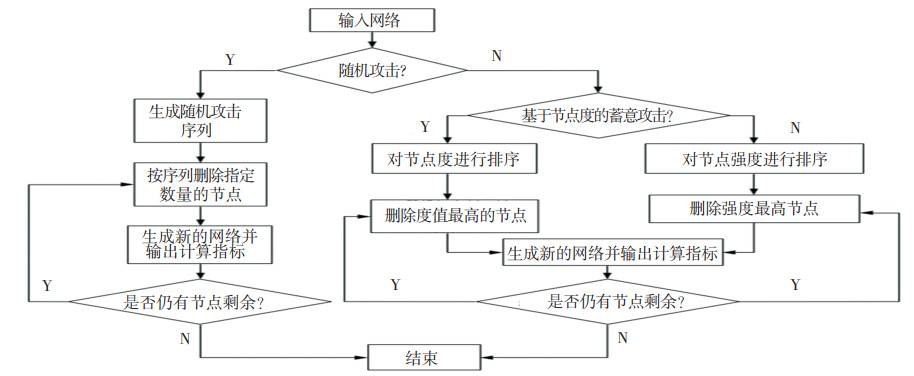
因去除连边对承载力的影响仅为在总承载力中减去该条连边的承载力,为简化计算,在此仅作针对节点的攻击。选取网络承载力作为承载力指标,网络连通率作为连通性指标,分析步骤如图 5所示。每轮攻击过程描述如下:
|
图 5 网络鲁棒性分析步骤 Fig. 5 Network robustness analysis steps |
步骤1 输入网络连接关系和连边权重。
步骤2 如果是随机攻击,将节点随机排序作为攻击序列;如果是蓄意攻击,针对度的攻击则将节点度从高到低排序作为攻击序列,针对节点承载力(即节点强度)的攻击,则将节点承载力(即节点强度)作为攻击序列。
步骤3 按照序列去除节点形成新的网络,输出网络承载力、连通率。
步骤4 如有节点剩余则接着按照序列删除节点并输出指标,若没有则攻击结束。
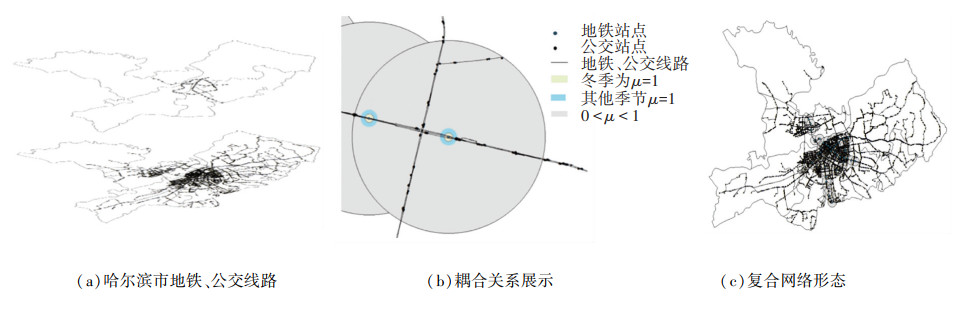
3 算例分析 3.1 双层网络构建及承载力计算选取哈尔滨市主城区(香坊区、南岗区、道里区、道外区、松北区)作为案例,以哈尔滨交通云公交电子站牌数据为主,高德地图数据为补充。哈尔滨主城区现有公交线路275条,同名站点合并后有站点1 906个,连边2 983条。哈尔滨地铁开通运营线路共有2条,分别为1号线、3号线,在建线路两条,分别为2号线一期工程、3号线二期工程,地铁站点共70个,连边73条。公交站点仅与离其最近的且距离在1 380 m之内的地铁站点构成层间换乘关系,经ArcGIS软件识别,与地铁构成连接关系的公交站点共714个。其网络形态如图 6所示。
|
图 6 哈尔滨市主城区复合公交网络建网过程 Fig. 6 Construction process of composite transportation network in the main urban area of Harbin |
通过计算,哈尔滨市冬季地铁-公交复合网络总承载力为7 960 594人/h,平均连边承载力为2 111人/h,平均节点承载力为8 057人/h。其他季节,总承载力为8 338 903人/h,平均连边承载力为2 207人/h,网络平均节点承载力为8 424人/h。由此数据可知,在网络结构相同的情况下,严寒城市冬季和其他季节的网络承载力也有着较为明显的变化。其中,冬季、其他季节承载力排名前20位的连边、站点及其节点度见表 3~6。
| 表 3 冬季连边承载力 Tab. 3 Carrying capacity of edges in winter |
| 表 4 其他季节连边承载力 Tab. 4 Carrying capacity of edges in other seasons |
| 表 5 冬季站点的节点度及其承载力 Tab. 5 Node degree and carrying capacity of stations in winter |
| 表 6 其他季节站点的节点度及其承载力 Tab. 6 Node degree and carrying capacity of stations in other seasons |
由前文知,冬季、其他季节在μij趋于0时R取值相似。由于连通性指标考虑的是“连通-不连通”的无权网络,即权重仅取0或1,为方便对比哈尔滨市地铁-公交网络在冬季与其他季节下网络承载力和连通性,由图 6可知,冬季和其他季节下接受度取75%和50%左右的网络其换乘意愿的斜率变化较为明显。在此选取这两种换乘意愿系数下的网络作鲁棒性分析,即R取75%和50%的居民可接受的站间步行距离。超出此距离的节点视为无换乘关系。冬季75%接受度下换乘距离为266.6 m,层间连边数为81条,50%接受度下耦合半径为414.4 m,层间连边数为190条;其他季节75%接受度下换乘距离为473.6 m,层间连边数为233条,50%接受度下耦合半径为681.9 m,层间连边数为406条。
使用Python的Networkx工具包对4个网络进行随机攻击与蓄意攻击,选取网络连边总权重和网络连通率作为衡量网络总承载力和连通性的衡量指标。为简化计算,每次攻击去除网络中5%的节点(10个),同时为避免随机攻击的偶然性,在此对4个网络分别作40轮随机节点攻击,最终结果取40轮攻击的平均值。分别选取当前网络的节点强度、节点度作为衡量节点承载力和连通性的指标,对4个网络进行蓄意攻击,最终输出结果如图 7所示。

|
图 7 不同攻击策略下网络鲁棒性分析 Fig. 7 Network robustness analysis under different attack strategies |
由图 7(a)、7(b)、7(g)、7(h)可看出,7个网络在随机攻击下指标变化均匀趋势基本一致,说明当前的攻击结果充分避免了随机攻击的偶然性。由结果可知,在同样的接受度和攻击策略下,冬季网络的连通性、网络总承载力和鲁棒性总体弱于其他季节。在节点度蓄意攻击策略下,75%和50%接受度下冬季网络总承载力曾阶段性地高于其他季节的网络,是因为对节点度的蓄意攻击相对于节点强度更加针对于网络的连通性,网络指标的变化会在连通性上(即网络连通率)反映得更明显、更相关和更具有针对性。
4 结论1) 本文建立了基于网络承载力和出行者换乘意愿地铁-公交双层网络模型,采集了严寒城市出行者不同季节关于地铁-公交换乘的最大接受距离,并拟合出距离和换乘意愿的数学关系,之后基于其拟合结果细化层间连边规则,该层间连边规则更符合居民实际出行意愿。
2) 通过对哈尔滨不同季节的地铁-公交复合网络承载力计算可以发现,严寒城市同一公共交通网络在不同季节,其网络承载力明显不同,冬季承载力要弱于其他季节,这可为严寒城市的交通管理与规划部门提供参考。
3) 对哈尔滨市地铁-公交复合网络节点进行了随机攻击和基于节点度、节点强度的蓄意攻击,结果表明,相同意愿下严寒城市其他季节地铁-公交网络的鲁棒性要高于冬季。
4) 受限于篇幅和数据等因素限制,本文还存在以下需进一步探讨的问题:在网络承载力层面,可以将节点承载力与职住数据、POI密度等结合,进一步探究公共交通网络与城市形态的耦合关系;在事故研究层面,还可以在相继故障、故障后恢复等方面深入研究。此外,突发事件造成的客流拥堵传播行为也可以进一步探讨。
| [1] |
高自友, 赵小梅, 黄海军, 等. 复杂网络理论与城市交通系统复杂性问题的相关研究[J]. 交通运输系统工程与信息, 2006, 6(3): 41. GAO Ziyou, ZHAO Xiaomei, HUANG Haijun, et al. Research on problems related to complex networks and urban traffic systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(3): 41. |
| [2] |
吴建军. 城市交通网络拓扑结构复杂性研究[D]. 北京: 北京交通大学, 2008 WU Jianjun. Studies on the complexity of topology structure in the urban traffic network[D]. Beijing: Beijing Jiaotong University, 2008 |
| [3] |
田晶, 方华强, 刘佳佳, 等. 运用复杂网络方法分析城市道路网的鲁棒性[J]. 武汉大学学报(信息科学版), 2019, 44(5): 771. TIAN Jing, FANG Huaqiang, LIU Jiajia, et al. Robustness analysis of urban street networks using complex network method[J]. Geomatics and Information Science of Wuhan University, 2019, 44(5): 771. DOI:10.13203/j.whugis20150334 |
| [4] |
党亚茹, 李雯静. 中美航空客流加权网络结构对比分析[J]. 交通运输系统工程与信息, 2011, 11(3): 156. DANG Yaru, LI Wenjing. Comparative analysis on weighted network structure of air passenger flow of China and US[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(3): 156. DOI:10.16097/j.cnki.1009-6744.2011.03.005 |
| [5] |
FENG Jia, LI Xiaoming, MAO Baohua, et al. Weighted complex network analysis of the Beijing subway system: train and passenger flows[J]. Physica A: Statistical Mechanics and its Applications, 2017, 474: 213. DOI:10.1016/j.physa.2017.01.085 |
| [6] |
BERCHE B, VON FERBER C, HOLOVATCH T, et al. Resilience of public transport networks against attacks[J]. The European Physical Journal B, 2009, 71(1): 125. DOI:10.1140/epjb/e2009-00291-3 |
| [7] |
DE REGT R, VON FERBER C, HOLOVATCH Y, et al. Public transportation in Great Britain viewed as a complex network[J]. Transportmetrica A: Transport Science, 2019, 15(2): 722. DOI:10.1080/23249935.2018.1529837 |
| [8] |
裴玉龙, 张枭, 塔建. 城市多模式公交拓扑网络的构建及特征分析[J]. 交通科技与经济, 2019, 21(5): 1. PEI Yulong, ZHANG Xiao, TA Jian. Construction and characteristic analysis of urban multi-modal public transport topology network[J]. Technology & Economy in Areas of Communications, 2019, 21(5): 1. DOI:10.19348/j.cnki.issn1008-5696.2019.05.001 |
| [9] |
裴玉龙, 金英群, 常铮. 城市多模式公交网络拓扑结构与布局均衡性研究[J]. 中国公路学报, 2021, 34(1): 127. PEI Yulong, JIN Yingqun, CHANG Zheng. Equilibrium of topology and layout of urban multimode public transit network[J]. China Journal of Highway and Transport, 2021, 34(1): 127. DOI:10.19721/j.cnki.1001-7372.2021.01.012 |
| [10] |
CRIADO R, FLORES J, GARCIA A, et al. A mathematical model for networks with structures in the mesoscale[J]. International Journal of Computer Mathematics, 2012, 89(3): 291. DOI:10.1080/00207160.2011.577212 |
| [11] |
ALETA A, MORENO Y. Multilayer networks in a nutshell[J]. Annual Review of Condensed Matter Physics, 2019, 10: 45. DOI:10.1146/annurev-conmatphys-031218-013259 |
| [12] |
WU J, PU C, LI L, et al. Traffic dynamics on multilayer networks[J]. Digital Communications and Networks, 2020, 6(1): 58. DOI:10.1016/j.dcan.2018.10.011 |
| [13] |
董有郁. 基于双层网络模型的公交网络通行能力和级联故障研究[D]. 杭州: 浙江工业大学, 2014 DONG Youyu. Research on traffic capacity and cascading failure of bus transport network based on layered model[D]. Hangzhou: Zhejiang University of Technology, 2014 |
| [14] |
张琳, 陆建, 雷达. 基于复杂网络和空间信息嵌入的常规公交-地铁复合网络脆弱性分析[J]. 东南大学学报(自然科学版), 2019, 49(4): 773. ZHANG Lin, LU Jian, LEI Da. Vulnerability analysis of bus-metro composite network based on complex network and spatial information embedding[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(4): 773. DOI:10.3969/j.issn.1001-0505.2019.04.022 |
| [15] |
孙晓璇, 吴晔, 冯鑫, 等. 高铁-普铁的实证双层网络结构与鲁棒性分析[J]. 电子科技大学学报, 2019, 48(2): 315. SUN Xiaoxuan, WU Ye, FENG Xin, et al. Structure characteristics and robustness analysis of multi-layer network of high speed railway and ordinary railway[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(2): 315. |
| [16] |
吴桐雨, 王健. 基于多层复杂网络的物流枢纽城市多尺度分析及发育评价[J]. 交通运输系统工程与信息, 2019, 19(1): 33. WU Tongyu, WANG Jian. Multi-scale analysis and development evaluation of logistics hub cities based on multi-layer complex networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(1): 33. DOI:10.16097/j.cnki.1009-6744.2019.01.006 |
| [17] |
陈晓明, 李引珍, 沈强, 等. 基于双层复杂网络的城市交通网络协同优化方法[J]. 计算机应用, 2019, 39(10): 307. CHEN Xiaoming, LI Yinzhen, SHEN Qiang, et al. Urban traffic networks collaborative optimization method based on two-layered complex networks[J]. Journal of Computer Applications, 2019, 39(10): 3079. DOI:10.11772/j.issn.1001-9081.2019030538 |
| [18] |
DING Rui, UJANG N, HAMID H B, et al. Heuristic urban transportation network design method, a multilayer coevolution approach[J]. Physica A: Statistical Mechanics and its Applications, 2017, 479: 71. DOI:10.1016/j.physa.2017.02.051 |
| [19] |
宋英华, 李玉枝, 霍非舟, 等. 城区内涝条件下城市公交-地铁双层交通网络的脆弱性分析[J]. 安全与环境工程, 2021, 28(2): 114. SONG Yinghua, LI Yuzhi, HUO Feizhou, et al. Vulnerability of two-layer traffic network of bus and subway under waterlogging condition based on complex network theory[J]. Safety and Environmental Engineering, 2021, 28(2): 114. DOI:10.13578/j.cnki.issn.1671-1556.2021.02.016 |
| [20] |
刘朝阳, 吕永波, 刘步实, 等. 城市轨道交通运输网络级联失效抗毁性研究[J]. 交通运输系统工程与信息, 2018, 18(5): 82. LIU Chaoyang, LV Yongbo, LIU Bushi, et al. Cascading failure resistance of urban rail transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(5): 82. DOI:10.16097/j.cnki.1009-6744.2018.05.013 |
 2022, Vol. 54
2022, Vol. 54


