2. 智能网络与网络安全教育部重点实验室 (西安交通大学),西安 710049;
3. 西安建筑科技大学 信息与控制工程学院,西安 710055
2. Ministry of Education Key Laboratory for Intelligent Networks and Network Security (Xi′an Jiaotong University), Xi′an 710049, China;
3. College of Information and Control Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China
锂离子电池凭借其能量密度高、循环寿命长、自放电率低等优点在生产生活中具有广泛的应用,但是锂电池在长期的使用过程中,随着充放电次数的不断增加,电池性能衰减影响着电池的寿命,造成电池故障等问题,更严重的会威胁使用者的安全。锂电池的故障会造成巨大的经济损失及环境破坏[1]。因此可靠的电池RUL预测方法可以保证更加规范有效地使用电池和降低故障率,能改善电池管理水平、提供维修策略和延长电池寿命[2-7]。
目前,对电池RUL的预测方法主要包括模型法和数据法。基于数据的方法不需要电池的具体描述,只需要通过大量实验数据和经验就能大致地预测出电池的RUL。此类方法只需要获取电池外部环境数据就能建立电池的退化趋势,从而评估电池性能和预测电池寿命[13]。基于数据的预测方法主要包括:人工神经网络、长短记忆循环神经网络、深度置信网、深度学习、支持向量机等[8-15]。此类方法虽然都能预测出电池的RUL,但是当电池内部变化不规律或发生明显变化时,其可行性和有效性将大大降低。而且,此类方法的精度依赖数据规模,当测量数据不足或者数据不准确时,预测性能也会受到明显影响。
基于模型的方法主要采用状态估计法,与数据方法不同,状态估计法主要依靠建立精确的电池模型,模型的准确性将直接影响估计性能。目前的电池模型大致可分为机理模型和经验模型,机理模型通过电池内部化学参数的关系而建立,其模型精度较高,但内部参数较多,关系较为复杂,使用困难较大。由于机理模型建立在实时的化学描述的基础上,所以对于电池未来容量的变化趋势的应用较为困难,而且此模型受到客观因素的影响很难适应性地反应电池退化过程,模型求解复杂,鲁棒性需要进一步提升也是此方法的局限性。不仅如此,机理模型与经验模型相比应用较为困难。而经验模型结构较为简单,描述电池容量的退化趋势也能得到保证,与现有的技术结合更加容易,应用更为广泛。由于电池退化过程表现出较强的非线性和非高斯特征,PF算法被广泛应用在基于经验模型的电池寿命预测研究中。文献[16]基于双指数退化模型使用扩展H∞PF算法获得相对精确的动力电池RUL。文献[17]使用扩展卡尔曼滤波优化PF算法采样过程提高估计精度,并实现较为准确的电池RUL预测。同样,文献[18-19]使用基于线性优化组合重采样的无迹PF算法进一步提升估计精度,并结合马尔科夫链蒙特卡洛方法和无迹卡尔曼滤波来解决粒子退化问题。此外,为了同时获得基于数据和模型方法的优势,相关的融合方法正逐渐成为研究热点。文献[20]提出一种基于支持向量机和自适应卡尔曼滤波算法的电池RUL预测方法,实现了多步预测,并取得良好效果。文献[21]使用多层感知机作为描述电池退化行为的工具,并结合改进PF算法更新神经网络参数对电池寿命进行预测。同样,文献[22]使用PF训练神经网络参数,并采用长短记忆神经网络对参数进行更新,得到了较好的RUL预测结果。
虽然上述方法能够保证一定的预测精度,但是仍存在固有问题:1)电池模型的精度问题,当电池外部环境如充电电压、充电电流和温度环境温度等发生改变的情况下,电池容量易受影响并发生突变,现有模型无法准确描述电池退化趋势,因此会直接影响到电池寿命的预测结果;2)PF自身估计精度问题,PF经多次迭代,其粒子将出现多样性丧失和精度下降的问题,也会影响寿命预测的精度。因此本文提出了一种自适应混合模型来表征电池退化行为,以提高外部环境因素变化的工况下模型的精度和适应性,同时使用BAS提升PF的粒子多样性,以避免粒子多样性丧失,从而实现更准确的寿命估计。
1 锂电池容量退化模型本节提出了一种新型电池退化模型,将经验模型与神经网络模型相结合。首先介绍标准经验模型,然后提出一种新型自适应混合模型。
1.1 经验模型电池容量是反映电池退化的重要指标,经验模型包括线性模型、对数线性模型、多项式模型和指数模型,其中最常用的是指数模型。随着充电次数的增加,锂电池的容量会逐渐减少,其下降趋势分为两个阶段,即缓慢阶段和快速阶段,表现为在循环初期容量下降速率较慢,而到了后期下降速率变快,其下降呈现非线性凹凸的退化趋势。对于线性模型,随着循环次数增加,此模型只能描述电池容量递减的趋势,难以捕捉容量的非线性退化特征,对于变化趋势的细节部分,其描述能力较差。对于对数线性模型其描述的容量变化速率较小,只能保证描述电池容量退化的其中一个阶段,对于另外一个阶段此模型将无法精确描述,因此,对数线性模型无法描述两阶段的容量退化趋势。对于多项式模型,其能描述容量退化的非线性特征,但不能保证更好的曲线逼近,特别地,其无法准确地捕捉到两阶段的非线性拐点。对于双指数模型,其使用两个指数形式的结构,对于非线性特征有较好的适应性,而且针对两个变化阶段,此模型也能更好地描述。综上所述,本文选择双指数模型作为电池的经验模型,使得模型的描述能力更强,更能准确表现电池容量退化趋势与特征。双指数模型为
| $ Q_1=f(k)=a_k \mathrm{e}^{b_k k}+c_k \mathrm{e}^{d_k k} $ | (1) |
式中:Q1表示电池容量,ak、bk、ck、dk为电池内部参数,ak、ck与电池的内阻有关,bk、dk与电池的退化率有关,k是周期数。
需要注意的是,该模型虽然可以表现出电池退化的一般特征,但没有考虑电池外部因素的变化。这会严重影响对电池退化行为的描述。因此,本文将神经网络模型与经验模型相结合,此混合模型既考虑了电池内部参数又考虑了环境的变化对电池容量的影响,因此,此模型能更好地表征电池的具体退化行为。
1.2 自适应混合模型经网络可以有效处理复杂系统内难以解析描述的规律性,具有很好的泛化能力。为了得到所需的混合模型,引入人工神经网络模型来描述电池外部环境与电池容量之间的关系,并描述此时的容量退化过程。需要强调的是,虽然在实际应用中电池容量可以直接测量,但在工作状态下,一般无法获得电池的实时容量。文献[13]基于外部数据建立了电池容量的退化模型,表明电池的容量退化过程与电池的充放电时间、电流、电压、温度等外界因素有着密切的联系。因此,本文采用神经网络训练获得电池退化模型。
由于径向基(radial basis function,RBF)神经网络具有最佳逼近、训练简洁、学习收敛速度快等特点,因此使用径向基神经网络作为描述电池外部变量与容量之间非映射关系的模型。图 1展示了RBF神经网络的具体结构。

|
图 1 RBF神经网络原理图 Fig. 1 Schematic diagram of RBF neural network |
如图 1所示,径向基神经网络模型包括3层:输入层、隐含层和输出层。‖dist‖表示求取输入向量和权值向量的距离,神经元radbas的输入为输入向量和权值向量的距离乘以阈值b,高斯函数radbas是典型的径向基函数。输入层与隐藏层之间的表达式为
| $ \| \text { dist }\|=\| I W_j-X \|=\sqrt{\sum_{i=1}^n\left(I W_{j, i}-x_i\right)^2} $ | (2) |
| $ h=\operatorname{radbas}\left(\left\|I W_j-X\right\| b_1\right)=\mathrm{e}^{-\left(\left\|I W_j-X\right\| b_1\right)^2} $ | (3) |
隐藏层与输出层的计算关系为
| $ y=\text { purelin }\left(L W_j h+b_2\right) $ | (4) |
式中:IW为输入向量的加权矩阵,LWj为隐藏层与输出层之间的权重,b2为偏差。
人工神经网络对电池容量与外部因素的关系表示为
| $ Q_2=\mathrm{NN}(I, U, W, T) $ | (5) |
式中:Q2为电池容量,I、U、W、T分别为电池充放电电流、电压、外部环境温度和充放电时间。
式(1)描述了电池容量与电池内部参数的关系,式(5)描述了电池容量与充放电电流等外部变量之间的映射关系。因此,根据式(1)和式(5),本文提出使用上述两个容量的综合表达作为电池容量的退化模型,因此定义容量表达式为
| $ Q=\alpha Q_1+\beta Q_2 $ | (6) |
式中:α为经验模型的置信度,β为神经网络模型置信度,且α+β=1。
式(6)中的混合模型由参数α和β决定,在PF算法中,被用作观测方程,因此,参数的选取直接决定了预测的精度程度。通过求解优化问题的方法定义模型参数值以期获取最佳的容量表达式。假设上一周期k=i的估计容量为
| $ Q_{\mathrm{L}}(i)=\alpha Q_1(i)+\beta Q_2(i) $ | (7) |
通过求解估计容量QL与真实容量QT之间的最小均方误差(mean square error, MSE)获得下一时刻所需的混合模型参数α和β:
| $ \text{Min}(\text { MSE }) $ | (8) |
| $ \mathrm{MSE}=\frac{1}{t} \sum_{i=1}^t\left[\left(Q_{\mathrm{L}}(i)-Q_{\mathrm{T}}(i)\right)^2\right] $ | (9) |
在PF的每次执行后,通过计算式(9)获得的模型参数α和β更新混合模型从而实现模型的自适应调整。其具体过程如下:1)输入初始α和β值,电池容量真实值QT,电池充放电电流I、电压U、外部环境温度W和充放电时间T;2)由式(1)计算经验模型容量Q1(i),由式(5)计算经验模型容量Q2(i),由式(7)得到混合模型容量QL(i);3)求解优化问题式(9);4)得到最优解α和β作为下一时刻混合模型参数。
2 电池RUL预测方法基于上一节提出的混合模型,本节提出了一种基于BAS-PF的RUL预测方法。
2.1 BAS-PF基于PF的状态估计所需动态系统模型为
| $ x_j=f\left(x_{j-1}, u_{j-1}\right)+v_j $ | (10) |
| $ y_j=h\left(x_j, u_j\right)+\eta_j $ | (11) |
其中:xj表示系统在j时刻的状态,u表示系统的输入,yj表示j时刻系统的测量值,f与h分别表示系统的状态转移函数和测量函数,υj和ηj表示系统的状态噪声和测量噪声。
xj的后验概率密度函数p(xj|y1∶j)的计算分为两步,包括预测和更新[23-24],预测步为
| $ p\left(x_j \mid y_{1: j-1}\right)=\int p\left(x_j \mid x_{j-1}\right) p\left(x_{j-1} \mid y_{1: j-1}\right) \mathrm{d} x_{j-1} $ | (12) |
根据贝叶斯滤波算法,更新步为
| $ p\left(x_j \mid y_{1: j}\right)=\frac{p\left(y_j \mid x_j\right) p\left(x_j \mid y_{j-1}\right)}{\int p\left(y_j \mid x_j\right) p\left(x_j \mid y_{1: j-1}\right) \mathrm{d} x_j} $ | (13) |
为避免复杂的积分运算,使用一组加权的随机样本(粒子)χj={xji, wji}i=1:P近似后验概率密度函数,其后验概率密度的近似表示为
| $ p\left(x_j \mid y_{1: j}\right) \approx \sum_{i=1}^P w_j^i \delta\left(x_j-x_j^i\right) $ | (14) |
其中:P为一组随机样本中的样本的个数(粒子数),i为该组样本的第i个样本,δ为狄拉克函数。
在概率密度函数p(xj|y1:j)中抽取粒子集较难,因此定义重要性概率密度函数q(xji)=p(xji|xj-1i)并从其中抽取粒子,此时,粒子权重wji的更新由式(15)给出:
| $ w_j^i \propto w_{j-1}^i p\left(y_j \mid x_j^i\right) $ | (15) |
其中wji是归一化权重,
| $ w_j^i=w_{j-1}^i / \sum_{i=1}^P w_j^i $ | (16) |
重采样后,各个粒子的权重为1/P,此时,j时刻的状态估计值由各个粒子加权而获得
| $ \tilde{x}=\sum_{i=1}^P w_j^i x_j^i $ | (17) |
需要强调的是,PF算法在经过数次迭代之后,会出现粒子退化,其主要表现为粒子集的权重集中于某个或数个粒子上,导致粒子多样性丧失,从而严重影响估计精度。目前常用的解决粒子退化的方案是重采样,但该方法也会带来粒子贫化问题并影响估计精度。
为了解决上述问题,引入基于BAS的重采样过程,将退化的粒子集优化至高似然值,根据优化阈值条件,产生新粒子集,从而在保证粒子群贴近真实后验分布的同时,增强了粒子的多样性。PF的估计状态由各个粒子加权获得,然而,在PF中,粒子的贫化问题降低了算法的性能。粒子贫化是由于重采样过程中不合理使得粒子多样性丧失,即重采样过程中,高权重粒子会被保留,低权重的粒子会被丢弃,虽然低权重粒子对状态估计影响小,但是其仍包含有用的状态信息。因此使用BAS优化PF的重采样过程。BAS优化PF的思想是将每个粒子作为天牛个体,通过目标函数分别计算天牛个体的适应度,然后将适应度最高的个体选为最优值。经过一定次数的迭代,使得每个天牛向最优位置靠近,最终得到全局最优解。这样,粒子集不断靠近高似然区,从而提高粒子的多样性和滤波算法的性能。BAS算法的具体步骤如下:
1) 对于n维空间优化问题,xL表示天牛的左须坐标,xR表示右须坐标,x表示质心坐标,d0表示两须距离,天牛朝向位置为dir。则左右须表达式分别为
| $ x_{\mathrm{L}}=x+d_0 \cdot d_{\mathrm{ir}} / 2 $ | (18) |
| $ x_{\mathrm{R}}=x-d_0 \cdot d_{\mathrm{ir}} / 2 $ | (19) |
2) 对于优化问题f,定义天牛前进步长St,
| $ f_{\mathrm{L}}=f\left(x_{\mathrm{L}}\right) $ | (20) |
| $ f_{\mathrm{R}}=f\left(x_{\mathrm{R}}\right) $ | (21) |
如果fL < fR,则天牛向左方向移动St:
| $ x=x+S_{\mathrm{t}} \cdot\left(x_{\mathrm{L}}-x_{\mathrm{R}}\right)+\widetilde{\omega} $ | (22) |
如果fL>fR,则天牛向右方向移动St:
| $ x=x-S_{\mathrm{t}} \cdot\left(x_{\mathrm{L}}-x_{\mathrm{R}}\right)+\widetilde{\omega} $ | (23) |
结合上述算法,具体的BAS-PF步骤如下:
步骤1 设置PF算法以及BAS算法参数。参数包括:粒子个数P,最大迭代次数Tmax,迭代阈值L,移动步长St,初始方向d0,调整因子$\tilde \omega $。
步骤2 从重要性概率密度函数中抽样产生N个粒子{xji}i=1N作为初始粒子。
步骤3 更新粒子位置计算各个粒子的适应度,将粒子集作为种群,更新当前个体最优值pB和种群最优值gB。通过引入最新观测量z到优化函数中,本文定义似然函数为适应度函数:
| $ {\mathop{\rm Min}\nolimits} \left( {\mathit{\Theta }\left( {x_j^i} \right)} \right) = {{\rm{e}}^{\left( { - \frac{{{{\left( {y_j^i - z} \right)}^2}}}{{2{\sigma ^2}}}} \right)}} $ | (24) |
步骤4 种群移动,更新pB和gB。根据式(22)、(23)计算种群移动位置,并根据式(24)更新个体与种群最优值。
步骤5 判断循环是否停止。当迭代时间t满足t < Tmax或者种群最优值满足迭代阈值gB < L时,则循环结束,否则转到步骤4。
步骤6 根据式(15)、(16)计算各个粒子权重,由式(17)得出估计状态。
2.2 电池RUL预测过程为了实现电池寿命的在线预测,提出一种新型电池寿命预测算法和电池退化模型,在所提出的模型的基础上更新电池参数,利用BAS-PF在线滚动估计电池内部参数。所提出的电池寿命预测方法流程如图 2所示。

|
图 2 电池寿命预测方法流程图 Fig. 2 Flow chart of RUL prediction method |
根据上述提出的电池退化模型建立电池的状态空间方程,其中电池的内部参数作为状态量,电池容量作为观测量,状态空间方程表示如下:
| $ \boldsymbol{x}_k=\left[a_k, b_k, c_k, d_k\right] $ | (25) |
| $ \begin{cases}a_k=a_{k-1}+\omega_a, & \omega_a \sim N\left(0, \sigma_a\right) \\ b_k=b_{k-1}+\omega_b, & \omega_b \sim N\left(0, \sigma_b\right) \\ c_k=c_{k-1}+\omega_c, & \omega_c \sim N\left(0, \sigma_c\right) \\ d_k=d_{k-1}+\omega_d, & \omega_d \sim N\left(0, \sigma_d\right)\end{cases} $ | (26) |
| $ y_k=Q_k=\alpha Q_{1 k}+\beta Q_{2 k}+\nu_k, \quad \nu_k \sim N(0, \sigma) $ | (27) |
式中N(0, σ)表示均值为0标准差为σ的高斯噪声。
结合上述建立的电池状态空间模型以及提出的BAS-PF算法,可以对电池RUL进行估计,具体步骤如下:
1) 利用测试电池可用的容量数据,在估计出当前周期电池的内部参数xk后,电池的容量可以表示为
| $ Q_k=\sum_{i=1}^N w_k^i Q_k^i $ | (28) |
2) 通过外推经验模型,获取k+l周期的电池容量
| $ Q_{k+l}=\sum_{i=1}^N w_k^i Q_{k+l}^i $ | (29) |
3) 在k个周期,通过第i个粒子的电池寿命可以得出
| $ f\left(x_k^i, L_k^i\right)=Q_{\mathrm{s}} $ | (30) |
式中Qs为使用寿命阈值的容量。
4) k循环周期,电池寿命的后验概率密度为
| $ p\left(L_k \mid Q_{1: k}\right) \approx \sum_{i=1}^N w_k^i \delta\left(L_k-L_k^i\right) $ | (31) |
5) 最终,电池的RUL可以被估计为
| $ L_k=\sum_{i=1}^N w_k^i L_k^i $ | (32) |
式中Lki为第i个粒子预测的RUL。
3 实验验证结果 3.1 实验数据集为了验证所提出的方法预测电池RUL的准确性,首先使用来自美国航空航天局的钴酸锂电池数据。使用标号为B0005、B0006的电池数据来验证本文的电池寿命预测方法。电池的测试环境条件如下:1)锂电池被放置在大约24 ℃的温度环境下进行充放电实验。锂离子电池(B0005、B0006)在室温下通过3种不同的操作模式(充电、放电和阻抗)。2)用电流为1.5 A的恒定电流和变化的充电电压充电,充电电压直到电池电压达到4.2 V,然后在恒定电压和可变电流条件下充电,直到充电电流降至20 mA。之后,用2 A左右大小的电流放电,直到电池电压分别降至2.7、2.5 V,电池阻抗测量采用电化学阻抗谱0.1~5 000 Hz进行扫描。3)当电池容量下降到额定容量的70%左右时,实验停止。
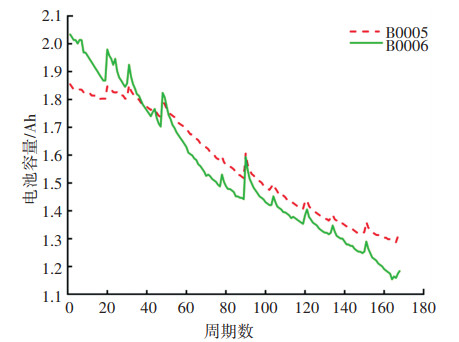
本次实验中,使用电池容量作为衡量电池健康状态的指标,当电池充放电容量达到额定容量的70%时,可认为电池达到最终寿命。B0005和B0006号电池的退化曲线如图 3所示。
|
图 3 B0005和B0006号电池的退化曲线 Fig. 3 Degradation curves of B0005 and B0006 batteries |
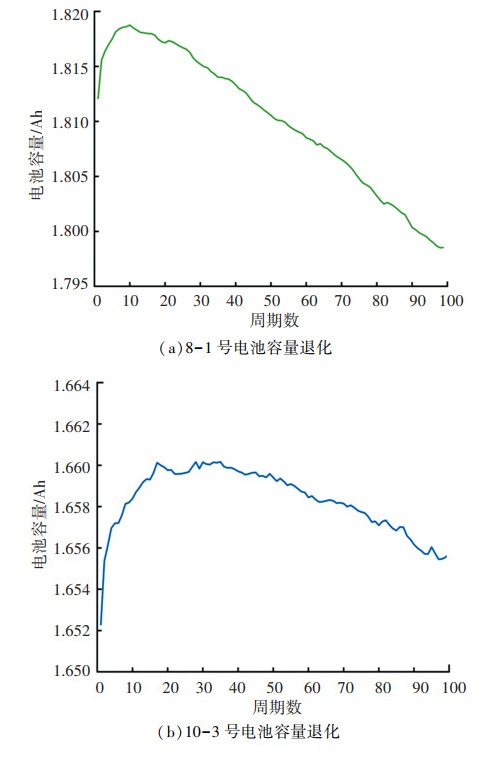
为进一步考察本文模型和所提算法的普适性,除上述的钴酸锂电池外,还增加了对于磷酸铁锂电池的验证。实验对象为CALCE电池数据组,标号为K2-06的数据组,其中两块电池标号为8-1和10-3,测试条件:1) 以2.6 A的恒定电流将电池放电;2) 放电直到电压为4.2 V;3) 在恒定电压下充电,直到电流小于0.08 A;4) 放置2 min,测量内阻;5) 放置1 min。两块电池的容量退化曲线如图 4所示。
|
图 4 8-1和10-3号电池的退化曲线 Fig. 4 Degradation curves of 8-1 and 10-3 batteries |
首先,验证所提出的电池退化模型的有效性,然后在此模型的基础上对电池RUL进行估计。对于神经网络模型,选取B0005号电池作为神经网络的训练数据,B0006号电池作为测试对象,同样,10-3号电池为训练数据,8-1为测试对象。在神经网络中,充放电电流、电压,实验温度和充放电时间作为输入,输出是电池容量。将测试电池作为参考,混合模型参数的初始值α和β分别为0.8和0.2。图 5展示了钴酸锂电池4种模型的退化曲线。图 6描述了描述磷酸铁锂电池4种模型的退化曲线。

|
图 5 钴酸锂电池不同模型容量退化曲线 Fig. 5 Capacity degradation curves of different models for lithium cobaltate batteries |
|
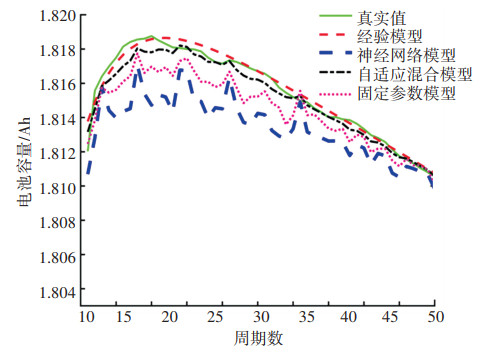
图 6 磷酸铁锂电池不同模型容量退化曲线 Fig. 6 Capacity degradation curves of different models for lithium iron phosphate batteries |
首先实验结果如图 5所示,其中,神经网络模型容量曲线较真实值相差较大,但能有效描述电池的突变行为;经验模型曲线较神经网络模型更加接近实际,但其描述电池突变的能力相对较差;相较上述两种模型,所提出混合模型不论是固定参数还是自适应参数,其描述电池容量变化的能力都更加准确。
上述实验结果的原因是,神经网络只考虑了外部环境因素的变化,而不能描述电池内部参数变化;而经验模型是通过内部参数描述电池退化趋势,忽略了外部环境变化量的影响。所提出自适应混合模型兼顾了上述两种模型的优势,因而获得性能的提升,此外,由于自适应法通过每一时刻的测量值求解优化问题实时获得模型参数,其性能优于固定参数模型。
表 1给出了上述4种模型与真实值的误差比较,此外,还增加了两组固定参数模型的对比数据。为衡量模型的精确度,使用平均绝对误差(mean absolute error,MAE)和MSE作为衡量模型的指标,可以看出,对于钴酸锂电池,神经网络模型的误差分别为7.1%和0.7%,远高于其他3种模型的误差。其次,经验模型的精确度相较神经网络模型的精确度有较大的提升,误差分别为4.7%和0.37%。而3种固定参数混合模型精度相差较小,其精度都比经验模型高。最后,自适应混合模型的MAE和MSE分别为3.39%和0.29%,其精度对比固定参数模型又有了明显的提升。对于磷酸铁锂电池的模型验证结果如图 6所示,可以看出本文所提出的混合模型更加接近于真实状态,从表中的误差结果可以得出,自适应混合模型的MSE和MAE分别为0.141%和1.12%,其误差均小于其他的模型。从模型结果和误差表现可以看出本文所提模型具有更高的精度而且适用于磷酸铁锂电池。综上可以得出,所提出的自适应混合模型具有更好的精度和描述电池容量退化的能力。
| 表 1 不同模型误差对比 Tab. 1 Error comparison of different models |
在长时间的循环使用中,锂电池容量会出现明显的退化现象,与其他机械和电气设备相同,锂电池的退化过程是不可逆的,由于锂电池内部存在复杂的物理和化学反应变化,而且化学成分在重复的充放电过程中会发生降解,这导致锂电池性能逐渐下降和可用容量不断减少[25-26]。由于复杂和非线性的电化学机理和各类应用场景的不同,电池可用容量衰减呈现锯齿状,这是电池容量再生现象所导致的,因此电池容量的衰减变化呈现出非平滑的下降趋势,由于此问题的出现导致对电池剩余使用寿命预测成为的热点和难点问题。
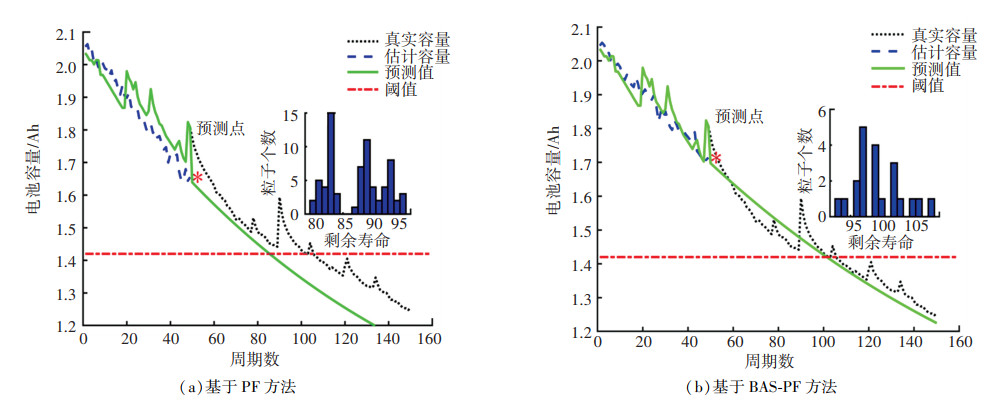
根据预测点之前数据拟合得出经验模型参数并作为PF的初始状态,在PF算法中,粒子的数量设置为100,电池的寿命阈值为1.42 Ah。基于自适应混合模型,使用改进PF算法对电池状态进行参数估计,其中ωa~ωc服从N(0, 0.1×10-4),νk服从N(0, 0.1)。钴酸锂电池的PF状态的初始参数为[1.57, -0.005 576, 0.489, 0.009 449],磷酸铁锂电池[1.823, -0.000 134 8, -0.010 63, -0.168 9],PF每次更新的参数都作为新的经验模型参数,PF算法和神经网络算法在MATLAB仿真实验平台上实现。为验证所提方法的有效性,分别选取预测开始时间为第50、第70、第90周期。同时使用PF和BAS-PF算法对电池RUL进行预测,并且得到预测点处粒子的概率分布,其预测效果如图 7~10所示。图中,分别给出了代表锂电池实际的衰退曲线,预测点之前的估计容量曲线,容量预测值曲线以及锂电池的寿命阈值曲线,并且在图 7~9中还标注出不同预测的时间点和预测结果附近的概率密度,图中剩余寿命指的是周期个数。
|
图 7 钴酸锂电池50个周期的预测结果 Fig. 7 Prediction results for 50 cycles of lithium cobaltate batteries |

|
图 8 钴酸锂电池70个周期的预测结果 Fig. 8 Prediction results for 70 cycles of lithium cobaltate batteries |
|
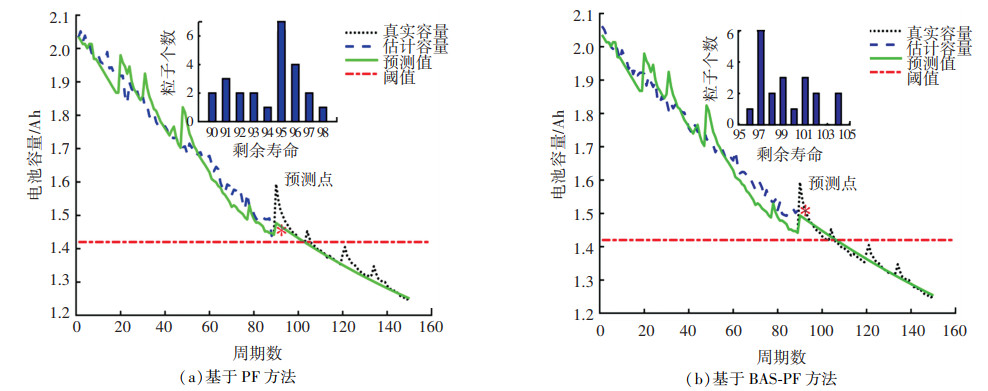
图 9 钴酸锂电池90个周期的预测结果 Fig. 9 Prediction results for 90 cycles of lithium cobaltate batteries |
|
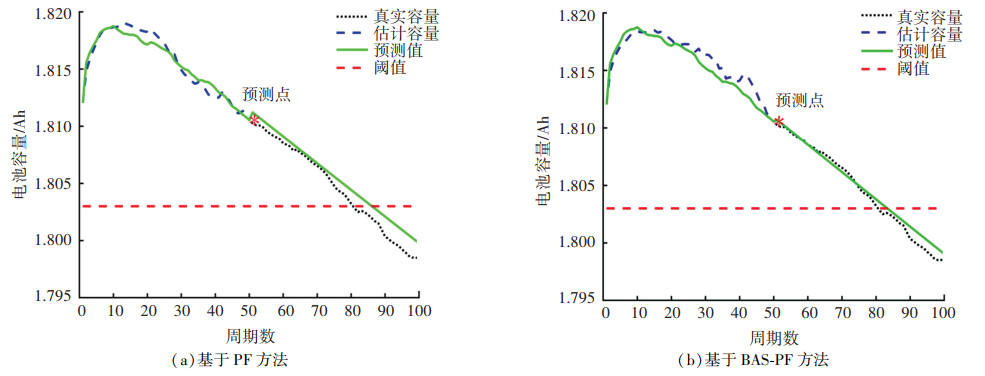
图 10 磷酸铁锂电池50个周期的预测结果 Fig. 10 Prediction results for 50 cycles of lithium iron phosphate batteries |
对于钴酸锂电池,图 7(a)、7(b)展示了基于自适应混合模型的前50个周期的容量数据更新的模型参数,误差由表 2给出。其中,基于PF算法的锂电池RUL预测结果为89个周期,误差为12.75%,而基于BAS-PF算法的预测结果为96个周期,误差为5.88%。图 8(a)、8(b)是前70个周期的数据的预测结果,PF的预测结果为109个周期,误差为6.86%,BAS-PF的预测结果分别为106个周期和3.92%。同样,90个周期数据的预测结果如图 9所示,基于PF方法预测结果是99个周期,2.94%的误差,BAS-PF预测为104个周期,误差为1.96%。由此看出基于BAS-PF的预测效果比PF的好。由于文章篇幅限制,本文给出了磷酸铁锂电池50周期的RUL预测结果,如图 10所示,相较于PF算法,所提出的改进PF算法在电池容量的预测准确性上更高,更能反应真实状态,误差分析由表 3给出,改进PF算法的RUL误差分别为3、1、0个周期而PF算法的误差为7、4、2个周期,改进算法误差均小于未改进算法。从结果上看,本文所提算法的RUL预测精度更高。而且预测表现和钴酸锂电池相同,即改进PF算法预测精度更高。
| 表 2 钴酸锂电池RUL预测结果 Tab. 2 RUL prediction results for lithium cobaltate batteries |
| 表 3 磷酸铁锂电池RUL预测结果 Tab. 3 RUL prediction results for lithium iron phosphate batteries |
随着预测点周期的增加,钴酸锂电池基于PF算法的锂电池RUL预测误差分别为12.75%、6.86%、2.94%,BAS-PF的预测误差则为5.88%、3.92%、1.96%。而磷酸铁锂电池的PF误差从8.75%下降到2.5%,基于BAS-PF的误差从3.75%下降到0。从表 2、3中可以观察到,随着预测周期的增加,RUL的预测结果越精确,而且BAS-PF比PF方法具有更准确的估计精度和预测结果。综合上述实验结果,本文所提模型和算法对于不同类型的锂电池有较好的适用。
本文所提出的电池寿命预测方法从原理上能够拓展应用到其他类型的电池。本方法主要包含建模及状态估计两个部分,首先,本文中所提出的混合模型是由神经网络模型和经验模型组合而成,并且模型参数通过求解优化问题实现自适应调整。其中,神经网络模型是使用采集到的外部数据(比如电流和电压)预测当前的电池容量,对于不同的电池模型系统,神经网络模型具有一般性和普适性并能直接使用。而对于经验模型,不同类型的锂电池随着充电次数的增加其容量都是出现逐渐下降的非线性趋势,并且下降速率具有明显的先慢后快的特点,本文使用的双指数模对于描述此类非线性变化趋势和特点具有较强的能力,所以经验模型对不同类型的锂电池容量下降趋势都有较好的适应性。因此,本文所建立的混合模型对于不同的锂电池都拥有较好的适用性。其次,由于寿命预测所使用的粒子滤波算法是结合所建立的模型基于状态估计获得电池寿命的预测值,一旦模型成功建立,粒子滤波算法便可以基于其自身的收敛特性对不同类型的锂电池进行状态估计,获得其寿命预测结果。因此,基于粒子滤波的寿命预测算法对于不同的锂电池也都具有较好的可行性。综上,本文所提出模型和方法对于不同类型的锂电池有较好的适用性。在后续的研究中,还将针对更多种类的常用锂电池,如三元锂电池、锰酸锂电池等,考察本文方法的普适性。
4 结论本文提出了一种自适应混合模型和改进的PF算法预测锂电池的RUL。并通过两组实验验证所提出方法的有效性,主要结论如下:
1) 所提出的自适应混合模型能精确表示电池容量退化特征,拥有更小的误差,MAE和MSE分别为3.39%、0.29%和1.12%、0.141%,远优于其他模型,说明此模型具有更好的描述电池退化趋势的能力。
2) 在建立模型的基础上,使用BAS算法对PF进行改进,改进PF算法具有更佳的估计精度和RUL预测结果。对于不同类型锂电池,BAS-PF的预测误差分别为5.88%、3.92%、1.96%和3.75%、1.25%、0,其误差均低于同期的PF算法的误差。说明基于BAS-PF算法的估计精度和锂电池的RUL预测结果较PF更加准确。
3) 预测周期数据越多其RUL预测结果越准确,选取50、70和90个周期为预测点,对于钴酸铁锂电池,其实际的使用寿命为102周期,在不同的预测点,预测结果分别为96、106和104个周期对于磷酸铁锂电池其实际使用寿命为80周期,预测结果为83、79和80个周期。
4) 本文提出的混合模型是神经网络模型与经验模型的组合,采用传统的神经网络模型,考虑改用估计性能更好精确度更高的神经网络代替现有的模型以提高模型精度。更加精确理想的经验模型也有助于提升性能,实现对锂电池RUL的精准预测。
| [1] |
石伟杰, 王海民. 基于锂离子电池热特性的SOH在线诊断模型研究[J]. 仪器仪表学报, 2020, 41(8): 206. SHI Weijie, WANG Haimin. On-line diagnosis model of SOH based on thermal characteristics of lithium-ion battery[J]. Chinese Journal of Scientific Instrument, 2020, 41(8): 206. DOI:10.19650/j.cnki.cjsi.J2006393 |
| [2] |
ZHANG Lijun, MU Zhongqiang, SUN Changyan. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter[J]. IEEE Access, 2018, 6: 17729. DOI:10.1109/ACCESS.2018.2816684 |
| [3] |
MO Baohua, YU Jingsong, TANG Diyin, et al. A remaining useful life prediction approach for lithium-ion batteries using Kalman filter and an improved particle filter[C]// 2016 IEEE International Conference on Prognostics and Health Management (ICPHM). Ottawa: IEEE, 2016: 1. DOI: 10.1109/ICPHM.2016.7542847
|
| [4] |
LIU Datong, LUO Yue, LIU Jie, et al. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm[J]. Neural Computing and Applications, 2014, 25(3/4): 557. DOI:10.1007/s00521-013-1520-x |
| [5] |
GUHA A, VAISAKH K V, PATRA A. Remaining useful life estimation of lithium-ion batteries based on a new capacity degradation model[C]// 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific. Busan: IEEE, 2016: 555. DOI: 10.1109/ITEC-AP.2016.7513015
|
| [6] |
MA Guijia, ZHANG Yong, CHENG Cheng, et al. Remaining useful life prediction of lithium-ion batteries based on false nearest neighbors and a hybrid neural network[J]. Applied Energy, 2019, 253: 113626. DOI:10.1016/j.apenergy.2019.113626 |
| [7] |
WEI Jingwen, DONG Guangzhong, CHEN Zonghai. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5634. DOI:10.1109/TIE.2017.2782224 |
| [8] |
WU Ji, ZHANG Chenbin, CHEN Zonghai. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks[J]. Applied Energy, 2016, 173: 134. DOI:10.1016/j.apenergy.2016.04.057 |
| [9] |
LI Xiaoyu, ZHANG Lei, WANG Zhenpo, et al. Remaining useful life prediction for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks[J]. Journal of Energy Storage, 2019, 21: 510. DOI:10.1016/j.est.2018.12.011 |
| [10] |
LI Penghua, ZHANG Zijian, XIONG Qingyu, et al. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network[J]. Journal of Power Sources, 2020, 459: 228069. DOI:10.1016/j.jpowsour.2020.228069 |
| [11] |
ZHANG Yongzhi, XIONG Rui, HE Hongwen, et al. A LSTM-RNN method for the lithuim-ion battery remaining useful life prediction[C]// 2017 Prognostics and System Health Management Conference (PHM-Harbin). Harbin: IEEE, 2017: 1. DOI: 10.1109/PHM.2017.8079316
|
| [12] |
ZHANG Yongzhi, XIONG Rui, HE Hongwen, et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5695. DOI:10.1109/TVT.2018.2805189 |
| [13] |
QIN Wei, LYU Huichun, LIU Chengliang, et al. Remaining useful life prediction for lithium-ion batteries using particle filter and artificial neural network[J]. Industrial Management & Data Systems, 2019, 120(2): 312. DOI:10.1108/IMDS-03-2019-0195 |
| [14] |
ZHAO Guangquan, ZHANG Guohui, LIU Yuefeng, et al. Lithium-ion battery remaining useful life prediction with deep belief network and relevance vector machine[C]//2017 IEEE International Conference on Prognostics and Health Management (ICPHM). Dallas: IEEE, 2017: 7. DOI: 10.1109/ICPHM.2017.7998298
|
| [15] |
SHEN Sheng, SADOUGHI M, CHEN Xiangyi, et al. A deep learning method for online capacity estimation of lithium-ion batteries[J]. Journal of Energy Storage, 2019, 25: 100817. DOI:10.1016/j.est.2019.100817 |
| [16] |
马彦, 陈阳, 张帆, 等. 基于扩展H∞粒子滤波算法的动力电池寿命预测方法[J]. 机械工程学报, 2019, 55(20): 36. MA Yan, CHEN Yang, ZHANG Fan, et al. Remaining useful life prediction of power battery based on extend H∞ particle filter algorithm[J]. Journal of Mechanical Engineering, 2019, 55(20): 36. |
| [17] |
DUAN Bin, ZHANG Qi, GENG Fei, et al. Remaining useful life prediction of lithium-ion battery based on extended Kalman particle filter[J]. International Journal of Energy Research, 2020, 44: 1724. DOI:10.1002/er.5002 |
| [18] |
ZHANG Heng, MIAO Qiang, ZHANG Xin, et al. An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction[J]. Microelectronics Reliability, 2018, 81: 288. DOI:10.1016/j.microrel.2017.12.036 |
| [19] |
ZHANG Xin, MIAO Qiang, LIU Zhiwen. Remaining useful life prediction of lithium-ion battery using an improved UPF method based on MCMC[J]. Microelectronics Reliability, 2017, 75: 288. DOI:10.1016/j.microrel.2017.02.012 |
| [20] |
XUE Zhiwei, ZHANG Yong, CHENG Cheng, et al. Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression[J]. Neurocomputing, 2020, 376: 95. DOI:10.1016/j.neucom.2019.09.074 |
| [21] |
WU Yi, LI Wei, WANG Youren, et al. Remaining useful life prediction of lithium-ion batteries using neural network and bat-based particle filter[J]. IEEE Access, 2019, 7: 54843. DOI:10.1109/ACCESS.2019.2913163 |
| [22] |
XIE Renyou, MA Rui, PU Sicheng, et al. Prognostic for fuel cell based on particle filter and recurrent neural network fusion structure[J]. Energy and AI, 2020, 2: 100017. DOI:10.1016/j.egyai.2020.100017 |
| [23] |
李天成, 范红旗, 孙树栋. 粒子滤波理论、方法及其在多目标跟踪中的应用[J]. 自动化学报, 2015, 41(12): 1981. LI Tiancheng, FAN Hongqi, SUN Shudong. Particle filtering: theory, approach, and application for multitarget tracking[J]. Acta Automatica Sinica, 2015, 41(12): 1981. DOI:10.16383/j.aas.2015.c150426 |
| [24] |
贺宁, 陈奕昕, 贺利乐, 等. 基于粒子滤波与压缩感知的管道泄漏定位[J]. 仪器仪表学报, 2019, 40(12): 36. HE Ning, CHEN Yixin, HE Lile, et al. Pipeline leak location based on particle filter and compressed sensing[J]. Chinese Journal of Scientific Instrument, 2019, 40(12): 36. DOI:10.19650/j.cnki.cjsi.J1905596 |
| [25] |
BARRÉ A, DEGUILHEM B, GROLLEAU S, et al. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications[J]. Journal of Power Sources, 2013, 241: 680. DOI:10.1016/j.jpowsour.2013.05.040 |
| [26] |
LI Yi, LIU Kailong, FOLEY A M, et al. Data-driven health estimation and lifetime prediction of lithium-ion batteries: a review[J]. Renewable and Sustainable Energy Reviews, 2019, 113: 109254. DOI:10.1016/j.rser.2019.109254 |
 2022, Vol. 54
2022, Vol. 54


