2. 磁浮技术与磁浮列车教育部重点实验室(西南交通大学),成都 611756
2. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle of Ministry of Education(Southwest Jiaotong University), Chengdu 611756, China
磁浮列车具有占用土地面积小,爬坡能力强, 噪音小等优点,可以很好地满足城市轨道交通的要求[1]。悬浮系统是保证列车在不同工况下稳定运行的前提条件,为了提高磁浮列车稳定性,国内外学者针对悬浮控制算法的设计与优化进行了广泛研究。文献[2]构造了一种同时考虑参数不确定性和外部扰动的T-S模糊模型,设计了基于粒子群优化的模糊自适应控制算法,实验验证了系统的悬浮稳定性和抗干扰能力,然而,该算法存在计算量大,对系统参数变化响应不及时等问题。文献[3]提出了一种磁悬浮系统的二维模糊滑膜控制算法,通过实验验证了该算法的悬浮稳定性,并未验证该算法在复杂工况下的鲁棒性和反馈跟踪能力。文献[4]采用逆系统方法对悬浮系统进行线性解耦,然后采用线性二次型(LQR)实现稳定悬浮,并利用非线性观测器补偿负载不确定性和模型误差的影响。但是由于控制器设计基于线性模型,在误差较大时,控制性能下降。文献[5]提出基于人工智能负载估计的磁浮列车主动控制方法,利用多层人工神经网络对悬浮系统进行主动控制,并采用非支配排序遗传算法进行参数优化,在较大负载扰动时仍能保持较小的误差。但是鉴于算法的复杂性和兼容性,并没有进行实验验证。文献[6]提出了实时补偿设定间隙的控制算法,仿真验证了该算法对悬浮间隙波动的抑制效果。但是算法需要快速准确地辨识出台阶以及台阶高度并完成算法切换,这一点不容易实现。为解决轨道不平顺对悬浮系统控制带来的问题,国内外学者进行了大量的研究,提出了一些有效的控制方案,解决悬浮列车由于轨道因素带来的各种问题[7]。但是,悬浮系统在过轨道台阶时的跟踪性和鲁棒性的矛盾没有得到一个完美的答案。
自抗扰控制(ADRC)不同于其他鲁棒控制方法,是一种新型的应对不确定性的控制算法,是韩京清于1995年提出的,2008年进行了全面的阐述[8]。它对系统模型的依赖性较弱,且具有较强的鲁棒性[9-10]。文献[11-12]将自抗扰控制应用于磁悬浮系统,实现了磁悬浮系统的稳定控制,但是没有考虑轨道问题对悬浮系统的影响。广义预测控制的基本思想是通过最小化在预测范围内定义的多级成本函数来计算未来的控制信号序列。它对开环不稳定系统具有很好的控制作用,但是其对模型参数敏感,在线计算量大[13]。广义预测控制在快速的、实时的系统中的应用还在不断探究中,针对悬浮控制系统这样一个实时的、快速的系统,降低广义预测控制的实时计算量是首先要解决的问题。文献[14]为了实现对时滞系统的高性能控制,将自抗扰控制和广义预测控制结合,提出自抗扰广义预测控制(LADRC-GPC)算法。LADRC-GPC不需要在线对系统进行参数辨识,很大程度上降低了算法的在线计算量,使得它在实时性要求很高的悬浮系统中应用成为可能。磁悬浮系统控制器需要强抗干扰性、强鲁棒性以及较高的实时性,基于这一特点,本文以贝加莱X20系列PLC为控制单元设计了的悬浮系统的自抗扰广义预测(LADRC-GPC)控制器,并通过实验验证了该控制器的有效性。
1 系统模型与自抗扰广义预测控制算法设计 1.1 系统模型磁浮列车每列车厢悬浮系统有5套悬浮架组成,各个悬浮架独立工作,共同完成车体的悬浮。每套悬浮架共有4套电磁铁,悬浮架两侧的电磁铁通过抗侧滚梁和吊杆弹性铰接,可以实现一定程度的机械解耦。为了简化系统模型,磁浮列车悬浮系统可以简化为几个单电磁铁悬浮系统,图 1给出了单电磁铁的物理结构,其中F(i, δ)为电磁铁产生的电磁力,m为单个电磁铁的质量,g为重力加速度,fd为在重力方向的干扰力,u(t)为线圈两端的电压;i(t)为流经电磁铁线圈的电流,δ(t)为悬浮气隙。由文献[15-16]可以得到单电磁铁的数学模型:
| $ \left\{ {\begin{array}{*{20}{l}} {F(i, \delta ) = K\frac{{i{{(t)}^2}}}{{\delta {{(t)}^2}}}}\\ {m\frac{{{{\rm{d}}^2}\delta (t)}}{{{\rm{d}}{t^2}}} = - F(i, \delta ) + mg + {f_{\rm{d}}}}\\ {u(t) = \frac{{2K}}{{\delta (t)}}\frac{{{\rm{d}}i(t)}}{{{\rm{d}}t}} - 2K\frac{{i(t)}}{{\delta {{(t)}^2}}}\frac{{{\rm{d}}\delta (t)}}{{{\rm{d}}t}} + Ri(t)} \end{array}} \right. $ | (1) |

|
图 1 单电磁铁结构示意图 Fig. 1 Single electromagnet structure diagram |
式中:R为线圈电阻,
文献[17]提出了双环串级控制的思想。通过设置电流环参数,不仅可以使电流迅速跟踪上电压变化,而且可以把电流环等效为比例环节,简化系统模型。
将状态变量定义为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} x_1}{\mathrm{~d} t}=x_2 \\ \frac{\mathrm{d} x_2}{\mathrm{~d} t}=\frac{f_{\mathrm{d}}}{m}+g-\frac{K}{m} \frac{i^2}{x_1^2} \end{array}\right. $ | (2) |
其中:i=u/Rt,Rt为等效电阻。
文献[18]在气隙环设计了分层控制器。内层采用反馈线性化控制进行预稳定,外层加入隐式广义预测控制。仿真结果证明了广义预测控制在快速系统中应用的有效性,并且能够很好地抑制过台阶波动。
本文采用双环串级控制思想,先简化电流环,然后气隙环采用分层控制的方法。内层采用自抗扰控制,以提高系统的抗干扰能力,外层使用广义预测控制抑制过台阶波动。
1.2 自抗扰广义预测控制将式(2)在平衡点进行线性化得
| $ \left\{\begin{array}{l} \frac{\mathrm{d} \Delta x_1}{\mathrm{~d} t}=\Delta x_2 \\ \frac{\mathrm{d} \Delta x_2}{\mathrm{~d} t}=\frac{f_{\mathrm{d}}}{m}+\frac{2 K}{m} \frac{i_0{ }^2}{\delta_0{ }^3 \Delta x_1}-\frac{2 K}{m} \frac{i_0}{\delta_0{ }^2} \frac{\Delta u}{R_{\mathrm{t}}} \end{array}\right. $ | (3) |
将式(3)中的
设计离散型状态观测器即ESO,对y1,y2,y3进行估计:
| $ \left\{\begin{array}{l} e(k+1)=z_1(k)-y_1(k) \\ z_1(k+1)=z_1(k)+h\left(z_2(k)-\beta_1 e(k)\right) \\ z_2(k+1)=z_2(k)+h\left(z_3(k)-\beta_2 e(k)+b_0 u(k)\right) \\ z_3(k+1)=z_3(k)+h\left(-\beta_3 e(k)\right) \end{array}\right. $ | (4) |
式中:β1、β2、β3分别为ESO的增益,e为观测误差,z1、z2、z3分别为x1、x2、x3估计值,b0为补偿因子。其中[β1, β2, β3]=[3ω0, 3ω02, ω03],ω0为观测器的带宽[19]。
设计控制律为
| $ \left\{\begin{array}{l} u=\frac{u_o-z_3}{b_0} \\ b_0=\frac{2 K}{m} \frac{i_0}{\delta_0^2} \frac{1}{R_{\mathrm{t}}} \end{array}\right. $ | (5) |
式中:u0为虚拟控制量,u为简化后系统的控制量。
通过扩张状态观测器中的z3变量对干扰变量x3进行动态补偿,系统可以简化为
| $ \frac{\mathrm{d}^2 x_1}{\mathrm{~d} t^2}=u $ | (6) |
在LADRC-GPC中,GPC针对简化后的积分串联型系统进行控制,在这里采用CARMA模型为
| $ A\left(z^{-1}\right) y(k)=B\left(z^{-1}\right) u(k-1)+C\left(z^{-1}\right) \xi(k) $ | (7) |
式中:ξ(k)为扰动信号;z-1为后移算子;A(z-1),B(z-1),C(z-1)为后移算子的多项式,其阶次分别为na,nb,nc。通常情况下C(z-1)=1。
| $ \left\{\begin{array}{l} A\left(z^{-1}\right)=1+a_1 z^{-1}+\cdots+a_{n_a} z^{-n_a} \\ B\left(z^{-1}\right)=b_0+b_1 z^{-1}+\cdots+b_{n_b} z^{-n_b} \end{array}\right. $ | (8) |
式中:ai为多项式系数,i=1, 2, …, na;bi为多项式系数,i=1, 2, …, nb。
基于CARMA模型,考虑式(9)中的丢番图方程:
| $ \left\{\begin{array}{l} 1=E_j\left(z^{-1}\right) A\left(z^{-1}\right)+z^{-j} F\left(z^{-1}\right) \\ E_j\left(z^{-1}\right) B\left(z^{-1}\right)=G_j\left(z^{-1}\right)+z^{-j} H_j\left(z^{-1}\right) \end{array}\right. $ | (9) |
式中:j=1, 2, …, N2-N1;Ej,Fj,Gj,Hj为后移算子z-1的多项式
| $ \left\{\begin{array}{l} E_j\left(z^{-1}\right)=e_1+e_2 z^{-1}+\cdots+e_j z^{-(j-1)} \\ F_j\left(z^{-1}\right)=f_{j, 1}+f_{j, 2} z^{-1}+\cdots+f_{j, n+1} z^{-n} \\ G_j\left(z^{-1}\right)=g_1+g_2 z^{-1}+\cdots+g_j z^{-(j-1)} \\ H_j(z-1)=h_{j, 1}+h_{j, 2} z^{-1}+\cdots h_{j, n-1} z^{-(n-2)} \end{array}\right. $ |
其中:ei、gi为多项式系数,i=1, 2, …, j; fj, i为多项式系数,i=1, 2, …, n+1; hi为多项式系数i=1, 2, …, n-1; n=1, 2, …, N2-N1。
由式(6)可得系统的传递函数为
| $ G(s)=\frac{1}{s^2} $ | (10) |
式中s为拉普拉斯算子。
采用零阶保持器将G(s)经Z变换得离散域传递函数:
| $ G\left(z^{-1}\right)=z^{-1} \frac{T^2\left(1+z^{-1}\right)}{2\left(1-z^{-1}\right)^2} $ | (11) |
式中: z为Z变换算子,T为采样周期。
忽略扰动信号,由式(7)可得
| $ G\left(z^{-1}\right)=z^{-1} \frac{B\left(z^{-1}\right)}{A\left(z^{-1}\right)} $ | (12) |
对比式(11)和式(12)得
| $ A\left(z^{-1}\right)=\left(1-z^{-1}\right)^2, B\left(z^{-1}\right)=\frac{T^2\left(1+z^{-1}\right)}{2} $ |
当确定采样频率后,可以离线求得系统丢番图方程的解:
| $ \left\{ {\begin{array}{*{20}{l}} {{e_j} = j}\\ {{f_{j, 1}} = j + 1, {f_{j, 2}} = - j}\\ {{g_j} = \frac{{{T^2}}}{2}(2j - 1)}\\ {{h_j} = j\frac{{{T^2}}}{2}} \end{array}} \right. $ | (13) |
广义预测控制性能指标函数为
| $ J=\sum\limits_{j=N_1}^{N_2}[y(k+j)-w(k+j)]^2+\sum\limits_{j=1}^{N_u} \lambda u^2(k+j-1) $ | (14) |
式中:y(k+j)为输出的预测序列,u(k+j-1)为控制量的预测序列,yr(k)为给定值的柔化序列,Nu为控制时域,λ为控制加权因子,w(k+j)的作用是使输出平稳达到设定值,其表达式为
| $ \boldsymbol{W}=\boldsymbol{\alpha} y(k)+(\bf{1}-\boldsymbol{\alpha}) y_{\mathrm{r}}(k) $ | (15) |
式中:W=[w(k+1),…,w(k+N2-N1)], αn为柔化因子,0 < αn < 1,α=[α1, α2, ..., αN2-N1]T。
将式(9)、(12)代入式(7),可得系统的j步预测输出y(k+j):
| $ y(k+j)=G_j u(k+j-1)+F_j y(k)+H_j u(k-1) $ | (16) |
将上式写为向量的形式:
| $ \boldsymbol{Y}=\boldsymbol{G} \boldsymbol{U}+\boldsymbol{H} \boldsymbol{U}(k-j)+\boldsymbol{F} \boldsymbol{Y}(k) $ | (17) |
Y=[y(k+N1), …, y(k+N2)]T为未来的预测输出。
U=[u(k), …,u(k+Nu-1)]T为当前和未来的控制量。
U(k-j)=[u(k-1), …,u(k+nb)]T为过去的控制量。
Y(k)=[y(k), …,y(k-na-1)]T为当前及过去的实际输出。
将式(14)写为向量形式:
| $ \boldsymbol{J}=(\boldsymbol{Y}-\boldsymbol{W})^{\mathrm{T}}(\boldsymbol{Y}-\boldsymbol{W})+\lambda \boldsymbol{U}^{\mathrm{T}} \boldsymbol{U} $ | (18) |
将式(17)代入式(18),得性能指标为最小的控制律:
| $ \begin{aligned} &\boldsymbol{U}=\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}}[\boldsymbol{W}-\boldsymbol{H} \boldsymbol{U}(k-j)-\boldsymbol{F} \boldsymbol{Y}(k)] \\ &u(k)=[1, 0, \cdots, 0]\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}}[\boldsymbol{W}-\boldsymbol{H} \boldsymbol{U}(k- \\ &j)-\boldsymbol{F} \boldsymbol{Y}(k)] \end{aligned} $ |
将u0=u(k)代入式(5)可以得到自抗扰广义预测控制下的控制律。
1.3 稳定性分析针对单电磁铁模型,Y(k)取y(k),U(k)取u(k-1),则控制律可以改写为
| $ \begin{aligned} u(k)=& {[1, 0, \cdots, 0]\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}}\left[(\bf{1}-\boldsymbol{\alpha}) y_{\mathrm{r}}(k)\right.} \\ &-(\boldsymbol{F}-\boldsymbol{\alpha}) y(k)-\boldsymbol{H} u(k-1)] \end{aligned} $ |
即
| $ T\left(z^{-1}\right) u(k)=R y_{\mathrm{r}}(k)-S y(k) $ | (19) |
式中:
| $ \begin{aligned} &T\left(z^{-1}\right)=1+z^{-1}[1, 0, \cdots, 0]\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}} \boldsymbol{H} \\ &R=[1, 0, \cdots, 0]\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}}(\bf{1}-\boldsymbol{\alpha}) \\ &S\left(z^{-1}\right)=[1, 0, \cdots, 0]\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{G}^{\mathrm{T}}(\boldsymbol{F}-\boldsymbol{\alpha}) \end{aligned} $ |
将y(k)=G(z-1)u(k)代入式(19),可得
| $ y(k)=\frac{G\left(z^{-1}\right) D\left(z^{-1}\right)}{1+G\left(z^{-1}\right) H\left(z^{-1}\right)} y_{\mathrm{r}}(k) $ | (20) |
式中:
| $ D\left(z^{-1}\right)=\frac{R}{T\left(z^{-1}\right)} ; H\left(z^{-1}\right)=\frac{S\left(z^{-1}\right)}{T\left(z^{-1}\right)} $ |
内模模型下系统的闭环控制结构如图 2所示,其中虚线框内传递函数为G(s)。
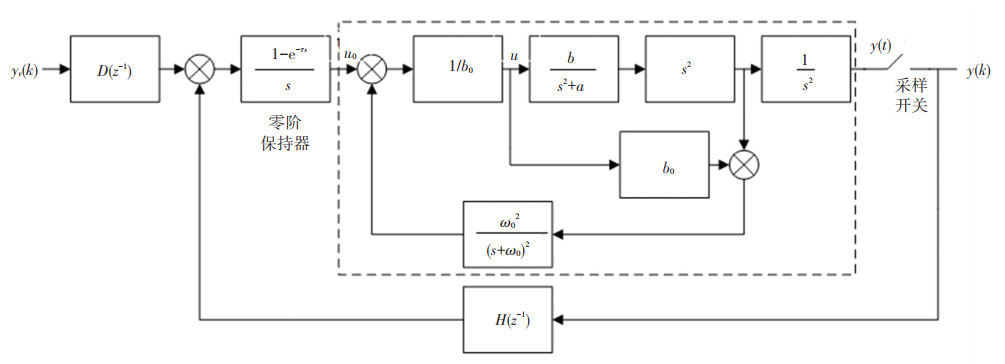
|
图 2 内模模型下系统的闭环反馈结构 Fig. 2 Closed-loop feedback structure of the system under internal model |
由文献[14]可得ESO回路的内模控制模型:
| $ z_2=\frac{\omega_0^2}{\left(s+\omega_0\right)^2}\left(s^2 y-b_0 u\right) $ | (21) |
单电磁铁系统开环传递函数[16]为
| $ G_1=\frac{\frac{K_i}{m R_{\mathrm{t}}}}{\frac{L_0}{R_{\mathrm{t}}} s^3+s^2-\frac{K_y}{m}} \approx \frac{\frac{K_i}{m R_{\mathrm{t}}}}{s^2-\frac{K_y}{m}} $ | (22) |
式中: Ki=2Ki0/y02, Ky=-2Ki02/y03。
可以将ESO和单磁铁系统转换为内模控制的标准结构,如图 2虚线框所示,其中b=Ki/mRt,a=Ky/m,可得
| $ G(s)=\frac{b\left(s+\omega_0^2\right)}{b_0\left(s^2+2 \omega_0 s\right)\left(s^2+a\right)+b \omega_0^2 s^2} $ | (23) |
式(23)可以整理为
| $ G(s)=\frac{\frac{b\left(s+\omega_0^2\right)}{b \omega_0^2+b_0 a}}{\frac{b_0\left(s^4+2 \omega_0 s^3\right)}{b \omega_0^2+b_0 a}+s^2+\frac{2 \omega_0 a b_0}{b \omega_0^2+b_0 a} s} $ | (24) |
对比式(10)可知,自抗扰广义预测控制算法稳定的前提是ω0必须满足:
| $ \left\{\begin{array}{l} \omega_0 \gg\left|\frac{b_0 a}{b}\right| \\ \omega_0 \gg\left|\frac{b_0}{b}\right| \end{array}\right. $ |
根据离散系统的稳定性条件,设
| $ G\left(z^{-1}\right)=Z\left[\frac{1-\mathrm{e}^{-\tau s}}{s} G(s)\right] $ |
图中的闭环系统的特征方程为
| $ 1+G\left(z^{-1}\right) H\left(z^{-1}\right)=0 $ | (25) |
在频域分析中,经常根据系统的开环传递函数选用奈式曲线定性分析算法的性能。如此需要考虑G(z-1)H(z-1)的频率响应:
| $ G\left(z^{-1}\right) H\left(z^{-1}\right)=\frac{z^{-1} B\left(z^{-1}\right) S\left(z^{-1}\right)}{A\left(z^{-1}\right) T\left(z^{-1}\right)} $ |
根据离散系统的奈氏判据,设等式中分母A(z-1)T(z-1)在单位圆外有P个根,点(-1,j0)被系统的开环传递函数G(z-1)H(z-1)的奈式曲线逆时针包围R圈,则P=R是系统稳定的充分必要条件[14],需要注意A(z-1)T(z-1)在单位圆上有根,则单位圆上的根的个数不计入P。
1.4 系统闭环控制结构图LADRC-GPC的结构图如图 3所示,LADRC-GPC算法由内层和外层组成:内层将电磁铁模型中不是积分串联型的部分看作总扰动,气隙传感器采集的悬浮气隙信号和虚拟控制量u0与补偿因子b0的乘积作为扩张状态观测器(ESO)的输入量,将输出的综合加速度反馈给系统实现动态补偿。外层将内层作为被控对象,以气隙信号和给定气隙值作为输入量,通过广义预测控制(GPC)对内层进行控制。
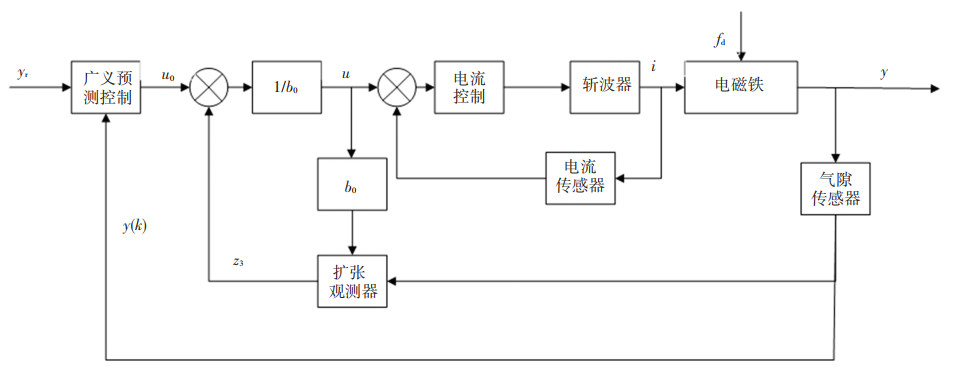
|
图 3 自抗扰广义预测控制的结构图 Fig. 3 Structure diagram of LADRC-GPC |
为了验证自抗扰广义预测控制在悬浮系统的有效性,利用MATLAB/Simulink软件进行仿真验证,并将LADRC-GPC与LADRC、PID控制进行仿真比较。主要进行以下研究:1)轨道由于各种客观因素会出现台阶现象。在实验中通过给定气隙的阶跃变化来模拟这种工况;2)在悬浮列车的运行中,某一悬浮电磁铁出现故障,相邻电磁铁负载变化较大。实验中,通过对系统加减载来模拟这种负载扰动。悬浮电磁铁的仿真模型参数见表 1。
| 表 1 悬浮电磁铁仿真模型参数 Tab. 1 Suspension electromagnet simulation model parameters |
系统起浮、加减负载及给定气隙突变工况下,LADRC-GPC的仿真结果如图 4~6所示。
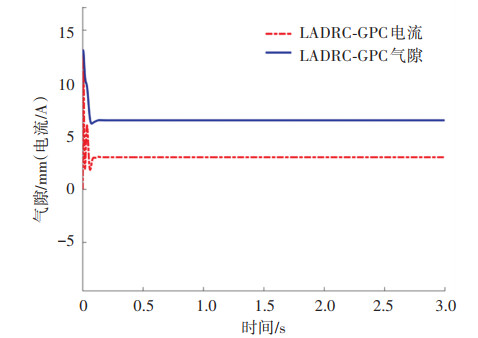
|
图 4 起浮时悬浮系统LADRC-GPC的仿真波形 Fig. 4 Simulation waveform of levitation system using LADRC-GPC during floating |

|
图 5 加减载时悬浮系统LADRC-GPC的仿真波形 Fig. 5 Simulation waveform of levitation system using LADRC-GPC during loading and unloading |

|
图 6 给定气隙突变时悬浮系统LADRC-GPC仿真波形 Fig. 6 Simulation waveform of levitation system using LADRC-GPC under reference mutation of air gap |
图 4给出了系统起浮时LADRC-GPC的电流和气隙波形。电磁铁从起始的13 mm气隙开始起浮,经过0.13 s调整,系统稳定悬浮在给定气隙6.5 mm,电流稳定在3.0 A。在此过程中,电流的最大值达到了12.8 A。
图 5给出了系统加减负载时LADRC-GPC的电流和气隙波形。在1.0 s时刻,系统加载50%(3.25 kg),电流迅速增大,峰值达到4.6 A,悬浮气隙在增大方向上产生0.5 mm的波动,经过0.05 s的调整,电流稳定在4.6 A,悬浮气隙恢复至6.5 mm。在2.0 s时刻,系统减载50%,电流迅速减小,谷值达到2.2 A,悬浮气隙在减小方向上产生0.4 mm的波动,经过0.05 s的调整,电流稳定在3.0 A,悬浮气隙恢复至6.5 mm。
图 6给出了系统在给定气隙突变时LADRC-GPC的电流和气隙波形。在1.0 s时刻给定气隙从6.5 mm突变到9.0 mm,电流首先突变到1.7 A,然后迅速增加,峰值达到4.6 A,悬浮气隙在增大的方向上产生0.2 mm的超调,经过0.11 s的调整,电流稳定在4.2 A,悬浮气隙跟踪给定气隙稳定在9.0 mm。1.5 s时刻,给定气隙从9.0 mm突变为4.0 mm,电流首先突变到6.8 A,然后迅速减小,谷值达到1.5 A,悬浮气隙在减小方向上产生0.4 mm的超调,经过0.12 s的调整,电流稳定在1.9 A,悬浮气隙跟踪给定气隙稳定在4.0 mm。
图 7给出了起浮和加减载工况下3种控制策略的悬浮气隙仿真波形。在起浮的过程中,PID控制和LADRC下,经过0.27 s完成起浮;由图 7可知,LADRC-GPC起浮更平滑,超调量更小,调整速度更快。
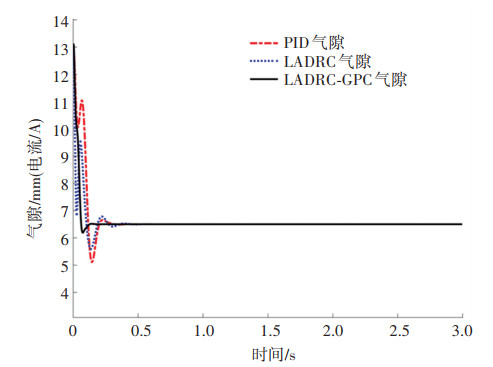
|
图 7 起浮时3种控制策略的气隙波形 Fig. 7 Air gap waveforms of three control strategies during floating |
图 8给出了系统50%加载和50%减载工况下3种控制策略的悬浮气隙仿真波形。PID控制下悬浮气隙发生了1.4 mm的变化, LADRC气隙变化1.1 mm,在两种控制策略下经过0.26 s调整,系统恢复稳态。LADRC相比PID控制,在加减载工况下,悬浮气隙的波动量较小,但是调整时间并没有减小。LADRC-GPC无论是起浮、50%加载、50%减载工况下,悬浮气隙波动量更小,响应速度更快。

|
图 8 负载突变时3种控制策略的气隙波形 Fig. 8 Air gap waveform of three control strategies under load mutation |
图 9给出了给定气隙突变的情况下3种控制策略的气隙仿真波形。1.0 s时刻,给定气隙从6.5 mm突变为9.0 mm,在PID控制下,悬浮气隙在增大方向上产生1.7 mm超调,调节时间为0.18 s;LADRC产生了0.9 mm超调,调节时间为0.29 s。在2.0 s时刻,给定气隙从9.0 mm突变为4.0 mm,在PID控制下,悬浮气隙在减小方向上产生2.5 mm超调,调节时间为0.20 s;LADRC悬浮气隙产生1.2 mm超调,调整时间为0.32 s。LADRC相比PID控制,超调量较小,但是调节时间变长了。由图 9可知,LADRC在给定气隙突变情况下,气隙超调量有明显的降低,而且可以更快地跟踪给定气隙。

|
图 9 给定气隙突变时3种控制策略的气隙波形 Fig. 9 Air gap waveform of three control strategies under reference mutation of air gap |
本文设计了基于贝加莱PLC的控制器,以实验室现有的磁悬浮小车为控制对象,验证ADRC-GPC算法在悬浮系统的有效性。
图 10给出了磁悬浮小车系统的主要组成部分,其中贝加莱PLC控制器中的X20CP3586是CPU模块,用于数据处理;X20AI4632是模拟量输入模块,用于输入悬浮气隙信号和线圈电流信号;X20DI4375是数字量输入模块,用于输入指令信号;X20AO4632是模拟量输出模块,用于将参考电流输出给斩波器。斩波器使悬浮电磁铁中的电流跟踪参考电流信号。

|
图 10 悬浮小车硬件系统 Fig. 10 Suspension vehicle hardware system |
控制参数的整定方法大体可以分为理论计算整定法和工程整定法两大类。基于数学模型通过计算直接得到的控制器的整定参数,其整定过程复杂,且由于磁悬浮系统是一个强非线性系统,而现有的数学模型是对悬浮系统的线性近似,故求得整定参数很不可靠。实际试验中采用工程整定法,首先以Ziegler-Nichols稳定边界整定法进行PID控制参数整定,然后以ITAE(时间误差绝对值积分)最小为目标进行参数优化[19]。LADRC-GPC控制器主要参数见表 2。
| 表 2 LADRC-GPC控制器主要参数 Tab. 2 Main parameters of LADRC-GPC controller |
表 2中N1为优化时域的初值,N2为优化时域终值,Nu为控制时域,λ为控制加权常数,α为柔化因子,T为采样时间,ω0为ESO带宽,h为ESO采样时间,b0为补偿因子。实验和仿真时的参数存在一定的差异。
扩张观测器的带宽ω0实验参数和仿真参数差别较大。根据实验调试发现,由于环境噪声和系统延时的影响,当ω0=240时,系统无论如何调试,始终处于降落、吸死的循环状态,无法达到稳定。当ω0≥800时,悬浮电磁铁悬浮在额定气隙时出现噪声,系统处于临界稳定状态。当ω0过小时,扩张状态观测不能有效地估计系统误差,系统无法达到稳定。当ω0过大时,输出被量测噪声污染。扩张观测器的带宽选择受到系统噪声能力的约束,综合分析,对于本磁悬浮系统ω0=600时动态性能较好。
优化时域的长度(N2 - N1)对系统影响较大。根据实验调试发现,N2需要平衡磁悬浮系统实时性和稳定性的影响,经过反复的测试,N2=20时,本悬浮系统具有期望的鲁棒性和快速性。
本磁悬浮系统,为了保证鲁棒性和实时性,取控制时域Nμ=1。
控制加权常数λ的作用是避免电流上升率过大,出现电磁体猛烈撞击轨道的现象。实验中选择λ=0作为初值,通过增大λ可以实现稳定控制,同时减弱了控制作用。根据调试的经验,λ较大时,给定气隙突变时会出现超调,调节时间变长;λ较小时,在起浮过程中,电流变化较为剧烈。同时,在保证系统稳定的前提下,λ减小,系统刚度增大,抗干扰能力增强。
柔化因子α的调节和N2、λ密切相关。当N2增大时,λ需要相应的增大,α需要相应减小才能保证系统的稳定性。保证其他参数合适的情况下,α较大时,系统的响应速度下降,α较小时,相应速度较快,超调量增大。通过实验发现,当α=0.997时,系统的动态性能最优。
补偿因子b0可以通过式(5)来确定,其中等效电阻Rt的确定和电流环密切相关,本磁悬浮系统取Rt=27,通过式(5)计算得到b0=-0.25可以在本磁悬浮系统中使用,在反复调试中发现b0=-0.23时动态性能最优。
3.3 实验结果与分析在图 11~13中,示波器通道1测量气隙波形,通道2测量电流波形。

|
图 11 起浮时3种控制策略的实验波形 Fig. 11 Experimental waveforms of three control strategies during floating |

|
图 12 加减载时3种控制策略的实验波形 Fig. 12 Experimental waveforms of three control strategies during loading and unloading |

|
图 13 给定气隙突变时3种控制策略的实验波形 Fig. 13 Experimental waveforms of three control strategies under reference mutation of air gap |
图 11给出了3种控制方式下系统空载状态起浮时的电流和气隙波形。在起浮的过程中为了避免电磁铁碰撞导轨,采用了缓起浮控制策略。由图 11(a)可知,在PID控制情况下,电流增加,最大可以达到5 A,经过1.2 s的调整稳定在3.0 A。电流达到一定值时,小车起浮,悬浮气隙减小,出现3.2 mm的超调,经过1.2 s的调整,悬浮气隙稳定在6.5 mm。由图 11(b)可知,在LADRC情况下,电流增加,峰值为5.0 A,经过0.4 s的调整稳定在3.2 A。经过短暂的延时,小车起浮,悬浮气隙减小,出现4.8 mm的超调,经过0.4 s的调整,悬浮气隙稳定在6.5 mm。由图 11(c)可知,在LADRC-GPC情况下,电流增加,峰值达到4.6 A,经过0.4 s调整,稳态电流为3.1 A。经过短暂的延时,小车起浮,悬浮气隙减小,出现4.0 mm的超调,经过0.4 s的调整,悬浮气隙稳定在6.5 mm。可以看出,在起浮工况下LADRC-GPC时气隙的相应速度最快,超调量最小。
图 12给出了3种控制方式下系统稳定悬浮时50%加减负载情况下的电流和气隙实验波形。在此针对加载进行分析。由图 12(a)可知在PID控制下,加载的瞬间,电流从2.8 A上升到4.8 A,悬浮气隙出现3.2 mm波动,经过1.0 s的调节,电流稳定在3.8 A,气隙恢复6.5 mm稳态。由图 12(b)可知,LADRC下,加载的瞬间,电流从3.0 A增加到4.5 A,悬浮气隙出现1.4 mm的波动,经过0.6 s的调节,电流稳定4.0 A,气隙达到6.5 mm稳态。由图 12(c)可知,在LADRC-GPC下,加载的瞬间电流从3.1 A增加至4.6 A,悬浮气隙出现1.0 mm的波动,经过0.6 s的调整,系统达到稳态。从实验波形可知,在50%加减载工况下,LADRC-GPC悬浮气隙波动最小,调整时间更短。因此,磁悬浮系统在LADRC-GPC下具有更强的抗干扰能力,控制性能更优越。
图 13给出了在3种控制策略下,给定气隙突变时,电流和气隙的实验波形。图 13(a)给出了在PID控制下,给定气隙突然增大时,电流从3.1 A迅速达到峰值5 A,经过0.6 s调整稳定在3.4 A,悬浮气隙出现了3.6 mm的超调,经过0.6 s的调节稳定在9.0 mm;给定气隙突然减小时,悬浮气隙出现3.2 mm的超调,经过1.2 s的调节,电流稳定在2.8 A,气隙达到4 mm的稳定状态。图 13(b)给出了LADRC下,给定气隙突然增大时,电流从3.1 A快速达到峰值3.9 A,悬浮气隙出现1.0 mm的超调,经过0.6 s的调节电流稳定在3.4 A,气隙达到9.0 mm稳态;给定气隙突然减小时,悬浮气隙出现了0.8 mm的超调,经过0.2 s的调节,电流稳定在2.8 A,气隙达到4 mm的稳定状态。图 13(c)给出了LADRC-GPC下,给定气隙突然增大时,气隙和电流基本不存在超调,经过0.3 s的调节,电流稳定在3.4 A,气隙达到9 mm稳态;给定气隙突然减小时,电流和悬浮气隙可以快速无超调地达到稳定状态。实验结果表明,在给定气隙突变工况下,LADRC-GPC悬浮气隙超调量更小,可以更快地跟踪给定气隙。因此,对导轨有更强适应性,对导轨的材料、制造工艺、安装精度等方面的要求有所降低。
综上比较,磁悬浮系统采用LADRC-GPC可以实现稳定悬浮,与PID控制、LADRC相比,无论起浮、加减载还是给定气隙突变工况,悬浮气隙波动最小,调整时间最短。表明LADRC-GPC算法应用在悬浮系统具有优越性。
4 结论1) 对磁悬浮系统的LADRC-GPC进行了详细的推导,并进行了仿真分析和实验验证。
2) 给定气隙突变和加减载对悬浮系统具有显著影响。LADRC-GPC相比于传统的控制策略具有更强的快速性、适应性和鲁棒性。
3) 本文是在悬浮电磁铁静态悬浮时,通过给定气隙突变和加减载来模拟实际磁浮列车的悬浮系统过接缝和负载扰动工况,与磁悬浮列车实际运行时工况存在一定差距。在后续研究中,可以通过动态悬浮实验,针对实际运行时存在的车轨耦合等工况进行算法改进。
| [1] |
徐飞, 罗世辉, 邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报, 2019, 41(3): 40. XU Fei, LUO Shihui, DENG Zigang. Study on key technologies and whole speed range application of maglev rail transport[J]. Journal of the China Railway Society, 2019, 41(3): 40. |
| [2] |
CHEN C, XU J, LIN G, et al. Fuzzy adaptive control particle swarm optimization based on T-S fuzzy model of maglev vehicle suspension system[J]. Journal of Mechanical Science and Technology, 2020, 34(1): 43. DOI:10.1007/s12206-019-1247-4 |
| [3] |
LI J, CHIOU J. Two-dimensional fuzzy sliding mode control of a field-sensed magnetic suspension system[J]. Mathematical Problems in Engineering, 2014, 2014: 1. |
| [4] |
HE G, LI J, CUI P. Nonlinear control scheme for the levitation module of maglev train[J]. Journal of Dynamic Systems, Measurement, and Control, 2016, 138(7): 0745037. |
| [5] |
陈琛, 徐俊起, 倪菲, 等. 基于人工智能负载估计系统的磁浮列车垂向振动主动控制[J]. 同济大学学报(自然科学版), 2020, 48(9): 1344. CHEN Chen, XU Junqi, NI Fei, et al. Active control of vertical vibration for maglev train based on artificial intelligence load estimation system[J]. Journal of Tongji University (Natural Science Edition), 2020, 48(9): 1344. |
| [6] |
林科文. 低速磁浮列车过轨道台阶的悬浮控制研究[D]. 长沙: 国防科学技术大学, 2010: 82 LIN Kewen. Research on suspension control of low-speed maglev train running on step railway[D]. Changsha: National University of Defense Technology, 2010: 82 |
| [7] |
周思洋. 中低速磁浮列车轨道台阶识别及波动抑制算法研究[D]. 长沙: 国防科学技术大学, 2017 ZHOU Siyang. Research of mid-low speed maglev track step recognition and fluctuation restrain algorithm[D]. Changsha: National University of Defense Technology, 2017 |
| [8] |
韩京清. 自抗扰控制技术[J]. 前沿科学, 2007(1): 24. HAN Jingqing. Auto disturbances rejection control technique[J]. Frontier Science, 2007(1): 24. |
| [9] |
CHEN Z, QIN B, SUN M, et al. Q-learning-based parameters adaptive algorithm for active disturbance rejection control and its application to ship course control[J]. Neurocomputing, 2020, 408: 51. DOI:10.1016/j.neucom.2019.10.060 |
| [10] |
WANG D, SUN H. Design of repetitive controller based on linear auto disturbance rejection control for active magnetic bearing spindles[C]//2nd International Conference on Cybernetics, Robotics and Control. Danver: IEEE, 2017: 106
|
| [11] |
郑安荣. 磁悬浮系统的自抗扰控制策略研究[D]. 沈阳: 沈阳工业大学, 2017: 62 ZHENG Anrong. Research on active disturbance rejection control strategy of maglev system[D]. Shenyang: Shenyang University of Technology, 2017: 62 |
| [12] |
何凌云. 磁悬浮系统的自抗扰控制[D]. 长沙: 国防科学技术大学, 2006: 24 HE Lingyun. Active disturbance rejection control of maglev system[D]. Changsha: National University of Defense Technology, 2006: 24 |
| [13] |
WU X, CHEN Z, ZHAO Y, et al. A comprehensive decoupling control strategy for a gas flow facility based on active disturbance rejection generalized predictive control[J]. Canadian Journal of Chemical Engineering, 2019, 97(3): 762. DOI:10.1002/cjce.23215 |
| [14] |
陈增强, 吴瑕, 孙明玮, 等. 基于频域的自抗扰广义预测控制的稳定性分析[J]. 哈尔滨工程大学学报, 2018, 39(6): 1046. CHEN Zengqiang, WU Xia, SUN Mingwei, et al. Stability of active disturbance rejection generalized predictive control based on frequency domain[J]. Journal of Harbin Engineering University, 2018, 39(6): 1046. |
| [15] |
LIANG D, ZHANG K, JIANG Q, et al. Mathematical model optimization of electromagnetic suspension system based on additional constraints[C]//14th IEEE Conference on Industrial Electronics and Applications. Xi'an: IEEE, 2019: 2309
|
| [16] |
YAN F, JIANG Q, XIAO S, et al. A load adaptive control strategy for electromagnetic levitation systems[C]//14th IEEE Conference on Industrial Electronics and Applications. Xi'an: IEEE, 2019: 1135
|
| [17] |
李云钢, 常文森. 磁浮列车悬浮系统的串级控制[J]. 自动化学报, 1999, 25(2): 3. LI Yungang, CHANG Wensen. Cascade control of an EMS maglev vehicle's levitation control system[J]. Acta Automatica Sinica, 1999, 25(2): 3. |
| [18] |
王育银. 磁悬浮系统的隐式广义预测控制器设计[D]. 长沙: 国防科学技术大学, 2013: 3 WANG Yuyin. Design of the implicit general predictive controller for the maglev system[D]. Changsha: National University of Defense Technology, 2013: 3 |
| [19] |
GAO Z. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the 2003 American Control Conference. Denver: IEEE, 2003: 4989
|
| [20] |
张文清. 基于磁通反馈的悬浮控制方法研究及实现[D]. 长沙: 国防科技大学, 2014: 25 ZHANG Wenqing. Research and realization of magnetic flux feedback control method in maglev system[D]. Changsha: National University of Defense Technology, 2014: 25 |
| [21] |
柴天佑, 岳恒. 自适应控制[M]. 1版. 北京: 清华大学出版社, 2016: 106. CHAI Tianyou, YUE Heng. Adaptive control[M]. 1st ed. Beijing: Tsinghua University Press, 2016: 106. |
 2022, Vol. 54
2022, Vol. 54


