2. 中国航天科技集团有限公司 空间结构与机构技术实验室,上海 201108
2. Space Structure and Mechanism Technology Laboratory of China Aerospace Science and Technology Group Co.Ltd, Shanghai 201108, China
随着航天事业的发展,深空探测、地球观测、射电天文学等航天任务对航天器的结构与可展机构的尺寸、质量、可靠性等提出了更高的要求。可展开薄膜具有质量轻、尺寸大等一系列优点,其广泛应用于太阳帆、大孔径天线、遮阳罩中,如NASA研制的NanoSail-D太阳帆[1],R3D2卫星中的P-DAHGR薄膜反射阵面天线[2]等。随着空间任务对大尺寸薄膜的需求越来越迫切,如何实现可展薄膜的大折展比折叠,折叠后如何实现高效有序展开,以及展开后如何保证薄膜表面的高精度成为研究热点之一。
Miura-ori是由Miura[3-4]提出的一种折纸方法,该研究的初衷是致力于解决地图的折叠问题,目前这种折纸方法广泛应用于航空航天、建筑等众多领域。如Wright等[5]开发了一种使用Miura-ori折叠方法的装配过程,以及一个用于制造3 m× 3 m太阳帆的原型装配台;Velez等[6]提出了一种基于扩展Miura-ori折纸图形的可折叠可重构深空通信天线;Yu等[7]设计了一种基于Miura-ori的气动可折叠驱动器驱动的爬行软体机器人;Li等[8]根据Miura-Ori原理提出了一种设计和制造可伸缩电路板的方法;Horner等[9]详细讨论了Miura-Ori太阳帆模型的构造技术,并概述了各种可能的展开方法;肖洪等[10]基于Miura-ori折纸原理提出薄膜防护罩折叠方法,并进行了参数分析。
薄膜在折叠过程中局部发生变形,由此产生折痕[11]。折痕改变了膜面材料的状态与行为,且在薄膜完全展开状态下具有一定的不可恢复性[12-13],对折叠态薄膜展开过程与展开结果产生了一定程度的影响。在研究折痕的弹塑性变形方面,国内外许多学者将薄膜折痕处假设为完全塑性变形,以便对折痕区域展开研究。Woo等[14]采用有限元法模拟薄膜折叠和单轴拉伸试验,以计算薄膜的有效模量;Furuya等[15-16]建立了由弹性铰链和板组成的一维可展开薄膜分析模型,通过数值分析研究了薄膜的抗弯刚度对结构的影响,还对一维Z型折叠薄膜进行了数值模拟和实验验证,将大变形理论作为弹性问题进行理论分析,研究了折叠膜结构太阳帆的展开性能;Satou等[17-18]采用有限元方法研究可展开薄膜的折叠特性,估计了折痕中可能出现的塑性变形,还对一维Z型折叠薄膜进行了弹塑性有限元分析,检验折痕的力学性能;Reynolds等[19]对光学应用的薄膜提出了一种弹性折叠方法,使用特定的最小半径折痕而不是刚性折痕;侯德高等[20]对薄硅橡胶板的交叉折叠进行了数值分析,研究了薄膜的变形和应力;谢志民等[21]对柔性复合薄膜材料的折叠损伤进行了实验研究,并讨论了由于压缩屈曲导致的复合薄膜在拉伸中出现的伸长破坏的现象。上述研究的薄膜折痕多数以一维折痕为研究对象,很少涉及二维折痕的研究,而且,目前对薄膜展开过程的分析大部分停留在理论分析阶段,没有实现相应的工程应用。深入研究折痕处的力学行为对薄膜展开过程是否顺畅以及展开后的表面精度至关重要,二维弹性折痕的可行性分析具有重大的研究意义。
本文提出基于Miura弹性折痕的可展薄膜构型,可以兼顾大尺度、轻量化、高展收可靠性等性能要求,并对折痕参数作出合理优化以实现大折展比及小折痕总长,同时建立数值模型,分析折痕在折叠过程中力学行为变化,验证薄膜二维弹性折痕的可行性,使得展开后薄膜的平整度及表面精度达到最优。
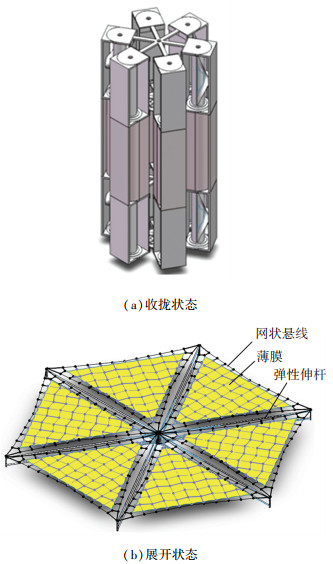
1 空间薄膜可展机构构型设计空间薄膜可展开机构通常由展开支撑机构、薄膜和张拉系统组成。基于六边形的几何构型,根据空间薄膜可展机构具有薄膜结构可折叠、轻量化、高折展比、高刚度和大尺寸等性能要求,本文提出了中心展开空间薄膜可展机构,如图 1所示。中心展开的展开方式具有良好的同步展开性并且易于控制,同时在面密度、收拢展开尺寸和动力学特性等方面也具有优势。
|
图 1 中心展开空间薄膜机构 Fig. 1 Central deployable space membrane mechanism |
中心展开空间薄膜可展机构选用开缝圆管弹性伸杆作为展开支撑机构,卷曲后能够发生较大的弹性变形,从而存储一定的弹性变形能;当解除约束后弹性变形自动恢复,实现自驱动展开,且杆件展开状态具有一定的弯曲刚度和强度。张拉系统采用网状悬线张拉方案,通过内外悬线以及连接线的合理配置,有效减轻了绳索总质量,并极大程度地消除了褶皱,提高了薄膜的表面精度和平整度,有效改善了中心展开空间薄膜可展机构整体系统的动力学特性。
中心展开空间薄膜可展机构将薄膜整体分解成了6个三角形薄膜,借鉴折纸方法Miura-ori来实现三角形薄膜的折叠展开。参照Miura-ori的谷线和脊线,合理配置薄膜的折痕,展开时靠近中心的薄膜角点固定,弹性伸杆带动边缘的薄膜角点进行展开,当弹性伸杆完全展开时完成整个薄膜的展开。而针对中心展开空间薄膜可展机构中的三角形薄膜,如何设计优化Miura-ori折痕参数,来满足机构性能要求,实现高折展比和对薄膜较小的塑性损伤,需要进一步深入研究。
塑性折痕会使薄膜产生塑性变形,甚至造成薄膜的损伤,不仅会影响薄膜的展开效率及展开稳定可靠度,而且可能存在残余应力以及应力集中的现象,导致薄膜产生褶皱乃至撕裂,影响薄膜的展开形态及表面精度。在完成优化的Miura-ori三角形薄膜折叠方法的基础上,研究其弹性折痕的可行性。而建立折痕的解析模型来分析其弹塑性,模型很复杂且很难可视化直观分析薄膜各处的应力分布情况。可以通过有限元来观察应力分布是否存在应力集中以及最大应力是否超过屈服强度来验证Miura-ori弹性折痕的可行性。在得到的优化折痕参数基础上建立数值分析模型,利用有限元软件ABAQUS/Explicit显示分析模块来模拟折叠过程,分析折叠后薄膜的应力分布并验证Miura-ori弹性折痕的可行性。
2 Miura-ori折痕参数分析和优化Miura-ori折叠方法中的两个主要折痕参数分别是折痕间距和折痕倾角,基于折痕参数的几何和数值关系建立分析模型,对折痕参数进行分析和优化,以提高薄膜的折展比,同时通过减小折痕总长来降低对薄膜的损伤。
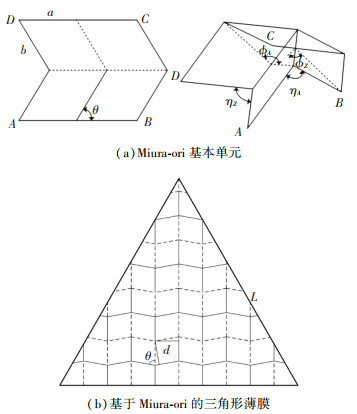
2.1 Miura-ori折叠薄膜折展比计算Miura-ori折叠因其快速简单的展开方式而广泛应用于卫星天线和太阳能聚光器等空间任务中,将Miura-ori折叠应用到中心展开空间薄膜机构的薄膜折叠设计中。图 2(a)中绘制了Miura-ori基本单元的折痕参数及折展构型,其构型由折痕长度a,b和折痕倾角θ这3个参数决定,并由4个二面角来描述其折展构型状态。由此基本单元可知,Miura-ori只需要一次折展即可完成折叠及展开,折展比大,折展效率高。中心展开空间薄膜可展机构由6个三角形薄膜组成,将Miura-ori应用于三角形构型,得到如图 2(b)所示的基于Miura-ori的三角形薄膜折痕分布图,图中d为折痕间距,L为薄膜边长,θ为折痕倾角,s为薄膜厚度。
|
图 2 Miura-ori折叠的基本单元及平面折痕图 Fig. 2 Basic unit and creases diagram of Miura-ori |
为了计算基于Miura-ori的三角形薄膜的折展比,需要先计算Miura-ori折叠的展开体积Vd和折叠体积Vf。根据几何关系,可以计算薄膜的展开体积为
| $ V_{\mathrm{d}}=\frac{\sqrt{3}}{4} L^2 s $ | (1) |
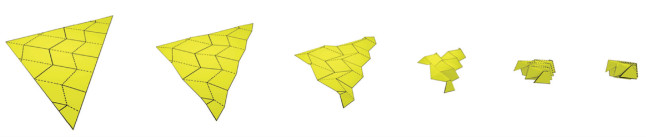
基于Miura-ori折叠的三角形薄膜折叠过程和收拢状态如图 3所示,其收拢状态的包络体积可被视为具有平行四边形底部的棱柱。反之,要展开基于Miura-ori折叠的三角形薄膜,只需要对3个角点进行张拉。
|
图 3 基于Miura-ori折叠的薄膜折叠过程和收拢状态 Fig. 3 Membrane folding process and folded state of Miura-ori |
棱柱的高度与薄膜的厚度和折叠后的薄膜层数有关,根据几何关系和棱柱体积计算公式,推导基于Miura-ori折叠的三角形薄膜的折叠体积为
| $ V_{\mathrm{f}}=\frac{d^2}{\sin \theta} \times\left[\left(\frac{L}{d}+2\right) \frac{L}{2 d}\right] s=\frac{d L s}{2 \sin \theta}\left(\frac{L}{d}+2\right) $ | (2) |
根据折展比的定义,进一步推导了基于Miura-ori的三角形薄膜的折展比表达式:
| $ \mathit{\Theta } = \frac{{{V_{\text{d}}}}}{{{V_{\text{f}}}}} = \frac{{\sqrt 3 L\sin \theta }}{{2L + 4d}} $ | (3) |
由式(3)可知,基于Miura-ori的三角形薄膜的折展比只与薄膜的折痕倾角θ和折痕间距d有关
当L=25 m,折痕间距不应超过薄膜边长,所以0 m≤d≤25 m,折痕倾角0°≤θ≤90°,绘制基于Miura-ori的三角形薄膜的折展比关于折痕参数的曲线,如图 4所示。由图 4可知,在折痕间距一定时,基于Miura-ori折叠的薄膜的的折展比随折痕倾角的增大而增大。在折痕倾角一定时,折展比随折痕间距的增大而减小。

|
图 4 Miura-ori折叠的折展比关于折痕参数的曲线 Fig. 4 Deployment ratio curve of Miura-ori with respect to crease parameters |
由基于Miura-ori折叠的平面折痕图(图 2)可知,Miura-ori折叠的折痕主要有竖直折痕和水平倾斜折痕两类。根据折痕分布规律以及相关几何关系,竖直折痕可看作0.5L/d条长度为
| $ L_{\mathrm{V}}=\frac{\sqrt{3} L^2}{4 d} $ | (4) |
计算水平倾斜折痕时,根据折痕分布规律以及相对称关系,可以将等边三角形薄膜看作边长为L/2和
| $ L_{\mathrm{H}}=\left[\frac{\sqrt{3} L}{2 d} \sin \theta-1\right] \times \frac{L}{2 \sin \theta} $ | (5) |
折痕总长为竖直折痕和水平倾斜折痕长度总和,即
| $ {\mathit{\Sigma }_L} = \frac{{\sqrt 3 {L^2}}}{{4d}} + \left[ {\frac{{\sqrt 3 L}}{{2d\sin \theta }} - 1} \right] \times \frac{L}{{2\sin \theta }} $ | (6) |
式中:θ为折痕倾角,L为薄膜边长,d为折痕间距,ΣL为折痕总长。由式(6)易知,Miura-ori折叠的折痕总长与折痕间距、折痕倾角和薄膜边长有关,合理设计这些参数可以有效缩短折痕长度,降低对薄膜造成的损伤程度。
2.3 薄膜折痕参数优化根据薄膜可展机构的设计要求,对折痕参数进行优化以实现高折展比、短折痕长度,综合折展比和折痕长度,定义折展比与折痕长度的比Θ/ΣL为优化目标,基于Miura-ori折叠的Θ/ΣL表达式为
| $ \mathit{\Theta /}{\mathit{\Sigma }_L} = \frac{{\sqrt 3 d{{\sin }^2}\theta }}{{(L + 2d)\left\{ {\frac{{\sqrt 3 L\sin \theta }}{2} + \left[ {\frac{{\sqrt 3 L}}{{2d\sin \theta }} - 1} \right] \times d} \right\}}} $ | (7) |
将三角形薄膜边长L=25 m带入式(7)中进行简化,可得最终的优化目标函数:
| $ \mathit{\Theta /}{\mathit{\Sigma }_L} = \frac{{\sqrt 3 d{{\sin }^2}\theta }}{{(25 + 2d)\left\{ {\frac{{25\sqrt 3 }}{2}\sin \theta + \left[ {\frac{{25\sqrt 3 }}{{2d\sin \theta }} - 1} \right] \times d} \right\}}} $ | (8) |
式中其他折痕参数均为已知量,只需求解d和θ两个设计变量的最优解。计算后求得基于Miura-ori折叠的最优折痕参数为θ=80°, d=0.25 m。
3 二维弹性折痕数值建模分析一维弹性折痕较为容易实现,而二维弹性折痕必然会存在折痕交点,此处会产生应力集中,容易产生塑性变形。为了分析二维弹性折痕,选择最为简单的四折痕基本单元进行分析,分别对折痕倾角θ=90°及θ < 90°的四折痕基本单元建立数值仿真模型,分析二维弹性折痕的可行性。图 2(a)中所示的Miura-ori基本单元,也可看作折痕倾角θ < 90°的四折痕基本单元,先对基本单元进行数值建模分析,为后续建立多折痕的Miura-ori弹性折痕分析模型奠定基础。
3.1 折痕倾角θ=90°弹性折痕有限元仿真分析为更好地分析薄膜的二维弹性折痕,对折痕倾角θ=90°的四折痕基本单元进行分析,建立如图 5所示的几何模型,薄膜基本几何参数为:厚度t=25 μm,有效边长L=100 mm。根据Euler-Bernoulli梁理论可知,当薄膜的材料参数确定,其弹性折痕的曲率半径与薄膜厚度成正比,数值模型以厚度为25 μm的聚酰亚胺薄膜为例来进行分析。为实现交叉折叠,根据折痕的峰线和谷线分布,第一步要将AD、BC两边沿着折痕EF对折,第二步则将AB、CD两边沿着折痕GH对折。选用ABAQUS/Explicit显示分析模块来进行薄膜折叠过程的数值分析。

|
图 5 折痕倾角θ=90°薄膜折叠过程仿真的计算模型 Fig. 5 Calculation model of membrane folding process simulation of θ=90° |
单元类型和网格尺寸直接决定了创建有限元模型的质量,进而影响仿真分析的计算速度和准确性。为了对薄膜折叠和展开过程进行比较准确的数值模拟,要选择正确的单元类型以及合适的网格尺寸。在确定网格尺寸时,不仅要保证薄膜折痕附近的网格质量和计算精度,而且要保证合适的计算时间。根据收敛性测试,最终网格划分均采用四边形进阶算法,网格大小设定为1 mm,薄膜选用M3D4R单元。此外,在进行显示分析步时,对计算时长的选取也会影响收敛性及计算速度。针对薄膜二维弹性折痕,每一个折叠过程划分为一个计算步,综合考虑仿真的准确性、收敛性以及计算速度,设定每一个分析步时间为0.1 s。综上,在ABAQUS中建立折痕倾角θ=90°薄膜的有限元模型,如图 5 (c)所示。薄膜添加的材料为聚酰亚胺,其常温(22 ℃)状态下的主要特性如表 1所示。
| 表 1 聚酰亚胺材料特性 Tab. 1 Material properties of polyimide |
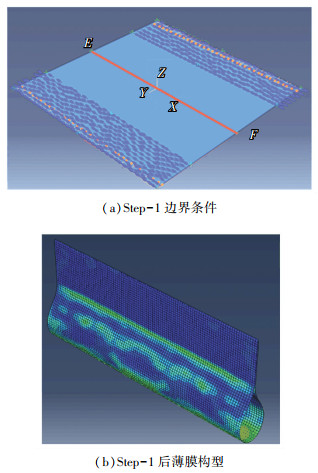
折痕倾角θ=90°的四折痕基本单元需要两步折叠得到最终的折叠构型,所以分别建立Step-1和Step-2两个计算步来进行边界条件的添加和折叠结果的计算。为了更好地观察折叠后的应力分布情况,边界条件添加到特定的节点上,通过控制节点来实现折叠,相较于将刚体与薄膜绑定之后控制刚体的边界条件添加方法,节点控制法对薄膜的构型影响更小,所得变形及应力结果只跟弹性折痕有关,不受刚体的影响,结果更加准确。如图 6(a)所示,在薄膜的中间定义一条路径EF以便于后处理提取路径上各节点应力值,Step-1中边界条件为如图 6所示的节点集向着中心点O沿着X轴旋转90°,得到如图 6(b)所示的折叠构型。
|
图 6 Step-1的过程及结果 Fig. 6 Process and result of Step-1 |
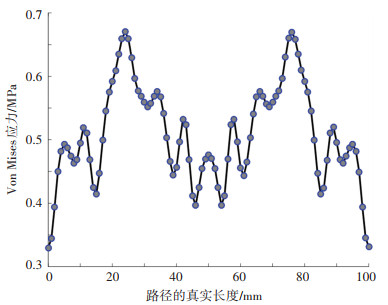
对Step-1的仿真结果进行后处理,提取所定义的路径EF上各节点应力值,绘制如图 7所示的Step-1后Von Mises应力沿路径分布图。由图 7可知,路径上各节点应力呈对称分布,在路径25 mm及75 mm处出现应力最大值,为0.67 MPa;而路径50 mm处应力值为0.48 MPa,造成这一应力分布的原因是,只在靠近边缘的特定节点处添加了边界条件,靠近中间处的节点处于自由状态,所以弹性折痕附近处的路径EF的应力分布应呈对称性,但应力最大处不一定出现在路径中点处,且各节点应力值都很小,非常接近。经历Step-1折叠后薄膜的应力值仍处于弹性范围内,未发生塑性变形,初步验证了一维弹性折痕的可行性。
|
图 7 Step-1后Von Mises应力沿路径分布 Fig. 7 Von Mises stress distribution along the path after Step-1 |
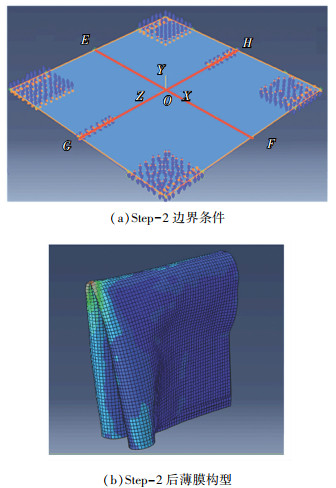
在Step-1基础上,进行第二步折叠Step-2的仿真计算。如图 8(a)所示,根据第二步折叠的特性,定义两条路径EF及GH以便于后处理提取路径上各节点应力值。Step-2中边界条件为如图 8(a)所示的节点集向着中心点O沿着Y轴旋转90°,得到如图 8(b)所示的折叠构型,即折痕倾角θ=90°的四折痕基本单元的最终折叠构型。
|
图 8 Step-2过程及结果 Fig. 8 Process and result of Step-2 |
并对Step-2的仿真结果进行后处理,提取所定义的路径EF及GH上各节点应力值,绘制如图 9所示的Step-2后Von Mises应力沿路径分布图。由图 9可知,两条路径上各节点应力总体呈对称分布,薄膜边界附近应力并不大,当靠近两条折痕交点时,应力急剧增大,并且在两条折痕交点处应力达到最大值,为2.794 MPa。通过和材料属性对比分析可知,经历Step-2折叠后薄膜的应力值仍处于弹性范围内,未发生塑性变形,初步验证了二维弹性折痕的可行性。路径EF的应力分布对称性较好,而路径GH的应力分布总体趋势呈现对称性,少量区域不完全对称,造成这一应力分布的原因是,OE和OF完全对称且受力情况相同,而OG会被折叠到OH的内侧,造成应力值存在一定的差异,但是两条路径的最大应力值都出现在点O处,因为点O为四折痕的交点,符合弹塑性力学规律。

|
图 9 Step-2后Von Mises应力沿路径的应力分布 Fig. 9 Von Mises stress distribution along the path after Step-2 |
为了进一步分析验证折痕倾角θ<90°的四折痕基本单元折叠过程,建立如图 10(a)所示的几何模型,薄膜基本几何参数为:厚度t=25 μm,有效边长L=100 mm。为了实现折痕倾角θ < 90°四折痕基本单元的折叠,实际上是根据折痕的脊线和谷线分布,将相邻表面沿着他们的连接折痕折叠实现的,而且仅需一个步骤就能完成所有折痕的折叠。同样选用ABAQUS/Explicit显示分析模块来进行折痕倾角θ < 90°四折痕基本单元折叠过程的数值分析。

|
图 10 ABAQUS中折痕倾角θ<90°的计算模型 Fig. 10 Calculation model of θ < 90° in ABAQUS |
在ABAQUS中建立折痕倾角θ < 90°四折痕基本单元的有限元模型,并在如图 10(b)所示的折痕处定义两条路径AOA′及BOB′,其中薄膜选用M3D4R单元,网格划分均采用四边形进阶算法,网格大小为1 mm,同样薄膜添加的材料为聚酰亚胺。利用建立的有限元模型,对薄膜折痕倾角θ < 90°四折痕基本单元的折叠过程进行仿真分析,如上所述其折叠过程只需要一个步骤,所以建立一个分析步Step-1来进行边界条件的添加和折叠结果的计算即可。如图 10(c)所示,两组相邻的表面分别沿着倾斜折痕旋转90°得到如图 11所示的折叠构型。

|
图 11 折痕倾角θ<90°的折叠过程 Fig. 11 Folding process of θ < 90° |
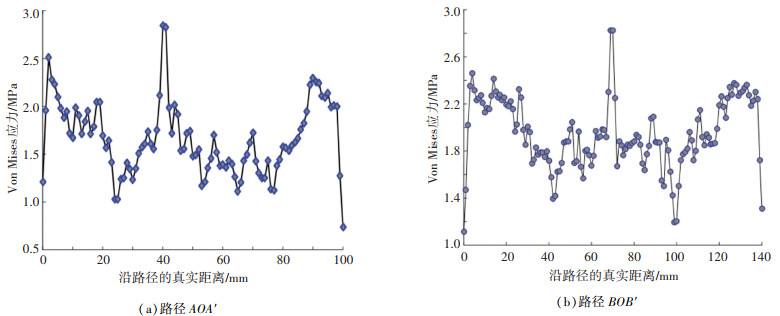
对仿真结果进行后处理,提取所定义的路径AOA′及BOB′上各节点应力值,分别绘制如图 12所示的Von Mises应力分布曲线。由图 12可知,在路径AOA′上,最大应力值发生在40 mm处,在路径BOB′上,最大应力值发生在70 mm处,这两处坐标对应位置均为O点,应力值为2.83 MPa,应力值仍处于弹性范围内,未发生塑性变形,初步验证了折痕倾角θ < 90°四折痕基本单元的二维弹性折痕的可行性。
|
图 12 折叠后的应力分布 Fig. 12 Von Mises stress distribution after folding |
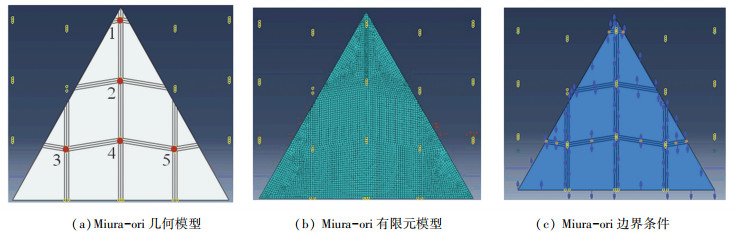
参照上一章中的数值模型建立方法,建立了如图 13(a)所示的基于Miura-ori的三角形薄膜的几何模型,薄膜基本几何参数为:厚度t=25μm,有效边长L=100 mm。同样的,Miura-ori折叠的实现是根据折痕的峰线和谷线分布,将相邻表面沿着他们的连接折痕折叠,并且仅需一个步骤就能完成所有折痕的折叠。在折痕交点处的5个节点分别定义为节点1、2、3、4、5,以便于分析折痕交点处的应力情况。同样选用ABAQUS/Explicit显示分析模块来进行基于Miura-ori薄膜折叠过程的数值分析。单元的类型、材料的属性以及网格尺寸均与上一章相同,进而得到如图 13(b)所示的基于Miura-ori薄膜弹性折叠的有限元模型。
|
图 13 ABAQUS中Miura-ori的计算模型 Fig. 13 Calculation model of Miura-ori in ABAQUS |
利用建立的有限元模型,对薄膜基于Miura-ori的折叠过程进行仿真分析,其折叠过程同样只需要一个步骤,所以建立一个分析步Step-1来进行边界条件的添加和折叠结果的计算即可。如图 13(c)所示,各组相邻的表面分别沿着倾斜折痕旋转90°,得到如图 14所示的折叠构型。

|
图 14 Miura-ori折叠过程 Fig. 14 Folding process of Miura-ori |
在上述仿真中,不难看出在折叠过程中多条折痕交点处的应力相比于薄膜其他位置应力更大,为此,提取上述5个节点的应力变化曲线,如图 15所示。可以观察出3个特征,首先,在折叠过程进行到一半左右,各个节点的应力达到最大值,其中节点2的应力峰值最大,为3.6 MPa,但折叠后薄膜的应力值仍处于弹性范围内,未发生塑性变形,验证了薄膜基于Miura-ori折叠多折痕弹性折痕的可行性;其次,可以发现节点1处的应力峰值最小,节点4、5的应力峰值与节点1相近,而节点1、4、5均为薄膜临近边界上的节点,相应可以得出结论,临近边界上的折痕交点相较于薄膜内部的折痕交点在折叠过程中产生的应力较小;最后,在几何模型中,节点3和节点5是成几何对称的,对于所得到的应力变化曲线中,节点3和节点5的应力变化在折叠前0.05 s内几乎完全一致,在后0.05 s内有一点偏差,符合应力分布变化规律。

|
图 15 薄膜各折痕交点处应力随时间变化曲线 Fig. 15 Stress curve at intersection of membrane creases with time |
根据所提出的空间薄膜可展机构构型设计方案,研制薄膜边长为2.5 m,厚度为25 μm的原理样机,其中薄膜基于Miura-ori的折痕参数设计优化方法,对三角形薄膜进行折痕参数优化及二维弹性折痕的研制。杆件采用碳纤弹性伸杆,悬线采用凯夫拉绳索,接头采用尼龙基玻璃纤维复合材料3D打印制作。空间可展开薄膜机构样机的收拢态及展开态构型如图 16所示。

|
图 16 空间薄膜可展机构原理样机 Fig. 16 Prototype of deployable space membrane mechanism |
整个机构在弹性伸杆的作用下沿着径向方向同步展开,并通过绳索驱动薄膜的展开,整个展开过程流畅无卡滞。利用样机进行多次重复展收实验,样机均顺利地实现了轴向的重复展收,且展收过程稳定可靠,验证了所提出的构型设计的合理性。样机中的薄膜展开过程如图 17所示,其中图 17(a)为Miura-ori薄膜的收拢态构型,收拢态体积符合上述计算公式,所占空间小,满足大折展比要求,且折痕总长数值较小,验证了薄膜折痕参数优化的有效性。根据Miura-ori的展开方法,在绳索牵引下张拉3个角点,实现薄膜的高效有序展开,得到图 17(d)所示的薄膜展开态构型,其展开形态平整,具有较高的表面精度,验证了可展薄膜的Miura弹性折痕的可行性及优越性。

|
图 17 薄膜展开过程 Fig. 17 Membrane unfolding process |
1) 本文设计了一种空间薄膜可展机构,满足薄膜结构可折叠、轻量化、高折展比、高刚度和大尺寸等性能要求。建立几何模型,计算了基于Miura-ori薄膜折叠方式的折展比和折痕总长,发现折展比和折痕总长与折痕倾角和折痕间距有关,并优化得到最优折痕参数。
2) 分别建立折痕倾角θ=90°及θ < 90°的四折痕基本单元以及基于Miura弹性折痕的三角形薄膜数值仿真模型,发现其关键路径上各节点应力值均处于弹性范围内,未发生塑性变形,验证了二维弹性折痕的可行性。
3) 研制了空间薄膜可展机构原理样机并进行了重复展收试验,展开过程流畅无卡滞,验证了机构构型设计的合理性,薄膜的大折展比和小折痕总长表明了折痕参数优化的有效性,薄膜展开后表面平整说明了二维弹性折痕的可行性及优越性。
通过对基于Miura弹性折痕的空间薄膜可展机构的构型设计、建模分析及样机研制,为空间薄膜可展开结构的弹性折痕设计分析和进一步研发提供了有益参考。后续将采用非接触测量的方法来测试可展薄膜Miura弹性折痕的应力分布情况,量化验证数值模拟工作的准确性。
| [1] |
JOHNSON L, WHORTON M, HEATON A, et al. NanoSail-D: a solar sail demonstration mission[J]. Acta Astronautica, 2011, 68(5/6): 571. DOI:10.1016/j.actaastro.2010.02.008 |
| [2] |
KELLY P K. A scalable deployable high gain antenna-DaHGR[C]//30th Annual AIAA/USU Conference on Small Satellites. Logan: AIAA, 2016: 1
|
| [3] |
MIURA K. Method of packaging and deployment of large membranes in space[J]. Institute of Space and Astronautical Science Report, 1980, 618: 1. |
| [4] |
MIURA K. Folded map and atlas design based on the geometric principle[C]//Proceedings of the 20th International Cartographic Conference. Beijing: ICACI, 2001: 1
|
| [5] |
WRIGHT T, LAUE G, HORNER G. A practical approach to large-area solar sail assembly utilizing the Miura-ori folding technique[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Huntsville: AIAA, 2003: 4663. DOI: 10.2514/6.2003-4663
|
| [6] |
VELEZ C A, KADDOUR A S, YNCHAUSTI C, et al. Deployable and reconfigurable Miura-ori reflectarray for mission-flexible satellite applications[C]//2021 IEEE Texas Symposium on Wireless and Microwave Circuits and Systems (WMCS). Waco: IEEE, 2021: 1. DOI: 10.1109/WMCS52222.2021.9493295
|
| [7] |
YU M, YANG W M, YU Y, et al. A crawling soft robot driven by pneumatic foldable actuators based on Miura-ori[J]. Actuators, 2020, 9(2): 26. DOI:10.3390/act9020026 |
| [8] |
LI Y K, LIU W X, DENG Y, et al. Miura-ori enabled stretchable circuit boards[J]. npj Flexible Electronics, 2021, 5(3): 1. DOI:10.1038/s41528-021-00099-8 |
| [9] |
HORNER G C, ELLIOTT M D. A fabrication and deployment approach for a Miura-ori solar sail model[C]//43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Denver: AIAA, 2002: 1708. DOI: 10.2514/6.2002-1708
|
| [10] |
肖洪, 王洪洋, 郭宏伟, 等. 空间相机重复展收机构薄膜防护罩设计及分析[J]. 光学精密工程, 2021, 29(12): 2877. XIAO Hong, WANG Hongyang, GUO Hongwei, et al. Design and analysis of the repeatable development and collapse mechanism film protective cover of space camera[J]. Optics and Precision Engineering, 2021, 29(12): 2877. DOI:10.37188/OPE.20212912.2877 |
| [11] |
HOSSAIN N M, WOO K, JENKINS C. Nonlinear material response of systematically creased membranes[C]// Proceedings of 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Rhode Island: AIAA, 2006: 1801. DOI: 10.2514/6.2006-1801
|
| [12] |
OKUIZUMI N, YAMAMOTO T. Centrifugal deployment of membrane with spiral folding: experiment and simulation[J]. Journal of Space Engineering, 2009, 2(1): 41. DOI:10.1299/spacee.2.41 |
| [13] |
MURPHEY T W. A nonlinear elastic constitutive model for wrinkled thin films[D]. Boulder: University of Colorado, 2000
|
| [14] |
WOO K, NANDURKAR K, JENKINS C H. Effective modulus of creased thin membranes[J]. Journal of Spacecraft and Rockets, 2008, 45(1): 19. DOI:10.2514/1.29282 |
| [15] |
FURUYA H, KAWASAKI Y. Effects of folding parameters on surface accuracy of deployable membrane space structures[C]//41st Structures, Structural Dynamics, and Materials Conference and Exhibit. Atlanta: AIAA, 2000: 1731. DOI: 10.2514/6.2000-1731
|
| [16] |
FURUYA H, MIYAZAKI Y K, TAKEUCHI H. Deployment characteristics of creased membrane for solar sail on geometrical configuration and fold pattern[C]//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Norfolk: AIAA, 2003: 1908. DOI: 10.2514/6.2003-1908
|
| [17] |
SATOU Y, FURUYA H. Folding properties of two-dimensional deployable membrane using FEM analyses[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology Japan, 2010, 8(27): 23. DOI:10.2322/tastj.8.Pc_23 |
| [18] |
SATOU Y, FURUYA H. Mechanical properties of z-fold membrane under elasto-plastic deformation[J]. Journal of Space Engineering, 2011, 4(1): 14. DOI:10.1299/spacee.4.14 |
| [19] |
REYNOLDS W D, MURPHEY T W. Elastic spiral folding for flat membrane apertures[C]//Spacecraft Structures Conference. Maryland: AIAA, 2014: 1036. DOI: 10.2514/6.2014-1036
|
| [20] |
HOU D, MA J, YAN C, et al. Analysis of cross folding an elastic sheet[C]// Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Cleveland: ASME, 2017: 67388. DOI: 10.1115/detc2017-67388
|
| [21] |
王友善, 谢志民, 杜星文. 柔性复合薄膜折叠损伤实验研究[J]. 哈尔滨工业大学学报, 2006, 38(8): 1292. WANG Youshan, XIE Zhimin, DU Xingwen. Experimental investigation of the folding damage of the flexible composite membranes[J]. Journal of Harbin Institute of Technology, 2006, 38(8): 1292. DOI:10.3321/j.issn:0367-6234.2006.08.022 |
 2023, Vol. 55
2023, Vol. 55


