无论是在传统能源的高效清洁利用,还是在新能源的可再生转化方面,多相反应过程均扮演着重要的角色,其中超过80%的多相反应过程采用多孔催化颗粒以提高反应速率或者合成特定产品。多孔催化颗粒内外表面难以避免发生积碳[1],积碳会覆盖活性位点,引起孔道变窄甚至堵塞,造成催化剂活性的迅速下降甚至失活[2]。为了实现工业上连续生产,积碳失活的催化剂需要及时进行氧化或气化等再生过程,以消除积碳并恢复催化活性[3]。因此,催化剂消碳再生技术一直是研究者们关注的焦点问题。
随着计算机水平的不断发展,数值模拟已广泛应用于多孔颗粒失活及再生过程。Yang等[4-5]采用MP-PIC方法,结合流体力学和积碳燃烧动力学模型,模拟了失活催化剂分布和水平挡板对工业紧凑型再生器性能的影响。研究表明,添加水平挡板和改善积碳催化剂分布,可以提高工业FCC再生器的性能。积碳消除过程不仅依赖于反应器宏观流动和传递特性,而且取决于颗粒内部孔隙结构[6]。Kern等[7]利用一维伪均质模型耦合再生反应动力学模型,分析了单催化剂颗粒内氧气和积碳负载量径向分布的瞬时变化,结果表明,在内扩散的作用下,氧气浓度和积碳负荷在催化颗粒内部径向呈现梯级分布。在固定床反应器内,孔扩散阻力对反应前沿宽度的影响比轴向扩散阻力更加显著。Zhang等[8]考虑颗粒内外热质传递,建立了丙烷脱氢Cr2O3/Al2O3催化剂再生的非均相模型。结果表明,随着反应温度的升高和积碳含量的增加,孔隙扩散对反应的影响更加显著。Reshetnikov等[9]基于反应器轴向和颗粒径向二维多尺度模型,研究了低氧浓度条件下绝热固定床反应器内CrF3/MgF2催化剂再生过程, 结果表明,在进口气体低于初始催化剂温度条件下,氧化再生反应只发生在催化剂颗粒外表面附近,易导致过热和催化剂损坏。
上述宏观模型往往忽略微观孔隙结构对反应和传质过程的影响,而积碳消除行为导致多孔催化颗粒内外表面孔隙结构的动态演变,传递-反应特性又直接依赖于真实复杂的孔隙结构。随着可控技术的发展,基于微观离散模型探索局部非均匀结构对反应和传递过程的影响,逐步成为研究热点[10]。因此,本文基于格子玻尔兹曼方法,开展多孔催化颗粒消碳行为的孔隙尺度模拟,分析消碳行为引起的孔隙结构演变特性和微纳尺度流动特性,评估气体稀薄效应下的消碳行为。
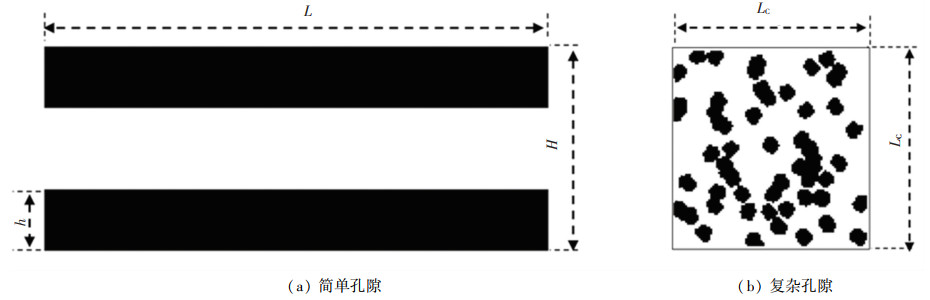
1 数学模型 1.1 物理模型本文开展简单孔隙结构和复杂随机孔隙结构的二维孔隙尺度模拟,如图 1(a)所示,简单孔隙结构的孔隙长L,高H,黑色代表积碳(固相),顶部和底部边界的积碳厚度均为h。采用四参数随机构造方法构建的复杂孔隙结构如图 1(b)所示,该孔隙结构的结构特性与真实催化剂结构相似[11]。
|
图 1 孔隙尺度积碳分布示意图 Fig. 1 Schematic diagram of coke deposition at pore scale |
采用格子玻尔兹曼(LB)方法描述气体稀薄效应下微纳孔隙传递过程,大孔存在条件下,催化颗粒孔隙内存在显著的黏性流动[12]。为了保持高努森数条件下的数值稳定性,本文采用正则化多松弛(MRT)模型来描述流动过程,其表达式为
| $ \begin{gathered} f_i\left(\boldsymbol{x}+\boldsymbol{c}_i \Delta t, t+\Delta t\right)=f_i^{\mathrm{eq}}(\boldsymbol{x}, t)+\bar{f}_i(\boldsymbol{x}, t)- \\ \boldsymbol{M}^{-1} \boldsymbol{S} \boldsymbol{M} \bar{f}_i(\boldsymbol{x}, t) \end{gathered} $ | (1) |
式中:
密度分布函数
| $ f_i^{\mathrm{eq}}(\boldsymbol{x}, t)=w_i \boldsymbol{\rho}\left(1+\frac{\boldsymbol{u} \cdot \boldsymbol{c}_i}{c_{\mathrm{s}}^2}+\frac{\left(\boldsymbol{u} \cdot \boldsymbol{c}_i\right)^2}{2 c_{\mathrm{s}}^4}-\frac{\boldsymbol{u} \cdot \boldsymbol{u}}{2 c_{\mathrm{s}}^2}\right) $ | (2) |
式中:wi、ci和cs分别代表格子权重、格子速度和格子声速,ρ和u为密度和速度。
正则化非平衡态分布函数fi可表示为
| $ \overline{f_i}=w_i\left[\frac{1}{c_i^2} H_{\mathrm{e}}^{(2)}\left(\boldsymbol{c}_i / c_{\mathrm{s}}\right) \sum\limits_{j=0}^8 f_j^{\mathrm{neq}} \boldsymbol{c}_j \boldsymbol{c}_j\right] $ | (3) |
式中,He(2)为二阶Hermite多项式. 非平衡态分布函数fineq可通过
对于孔隙尺度扩散和反应过程,采用被动标量模型来描述反应输运过程[11],对应的对流扩散方程如下:
| $ \frac{\partial C}{\partial t}+(\boldsymbol{u} \cdot \nabla) C=\nabla \cdot(D \nabla C) $ | (4) |
式中,C和D分别为组分浓度和分子扩散系数。
基于LBM方法,其演化方程为
| $ \begin{gathered} g_{C i}\left(\boldsymbol{x}+\boldsymbol{c}_i \Delta t, t+\Delta t\right)-g_{\mathrm{C} i}(\boldsymbol{x}, t)= \\ -\tau_{\mathrm{gs}}^{-1}\left[g_{C i}(\boldsymbol{x}, t)-g_{C i}^{\mathrm{eq}}(\boldsymbol{x}, t)\right] \end{gathered} $ | (5) |
式中:gCi为表示浓度的分布函数;gCieq为浓度的平衡态分布函数,且
| $ g_{C_i}^{\mathrm{eq}}(\boldsymbol{x}, t)=w_i C\left(1+\frac{\boldsymbol{u} \cdot \boldsymbol{c}_i}{c_{\mathrm{s}}^2}+\frac{\left(\boldsymbol{u} \cdot \boldsymbol{c}_i\right)^2}{2 c_{\mathrm{s}}^4}-\frac{\boldsymbol{u} \cdot \boldsymbol{u}}{2 c_{\mathrm{s}}^2}\right) $ | (6) |
无量纲松弛时间τgs=3D+0.5。
宏观浓度C可通过式(7)计算:
| $ C=\sum\limits_{i=0}^8 g_{C i} $ | (7) |
对于流动过程以及进口和出口,采用Zou-He压力边界指定压力,具体表达形式可参考文献[15]。采用反弹-镜面反射组合边界条件描述气固交界面速度滑移现象[16]:
| $ f_i(\boldsymbol{x}, t)=(1-r) f_i^{\mathrm{sr}}(\boldsymbol{x}, t)+r f_i^{\mathrm{bb}}(\boldsymbol{x}, t) $ | (8) |
其中,
对于扩散-反应过程,一般性浓度边界条件可表示为
| $ b_1 \frac{\partial C}{\partial \boldsymbol{n}}+b_2 C=b_3 $ | (9) |
式中:
基于赵建平等[18]的热重分析实验,积碳催化剂在O2/CO2气氛中的再生反应是一级反应。因此,这里将消碳反应表达式和反应速率简化为:
| $ \text { Reactant }_{(\text {gas })}+\text { Coke }_{(\text {solid })} \rightarrow \text { Product }_{(\text {gas })} $ | (10) |
| $ R=k_{\mathrm{r}} \cdot C_{\mathrm{R}} $ | (11) |
式中:R为反应速率,kr为反应常数,CR为浓度,反应表面的浓度可通过下式计算:
| $ C_{\mathrm{w}}=\frac{C_{\mathrm{f}}+0.5 \Delta x \boldsymbol{n} \cdot \boldsymbol{c}_i b_3 / b_1}{1.0+0.5 \Delta x \boldsymbol{n} \cdot \boldsymbol{c}_i b_2 / b_1} $ | (12) |
式中:Cf为边界处气相格子的浓度,n为反应表面法向矢量。
1.4 固相更新方法采用固相更新方法实现消碳反应导致的孔隙结构的改变。气相和固相均采用控制体积Vm标记。起初,固相和气相控制体积分别标记为1和0。当Vm≤0时,固相格子转变为气相格子。边界固相格子的控制体积随消碳反应变化可表示为[11]
| $ V_{\mathrm{m}}(t+\Delta t)=V_{\mathrm{m}}(t)-\overline{V_{\mathrm{m}}} a_{\mathrm{m}} R \Delta t $ | (13) |
式中am、R和Vm分别为比表面积、反应速率和摩尔体积。
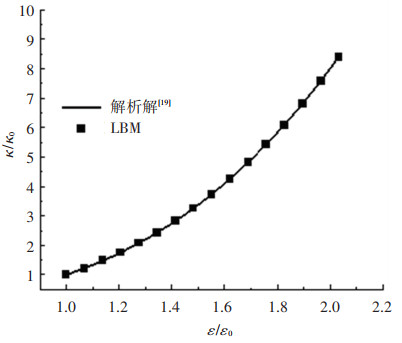
1.5 模型验证微尺度流动-扩散和反应模型在文献[11]中已得到验证。为了验证固相更新方法,模拟了二维简单孔隙的溶解过程,如图 2所示。当达姆科勒数(Dam)取0.000 1,积碳壁面发生均匀溶解时,该问题存在解析解。无量纲渗透率和孔隙率遵循指数为3的函数关系[19]。比较渗透率-孔隙度理论关系与LBM溶解模拟值发现,模拟得到的关系式与理论值相符合,从而验证了固相更新方法的有效性。
|
图 2 积碳消除行为的模拟验证 Fig. 2 Model verification of coke removal behavior |
通过网格独立性分析,选用250×100格子数目作为最终的计算网格。基于开源数值计算软件GNU Octave进行孔隙尺度模拟。
2 结果与讨论 2.1 简单孔隙的结构和传递特性变化采用无量纲参数(初始努森数Kn0)表征孔隙结构特性。图 3给出了基准工况(Kn0=0.1)条件下消碳过程的孔隙结构瞬时变化。由图 3可知,入口附近积碳首先消除,随着时间的推移,入口消碳显著,沿轴向孔隙的变化幅度增大。
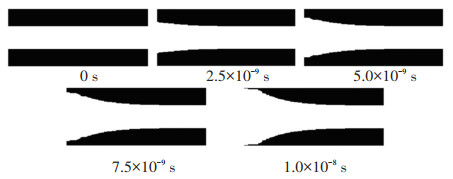
|
图 3 简单孔隙结构的瞬时变化(Kn0=0.1) Fig. 3 Transient variation of simple pore structure (Kn0=0.1) |
为了表征消碳过程孔隙结构演变对传递和反应特性的影响,图 4给出了基准工况下速度和反应物分布的瞬时变化。

|
图 4 孔隙结构内速度和浓度分布(Kn0=0.1) Fig. 4 Distribution of velocity and concentration inside pore structure (Kn0=0.1) |
由图 4(a)可知,随着消碳反应进行,整体流动阻力减小,导致整体流动速度升高。图 4(b)给出了入口处径向速度分布。由图 4(b)可以观察到努森层作用下的速度滑移现象。随着时间的推移,孔径增大导致滑移速度不断减小,这说明消碳过程削弱了气体稀薄效应。图 4(c)给出了生成物浓度的瞬时变化。由图 4(c)可知,随着反应的进行,生成物浓度沿轴向逐渐上升。但随着时间推移,生成物浓度上升的速率反而有所降低。这主要归因于孔隙的变宽削弱了气体稀薄效应,消碳反应速率也随之下降。
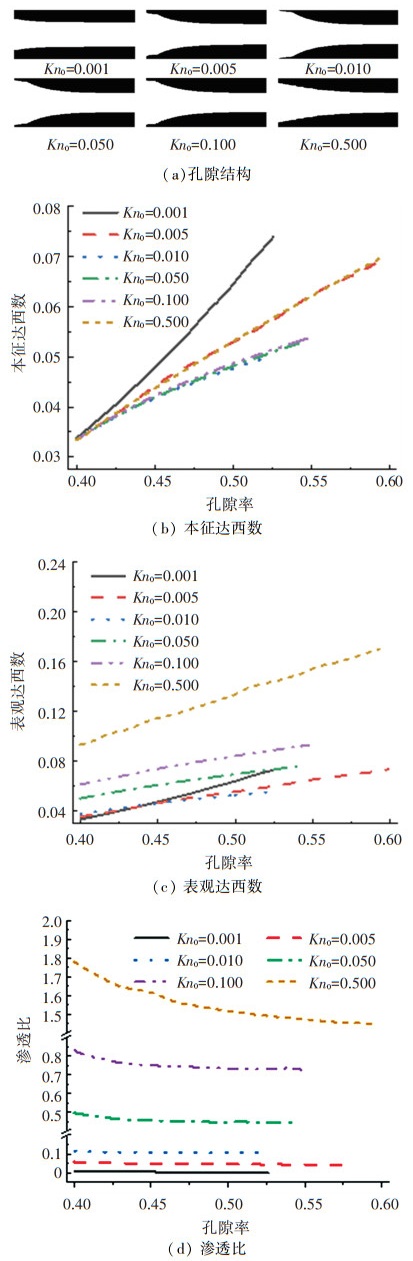
2.2 初始努森数的影响用初始努森数Kn0表征孔径大小,分析其对孔隙结构演变和主相气体输运机制的影响。孔隙结构随不同初始努森数的变化如图 5(a)所示。由图 5(a)可知,当初始努森数<0.01时。初始努森数的增大导致入口处消碳反应更加显著,孔隙结构更加不均匀。这归因于气体高稀薄效应下,努森扩散对主相气体输运的贡献愈发重要,强化了局部传质速率。当初始努森数>0.01时,孔隙局部变宽,削弱了气体稀薄效应的影响,抑制了上述气体高稀薄效应下消碳反应的入口效应。上述分析表明,“大孔”和“小孔”内均匀分布的积碳,更容易均匀地消除,而“中孔”内均匀分布的积碳,受到入口效应的影响更加显著。因此,对不同孔径的孔隙结构应采用对应的消碳方式,以提高消碳效率。引入本征达西数Dain、表观达西数Daapp和渗透比RKn来评价主相气体输运特性变化。将表征黏性流的本征渗透率κin采用孔径Dp的平方无量纲化得到本征达西数,将表征气体主相总输运(即黏性流动和努森扩散之和)的表观渗透率κapp采用孔径的平方无量纲化得到表观达西数,将努森扩散等价的渗透率κKn和本征渗透率κin之比定义为渗透比,表达式分别如下:
|
图 5 不同初始努森数下流动特征参数的变化 Fig. 5 Effect of initial Knudsen number on flow characteristic parameters |
| $ \begin{aligned} & D a_{\text {in }}=\frac{\kappa_{\text {in }}}{D_{\mathrm{p}}^2}, \\ & D a_{\text {ap }}=\frac{\kappa_{\text {app }}}{D_{\mathrm{p}}^2}, \\ & D a_{\kappa n}=\frac{\kappa_{K n}}{\kappa_{\mathrm{in}}} \end{aligned} $ | (14) |
由图 5(b)可知,随着消碳反应进行,黏性流动在不同的初始努森数下均大大增强,本征达西数随孔隙率增大而不断升高。对应孔隙结构的变化,随着初始努森数的增大,本征达西数升高的速率先减小后增大。从图 5(c)可知,初始阶段的表观达西数随着初始努森数的增大而增大。这归因于较高的初始努森数意味着努森扩散对主相气体输运的贡献更加显著。随着消碳反应进行,黏性流动和努森扩散均得到增强,因此表观达西数的升高速率明显快于本征达西数。类似于本征达西数,表观达西数的升高速率随初始努森数的变化同样存在临界阈值,表明“中孔”内积碳消除引起的传质速率提高受到一定的限制。由图 5(d)可知,不同初始努森数条件下渗透比均随着孔隙率的增大而减小。随着初始努森数的增大,渗透比的下降速率也显著提高,表明气体高稀薄效应下消碳反应导致孔隙结构演变对黏性流动的促进作用比努森扩散更加显著。
2.3 达姆科勒数的影响孔隙结构演变特性与反应特性密切相关,达姆科勒数对消碳过程中孔隙结构演变机制和气体输运机制的影响见图 6。图 6(a)为同一孔隙率下,孔隙结构随不同达姆科勒数的变化情况。由图 6(a)可知,当达姆科勒数<0.010时,积碳消除过程中积碳分布较为均匀;当达姆科勒数进一步增大,尤其是达姆科勒数为1.000时,入口效应将十分显著。表明当反应物具有高反应速率或低扩散速率时,孔隙深处的积碳更加不容易消除。图 6(b)给出了不同达姆科勒数条件下,渗透比随着孔隙率的变化。由图 6(b)可知,随着达姆科勒数的增大,渗透比下降的速率也明显加快,并且更早达到稳定状态。表明高反应速率条件下,消碳反应导致孔隙结构演变对黏性流动的促进作用比努森扩散更加显著。

|
图 6 达姆科勒数对孔隙结构和流动特征参数的影响 Fig. 6 Effect of Damköhler number on pore structure and flow characteristic parameters |
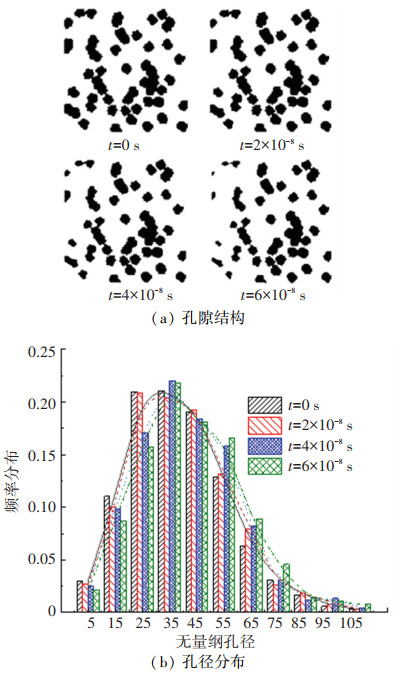
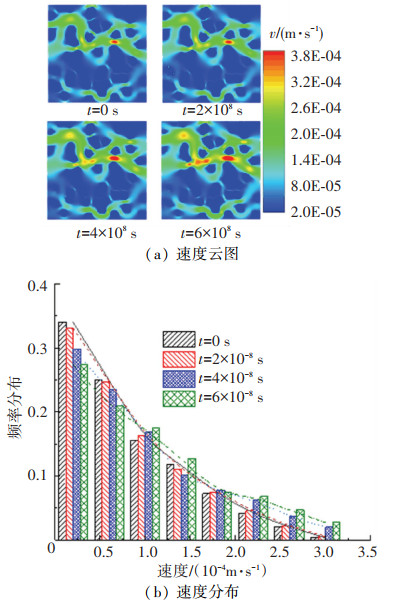
图 7给出了复杂孔隙结构特性的瞬时变化。由图 7可知,随着消碳反应进行,可以观察到孔隙的变宽和合并,并且入口附近积碳首先消除,这与单孔相似。但在积碳消除过程中,孔径始终呈钟形分布。随着孔隙变宽和合并,导致孔径频率分布的峰右移和降低,这表明孔径分布变得更加均匀。复杂孔隙结构的演变也引起了流动特性的变化。从图 8可知,孔隙变宽和合并,大大减小了复杂孔隙内的气体流动阻力,导致流速升高。速度的频率分布也随之发生变化,低速度的频率降低而高速度的频率升高。
|
图 7 复杂孔隙结构特性的瞬时变化 Fig. 7 Transient variation of structure characteristics inside complex pore |
|
图 8 复杂孔隙速度特性的瞬时变化 Fig. 8 Transient variation of velocity characteristics inside complex pore |
基于格子玻尔兹曼方法以及固相更新方法,构建了消碳反应的孔隙尺度模型,开展了孔隙尺度消碳行为的数值模拟,主要结论如下:
1) 简单孔隙内积碳均匀分布条件下,入口附近积碳首先消除,形成沿轴向随时间延长变化幅度明显的孔隙结构。消碳过程减弱了气体稀薄效应,降低了传质速率和反应速率。
2)“大孔”和“小孔”简单孔隙内均匀分布的积碳,更容易均匀地消除,而“中孔”内积碳,入口效应更加显著,消碳反应引起的传质速率升高也受到了抑制。
3) 气体高稀薄效应和高反应速率条件下,消碳反应导致简单孔隙结构演变对黏性流动的促进作用比努森扩散更加显著。
4) 对于复杂的随机孔隙结构,同样存在入口效应,并且积碳消除会导致孔径频率分布峰值的右移和下降。
| [1] |
PHAM M D, PHAM X H, SIANG T J, et al. Review on the cataly-tic tri-reforming of methane: Part I: Impact of operating conditions, catalyst deactivation and regeneration[J]. Applied Catalysis A: General, 2021, 621: 118202. DOI:10.1016/j.apcata.2021.118202 |
| [2] |
YE G H, WANG H Z, DUAN X Z, et al. Pore network modeling of catalyst deactivation by coking, from single site to particle, during propane dehydrogenation[J]. AIChE Journal, 2019, 65(1): 140. DOI:10.1002/aic.16410 |
| [3] |
ZHOU J B, ZHAO J P, ZHANG J L, et al. Regeneration of catalysts deactivated by coke deposition: A review[J]. Chinese Journal of Catalysis, 2020, 41(7): 1048. DOI:10.1016/S1872-2067(20)63552-5 |
| [4] |
YANG Z J, ZHANG Y M, OLORUNTOBA A, et al. MP-PIC simulation of the effects of spent catalyst distribution and horizontal baffle in an industrial FCC regenerator. Part I: Effects on hydrodynamics[J]. Chemical Engineering Journal, 2021, 412: 128634. DOI:10.1016/j.cej.2021.128634 |
| [5] |
YANG Z J, ZHANG Y M, LIU T B, et al. MP-PIC simulation of the effects of spent catalyst distribution and horizontal baffle in an industrial FCC regenerator. Part Ⅱ: Effects on regenerator performance[J]. Chemical Engineering Journal, 2021, 421: 129694. DOI:10.1016/j.cej.2021.129694 |
| [6] |
TAKENAKA S, OTSUKA K. Specific reactivity of the carbon filaments formed by decomposition of methane over Ni/SiO2: gasification with CO2[J]. Chemistry Letters, 2001, 30(3): 218. DOI:10.1246/cl.2001.218 |
| [7] |
KERN C, JESS A. Regeneration of coked catalysts: modelling and verification of coke burn-off in single particles and fixed bed reactors[J]. Chemical Engineering Science, 2005, 60(15): 4249. DOI:10.1016/j.ces.2005.01.024 |
| [8] |
ZHANG X P, SUI Z J, ZHOU X G, et al. Modeling and simulation of coke combustion regeneration for coked Cr2O3/Al2O3 propane dehydrogenation catalyst[J]. Chinese Journal of Chemical Engineering, 2010, 18(4): 618. DOI:10.1016/S1004-9541(10)60265-0 |
| [9] |
RESHETNIKOV S I, PETROV R V, ZAZHIGALOV S V, et al. Mathematical modeling of regeneration of coked Cr-Mg catalyst in fixed bed reactors[J]. Chemical Engineering Journal, 2020, 380(5): 122374. DOI:10.1016/j.cej.2019.122374 |
| [10] |
DENG H, HOU Y, CHEN W, et al. Lattice Boltzmann simulation of oxygen diffusion and electrochemical reaction inside catalyst layer of PEM fuel cells[J]. International Journal of Heat and Mass Transfer, 2019, 143: 118538. DOI:10.1016/j.ijheatmasstransfer.2019.118538 |
| [11] |
WANG S, YANG X S, HE Y R. Pore-scale study of reactive transfer process involving coke deposition via lattice Boltzmann method[J]. AIChE Journal, 2022, 68(3): e17478-1. DOI:10.1002/aic.17478 |
| [12] |
OLIVEIRA E L G, GRANDE C A, RODRIGUES A E. Methane steam reforming in large pore catalyst[J]. Chemical Engineering Science, 2010, 65(5): 1539. DOI:10.1016/j.ces.2009.10.018 |
| [13] |
GUO Z L, ZHENG C G, SHI B C. Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2008, 77(3): 036707. DOI:10.1103/PhysRevE.77.036707 |
| [14] |
MICHALIS V K, KALARAKIS A N, SKOURAS E D, et al. Rarefaction effects on gas viscosity in the Knudsen transition regime[J]. Microfluidics and Nanofluidics, 2010, 9(4/5): 847. DOI:10.1007/s10404-010-0606-3 |
| [15] |
ZOU Q S, HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591. DOI:10.1063/1.869307 |
| [16] |
SUCCI S. Mesoscopic modeling of slip motion at fluid-solid interfaces with heterogeneous catalysis[J]. Physical Review Letters, 2002, 89(6): 064502. DOI:10.1103/PhysRevLett.89.064502 |
| [17] |
LI Q, HE Y L, TANG G H, et al. Lattice Boltzmann modeling of microchannel flows in the transition flow regime[J]. Microfluidics and Nanofluidics, 2011, 10(3): 607. DOI:10.1007/s10404-010-0693-1 |
| [18] |
赵建平, 赵银峰, 叶茂, 等. MTO积炭催化剂在O2/CO2气氛中的再生动力学[J]. 化学反应工程与工艺, 2019, 35(5): 410. ZHAO Jianping, ZHAO Yinfeng, YE Mao, et al. Regeneration kinetic study of coked MTO catalyst in O2 & CO2[J]. Chemical Reaction Engineering and Technology, 2019, 35(5): 410. DOI:10.11730/j.issn.1001-7631.2019.05.0410.06 |
| [19] |
KANG Q J, CHEN L, VALOCCHI A J, et al. Pore-scale study of dissolution-induced changes in permeability and porosity of porous media[J]. Journal of Hydrology, 2014, 517: 1049. DOI:10.1016/j.jhydrol.2014.06.045 |
 2023, Vol. 55
2023, Vol. 55


