2. 大连理工大学 汽车工程学院,辽宁 大连 116024
2. School of Automotive Engineering, Dalian University of Technology, Dalian 116024, Liaoning, China
驱动系统的成本和效率一直是制约燃料电池汽车大规模推广应用的关键问题。燃料电池汽车驱动系统通常采用电-电混合驱动组成形式[1],即由燃料电池提供车辆运行所需的平均功率,而由动力电池或超级电容等储能部件提供动态辅助功率,以改善车辆的动态特性[2-3],其拓扑方案中通常包含DC/DC变换器[4]。由于燃料电池的所有能量均经过DC/DC转换,故要求DC/DC变换器的功率及体积较大,同时带来制造成本高和功率损失等问题[5]。为避免DC/DC环节带给燃料电池汽车驱动系统成本及效率方面的压力,国内外研究者提出双电源直接为电机供电的驱动系统方案[6-7],由于该方案中双电源共同为一套定子绕组供电,使得双电源之间的能量传输与电机转矩控制相互影响,且该方案中双逆变器协同控制时存在零序电流与共模电压问题。为了提高双逆变器的协同控制性能,Zhong等[8]采用三电平逆变器,但增加的功率器件增加了系统成本并加大了控制难度。
本文所研究的燃料电池汽车双源电机驱动系统采用双电源直接为电机供电的驱动方案,但双源电机定子上有两套绕组,并分别由燃料电池、动力电池独立供电,通过对两套绕组内电流的控制,可以使双源电机在多种模式下工作,并能够在复杂工况下实现燃料电池汽车双电源之间的能量传输及对应转矩的独立控制。首先建立燃料电池汽车双源电机驱动系统模型;然后针对燃料电池汽车双电源之间的能量传输及输出转矩的独立控制问题,讨论双源电机的多种工作模式,并就双源电机两套绕组之间存在的电压耦合现象提出解耦控制策略;最后,在试验台架上验证双源电机及其控制系统在燃料电池汽车不同工况下的输出性能。
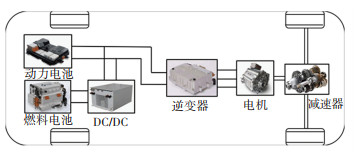
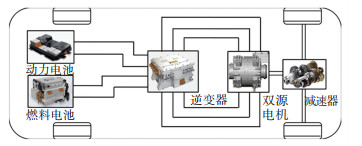
1 驱动系统模型 1.1 双源电机模型作为双源驱动系统的核心部件,双源电机承担着车辆动力需求及燃料电池与动力电池之间能量交换的任务。因为永磁同步电机具有高效率、高可靠性的特点[9-10],所以将双源电机设计为定子上有两套独立绕组的永磁同步电机。传统燃料电池汽车驱动系统通过DC/DC将燃料电池与动力电池并联以驱动电机及其控制器,如图 1所示。与三相永磁同步电机不同,双源电机的定子上有两套中性点相互隔离的Y型绕组,并通过逆变器分别由燃料电池、动力电池供电,如图 2所示。由于两套定子绕组共用1个转子,双源电机驱动系统相比于采用两个独立电机的驱动系统结构更为紧凑,可以节省车内可用空间,并降低电机制造成本。
|
图 1 燃料电池汽车DC/DC驱动系统 Fig. 1 DC/DC drive system of fuel cell vehicles |
|
图 2 燃料电池汽车双源电机驱动系统 Fig. 2 Dual-power source electric motor drive system of fuel cell vehicles |
双源电机的定子电压方程[11]为
| $ \left\{\begin{array}{l} v_{d 1}=R_{\mathrm{s}} i_{d 1}-\omega \psi_{q 1}+\mathrm{d} \psi_{d 1} / \mathrm{d} t \\ v_{q 1}=R_{\mathrm{s}} i_{q 1}+\omega \psi_{d 1}+\mathrm{d} \psi_{q 1} / \mathrm{d} t \\ v_{d 2}=R_{\mathrm{s}} i_{d 2}-\omega \psi_{q 2}+\mathrm{d} \psi_{d 2} / \mathrm{d} t \\ v_{q 2}=R_{\mathrm{s}} i_{q 2}+\omega \psi_{d 2}+\mathrm{d} \psi_{q 2} / \mathrm{d} t \end{array}\right. $ | (1) |
式中:vd1、vd2、vq1、vq2分别为燃料电池绕组、动力电池绕组对应的d、q轴电压;id1、id2、iq1、iq2分别为两套绕组的d、q轴等效电流;ψd1、ψd2、ψq1、ψq2分别为两套绕组的d、q轴等效磁链;Rs为绕组的等效电阻,ω为电机电角速度。
双源电机的磁链方程可表示为
| $ \left\{\begin{array}{l} \psi_{d 1}=L_{d 1} i_{d 1}+M_{d 12} i_{d 2}+\psi_{\mathrm{f}} \\ \psi_{q 1}=L_{q 1} i_{q 1}+M_{q 12} i_{q 2} \\ \psi_{d 2}=M_{d 21} i_{d 1}+L_{d 2} i_{d 2}+\psi_{\mathrm{f}} \\ \psi_{q 2}=M_{q 21} i_{q 1}+L_{q 2} i_{q 2} \end{array}\right. $ | (2) |
式中:Ld1、Ld2、Lq1、Lq2分别为燃料电池绕组、动力电池绕组对应的d、q轴等效自感;Md12 = Md21和Mq12 = Mq21分别为两套绕组之间的d、q轴等效互感;ψf为双源电机转子磁链。
双源电机的转矩方程为
| $ T=1.5 p_0\left(\psi_{d 1} i_{q 1}-\psi_{q 1} i_{d 1}+\psi_{d 2} i_{q 2}-\psi_{q 2} i_{d 2}\right) $ | (3) |
式中:T为双源电机的电磁转矩,p0为极对数。
当采用id=0策略对双源电机进行控制时,id1=id2=0,此时,双源电机的转矩方程为
| $ T=1.5 p_0 \psi_f\left(i_{q 1}+i_{q 2}\right)=T_1+T_2 $ | (4) |
式中,T1、T2分别为双源电机燃料电池绕组、动力电池绕组中的电流与电机转子磁链相互作用产生的转矩。
双源电机的输出功率为
| $ \left\{\begin{array}{l} P=1.5 \omega p_0 \psi_{\mathrm{f}}\left(i_{q 1}+i_{q 2}\right) \\ P_1=1.5 \omega p_0 \psi_{\mathrm{f}} i_{q 1} \\ P_2=1.5 \omega p_0 \psi_{\mathrm{f}} i_{q 2} \end{array}\right. $ | (5) |
式中:P为双源电机的输出功率;P1、P2分别为燃料电池、动力电池对双源电机的输出功率。
由式(4)和式(5)可以看出,采用零直轴电流控制策略令id = 0,通过对双源电机电压方程中q轴电流iq1、iq2的控制,可以实现对燃料电池及动力电池的转矩分配及输出功率调节。
1.2 燃料电池模型燃料电池工作在封闭、复杂环境下,是一个具有多回路、多相流电化学反应的非线性系统[12]。质子交换膜燃料电池模型[13]为
| $ V_{\mathrm{FC}}=E_{\mathrm{oc}}-N A \ln \left(\frac{i_{\mathrm{FC}}}{i_0}\right) \frac{1}{s T_{\mathrm{d}} / 3+1}-R_{\mathrm{ohm}} i_{\mathrm{FC}} $ | (6) |
式中:VFC、iFC分别为燃料电池的输出电压、输出电流;Eoc、N分别为燃料电池的开路电压、单体电池数;Td、Rohm、i0分别为燃料电池的响应时间、内阻及交换电流;A为Tafel斜率。
式(6)代表燃料电池在给定温度和压力下的工作状态,模型中的参数可根据制造商提供的极化曲线确定。
1.3 动力电池模型车辆在运行过程中,存在频繁的启动、加速、爬坡等工况,要求驱动电机具有快速的输出转矩响应能力。由于双源电机的输出转矩为燃料电池及动力电池对应的转矩之和,而燃料电池输出特性偏“软”,动态响应性能欠佳[14],故燃料电池无法提供车辆瞬态负荷变化的功率。为了提高驱动系统的动态响应能力,发挥动力电池高功率密度的特点,由动力电池提供车辆所需的瞬时功率[15],而利用燃料电池高能量密度的特点使之提供车辆所需的平均功率。即动力电池对车辆需求功率起到“削峰填谷”的调节作用[16],从而减少燃料电池启停及变载次数,避免燃料电池输出电流的突变,延长燃料电池的使用寿命。
动力电池的等效内阻模型为
| $ C \mathrm{~d} V_c / \mathrm{d} t=i_{\mathrm{B}}-V_c / R_2 $ | (7) |
| $ V_{\mathrm{B}}=V_{\mathrm{oc}}-V_c-i_{\mathrm{B}} R_1 $ | (8) |
式中:R1、R2为动力电池等效内阻,Vc为电容C的端电压,VB、iB分别为动力电池的端电压及输出电流,Voc为动力电池开路电压。
2 双源电机驱动系统的控制 2.1 双源电机多工作模式为了满足不同道路条件下车辆对动力的需求,并最大程度地延长电源的使用寿命,双源电机需根据燃料电池、动力电池的状态及车辆的需求功率,运行在多种工作模式下,并在复杂工况下进行不同工作模式之间的切换。
双源电机的燃料电池绕组、动力电池绕组分别在逆变器控制下通入三相对称交流电,此时双源电机的输出转矩T等于燃料电池绕组、动力电池绕组内电流与电机转子磁场相互作用所产生的转矩T1和T2之和,即T = T1 + T2,故双源电机在合理的控制下可以看作为两台独立工作的电机。根据燃料电池、动力电池的电流方向及双源电机两套定子绕组与转子相互作用产生的转矩不同,双源电机存在以下几种工作模式:Mode A,燃料电池和动力电池共同供电电机来驱动车辆运动,T1、T2均为正数;Mode B,燃料电池单独供电电机来驱动车辆运动,T1为正、T2为零;Mode C,燃料电池单独供电电机来驱动车辆运动,同时燃料电池向动力电池充电,T1为正、T2为负且T为正;Mode D,动力电池单独供电电机来驱动车辆运动,T1为零、T2为正;Mode E,车辆处于制动能量回收模式,T1为零、T2为负。双源电机各种工作模式下的电流流向及转矩情况如图 3所示。

|
图 3 双源电机的工作模式 Fig. 3 Operating modes of dual-power source electric motor |
由式(2)可知,燃料电池绕组磁链ψd1、ψq1不仅受到id1、iq1影响,还受到动力电池绕组电流id2、iq2影响;同理ψd2、ψq2亦受到id1、iq1影响。故结合式(1)可知,双源电机两套绕组之间存在电压耦合,这使得对燃料电池绕组内的电流id1、iq1进行控制时,动力电池绕组的电压vd2、vq2也会受到影响,此时动力电池绕组产生的电流id2、iq2亦会对燃料电池绕组电压vd1、vq1造成影响,反之亦然。此外,燃料电池(动力电池)绕组内d、q轴之间也存在电压耦合。耦合现象的存在为双源电机两套绕组内电流的独立控制带来困难,使得双源电机的动态性能变差。同时,动力电池转矩T2发生变化时,燃料电池转矩T1及功率P1不得不相应改变,这恶化了燃料电池的工作条件,不利于燃料电池的稳定工作。为了实现两套绕组内电流的独立控制,进而实现燃料电池与动力电池对应转矩的独立控制,本文采用前馈控制技术对耦合电压进行补偿,令
| $ \left\{\begin{array}{l} v_{d 1 \mathrm{de}}=v_{d 1}-v_{d 1 \mathrm{fw}} \\ v_{q 1 \mathrm{de}}=v_{q 1}-v_{q 1 \mathrm{fw}} \\ v_{d 2 \mathrm{de}}=v_{d 2}-v_{d 2 \mathrm{fw}} \\ v_{q 2 \mathrm{de}}=v_{q 2}-v_{q 2 \mathrm{fw}} \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} v_{d 1 \mathrm{fw}}=\omega L_{q 1} i_{q 1}+\omega M_{q 12} i_{q 2}-M_{d 12} \mathrm{~d} i_{d 2} / \mathrm{d} t \\ v_{q 1 \mathrm{fw}}=-\omega\left(L_{d 1} i_{d 1}+M_{d 12} i_{d 2}+\psi_{\mathrm{f}}\right)-M_{q 12} \mathrm{~d} i_{q 2} / \mathrm{d} t \\ v_{d 2 \mathrm{fw}}=\omega M_{q 21} i_{q 1}+\omega L_{q 2} i_{q 2}-M_{d 21} \mathrm{~d} i_{d 1} / \mathrm{d} t \\ v_{q 2 \mathrm{fw}}=-\omega\left(M_{d 21} i_{d 1}+L_{d 2} i_{d 2}+\psi_{\mathrm{f}}\right)-M_{q 21} \mathrm{~d} i_{q 1} / \mathrm{d} t \end{array}\right. $ | (10) |
式中:vd1de、vq1de、vd2de、vq2de为双源电机各个轴上经过前馈补偿后的解耦电压分量,vd1fw、vq1fw、vd2fw、vq2fw为对应前馈电压补偿量。则式(1)可写为
| $ \left\{\begin{array}{l} v_{d 1 \mathrm{de}}=R_{\mathrm{s}} i_{d 1}+L_{d 1} \mathrm{~d} i_{d 1} / \mathrm{d} t \\ v_{q 1 \mathrm{de}}=R_{\mathrm{s}} i_{q 1}+L_{q 1} \mathrm{~d} i_{q 1} / \mathrm{d} t \\ v_{d 2 \mathrm{de}}=R_{\mathrm{s}} i_{d 2}+L_{d 2} \mathrm{~d} i_{d 2} / \mathrm{d} t \\ v_{q 2 \mathrm{de}}=R_{\mathrm{s}} i_{q 2}+L_{q 2} \mathrm{~d} i_{q 2} / \mathrm{d} t \end{array}\right. $ | (11) |
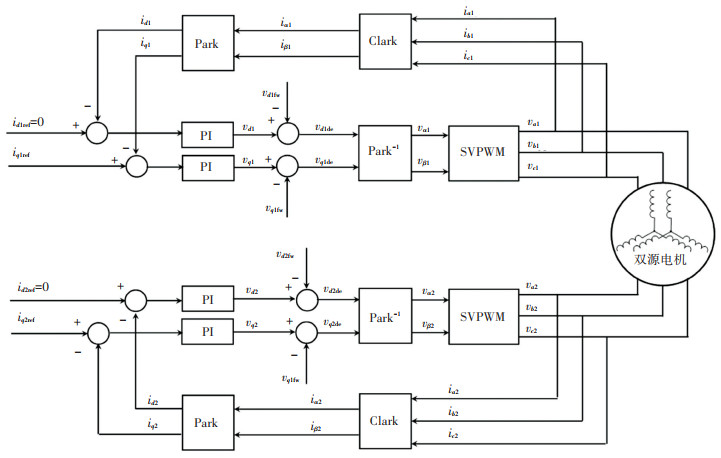
由式(11)可以看出,前馈控制技术将电压耦合项vd1fw、vq1fw、vd2fw、vq2fw从对应电压分量中去掉,使得解耦电压分量vd1de、vq1de、vd2de、vq2de与对应电流分量id1、iq1、id2、iq2为一阶关系,故经过前馈解耦后的双源电机各轴电压方程可以等效为一阶系统,可采用PI控制器对各轴电流进行反馈调节。双源电机驱动系统的控制框图如图 4所示。
|
图 4 双源电机驱动系统的控制框图 Fig. 4 Control diagram of dual-power source electric motor drive system |
在Simulink仿真环境中对图 4中双源电机驱动系统进行仿真,如图 5所示(驱动系统仿真模型参数见表 1)。从图 5可以看出,在未进行前馈补偿控制之前,双源电机d1、q1、d2、q2轴电流存在明显的耦合效应。iq1的脉冲变化会使得id1波动,d2、q2轴电流id2、iq2出现电流尖峰,这对实现燃料电池及动力电池转矩的独立控制及功率分配极为不利。与解耦前两套绕组对应的d、q轴的电流波形相比,在解耦后的控制系统中iq1的脉冲变化对于id1、id2和iq2没有影响,故通过上述前馈补偿实现了对双源电机两套绕组中d、q轴电流的独立控制。

|
图 5 解耦前后两套绕组d-q轴电流仿真波形 Fig. 5 Simulation of d-q currents in two windings before and after decoupling |
| 表 1 双源电机驱动系统仿真参数 Tab. 1 Simulation parameters of dual-power source electric motor drive system |
为了对所研究的燃料电池汽车驱动系统进行性能验证,搭建了双源电机驱动系统模拟试验台架。试验台架系统由加拿大D & V公司的高性能测功机及其上位机、燃料电池模拟器、动力电池、双源电机、双源电机控制器、功率分析仪、维克多VX1060高速测量标定系统及其上位机CANape软件组成,如图 6所示。其中燃料电池模拟器的输出可以根据需求进行编程控制,用以模拟燃料电池的输出特性。

|
图 6 双源电机驱动系统模拟试验台架 Fig. 6 Simulation bench for test of dual-power source electric motor drive system |
试验台架各主要部件的参数见表 2。试验时,通过上位机给双源电机控制器发送转矩指令来模拟车辆的启动、加速、减速、制动能量回收等工况。
| 表 2 双源电机驱动系统模拟试验台架参数 Tab. 2 Parameters of simulation bench for test of dual-power source electric motor drive system |
图 7为双源电机在实验室设计工况下的转矩输出及对应定子绕组q轴电流。T为双源电机需求转矩指令值;Tt为双源电机实际输出转矩;T1、T2分别为双源电机控制器接收到的燃料电池及动力电池转矩指令值,且T = T1 + T2;iq1、iq2分别为燃料电池绕组及动力电池绕组的q轴电流。

|
图 7 实验室设计工况下双源电机输出转矩及对应定子q轴电流 Fig. 7 Output torque and corresponding stator q-axis current of the dual-power source electric motor under laboratory-designed operating condition |
在0~1 s,模拟车辆处于驻车状态,此时双源电机的输出转矩Tt为0。在1~2 s,车辆处于起步行驶状态,双源电机工作在Mode D。在2~10 s,车辆起步运行后加速行驶,双源电机输出转矩Tt增大,在此过程中燃料电池加载,动力电池随着燃料电池输出电流的增加逐步退出驱动,双源电机在Mode A下工作。在10~11 s,车辆进入平稳行驶阶段,双源电机输出转矩Tt不变,双源电机工作在Mode B。在11~12 s,车辆进入上坡路段,双源电机输出转矩Tt也相应增加;为了维持燃料电池输出平稳,由动力电池满足突然增加的功率需求,此时双源电机工作在Mode A,动力电池绕阻电流iq2随着其转矩指令T2的增加而增加。在12~13 s,车辆进入功率需求较小的下坡路段,双源电机输出转矩Tt减小,燃料电池输出仍维持平稳,由动力电池响应突然减小的功率需求,双源电机进入Mode C。在13~17 s,车辆进入低速行驶阶段,燃料电池进入降载阶段,燃料电池绕组q轴电流iq1逐渐减小至0;动力电池对应转矩T2由负值逐渐增加以维持输出转矩Tt不变,直至双源电机的输出转矩完全由动力电池提供,双源电机的工作状态由Mode C过渡到Mode A。在17~18 s,车辆减速并准备进入驻车状态,此时双源电机进入制动能量回收状态,即Mode E,动力电池转矩由表示制动的负值逐渐到0。
当双源电机运行在Mode A~E时,双源电机的输出转矩Tt与其需求转矩指令T基本重合,二者偏差<5%,输出转矩响应时间<100 ms。在燃料电池启动后,其对应绕组电流iq1恒定以维持燃料电池输出平稳,动力电池绕组电流iq2响应需求转矩T的瞬态变化。故双源电机驱动系统能够实现对需求转矩的快速响应,并通过多种工作模式实现燃料电池与动力电池的能量分配与传输。
由图 7可知,燃料电池转矩T1、动力电池转矩T2与对应的q轴电流波形iq1、iq2一致,验证了零直轴电流控制策略的有效性。在10~13 s,动力电池绕组电流iq2进行了阶跃变化,双源电机输出转矩Tt变化与动力电池转矩指令T2变化相同,燃料电池转矩指令T1及对应电流iq1均不变,验证了前馈补偿控制方法的有效性,消除了两套绕组间的耦合效应。所采用的控制方法实现了对双源电机燃料电池、动力电池绕组电流及对应转矩的独立控制。
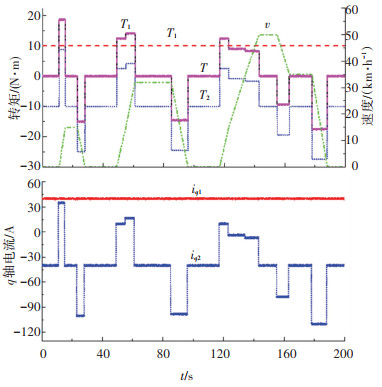
为了验证双源电机驱动系统在实际工况下的性能,根据GB/T 18386—2017 B.2.2,采用电动汽车基本市区循环试验工况进行测试。其中,基本市区循环试验工况的车速为v,对双源电机的需求转矩为T,试验结果如图 8所示。在测试过程中,双源电机的实际输出转矩Tt与其需求转矩T曲线基本重合,二者偏差<5%,输出转矩响应时间<100 ms。试验过程中,为维持燃料电池输出平稳,燃料电池转矩指令值T1保持恒定,动力电池转矩指令T2响应需求转矩T的瞬态变化;燃料电池绕组、动力电池绕组电流iq1、iq2与二者转矩指令T1、T2波形一致,在iq2响应动力电池转矩指令T2而进行阶跃变化时,iq1仍响应燃料电池转矩指令T1维持平稳输出,证明了所采用的解耦控制算法在实际工况下实现了对燃料电池、动力电池的电流及对应转矩的独立控制。
|
图 8 基本市区循环工况下双源电机输出转矩及对应定子q轴电流 Fig. 8 Output torque and corresponding stator q-axis current of the dual-power source electric motor under basic urban drive cycle |
在基本市区循环试验工况中,燃料电池绕组电流iq1维持恒定正值,动力电池绕组电流iq2为正值时,动力电池侧转矩输出为正,此时双源电机工作在Mode A,即燃料电池、动力电池共同驱动;动力电池绕组电流iq2为负值时,动力电池侧转矩输出为负,此时双源电机工作在Mode C,即燃料电池单独驱动且向动力电池充电,故双源电机驱动系统在实际工况下通过对燃料电池、动力电池绕组电流及对应转矩的独立控制,实现了双电源之间的能量分配与传输。
4 结论1) 为避免DC/DC带给燃料电池汽车驱动系统成本及效率方面的压力,实现双电源之间能量传输及转矩独立控制,研究了燃料电池汽车双源电机驱动系统,建立了双源电机模型、燃料电池模型及动力电池模型。
2) 针对燃料电池汽车在实际运行过程中的启动、加速、下坡、制动等工况给出了双源电机相应的工作模式Mode A~E。针对双源电机两套绕组中的电压耦合问题,采用前馈补偿及零直轴电流控制策略,实现了对两套绕组中电流的独立控制。
3) 搭建了燃料电池汽车双源电机驱动系统模拟试验台架,并对双源电机在不同工作模式下的转矩响应性能进行了模拟试验验证。试验结果表明,燃料电池汽车双源电机驱动系统能够满足燃料电池汽车在不同工况下的转矩需求,在实际工况下实现燃料电池与动力电池之间的能量传输及对应转矩的独立控制。
| [1] |
JIANG Hongliang, XU Liangfei, LI Jianqiu, et al. Energy management and component sizing for a fuel cell/battery/supercapacitor hybrid powertrain based on two-dimensional optimization algorithms[J]. Energy, 2019, 177: 386. DOI:10.1016/j.energy.2019.04.110 |
| [2] |
SUN Haochen, FU Zhumu, TAO Fazhan, et al. Data-driven reinforcement-learning-based hierarchical energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles[J]. Journal of Power Sources, 2020, 455: 227964. DOI:10.1016/j.jpowsour.2020.227964 |
| [3] |
LI Huan, RAVEY A, N'DIAYE A, et al. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation[J]. Energy Conversion and Management, 2019, 192: 133. DOI:10.1016/j.enconman.2019.03.090 |
| [4] |
LI Xiyun, WANG Yujie, YANG Duo, et al. Adaptive energy management strategy for fuel cell/battery hybrid vehicles using Pontryagin's minimal principle[J]. Journal of Power Sources, 2019, 440: 227105. DOI:10.1016/j.jpowsour.2019.227105 |
| [5] |
LIU Yonggang, LIU Junjun, QIN Datong, et al. Online energy management strategy of fuel cell hybrid electric vehicles based on rule learning[J]. Journal of Cleaner Production, 2020, 260: 121017. DOI:10.1016/j.jclepro.2020.121017 |
| [6] |
贾一帆. 车用双电源开绕组永磁同步电机驱动系统的控制方法研究[D]. 长春: 吉林大学, 2020 JIA Yifan. Research on control methods of open-end winding permanent magnet synchronous motor drive systems for electric vehicles[D]. Changchun: Jilin University, 2020 |
| [7] |
CHEN Min, SUN Dan. A unified space vector pulse width modulation for dual two-level inverter system[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 889. DOI:10.1109/TPEL.2016.2585223 |
| [8] |
ZHONG Liping, HU Song. Reference voltage self-equalization-based modulation strategy for open-end winding PMSM fed by dual three-level inverters with common DC bus[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 196. DOI:10.1109/JESTPE.2021.3069351 |
| [9] |
曾冲, 黄嵩, 杨永明. 永磁同步电机定子齿磁通分析与偏心故障在线诊断[J]. 哈尔滨工业大学学报, 2020, 52(3): 186. ZENG Chong, HUANG Song, YANG Yongming. Tooth flux analysis and eccentricity fault diagnosis for permanent magnet synchronous motor[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 186. DOI:10.11918/201812125 |
| [10] |
夏薇, 王凯, 张建亚, 等. 基于谐振控制器的谐波削极型永磁同步电机转矩脉动抑制策略[J]. 中国电机工程学报, 2019, 39(18): 5499. XIA Wei, WANG Kai, ZHANG Jianya, et al. Torque ripple suppression of permanent magnet synchronous motor with harmonic shaped rotors based on resonance controllers[J]. Proceedings of the CSEE, 2019, 39(18): 5499. DOI:10.13334/j.0258-8013.pcsee.181505 |
| [11] |
HE Shuai, LI Yaoheng, ZHOU Guangming, et al. Digital collaborative development of a high reliable auxiliary electric drive system for etransportation: from dual three-phase PMSM to control algorithm[J]. IEEE Access, 2020, 8: 178755. DOI:10.1109/ACCESS.2020.3027633 |
| [12] |
谢长君. 基于多模型控制的燃料电池汽车混合动力系统优化研究[D]. 武汉: 武汉理工大学, 2009 XIE Changjun. Optimization research for hybrid power system of fuel cell vehicles[D]. Wuhan: Wuhan University of Technology, 2009 |
| [13] |
CHEN Jian, XU Chenfeng, WU Chengshuai, et al. Adaptive fuzzy logic control of fuel-cell-battery hybrid systems for electric vehicles[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 292. DOI:10.1109/TⅡ.2016.2618886 |
| [14] |
ZHOU Yue, OBEID H, LAGHROUCHE S, et al. A novel second-order sliding mode control of hybrid fuel cell/super capacitors power system considering the degradation of the fuel cell[J]. Energy Conversion and Management, 2021, 229: 113766. DOI:10.1016/j.enconman.2020.113766 |
| [15] |
FU Zhumu, ZHU Longlong, TAO Fazhan, et al. Optimization based energy management strategy for fuel cell/battery/ultracapacitor hybrid vehicle considering fuel economy and fuel cell lifespan[J]. International Journal of Hydrogen Energy, 2020, 45(15): 8875. DOI:10.1016/j.ijhydene.2020.01.017 |
| [16] |
RAHMAN A, AHMAD I, MALIK A. Variable structure-based control of fuel cell-supercapacitor-battery based hybrid electric vehicle[J]. Journal of Energy Storage, 2020, 29: 101365. DOI:10.1016/j.est.2020.101365 |
 2023, Vol. 55
2023, Vol. 55


