燃油的运输及存储中极易发生泄露,从而引发火灾,导致重大的工业安全事故,火灾危害程度很大程度取决于燃油的燃烧速率。燃烧速率本质上为燃油汽化过程中的“汽化速率”,受燃油种类、油池直径、油池厚度以及温度等因素影响,并与燃油的传热和流动密切相关。燃油接收的热反馈包括热传导、热对流和热辐射。在小尺度池火中,池壁热传导对液相的传热具有显著影响[1],而在中等尺度池火中,池壁的热传导则可忽略不计,热辐射占据主导[2],热辐射可传递至燃油内部[3]。燃油的流动由浮力效应以及马兰戈尼效应共同驱使[4]。因不均匀分布的热反馈,液面存在较大的温度梯度以及表面张力梯度,导致马兰戈尼流动[5]。过去,液相流动被认为只由浮力所驱动,马兰戈尼效应一直被忽视。目前,众多关注液相区域的池火实验研究表明:当燃油处于无燃烧状态时,液相流动呈现出相对较规律的分布;当燃油处于燃烧状态时,液相流动会变得更加复杂。Farahani[5]在正辛烷池火中观察到燃油由池中心流向池壁的现象;Vali等[6-7]在甲醇池火的池边缘处观察到了一对反漩涡;Sefiane等[8]的研究表明马兰戈尼效应能够加强液相的流动以及蒸发过程。
考虑到实验测量难度,数值模拟方法是研究该问题的合适手段。在已有数值模拟文献中,大多数研究[9-10]使用经验公式确定燃烧速率。Babrauskas[2]提出的经典经验公式在计算燃烧速率时,仅需输入油池尺寸及燃料特定常数。Ditch等[11]用全局能量平衡方法得到了考虑辐射和碳烟的经验公式。然而,这类经验公式仅能获得稳态燃烧阶段的时均燃烧速率,同时由于燃烧速率受众多因素影响,经验公式难以具备广适性。计算燃烧速率的另一类方法是采用基于薄膜理论的蒸发模型,但是当前大部分研究[12-13]忽略了液相流动的影响,将燃油作为热厚固体进行处理,计算燃烧速率时仅考虑表面液体层。Sikanen等[14]通过有效的热传导系数等效模拟液相的流动和传热过程,但并不能准确还原真实的液相物理过程。Fukumoto等[15]在小尺度油池模拟中考虑了液相的流动,发现马兰戈尼效应对小尺度池火稳定阶段的燃烧速率影响较小,忽略浮力将大幅降低燃烧速率,但其未对中等尺度池火开展研究。国内相关研究大多直接将燃烧速率作为恒定输入参数,其数值通过实验测量[16-17]或经验公式[18]确定,由于湍流燃烧火焰的热反馈具有显著的瞬态性和分布不均匀性,燃烧速率同样具有瞬态性及分布不均匀性,采用恒定的燃烧速率并不能准确模拟池火燃烧过程;杨娴等[19]使用商业软件FDS模拟池火,通过蒸发模型计算燃烧速率,但其忽略了液相区域流动的影响。综上所述,针对中等尺度池火,目前尚未存在充分考虑液相传热和流动的数值模拟研究,浮力效应、马兰戈尼效应对中等尺度池火燃烧速率的影响尚需深入分析。
为准确模拟池火完整的燃烧过程,本文提出基于气液双向耦合的三维数值模型,对液相流动进行直接求解,基于“薄膜理论”方法计算燃油的燃烧速率,使用共轭传热方法求解气液两相间的热量传递。通过两种不同直径的厚层甲醇池火实验以及薄层庚烷池火实验验证提出的数值模型,并分析在不同直径、燃油种类及燃油厚度条件下,浮力效应、马兰戈尼效应对中等尺度池火的液相流动、传热以及燃烧速率的影响。
1 数学模型中等尺度池火湍流雷诺数较小[3],属于低雷诺数流动。本文基于开源CFD平台OpenFOAM,搭建气相可压缩求解器以及液相不可压缩求解器,通过交界面处的耦合边界条件实现两相间的双向耦合。
1.1 气相区域基于OpenFOAM平台扩展的FireFOAM[20]求解器对气相区域的湍流池火进行求解。该求解器使用LES方法求解经过滤波过滤的考虑浮力效应的可压缩N-S方程;通过单方程亚网格湍流模型[21]对方程组中的亚网格湍流源项进行封闭;根据扩展的涡耗散模型[4]计算湍流燃烧源项;使用扩展的基于烟点高度的层流碳烟模型[20]进行碳烟源项计算;使用基于有限容积的DOM辐射模型封闭辐射源项[22],并采用灰气体平均吸收发射系数,考虑碳烟的辐射作用,忽略散射。以上模型的详细信息见文献[20]。
1.2 液相区域基于Boussinesq近似的液相不可压缩层流控制方程如下:
| $ \nabla \cdot \boldsymbol{u}=0 $ | (1) |
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\nabla \cdot(\boldsymbol{u} \boldsymbol{u})=-\nabla p+\mu \nabla^2 \boldsymbol{u}+\left[1-\beta\left(T-T_{\text {ref }}\right)\right] \boldsymbol{g} $ | (2) |
| $ \frac{\partial T}{\partial t}+\nabla \cdot(\boldsymbol{u} T)=\alpha \nabla^2 T-\dot{m}^{\prime \prime \prime} \cdot \Delta H_{\mathrm{v}}+\frac{\partial Q_{\mathrm{dep}}}{\partial \boldsymbol{n}} \frac{1}{\rho c_p} $ | (3) |
式中:
燃烧速率依据Sikanen和Hostikka提出的“薄膜理论”的蒸发模型进行计算,计算表达式[14]为
| $ \dot{m}^{\prime \prime}=h_m \frac{p}{R_{\mathrm{f}} T_{\mathrm{g}}} \ln \left(\frac{X_{\mathrm{f}, \mathrm{g}}-1}{X_{\mathrm{f}, 1}-1}\right) $ | (4) |
式中:hm为传质系数,Rf为气体常数,Tg及Xf, g分别为气相温度以及邻近液面的第一层气相网格的气态燃油摩尔分数。Xf, l为在液面温度Ts下气态燃油处于平衡压力时的摩尔分数。
1.3.2 动量条件——考虑马兰戈尼效应的速度边界条件由于液面热通量的高度不均匀分布,液面出现温度分布梯度,导致燃油在表面张力的作用下出现对流运动。忽略气相切应力的作用,马兰戈尼对流运动的速度依赖于表面张力σ梯度:
| $ \mu \frac{\partial u}{\partial z}=\frac{\partial \sigma}{\partial T} \frac{\partial T}{\partial x} $ | (5) |
| $ \mu \frac{\partial v}{\partial z}=\frac{\partial \sigma}{\partial T} \frac{\partial T}{\partial y} $ | (6) |
式中u和v为液面x和y方向上的速度分量。竖直方向的速度分量计算表达式为
| $ w=\frac{\sum \dot{m}^{\prime \prime} A_i}{\rho \sum A_i} $ | (7) |
其中Ai为液面处单个网格的面积。使用液面竖直方向的速度分量对网格进行更新,重新分布网格点,以模拟薄层燃油的液面下降过程。气相的液面入口速度为
| $ \boldsymbol{u}_i^{\mathrm{g}}=\frac{\dot{m}_i^{\prime \prime}}{\rho A_i} \cdot \boldsymbol{n}+\boldsymbol{u}_i^{\mathrm{f}} $ | (8) |
式中:uig和uif分别为交界面上的网格i对应的气相侧、液相侧速度矢量。
1.3.3 能量条件——基于共轭传热的热边界条件| $ T_{\mathrm{f}, \mathrm{int}}=T_{\mathrm{g}, \mathrm{int}} $ | (9) |
| $ \left.k_{\mathrm{f}} \frac{\partial T_{\mathrm{f}}}{\partial \boldsymbol{n}}\right|_{\mathrm{int}}=\left.k_{\mathrm{g}} \frac{\partial T_{\mathrm{g}}}{\partial \boldsymbol{n}}\right|_{\mathrm{int}} $ | (10) |
式中:下标f, g和int分别表示燃油、气体和内部相,kf和kg分别为燃油和气相混合气体的导热系数。由于液面处雷诺数较低且存在瞬态不均匀分布的质量流量,本文对液面边界层进行直接求解。
2 问题描述甲醇和庚烷是具有代表性的醇类和碳氢类燃料,前者无碳烟生成,辐射热反馈较低,后者有碳烟生成且辐射热反馈较高。采用甲醇和庚烷实验验证提出的模型,验证数据来自0.3 m直径的厚层甲醇池火实验[23-24] (Case 1)、1.0 m直径的厚层甲醇池火实验[25] (Case 2)以及0.3 m直径的薄层庚烷池火实验[26] (Case 3)。3组实验的唇口高度分别为0.5、1.0、2.7 cm,燃烧器均置于开放空间。甲醇实验在稳定燃烧后开始采集数据,庚烷实验采集了整个阶段的瞬时数据。实验中使用细线热电偶测量气相和液相温度,通过质量传感器监测燃油质量损失速率,采用辐射计量仪测量辐射热通量。庚烷实验未对燃油进行补充,使用动网格降模拟液面的下降过程。考虑到液态甲醇和庚烷的物性随温度变化幅度较小,采用恒定的物性参数。气态组分使用OpenFOAM中的变热物性参数。实验条件和燃油物性参数分别见表 1、2。
| 表 1 实验条件 Tab. 1 Experiment conditions |
| 表 2 燃油物性 Tab. 2 Fuel properties |
3种工况的计算域分别为ϕ1.6 m×2.5 m、ϕ2.5 m×4 m和ϕ1.6 m×2.5 m的圆柱体,燃烧器均设置于计算域底部中心位置,如图 1中所示。3种工况的气相区域网格数量分别为67万、174万以及67万,液相区域网格数量分别为24万、60万以及9.4万。为准确求解气相燃油表面边界层,对所有算例中的燃烧器唇口段的网格在竖直方向进行了加密,满足Y+ < 1.5。燃烧器壁面边界设为绝热边界条件,气相区域的侧部面以及顶部面设为自由边界,允许空气流进流出。
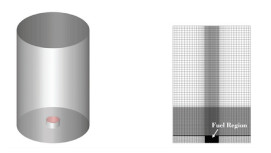
|
图 1 计算区域及计算网格 Fig. 1 Computational domain and computational grid |
设置3种网格分辨率,对Case 1进行网格敏感性研究。第2节描述的网格为中等网格,精细网格尺寸和粗糙网格尺寸约为中等网格的0.75倍和1.50倍,网格总数分别51万和321万。稳定燃烧阶段的预测瞬时燃烧速率以及气相预测时均温度如图 2。图 2中粗糙网格的预测结果偏高,而中等网格与精细网格的预测结果吻合较好,因此使用的网格分辨率满足计算要求。

|
图 2 网格敏感性研究 Fig. 2 Grid sensitivity study |
图 3为实验拍摄的可视火焰[24]与预测火焰(800 K等温面)的对比。图中预测火焰从液面边缘卷向液面中心,中心线处出现明显狭长透明火焰羽流,与实验火焰高度一致。在稳定燃烧阶段,预测热释放速率时均值为19.7 kW,预测火焰脉动频率为2.61 Hz,接近于实验测量值20.3 kW及2.64 Hz,误差为3.0%及1.1%。

|
图 3 Case 1: 预测火焰(下)与实验火焰(上)的对比 Fig. 3 Case 1: comparison between predicted flame shapes (bottom) and images from experiment (top) |
图 4为20~50 s时间段,0.3 m直径甲醇池火中高于燃烧器顶部面0.007 m处时均入射辐射热通量随径向距离变化图。由图 4可知,预测结果出现中心高、边缘低的特征,与实验值的平均误差为12.7%。图 5为20~50 s时间段,唇口上方3.3、30.3、60.3 cm处时均温度与实验时均温度的对比。由图 5可知,3种高度下,边缘位置的预测时均温度略低于实验值,但整体与实验值较为接近,整体平均误差为8.9%。以上结果证明了本文提出模型在气相区域的准确性。

|
图 4 Case 1: 预测时均辐射热通量与实验值的对比 Fig. 4 Case 1: comparison between predicted time-averaged radiative heat flux and measured values |
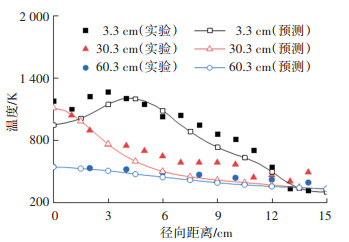
|
图 5 Case 1: 预测气相时均温度与实验值的对比 Fig. 5 Case 1: comparison between predicted gas phase time-averaged temperatures and measured values |
图 6为不同情况下的预测液面最大流速以及液相平均流速。图 6中只考虑浮力效应的液面、液相预测流速远低于另外两条曲线,前者峰值是后两者的34.3%,这表明在该工况的前期阶段下,浮力效应对液相流动的贡献较低,而马兰戈尼效应有效促进了燃油表面及内部流动。随着时间推移,液面温度梯度减小,只考虑马兰戈尼效应情况下,预测流速均降至0,而浮力效应的影响贯穿整个燃烧过程,流速在稳定燃烧后仍保持一较低数值。
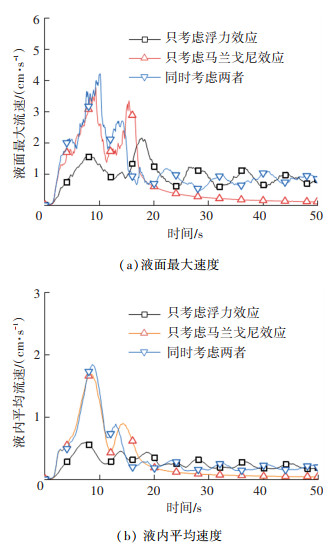
|
图 6 Case 1: 预测液相速度 Fig. 6 Case 1: predicted liquid phase velocities |
图 7为10 s时4种情况下液面温度在径向方向上的分布情况。在无流动情况下,液面温度受热反馈的影响,分布极其不均匀,最大值与最小值相差9.7%;只考虑浮力效应情况下,由于存在一定的流向池中心的速度,液面中心位置温度为326.3 K,高于无流动情况的307.0 K;只考虑马兰戈尼效应时,张力梯度的存在致使温度较高区域流向温度较低处,液面温度分布较为均匀,其最大值与最小值相差2.9%,相较于无流动情形降低了70.1%;同时考虑浮力效应和马兰戈尼效应时,其液面温度分布综合了浮力效应和马兰戈尼效应的共同影响,温度最大值与最小值仅相差3.4 K。结果表明:发展阶段,马兰戈尼效应加强了液面横向传热,使得液面温度分布更为均匀;忽略马兰戈尼效应将导致预测液面温度过高。

|
图 7 Case 1: 10 s时预测液面温度 Fig. 7 Case 1: predicted liquid surface temperatures at 10 s |
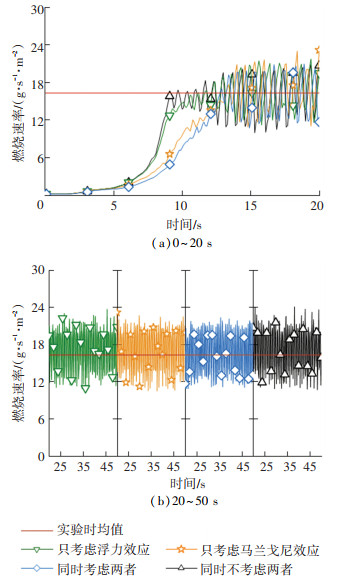
由于实验未测量瞬时燃烧速率,采用预测瞬时燃烧速率与实验时均值进行对比,见图 8。10~15 s时间段,无流动情况下瞬时燃烧速率快速上升,最早达到稳定燃烧;考虑液相流动时,瞬时燃烧速率的上升速率明显放缓,相比于无流动情况降低55%。当池火达到稳定燃烧阶段后,4种情况下的瞬时燃烧速率较为接近。考虑液相流动的预测瞬时燃烧速率时均值为12.91 g/(s·m2),相比于实验值,误差为1.5%。

|
图 8 Case 1: 预测瞬时燃烧速率与实验时均值的对比 Fig. 8 Case 1: comparison between predicted instantaneous mass burning rates and measured values |
图 9为20~50 s时均燃烧速率在径向方向上的分布图。由于稳定燃烧阶段温度梯度减小,马兰戈尼效应和浮力效应减弱,其对流动和传热的影响降低,因此4种计算条件下的时均燃烧速率分布较为接近。当无流动时,燃烧速率最大值出现在距中心位置10 cm处,而中心位置较低;考虑浮力效应后,池边缘的涡流使燃烧速率在局部位置略有上升;由于温度梯度的存在, 考虑马兰戈尼效应时,距中心位置10 cm处的燃烧速率明显上升,其原因为马兰戈尼效应使得该处热量传递加快,其温度上升更快,导致局部燃烧速率更大。预测时均燃烧速率的分布趋势与两组实验值均存在一定差异,其原因为:为了测量局部燃烧速率,实验使用了隔板将油池分隔成多个环形形状,影响燃油的流动和传热,进而影响了燃烧速率的分布。Hamins与Aktia的分布趋势存在较大差异,证明了此观点。

|
图 9 Case 1: 预测时均燃烧速率与实验值的对比 Fig. 9 Case 1: comparison between predicted time-averaged mass burning rates and measured values |
图 10为10 s时燃油垂直中截面流线图。在液面处,不均匀分布的温度产生表面张力,具有较高表面张力的区域会将流体拉向自身,引起液面流动;在液内区域,上下温差产生浮力,引起液内流动。在两种流动的共同作用下,液内出现如图 10中所示的漩涡,其与Vali[6]实验观察到的反旋涡较相似。

|
图 10 Case 1: 液相中截面流动图 Fig. 10 Case 1: predicted streamline at middle plane |
1.0 m直径的厚层甲醇池火达到稳定燃烧后,火焰预测脉动频率为1.51 Hz,接近于经验值1.50 Hz。图 11为预测瞬时燃烧速率和实验时均燃烧速率的对比。在池火发展阶段,仅考虑马兰戈尼效应与同时考虑浮力效应和马兰戈尼效应的燃烧速率较为接近,同时仅考虑浮力效应的结果与无流动情形的结果高度吻合,表明该阶段浮力效应贡献较低。相比于Case 1,当不考虑马兰戈尼效应时,燃烧速率上升得更快。可推断:在池火的发展阶段,随着池火直径的增加,浮力效应对燃烧速率的影响逐渐减弱,而马兰戈尼效应的贡献占比逐渐增加。当达到稳定燃烧阶段后,浮力效应与马兰戈尼效应对池火燃烧速率的影响较低。考虑马兰戈尼效应和浮力效应的预测瞬时燃烧速率时均值为16.8 g/(s·m2),误差为3%。
|
图 11 Case 2: 预测瞬时燃烧速率与实验时均值的对比 Fig. 11 Case 2: comparison between predicted instantaneous mass burning rates and measured time-averaged values |
采用有碳烟生成且辐射热反馈较大的庚烷进行分析验证。图 12为距离燃烧器底部10.9 mm处的液内温度随时间变化。同时不考虑两种效应时,预测温度与实验值平均误差较大,为20.1%;而仅考虑浮力时,预测温度略有升高,但依然低于实验值;考虑马兰戈尼效应后,预测温度明显上升,这表明马兰戈尼效应可加强液相热量传递;在浮力效应和马兰戈尼效应同时存在时,预测温度与实验温度几乎完全吻合,平均误差为6.1%。结果表明,同时考虑浮力效应以及马兰戈尼效应有助于准确预测薄层燃油液内的流动及传热过程。
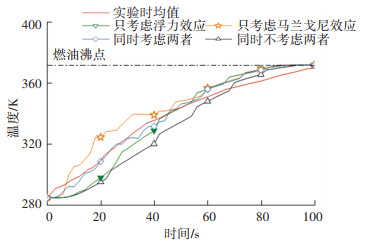
|
图 12 Case 3: 距离燃烧器底部10.9 mm处的预测液体温度 Fig. 12 Case 3: predicted liquid temperatures at 10.9 mm above the bottom of the burner |
图 13为瞬时燃烧速率预测值与实验值的对比。

|
图 13 Case3:瞬时燃烧速率预测值与实验值的对比 Fig. 13 Case3: comparison between predicted instantaneous mass burning rates and measured values |
0~50 s段,不考虑马兰戈尼效应对应的预测燃烧速率明显高于实验值;当加入马兰戈尼效应后,燃烧速率更贴合于实验值。预测误差分别为10.2%(浮)、7.6%(马)、6.9%(都有)和18.1%(都无)。忽略液相流动使误差增加了11.2%。与Case 1相比,浮力效应有所减弱。50 ~ 100 s,浮力和马兰戈尼对燃烧速率的影响减弱,无流动时预测燃烧速率偏低。
图 14为液面下降过程对燃烧速率的影响。考虑液面下降过程的预测误差为12.6%。将液面固定时,瞬时燃烧速率上升较慢,预测误差明显增大,为31.8%。预测值在前20 s内与实验值存在一定偏差,这可能由池壁使用的绝热边界条件导致。

|
图 14 Case 3: 液面下降对燃烧速率的影响 Fig. 14 Case 3: effect of liquid surface drop on burning rates |
本文建立了基于气液双向耦合的三维数值模型,并通过3个不同燃油尺寸、燃油厚度以及燃油种类的池火实验进行了验证,预测结果与实验测量数据整体吻合良好,得到如下结论:
1) 对中等尺度池火,在池火发展阶段,马兰戈尼效应、浮力效应对燃油表面、燃油内部的流动、传热均具有明显影响;忽略两者后,液相最大流速下降34.3%,液面温差增大70.1%;随着时间推移,马兰戈尼效应的影响逐渐减弱;
2) 对中等尺度池火,在池火发展阶段,忽略液相流动会导致过高预测液面温度,从而影响燃烧速率的预测精度,使误差增加11.2%;
3) 燃油的对流运动由浮力效应和马兰戈尼效应共同驱动。对中等尺度池火,在池火发展阶段,相比于浮力效应,马兰戈尼效应对池火的流动、传热以及燃烧速率的影响更大,而在达到稳定燃烧阶段后,浮力效应的影响更为明显。随着油池直径的增加或燃油厚度的减小,浮力效应的贡献越来越小。
4) 在池火稳定燃烧阶段,浮力效应、马兰戈尼效应对池火整体瞬时燃烧速率的影响逐渐降低,而马兰戈尼效应对局部位置的燃烧速率仍具有一定影响。
5) 对中等尺度池火,在薄层燃油池火的数值模拟中,必须考虑液面的下降过程,忽视下降过程将导致预测燃烧速率误差增加19.2%。
| [1] |
NAKAKUKI A. Heat transfer in small scale pool fires[J]. Combustion and Flame, 1994, 96(3): 320. DOI:10.1016/0010-2180(94)90018-3 |
| [2] |
BABRAUSKAS V. Estimating large pool fire burning rates[J]. Fire Technology, 1983, 19(4): 252. DOI:10.1007/BF02380810 |
| [3] |
ZHAO Jinlong, HUANG Hong, JOMAAS G, et al. Experimental study of the burning behaviors of thin-layer pool fires[J]. Combustion and Flame, 2018, 193: 331. DOI:10.1016/j.combustflame.2018.03.018 |
| [4] |
PORTER J, SANCHEZ P S, SHEVTSOVA V, et al. A review of fluid instabilities and control strategies with applications in microgravity[J]. Mathematical Modelling of Natural Phenomena, 2021, 16: 24. DOI:10.1051/mmnp/2021020 |
| [5] |
FARAHANI H F, JOMAAS G, RANGWALA A S. Effects of convective motion in n-octane pool fires in an ice cavity[J]. Combustion and Flame, 2015, 162(12): 4647. DOI:10.1016/j.combustflame.2015.09.021 |
| [6] |
VALI A, NOBES D S, KOSTIUK L W. Transport phenomena within the liquid phase of a laboratory-scale circular methanol pool fire[J]. Combustion and Flame, 2014, 161(4): 1081. DOI:10.1016/j.combustflame.2013.09.028 |
| [7] |
VALI A, NOBES D S, KOSTIUK L W. Fluid motion and energy transfer within burning liquid fuel pools of various thicknesses[J]. Combustion and Flame, 2015, 162(4): 1483. DOI:10.1016/j.combustflame.2014.11.013 |
| [8] |
SEFIANE K, WARD C A. Recent advances on thermocapillary flows and interfacial conditions during the evaporation of liquids[J]. Advances in Colloid and Interface Science, 2007, 134: 201. DOI:10.1016/j.cis.2007.04.020 |
| [9] |
SUARD S, FORESTIER M, VAUX S. Toward predictive simulations of pool fires in mechanically ventilated compartments[J]. Fire Safety Journal, 2013, 61(4): 57. DOI:10.1016/j.firesaf.2013.08.010 |
| [10] |
WAHLQVIST J, VAN HEES P. Implementation and validation of an environmental feedback pool fire model based on oxygen depletion and radiative feedback in FDS[J]. Fire Safety Journal, 2016, 85: 36. DOI:10.1016/j.firesaf.2016.08.003 |
| [11] |
DITCH B D, DE RIS J L, BLANCHAT T K, et al. Pool fires: An empirical correlation[J]. Combustion and Flame, 2013, 160(12): 2963. DOI:10.1016/j.combustflame.2013.06.020 |
| [12] |
SIKANEN T, HOSTIKKA S. Predicting the heat release rates of liquid pool fires in mechanically ventilated compartments[J]. Fire Safety Journal, 2017, 91: 266. DOI:10.1016/j.firesaf.2017.03.060 |
| [13] |
RENGEL B, MATA C, PASTOR E, et al. A priori validation of CFD modelling of hydrocarbon pool fires[J]. Journal of Loss Prevention in the Process Industries, 2018, 56: 18. DOI:10.1016/j.jlp.2018.08.002 |
| [14] |
SIKANEN T, HOSTIKKA S. Modeling and simulation of liquid pool fires with in-depth radiation absorption and heat transfer[J]. Fire Safety Journal, 2016, 80: 97. DOI:10.1016/j.firesaf.2016.01.002 |
| [15] |
FUKUMOTO K, WEN J X, LI Manhou, et al. Numerical simulation of small pool fires incorporating liquid fuel motion[J]. Combustion and Flame, 2020, 213: 446. DOI:10.1016/j.combustflame.2019.11.047 |
| [16] |
苗磊. 大风环境中航空煤油池火数值模拟[D]. 哈尔滨: 哈尔滨工程大学, 2015 MIAO Lei. Numerical simulation of aviation fuel pool fire under high speed wind[D]. Harbin: Harbin Engineering University, 2015 |
| [17] |
党晓贝, 何亚平, 汪箭. 不同边沿高度油池火燃烧行为的实验和数值模拟研究[J]. 火灾科学, 2018, 27(4): 216. DANG Xiaobei, HE Yaping, WANG Jian. Experimental and numerical study on burning behavior of pool fire with different lip heights[J]. Fire Safety Science, 2018, 27(4): 216. DOI:10.3969/j.issn.1004-5309.2018.04.03 |
| [18] |
赵金龙. 持续泄漏溢油流淌火扩散和燃烧机理与模型研究[D]. 北京: 清华大学, 2018 ZHAO Jinlong. Experimental and model study on the spread and burning behaviors of continuous liquid spill fires[D]. Beijing: Tsinghua University, 2018 |
| [19] |
杨娴, 从伟, 汪书苹, 等. 不同燃料液面深度的变压器套管油池火燃烧特性数值模拟[J]. 消防科学与技术, 2021, 40(12): 1725. YANG Xian, CONG Wei, WANG Shuping, et al. Numerical study on burning behavior of transformer bushing oil pool fire with different lip heights[J]. Fire Science and Technology, 2021, 40(12): 1725. DOI:10.3969/j.issn.1009-0029.2021.12.005 |
| [20] |
CHEN Zhibin, WEN J, XU Baopeng, et al. Large eddy simulation of a medium-scale methanol pool fire using the extended eddy dissipation concept[J]. International Journal of Heat and Mass Transfer, 2014, 70: 390. DOI:10.1016/j.ijheatmasstransfer.2013.11.010 |
| [21] |
MENON S, YEUNG P K, KIM W W. Effect of subgrid models on the computed interscale energy transfer in isotropic turbulence[J]. Computers & Fluids, 1996, 25(2): 166. DOI:10.1016/0045-7930(95)00036-4 |
| [22] |
STAGGS J. The effects of gas-phase and in-depth radiation absorption on ignition and steady burning rate of PMMA[J]. Combustion and Flame, 2014, 161(12): 3232. DOI:10.1016/j.combustflame.2014.06.007 |
| [23] |
SUNG K, FALKENSTEIN-SMITH R, HAMINS A. Velocity and temperature structure of medium-scale pool fires[Z]. Gaithersburg: National Institute of Standards and Technology, 2021. DOI: 10.6028/NIST.TN.2162
|
| [24] |
HAMINS A, HAMINS A, LOCK A. The structure of a moderate-scale methanol pool fire[Z]. Gaithersburg: National Institute of Standards and Technology, 2016. DOI: 10.6028/NIST.TN.1928
|
| [25] |
SUNG K, CHEN Jian, BUNDY M, et al. The thermal character of a 1 m methanol pool fire[Z]. Gaithersburg: National Institute of Standards and Technology, 2020. DOI: 10.6028/NIST.TN.2083
|
| [26] |
KANG Quansheng, LU Shouxiang, CHEN Bing. Experimental study on burning rate of small scale heptane pool fires[J]. Chinese Science Bulletin, 2010, 55(10): 973. DOI:10.1007/s11434-009-0741-y |
 2023, Vol. 55
2023, Vol. 55


