2. 山东大学 机械工程学院,济南 250061
2. School of Mechanical Engineering, Shandong University, Jinan 250061, China
基于铁磁材料磁化理论的磁性无损检测技术近年来发展迅速,该技术不仅能够快速检测材料的应力状态,还能评估材料的损伤状态[1-2]。电磁无损检测是将缺陷、应力、损伤等因素对铁磁材料固有特性或磁化强度的影响转化为可测量的特征磁场,以获得相应电信号的变化[3]。王威[4]根据能量守恒定律,即单位体积的磁化功之差应等于由机械外力所引起的单位磁积能的变化量,研究了磁导率随应力的变化情况。常福清等[5]依据能量最小原理和拉格朗日乘数法得到了一个外力下铁磁体内应力和磁化率改变间的线性关系式。赵维义等[6]从等效应力磁场出发,给出了存在应力影响的材料磁导率与应力间的一个表达式。上述3篇文献从不同的角度经过一定的变换来研究材料磁导率模型,具有一定的等效性。铁磁材料磁导率与应力和磁场之间存在非线性耦合关系,可以由材料的力磁耦合模型依据磁导率与磁化强度的关系获得。近年来力磁耦合理论的研究也在不断进步,Ren等[7-8]研究了复杂磁机械效应下铁磁材料应力与磁化强度及热力学能之间的关系,建立了应力诱磁的微观模型。在定量化磁致伸缩实验中,Kuruzar等[9]发现磁致伸缩应变是关于磁化强度的偶函数。Jiles [10]研究了铁磁性材料磁化过程中的定量化磁力学关系,得到了磁致伸缩模型和磁化磁滞模型(J-A模型)。郑晓静等[11-13]基于宏观热力学理论,结合磁化过程中磁畴壁的微观运动,建立了能够准确模拟磁致伸缩材料磁化过程的磁机械耦合模型(Z-L模型)。Shi[14]在引入形状因子和无应力状态标准方程后,得到了更精确的四阶磁化项下的磁致伸缩模型。Kim等[15]通过引入六阶磁化和非线性惯性跳跃函数,建立了一个广义非线性磁致伸缩模型,它可以充分解释拉压应力对软铁磁材料中磁致伸缩应变的影响。尽管如此,Z-L模型[11-13]及其修改形式[14-15]在描述压应力下磁致伸缩应变时仍然存在较大的误差,且无法描述铁磁材料的磁滞磁化强度。Hu等[16]通过引入整体耦合因子和应力惯性函数,提出了一种新的磁致伸缩应变方程,可以更准确地描述拉应力和压应力对磁致伸缩应变的影响。因此,基于Hu等[16]的磁致伸缩方程,结合有效场方程、J-A磁滞方程[10]和弹性模量方程,可以获得新的非线性磁化本构模型,该模型能够更准确地描述材料的磁力学效应和变刚度效应。
数值模拟是分析漏磁场分布与铁磁材料损伤或其他物理特性之间定量关系的有效方法,是铁磁材料理论研究的重要组成部分。Li等[17]利用数值模拟软件分析了管线钢中的缺陷与漏磁通密度的关系,为管线钢缺陷的定量分析提供了依据。Ma等[18]采用改进的磁力耦合模型对钢丝绳进行模拟,为钢丝绳损伤定量评估奠定了研究基础。以往的数值模拟过程中很少考虑材料的磁导率等参数随磁场和应力的变化。因此,将磁导率与应力、磁场的耦合关系导入数值分析软件,可以更准确地呈现磁化的仿真结果。
本文基于铁磁性材料磁化过程中的热力学关系、有效磁场理论以及修正的磁致伸缩应变方程,建立了杨氏模量方程、非线性磁化本构模型和变刚度模型(ΔE模型),并分析了铁磁材料的磁机械效应和变刚度效应,用数值分析软件将理论模型的输出结果与仿真过程相结合,通过仿真结果与已有研究成果的对比,验证模型用于仿真分析的可行性和准确性,同时研究应力、缺陷尺寸和缺陷位置对漏磁信号的影响。
1 理论模型当棒状铁磁材料所受应力方向和外加磁场方向相同,且其均沿材料轴向分布时,Kuruzar等[9]的实验结果和之前的模型[10-16]证明了磁致伸缩应变和磁化强度之间的偶函数关系。在理论模型中,J-A模型[10]、Z-L模型[11-13]、Shi模型[14]未考虑应力对磁化的惯性阻抗效应,因此磁致伸缩应变的理论预测结果与文献[9]的实验结果偏差较大。尽管Kim模型[15]考虑了低磁化区的应力惯性阻抗作用,但是其在描述压应力作用下的磁致伸缩应变时仍存在较大误差。相对而言,Hu等[16]的模型在描述压应力作用下的磁致伸缩和磁化强度方面具有更高的精度,其应变方程可表示为
| $ \varepsilon=\sigma / E_{\mathrm{s}}+\lambda_0+\lambda $ | (1) |
式中:σ为应力,Es为饱和杨氏模量,λ0为应力单独作用下磁畴移动导致的磁致伸缩应变,λ为应力磁场共同作用下的磁致伸缩应变。
根据热力学关系,可得到铁磁材料的无磁滞有效磁场Heff与应变ε的关系:
| $ H_{\text {eff }}=H+\alpha M-N_{\mathrm{d}} M-\mu_0^{-1} \partial\left(\int \varepsilon \mathrm{d} \sigma\right) / \partial M $ | (2) |
式中:H为磁场强度,α为表征磁畴内部耦合的平均场系数,M为材料实际磁化时的磁化强度,Nd为退磁系数(退磁系数与材料几何形状和材料内部缺陷有关),μ0为真空磁导率。通过替换M为Man(Man为无磁滞磁化强度,即理想磁材料的磁化强度),可以获得无磁滞磁化的有效场Heff(Man)。
Langevin方程可以描述无磁滞磁化强度如下:
| $ M_{\mathrm{an}}=M_{\mathrm{s}}\left[\operatorname{coth}\left(\frac{H_{\mathrm{eff}}\left(M_{\mathrm{an}}\right)}{a}\right)-\frac{a}{H_{\mathrm{eff}}\left(M_{\mathrm{an}}\right)}\right] $ | (3) |
式中:Ms是饱和磁化强度,a为材料规划常数。
| $ \mathrm{d} M / \mathrm{d} H=c \mathrm{~d} M_{\text {an }} / \mathrm{d} H+(1-c) \mathrm{d} M_{\mathrm{irr}} / \mathrm{d} H $ | (4) |
| $ \int {{M_{{\text{an}}}}} {\text{d}}{H_{\text{e}}} - \int M {\text{d}}{H_{\text{e}}} = \left( {\delta k/{\mu _0}} \right)\int {\left( {{\text{d}}{M_{{\text{irr}}}}/{\text{d}}{H_{\text{e}}}} \right)} {\text{d}}{H_{\text{e}}} $ | (5) |
可得到非线性磁化本构模型如下:
| $ \frac{\mathrm{d} M}{\mathrm{~d} H}=\frac{c \mathrm{~d} M_{\mathrm{an}} / \mathrm{d} H+(1-c) \mu_0\left(M_{\mathrm{an}}-M\right) / \delta k}{1+(1-c) k_1 M / \delta k-(1-c) \frac{\mu_0\left(M_{\mathrm{an}}-M\right)}{\delta k} \cdot X} $ | (6) |
式中:c为可逆系数;Mirr为可逆磁化强度;He为实际磁化时的有效磁场强度; k为钉扎系数,表示由材料内部钉扎点造成的磁滞损耗;δ为方向系数,
| $ \begin{aligned} X= & \alpha-N_{\mathrm{d}}+\left[\gamma(\sigma)+\varphi(\sigma) \lambda_{\mathrm{ws}}\right] /\left(\mu_0 M_{\mathrm{ws}}^2\right)- \\ & 12 \sigma \vartheta \lambda_{\mathrm{ws}} M^2 /\left(\mu_0 M_{\mathrm{ws}}^4\right)-5 \lambda_{\mathrm{ws}} \psi(\sigma) M^4 /\left(\mu_0 M_{\mathrm{ws}}^6\right) \end{aligned} $ |
其中,k1为与磁畴旋转相关系数,Mws为无应力时的饱和壁移磁化强度,λws为无应力状态下,与磁畴位移有关的最大磁致伸缩应变,γ(σ)、φ(σ)、ψ(σ)的计算公式可从文献[16]获得,
由文献[21]可知,杨氏模量E和应力微分之间的关系为
| $ E^{-1}=E_{\mathrm{s}}^{-1}+\partial \lambda_0(\sigma) / \partial \sigma+\partial \lambda / \partial \sigma $ | (7) |
假设
| $ \begin{aligned} Y= & {\left[M\left(\gamma^{\prime}(\sigma)+\lambda_{\mathrm{ws}} \varphi^{\prime}(\sigma)\right)\right] /\left(\mu_0 M_{\mathrm{ws}}^2\right)-} \\ & \lambda_{\mathrm{ws}} M^3 /\left(\mu_0 M_{\mathrm{ws}}^4\right)\left(4 \vartheta+M^2 \psi^{\prime}(\sigma) / M_{\mathrm{ws}}^2\right)+ \\ & 27 \vartheta \lambda_{\mathrm{ws}} f^2(\sigma) /\left(16 \mu_0 M_{\mathrm{ws}}\right)\left[3 \sigma f^{\prime}(\sigma)+\right. \\ & f(\sigma)] \end{aligned} $ | (8) |
其中:
将式(6)转化为磁化强度与应力的微分形式,结合式(8)可得
| $ \frac{\mathrm{d} M}{\mathrm{~d} \sigma}=\frac{\mu_0(1-c)\left(M_{\mathrm{an}}-M\right) Y+\delta k c \cdot \mathrm{d} M_{\mathrm{an}} / \mathrm{d} \sigma}{\left[\delta k+(1-c) k_1 M\right]-\mu_0(1-c)\left(M_{\mathrm{an}}-M\right) X} $ | (9) |
根据相对磁导率与磁化强度的关系μr=1+M/H,求出M后即可得到磁导率。
假设
| $ \begin{aligned} Q_1= & \frac{27 \vartheta}{16} f^3(\sigma)+\frac{M^2}{M_{\mathrm{ws}}^2}\left(1+\frac{27 \delta_0}{16} f^3(\sigma)-\right. \\ & \left.\frac{405 \kappa f^9(\sigma)}{2048}\right)+\frac{3 \kappa f^5(\sigma) M^6}{8 M_{\mathrm{ws}}^6} \end{aligned} $ | (10) |
| $ \begin{aligned} Q_2= & \frac{3}{2} f(\sigma)+\frac{81 \delta_0}{128} f^4(\sigma)-\frac{243 \kappa f^{10}(\sigma)}{8\,192}- \\ & \frac{4 \vartheta M^2}{M_{\mathrm{ws}}^2}-\left(2 \delta_0-\frac{3 \kappa f^6(\sigma)}{32}\right) \frac{3 M^4}{M_{\mathrm{ws}}^4} \end{aligned} $ | (11) |
式中:δ0为全局耦合因子,κ为与磁畴位移有关的耦合因子。
| $ \frac{\partial \lambda}{\partial \sigma}=\frac{3}{4} \lambda_{\mathrm{ws}} \cdot Q_1 \cdot f^{\prime}(\sigma)+\frac{\lambda_{\mathrm{ws}} M}{M_{\mathrm{ws}}^2} \cdot Q_2 \cdot \frac{\mathrm{d} M}{\mathrm{~d} \sigma} $ | (12) |
结合式(7)可得杨氏模量
| $ E=1 /\left[\frac{1}{E_{\mathrm{s}}}+\frac{3}{4} \lambda_{\mathrm{ws}} \cdot Q_1 \cdot f^{\prime}(\sigma)+\frac{\lambda_{\mathrm{ws}} M}{M_{\mathrm{ws}}^2} \cdot Q_2 \cdot \frac{\mathrm{d} M}{\mathrm{~d} \sigma}\right] $ | (13) |
根据饱和杨氏模量与ΔE的关系可知
| $ \Delta E=\left[E_{\mathrm{s}}-E(H, \sigma)\right] / E(H, \sigma) \times 100 \% $ | (14) |
ΔE效应是磁致伸缩材料在应力和磁场作用下磁矩旋转的结果,表现出应力和磁场的双重依赖性。
2 磁机械效应和变刚度效应分析 2.1 磁机械效应将提出模型的参数设置为:Mws=1×106 A/m,λws=4.17×10-6,σs=300 MPa,β=2.5,k/μ0=500,a=2 500,k1=-1.832 5×10-12,α=1.44×10-3,κ=0.005,δ0=0.015,
|
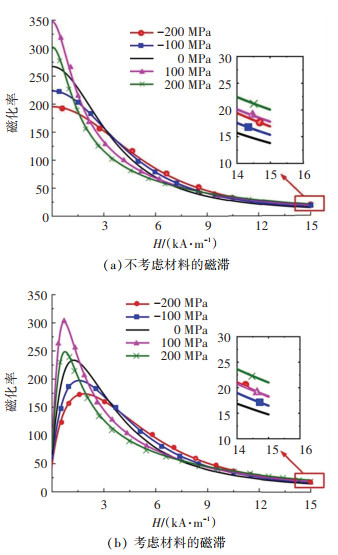
图 1 不同应力条件下磁化率随磁场的变化 Fig. 1 Variation of magnetic susceptibility with magnetic field under different stress conditions |
由图 1可知,磁化率随着磁场增大而降低,直至趋于饱和。应力使材料的磁化率饱和值增大,且饱和值与应力成正比;与压应力相比,拉应力对饱和磁化强度的增加有更大的影响。从图 1(a)可以看出,不考虑材料的磁滞时,磁化率的初始值随应力的增加而减小。拉应力状态下材料的无磁滞磁化率的初始值高于无应力状态,而压应力状态下的磁化率则低于无应力状态。随着磁场的增加,压应力下的无磁滞磁化率值逐渐增大,并超过拉应力下的值,直到接近饱和时再次变化。上述观察结果与Kim等[15]的研究结果一致。而在实际磁化过程中,材料内部不可避免地存在缺陷、位错、晶格滑移等钉扎点,从而阻碍磁畴运动,导致磁滞损耗。因此,在考虑材料的磁滞时(图 1(b)),材料的磁化率在低磁场时会出现一个转折点,这会造成磁化率随磁场的增大先增大后减小,而其他变化均与不存在磁滞时一致。
2.2 ΔE效应ΔE效应是指铁磁材料的杨氏模量在磁机械耦合过程中表现出磁场和应力的耦合函数特性。文献[16]验证了磁致伸缩应变方程,本节研究不同磁场下ΔE与应力之间的关系,以实现材料在应力作用下变刚度现象的可视化。
将本节模型的参数设置为a=1 500,δ0=0.18,
|
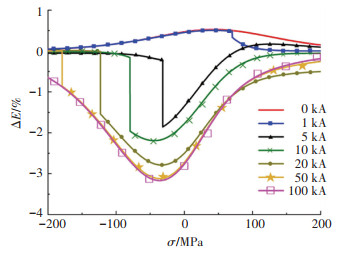
图 2 不同磁场下铁磁材料ΔE与应力的关系 Fig. 2 Relationship between ferromagnetic material ΔE and stress under different magnetic fields |
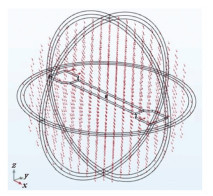
在数值仿真过程中,利用均匀磁场和磁导率模型建立了应力、磁场和磁导率之间的关系。在引入材料磁导率与应力的数值关系后,首先加载试件得到内部节点的应力值,然后进行磁耦合求解。模型仿真过程中施加的磁场如图 3所示。
|
图 3 仿真过程中施加到模型的磁场 Fig. 3 Magnetic field applied to the model during simulation |
为验证本文提出的数值仿真方法的可行性,利用具有不同缺陷的样品进行仿真,得到采集线上的漏磁场信号和漏磁通密度信号,并将仿真结果与实验结果[22-24]进行比较。
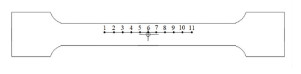
3.1.1 中心孔缺陷本文设计的中心孔半径为1.6 mm、深度为2 mm,其信号采集路线如图 4所示。将仿真得到的漏磁场法向分量和切向分量与文献[22]中图 7的数据进行比较,结果如图 5所示。
|
图 4 中心孔缺陷的信号采集路线 Fig. 4 Signal acquisition route for central hole defect |

|
图 5 样品表面不同位置的漏磁场信号变化情况 Fig. 5 Variation of leakage magnetic field signal at different positions on the sample surface |
|
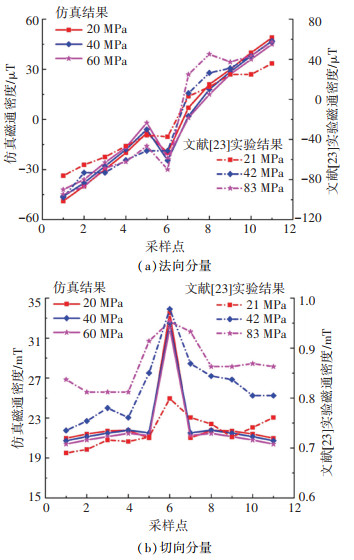
图 6 不同拉伸载荷下不同位置的漏磁通强度分布情况 Fig. 6 Leakage flux intensity distribution at different positions under different tensile loads |

|
图 7 焊接试样 Fig. 7 Weld test sample |
图 5表明漏磁场的法向分量过零点,切向分量存在极值。仿真得到漏磁场分量的变化与文献[22]中漏磁场的变化一致。图 5中也存在一定的差异,主要体现在本文模拟结果的数值与文献[22]的实验结果之间有一定的偏差,因为仿真模型中使用的磁场为250 A /m,而文献[22]的研究中的磁场是地磁场。但是,从总体趋势来看,本文模拟模型得到的结果与文献[22]的研究结果有很好的一致性。说明本文的仿真模型在描述铁磁材料缺陷引起的漏磁场变化方面表现良好。
仿真获得的漏磁通信号法向和切向分量与樊清泉等[23]实验结果的对比见图 6。图 6(a)为不同拉伸载荷下中心孔缺陷对不同位置的漏磁通密度法向分量的影响。由图 4可知,点6在圆形缺陷的边缘。漏磁通信号的法向曲线在采集点1~5和7~11处近似为一条斜线,信号值随应力的增大而增大。如图 6(a)所示,采集点1~4和7~11的信号关于坐标点(6, 0)中心对称,而在缺陷圆周方向的点6存在一定的突变,且点6的信号突变值随着拉伸载荷的增加而增加。如图 6(b)所示,采集点1~5和7~11的漏磁通切向信号关于x=6轴对称,且峰值出现在采集点6处。根据图 6结果及上述分析可知,均匀磁场磁化下的仿真结果与文献[23]的实验结果较吻合。
3.1.2 焊接区裂纹Wilson等[24]测量了焊缝裂纹区域的磁场分布,试样的焊缝裂纹分布如图 7所示。试样由两2块300 mm×180 mm×12 mm钢材组成,测量曲线垂直于焊缝裂纹。
仿真获得的漏磁通强度与Wilson等[24]实验结果比较见图 8。由图 8(a)可知,法向磁场分量分布呈倒S形,切向磁场分量对称分布在裂纹两侧,在裂纹处有一个极值(如图 8(b)所示)。总体而言,仿真结果的变化趋势与Wilson等[24]的实验结果吻合较好。但仿真得到的磁场法向分量或切向分量与Wilson等[24]的实验结果分别相差一个或两个数量级,这可能是由于本文中的磁场为250 A/m,而Wilson等[24]研究中的磁场是地磁场。另外,在Wilson等[24]的研究中,缺陷两侧对称位置的磁场值不同,这可能是在实验中,焊缝附近存在复杂的应力分布,而本文的仿真将焊缝等效为缺陷,因此使仿真结果和Wilson等[24]的实际实验结果存在一定的差异。

|
图 8 焊缝裂纹区漏磁通强度分布情况 Fig. 8 Leakage magnetic flux intensity distribution in the weld crack area |
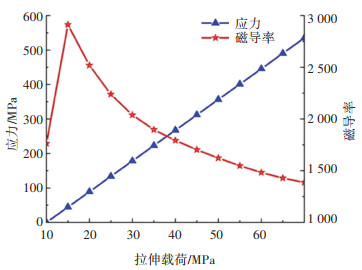
对具有圆孔缺陷的样品分别施加0、5、10、30、50 MPa的拉伸载荷,研究应力对样品漏磁场信号的影响。图 4中信号采集路径上点6的应力和磁导率值如图 9所示。
|
图 9 不同拉伸载荷下磁导率和应力的变化 Fig. 9 Variation of magnetic permeability and stress under different tensile loads |
带中心孔缺陷样品的漏磁场信号见图 10.
|
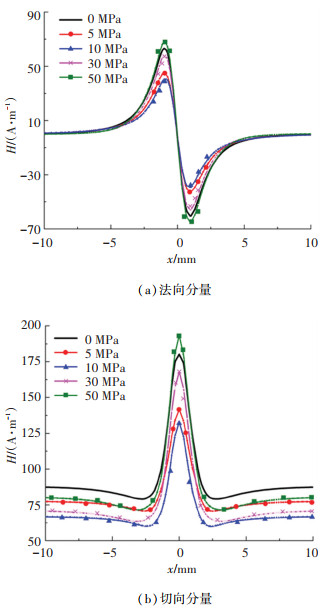
图 10 带中心孔缺陷样品的漏磁场信号 Fig. 10 Leakage magnetic field signals of samples with central hole defects |
由图 10可知,在采集路径上,法向磁场信号呈类S形曲线,切向磁场信号呈类锥形曲线,且随着拉伸载荷增大,二者的极值均先减小后增大。在x=0 mm处,出现切向磁场信号的峰值,在50 MPa的拉伸载荷下,切向磁场的峰值最大。距缺陷一定距离处的切向漏磁场信号与缺陷边缘处的信号存在明显的差异。距缺陷一定距离处的磁场值随着拉伸载荷的增加先减小后增大,切向漏磁场信号分量在无应力状态下最大。同时可看出,不同拉伸载荷下的材料漏磁场信号存在一定差异,这是由于在无应力状态下,铁磁材料的磁畴处于无序状态,而在施加于铁磁材料的应力和磁场下,由于磁机械耦合效应,磁畴壁在材料内部发生微观运动,进而导致不同应力下的表面漏磁场存在差异。
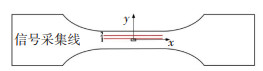
改变矩形孔缺陷长度后的漏磁场信号采集线如图 11所示。图 12为不同缺陷长度下漏磁场信号沿采集路径1的变化曲线。
|
图 11 矩形孔缺陷处漏磁场的信号采集路径 Fig. 11 Signal acquisition path of leakage magnetic field at rectangular hole defect |

|
图 12 路径1上漏磁场信号随缺陷长度的变化 Fig. 12 Variation of leakage magnetic field signal on route 1 with defect length |
如图 12(a)所示,缺陷中心位置对应的法向磁场分量接近于零,漏磁场的峰值随着缺陷长度的增加而逐渐减小。峰谷之间的距离随着缺陷长度的增加而增加,呈正相关。如图 12(b)所示,切向漏磁场分量的最大值随着缺陷长度的增加而减小。在缺陷边缘,切向漏磁场分量呈凹形对称曲线。随着缺陷长度的增加,切向漏磁场分量的峰跨度呈线性关系增大,即切向漏磁场的峰跨度越大,缺陷长度越大。
图 13为漏磁场信号沿采集路径2的变化曲线。如图 13(a)所示,缺陷中心位置对应的法向漏磁场分量几乎为零。法向漏磁场分量的峰值随着缺陷长度的增加而增加,呈正相关。峰谷间距不随缺陷长度变化,这与采集路径1上的信号分布不同。如图 13(b)所示,缺陷中心位置对应的切向漏磁场分量大于相邻两侧的漏磁场分量,呈中间高,两侧低的凸形。切向漏磁场分量的峰值随着缺陷长度的增加而增加,呈正相关。即切向漏磁场分量的峰值越大,缺陷长度越大。同时,漏磁场的峰值跨度与缺陷长度呈明显的正线性相关,即切向漏磁场分量的跨度随缺陷长度的增大而增大。

|
图 13 路径2上漏磁场信号随缺陷长度的变化 Fig. 13 Variation of leakage magnetic field signal on route 2 with defect length |
本文将物理模型与数值分析过程相结合,通过数值仿真软件对铁磁材料在均匀磁场磁化作用下的漏磁信号分布进行了分析,可以得出以下结论:
1) 建立了新的磁弹耦合模型和ΔE模型,分析了铁磁材料的磁机械效应和变刚度效应。通过数值分析软件得到拉伸载荷下缺陷试样的表面漏磁信号,结果与已有文献的研究结果一致,证明了该方法在铁磁材料数值分析中的可行性和准确性。
2) 在拉伸载荷作用下,法向磁场信号呈类S形曲线,切向磁场信号呈类锥形曲线,其极值均随载荷增加先减小后增大。由于磁机械耦合效应的存在,漏磁场切向分量在缺陷中心位置处50 MPa的拉应力状态下最大,而在远离缺陷处无应力状态下最大。
3) 不同采集路径获取的信号存在很大的差异,采集路线1和2上对应缺陷中心位置的切向信号分别显示为凹形和凸形。缺陷边缘路径上漏磁场峰值与缺陷长度呈负相关,而峰值距离和跨度却相反。远离缺陷的采集路线上,漏磁场信号的峰值和跨度均与缺陷长度呈正相关。该研究结果为磁性无损检测中缺陷的准确定位提供一定的参考。
4) 磁信号的影响因素较多,而且具有一定的耦合特性。因此,要明确各种干扰因素对磁信号的影响,提高检测信号的准确性,还需要结合其他技术和信号分析方法进行进一步研究。
| [1] |
BAO Sheng, FU Meili, LOU Huangjie, et al. Evaluation of a stress concentration of a low-carbon steel based on residual magnetic field measurements[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2016, 58(12): 678. DOI:10.1784/insi.2016.58.12.678 |
| [2] |
SHI Pengpeng, SU Sanqing, CHEN Zhenmao. Overview of researches on the nondestructive testing method of metal magnetic memory: status and challenges[J]. Journal of Nondestructive Evaluation, 2020, 39(2): 43. DOI:10.1007/s10921-020-00688-z |
| [3] |
刘美全, 郎宾, 陶斌坤, 等. 磁性无损检测技术研究进展[J]. 应用物理, 2020, 10(8): 374. LIU Meiquan, LANG Bin, TAO Binkun, et al. Research progress of magnetic nondestructive testing technology[J]. Applied Physics, 2020, 10(8): 374. DOI:10.12677/app.2020.108050 |
| [4] |
王威. 钢结构磁力耦合应力检测基本理论及应用技术研究[D]. 西安: 西安建筑科技大学, 2005 WANG Wei. The basic theory and application technology of stress NDT & E based on magnetic-mechanical coupling effects for steel structure[D]. Xi'an: Xi'an University of Architecture & Technology, 2005 |
| [5] |
常福清, 刘东旭, 刘峰. 磁记忆检测中的力-磁关系及其实验观察[J]. 实验力学, 2009, 24(4): 369. CHANG Fuqing, LIU Dongxu, LIU Feng. Stress-magneto relationship in magnetic memory testing and experimental observation[J]. Journal of Experimental Mechanics, 2009, 24(4): 369. |
| [6] |
赵维义, 喻力华, 邹畹珍. 利用等效应力磁场测平面残余应力[J]. 华中理工大学学报, 1999, 27(12): 100. ZHAO Weiyi, YU Lihua, ZOU Wanzhen. Measuring the plane residual stresses by equivalent stress magnetic field[J]. Journal of Huazhong University of Science & Technology, 1999, 27(12): 100. DOI:10.13245/j.hust.1999.12.034 |
| [7] |
REN Shangkun, REN Xianzhi, DUAN Zhenxia, et al. Studies on influences of initial magnetization state on metal magnetic memory signal[J]. NDT & E International, 2019, 103: 77. DOI:10.1016/j.ndteint.2019.02.002 |
| [8] |
REN Shangkun, REN Xianzhi. Studies on laws of stress-magnetization based on magnetic memory testing technique[J]. Journal of Magnetism and Magnetic Materials, 2018, 449: 165. DOI:10.1016/j.jmmm.2017.09.050 |
| [9] |
KURUZAR M E, CULLITY B D. The magnetostriction of iron under tensile and compressive stress[J]. International Journal of Magnetism, 1971, 1(4): 323. |
| [10] |
JILES D C. Theory of the magneto-mechanical effect[J]. Journal of Physics D: Applied Physics, 1995, 28(8): 1537. DOI:10.1088/0022-3727/28/8/001 |
| [11] |
ZHENG Xiaojing, SUN Le. A nonlinear constitutive model of magneto-thermo-mechanical coupling for giant magnetostrictive materials[J]. Journal of Applied Physics, 2006, 100(6): 063906-2. DOI:10.1063/1.2338834 |
| [12] |
SHI Pengpeng, JIN Ke, ZHENG Xiaojing. A general nonlinear magneto-mechanical model for ferromagnetic materials under a constant weak magnetic field[J]. Journal of Applied Physics, 2016, 119(14): 145103-3. DOI:10.1063/1.4945766 |
| [13] |
SHI Pengpeng, JIN Ke, ZHENG Xiaojing. A magneto-mechanical model for the magnetic memory method[J]. International Journal of Mechanical Sciences, 2017, 124/125: 229. DOI:10.1016/j.ijmecsci.2017.03.001 |
| [14] |
SHI Pengpeng. Magneto-elastoplastic coupling model of ferromagne-tic material with plastic deformation under applied stress and magnetic fields[J]. Journal of Magnetism and Magnetic Materials, 2020, 512: 166980-2. DOI:10.1016/j.jmmm.2020.166980 |
| [15] |
KIM S, KIM K, CHOE K, et al. A nonlinear magneto-mechanical coupling model for magnetization and magneto-striction of ferromagnetic materials[J]. AIP Advances, 2020, 10(8): 085304-3. DOI:10.1063/5.0016489 |
| [16] |
HU Xiangyi, FU Zhensheng, WANG Zhongcheng, et al. Research on a theoretical model of magnetic nondestructive testing for ferromagnetic materials based on the magneto-mechanical coupling effect[J]. Journal of Physics D: Applied Physics, 2021, 54(41): 415002-4. DOI:10.1088/1361-6463/AC100C |
| [17] |
LI Xunbo, LI Xiang, CHEN Liang, et al. Numerical simulation and experiments of magnetic flux leakage inspection in pipeline steel[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 111. DOI:10.1007/s12206-008-1005-5 |
| [18] |
MA Xiaoping, SU Sanqing, WANG Wei, et al. Damage location and numerical simulation for steel wire under torsion based on magnetic memory method[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 60(2): 233. DOI:10.3233/JAE-180075 |
| [19] |
JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetism and Magnetic Materials, 1986, 61(1/2): 48. DOI:10.1016/0304-8853(86)90066-1 |
| [20] |
罗旭, 朱海燕, 丁雅萍. 基于力磁耦合效应的铁磁材料修正磁化模型[J]. 物理学报, 2019, 68(18): 187501-4. LUO Xu, ZHU Haiyan, DING Yaping. A modified model of magneto-mechanical effect on magnetization in ferromagnetic materials[J]. Acta Physica Sinica, 2019, 68(18): 187501-4. DOI:10.7498/aps.68.20190765 |
| [21] |
牛牧青, 杨斌堂, 杨诣坤, 等. 磁致伸缩主被动隔振装置中的磁机耦合效应研究[J]. 力学学报, 2019, 51(2): 327. NIU Muqing, YANG Bintang, YANG Yikun, et al. Research on the magneto-mechanical effect in active and passive magneto-strictive vibration isolator[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 327. DOI:10.6052/0459-1879-18-254 |
| [22] |
苏三庆, 刘馨为, 王威, 等. 金属磁记忆检测技术研究新进展与关键问题[J]. 工程科学学报, 2020, 42(12): 1565. SU Sanqing, LIU Xinwei, WANG Wei, et al. Progress and key problems in the research on metal magnetic memory testing technology[J]. Chinese Journal of Engineering, 2020, 42(12): 1565. DOI:10.13374/j.issn2095-9389.2020.05.10.002 |
| [23] |
樊清泉, 任尚坤, 任仙芝, 等. 外加磁场对Q235钢力磁效应影响试验研究[J]. 中国测试, 2019, 45(6): 48. FAN Qingquan, REN Shangkun, REN Xianzhi, et al. Experimental study on the influence of external magnetic field on magneto-mechanical effect for Q235 steel[J]. China Measurement & Test, 2019, 45(6): 48. DOI:10.11857/j.issn.1674-5124.2018070108 |
| [24] |
WILSON J W, TIAN Guiyun, BARRANS S. Residual magnetic field sensing for stress measurement[J]. Sensors and Actuators A: Physical, 2007, 135(2): 386. DOI:10.1016/j.sna.2006.08.010 |
 2023, Vol. 55
2023, Vol. 55


