目前,随着芯片、微器件、光学元件等超精加工以及医疗、食品等行业的超净加工的要求越来越高,工件在智能制造生产线上进行搬运时,需要保持工件表面的零污染。传统的接触式搬运例如接触式真空吸盘、带传送和机械夹持等方式,极易污染工件,还可能损坏其表面结构,难以满足要求。非接触式真空吸盘凭借其无接触、绿色环保、使用方便等优点在超精、超净制造中得到了广泛应用[1]。目前,非接触式真空吸盘按其工作原理主要可分为伯努利式与涡旋式。伯努利式吸盘通过在工件表面产生高速气流使吸盘与工件的间隙处产生负压以吸取工件,其空气消耗量较大;涡旋式吸盘则是通过内部气腔涡旋气流的离心力效应在工件表面产生负压进行工作。与伯努利式吸盘相比,涡旋吸盘在产生相同吸力时消耗的空气流量更少,因此更加节能和环保,应用前景更加广阔[2]。
国内外学者针对涡旋式非接触真空吸盘进行了大量的研究工作,Wu等[3]在吸盘中心加入绕流体结构以提高吸盘的吸力和悬浮刚度。Chandran等[4]的研究表明,使用正锥形涡旋气腔可以提高涡旋吸盘的吸力。Zhao等[5-6]发现增加环形间隙宽度可以改变吸盘的稳定悬浮区域,提高其吸力;而间隙处的不均匀流场会导致出口回流,减小吸盘最大吸力。Wang等[7]研究发现,随着吸盘涡旋气腔直径的增加,吸盘的最大吸力首先明显上升,而后有平稳下降的趋势。由于涡旋式吸盘是依靠高速旋转气流产生真空,工作时不可避免地对工件产生周向转矩,从而使工件发生旋转和侧倾,极易导致非接触吸取的失效。Li等[8-9]研究了旋转流场的动力学模型,发现环形间隙的气膜可以抑制工件振动。Li等[10]提出了一种单涡旋吸盘成对并列使用、旋向相反、对称安装的技术方法,有效地抑制了较大尺寸被吸工件的旋转。Iwasaka等[11]将两个通入不同旋向涡旋气流的气腔错位布置以防止工件的旋转。郭丽媛[12]在吸盘底部增设了稳流网与分流孔结构,具有抑制工件旋转的效果,但一定程度上增加了吸盘加工的难度。李剑锋等[13]设计了一种由6个单进气喷嘴吸盘组成的非接触搬运吸盘装置,该装置比单吸盘减小了52.6%的转矩。
本文提出一种同心双涡旋的非接触式真空吸取技术方案,探讨结构参数和工作参数对吸盘性能的影响规律,旨在有效抑制吸盘工作时工件的旋转,提高非接触吸取的可靠性。
1 工件旋转机理及防旋方案提出如图 1所示,涡旋式非接触真空吸盘的工作原理如下:压缩空气经切向喷嘴射入涡旋气腔,气流沿腔室内壁高速旋转形成涡旋,由于离心效应,气腔中心区域形成负压,被吸工件上下表面的气压差使工件获得向上的吸力。由吸盘与工件的间隙中形成的气流层实现工件的非接触式吸取。

|
图 1 涡旋吸盘工作原理 Fig. 1 Working principle of vortex gripper |
由于单方向的涡旋气流流经工件表面时会对工件产生黏性摩擦转矩,使工件发生旋转,一旦工件与吸盘发生碰撞或者工件脱离了正常的吸取工作范围,则会导致非接触吸取的失效。为此,滕燕等[14]提出了一种同心双涡旋非接触真空吸盘技术方案,如图 2所示,内、外两个涡旋气腔结构同心但气流旋向相反,内涡旋产生真空提供吸力,外涡旋反向气流用于平衡内涡旋对工件产生的摩擦转矩。

|
图 2 同心双涡旋吸盘工作原理 Fig. 2 Working principle of concentric double-vortex gripper |
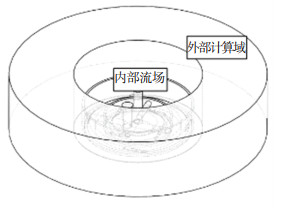
用Fluent软件对吸盘进行仿真研究。建立了该型吸盘的流场仿真模型,并进行了网格划分,如图 3所示。设工件与吸盘之间的间隙厚度为0.3 mm,由于内部流场结构复杂,故将其划分为四面体非结构网格,网格总数约为400万个,平均斜度为0.20。涡旋式非接触真空吸盘涡旋腔内气流为湍流流动,在环形间隙区域,仅当间隙厚度相对很小时可看作层流[15]。对于吸盘的湍流流场,目前主要采用k-ε湍流模型和雷诺应力模型对吸盘流场进行数值模拟,其中雷诺应力模型理论上比其他模型要更加精确,但是计算花费时间大大增加,Realizable k-ε湍流模型可以较为精确地模拟吸盘喷嘴射流的扩散速度和缝隙平面中的流动,计算结果较为符合真实情况,因此使用Realizable k-ε湍流模型。由于仿真时用完全的整体流场,使用压力入口符合实际试验情况且能保证较好的收敛速度,故边界条件设置为压力入口和大气压压力出口。由于间隙出口流动较复杂,若将间隙出口直接定义为压力出口,会导致计算得到的吸盘流量特性及间隙压力分布产生较大误差,所以在吸盘流场外围额外固定一个足够大的外部计算区域,如图 4所示,并把外部区域的边界定义为大气压压力出口,以保证结果的准确性。考虑到计算速度,将外部计算域划分为六面体结构化网格。

|
图 3 双涡旋吸盘流场网格 Fig. 3 Mesh of double-vortex gripper flow field |
|
图 4 计算域定义 Fig. 4 Calculation domain definition |
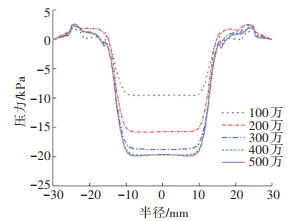
为了验证吸盘流场模型网格的网格无关性,取吸盘的最为重要的性能指标吸力作为验证比较的依据,吸力主要由工件表面的压力分布决定。分别调整网格划分的密度,将吸盘流场模型划分成不同密度的网格,仿真得到网格数与0.3 mm间隙处的径向压力分布变化(如图 5所示)。根据曲线分布,在R < 15.5 mm范围内即吸盘内涡旋气腔区域内为内涡旋真空发生区域,当网格数大于400万时内涡旋真空度不再发生明显变化。此外,在R>10 mm范围内,真空度变化幅度不大,且当网格数大于300万时,该区域内的压力曲线趋势基本一致,可以认为网格数在400万以上时可获得网格无关解。
|
图 5 不同网格数下0.3 mm间隙厚度的工件表面径向压力 Fig. 5 Radial pressure distribution on workpiece surface with 0.3 mm gap thickness under different mesh numbers |
如图 6所示,在工件表面按等角度均匀选择4条径向分布直线,初步研究当内、外涡旋气腔供气压力均为200 kPa时(供气压力均为表压,下同),不同直径方向上的周向切应力分布。仿真计算得到4条直径上的周向切应力分布(如图 7所示)。

|
图 6 工件俯视示意图 Fig. 6 Top view of workpiece |

|
图 7 工件表面的周向切应力分布 Fig. 7 Circumferential shear stress distribution on workpiece surface |
由图 7可知,4个方向的切应力分布趋势大体相同,但最大值间存在差异。在内、外涡旋腔区域内,存在方向相反的切应力,且在靠近涡旋腔壁面的区域内,切应力分别达到最大值。对4条线的周向切应力平均值进行积分可得总摩擦转矩为
| $ M=2 \rm{ \mathsf{ π}} \int_0^R r^2 \bar{\tau} \mathrm{d} r $ | (1) |
式中: r为半径,
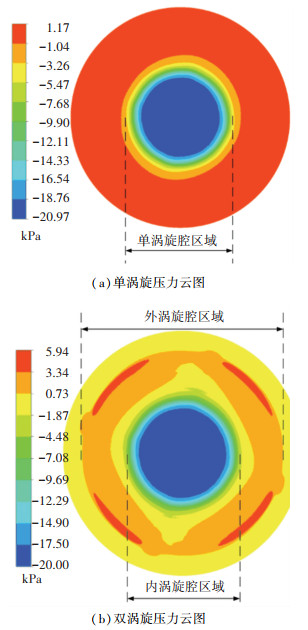
分别对单涡旋吸盘与双涡旋吸盘在不同供气压力下吸取时工件的表面压力分布进行了仿真,图 8给出了当供气总压力为200 kPa时的仿真结果。
|
图 8 工件表面压力分布云图 Fig. 8 Contour of pressure distribution on workpiece surface |
可以看出:两种吸盘的负压产生区域均集中在中心内涡旋腔区域,最大负压相差仅有约800 Pa;进一步计算得到单涡旋吸盘吸力约为10.5 N,双涡旋吸盘吸力约为8.5 N。双涡旋吸盘吸力与单涡旋相比基本相当,略有下降。分析其原因主要为:在同样的供气条件下,对双涡旋吸盘而言,供气流量要同时分配给内、外两个涡旋,从而导致内涡旋的供气流量比单涡旋吸盘的供气量要少,一定程度上影响了吸力的大小。
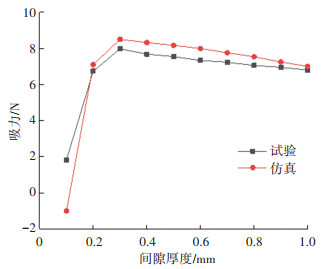
2.3 试验验证通过初步试验,得到吸盘内、外涡旋气腔入口供气压力均为200 kPa时的试验结果。图 9为吸盘静态试验和数值仿真得到的吸盘吸力随间隙厚度变化的曲线图。由图 9可知,在静态试验中,随着间隙厚度的增大,吸力先增大后减小,最大值出现在约0.3 mm间隙厚度处,最大吸力约为8.0 N。与仿真结果比较发现,当间隙厚度δ≥0.2 mm时,在相同供气流量和间隙厚度的条件下,吸盘的吸力均略小于仿真值,最大值均出现在间隙厚度为0.3 mm左右。当间隙厚度为0.1 mm时,试验测得的吸力值为正值,而仿真值为负值,即产生斥力,这与吸盘的工作原理相符,试验值为正值的现象可能是吸盘内、外涡旋气腔底座的装配误差造成。当间隙厚度δ>0.1 mm时,吸力的误差均<10%,可以认为所建立的仿真模型是正确的,仿真结果是可信的,为进一步研究奠定了理论基础。
|
图 9 吸力与间隙厚度关系 Fig. 9 Relationship between suction force and gap thickness |
图 10为双涡旋吸盘剖面结构示意图。

|
图 10 双涡旋吸盘剖面示意图 Fig. 10 Section diagram of double-vortex gripper |
由于绕流体下的速度流动非常小[3],故将绕流体下(r<R1)的压力值设为定值,记作p0。可得R1<r<R2区域内的压力梯度为
| $ \frac{\partial p}{\partial r}=\rho \frac{u_\alpha^2}{r} $ | (2) |
式中:p为压强,ρ为密度,uα为半径r处流体的切向速度。假设切向速度与半径成正比,即
| $ u_\alpha=\omega r $ | (3) |
式中ω为内涡旋气腔内流体角速度。记大气压力为pa,当外涡旋气腔未供气时,吸盘中心理论最大吸力在p(R2)=pa时取得,据此边界条件,对式(2)积分可得
| $ p=\frac{\rho \omega^2}{2}\left(r^2-R_2^2\right)+p_{\mathrm{a}} $ | (4) |
假设内涡旋气腔边界最大流速为V,则式(4)积分可得吸盘内涡旋气腔区域理论最大吸力为
| $ F_{\mathrm{m}}=\frac{ \rm{π} \rho V^2}{4}\left(R_2^2-\frac{R_1^4}{R_2^2}\right) $ | (5) |
由于绕流体半径与吸盘悬浮刚度及中心压力分布均匀性有关[3],在此设为固定值,则由式(5)可知,吸盘的最大吸力正相关于V和R2,V则与喷嘴直径和位置有关。
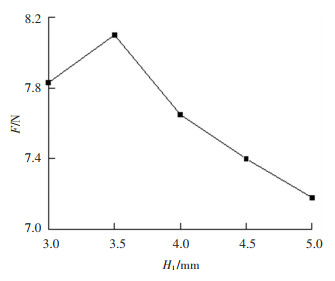
固定间隙厚度δ=0.3 mm,内、外涡旋气腔供气压力ps1、ps2均为200 kPa,进一步研究该型吸盘的关键结构参数内涡旋腔半径R2、内涡旋腔高度H1和喷嘴距内涡旋腔上壁面距离H2与吸盘吸力的关系,结果分别如图 11~13所示。可以看出,R2、H1、H2均存在一个吸盘吸力最优的值。进行了正交试验,通过仿真获得正交试验结果如表 1所示,选择各个因素的单水平均值的最大值为最优水平,可得最优选择:R2=17 mm,H1=4 mm,H2=1 mm。

|
图 11 F与R2的关系 Fig. 11 Relationship between F and R2 |
|
图 12 F与H1的关系 Fig. 12 Relationship between F and H1 |

|
图 13 F与H2的关系 Fig. 13 Relationship between F and H2 |
| 表 1 正交试验表 Tab. 1 Orthogonal experimental design table |
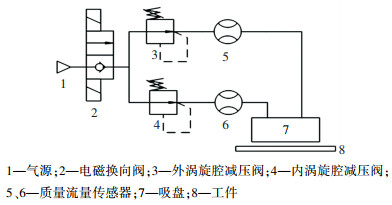
根据结构分析优化结果,使用光固化技术加工了吸盘样机,其精度为200 μm,样机实物如图 14所示。试验装置见图 15。调节装置用于调节吸盘的高度,并由激光位移传感器进行测量,扭矩传感器用于测量工件所受的摩擦转矩,其量程为2 N·m,综合精度0.1%,力传感器用于测量吸力。试验的气动回路如图 16所示。

|
图 14 吸盘实物照片 Fig. 14 Photograph of gripper |

|
图 15 转矩/力测量试验装置 Fig. 15 Torque/force measurement experiment device |
|
图 16 气动回路 Fig. 16 Air supply circuit |
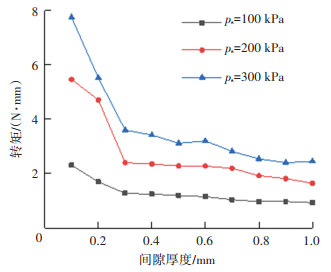
首先,调节单涡旋腔供气压力ps分别为100、200、300 kPa,间隙厚度δ分别为0.1、0.2、0.3、…、1.0 mm,测试了单涡旋吸盘吸取时工件所受的摩擦转矩,结果见图 17。由图 17可以看出,随着间隙厚度增大,工件受到的摩擦转矩总体呈现减小的趋势,当δ>0.3 mm后,这种下降的趋势变缓;另一方面,供气压力越大,工件所受到的转矩越大。
|
图 17 单涡旋吸盘吸取工件所受的转矩 Fig. 17 Torque of workpiece sucked by single-vortex gripper |
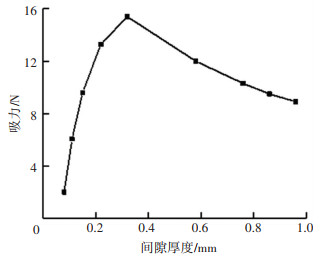
图 18为供气压力ps为300 kPa时吸盘吸力随间隙δ变化的试验结果。由图 18可知,吸力F随δ增大先增后减,最大吸力出现在δ=0.32 mm处,约为15.4 N。
|
图 18 单涡旋吸盘吸力 Fig. 18 Suction force of single-vortex gripper |
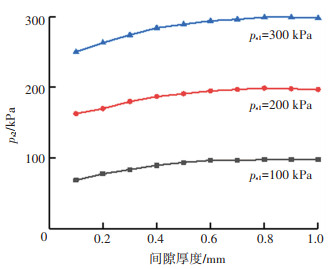
分别调节并固定同心双涡旋吸盘的内涡旋腔供气压力ps1为100、200和300 kPa,间隙厚度δ分别为0.1、0.2、0.3、…、1.0 mm,缓慢调节同心双涡旋吸盘的外旋腔供气压力ps2,当工件所受转矩为零时,记录此时的ps2,多次测量取其均值,得到吸盘内、外涡旋腔供气压力的关系见图 19。由图 19可知,在所有试验中,均为ps2<ps1,且当ps1一定时,ps2均随δ的增大而增大,最终趋向于ps1。当δ=0.3 mm时对应的3组内、外旋腔供气压力分别为:组A,ps1=100 kPa,ps2=84 kPa;组B,ps1=200 kPa,ps2=180 kPa;组C,ps1=300 kPa,ps2=274 kPa。
|
图 19 不同条件下所需的外涡旋供气压力 Fig. 19 External vortex supply pressure required under different conditions |
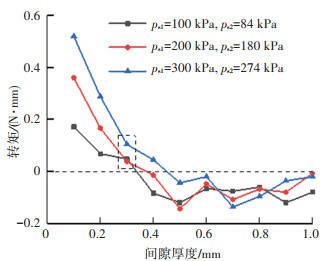
进一步调节间隙厚度δ分别为0.1、0.2、0.3、…、1.0 mm,供气压力分别取组A、组B、组C数据时,同心双涡旋吸盘对工件产生的摩擦转矩如图 20所示,与单涡旋吸盘(图 17)对比可以看出:在本次所有的试验条件下,同心双涡旋吸盘对工件产生的最大转矩均<0.6 N·mm,远远低于单涡旋吸盘对工件产生的转矩;当δ=0.3 mm时,同心双涡旋吸盘对工件产生的转矩<0.12 N·mm,比同等条件下单涡旋吸盘产生的转矩减小了90%左右。
|
图 20 双涡旋吸盘吸取工件所受的转矩 Fig. 20 Torque of workpiece sucked by double-vortex gripper |
图 21为吸盘内、外旋腔供气总压力为300 kPa时,吸盘吸力随间隙δ变化的试验结果。由图 21可知:同心双涡旋吸盘的吸力F随δ的增大先增后减,最大吸力出现在δ=0.34 mm处,约为13.7 N,与单涡旋吸盘相比,在同等供气压力条件下吸力略有下降。分析其原因主要在于:同样的供气条件下,双涡旋吸盘的供气流量因为要同时分配给内、外两个涡旋,从而导致内涡旋的供气流量比单涡旋吸盘的供气量要少,一定程度上影响了吸力的大小;这也说明,若增加供气压力或供气流量,对提高双涡旋吸盘的吸力是有益的。

|
图 21 双涡旋吸盘吸力 Fig. 21 Suction force of double-vortex gripper |
针对单涡旋吸盘工作时被吸工件易旋转从而导致非接触吸取失效的问题,提出了一种同心双涡旋非接触式真空吸盘技术方案,仿真和试验研究得到如下结论:
1) 研究分析了涡旋式非接触真空吸盘工作时工件旋转的机理,提出了一种同心双涡旋非接触真空吸盘结构方案,内涡旋产生真空提供吸力,外涡旋用于平衡摩擦转矩以抑制工件的旋转。
2) 仿真分析了同心双涡旋真空吸盘的工件表面压力场和摩擦转矩,研究了结构设计参数对吸盘吸力的影响规律,对吸盘的结构优化奠定了理论基础。
3) 对吸盘样机进行的试验结果表明,同等工作条件下,同心双涡旋非接触真空吸盘可以在保证一定吸取能力的情况下很好地抑制被吸工件的旋转,提高吸取搬运的稳定性和可靠性。
| [1] |
钟伟, 顾小玉, 黎鑫. 气悬浮技术在无接触输运领域的研究进展[J]. 机械工程学报, 2018, 54(20): 40. ZHONG Wei, GU Xiaoyu, LI Xin. Review on contactless transport using pneumatic levitation[J]. Journal of Mechanical Engineering, 2018, 54(20): 40. DOI:10.3901/JME.2018.20.040 |
| [2] |
LI Xin, LI Ning, TAO Guoliang, et al. Experimental comparison of Bernoulli gripper and vortex gripper[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(10): 2081. DOI:10.1007/s12541-015-0270-3 |
| [3] |
WU Qiong, YE Qian, MENG G X. Experimental and numerical study of vortex gripper with a diversion body[J]. Journal of Mecha-nical Engineering Science, 2012, 226(6): 1526. DOI:10.1177/0954406211423585 |
| [4] |
CHANDRAN C S A, SAJIKUMAR K S, JAYARAJ K. Numerical characterisation of the performance of flow rate on a non-contact vortex gripper[J]. Journal of Physics: Conference Series, 2019, 1355: 1. DOI:10.1088/1742-6596/1355/1/012001 |
| [5] |
ZHAO Jianghong, WANG Ching, LI Xin. Gap flow with circumferential velocity in annular skirt of vortex gripper[J]. Precision Engineering, 2019, 57: 64. DOI:10.1016/j.precisioneng.2019.03.007 |
| [6] |
ZHAO Jianghong, LI Xin. Two-dimensional pressure field and backflow in the annular skirt of vortex gripper[J]. Journal of Mechanical Engineering Science, 2020, 235(20): 4954. DOI:10.1177/0954406220974044 |
| [7] |
WANG Ching, ZHAO Jianghong, LI Xin. Effect of chamber diameter of vortex gripper on maximum suction force and flow field[J]. Advances in Mechanical Engineering, 2019, 11(3): 1. DOI:10.1177/16878140198-37401 |
| [8] |
LI Xin, KAWASHIMA K, KAGAWA T. Dynamic characteristics of vortex levitation[C]// 2008 SICE Annual Conference. Chofu: IEEE, 2008: 1175. DOI: 10.1109/SICE.2008.4654838
|
| [9] |
LI Xin, KAWASHIMA K, KAGAWA T. Dynamic modeling of vortex levitation[C]// 2008 Asia Simulation Conference. Beijing: IEEE, 2008: 218. DOI: 10.1109/ASC-ICSC.2008.4675358
|
| [10] |
LI Xin, KAWASHIMA K, CAI M, et al. Research on a non-contact handling system using swirling flow[J]. Transactions of the Japan Fluid Power System Society, 2011, 42(4): 67. |
| [11] |
IWASAKA H, HIDEYUKI T. The swirling flow formation body and the non-contact transport apparatus: Japan, P2007-324382A[P]. 2011-05-18
|
| [12] |
郭丽媛. 非接触硅片夹持装置的研究[D]. 杭州: 浙江大学, 2010: 35 GUO Liyuan. Research of non-contact wafer holder[D]. Hangzhou: Zhejiang University, 2010: 35 |
| [13] |
李剑锋, 梁冬泰, 路波, 等. 非接触搬运吸盘系统研究[J]. 仪器仪表学报, 2018, 39(10): 108. LI Jianfeng, LIANG Dongtai, LU Bo, et al. Research on non-contact handling sucker system[J]. Chinese Journal of Scientific Instrument, 2018, 39(10): 108. DOI:10.19650/j.cnki.cjsi.J1803631 |
| [14] |
滕燕, 谢玉飞, 李小宁. 一种同心双涡旋非接触式真空吸取装置: 中国, CN111268424B[P]. 2021-04-16 TENG Yan, XIEYufei, LI Xiaoning. Concentric double-vortex non-contact vacuum suction device: China, CN111268424B[P]. 2021-04-16 |
| [15] |
吴琼. 含导流体的旋流非接触吸盘的内部流场研究及其优化设计[D]. 上海: 上海交通大学, 2013: 36 WU Qiong. Investigation on internal flow field of vortex gripper with the division body and multi-objective optimization design[D]. Shanghai: Shanghai Jiao Tong University, 2013: 36 |
| [16] |
章梓雄, 董曾南. 黏性流体力学[M]. 北京: 清华大学出版社, 1998: 150. ZHANG Zixiong, DONG Zengnan. Viscous fluid mechanics[M]. Beijing: Tsinghua University Press, 1998: 150. |
 2023, Vol. 55
2023, Vol. 55


