功率超声应用为液体空化[1]、工业零件清洗[2]、线束焊接[3]、塑料焊接[4]、异种金属焊接[5]等行业提供了新的思路。随着超声清洗[6]、超声焊接[7]等功率超声应用的发展,大功率超声设备的需求日益明显。压电换能器的输出功率是影响超声设备功率能力的直接因素[8],例如:随着被焊接件厚度和焊接面积的增加,超声金属焊接对压电换能器的功率需求呈指数性增加[9]。因此,大功率压电换能器的设计、装配与测试引起了研究者的关注。
压电换能器是功率超声应用中的核心装置,其利用逆压电效应进行高频电-声能量转换并向外输出能量[10]。在压电陶瓷功率密度一定的情况下,增加压电陶瓷组径向尺寸是提升压电换能器输出功率最有效的方法,也是一种广泛使用的方法。随着压电换能器径向尺寸的增加,尤其是当径向尺寸高于纵振频率下压电陶瓷材料中纵波波长的1/4时,压电换能器的纵向与径向的耦合振动问题不可忽略,且需要对其进行控制[11]。同时,径向尺寸的增加意味着在同等预应力下,装配所需的预紧力增加。压电换能器的高预紧力装配是压电换能器设计时需要考虑的问题[12]。
文献[13]对大功率压电换能器的内部动应力分布进行了分析,并使用电荷测量的方法确定装配过程中的拧紧力矩,指出压电换能器动态特性是压电换能器设计时需要考虑的关键问题。针对预应力引起的谐振频率漂移,文献[14]基于各部件间的有效截面差异建立了压电换能器电阻抗数学模型,结果表明,预应力与零件的有效耦合成正比关系,且预应力需高于30 MPa。文献[15]针对机械极限对高功率压电换能器的功率限制,使用ATILA有限元程序分析了高功率压电换能器预紧后的静态应力场和高驱动水平下的动态应力,并研究了压电陶瓷平面度对高功率压电换能器内部应力的影响,结果表明,使用有限元软件分析压电换能器材料的疲劳和失效是研究压电换能器机械极限的一种有效手段,较差的压电陶瓷表面性能会严重影响高驱动水平下的压电换能器性能并导致较为严重的发热问题。文献[16]针对20 kHz夹心式压电换能器开展了设计与装配研究,提出了夹层压电换能器数字化装配技术,装配后的压电换能器阻抗稳定在8.5 Ω附近。文献[17]提出了一种通过检测谐振电阻来确定最佳预紧力的方法,结果表明,谐振电阻处于最小值时,换能器前端振幅达到最大值,但最大振幅对应的最佳预紧扭矩与最小谐振电阻对应的最佳预紧扭矩约有5 N·m的偏差。为实现压电换能器的自动装配并提高装配精度,文献[18-19]设计了四立柱压电换能器装配机,通过压电陶瓷组的电压值来反馈控制装配扭矩进行压电换能器装配。
随着拧紧装配研究的深入和装配经验的积累,拧紧装配已经可以实现小尺寸压电换能器的精确装配。但对于大尺寸的压电换能器,拧紧装配较难实现高装配扭矩需求[20]。高装配扭矩在装配过程中还会对压电换能器的阻抗特性和接触面造成影响。此外,压电换能器的装配方式也直接影响压电换能器的结构设计。在设计大尺寸压电换能器时,应该重点考虑装配后的应力分布问题。
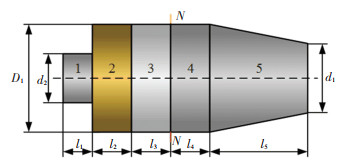
1 压电换能器设计 1.1 压电换能器的结构设计压电换能器的性能指标见表 1,基本组成见图 1,N-N为理想节面位置。预紧螺栓与前端盖通过螺纹配合,产生的预紧力通过后端盖施加于压电陶瓷表面。预紧力使压电陶瓷在工作时始终处于受压状态,避免压电陶瓷工作时的破碎[21]。
| 表 1 压电换能器的性能指标 Tab. 1 Performance indexes of piezoelectric transducer |
|
1—预紧螺栓; 2—后端盖; 3—压电陶瓷组; 4—前端盖-1; 5—前端盖-2 图 1 压电换能器的基本组成 Fig. 1 Basic composition of piezoelectric transducer |
为了尽可能提高压电换能器前后端面的振幅比,根据动量守恒原理,节面后部材料的密度应尽可能比节面前部材料的密度高[21],因此后端盖采用黄铜材料。由于前端盖需要与双头螺柱配合,为了保证连接强度,螺纹连接处采用TC4钛合金,非连接处采用7075铝合金。此外,令前端盖-1的螺纹配合段尽可能远离压电陶瓷组,以减少应力集中对压电陶瓷组表面应力分布均匀性的影响。4片PZT-8压电陶瓷尺寸为:外径D1=62 mm、内径D2=22 mm、厚度t=5 mm。压电陶瓷通过5片厚度t0=0.25 mm的黄铜电极片施加电激励。组成压电换能器基本结构的各零件材料及性能参数见表 2。
| 表 2 压电换能器各零件材料及性能参数 Tab. 2 Materials and parameters of piezoelectric transducer components |
首先,根据目标谐振频率计算压电换能器各部分的纵向长度。根据节面位置N-N可将压电换能器分解为2个1/4波长振子。左侧1/4波长振子由圆螺母、后端盖和压电陶瓷组构成,右侧1/4波长振子为压电换能器的前盖板,由前端盖-1和前端盖-2构成。确定纵向尺寸时不考虑各零件的连接和预紧等问题,各零件均视为实心结构。取l1=8 mm、l3=20 mm、l4=20 mm,径向长度D1=62 mm、d1=40 mm、d2=30 mm。l2和l5需通过计算确定。
利用传输线原理,右侧1/4波长振子和左侧1/4波长振子的频率方程分别为[21]:
| $ \tan \left(k_4 l_4\right) \tan \left(k_5 l_5\right)=\frac{z_4}{z_5} $ | (1) |
| $ \begin{gathered} \frac{z_3}{z_2} \tan \left(k_2 l_2\right) \tan \left(k_3 l_3\right)+\frac{z_3}{z_1} \tan \left(k_1 l_1\right) \tan \left(k_3 l_3\right)+ \\ \frac{z_2}{z_1} \tan \left(k_1 l_1\right) \tan \left(k_2 l_2\right)=1 \end{gathered} $ | (2) |
式中:zi为波阻抗,zi=ρiciSi,ρi为密度,ci为纵波波速,Si为横截面积;ki为波数,ki=ω/ci,ω为振动圆频率;li为纵向长度。
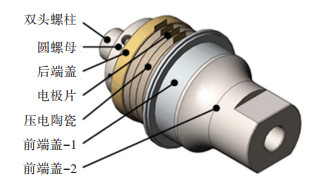
求解式(1)和式(2)得:l2=23.92 mm、l5=52.74 mm。确定纵向长度后,需要考虑装配方式和安装等因素对结构做进一步调整。为了适应装配方法,压电换能器由双头螺柱和螺母配合进行预紧。考虑到防松性能和接触面能量的有效传递,双头螺柱采用M20×1的细牙螺纹。针对前端盖的聚能和放大振幅的作用,前端盖-2由圆锥形更改为带圆弧过渡的阶梯型。前端盖-1设计出突出的节面以方便固定压电换能器或安装保护壳进行高压电隔离。本文所设计的半波长压电换能器见图 2。
|
图 2 半波长压电换能器 Fig. 2 Half-wavelength piezoelectric transducer |
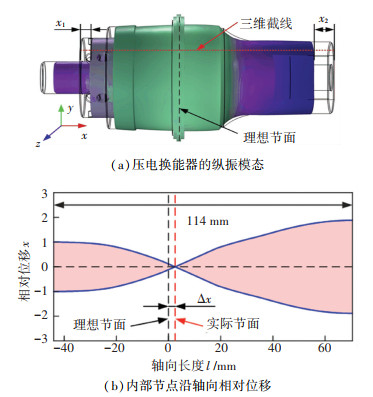
压电换能器的纵振频率f、振幅比A和节面位置偏差Δx是评价压电换能器设计的重要机械性能指标。基于模态分析的仿真设计可以快速得到压电换能器的机械性能参数和各模态下的振型[22]。纵振频率f可以通过模态分析直接得到,振幅比A和节面位置偏差Δx需要对分析结果进行后处理得到。压电换能器在纵振时可近似看作一维轴向振动,即内部实体同一轴截面上的点具有相同的位移。压电换能器的纵向振动模态仿真结果见图 3。
|
图 3 压电换能器的纵振仿真 Fig. 3 Longitudinal vibration simulation of piezoelectric transducer |
定义前端盖-1突出的节面中心截面为理想节面位置。在仿真软件三维坐标系中,理想节面位置圆心坐标(x, y, z)=(0, 0, 0),即x0=0。压电换能器的轴线与x轴重合。为了得到压电换能器的轴向相对位移分布,在压电换能器实体结构中插入一条与x轴平行的三维截线。当三维截线与实体相交时会输出相对位移结果,因此,将三维截线沿y轴正向平移17 mm。定义螺母外端面的相对位移为±1。
三维截线上相对位移为0的点所在的轴截面即为实际节面位置x0′。节面位置偏差Δx为实际节面位置x0′与理想节面位置x0之差。振幅比A为前端盖- 2输出端振幅x2与螺母最外端振幅x1的比值。
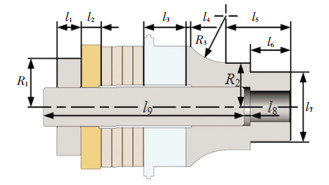
1.3 尺寸参数的灵敏度分析为了满足机械性能指标要求,需进一步调整压电换能器的尺寸参数。压电换能器有12个可以调节的尺寸参数,见图 4。
|
图 4 压电换能器的参数 Fig. 4 Parameters of piezoelectric transducer |
在尺寸参数调整前,需要分析各参数对机械性能的灵敏度。Morris灵敏度分析是一种研究模型各参数对系统输出影响的方法。该方法与单一参数灵敏度分析方法相比,考虑了模型各参数同时变化对系统输出的影响。参数xj对系统输出影响的灵敏度分析结果会以基本影响绝对值的均值μj和方差σj呈现。用μj来表征该参数的灵敏度,μj越大说明系统输出受参数xj变化的影响越大,系统输出对参数xj越敏感;方差σj表征该参数与其他参数的耦合性,σj越大说明参数xj与系统其他输入参数的耦合性越强,参数xj对系统输出的影响非线性越强。
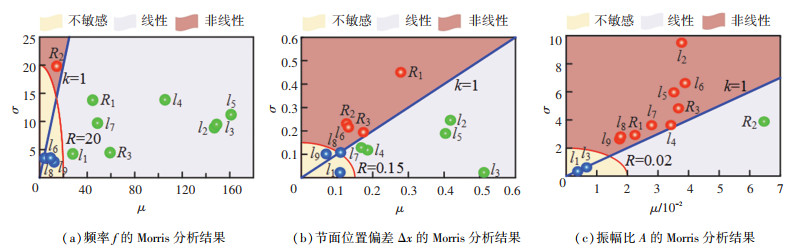
对压电换能器进行Morris方法的灵敏度分析,系统输入x=L,L为尺寸参数向量,由图 4可知L=[l1 l2 l3 l4 l5 l6 l7 l8 l9 R1 R2 R3]。系统输出y =[f A Δx]。对尺寸参数向量L中的12个因素各等间距取9个水平,即p=9。各因素的取值见表 3。对尺寸参数进行9次随机抽样,即r=9,进行9条轨道的模态分析。尺寸参数对纵振频率f、节面位置偏差Δx和振幅比A的Morris灵敏度分析结果见图 5。
| 表 3 压电换能器灵敏度分析的参数及取值 Tab. 3 Parameters and values of sensitivity analysis of piezoelectric transducer |
|
图 5 Morris分析结果 Fig. 5 Morris analysis results |
纵振频率f的尺寸参数灵敏度顺序为:l5>l3>l2>l4>R3>l7>R1>l1>R2>l9>l6>l8。除R2外,各参数均位于直线σ=μ下方,说明各参数基本独立影响纵振频率f。纵振频率f对纵向尺寸l2、l3、l4和l5具有较高的敏感性,说明纵向长度仍是决定压电换能器纵振频率f的主要因素。节面位置偏差Δx的尺寸参数灵敏度顺序为:l3>l2>l5>R1>l4>R3>l7>l6>R2>l8>l1>l9。节面位置偏差Δx对纵向尺寸l2、l3和l5具有较高的敏感性。纵向尺寸l2、l3和l5基本独立影响节面位置偏差Δx,径向尺寸R1、R2和R3对节面位置偏差Δx的影响则具有较高的非线性。振幅比A的尺寸参数灵敏度顺序为:R2>l6>l2>R3>l5>l4>l7>R1>l8>l9>l3>l1。除R2外,各参数均位于直线σ=μ上方,说明各参数影响振幅比A时具有较强的相互作用。
参数l2对纵振频率f、振幅比A和节面位置偏差Δx的灵敏度均较高。对参数l2调整时,需要综合考虑对3个输出的影响。因此,在参数l2确定后,非必要情况下应尽可能避免对其进行调整。尺寸参数对纵振频率f和节面位置偏差Δx的影响具有较高的重合性,例如:二者均对参数l2、l3和l5具有较高的敏感性,均对参数R2、l8和l9具有较低的敏感性。因此参数l3和l5的调整需要综合考虑对纵振频率f和节面位置偏差Δx的影响。
振幅比A对参数R2和l6具有较高的敏感性,而纵振频率f和节面位置偏差Δx对参数R2和l6的敏感性较低。因此可以在保证纵振频率f和节面位置偏差Δx基本不变的情况下,调节参数R2和l6满足振幅比A要求。参数l1、l8和l9对纵振频率f、节面位置偏差Δx和振幅比A的敏感性均较低。这说明圆螺母厚度、双头螺柱长度及配合后的残余间隙对机械性能基本没有影响。
针对目标输出结果,通过调节压电换能器的高灵敏度参数,实现了压电换能器结构设计。压电换能器各结构参数最终取值见表 4。该尺寸参数下压电换能器纵振频率f=19 522 Hz,振幅比A=1.88,节面位置偏差Δx=2.28 mm。
| 表 4 压电换能器的主要结构参数 Tab. 4 Main structural parameters of piezoelectric transducer |
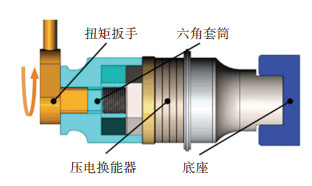
通常,压电换能器通过扭矩扳手等设备拧紧螺栓进行预紧,通过控制拧紧力矩来控制预紧力。拧紧装配示意见图 6。压电陶瓷所需的预应力约为50 MPa,计算可得本文采用的压电陶瓷需要的预紧力约为130 kN,对应拧紧力矩T在800~1 600 N·m之间,这需要依靠特定的高扭矩输出设备。
|
图 6 压电换能器拧紧装配示意 Fig. 6 Tighten assembly diagram of piezoelectric transducer |
接触面粗糙度、润滑程度等因素使摩擦系数难以确定。因此,无法确定特定目标预紧力下的拧紧力矩T,这将严重影响装配后压电换能器性能的一致性。此外,装配过程中各零件间会产生相对转动,造成接触面破坏,影响压电换能器工作时的能量传输,甚至造成局部发热,影响压电换能器正常工作。
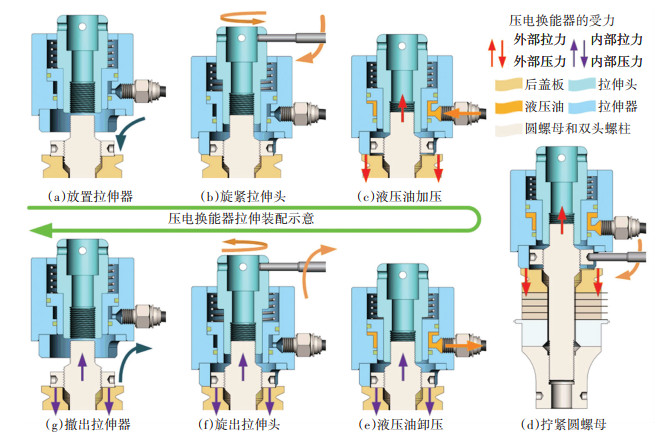
针对拧紧装配方法存在的不足,本文提出一种以液压作为动力的压电换能器拉伸装配方法,装配过程示意见图 7。
|
图 7 压电换能器拉伸装配示意 Fig. 7 Tensile assembly diagram of piezoelectric transducer |
液压拉伸器以后端盖为支承,拉伸头与双头螺柱配合。液压油加压使拉伸头沿轴向运动,后端盖、压电陶瓷组等部件受压被轴向压缩,双头螺柱受拉被轴向拉伸。因此,圆螺母与后端盖之间产生间隙。通过拨杆旋动圆螺母使其与后端盖完全贴合。液压油卸压后,拉伸器施加于压电换能器外部的拉压力即可转化为压电换能器内部的预紧力。在拉伸过程中,压电换能器同时受拉压力。液压油卸压过程中,协调变形主要发生在圆螺母上,变形协调极小。因此,拉伸力可近似完全转化为预紧力。
压电换能器在装配过程中存在2个关键状态。当拉伸器的拉伸力加载到目标值且圆螺母未拧紧时,压电换能器承受的外部拉压力最大,见图 7(d),称为“装配时”;当圆螺母拧紧且拉伸器退出时,压电换能器完全受内部拉压力,对应状态见图 7(g),称为“装配后”。拉伸装配过程较为缓慢,可以视为“准静态”。因此,通过静应力仿真对装配过程中的2个关键状态进行分析。仿真过程忽略电极片以及零部件的加工误差等影响。定义距后端盖轴向距离由近及远的压电陶瓷编号为1~4。
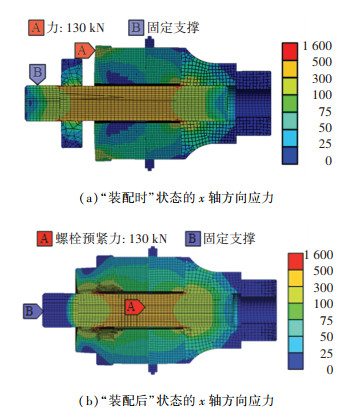
“装配时”状态,后端盖与圆螺母之间会出现间隙。仿真时定义后端盖与圆螺母的接触类型为“无摩擦”。其余接触面的接触类型定义为“绑定”。定义拉伸头和双头螺柱的配合部分为“固定支撑”,在后端盖内径为51 mm、外径为64 mm的圆环上施加130 kN的均布力。“装配后”状态,圆螺母会与压电换能器的其他部分发生协调变形,但该协调变形较小。仿真时,所有接触面的接触类型定义为“绑定”。在双头螺柱中部施加130 kN的螺栓预紧力。定义双头螺柱后端面为“固定支撑”。2个状态的x轴方向应力见图 8。可以看出,2个状态下的双头螺柱承受的拉力均约为400 MPa。
|
图 8 压电换能器的静应力仿真 Fig. 8 Static stress simulation of piezoelectric transducer |
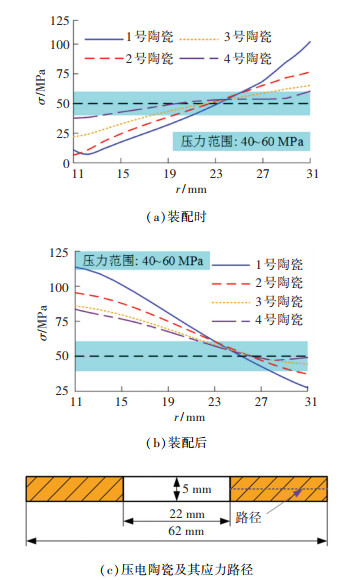
压电换能器的结构和仿真时所施加的载荷均周向对称。因此,在装配过程中压电换能器内部的应力周向对称、沿径向变化。压电换能器的静应力仿真结果也表明轴截面上的应力沿径向呈环状分布。在每片压电陶瓷内部中间厚度处添加一条径向路径,径向路径见图 9(c)。通过后处理导出径向位置向量r=(r1, r2, r3, …, rn)及其对应的径向应力分布向量σ=(σ1, σ2, σ3, …, σn),各压电陶瓷径向应力分布情况见图 9。
|
图 9 压电陶瓷的径向应力分布 Fig. 9 Radial stress distribution of piezoelectric ceramics |
压电陶瓷在2个状态的径向应力分布趋势相反,“装配时”状态的压电陶瓷主要外环受力,径向应力由内环向外环递增,压电陶瓷组内环出现了一个低于35 MPa的锥形低应力区。“装配后”状态的压电陶瓷主要内环受力,径向应力由内环向外环递减,压电陶瓷组内环出现了一个高于75 MPa的锥形高应力区。压电陶瓷组在2个状态下的最大应力均高于100 MPa。但从1号陶瓷到4号陶瓷的应力分布逐渐均匀。
2.2 基于静应力分析的后端盖结构改进压电陶瓷组沿径向不均匀的应力分布极大可能在装配过程中导致压电陶瓷破碎,还会对接触面间的能量传输造成影响,进而影响压电换能器的阻抗特性。本质上,以上问题是装配力和螺栓预紧力在后端盖分布位置不合理造成的。当力主要分布于后端盖环形端面中央时,施加于压电陶瓷组的应力将得到明显改善。
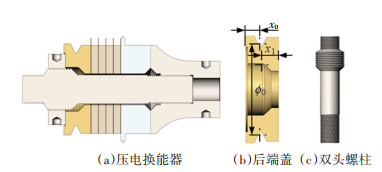
改善以上问题最直接的办法是增大后端盖的轴向长度l2,即增加厚度。但Morris分析结果表明,机械性能对参数l2极为敏感。过多地增加后端盖厚度将导致压电换能器的纵振频率大幅度降低。本文通过在后端盖加V型槽来解决“装配时”压电陶瓷组外环应力过高的问题。为了解决“装配后”压电陶瓷组内环应力过高的问题,将双头螺柱与圆螺母配合尺寸由M20×1增加至M30×1。此外,还增加了前端盖-1和前端盖-2的接触位置的倒角尺寸。改进后的压电换能器三维模型见图 10。
|
图 10 结构调整后的压电换能器三维模型 Fig. 10 Three-dimensional model of piezoelectric transducer after structural adjustment |
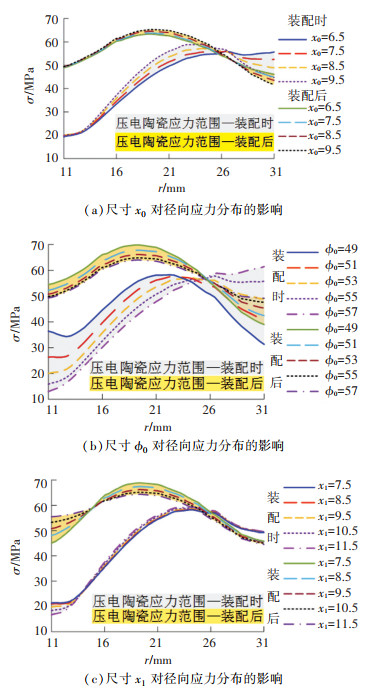
影响压电陶瓷组应力分布的后端盖结构尺寸主要有V型槽槽心位置尺寸x0、槽心直径尺寸ϕ0和内环厚度尺寸x1。根据图 9的结果,选取应力分布最不均匀的1号压电陶瓷进行分析。1号压电陶瓷的应力分布越均匀,则压电陶瓷组内的所有陶瓷应力分布越均匀。后端盖结构尺寸参数取不同参数值时,1号压电陶瓷的径向应力分布见图 11。
|
图 11 后端盖尺寸参数对径向应力分布的影响 Fig. 11 Effect of dimension parameters of back cover on radial stress distribution |
槽心位置尺寸x0的大小表示V型槽槽心距离后端盖后部的距离。随着x0参数值的增大,V型槽距离后端盖后部越远,1号压电陶瓷“装配时”状态的内环应力基本不变、外环应力减小、应力峰值增大、应力峰值位置向内移动,“装配后”状态内环应力基本不变、外环应力减小、应力峰值增大、应力峰值位置不变。
槽心直径尺寸ϕ0表示V型槽底部圆弧圆心所处的圆的直径。随着ϕ0参数值的增大,V型槽越浅,1号压电陶瓷“装配时”状态的内环应力减小、外环应力增大、应力峰值基本不变、应力峰值位置向外移动,“装配后”状态内环应力减小、外环应力增大、应力峰值减小、应力峰值位置不变。
内环厚度尺寸x1表示后端盖与压电陶瓷内环接触部分的厚度。随着x1参数值的增大,后端盖与压电陶瓷接触的内环厚度增加,1号压电陶瓷“装配时”状态的内环应力减小、外环应力和应力峰值基本不变、应力峰值位置向外移动,“装配后”状态内环应力增大、外环应力不变、应力峰值减小、应力峰值位置不变。
可以看出,槽心位置尺寸x0主要影响压电陶瓷组在“装配时”状态的外环应力分布情况。内环厚度尺寸x1主要影响压电陶瓷组在“装配后”状态的内环应力分布情况。槽心直径尺寸ϕ0则同时影响“装配时”状态和“装配后”状态的内、外环应力分布情况,还会对应力峰值的位置产生影响。
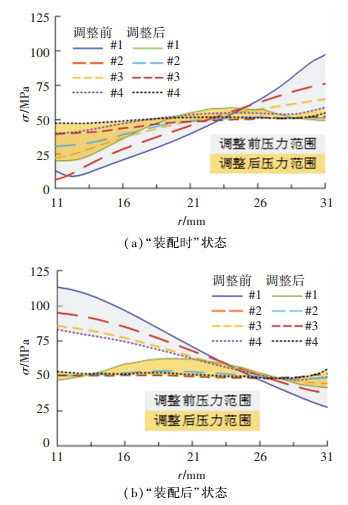
根据以上分析结果,取x0=8.5 mm、ϕ1=53 mm、x1=9.5 mm。压电换能器的后端盖和双头螺柱结构调整前后,压电陶瓷的径向应力区间与区间宽度见表 5,各压电陶瓷的径向应力分布见图 12。
| 表 5 结构调整前后的压电陶瓷径向应力对比 Tab. 5 Comparison of radial stress of piezoelectric ceramics before and after structural adjustment |
|
图 12 结构调整前后压电陶瓷组的径向应力分布 Fig. 12 Radial stress distribution of piezoelectric ceramics before and after structural adjustment |
结构调整明显提高了各压电陶瓷在2种装配状态的内环应力,降低了外环应力和径向应力区间。此外,结构调整会对压电换能器的纵振频率f、振幅比A和节面位置偏差Δx产生影响。在结构调整后,再次调整Morris灵敏度分析中的高灵敏度参数以实现设计需求,结构参数的调整在此不再赘述。
3 压电换能器的拉伸装配试验设计的拉伸装配装置见图 13(a),通过该拉伸装置对压电换能器进行装配。液压源的压力范围为0~70 MPa,最高可产生170 kN的拉伸力。拉伸器内有M20×1的螺纹,可与压电换能器的双头螺柱相配合而施加拉伸力。使用拉伸装配装置对压电换能器进行装配,试验过程中保持压电陶瓷组的正负极短路,对装配后的压电换能器使用阻抗分析仪进行性能测试,性能测试见图 13(b)。

|
图 13 压电换能器的拉伸装配装置及性能测试 Fig. 13 Tensile assembly device and performance test of piezoelectric transducer |
对压电换能器进行20次拉伸装配试验。随着液压油压力P的升高,装配预紧力F增加,串联谐振阻抗Zs逐渐降低,达到最低值时又开始回升。当液压油压力P达到40 MPa以上且串联谐振阻抗Zs开始增加时,停止装配。压电换能器拉伸装配后的性能测试结果见图 14。
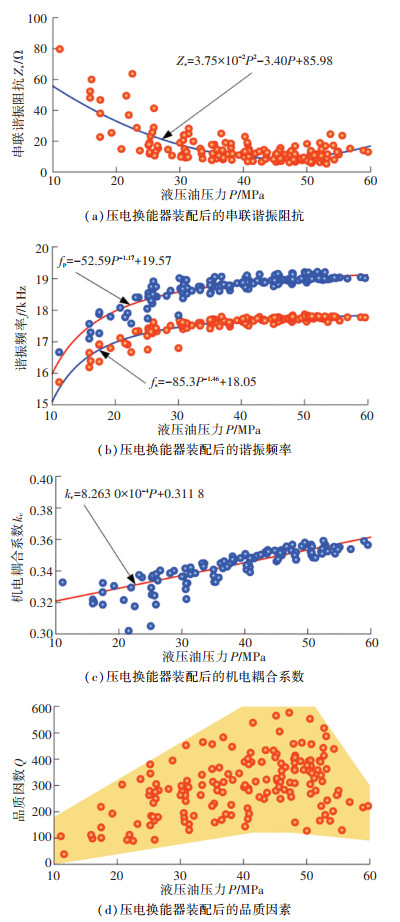
|
图 14 压电换能器拉伸装配后的性能 Fig. 14 Performance of piezoelectric transducer after tensile assembly |
随着液压油压力P升高,串联谐振阻抗Zs先降低后又升高。当液压油压力P低于40 MPa时,串联谐振阻抗Zs随着液压油压力P的升高而降低。当液压油压力P高于50 MPa时,串联谐振阻抗Zs随着液压油压力P的升高而升高。当液压油压力P在40~50 MPa之间时,串联谐振阻抗Zs基本达到极小值,为10 Ω左右。对试验结果使用二次多项式拟合,结果为Zs=3.75×10-2P2-3.40P+85.98。拟合曲线计算所得的最小串联谐振阻抗Zs值为8.80 Ω,在液压油压力P为45.37 MPa时取得。
串联谐振频率fs与并联谐振频率fp随着液压油压力P的增加而增加,在40 MPa后增速均趋于平缓。函数f=a·Pb+c对试验数据点具有较好的拟合效果,拟合结果分别为fs=-85.3P-1.46+18.05和fp= -52.59P-1.17+19.57。说明串联谐振频率fs的极限值在18.05 kHz附近,并联谐振频率fp的极限值在19.57 kHz附近,二者相差约1.52 kHz。频率间隔Δf随着液压油压力P增加而增加。受实际材料特性偏差以及仿真设置等影响,装配后的压电换能器与模态分析结果存在一定的偏差。
机电耦合系数kc随液压油压力P的增加而增加。在40~50 MPa的液压油范围内,串联谐振阻抗Zs基本取得极小值,对应机电耦合系数kc在0.34~0.36之间。对数据点进行直线拟合,拟合结果为kc=8.263 0×10-4P+ 0.311 8。整体上,品质因数Q的离散性较大,这可能是受接触面的粗糙度、压电陶瓷性能等因素影响。但总体上,在10~40 MPa的液压油压力范围内,试验结果随着液压油压力P的增加而增加。在50~60 MPa的液压油压力范围内,试验结果开始逐渐下降。在40~50 MPa的液压油压力范围内,品质因数Q的试验结果较大,这也与最小串联谐振阻抗Zs的液压油压力范围对应一致。
通过对压电换能器装配过程中串联谐振阻抗Zs、串联谐振频率fs、并联谐振频率fp、机电耦合系数kc和品质因数Q随液压油压力P变化的分析可以发现,在40~50 MPa的液压油压力范围内,串联谐振阻抗Zs取得极小值,串联谐振频率fs和并联谐振频率fp趋于稳定,机电耦合系数kc基本取得理想值,品质因数Q取得极大值。这些参数的变化趋势说明压电换能器的最佳装配液压油压力P的范围在40~50 MPa之间。
4 结论1) 基于传输线方法和模态分析完成了压电换能器的基本构型,并利用Morris方法分析了压电换能器结构参数对压电换能器串联谐振频率、节面位置偏差和振幅比影响的灵敏度顺序。分析结果表明前后端盖的轴向尺寸对压电换能器的机械性能影响较为明显。
2) 设计了后端盖带有V型槽的新型压电换能器,使陶瓷组应力跨度在“装配时”和“装配后”状态相较于常规构型分别减小了57.47%和75.77%。
3) 采用拉伸装配方法进行了压电换能器装配试验,验证了所提出拉伸式装配的可行性,得到了压电换能器串联谐振阻抗、机电耦合系数、串并联谐振频率和品质因数受装配装置液压油压力变化影响的规律。依据试验结果,得到了所设计的压电换能器最佳装配预紧力为40~50 MPa。
| [1] |
PÉRE-SÁNCHEZ A, SEGURA J A, RUBIO-GONZALEZ C, et al. Numerical design and analysis of a Langevin power ultrasonic transducer for acoustic cavitation generation[J]. Sensors and Actuators A: Physical, 2020, 311: 112035. DOI:10.1016/j.sna.2020.112035 |
| [2] |
PRIHODKO V, KAZANCEV V, KARAGODIN V, et al. Peculiarities of high-amplitude ultrasonic cleaning of parts[J]. Bulletin of Bryansk State Technical University, 2019, 2019(12): 76. DOI:10.30987/1999-8775-2019-2019-12-76-81 |
| [3] |
SCHEMMEL R, HEMSEL T, DYMEL C, et al. Using complex multi-dimensional vibration trajectories in ultrasonic bonding and welding[J]. Sensors and Actuators A: Physical, 2019, 295: 653. DOI:10.1016/j.sna.2019.04.025 |
| [4] |
TROUGHTON M J. Handbook of plastics joining: a practical guide[M]. 2nd ed. Norwich: William Andrew Inc, 2008: 15.
|
| [5] |
TUCKER M C, LAU G Y, JACOBSON C P. Joining of dissimilar materials[J]. CIRP Annals, 2015, 64(2): 679. |
| [6] |
MASON T J. Ultrasonic cleaning: an historical perspective[J]. Ultrasonics Sonochemistry, 2016, 29: 519. DOI:10.1016/j.ultsonch.2015.05.004 |
| [7] |
KICUKOV E, GURSEL A. Ultrasonic welding of dissimilar materials: a review[J]. Periodicals of Engineering and Natural Sciences (PEN), 2015, 3(1): 1. |
| [8] |
MASON T J. Sonochemistry and sonoprocessing: the link, the trends and (probably) the future[J]. Ultrasonics Sonochemistry, 2003, 10(4/5): 175. DOI:10.1016/S1350-4177(03)00086-5 |
| [9] |
PESHKOVSKY A S, PESHKOVSKY S L. Industrial-scale processing of liquids by high-intensity acoustic cavitation: the underlying theory and ultrasonic equipment design principles[M]// NOWAK F M. Sonochemistry: Theory, Reactions, Syntheses, and Applications. [S. l. ]: Nova Science Publishers Inc., 2010: 63
|
| [10] |
SHEN Wenqiang, JIA Ying, LI Dongming, et al. Design and experimental study of concave longitudinal vibration piezoelectric ultra-sonic transducer[C]// 2020 3rd International Conference on Electron Device and Mechanical Engineering (ICEDME). Suzhou: IEEE, 2020: 565
|
| [11] |
胡理情, 林书玉.. 声子晶体结构在功率超声换能器中的应用[J]. 应用声学, 2021, 40(3): 323. HU Liqing, LIN Shuyu. Application of phononic crystal structure in power ultrasonic transducer[J]. Journal of Applied Acoustics, 2021, 40(3): 323. DOI:10.11684/j.issn.1000-310X.2021.03.001 |
| [12] |
张震. 引线焊接高频超声换能器的设计和模态频率的优化[D]. 杭州: 中国计量学院, 2013: 10 ZHANG Zhen. Design of high frequency ultrasonic transducer for wire bonding application and optimization of modal frequencies[D]. Hangzhou: China Jiliang University, 2013: 10 |
| [13] |
ABDULLAH A, SHAHINI M, PAK A. An approach to design a high power piezoelectric ultrasonic transducer[J]. Journal of Electro-ceramics, 2009, 22(4): 369. DOI:10.1007/s10832-007-9408-8 |
| [14] |
ARNOLD F J, MVHLEN S S. The mechanical pre-stressing in ultrasonic piezotransducers[J]. Ultrasonics, 2001, 39(1): 7. DOI:10.1016/S0041-624X(00)00048-2 |
| [15] |
DUBUS B, DUBUS J C, DECARPIGNY J N, et al. Analysis of mechanical limitations of high power piezoelectric transducers using finite element modelling[J]. Ultrasonics, 1991, 29(3): 201. DOI:10.1016/0041-624X(91)90057-F |
| [16] |
FENG Xinyu, ZHU Xijing, LI Xiangmeng. Analysis on digital automatic assembly technology under ultrasonic transducer[J]. International Journal of Mechatronics and Applied Mechanics, 2020, 1(8): 167. |
| [17] |
JIANG Xinggang, WANG Kaiqiang, ZHANG Deyuan. Determining the optimal pre-tightening force of a sandwich transducer by measuring resonance resistance[J]. Applied Acoustics, 2017, 118: 8. DOI:10.1016/j.apacoust.2016.11.009 |
| [18] |
张云电, 姚晓峰. 四立柱压电换能器装配机研制[J]. 机电工程, 2015, 32(7): 925. ZHANG Yundian, YAO Xiaofeng. Developing of four pillars piezo-electric transducer assembly machine[J]. Journal of Mechanical & Electrical Engineering, 2015, 32(7): 925. DOI:10.3969/j.issn.1001-4551.2015.07.007 |
| [19] |
ZHANG Yundian, WANG Peng. Developing of high-power sandwich type piezoelectric transducer automatic assembly machine[J]. Applied Mechanics and Materials, 2014, 602/603/604/605: 1034. DOI:10.4028/www.scientific.net/AMM.602-605.1034 |
| [20] |
ZHANG Yundian, YU Fang, CHEN Yan, et al. Study of constant torsion assembly method of piezoelectric transducer based on PC control[C]// IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications. Beijing: IEEE, 2006: 4077759. DOI: 10.1109/MESA.2006.296932
|
| [21] |
林书玉. 超声换能器的原理及设计[M]. 北京: 科学出版社, 2004: 91. LIN Shuyu. Principle and design of ultrasonic transducer[M]. Beijing: Science Press, 2004: 91. |
| [22] |
ABDULLAH A, PAK A. Correct prediction of the vibration behavior of a high power ultrasonic transducer by FEM simulation[J]. The International Journal of Advanced Manufacturing Technology, 2008, 39: 21. DOI:10.1007/s00170-007-1191-9 |
 2023, Vol. 55
2023, Vol. 55


