2. 中车戚墅堰机车车辆工艺研究所有限公司, 江苏 常州 213011
2. CRRC Qishuyan Institute Co., Ltd., Changzhou 213011, Jiangsu, China
在动车高速行驶的过程中,齿轮箱滚动轴承易发生裂纹、点蚀等故障,但由于运行工况复杂多变,使得所能采集到的故障信号往往具有非平稳的特点,转速的时变性进一步加剧了信号的非平稳性。滚动轴承的故障特征随转速分布在非平稳信号的各处,传统的故障诊断方法无法有效从中准确提取出故障特征。因此,从变转速信号中将滚动轴承的故障特征有效提取出来,对保障动车的安全行驶具有重要意义。
针对变转速下的轴承时变信号,文献[1]提出了使用短时傅里叶变换(short-time Fourier transform, STFT)的时频分析方法提取交流无刷电机中的球轴承故障特征。该方法在传统频谱分析法基础上引入时间窗,实现了对信号频率成分随时间变化的表征。文献[2]对齿轮箱中滚动轴承的变转速信号进行了STFT分析,并与脊线提取方法相结合,成功从复杂的时变信号中提取出转速变化曲线。但由于STFT时间窗为固定值,一经选取无法改变,因此时频分析中无法同时兼顾时间分辨率与频率分辨率。针对上述问题,文献[3]提出了基于快速路径优化的STFT分析方法,利用快速路径优化方法改善了STFT中的时间窗固定问题,获得了更为恰当的时频分辨率。但由于STFT仍属于线性时频分析方法,时频分辨率之间的矛盾性依旧无法有效解决。文献[4]采用了一种魏格纳-威尔分布(Winger- Ville distribution, WVD)的时频分析方法,实现了滚动轴承的故障诊断。该方法是利用二次变换的时频分析方法,虽然解决了STFT中窗函数带来的分辨率问题,但其本身在处理多分量信号时,会出现交叉项的干扰,为故障诊断结果带来影响。文献[5]将循环谱密度与WVD相结合,通过对滚动轴承故障信号的处理验证了该方法能很好地抑制WVD中的交叉项。文献[6]采用WVD、STFT等时频分析方法对滚动轴承非平稳信号进行了研究,并对比处理结果分析了这些方法各自的优缺点。时频分析方法虽然可以用来分析频率与时间的变化规律,但若需要进一步检测出滚动轴承是否发生故障,还需要和其他方法相结合,进行深入分析。文献[7]采用Crazy Climber算法对列车轴承的时变信号进行了频率脊线提取,从中筛选出转速曲线对应的成分,实现了对时变信号的阶次分析。但采用Crazy Climber算法得到的转速曲线与实际曲线存在较大误差,且效率较低。为解决上述问题,文献[8]对Crazy Climber算法在频率脊线提取时的移动规则进行了改进,并将其与STFT相结合,准确提取出故障特征,实现滚动轴承的故障诊断。但改进的Crazy Climber仍旧是对STFT时频矩阵进行脊线提取,受限于STFT本身的时频聚集性影响,会存在较大的转速脊线提取误差。
目前,如何有效、精确地提取出滚动轴承时变信号是故障诊断领域的关注重点。本文针对变转速工况下的滚动轴承时变信号,提出了一种基于融合时频分析算法的滚动轴承转速提取和故障诊断方法。将WVD的频率高聚集性和STFT无干扰项的优点相结合,得到时变信号的时频分布;并针对融合算法的特点,采用动态路径规划算法对时频分布结果进行处理,实现滚动轴承的转速提取;最后利用阶次分析方法,对滚动轴承进行故障诊断。滚动轴承的数值仿真与实验验证均表明了所提方法的可行性。
1 基于融合时频分析算法的变转速提取 1.1 融合时频分析算法STFT得到的时频矩阵没有交叉项的干扰,但时频聚集性无法兼得;而WVD恰恰相反,其时频矩阵能兼顾时频聚集性,但对多分量信号进行处理会产生交叉项。为获得时频聚集性良好的时频矩阵,以STFT和WVD为基础,提出了一种融合时频分析算法。
令滚动轴承的故障时变信号表示为s(t),则其STFT变换可表示为
| $ S(\tau, f)=\int_{-\infty}^{+\infty} s(t) \omega(t-\tau) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} t $ | (1) |
式中ω(t)为选取的窗函数。
式(1)中,STFT以固定的窗长将信号s(t)变换为时间和频率的二维函数,每段窗内的信号近似成平稳信号来处理,通过傅里叶变换得到局部特征,信号的时变性通过不同时刻的局部特征表现出来。如果所选窗长过大,信号的所有特征都会显示在当前时刻,无法体现瞬时频率随时间变化的特点;而当窗长短至一定程度,短时信号的频谱会很宽,此时时间分辨率会很精确,但频率分辨率很差。因此,对信号进行分析时,频率分辨率和时间分辨率满足Heisenberg测不准原理[9],是相互矛盾的,需要在这两者中进行取舍。
信号s(t)的WVD变化见下式:
| $ V_{\mathrm{WD}}(t, f)=\int_{-\infty}^{+\infty} s\left(t+\frac{\tau}{2}\right) \times s^*\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} \tau $ | (2) |
式中:s*(t)为函数s(t)的共轭,
在WVD算法中,选取了信号某点处前后等长度的部分进行乘积,s(t)出现了2次,并且没有使用窗函数进行截断,所以避免了时域和频域分辨率矛盾的现象,二者可以同时拥有较优表现。但在针对多分量信号时,WVD缺乏可加性, 如含有3个分量的信号s(t)=s1(t)+s2(t)+s3(t),对其进行WVD将得到如下结果:
| $ \begin{aligned} V_{\mathrm{WD}=} & V_{\mathrm{WD}_1}(t, f)+2 \operatorname{Re}\left|V_{\mathrm{WD}_1 \mathrm{WD}_2}(t, f)\right|+ \\ & 2 \operatorname{Re}\left|V_{\mathrm{WD}_1 \mathrm{WD}_3}(t, f)\right|+2 \operatorname{Re}\left|V_{\mathrm{WD}_2 \mathrm{WD}_3}(t, f)\right|+ \\ & V_{\mathrm{WD}_2}(t, f)+V_{\mathrm{WD}_3}(t, f) \end{aligned} $ | (3) |
式中:
若初始信号含有3个分量,会产生3个交叉项,而n个分量则会产生Cn2个交叉项,这些交叉项在时频面内产生振荡,会使得时频图内出现假频、模糊等现象。
上述2种算法有各自的优缺点,为使得到的时频图有较高的时间-频率分辨率,同时降低交叉项的干扰,本文将其优点相结合,形成了融合时频分析算法。
考虑到2种变换的幅值尺度不尽相同,因此在得到融合算法前,需要对二者的时频矩阵各自进行归一化处理:
| $ \boldsymbol{T}^*(t, f)=\frac{\boldsymbol{T}(t, f)-\boldsymbol{T}_{\min }(t, f)}{\boldsymbol{T}_{\max }(t, f)-\boldsymbol{T}_{\min }(t, f)} $ | (4) |
式中:Tmax(t, f)为时频矩阵中的最大值,Tmin(t, f)为时频矩阵中的最小值,T*(t, f)是对时频矩阵进行归一化处理后的结果。
时频矩阵中能量最高点所对应的能量记为1,能量最小点所对应的能量记为0,其余能量通过式(4)的归一化方法进行尺度转化,转化后的取值均介于0~1之间。不同时频分析方法得到的时频矩阵存在能量尺度的差异,通过式(4)的归一化后,能量尺度得到了统一。
在一个时频域内,当且仅当WVD及STFT的时频图都存在明显时频特征,信号在该时间及频率下的能量分布才是真实的;若WVD及STFT的结果均不存在明显时频特征,则表明信号在该时间及频率下无能量分布;若WVD时频特征明显但是STFT在该处没有明显特征,则说明WVD中该时频特征为交叉项;若STFT中时频成分明显而WVD没有,则是因为STFT的时频聚集性不如WVD差,能量过于分散。为此,提出融合STFT与WVD的算法如下:
| $ \begin{aligned} \boldsymbol{T}_3= & \min \left[\min \left(\boldsymbol{T}_1(t, f), \boldsymbol{T}_2(t, f)\right) \times\left(\boldsymbol{T}_1(t, f)+\right.\right. \\ & \left.\left.\boldsymbol{T}_2(t, f)\right), 1\right] \end{aligned} $ | (5) |
式中:min为二者比较取较小值的函数命令,T1为对STFT进行归一化后的结果,T2为对WVD进行归一化后的结果,T3为融合算法得到的结果。该融合算法得到的结果保留了WVD时频聚集性高的优势,且大大降低交叉项对后续分析的影响。
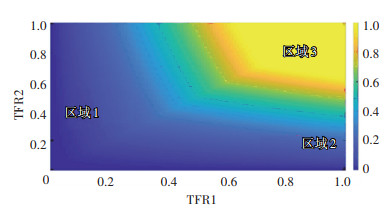
图 1为式(5)的融合时频能量分布示意,TFR1表示模拟的STFT能量大小,区间为[0, 1];TFR2表示模拟的WVD能量大小,区间为[0, 1];示意图的能量分布区间为[0, 1]。从图 1中可以发现,区域1代表WVD能量高而STFT能量低,这表示WVD产生了如式(3)所示的交叉项,通过式(5)的算法可将交叉项带来的能量虚假成分滤除;区域2代表STFT能量高而WVD能量低,这是由于式(1)中STFT算法采用窗函数导致了能量分散,通过式(5)同样可以将该区域的能量抑制。区域3的能量显著高于区域1和区域2,该区域代表WVD与STFT均具有较高的能量,此时便可认为该区域内的能量成分是真实有效的,式(5)的运算将该区域的能量很好地显示出来。
|
图 1 融合时频矩阵能量示意 Fig. 1 Schematic of fusion time-frequency matrix energy |
在获得融合时频矩阵后,需要准确地将矩阵中转速相关信息提取出来。本文采用动态路径规划方法对融合时频矩阵进行转速曲线的提取[10]。在动态路径规划算法中,代价函数的构造直接关系到最终提取出的转速结果,传统的代价函数见式(6):
| $ \begin{gathered} \boldsymbol{F}\left[\boldsymbol{T}_3\left(t_n, f_m\right), f_m, f_k\right]=\lg \left(\boldsymbol{T}_3\left(t_n, f_m\right)\right)- \\ \alpha\left|f_m-f_k\right| \end{gathered} $ | (6) |
式中:T3(tn, fm)是1.1节中的融合时频矩阵,α为权重系数,fm与fk分别为不同时刻的频率。
由于本文采用了归一化后的融合时频分析算法,时频矩阵的取值范围为[0, 1],这导致式(6)中代价函数的对数函数项的计算值均为负数,且部分能量接近0的位置所对应的lg函数取值接近于负无穷,严重影响了该算法的可行性。为了能够使该算法适用于融合时频分布矩阵,将式(6)的代价函数进行了改进,得到下式:
| $ \begin{gathered} \boldsymbol{F}\left[\boldsymbol{T}_3\left(t_n, f_m\right), f_m, f_k\right]=\exp \left(\boldsymbol{T}_3\left(t_n, f_m\right)\right)- \\ \alpha\left|f_m-f_k\right| \end{gathered} $ | (7) |
在保留原对数函数单调递增特性的前提下,将其替换为指数函数ex,对应的取值范围在[1, e]之间,解决了归一化后代价函数均为负数的问题。
改进的动态路径规划方法的具体思路如下:
1) 采用对数变换的形式对各点幅值进行重构,同时为抑制相邻时刻的脊线频率跳动,构造权重系数α对其进行调制。
2) 定义2个与时频矩阵维数相同的N×M维空矩阵Q和U。其中U矩阵为计量矩阵,用于存储代价函数计算得到的累加值;Q矩阵为度量矩阵,用于存储频率的位置序号,该序号取决于当前时刻与上一时刻代价函数值相累加得到的最大值位置。其计算式如下:
| $ \left\{\begin{array}{l} \boldsymbol{Q}(n, 1)=0, n=1, 2, \cdots, N \\ \boldsymbol{Q}(n, m)=\underset{k}{\operatorname{argmax}}\left\{\boldsymbol{F}\left[\boldsymbol{T}_3\left(t_n, f_m\right), f_m, f_k\right]+\boldsymbol{U}\left(t_{n-1}, f_k\right)\right\} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m=2, 3, \cdots, M ; k=1, 2, \cdots, M \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} \boldsymbol{U}(n, 1)=\lg \left(\boldsymbol{T}_3\left(t_n, f_1\right)\right), n=1, 2, \cdots, N ; k=1 \\ \boldsymbol{U}(n, m)=\boldsymbol{F}\left[\boldsymbol{T}_3\left(t_n, f_m\right), f_m, f_{\boldsymbol{Q}(n, k)}\right]+\boldsymbol{U}(n-1, \boldsymbol{Q}(n, k)) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m=1, 2, \cdots, M ; k=2, \cdots, M \end{array}\right. $ | (9) |
3) 结合度量矩阵Q和计量矩阵U。首先以矩阵U最后一列作为起始搜索点,选取其最大值的位置作为起点,记D(M);接下来寻找该点对应的矩阵Q中的元素值,以此值作为追踪线索确定上一时刻的最佳脊点位置。以此类推,最终得到全时刻最佳脊点位置集合D,结合式(10)计算最佳脊线:
| $ R=D \times \Delta f $ | (10) |
式中Δf为时频分布中频率的分辨率。
2 基于插值重采样的阶次分析方法在成功提取出转速信号后,需要根据转速信号对原时变信号进行阶次分析。传统的阶次分析的核心方法是基于角域采样理论[11],利用转速信号构建累积转动角度,随后根据角度信息对初始时变信号进行重采样。由于计算的转角与真实转角容易产生较大误差,因此对最终计算精度会产生影响。为了提高阶次计算的精度和效率,本文对阶次分析的重采样方法进行了改进,直接利用转速信息重构变转速信号的时间轴,并以新的时间轴对原信号进行插值拟合,实现非平稳信号到平稳信号的转变。
若所采集的滚动轴承故障信号为x[k],采样频率为fs,初始的采样时间间隔为t[k],提取的转速变化曲线为r[k],由于采样频率固定,采样时间的表达式如下:
| $ t[k]=k / f_{\mathrm{s}} $ | (11) |
利用拉伸采样的方法对信号在时域上进行拉伸处理,使得拉伸后信号的时间与转速相关:
| $ \begin{aligned} \hat{t}[k]= & \hat{t}[k-1]+\Delta \hat{t}[k]=\hat{t}[k-1]+ \\ & r^{\prime}(t[k]) \Delta t \end{aligned} $ | (12) |
式中:
当滚动轴承处于匀加速运动状态时,
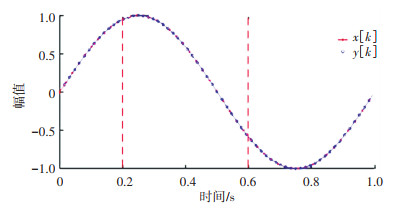
信号的插值重采样结果见图 2。这里假设插值重采样的频率为fr,分析的信号最大阶次为Omax,最终得到的插值新数组为y[k]。采样频率在此依旧需要满足奈奎斯特采样定理fr≥2Omax,重采样后的插值时间tr[n]表达式为
|
图 2 插值重采样示例 Fig. 2 Example of interpolation resampling |
| $ t_{\mathrm{r}}[n]=n / f_{\mathrm{r}}, n=1, 2, \cdots, k $ | (13) |
三次样条插值对应的插值函数为
| $ x(t)=a+b t+c t^2+d t^3 $ | (14) |
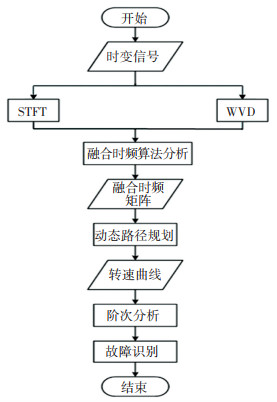
算法具体流程为:1)对时变信号分别采用STFT和WVD进行变换,将得到的2组时频矩阵归一化融合,得到1组新的时频分布矩阵;2)对时频分布矩阵采用动态路径规划方法,提取出其中的转速信息成分;3)根据转速信息对时变信号进行阶次分析,判别其是否存在故障特征,达到滚动轴承变转速下的故障诊断目的。流程见图 3。
|
图 3 滚动轴承时变信号故障诊断流程图 Fig. 3 Flow chart of time-varying signal fault diagnosis for rolling bearing |
为验证本文算法在提取转速瞬时频率方面的准确性,设计了一个含有2个分量的仿真信号:
| $ \begin{aligned} x= & \sin \left(2 \pi \times\left(10 t+15 t^2\right)\right)+2 \sin (2 \pi \times(30 t+ \\ & \left.\left.45 t^2\right)\right) \end{aligned} $ | (15) |
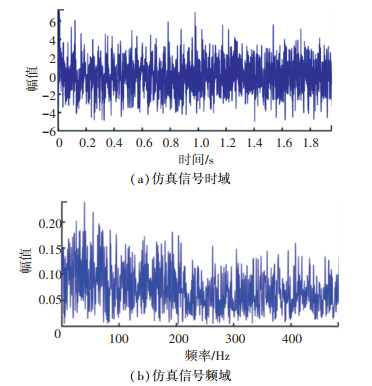
式中:设定的采样频率fs为1 000,构建的数组长度为2 048。构造的信号转频为10+30t,加入信噪比为-4 dB的高斯白噪声,信号的时域、频域见图 4。
|
图 4 仿真信号时频域 Fig. 4 Time and frequency domain of simulation signal |
图 4中,由于仿真信号的频率随时间发生变化,转速频率的变化范围从0至61.44 Hz均存在能量,导致频谱成分模糊,无法提取出有效信息。下面对该信号分别进行STFT和WVD变换。
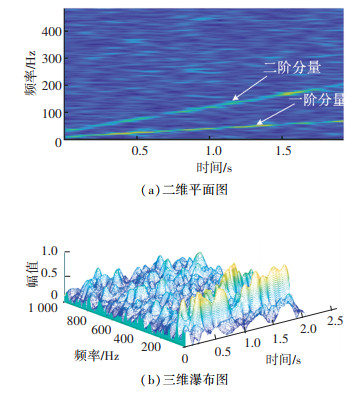
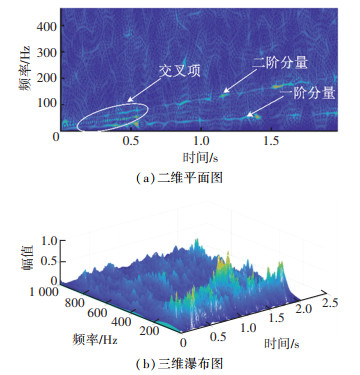
图 5和图 6分别为STFT与WVD的时频分布结果。可以发现,图 5(a)中STFT的时频图没有干扰项,但是2组分量的瞬时频率曲线频率段模糊,时频聚集性不高;而图 6(a)中WVD的时频图聚集性较高,但却出现了交叉项,且交叉项的能量不低,会对后续时频矩阵的分析处理产生影响。此外,从图 5(b)与图 6(b)的瀑布图可以发现,噪声成分的幅值较高,且噪声分布在各频段中,由此看出使用单一时频分析方法得到的时频图信噪比很低。同时,由于噪声成分之间也会产生交叉项,故图 6(b)中的瀑布图相较于图 5(b)更为复杂。
|
图 5 STFT时频图 Fig. 5 STFT time-frequency diagram |
|
图 6 WVD时频图 Fig. 6 WVD time-frequency diagram |
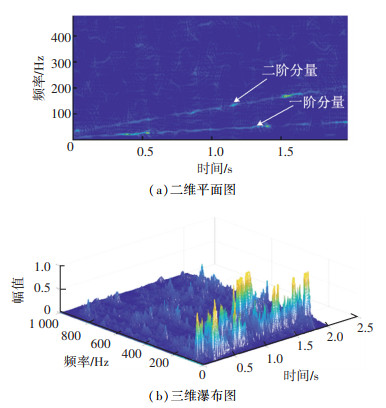
融合算法时频分布见图 7。图 7(a)中,噪声产生的影响被极大地抑制,交叉项的干扰也消失了,并且时频聚集性相较于STFT与WVD,有了显著的提升,可以清晰地看出2条瞬时频率变化曲线。相比图 5(b)与图 6(b),图 7(b)的瀑布图呈现出更高的信噪比,噪声成分的幅值更低,且噪声的分布范围也有所减小。
|
图 7 融合算法时频图 Fig. 7 Time-frequency diagram of fusion algorithm |
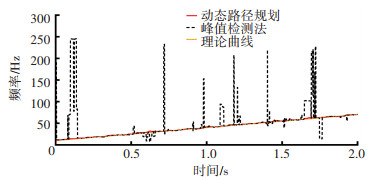
图 8是对融合算法得到的时频矩阵进行瞬时频率提取后得到的频率曲线。其中,由改进的动态路径规划算法得到的瞬时频率与理论值几乎一致,而当采用传统峰值检测法时,由于噪声的干扰并未完全消除,提取的瞬时频率会产生巨大误差。
|
图 8 同方法提取的瞬时频率 Fig. 8 Instantaneous frequency extracted by different methods |
为了直观地表现出不同强度噪声下提取瞬时频率的准确性,采用相对误差计算方法[14]来定量地表现不同方法的估计值与理论值偏差。相对误差计算式如下:
| $ \xi=\frac{\left\|F_{\text {req }}(t)-F_{\text {req }}^{\prime}(t)\right\|_2}{\left\|F_{\text {req }}(t)\right\|_2} \times 100 \% $ | (16) |
式中:Freq(t)为通过算法提取的转速曲线,Freq′(t)为理论的转速曲线,ξ为相对误差。
不同噪声强度下,2种方法提取脊线的误差见图 9。随着信噪比逐渐降低,噪声对信号的干扰也逐渐增强,当信噪比达到-7 dB以后,通过峰值检测法提取的脊线误差几乎趋于100%,而采用动态路径规划方法提取的脊线误差依旧很低。由此可见,本文所提方法对噪声的鲁棒性更强。

|
图 9 不同强度噪声下的相对误差 Fig. 9 Relative error under different intensity noise |
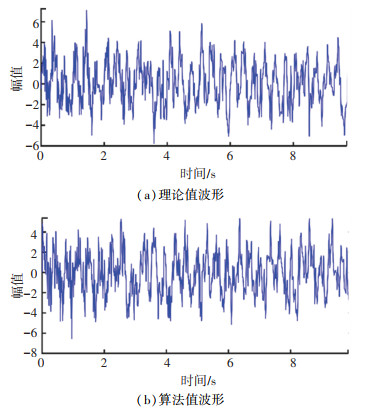
分别以理论转频脊线和通过动态路径规划算法提取出的转频脊线作为转频基准,对仿真信号的时域进行拉伸,变换后的信号波形见图 10。由于算法与理论值的误差不大,故图 10(a)~(b)在波形上的差异并不明显,但通过算法提取转频,并对时域拉伸后,信号的能量有所降低。随后,对拉伸后的信号进行插值重采样,其傅里叶变换后的频谱对应的便是仿真信号的阶次谱。
|
图 10 时域拉伸后的波形 Fig. 10 Waveform after time domain stretching |
插值重采样率fr设定为50,并对图 10的信号进行重采样,最终得到如图 11所示的2组阶次谱。图 11(a)对应图 10(a)信号的阶次谱,图 11(b)对应图 10(b)信号的阶次谱。图 10中能量降低的现象在图 11中表现得更为直观。

|
图 11 仿真信号阶次谱 Fig. 11 Simulation signal order spectrum |
表 1从计算精度及计算耗时2个方面对基于插值重采样的阶次分析和传统的阶次分析方法进行比较。表中列举了通过不同方法得到的阶次谱,并与理论阶次谱进行对比,由于计算精度,理论转频对应的实际阶次谱与设定值存在细微的偏差。当采用通过算法得到的转频进行阶次分析时,与原信号的理论阶次仅存在2%的误差,同时幅值都有一定的降低。而传统的重采样方法耗时长,与理论阶次之间的误差高于本文所提方法。综合阶次精度以及计算耗时,本文所提的插值重采样方法误差低,计算耗时减少了18%,并且当提取的转频与理论转频有误差时,对阶次分析的影响程度较小。
| 表 1 不同采样方法的计算结果 Tab. 1 Calculation results of different sampling methods |
考虑到实际工况中信号成分更为复杂,为进一步验证基于融合算法的动态路径规划瞬时频率提取方法的可靠性,与中车戚墅堰机车车辆工艺研究所有限公司合作搭建了动车组齿轮箱滚动轴承试验台,并对产生外圈裂纹缺陷的滚动轴承进行了变转速实验分析。
图 12是试验台的整体结构。该试验台与实际动车组上的齿轮箱尺寸结构相同,主要由高速驱动电机、纵向旋转枢轴、支撑轴承座等装置组成。

|
1—被测齿轮箱;2—被测齿轮箱轴承支座;3—吊挂支撑;4—联轴器;5—高速驱动电机;6—驱动电机支承座 图 12 滚动轴承试验台 Fig. 12 Rolling bearing test bench |
实验中,电机带动测试轴以0~50 Hz的转速转动,电机与测试轴承之间的转速传动比为2.5。选择NU1007圆柱滚子轴承进行研究,故障轴承放置在齿轮箱大端。传感器使用振动加速度传感器,放置位置见图 13。传感器的型号为608A11,频率响应范围为0.5~10 kHz,传感器的分辨率为350 μg,实验中设置的采样频率为20 kHz。选择图 13中的大端轴承传感器的纵向信号进行分析。轴承参数见表 2。

|
1—小端轴承传感器;2—大端轴承传感器 图 13 振动加速度传感器布置位置 Fig. 13 Layout of vibration acceleration sensors |
| 表 2 NU1007轴承参数 Tab. 2 NU1007 bearing parameters |
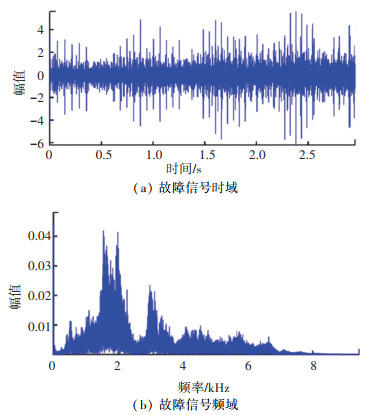
图 14是采集的一段滚动轴承外圈裂纹故障信号。故障裂纹深为0.177 mm,电机转频变化范围从34.85 Hz逐渐升高至48.95 Hz,对应的滚动轴承转频变化范围为[13.94, 19.85]。从图 14(a)的时域波形可以看出该段信号是处于升速运动阶段。随着转速的提升,故障冲击能量不断增强,振幅不断升高,滚动体每次撞击故障裂纹处的时间间隔逐渐减小,故障频率逐渐升高。图 14(b)是该信号所对应的频域波形,由于变转速工况,故障特征频率在[96.2, 135.1]范围内随转速变化,不再是固定值。整体的频域波形因转速的变化而模糊,无法有效识别故障频段。由于高频段的能量明显高于转速所处的频率范围,在对信号进行时频分析前,设计一个低通滤波器。为尽可能保留转速瞬时旋转频率(instantaneous rotation frequency, IRF)及其倍频,在此设置低通滤波器的通带为150 Hz,阻带衰减为80 dB。此外,由于采样点数过大,对时频分析的效率产生一定的影响,故先对滤波后的信号以低采样频率进行重采样,再进行时频分析,重采样频率为1 024 Hz。
|
图 14 外圈裂纹故障轴承信号 Fig. 14 Outer race fault of bearing signal |
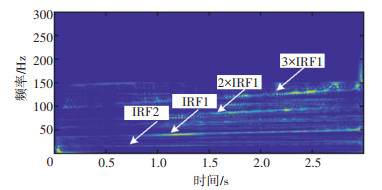
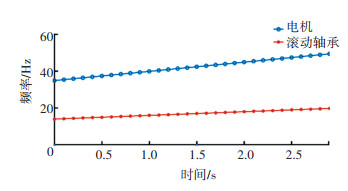
图 15是通过融合算法得到的时频,IRF1表示电机转速的瞬时旋转频率,IRF2表示滚动轴承的瞬时旋转频率。可以看到IRF1的分量最为明显,聚集性相对较高。此外,IRF1的2倍频与3倍频能量也较为显著,相比之下滚动轴承对应的IRF2分量能量较弱,因该分量与电机转速存在倍数关系,只需将最终提取出的电机转速除以2.5即可得到滚动轴承的转速变化曲线。提取的转速变化曲线见图 16。
|
图 15 融合算法时频 Fig. 15 Time-frequency of fusion algorithm |
|
图 16 转速曲线 Fig. 16 Speed curves |
实验截取的信号IRF1对应的转速频率变化范围为34.48~49.53 Hz。对提取的曲线通过拟合平滑,电机转频IRF1的曲线表达式可以近似为5t+34.85,滚动轴承转频为电机转频的1/2.5,与理论值误差在0.81%,可能是由于设备受实际加工、安装精度影响或电机旋转过程中的能量损耗。为了识别滚动轴承是否发生故障,以滚动轴承故障特征阶作为故障特征指标[15]。外圈发生裂纹故障时,滚动轴承的故障特征阶见下式:
| $ \begin{aligned} F_{\text {out }}= & Z \frac{\left|\omega_{\mathrm{o}}+\omega_{\mathrm{c}}\right|}{2 \pi I}= \\ & Z \frac{(D-d \cos \alpha)\left|\omega_{\mathrm{o}}-\omega_{\mathrm{i}}\right|}{4 D \pi I}= \\ & \frac{Z}{2}\left(1-\frac{d \cos \alpha}{2}\right) \end{aligned} $ | (17) |
式中:ωo、ωi、ωc分别为轴承的外圈角速度、内圈角速度以及保持架带动滚动体转动的角速度,Z为滚动体的个数,d为滚动体的直径,D为轴承的节径,α为轴承滚动体与内外滚道接触点所受的载荷与轴承径向平面之间的接触角,I为滚动轴承的转速。
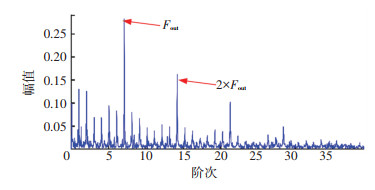
根据表 2中滚动轴承数据可知,当滚动轴承外圈发生故障时,对应的故障特征阶为6.9。图 17是根据提取转速对滚动轴承的故障信号进行阶次分析的阶次谱。其中,谱峰位于6.9阶次处,对应滚动轴承外圈故障特征阶,次谱峰位于13.8阶次处,对应滚动轴承外圈故障特征阶的2倍频。
|
图 17 轴承故障信号阶次谱 Fig. 17 Order spectrum of bearing fault signal |
为进一步验证所提方法的可行性,对一组无故障信号进行处理,将结果与外圈故障信号的处理结果相比较。
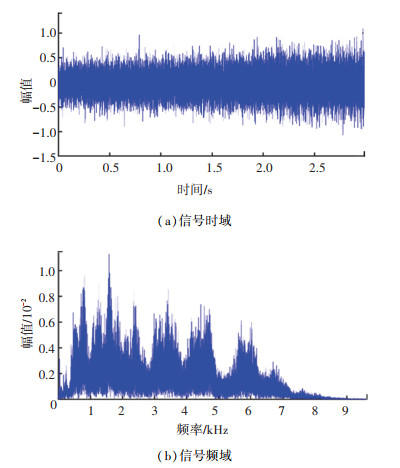
如图 18所示,是一组正常状态下运行的滚动轴承信号。图 18(a)是其时域,从图 18(a)中可以发现,幅值有着明显的上升趋势,但时域中不存在和图 14(a)相似的冲击间隔。这是由于正常状态下的轴承随转速升高,对应的能量也会有所提升,但由于不存在故障缺陷,滚动轴承每旋转一圈都是随机的无规则运动,故时域信号不存在明显规律。图 18(b)是该信号的频域,该频域中的能量相较图 14(b)的能量更低,且频率成分随变转速运动,在频域内更为分散。这同样是因为不存在故障的情况下,轴承旋转一圈不再产生冲击,运动的不规律性直观地表现为频率的分散性。
|
图 18 无故障轴承信号 Fig. 18 Fault free bearing signal |
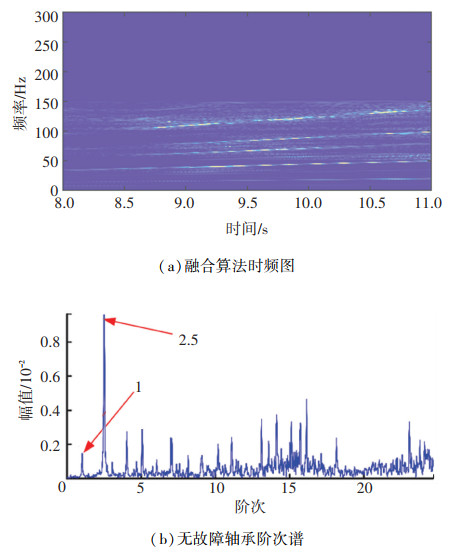
图 19是对无故障轴承进行转速提取与阶次分析的结果。图 19(a)是对无故障轴承信号进行的融合时频算法分析,从图中可以清晰地看到电机转速IRF1和轴承转速IRF2相对较为微弱,同样提取出电机转速IRF1后,通过倍数关系便可得到滚动轴承的转速。在提取出滚动轴承转速后,通过本文所提插值重采样方法,得到如图 19(b)所示的阶次谱。阶次谱中,幅值最为明显的地方位于2.5阶次处,由于该阶次谱是根据滚动轴承转速进行重构的,阶次为1处对应的是滚动轴承自身转速特征阶,其2.5倍位置对应的恰好是电机转速特征阶,该处特征与图 19(a)中电机转速最为明显相呼应。此外,在滚动轴承外圈故障特征阶6.9对应的位置不存在谱峰,说明该轴承不存在外圈故障。
|
图 19 无故障轴承阶次分析 Fig. 19 Order analysis of fault free bearing |
对比图 19(b)和图 17,当存在外圈故障时,滚动轴承每旋转一圈均会产生冲击,使得阶次谱中对应的故障特征阶具有明显的幅值,且由于冲击能量相较轴承自身旋转能量偏高,使得故障特征阶位于阶次谱的谱峰处(图 17);而无故障轴承在运行时,故障特征阶由于不存在故障冲击,在阶次谱中十分微弱,阶次谱中比较明显的成分是电机与滚动轴承转速所对应的特征阶(图 19(b))。因此,本文所提方法可以有效识别出滚动轴承在变转速工况下的故障。
6 结论1) 提出了一种滚动轴承故障诊断方法。首先通过融合时频分析得到变转速故障信号的时频矩阵,再利用改进的动态路径规划方法提取出转速曲线,最后以转速曲线对时变信号进行插值重采样,实现滚动轴承的故障诊断。
2) 所提方法不仅适用于分析动车组齿轮箱滚动轴承的故障信号,还可用于分析诊断各类旋转机械的故障,如风电齿轮箱、机床等。此外,本文所处理的信号是通过加速度传感器采集的振动信号,该方法同样适用于分析通过声音传感器采集设备的声音故障信号。
3) 针对实际工况中采集到的包含强背景噪声的故障信号,需要对采集的信号先进行降噪预处理,随后再使用本文方法对降噪后的信号进行处理,同样可以得到较好的故障诊断结果。
| [1] |
COCCONCELLI M, ZIMROZ R, RUBINI R, et al. STFT based approach for ball bearing fault detection in a varying speed motor[M]. Berlin: Springer, 2012: 41.
|
| [2] |
LIU Chang, CHENG Gang, LIU Bing, et al. Bearing fault diagnosis method with unknown variable speed based on multi-curve extraction and selection[J]. Measurement, 2020, 153: 107437. DOI:10.1016/j.measurement.2019.107437 |
| [3] |
包文杰, 涂晓彤, 李富才, 等. 参数化的短时傅里叶变换及齿轮箱故障诊断[J]. 振动、测试与诊断, 2020, 40(2): 272. BAO Wenjie, TU Xiaotong, LI Fucai, et al. Parametric short time Fourier transform and gearbox fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(2): 272. DOI:10.16450/j.cnki.issn.1004-6801.2020.02.009 |
| [4] |
陈维兴, 孙习习, 王涛. 基于SPWVD-CNN的滚动轴承故障诊断[J]. 机床与液压, 2020, 48(12): 147. CHEN Weixing, SUN Xixi, WANG Tao. Fault diagnosis for rolling bearings based on SPWVD-CNN[J]. Machine Tool & Hydraulics, 2020, 48(12): 147. DOI:10.3969/j.issn.1001-3881.2020.12.021 |
| [5] |
ZHOU Y, CHEN J, DONG G M, et al. Wigner-Ville distribution based on cyclic spectral density and the application in rolling element bearings diagnosis[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225(12): 2831. DOI:10.1177/0954406211413215 |
| [6] |
KIM B S, LEE S H, LEE M G, et al. A comparative study on damage detection in speed-up and coast-down process of grinding spindle-typed rotor-bearing system[J]. Journal of Materials Processing Technology, 2007, 187: 30. DOI:10.1016/j.jmatprotec.2006.11.222 |
| [7] |
王超, 孔凡让, 胡飞, 等. Crazy Climber算法与重采样技术在消除多普勒效应及列车轴承诊断中的应用[J]. 振动工程学报, 2014(5): 770. WANG Chao, KONG Fanrang, HU Fei, et al. Application of Crazy Climber algorithm and re-sampling technique in the Doppler effect removal and train bearings diagnosis[J]. Journal of Vibration Engineering, 2014(5): 770. DOI:10.3969/j.issn.1004-4523.2014.05.018 |
| [8] |
陈剑, 杨斌, 黄凯旋, 等. 一种脊线提取方法在轴承故障诊断中的应用[J]. 中国机械工程, 2021, 32(10): 1157. CHEN Jian, YANG Bin, HUANG Kaixuan, et al. Applications of a ridgeline extraction method in bearing fault diagnosis[J]. China Mechanical Engineering, 2021, 32(10): 1157. DOI:10.3969/j.issn.1004-132X.2021.10.003 |
| [9] |
张宇辉, 刘梦婕, 黄南天, 等. 频率切片小波变换在局部放电信号分析中的应用[J]. 高电压技术, 2015, 41(7): 2283. ZHANG Yuhui, LIU Mengjie, HUANG Nantian, et al. Application of frequency slice wavelet transform in partial discharge signal analysis[J]. High Voltage Engineering, 2015, 41(7): 2283. DOI:10.13336/j.1003-6520.hve.2015.07.023 |
| [10] |
IATSENKO D, MCCLINTOCK P V E, STEFANOVSKA A. Extraction of instantaneous frequencies from ridges in time-frequency representations of signals[J]. Signal Processing: The Official Publication of the European Association for Signal Processing (EURASIP), 2016, 1(24): 290. DOI:10.1016/j.sigpro.2016.01.024 |
| [11] |
EL BADAOUI M, BONNARDOT F. Impact of the non-uniform angular sampling on mechanical signals[J]. Mechanical Systems and Signal Processing, 2014, 44(1/2): 199. DOI:10.1016/j.ymssp.2013.10.008 |
| [12] |
YAN Cang, ZHANG Rubo. The application of short time fractional Fourier transform in processing underwater multi-frequency LFM signal[C]// Proceedings of 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference. Harbin: IEEE, 2011: 1472. DOI: 10.1109/CSQRWC.2011.6037244
|
| [13] |
FYFE K R, MUNCK E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997, 11(2): 187. DOI:10.1006/mssp.1996.0056 |
| [14] |
HU Yue, TU Xiaotong, LI Fucai, et al. An adaptive and tacholess order analysis method based on enhanced empirical wavelet transform for fault detection of bearings with varying speeds[J]. Journal of Sound and Vibration, 2017, 409: 241. DOI:10.1016/j.jsv.2017.08.003 |
| [15] |
王天杨, 李建勇, 程卫东. 基于瞬时故障特征频率趋势线和故障特征阶比模板的变转速滚动轴承故障诊断[J]. 振动工程学报, 2015, 28(6): 1006. WANG Tianyang, LI Jianyong, CHENG Weidong. The instan-taneous fault characteristic frequency and fault characteristic order template based fault diagnosis algorithm for rolling bearing under time-varying rotational speed[J]. Journal of Vibration Engineering, 2015, 28(6): 1006. DOI:10.16385/j.cnki.issn.1004-4523.2015.06.020 |
 2023, Vol. 55
2023, Vol. 55


