2. 河北省电力机械装备健康维护与失效预防重点实验室(华北电力大学), 河北 保定 071003
2. Hebei Key Laboratory of Electric Machinery Health Maintenance & Failure Prevention (North China Electric Power University), Baoding 071003, Hebei, China
在早春或初冬,由于过冷水滴撞击到导线形成水膜并冻结的自然现象被称为输电线覆冰[1-2]。覆冰常常导致输电线路倒杆、倒塔、导线断线和舞动等一系列重大事故,严重威胁电力系统安全平稳运行[3-6]。现有积冰研究主要集中在飞机结冰,对输电线覆冰的讨论还停留在二维时不变模型上。与飞机结冰主要发生在高速和小液滴条件下不同,输电线结冰发生在风速较低且液滴尺寸较大的条件下。因此,有必要针对输电线三维变参数积冰模型进行研究。
目前针对输电线路导线覆冰机理的研究,主要从流体力学和热力学两个角度进行。热力学观点中,输电线覆冰是液态过冷水释放潜热固化的过程,热量交换与传递在其中起到重要的作用,导线表面的覆冰形状、覆冰质量与密度等都取决于覆冰表面的热平衡状态[7-8]。文献[9]运用热力学原理分析了雨凇形成过程的热现象;文献[10]通过计算撞击到圆柱表面上的水流量函数及求解积冰表面热平衡方程,导出适用范围更广的积冰模型;文献[11-12]提出积冰表面的热平衡方程,并以此建立数值模型来研究积冰与气象条件的关系;文献[13]对输电线覆冰的形态进行研究,指出覆冰过程需要充分考虑固液相变的热平衡方程;文献[14-16]提出一种新的二维积冰模型来计算输电线上积冰过程,并通过一系列风洞试验验证了该模型;文献[1]首次基于润滑理论建立了考虑水膜厚度、冰厚、导体运动和传热等因素的二维雨凇积冰模型,并讨论了水膜流动对输电线覆冰的影响。
流体力学的观点认为,输电线上覆冰是导线捕获气流中过冷水滴的一种随机物理现象。文献[17]计算出了液滴流经圆柱体表面的轨迹;文献[18]提出了覆冰类型与环境温度、风速和空气中液态水含量的关系;文献[19]发现在覆冰表面水膜的回流并形成积冰;文献[20-22]建立了由重力、表面张力和空气剪切力驱动水膜在冰层上运动的模型,并发现水膜流动数值计算结果与试验结果相符,为典型的自由表面薄膜流动;文献[23]将Myers的模型扩展为一种隐式-显式计算方法来计算三维曲面上的积冰过程,验证结果表明,该方法可以得到与基于Messinger理论提出的LEWICE模型相近的结果。
上述研究多为二维不变参数模型,并未考虑实际覆冰环境中复杂的气象条件。为提高计算的准确性,本文提出了基于Fluent和ICING软件的三维导线时变参数积冰计算法,通过引入真实输电导线积冰试验数据验证模型有效性,并重点研究输电线倾斜角度、导线直径对导线覆冰形貌、积冰质量的影响。
1 ICING积冰理论 1.1 基本方程ICING[24-25]集成液滴收集效率、传热系数及水膜流动控制方程。对于冰面顶部有液态水的结冰环境,水膜流动可利用Navier-Stokes方程对流体层的运动进行计算,并基于润滑理论进行简化。对于在低风速不可压缩流体的仿真模拟中,ICING也可以对相应情况进行计算。
1) 流场计算模型。对于流场计算,通常选择Spalart-Allmaras[26]湍流模型,该模型非常适合模拟导线、风力涡轮机和飞机结冰期间的气流。
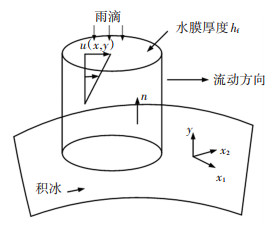
2) 水膜运动方程。图 1为液滴撞击覆冰导线形成相应水膜的示意。由于气流和重力产生的剪切应力,水膜会在冰面流动。水膜速度是表面坐标x=(x1, x2)和y(法线)的函数。引入垂直于壁面法线的水膜速度vf(x, y)的线性剖面。同时,为了简化问题,在壁面处设置速度为0。
|
图 1 水膜流动示意 Fig. 1 Schematic of water film flow |
| $ \boldsymbol{v}_{\mathrm{f}}(\boldsymbol{x}, y)=\frac{y}{\mu_{\mathrm{f}}} \boldsymbol{\tau}_{\text {wall }}(\boldsymbol{x}) $ | (1) |
式中τwall为水膜所受切向力的合力。
在所有固体表面上分别求解质量守恒和能量守恒2个偏微分方程。
3) 质量守恒方程。质量守恒偏微分方程见式(2),右侧3项分别对应于水滴撞击(水膜来源)、蒸发逃离和积冰(水膜冻结)的传质。
| $ \rho_{\mathrm{f}}\left[\frac{\partial h_{\mathrm{f}}}{\partial t}+\nabla \cdot\left(v_{\mathrm{f}} h_{\mathrm{f}}\right)\right]=v_{\infty} \omega_{\mathrm{LWC}} \beta-\dot{m}_{\text {evap }}-\dot{m}_{\text {ice }} $ | (2) |
式中:
4) 能量守恒方程。能量守恒偏微分方程见式(3),右侧前3项模拟了由过冷水滴撞击、蒸发和积冰产生的热传递;后3项为耗散、对流和一维传导热通量。
| $ \begin{aligned} & \rho_{\mathrm{f}}[\left.\frac{\partial h_{\mathrm{f}} c_{\mathrm{f}} T}{\partial t}+\nabla \cdot\left(v_{\mathrm{f}} h_{\mathrm{f}} c_{\mathrm{f}} T_{\mathrm{f}}\right)\right]=\left[c_{\mathrm{f}}\left(T_{\infty}-T_{\mathrm{f}}\right)+\right. \\ &\;\;\;\;\left.\frac{\left\|v_{\mathrm{d}}\right\|^2}{2}\right] v_{\infty} \omega_{\mathrm{LWC}} \beta-L_{\text {evap }} \dot{m}_{\text {evap }}+ \\ &\;\;\;\;\left(L_{\text {fusion }}-c_{\mathrm{s}} T\right) \dot{m}_{\text {ice }}+\sigma \varepsilon\left(T_{\infty}^4-T_{\mathrm{f}}^4\right)- \\ &\;\;\;\; c_{\mathrm{h}}\left(T_{\mathrm{f}}-T_{\text {ice, rec }}\right) \end{aligned} $ | (3) |
式中:
时变参数(多步)积冰计算中,ICING软件将计算过程划分为流场、液滴碰撞和结冰计算三部分。总积冰时间由人为指定,并基于导线覆冰速率及环境条件选择合适的时间步长。每完成一个时间步后调整覆冰外形,对网格进行重新划分,更新式(1)~(3)中流场、水膜流动、能量质量守恒方程的流固参数;不断重复此项程序,直至达到所设定的总覆冰时间。计算流程见图 2。

|
图 2 覆冰计算流程图 Fig. 2 Ice accretion calculation flow chart |
在多步时变覆冰预测中,计算步数对于覆冰外形的预测精准度是一个关键参数。计算步数过少,每步时间过长,覆冰外形对覆冰增长形式的影响将减小。而过大的步数会导致每个时间步所产生的误差不断叠加,降低计算准确性,并增加计算的时间。本文所用步数取决于所研究几何体的形状,根据文献[27]中每一步的覆冰厚度都不应该超过几何体弦长(或直径)1%的理论,采用下式估计覆冰步数:
| $ X=\frac{1}{n_{\text {step }} c}\left(\frac{\omega_{\mathrm{LWC}}}{\rho_{\mathrm{i}}} v_{\infty} t_{\exp }\right) $ | (4) |
式中:nstep为计算步数,c为模型的直径,ρi为覆冰密度,texp为积冰计算时间,X为覆冰厚度与直径的比值。
文献[27]指出,对于小几何体(如圆柱体),采用X=1%的数值可能会导致计算步数过高,且在相关文献和LEWICE的说明中没有提及对于小几何体和圆柱体推荐使用的X值。因此本文X的取值将根据时间算法的收敛程度确定步数。
覆冰厚度计算采用文献[22]中所提出的流体在任意三维表面流动、凝固的简化方程进行求解。
1) 雾凇覆冰。通常在温度低于-5 ℃时会形成雾凇,所有水滴撞击到输电线表面后会立即结冰,不会形成水膜。覆冰厚度b由简化的质量平衡方程得出:
| $ b=\frac{\omega_{\mathrm{LWC}}}{\rho_{\mathrm{i}}} \beta v_{\infty} t_{\exp } $ | (5) |
2) 雨凇覆冰。雨凇形成于-5 ℃~0 ℃温度范围内,由于温度较高,当水滴接触到输电线表面冰层后,只有一部分水滴会立即冻结,剩余水滴仍会保持液态,在原有冰层上形成一层水膜,并在重力和气流的剪切力作用下在冰层表面流动。覆冰厚度求解方程为
| $ \rho_{\mathrm{i}} \frac{\partial b}{\partial t}+\rho_{\mathrm{f}}\left(\frac{\partial h_{\mathrm{f}}}{\partial t}+\frac{\partial Q_{x_1}}{\partial x_1}+\frac{\partial Q_{x_2}}{\partial x_2}\right)=\omega_{\mathrm{LWC}} \beta t_{\exp } $ | (6) |
式中Qx1、Qx2分别为水膜沿x1、x2方向的流量通量。
对Qx1、Qx2通量的求解需化简水膜运动方程(式(1)):
| $ \left\{\begin{array}{l} Q_{x_1}=\frac{h^3}{3 \mu_\omega}\left[\sigma \frac{\partial^3 h_{\mathrm{f}}}{\partial x_1^3}-G_1-\frac{\partial P_{\mathrm{a}}}{\partial x_1}\right]+A_1 \frac{h_{\mathrm{f}}^2}{2 \mu_\omega} \\ Q_{x_2}=\frac{h^3}{3 \mu_\omega}\left[\sigma \frac{\partial^3 h_{\mathrm{f}}}{\partial x_2^3}-G_2-\frac{\partial P_{\mathrm{a}}}{\partial x_2}\right]+A_2 \frac{h_{\mathrm{f}}^2}{2 \mu_\omega} \end{array}\right. $ | (7) |
式中:μω为水膜动态黏度,σ为水膜表面张力,Pa为环境压力,(G1, G2)和(A1, A2)分别为x1、x2方向上重力和剪应力的分量。
同时结合能量守恒方程(式(3))对雨凇覆冰厚度进行求解。
2 输电线积冰计算结果与验证 2.1 CFD建模积冰计算采用三维导线模型。为增加积冰计算的准确性,同时考虑到计算时间成本等问题,采用长方体为计算区域。流场计算域由ANSYS Fluent 21.0完成,图 3、4分别为三维CFD输电导线的流体模型和输电导线区域的局部放大图。流场域尺寸为20D×20D×40D,输电导线中心距边界面同为10D,D为输电导线的直径(选取19.05 mm和34.9 mm两种)。计算域的边界面参数见表 1。

|
图 3 三维流场计算域 Fig. 3 Three-dimensional flow field calculation domain |

|
图 4 输电线结构局部放大 Fig. 4 Partial enlarged view of calculation domain of transmission line structure |
| 表 1 流场各边界参数 Tab. 1 Boundary parameters of flow field |
为验证本文导线覆冰计算方法的有效性,选取文献[14]中的4组数据进行验证,见表 2。其中工况1、2环境温度-15 ℃对应覆冰形式为雾凇(干覆冰),工况3、4环境温度-5 ℃对应覆冰形式为雨凇(湿覆冰)。4种工况下的覆冰时间均为30 min。
| 表 2 模型验证参数 Tab. 2 Model validation parameters |
积冰整体呈现出均匀生长,对称式分布。图 5为截取中间段10 mm长导线的覆冰形貌,输电线直径为19.05 mm,环境温度-15 ℃,环境风速5 m/s情况下覆冰30 min计算结果。从图 5中可以看出导线上积冰主要沿迎风面向外生长,积冰速度最大处位于迎风面前沿。后续与文献[14]的试验数据相对比时,截取导线中央轴向截面图形进行比较。

|
图 5 CFD计算30 min后覆冰结果 Fig. 5 CFD calculation results of 30 min ice accretion |
工况1(图 6)和工况2(图 7)为干覆冰条件下的积冰模拟。工况1(图 6)中,通过将模型预测冰形与试验冰形比较,观察到单步和多步覆冰法均可正确预测积冰的生长趋势。积冰沿轴向向外增长,冰形与风向垂直。对比单步覆冰形貌和试验生成的冰形,试验生成冰形前沿较为平坦,且积冰上、下部有较为明显的棱角生成;而单步覆冰法所生成的冰形整体呈现出较为光滑的圆弧形,相同时间内积冰轴向生长与试验冰形相差约8.8%,整体覆冰截面面积约为试验生成冰形截面面积的71.3%,相差较大。对比多步覆冰形貌和试验生成积冰,多步覆冰形貌前缘和上下边缘较为平缓,形貌上与试验生成的冰形相符合,整体覆冰截面面积相差约5.6%。但在积冰轴向长度和上部边缘厚度上有出入,多步法所计算出的积冰轴向长度比试验冰形长约13.5%,分析原因可能为试验生成冰形密度(文献[19]中未标明冰形密度值)与模型中所用密度有差异,当覆冰密度较小时,附着在前缘的冰晶由于黏附力较低,在切向力的拖拽下沿冰形向后移动,堆积在冰形上部边缘。总体看多步覆冰结果是令人满意的,且基于时间标准的迭代法在第6次时已经达到收敛标准,与10次和20次迭代所产生的结果相差甚小。每一步的冰层厚度平均值可以定义为:在整个计算时间所取得的最大覆冰厚度除以计算步数。对于这6次计算,计算出X=5.54%低于通过式(4)所计算的六步积冰的值X=7.83%。

|
图 6 工况1下覆冰30 min的试验对比 Fig. 6 Comparison of 30 min icing under working condition 1 |

|
图 7 工况2下覆冰30 min的试验对比 Fig. 7 Comparison of 30 min icing under working condition 2 |
工况2(图 7)中除导线直径改为19.05 mm和DMVD改为35 μm外,其他条件与工况1相同。由图 7可以看出,单步计算的覆冰结果与试验外形相差过大;多步计算的覆冰外形与试验生成的冰形基本一致,覆冰外形前沿与试验外形高度一致,但在覆冰上边缘平均厚度计算结果与试验结果相差约6.8%。对比覆冰外形截面面积,多步法覆冰截面面积与试验生成冰形截面面积相差约8.6%,显示出较高的相似度。每一步冰厚计算值约为导线直径的7.34%(X=7.34%),采用式(4)计算结果约为X=1.079%。
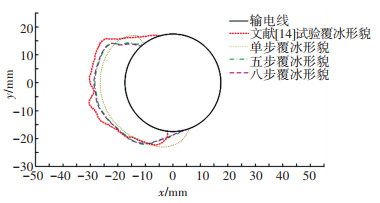
工况3(图 8)为大直径导线湿覆冰条件下的积冰计算结果,据其可评估出模型的可靠度。如图 8积冰轮廓所示,对比单步覆冰形貌和真实形貌,单步覆冰形貌在厚度上与真实覆冰形貌相差约12.6%;冰形的上部形成尖端突起,且下半部分积冰量过多,与真实外形不相符。对比五步覆冰形貌和试验生成冰形形貌,覆冰的整体生长趋势和外形与试验形貌相近,五步覆冰形貌厚度与试验覆冰形貌相差约4.6%,外部形貌较为光滑,总体满足模拟效果。对比五步覆冰形貌和八步覆冰形貌,观察到两者外形和厚度相差甚小,证明在五步覆冰时已经达到收敛。每一步积冰厚度约为导线直径的6.64%,由式(4)计算结果为X=12.61%。
|
图 8 工况3下覆冰30 min的试验对比 Fig. 8 Comparison of 30 min icing under working condition 3 |
工况4(图 9)为小直径导线湿覆冰条件下的积冰模拟,与工况3(图 8)的结果类似,单步和多步覆冰形貌与试验形貌具有大致相同的轮廓,但单步计算出的覆冰外形在厚度和冰形上下部轮廓差异较大,与试验结果不符。对比多步法覆冰外形,在第6个仿真步骤后已经达到收敛,且外形轮廓及厚度与试验覆冰形貌基本相符。模拟计算所得X约为8.39%,再通过式(8)计算得X=10.27%。

|
图 9 工况4下覆冰30 min的试验对比 Fig. 9 Comparison of 30 min icing under working condition 4 |
为与文献[14]的覆冰质量试验结果进行对比,采用相同环境条件与导线参数计算覆冰质量,得到覆冰质量与时间变化曲线,见图 10。计算所用参数如下:导线直径分别为34.9 mm和19.05 mm,环境温度为-10 ℃,环境风速为8 m/s,液滴中值体积直径为15 μm,空气中液态水含量为0.5 g/m3。由图 10可知,模型计算所得到的质量-时间曲线与文献[14]试验所得结果相符。

|
图 10 覆冰质量随时间变化曲线 Fig. 10 Variation curves of ice accretion mass with time |
综上,所提模型在计算干增长和湿增长条件下的覆冰生长、外形及质量方面均表现出良好性能,与试验积冰数据相符合,进一步证明该模型的可行性。
3 三维导线积冰计算为接近真实工况下输电线的积冰,以表 2条件为试验参数,并增加输电线倾斜角度,分析在不同倾斜角度下输电线覆冰特征。导线在流场中的布置见图 11。导线长度选取时结合文献[14]的试验数据并综合考虑文献[27]的风洞试验参数,最终选取100 mm长导线。风水平吹向导线节段模型,其中α为节段模型的倾斜角,β为节段模型的风偏角。计算中,风偏角β取90°固定值,导线倾角α分别取0°、15°、30°、45°、60°,并对各个倾斜角度导线积冰后的形貌、积冰质量进行分析,探究导线倾斜角度对积冰的影响。各工况下积冰计算时间均为30 min。

|
图 11 导线模型倾角和风向角定义 Fig. 11 Inclination angle and wind direction angle definitions for transmission line model |
将导线水平放置于计算域中(α=0°),积冰计算30 min后结果见图 12。干覆冰条件下(工况1、工况2)积冰计算结果与2节中覆冰形貌验证结果相近,积冰主要聚集于导线迎风面前端,表面光滑,且积冰上下侧较为平坦。湿覆冰条件下(工况3、工况4)积冰计算结果呈现出2节计算结果中未展现的轴向特征。2种积冰条件下,积冰表面均出现凹凸不平的沟壑状特征。工况3中,撞击到输电线表面的液滴主要冻结于导线迎风面前端,剩余未立即冻结的液滴在切向力和重力的拖拽下向导线背风面移动。对未冻结的水膜分两部分进行分析,其上部水膜所受重力与流场对水膜的切向力方向相反,风切力拖拽水膜在导线上部振荡,延缓其向下流动的趋势,并最终凝固;下部水膜所受重力与风切力方向相同,推动水膜向背风面移动,从而在输电线上下端形成明显的水线。工况4中,积冰计算结果主要为表面鱼鳞状特征,积冰平均厚度与2节中计算结果一致。

|
图 12 导线倾角α =0°时积冰30 min导线形貌 Fig. 12 Ice accretion morphology of transmission line after 30 min under inclination angle α= 0° |
导线倾角α=15°时积冰计算结果见图 13。将此次计算结果与导线水平放置计算结果进行对比。工况1、2的积冰结果与水平放置积冰计算结果相近,积冰质量差不超过3%。工况3中,倾斜导线表面积冰面积减小约38.7%,上下水线消失,分析为随导线倾斜,撞击到导线表面上的液滴受重力影响增大,液滴易沿导线倾斜方向流动,向背风面流动的趋势减小。工况4中,可以更加明显地看出湿覆冰凝固过程中释放的大量潜热无法通过对流或热传导消散,从而导致热量在计算模型覆冰表面局部聚集,因此只有小部分过冷水滴在撞击时被冻结成固态冰,其余仍保持液态,在模型周围气流的驱动下,形成小河状流动状态。同时气流对水膜流动存在不确定性扰动,在导线倾斜状态下,水膜更易沿背风面斜向下流动,最终冻结成鱼鳞状固体。

|
图 13 导线倾角α =15°时积冰30 min导线形貌 Fig. 13 Ice accretion morphology of transmission line after 30 min under inclination angle α=15° |
导线倾斜30°积冰计算结果见图 14。工况1、2积冰条件下,导线水平放置与导线倾斜15°积冰计算结果对比,积冰表面无明显变化,表面光滑,积冰质量计算结果相似。工况3条件下积冰计算外形与导线倾斜15°积冰计算外形相近,但积冰质量较后者减小约4.45%,主要原因是:随着导线倾斜角度增大,未冻结的水膜在重力及气流驱动下,向导线下游流动致使覆冰量减少。工况4中,下水线位置沿导线上端向导线下端逐渐向背风面移动,导线下端积冰覆盖面积明显大于导线上端,但积冰质量比导线倾斜15°积冰计算结果减小约10.54%。结合图 14(b),导线表面堆积的雨凇覆冰层沿方位角方向分布更加均匀,已经没有了如图 13(b)所示覆冰沟壑状外形,这与导线倾斜角度增加未冻结水膜更易流动密切相关。

|
图 14 导线倾角α =30°时积冰30 min导线形貌 Fig. 14 Ice accretion morphology of transmission line after 30 min under inclination angle α=30° |
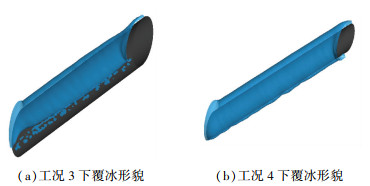
图 15为导线倾斜45°积冰计算结果。在工况1、2条件下,其积冰形貌与导线水平、导线倾斜15°、30°计算结果无明显差异,不再赘述。在工况3的积冰计算结果中,可明显发现积冰表面粗糙度减小,积冰外形逐渐圆润呈现出流线型,鱼鳞状的水膜流动特征消失,对比导线倾斜30°积冰结果,积冰质量减少约8.98%。工况4中,积冰表面同样展现出流线型特征,积冰表面光滑,较导线倾斜30°积冰结果积冰质量减少约8.85%。2种湿覆冰工况下,覆冰表面粗糙度相比之前明显减小,一方面重力对于水膜的流动起到了主要作用,气流流动对水膜运动的扰乱降低;另一方面导线上水膜起到润滑的作用使气流在导线表面更平稳地流动。
|
图 15 导线倾角α =45°时积冰30 min导线形貌 Fig. 15 Ice accretion morphology of transmission line after 30 min under inclination angle α=45° |
当导线倾角达到60°时观察积冰计算结果(图 16),在4种积冰工况下,导线覆冰外形趋同现象明显,覆冰表面光滑,这与上文提到水膜润滑作用及导线倾斜角度有关。水膜润滑作用使导线表面的边界气流层不易与导线分离,水膜能在导线表面更好地铺展。导线较大的倾斜角度,使导线上下部水膜所受重力与流场的切向力夹角接近垂直状态,原本导线上部处于振荡状态的水膜向导线背风面移动,而导线下部向背风面流动的水膜由于所受合力的减小,进而减缓向背风面流动趋势,使覆冰更加均匀。同时导线下端都出现明显积冰聚集,湿覆冰(工况3和工况4)条件下,液滴向导线下端流动趋势明显强于干覆冰(工况1和工况2)条件时积冰。此外,工况3条件下积冰质量较导线倾斜角α=45°再减小约5.46%。

|
图 16 导线倾角α =60°时积冰30 min导线形貌 Fig. 16 Ice accretion morphology of transmission line after 30 min under inclination angle α=60° |
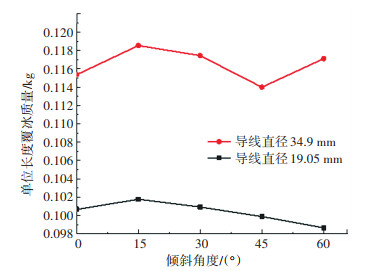
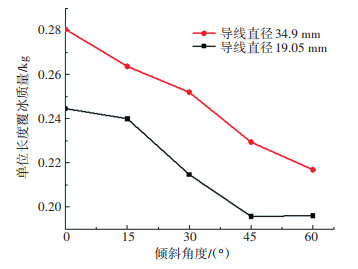
4种积冰工况在各倾斜角度下的积冰质量见图 17、18。干覆冰条件下,随导线倾斜角度增加,积冰质量没有明显变化,主要原因是:干覆冰条件温度较低,过冷液滴撞击到导线后会立即冻结,减少水膜流动过程。另外,观察到大直径导线上的积冰质量明显大于直径较小导线积冰质量,这一点与文献[19]所得结论一致。湿覆冰条件下,大直径导线积冰质量大于小直径导线积冰质量,干覆冰条件下积冰相同;随导线倾斜角度增加,2种工况的积冰质量都不同程度降低,分析为湿覆冰条件积冰温度较高(通常为-5 ℃~0 ℃),撞击到导线上的液滴不能及时冻结,进而沿导线倾斜方向流动,最终脱离导线,同时导线上端缺乏液滴补充,造成积冰质量减小。
|
图 17 干覆冰条件下(工况1、工况2)积冰质量 Fig. 17 Ice accretion mass under dry icing conditions(working conditions 1, 2) |
|
图 18 湿覆冰条件下(工况3、工况4)积冰质量 Fig. 18 Ice accretion mass under wet icing conditions(working conditions 3, 4) |
1) 以流体动力学和热力学为基础,应用ANSYS-Fluent ICING模块计算了三维导线覆冰过程,通过与文献[14]的试验数据对比,验证了所提模型的有效性和可行性。此外,本文模型可以完整描述导线上覆冰的三维结构、积冰过程并计算覆冰质量。
2) 在相同的积冰条件下,多步积冰计算法的精准度较单步积冰计算法提高约8%,更适合于积冰计算。
3) 干覆冰条件下,随输电线倾斜角度增大,输电线上积冰形貌和积冰质量都没有明显的变化。干覆冰条件温度较低,过冷液滴撞击到输电线后会立即冻结,减少水膜流动过程,因此导线倾斜对积冰计算结果无明显影响。
4) 湿覆冰条件下,随输电线倾斜角度增大,输电线表面上的液滴更易受到重力影响,沿输电线倾斜方向流动,向背风面流动趋势减缓,使得导线表面积冰覆盖面积减小,积冰形貌逐渐圆滑,呈现出流线型。同时积冰质量随导线倾角增加降低约21%,主要原因分析为:未冻结的液滴沿输电线倾斜方向流动最终脱离输电线,而输电线上游没有液滴及时补充。
| [1] |
ZHOU Chao, YIN Jiaqi. Glaze icing process of moveable overhead conductor and its aerodynamic characteristics with numerical method[J]. International Journal of Heat and Mass Transfer, 2021, 176: 121436. DOI:10.1016/j.ijheatmasstransfer.2021.121436 |
| [2] |
ZHOU Chao, YIN Jiaqi, LIU Yibing. Theoretical study of glaze ice accretion on an oscillating cylinder and its aerodynamic characteristics[J]. Journal of Fluids and Structures, 2021, 103: 103231. DOI:10.1016/j.jfluidstructs.2021.103231 |
| [3] |
苑吉河, 蒋兴良, 易辉, 等. 输电线路导线覆冰的国内外研究现状[J]. 高电压技术, 2004(1): 6. YUAN Jihe, JIANG Xingliang, YI Hui, et al. The present study on conductor icing of transmission lines[J]. High Voltage Engineering, 2004(1): 6. DOI:10.13336/j.1003-6520.hve.2004.01.003 |
| [4] |
MAKKONEN L. A model of hoarfrost formation on a cable[J]. Cold Regions Science and Technology, 2013, 85: 256. DOI:10.1016/j.coldregions.2012.10.001 |
| [5] |
陈俊旗, 王伟. 覆冰输电塔线体系风振响应数值模拟[J]. 哈尔滨工业大学学报, 2011, 43(增刊1): 147. CHEN Junqi, WANG Wei. Numerical simulation on wind-induced vibration of iced transmission line systems[J]. Journal of Harbin Institute of Technology, 2011, 43(S1): 147. |
| [6] |
JIANG Xingliang, FAN Songhai, ZHANG Zhijin, et al. Simulation and experimental investigation of DC ice-melting process on an iced conductor[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 919. DOI:10.1109/tpwrd.2009.2037632 |
| [7] |
蒋兴良, 陈凌, 赵阳, 等. 雨凇冰层热导率影响因素的试验分析[J]. 高电压技术, 2011, 37(8): 2032. JIANG Xingliang, CHEN Ling, ZHAO Yang, et al. Experimental analysis on influencing factors of thermal conductivity of rain-glace layer[J]. High Voltage Engineering, 2011, 37(8): 2032. DOI:10.13336/j.1003-6520.hve.2011.08.031 |
| [8] |
蒋兴良, 肖丹华, 陈凌, 等. 基于界面移动理论的导线覆冰过程分析[J]. 高电压技术, 2011, 37(4): 982. JIANG Xingliang, XIAO Danhua, CHEN Ling, et al. Physical process of icing on fixed wires by interface movement theory[J]. High Voltage Engineering, 2011, 37(4): 982. DOI:10.13336/j.1003-6520.hve.2011.04.034 |
| [9] |
MESSINGER B L. Equilibrium temperature of an unheated icing surfaces as a function of air speed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29. DOI:10.2514/8.2520 |
| [10] |
LOZOWSKI E P, STALLABRASS J R, HEARTY P F. The icing of an unheated, nonrotating cylinder. Part I: a simulation model[J]. Journal of Applied Meteorology and Climatology, 1983, 22(12): 2053. DOI:10.1175/1520-0450(1983)022<2053:TIOAUN>2.0.CO;2 |
| [11] |
MAKKONEN L. Heat transfer and icing of a rough cylinder[J]. Cold Regions Science and Technology, 1985, 10(6): 105. DOI:10.1016/0165-232x(85)90022-9 |
| [12] |
MAKKONEN L. Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology, 1984, 23(5): 929. |
| [13] |
SZILDER K, LOZOWSKI E P, FARZANEH M. Morphogenetic modelling of wet ice accretions on transmission lines as a result of freezing rain[J]. International Journal of Offshore and Polar Engineering, 2001, 11(1): 16. |
| [14] |
FU Ping, FARZANEH M, BOUCHARD G. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J]. Cold Regions Science and Technology, 2006, 46(2): 132. DOI:10.1016/j.coldregions.2006.06.004 |
| [15] |
FU Ping, FARZANEH M, BOUCHARD G. Simulation of ice accumulation on transmission line cables based on time dependent airflow and water droplet trajectory calculations[C] //Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering. Vancouver: ASME, 2004. DOI: 10.1115/OMAE2004-51389
|
| [16] |
FU Ping, FARZANEH M. Simulation of the ice accretion process on a transmission line cable with differential twisting[J]. Canadian Journal of Civil Engineering, 2007, 34(2): 147. DOI:10.1139/l06-109 |
| [17] |
KRULL U J, THOMPSON M, WONG H E. Simple instrumentation for Langmuir-Blodgett technology[J]. Analyst, 1985, 110(11): 1299. DOI:10.1039/an9851001299 |
| [18] |
LUDLAM F H. The heat economy of a rimed cylinder[J]. Quarterly Journal of the Royal Meteorological Socirty, 1951, 77(334): 663. DOI:10.1002/qj.49707733410 |
| [19] |
PERSONNE P, GAYET J F F. Ice accretion on wires and anti-icing induced by Joule effect[J]. Journal of Applied Meteorology and Climatology, 1988, 27(2): 101. DOI:10.1175/1520-0450(1988)027<0101:iaowaa>2.0.co;2 |
| [20] |
MYERS T G, HAMMOND D W. Ice and water film growth from incoming supercooled droplets[J]. International Journal of Heat and Mass Transfer, 1999, 42(12): 2233. DOI:10.1063/S0017-9310(98)00237-3 |
| [21] |
MYERS T G, CHARPIN J P F, THOMPSON C P. Slowly accreting ice due to supercooled water impacting on a cold surface[J]. Physics of Fluids, 2002, 14(1): 240. DOI:10.1016/1.1416186 |
| [22] |
MYERS T G, CHARPIN J P F, CHAPMAN S J. The flow and solidification of a thin fluid film on an arbitrary three-dimensional surface[J]. Physics of Fluids, 2002, 14(8): 2788. DOI:10.1063/1.1488599 |
| [23] |
HOU Shuo, CAO Yihua. Numerical simulation of two-dimensional ice accretion based on lubrication theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1442. DOI:10.13700/j.bh.1001-5965.2013.0625 |
| [24] |
ANSYS, Inc. ANSYS fluent user's guide[Z]. Canonsburg: ANSYS, 2021
|
| [25] |
ANSYS, Inc. ANSYS FENSAP-ICE user manual[Z]. Canonsburg: ANSYS, 2021
|
| [26] |
MAKKONEN L, ZHANG Jian, KARLSSON T, et al. Modelling the growth of large rime ice accretions[J]. Cold Regions Science and Technology, 2018, 151: 133. DOI:10.1016/j.coldregions.2018.03.014 |
| [27] |
WRIGHT W B. User manual for the NASA Glenn ice accretion code LEWICE[Z]. Cleveland: NASA, 2002
|
 2023, Vol. 55
2023, Vol. 55


