2. 江苏地质矿产设计研究院, 江苏 徐州 221002
2. Jiangsu Geology and Mineral Resources Design and Research Institute, Xuzhou 221002, Jiangsu, China
在装配式混凝土结构中,新老混凝土界面及其两侧一定范围内受影响的混凝土(称为界面区)是天然的薄弱部位。文献[1]研究表明,新老混凝土界面的渗透性大于新、老混凝土本体的渗透性,且渗透系数一般相差一个数量级;大量研究表明,新老混凝土界面的抗拉强度和抗剪强度相对于本体混凝土均有显著降低[2-3];文献[4]研究发现,装配式结构新老混凝土界面区的碳化速度明显大于本体混凝土;文献[5-6]研究发现,装配式结构新老混凝土界面区氯离子传输存在明显漏斗效应,其中恒定压应力对漏斗效应产生削弱乃至逆转作用。
在新老混凝土界面区,粗骨料的分布显著减少,同时水泥砂浆的孔隙率显著增大。弄清二者的定量分布模型,对于定量研究界面区力学及耐久性能弱化问题极为必要[7-8]。笔者前期已完成了界面区粗骨料分布模型的研究[9],本文进一步对界面区水泥砂浆孔隙率分布模型开展研究。
对于混凝土或水泥砂浆本体孔结构及孔隙率的研究工作非常之多。早在1958年,文献[10]就研究了混凝土孔结构及孔隙率与抗渗系数的关系。近年来,水泥基材料孔结构与孔隙率的研究工作不断深入,文献[11]分析了混凝土强度与孔隙率和孔径分布之间的关系,并建立了孔结构复合体模型;文献[12]研究了水泥砂浆孔结构的分形特征;文献[13]研究了养护条件对水泥基材料孔结构的影响;文献[14]研究了养护龄期、水胶比、骨料含量对水泥基材料与骨料界面过渡区孔隙率的影响;文献[15]研究了低气压环境对水泥基材料孔结构特征的影响规律。然而,对于装配式结构新老混凝土界面区孔结构及孔隙率的研究工作还极少。
本文采用扫描电镜法(scanning electron microscopy,SEM)并结合数字图像处理技术,对不同水灰比搭配的新老混凝土竖缝平整界面区的孔隙率进行测试。根据测试结果分析界面区孔隙率分布特征,在此基础上建立平整及凿毛界面区孔隙率的分布模型。
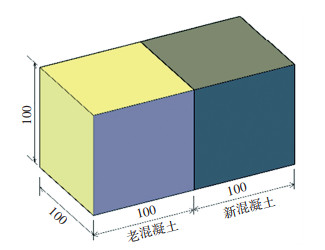
1 试验方案 1.1 试件设计与制作每个试件均由一个先浇筑的老混凝土块和一个后浇筑的新混凝土块接合而成,二者的轮廓尺寸均为100 mm×100 mm×100 mm,见图 1。
|
图 1 新老混凝土接合试件设计(mm) Fig. 1 Design of annectent new and old concrete specimen (mm) |
老混凝土块的强度等级按C30设计,水灰比为0.6。新混凝土块的强度等级分别按C30、C40和C50设计,水灰比分别为0.6、0.5和0.4,具体配合比见表 1。
| 表 1 试件混凝土配合比 Tab. 1 Mix proportion of concrete specimens |
水泥采用P·O 42.5普通硅酸盐水泥(中国联合水泥公司生产)。水为普通饮用自来水。细骨料采用表观密度为2 662 kg/m3、细度模数为2.8的天然河砂。粗骨料采用表观密度为2 850 kg/m3、公称粒径为5~16 mm连续级配的碎石骨料,颗粒级配见表 2。
| 表 2 试件混凝土粗骨料颗粒级配 Tab. 2 Particle gradation of coarse aggregate in concrete specimens |
试件制作过程为:首先浇筑100 mm×100 mm×100 mm的老混凝土块,浇筑完24 h后脱模,并将脱模后的老混凝土块置于温度为(20 ± 5) ℃、相对湿度为95%的养护室养护14 d,然后选择一个侧表面作为一个侧面模板, 浇筑后浇新混凝土块,从而形成一个尺寸为200 mm×100 mm×100 mm的新老混凝土接合试件。
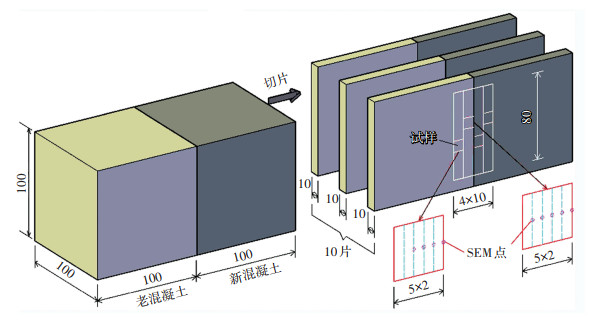
1.2 SEM取样与测试首先将每个新老混凝土接合体试件垂直于接缝面按每10 mm厚度进行剖切(图 2),并选取其中距离试件表面30~60 mm深度的3个薄片作为取样母片。然后在每个取样母片界面周围40 mm×80 mm的范围内进一步切取边长约10 mm的立方体小块作为SEM试样,切样区域尽量少包含粗骨料。每一个试件中,老混凝土部分只在距界面0~10 mm和10~20 mm范围内各切取1个试样,而新混凝土部分则在距界面0~10 mm和10~20 mm范围内各切取3个试样。试样获取与测点布置见图 2,试样编号见表 3。
|
图 2 SEM试样获取与测点布置(mm) Fig. 2 SEM specimen sampling and measuring points arrangement (mm) |
| 表 3 SEM试样编号 Tab. 3 SEM specimens designation |
电镜扫描前,为了增强混凝土试样的导电性,先在其待测表面进行喷金处理。扫描时,在各SO/N-1试样(其边界即为新老混凝土试件界面)中分别选取距各自边界0、2、4、6、8 mm的5个点进行扫描,在SO/N-2试样(其边界距新老混凝土试件界面10 mm)中分别选取距各自边界0、2、4、6 mm的4个点进行扫描。最终每组试样可得到距新老混凝土试件界面0、2、4、6、8、10、12、14、16 mm 9个点的SEM图像。图像放大倍数为1万倍。选点时须避免选到粗骨料点。
1.3 SEM图像处理与名义孔隙率提取通过电镜扫描直接获得的灰度图像,其画面品质不够理想,为此利用Photoshop和MATLAB图像处理工具箱进行图像信息增强处理。对于增强的灰度图像,进一步采用MATLAB工具箱中im2bw函数功能进行二值化处理,使图像变为只有0和255两个像素值的黑白图像。二值化处理后,0值像素代表孔隙,255值像素代表水泥砂浆基体。对每一个二值图像,统计出0值像素个数占总像素个数的比例,即得到扫描孔隙面积比。由于一万倍电子显微镜仅能观测到直径大于1 μm的孔隙,因此扫描孔隙面积比不足以反映混凝土中水泥砂浆的真实孔隙率,所以本文将扫描孔隙面积比定义为名义孔隙率,记作pN。
2 试验结果与分析 2.1 界面区水泥砂浆SEM图像及二值图像3个新老混凝土试件中,共有3个水灰比同为0.6的C30老混凝土块。对于每个老混凝土块,在距界面0~10 mm和10~20 mm区间各取出1个有效试样。对每个试样,从其边界开始每2 mm测得1个SEM图像,其中第1个试样测得距界面0、2、4、6、8 mm共5个图像,第2个试样测得距界面10、12、14、16 mm共4个图像,这样,每个老混凝土块共测得9个SEM图像。全部3个老混凝土块共测得27个SEM图像。每个SEM图像经MATLAB处理后获得了相应的二值图像。部分测点SEM图像及相应的二值图像见图 3。

|
图 3 C30老混凝土块距界面不同距离处3个测点的SEM图像及其二值图像 Fig. 3 SEM and binary images of three scanning points at different distances from interface in C30 old concrete block |
3个新老混凝土试件中,共有1个水灰比为0.6的C30新混凝土块。对于该新混凝土块,在距界面0~10 mm和10~20 mm区间各取出3个有效试样进行测试。对每个试样的测点取位均与前述老混凝土块相同,最终从该新混凝土块中也测得27个SEM图像并获得了相应的二值图像,部分图像见图 4。

|
图 4 C30新混凝土块距界面不同距离处3个测点的SEM图像及其二值图像 Fig. 4 SEM and binary images of three scanning points at different distances from interface in C30 new concrete block |
同样,3个新老混凝土试件中还有1个水灰比为0.5的C40新混凝土块和1个水灰比为0.4的C50新混凝土块,每个新混凝土块也同样测得了27个SEM图像并获得了相应的二值图像,部分图像见图 5、6。

|
图 5 C40新混凝土块距界面不同距离处3个测点的SEM图像及其二值图像 Fig. 5 SEM and binary images of three scanning points at different distances from interface in C40 new concrete block |

|
图 6 C50新混凝土块距界面不同距离处3个测点的SEM图像及其二值图像 Fig. 6 SEM and binary images of three scanning points at different distances from interface in C50 new concrete block |
通过对本文二值图像的统计,获得了各观测点水泥砂浆名义孔隙率的3个测试值,见表 4。表中粗体表示测试值与3个测试值的平均值误差超过了20%,这些值视作无效而舍弃。
| 表 4 名义孔隙率SEM测试结果 Tab. 4 SEM results of nominal porosity |
各混凝土块中水泥砂浆的名义孔隙率pN随距界面距离s的分布见图 7。可以看出,不管是老混凝土,还是不同强度等级(水灰比)的新混凝土,其水泥砂浆的名义孔隙率均在界面处最大。随着距界面距离的增大,名义孔隙率逐渐减小,最后趋于稳定,总体变化趋势具有高斯函数特征。不同强度等级混凝土相比,随着强度等级增大,从界面到内部各部位的名义孔隙率均呈相对减小趋势。

|
图 7 界面区水泥砂浆名义孔隙率分布特征 Fig. 7 Distribution characteristics of nominal porosity of cement mortar in interfacial zones |
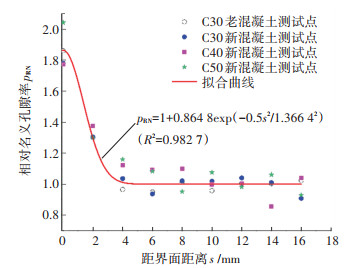
将各强度等级混凝土内部趋于稳定(距界面8~16 mm)的名义孔隙率取平均值作为混凝土内部名义孔隙率代表值,记作pNC;然后将各测点实测名义孔隙率pN分别除以pNC,得到各测点相对名义孔隙率pRN。界面区各强度等级新老混凝土块的相对名义孔隙率分布见图 8。图中相对名义孔隙率计算所需各测点名义孔隙率由其3个测试值的平均值所得。图 8表明,各强度等级混凝土中水泥砂浆的相对名义孔隙率在界面区的分布特征及量值较为一致,说明混凝土的强度等级及制作方式(预制或后浇)对界面区水泥砂浆相对名义孔隙率的分布基本没有影响。
|
图 8 界面区水泥砂浆相对名义孔隙率分布特征 Fig. 8 Distribution characteristics of relative nominal porosity of cement mortar in interfacial zones |
与界面区名义孔隙率分布特征类似,界面区相对名义孔隙率分布也具有高斯函数特征。经回归分析,其高斯函数模型见式(1),回归决定系数R2=0.982 7。
| $ p_{\mathrm{RN}}=1+0.864\;8 \exp \left(-0.267\;8 s^2\right) $ | (1) |
式中:s为距界面距离,pRN为相对名义孔隙率。
3.2 界面区水泥砂浆孔隙率分布模型前已述及,名义孔隙率无法反映真实孔隙率。不过,有学者[16]利用偏光显微镜对混凝土内部直径2 μm以上的孔隙进行了测试,同时使用压汞仪对混凝土孔隙进行辅助测试。测试结果对比发现,虽然二者测试值不同,但总体所呈现趋势却一致,主要原因是不同孔径的孔隙在水泥砂浆中所占比例相对稳定。本文拟根据这一研究结论寻找名义孔隙率与真实孔隙率之间的相关关系,从而由名义孔隙率推算出真实孔隙率。
文献[17]采用压汞法测试得到了水灰比分别为0.4、0.5、0.6的水泥砂浆在不同砂灰比时的孔隙率。据此可得到本文试验中3个水灰比混凝土块内部远离界面处水泥砂浆的稳定孔隙率,见表 5中的推算内部孔隙率。
| 表 5 混凝土内部水泥砂浆孔隙率 Tab. 5 Porosity of cement mortar of interior concrete |
对表 5中水灰比、名义内部孔隙率及推算内部孔隙率数据进行回归,得到名义内部孔隙率与水灰比之间的二次函数关系模型,并推算内部孔隙率与水灰比及名义内部孔隙率之间的幂函数关系模型,分别见式(2)和式(3):
| $ p_{\mathrm{NC}}=-0.175 r^2+0.249 r-0.019 $ | (2) |
| $ p_{\mathrm{C}}=1.374 r^{0.021} p_{\mathrm{NC}}^{0.577} $ | (3) |
式中:r为水灰比,pNC为名义内部孔隙率,pC为内部孔隙率。
将式(2)代入式(3),即可得到水泥砂浆内部孔隙率与水灰比之间的关系模型:
| $ p_{\mathrm{C}}=1.374 r^{0.021}\left(-0.175 r^2+0.249 r-0.019\right)^{0.577} $ | (4) |
根据式(4)计算出本文试验3个水灰比混凝土块内部孔隙率,见表 5中内部孔隙率回归值,其与推算内部孔隙率之间的误差在2%以内。
假定界面区孔隙率相对值的分布与名义孔隙率相对值的分布相同,则将式(1)与式(4)相乘便可得到不同强度等级(水灰比)混凝土界面区水泥砂浆孔隙率随水灰比和距界面距离变化的模型,见式(5)。模型曲线见图 9。

|
图 9 界面区水泥砂浆孔隙率分布模型曲线 Fig. 9 Distribution model curves of cement mortar porosity in interfacial zone |
| $ \begin{aligned} p= & 1.374 r^{0.021}\left(-0.175 r^2+0.249 r-0.019\right)^{0.577}[1+ \\ & \left.0.864\;8 \exp \left(-0.267\;8 s^2\right)\right] \end{aligned} $ | (5) |
式中p为孔隙率。
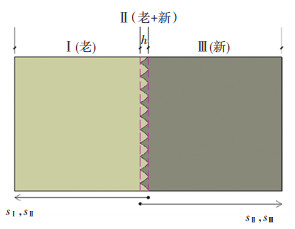
3.3 凿毛界面区水泥砂浆孔隙率分布模型老混凝土凿毛后,后浇筑的新混凝土会充填凿坑。于是,凿毛界面区由三部分组成:凿坑深度h以外的老混凝土区(图中Ⅰ区),原凿毛表面另一侧的新混凝土区(图中Ⅲ区)以及凿坑深度h范围内的新老混凝土啮合区(图中Ⅱ区),见图 10。
|
图 10 凿毛界面区新老混凝土啮合示意 Fig. 10 Diagram of meshing of new and old concrete in chiseled interfacial zone |
其中,老混凝土区和新混凝土区中的水泥砂浆孔隙率随各自s(sⅠ和sⅢ)的分布模型直接按式(5)计算,即:
| $ \begin{aligned} p_\text{O}\left(s_{\mathrm{Ⅰ}}\right)= & 1.374 r_\text{O}^{0.021}\left(-0.175 r_\text{O}^2+0.249 r_\text{O}-\right. \\ & 0.019)^{0.577}[1+0.864\;8 \cdot \\ & \left.\exp \left(-0.267\;8 s_{\mathrm{Ⅰ}}^2\right)\right], s_{\mathrm{Ⅰ}} \geqslant h \end{aligned} $ | (6) |
| $ \begin{aligned} p_{\mathrm{N}}\left(s_{\mathrm{Ⅲ}}\right)= & 1.374 r_{\mathrm{N}}^{0.021}\left(-0.175 r_{\mathrm{N}}^2+0.249 r_{\mathrm{N}}-\right. \\ & 0.019)^{0.577}[1+0.864\;8 \cdot \\ & \left.\exp \left(-0.267\;8 s_{\mathrm{Ⅲ}}^2\right)\right], s_{\mathrm{Ⅲ}} \geqslant h \end{aligned} $ | (7) |
式中:sⅠ、sⅢ分别为老混凝土区和新混凝土区中各点距离初始界面(即老混凝土未凿毛时的表面)的距离;pO(sⅠ)、pN(sⅢ)分别为老混凝土区和新混凝土区中的水泥砂浆孔隙率;rO、rN分别为老混凝土和新混凝土的水灰比;h为凿坑深度。
在凿坑深度范围内的新老混凝土啮合区中,距离初始界面任一深度sⅡ所在的横截面(平行于初始界面),其面积A(sⅡ)均由一部分老混凝土所占面积AO(sⅡ)与一部分新混凝土所占面积AN(sⅡ)相加而成,即:
| $ A\left(s_{\mathrm{Ⅱ}}\right)=A_\text{O}\left(s_{\mathrm{Ⅱ}}\right)+A_{\mathrm{N}}\left(s_{\mathrm{Ⅱ}}\right) $ | (8) |
式中:sⅡ为新老混凝土啮合区中任一点距离初始界面的距离;A(sⅡ)、AO(sⅡ)、AN(sⅡ)分别为新老混凝土啮合区中距离初始界面任一深度sⅡ所在横截面的总面积以及老混凝土和新混凝土各自所占的面积。
因此,在距离初始界面sⅡ深度处的新老混凝土啮合截面中,水泥砂浆平均孔隙率即为该截面处老混凝土和新混凝土各自的水泥砂浆孔隙率按各自所占面积加权平均而得,即:
| $ p_{\mathrm{ON}}\left(s_{\mathrm{Ⅱ}}\right)=p_\text{O}\left(s_{\mathrm{Ⅱ}}\right) \frac{A_\text{O}\left(s_{\mathrm{Ⅱ}}\right)}{A\left(s_{\mathrm{Ⅱ}}\right)}+p_{\mathrm{N}}\left(h-s_{\mathrm{Ⅱ}}\right) \frac{A_{\mathrm{N}}\left(s_{\mathrm{Ⅱ}}\right)}{A\left(s_{\mathrm{Ⅱ}}\right)} $ | (9) |
式中:pON(sⅡ)、pO(sⅡ)、pN(h-sⅡ)分别为新老混凝土啮合区中距离初始界面任一深度sⅡ所在横截面上全部水泥砂浆的平均孔隙率以及老混凝土水泥砂浆和新混凝土水泥砂浆的孔隙率,其中,pO(sⅡ)和pN(h-sⅡ)直接按式(5)计算,即:
| $ \begin{aligned} p_\text{O}\left(s_{\mathrm{Ⅱ}}\right)= & 1.374 r_\text{O}^{0.021}\left(-0.175 r_\text{O}^2+0.249 r_\text{O}-\right. \\ & 0.019)^{0.577}[1+0.864\;8 \cdot \\ & \exp \left(-0.267\;8 s_{\mathrm{Ⅱ}}^2\right) \end{aligned} $ | (10) |
| $ \begin{aligned} p_{\mathrm{N}}\left(h-s_{\text {Ⅱ }}\right)= & 1.374 r_{\mathrm{N}}^{0.021}\left(-0.175 r_{\mathrm{N}}^2+0.249 r_{\mathrm{N}}-\right. \\ & 0.019)^{0.577}[1+0.864\;8 \cdot \\ & \left.\exp \left(-0.267\;8\left(h-s_{\text {Ⅱ }}\right)^2\right)\right] \end{aligned} $ | (11) |
式中0≤sⅡ≤h。
笔者前期在凿毛界面区粗骨料分布模型研究中得到了AO(sⅡ)/A(sⅡ)的分布模型,见式(12)[9]:
| $ \frac{A_\text{O}\left(s_{\mathrm{Ⅱ}}\right)}{A\left(s_{\mathrm{Ⅱ}}\right)}=\left(\frac{s_{\mathrm{Ⅱ}}}{h}\right)^x $ | (12) |
式中
进一步,AN(sⅡ)/A(sⅡ)的分布模型见式(13):
| $ \frac{A_{\mathrm{N}}\left(s_{\mathrm{Ⅱ}}\right)}{A\left(s_{\mathrm{Ⅱ}}\right)}=1-\left(\frac{s_{\mathrm{Ⅱ}}}{h}\right)^x $ | (13) |
将式(10)~(13)代入式(9),即可得到新老混凝土啮合区中任一截面的平均孔隙率计算模型,见式(14):
| $ \begin{aligned} & p_{\mathrm{ON}}\left(s_{\mathrm{Ⅱ}}\right)=1.374 r_\text{O}^{0.021}\left(-0.175 r_\text{O}^2+0.249 r_\text{O}-\right. \\ & 0.019)^{0.577}\left[1+0.8648 \cdot \exp \left(-0.2678 s_{\mathrm{Ⅱ}}^2\right)\right] \cdot \\ & \quad\left(\frac{s_{\mathrm{Ⅱ}}}{h}\right)^x+1.374 r_{\mathrm{N}}^{0.021}\left(-0.175 r_{\mathrm{N}}^2+\right. \\ & \left.0.249 r_{\mathrm{N}}-0.019\right)^{0.577}[1+0.864\;8 \cdot\\ & \left.\exp \left(-0.2678\left(h-s_{\mathrm{Ⅱ}}\right)^2\right)\right] \cdot\left[1-\left(\frac{s_{\mathrm{Ⅱ}}}{h}\right)^x\right] \end{aligned} $ | (14) |
式中0≤sⅡ≤h。
于是,新老混凝土凿毛界面区水泥砂浆孔隙率分布模型由式(6)、(7)、(14)三段函数组成。其自变量包括老混凝土和新混凝土本体的水灰比rO和rN、凿坑深度h、以及距新老混凝土原始界面的距离s(包括sⅠ、sⅡ和sⅢ)。凿毛技术指标要求与文献[18]相同。函数的模型曲线见图 11。
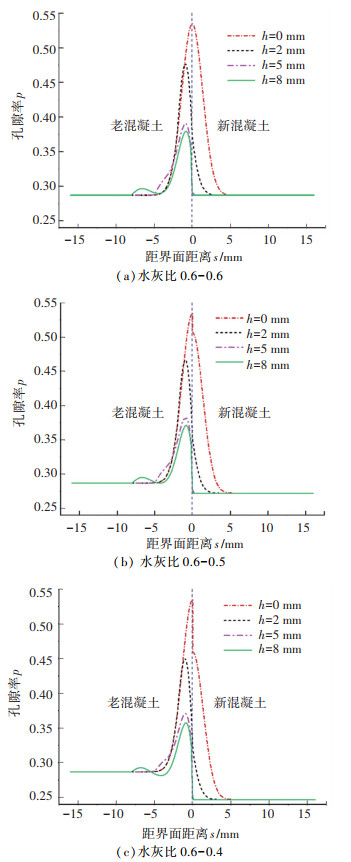
|
图 11 凿毛界面区水泥砂浆孔隙率分布模型曲线 Fig. 11 Distribution model curves of cement mortar porosity in chiseled interfacial zone |
1) 装配式结构新老混凝土竖缝界面区水泥砂浆名义孔隙率在界面处最大,然后向混凝土内部逐渐减小,最后趋于稳定,总体变化趋势具有高斯函数特征。
2) 随着水灰比增大,从界面到内部各部位的名义孔隙率均呈现相对增大趋势,但不同水灰比混凝土各自界面区与内部稳定区的相对名义孔隙率接近一致。
3) 基于名义孔隙率与真实孔隙率之间的稳定关系,建立了装配式结构竖缝式新老混凝土平整界面区孔隙率的分布模型。进一步,考虑凿毛区新老混凝土含量连续变化关系,建立了凿毛界面区孔隙率的分布模型。
| [1] |
李平先, 张雷顺, 赵国藩, 等. 新老混凝土粘结面渗透性能试验研究[J]. 水利学报, 2005, 36(5): 602. LI Pingxian, ZHANG Leishun, ZHAO Guofan, et al. Experimental study on permeability of fresh-old concrete bonding interface[J]. Journal of Hydraulic Engineering, 2005, 36(5): 602. DOI:10.3321/j.issn:0559-9350.2005.05.016 |
| [2] |
ESPECHE A D, LEÓN J. Estimation of bond strength envelopes for old-to-new concrete interfaces based on a cylinder splitting test[J]. Construction and Building Materials, 2011, 25(3): 1222. DOI:10.1016/j.conbuildmat.2010.09.032 |
| [3] |
MAILI C, JING M. Experimental study on shear behavior of the interface between new and old concrete with reinforced[J]. KSCE Journal of Civil Engineering, 2018, 22(5): 1882. DOI:10.1007/s12205-017-2007-6 |
| [4] |
LI Guoping, HU Hao, REN Cai. Resistance of segmental joints to carbonation[J]. ACI Materials Journal, 2017, 114(1): 137. DOI:10.14359/51689487 |
| [5] |
LI Fumin, LUO Xiaoya. Interfacial zone effects of chloride penetrations in precast concrete member joints[J]. Advances in Cement Research, 2019, 31(6): 279. DOI:10.1680/jadcr.17.00211 |
| [6] |
ZHAO Jie, LI Fumin, LUO Xiaoya. Influence of compressive stress on chloride transport in the interfacial zone of precast and cast-in-place concrete[J]. Structural Concrete, 2021, 22(5): 2624. DOI:10.1002/suco.201900147 |
| [7] |
KREIJGER P C. The skin of concrete composition and properties[J]. Matériaux et Construction, 1984, 17(4): 275. DOI:10.1007/BF02479083 |
| [8] |
LIU Peng, CHEN Ying, SHA Fei, et al. Study on micro structure and composition distribution of concrete surface zone based on fractal theory and XCT technology[J]. Construction and Building Materials, 2020, 263: 120209. DOI:10.1016/j.conbuildmat.2020.120209 |
| [9] |
ZHAO Jie, LI Fumin, CHEN Zhixiang. Modeling coarse aggregate distribution in interfacial zone of new-old concrete in precast concrete structures[J]. Structural Concrete, 2022. DOI:10.1002/suco.202100848 |
| [10] |
POWERS T C. Structure and physical properties of hardened Portland cement paste[J]. Journal of the American Ceramic Society, 1958, 41(1): 1. DOI:10.1111/j.1151-2916.1958.tb13494.x |
| [11] |
金南国, 金贤玉, 郭剑飞. 混凝土孔结构与强度关系模型研究[J]. 浙江大学学报(工学版), 2005, 39(11): 1680. JIN Nanguo, JIN Xianyu, GUO Jianfei. Relationship modeling of pore structure and strength of concrete[J]. Journal of Zhejiang University (Engineering Science), 2005, 39(11): 1680. |
| [12] |
金珊珊, 张金喜, 陈春珍, 等. 水泥砂浆孔结构分形特征的研究[J]. 建筑材料学报, 2011, 14(1): 92. JIN Shanshan, ZHANG Jinxi, CHEN Chunzhen, et al. Study on pore fractal characteristic of cement mortar[J]. Journal of Building Materials, 2011, 14(1): 92. DOI:10.3969/j.issn.1007-9629.2011.01.019 |
| [13] |
罗明勇, 曾强, 庞晓贇, 等. 养护条件对水泥基材料孔隙结构的影响[J]. 硅酸盐学报, 2013, 41(5): 597. LUO Mingyong, ZENG Qiang, PANG Xiaoyun, et al. Effect of curing conditions on pore structure of cement based materials[J]. Journal of the Chinese Ceramic Society, 2013, 41(5): 597. DOI:10.7521/j.issn.0454-5648.2013.05.04 |
| [14] |
GAO Y, SCHUTTER G D, YE G, et al. The ITZ microstructure, thickness and porosity in blended cementitious composite: effects of curing age, water to binder ratio and aggregate content[J]. Composites Part B: Engineering, 2014, 60(1): 1. DOI:10.1016/j.compositesb.2013.12.021 |
| [15] |
刘旭, 陈歆, 李立辉, 等. 负压成型水泥基材料孔结构特征[J]. 哈尔滨工业大学学报, 2021, 53(9): 26. LIU Xu, CHEN Xin, LI Lihui, et al. Characterization of pore structure of cement-based materials produced in negative pressure[J]. Journal of Harbin Institute of Technology, 2021, 53(9): 26. DOI:10.11918/202007097 |
| [16] |
连丽. 混凝土显微结构的研究[D]. 武汉: 武汉理工大学, 2006 LIAN Li. Study on microstructure of concrete[D]. Wuhan: Wuhan University of Technology, 2006 |
| [17] |
周继凯, 金龙, 丁宁. 含砂量对水泥砂浆强度与孔结构的影响[J]. 科学技术与工程, 2013, 13(20): 5855. ZHOU Jikai, JIN Long, DING Ning. Effect of sand content on strength and pore structure of cement mortar[J]. Science Technology and Engineering, 2013, 13(20): 5855. DOI:10.3969/j.issn.1671-1815.2013.20.023 |
| [18] |
陈志祥, 李富民, 方渝钰, 等. 混凝土表面粗糙度评价指标的相关性研究[J]. 建筑结构学报, 2021, 42(12): 193. CHEN Zhixiang, LI Fumin, FANG Yuyu, et al. Study on depen-dencies among evaluation indexes for concrete surface roughness[J]. Journal of Building Structures, 2021, 42(12): 193. DOI:10.14006/j.jzjgxb.2020.0044 |
 2023, Vol. 55
2023, Vol. 55


