2. 上海市动力工程多相流动与传热重点实验室(上海理工大学), 上海 200093;
3. 江苏东华测试技术股份有限公司, 江苏 靖江 214500
2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer for Power Engineering (University of Shanghai for Science and Technology), Shanghai 200093, China;
3. Jiangsu Donghua Testing Technology Co., Ltd., Jingjiang 214500, Jiangsu, China
中国浅海风资源开发趋于饱和[1],深海风资源较为丰富,因此海上风电正逐步向深海发展[2]。漂浮式风力机作为深海风能主要开发设备,在长期受海水腐蚀及复杂海洋环境载荷作用下,系泊极易失效进而影响整个漂浮式风力机的安全稳定运行。因此,采用合理有效的故障诊断方法,在系泊蠕变早期阶段实现预警,对保证漂浮式风力机安全运行及延长其使用寿命具有重要意义。
文献[3]提出采用变分模态分解(variational mode decomposition, VMD)对故障信号进行预处理,可有效改善上述问题,并具有良好的鲁棒性和运算效率;文献[4]采用VMD方法开展了轴承的故障诊断,研究发现VMD可提取多个特征;文献[5]将快速傅里叶变换、包络分析与VMD结合,实现了更有效的智能故障诊断;文献[6]研究了VMD方法在故障特征提取中的应用,结果表明VMD与EMD和EEMD相比更有效。但现有振动分析法在强噪声环境下难以有效识别故障状态[7]。因此,须引入新方法对非线性特征进行表征与反映。
分形学为表征振动信号的非线性特征提供了一种分析方法。因故障信号具有明显自相似性[8],故可利用分形对其进行分析。分形维数是描述信号非线性程度的特征量,包含Hausdorff位数、盒维数和关联维数等。其中,盒维数抗噪性好,可有效表现信号的非线性特征,在故障诊断领域已取得广泛应用[9]。文献[10]将分形盒维数应用于轴承信号的特征提取和故障诊断,证明了其在故障状态识别上的有效性;文献[11]结合盒维数与EMD方法,在传统单一分形维数判断的基础上,提高了特征提取的效率和准确性;文献[12]采用多重分形去趋势波动分析(multifractal detrended fluctuation analysis, MF-DFA)方法对机械故障非线性特征进行分析,以多重分形的多测度刻画分形特征优势弥补了单分形维数存在的缺陷。
目前国内外学者对风力机故障诊断的研究主要集中于发电机与齿轮箱方面,对海上风力机系泊故障诊断研究鲜见。本文以搭载NREL 5 MW风力机ITI Energy Barge平台的系泊系统为研究对象,分析不同位置系泊蠕变及其失效后对漂浮式风力机动态响应的影响;通过VMD对不同位置系泊蠕变下的平台响应数据进行解耦,结合分形盒维数对分量进行优选,提取系泊故障信号中更具代表性的非线性特征;并采用MF-DFA方法解析系泊故障信号多重分形特征,为漂浮式风力机系泊健康状况诊断提供了理论基础和技术支持。
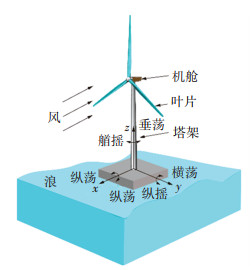
1 研究对象 1.1 漂浮式风力机模型以ITI Energy Barge平台的NERL 5 MW漂浮式风力机为研究对象,其整机系统见图 1,主要参数见表 1,漂浮式平台主要参数见表 2[13]。
|
图 1 Barge平台漂浮式风力机 Fig. 1 Floating wind turbine of Barge platform |
| 表 1 NREL 5 MW风力机参数 Tab. 1 Parameters of NREL 5 MW wind turbine |
| 表 2 ITI Energy Barge平台参数 Tab. 2 Parameters of ITI Energy Barge platform |
海上漂浮式风力机平台需安装系泊系统,减小平台位移并确保平台相对于海面的位置,实现在深海较恶劣环境下运行[14]。常见系泊方式有悬链线式系泊和张紧式系泊2种。
系泊系统中各根系泊能通过辐射状布置提供各方向的回复力。目前系泊缆通常为合成纤维缆,其为工程提供了便利,但相较传统锚链及钢丝绳具有更加复杂的非线性特征,为相关研究带来更大的难度。系泊发生蠕变时特征为刚度与系泊长度的小幅变化,在数值模拟上常通过系泊刚度与长度按百分比变化实现。
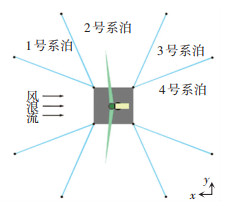
Barge平台利用8根从四角上导缆孔引出的系泊与海底锚点相连,采用悬链线式系泊,平台俯视图见图 2,系泊参数见表 3[15]。
|
图 2 系泊示意 Fig. 2 Mooring diagram |
| 表 3 系泊参数 Tab. 3 Mooring parameters |
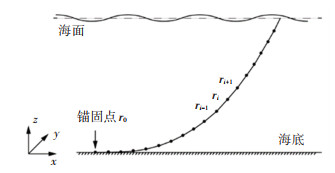
集中质量法常应用于求解动态系泊模型[16],见图 3。自底部锚固点开始,将系泊缆切分为以N+1个节点连接的N个大小相等的系泊段,每个系泊线段i+1/2具有相同的未拉伸长度L、体积等效直径d、弹性模量E和惯性阻尼系数Cint等特性。每个节点i位置由位置向量ri定义,包含节点位置的三维坐标。
|
图 3 动态系泊模型示意 Fig. 3 Diagram of dynamic mooring model |
在集中质量法中,通过将每个节点分配为相邻2个线段的组合质量的一半,将系泊缆的质量离散为每个节点的点质量。线段i+1/2的内部刚度和阻尼力分别表示为Ti+1/2和Ci+1/2,在节点i集中的线段的质量记为Wi,Bi为节点i的净浮力。
节点i的3×3质量矩阵表示为
| $ \boldsymbol{m}_i=\frac{\pi}{4} d^2 L \rho i \boldsymbol{I} $ | (1) |
式中:ρ为系泊缆的密度, I为单位矩阵。
节点i的附加质量矩阵表示为
| $ \boldsymbol{a}_i=\boldsymbol{a}_{\mathrm{p} i}+\boldsymbol{a}_{\mathrm{q} i}=\rho \frac{\boldsymbol{\pi}}{4} d^2 L\left[C_{\mathrm{an}}\left(\boldsymbol{I}-\hat{\boldsymbol{q}}_i \hat{\boldsymbol{q}}_i^{\mathrm{T}}\right)+C_{\mathrm{at}}\left(\hat{\boldsymbol{q}}_i \hat{\boldsymbol{q}}_i^{\mathrm{T}}\right)\right] $ | (2) |
式中:api和aqi分别对应横向和切向附加质量矩阵,Can(=0.865)和Cat(=0.269)分别为横向和切向附加质量系数,
节点处切线方向可表示为
| $ \hat{\boldsymbol{q}}_i=\frac{\boldsymbol{r}_{i+1}-\boldsymbol{r}_{i-1}}{\left\|\boldsymbol{r}_{i+1}-\boldsymbol{r}_{i-1}\right\|} $ | (3) |
式中ri为节点i的位置向量。
进而,各节点i的系泊缆运动方程为
| $ \begin{gathered} F_{\text {м }}=\sum\limits_{i=1}^N\left(\boldsymbol{m}_i+\boldsymbol{a}_i\right) \ddot{\boldsymbol{r}}_i=\sum\limits_{i=1}^N\left(T_{i+1 / 2}-T_{i-1 / 2}+\right. \\ \left.C_{i+1 / 2}-C_{i-1 / 2}+W_i+B_i+D_{\mathrm{p} i}+D_{\mathrm{q} i}\right) \end{gathered} $ | (4) |
式中Dpi和Dqi分别为横向和切向上的阻力。
2 环境载荷与参数复杂的海洋环境下,漂浮式风力机会受到风浪流等多种载荷作用,其中上部风轮受到的风载荷及下部漂浮式平台受到的海流与波浪载荷影响最大[17]。
2.1 风载荷基于叶素动量理论,通过动态入流理论对风轮平面的诱导速度进行求解,进而解得沿叶片展向各位置攻角[18]。
其中,诱导速度可表示为
| $ \lambda(r, \tilde{\psi})=v_0+v_{\mathrm{s}} u \sin \tilde{\psi}+v_{\mathrm{c}} u \cos \tilde{\psi} $ | (5) |
式中:v0、vs及vc分别为诱导速度的平均、水平和垂直分布,u为半径比,
进而,叶片所受推力与扭矩可表示为
| $ \left\{\begin{array}{l} \mathrm{d} Q=\frac{1}{2} \rho c \frac{(\mathit{\Omega} r(1+b))^2}{\cos ^2 \theta}\left(C_1 \sin \theta-C_{\mathrm{d}} \cos \theta\right) \mathrm{d} r \\ \mathrm{~d} N=\frac{1}{2} \rho c \frac{U_{\infty}^2(1-a)^2}{\sin ^2 \theta}\left(C_1 \cos \theta-C_{\mathrm{d}} \sin \theta\right) \mathrm{d} r \end{array}\right. $ | (6) |
式中:ρ为空气密度,c为距轮毂中心r处风力机叶片弦长,Ω为风轮转速,b为切向诱导因子,a为轴向诱导有因子,θ为来流攻角,U∞为来流速度,Cl为升力系数,Cd为阻力系数。
2.2 海流载荷一般情况下海流速度较缓,对海工结构的主要作用力为拖曳力,可表示为
| $ F_{\mathrm{c}}=\frac{1}{2} \rho_{\mathrm{s}} C_{\mathrm{d}} A U_{\mathrm{o}}{ }^2 $ | (7) |
式中:A为平台沿海流方向等效面积,Uo为流速,Cd为阻力系数,ρs为海水密度。
2.3 波浪载荷由于Barge平台体型较大,其对波浪场的影响不可忽略,但须考虑平台在海水中的绕射效应,故本文采用辐射/绕射理论求解Barge平台在海水中的波浪载荷,速度势函数可表示为[19]
| $ \varphi=\varphi_{\mathrm{i}}+\varphi_{\mathrm{d}}+\sum\limits_{j=1}^6 \varphi_{\mathrm{r}} $ | (8) |
式中:φi为入射势,φd为绕射势,φr为辐射势。
其中,速度势函数需满足拉普拉斯方程与边界条件:
| $ \left\{\begin{array}{l} \partial^2 \varphi / \partial x^2+\partial^2 \varphi / \partial y^2+\partial^2 \varphi / \partial z^2=0 \\ \partial \varphi / \partial z=0 \\ g \partial \varphi / \partial z+\partial^2 \varphi / \partial t^2=0 \\ \partial \varphi / \partial z=\partial \eta / \partial t+(\partial \eta / \partial x)(\partial \varphi / \partial x)+ \\ \quad(\partial \eta / \partial y)(\partial \varphi / \partial y) \\ \partial \varphi / \partial \boldsymbol{n}=0 \end{array}\right. $ | (9) |
式中:g为重力加速度,d为海深,η为入射波波面函数,n为浮体湿表面外法向量。
漂浮式风力机平台受到的波浪力与波浪力矩可表示为:
| $ \boldsymbol{F}_{\mathrm{W}}=\iint_{S_{\mathrm{B}}}-p \boldsymbol{n} \mathrm{d} S_{\mathrm{B}} $ | (10) |
| $ \boldsymbol{M}_{\mathrm{W}}=\iint_{S_{\mathrm{B}}}-p(\boldsymbol{r} \times \boldsymbol{n}) \mathrm{d} S_{\text {в }} $ | (11) |
式中:p为压强,FW为波浪力,SB为浮体湿表面积;MW为波浪力矩,r为结构物表面到基点矢量。
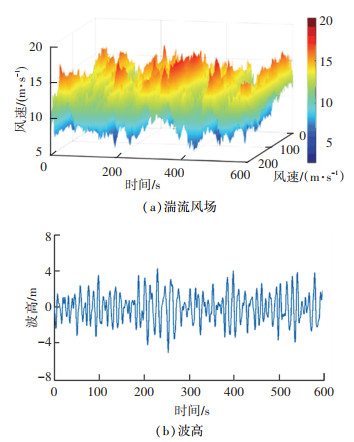
2.4 环境参数基于TurbSim[20],参照IEC 61400-3,选用Kaimal风谱,生成11.4 m/s湍流风场,见图 4(a)。海流为均匀流,流速0.8 m/s。波浪基于P-M谱,谱峰周期10.1 s,有义波高6 m,水深为150 m,不规则波高时域曲线见图 4(b)。
|
图 4 湍流风场与波高时间序列 Fig. 4 Turbulent wind speed spectrum and time series of wave height |
变分模态分解算法基于外差解调、Hilbert变换和维纳滤波,将原始信号分解为K个模态分量,可有效抑制EMD及EEMD等方法存在的模态混淆现象[10]。
建立约束变分模型表达式如下:
| $ \begin{aligned} & \min _{\left\{u_k, \omega_k\right\}}\left\{\sum\limits_k\left\|\partial_t\left[\left(\sigma(t)+\frac{\mathrm{j}}{\pi t}\right) * u_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_2^2\right\} \\ & \text { s.t. } \sum\limits_{k=1}^K u_k(t)=f(t) \end{aligned} $ | (12) |
式中:K为模态分量数,j为虚数单位,σ(t)为单位脉冲函数,∂t为偏导运算,*为卷积运算,uk = u1, u2, u3, …, uK、ωk = ω1, ω2, ω3, …, ωK分别为经变分模态分解得到的K个模态分量与其中心频率。
同时,利用惩罚系数α和拉格朗日乘子λ(t)求解变分约束问题。其增广拉格朗日表达式为
| $ \begin{aligned} & L\left(\left\{u_k\right\}, \left\{\omega_k\right\}, \lambda\right)= \\ & \alpha \sum\limits_{k=1}^K\left\|\partial_t\left[\left(\delta(t)+\frac{\mathrm{j}}{\pi t}\right) * u_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_k t}\right\|_2^2+ \\ & \quad\left\|f(t)-\sum\limits_{k=1}^K u_k(t)\right\|_2^2+\langle\lambda(t), f(t)- \\ & \left.\sum\limits_{k=1}^K u_k(t)\right\rangle \end{aligned} $ | (13) |
变分模态分解利用交替方向乘子法单独交替迭代ukn+1、ωkn+1、λn+1,进而收敛得到变分模型最优可行解。
其迭代表达式为:
| $ \hat{u}_k^{n+1}(\omega)=\frac{\hat{f}(\omega)-\sum\limits_{i=1}^{k-1} \hat{u}_i^{n+1}(\omega)-\sum\limits_{i=k+1}^K \hat{u}_i^n(\omega)+\frac{\hat{\lambda}_i(\omega)}{2}}{1+2 \alpha\left(\omega-\omega_k^n\right)^2} $ | (14) |
| $ \omega_k^{n+1}=\frac{\int_0^{\infty} \omega\left|\hat{u}_k^{n+1}(\omega)\right|^2 \mathrm{~d} \omega}{\int_0^{\infty}\left|\hat{u}_k^{n+1}(\omega)\right|^2 \mathrm{~d} \omega} $ | (15) |
| $ \hat{\lambda}^{n+1}(\omega)=\hat{\lambda}^n(\omega)+\tau\left(\hat{f}(\omega)-\sum\limits_{k=1}^K \hat{u}_k^{n+1}(\omega)\right) $ | (16) |
式中:τ为保真系数,^为傅里叶变换,n为迭代次数。
求解过程中各模态分量的带宽和中心频率亦不停迭代,直至达到更新停止条件,其判别表达式为
| $ \sum\limits_{k=1}^K\left(\left\|\hat{u}_k^{n+1}(\omega)-\hat{u}_k^n(\omega)\right\|_2^2 /\left\|\hat{u}_k^n(\omega)\right\|_2^2\right)<\beta $ | (17) |
式中β为判别精度。
3.2 盒维数考虑分形具有自相似性、无标度性及自仿射性,而分形维数是一种刻画分形不规则性的有效度量方式,其中盒维数因其原理简单及抗噪性好的特点,广泛用于信号处理中,可度量信号的不规则度。其定义为
| $ D_{\mathrm{c}}=\lim \limits _{\varepsilon \rightarrow 0} \frac{\log N(\varepsilon)}{-\log \varepsilon} $ | (18) |
设离散信号y(i)⊂Y,Y为n维欧氏空间Rn上的闭集。利用网格划分Rn,网格ε尽量小,Nε为划分网格数。仅定义难以求得,故采用近似法求解。扩大网格ε至kε,
| $ \begin{gathered} P(k \varepsilon)=\sum\limits_{i=1}^{N / k} \mid \max \left\{y_{k(i-1)+1}, y_{k(i-1)+2}, \cdots, y_{k(i-1)+k+1}\right\}- \\ \min \left\{y_{k(i-1)+1}, y_{k(i-1)+2}, \cdots, y_{k(i-1)+k+1}\right\} \mid \end{gathered} $ | (19) |
| $ N_{k \varepsilon}=P(k \varepsilon) /(k \varepsilon)+1 $ | (20) |
式中:i=1, 2, …, N/k;N为采样点数;k=1, 2, …, M, M < N;Nkε为网格计数。
自lg(kε)-lg Nkε选取线性程度良好的范围,令其两端点分别为k1与k2,则:
| $ \lg N_{k \varepsilon}=a \lg (k \varepsilon)+b \quad k_1 \leqslant k \leqslant k_2 $ | (21) |
通过数据拟合范围内曲线斜率:
| $ \hat{a}=-\frac{\left(k_2-k_1+1\right) \sum\limits_{k=1}^M \lg k \lg N_{k \varepsilon}-\sum\limits_{k=1}^M \lg k \sum\limits_{k=1}^M \lg N_{k \varepsilon}}{\left(k_2-k_1+1\right) \sum\limits_{k=1}^M \lg ^2 k-\left(\sum\limits_{k=1}^M \lg k\right)^2} $ | (22) |
可计算得盒维数DB为
| $ D_{\mathrm{B}}=\hat{a} $ | (23) |
系泊蠕变下平台响应信号较为复杂,单分形仅从单一测度无法准确描述信号的分形特性[21]。多重分形是在分形结构上具有多个标度指数的奇异测度组成的集合,可对分形测度或物理量在支集上的分布情况进行精细刻画[22],弥补单测度分析时易导致判别位置混淆的缺陷,且保留了单分形维数抗噪性优势。因此,本文采用多重分形去趋势波动分析法,研究不同位置系泊蠕变下平台响应信号的多重分形特征。
4.1 广义Hurst指数现有振动信号分析法在强噪声环境下难以有效识别故障状态,为研究非平稳信号的动力学特性,采用MF-DFA进行分析,具体步骤为[23]:
1)计算振动信号{x(k), k=1, 2, …, N}的均值累积离差Y(i):
| $ Y(i)=\sum\limits_{k=1}^i[x(k)-\bar{x}] \quad i=1, 2, \cdots, N $ | (24) |
式中x为x(k)的均值。
2) 等分划分区间Y(i),m为子区间个数,s为子区间长度。因m可能为非整数,反向重复划分,共得2m个子区间。
3) 子区间均方差F2(s, v)常以最小二乘多项式拟合:
| $ F^2(s, v) \equiv \frac{1}{s} \sum\limits_{i=1}^s\left\{Y[(v-1) s+i]-y_v(i)\right\}^2 $ | (25) |
式中v=1, 2, …, m。
区间Y(i)无法单向等分划分时:
| $ F^2(s, v) \equiv \frac{1}{s} \sum\limits_{i=1}^s\left\{Y[N-(v-m) s+i]-y_v(i)\right\}^2 $ | (26) |
式中:v=m+1, m+2, …, 2m;yv(i)为子区间v的拟合多项式。
4) 通过二元多项式拟合计算得到测度波动函数Fq(s)为
| $ F_q(s) \equiv\left\{\frac{1}{2 m} \sum\limits_{v=1}^{2 m}\left[F^2(s, v)\right]^{q / 2}\right\}^{1 / q} $ | (27) |
当q等于2时,式(27)则为去趋势波动分析。
5) 改变子区间长度s,重复上述步骤。若x(k)存在长程相关性,可知q和hq、Fq(s)和s关系如下:
| $ F_q(s) \propto s^{h_q} $ | (28) |
若广义Hurst指数hq不随q变化而发生变化,可知x(k)具有单分形特征;当广义Hurst指数hq随q变化而变化,则x(k)具有多重分形特性。
4.2 多重分形谱通过配分函数得关系式为
| $ \tau_q=q h_q-1 $ | (29) |
通过勒让德变换得奇异指数α和多重分形谱f(α)为
| $ \alpha_q=\mathrm{d} \tau_q / \mathrm{d} q $ | (30) |
| $ f(\alpha)=q \alpha_q-\tau_q $ | (31) |
利用式(29)~(31)计算,得奇异指数α、谱函数f(α)及广义Hurst指数hq间的关系为:
| $ \alpha_q=h_q+q \mathrm{~d} h_q / \mathrm{d} q $ | (32) |
| $ f(\alpha)=q\left(\alpha_q-h_q\right)+1 $ | (33) |
多重分形谱f(α)反映了x(k)的分形情况。若f(α)图像表现为单峰状曲线,则为多重分形;若f(α)图像为水平的直线,则仅为单重分形。
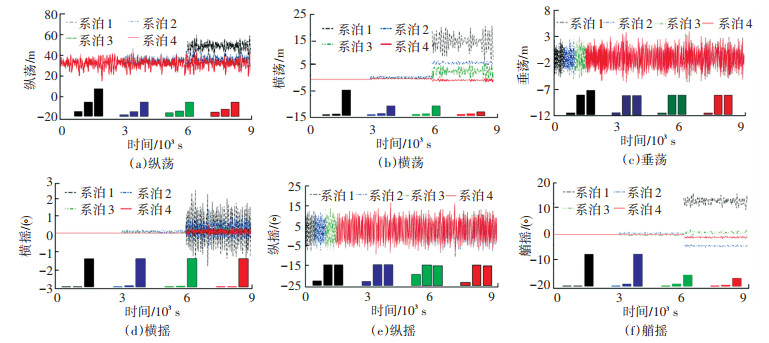
5 结果与分析 5.1 动态响应分析设置风浪流均以垂直风力机平面方向入射,因Barge平台8根系泊对称分布,故仅对其中4根进行分析。漂浮式风力机平台于系泊正常、发生蠕变及失效3种情况下六自由度上响应曲线与1~4号系泊在各阶段最大响应幅值对比见图 5。
|
图 5 系泊正常、蠕变及失效下平台六自由度响应 Fig. 5 Platform responses in six-degree-of-freedom under normal mooring, creep, and failure situations |
如图 5所示,0~3 000 s,3 000~6 000 s,6 000~9 000 s分别为系泊正常、蠕变及失效情况,图中上部各曲线分别表示各系泊在3个阶段的漂浮式风力机平台动态响应,系泊1~4在3个阶段的最大响应幅值对应图中下部柱状图。通过对比图 5中平台于系泊不同状况下在六个自由度上的响应曲线及响应幅值可知,系泊发生蠕变与失效后平台响应产生不同程度地增大。其中,纵荡、横荡、横摇及艏摇受到的影响最大,对纵摇和横荡影响较小;系泊蠕变后,平台响应幅值增加极小,系泊失效后,响应幅值急剧增大;不同位置系泊状态变化对平台动态响应影响不一,靠近迎风浪侧的1~2号系泊对平台影响较大,远离迎风浪侧的3~4号系泊影响较小。
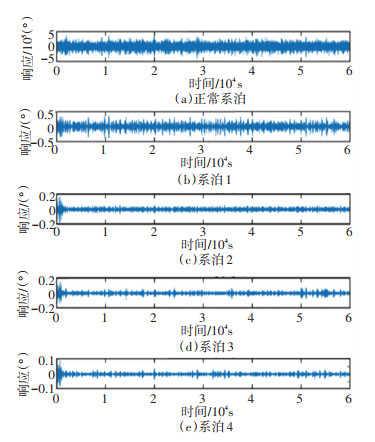
5.2 信号处理由上述分析可知,平台艏摇响应在各自由度中最为敏感,故下文对各系泊蠕变状态下的平台艏摇响应数据进行分析。正常系泊平台艏摇时域信号与上节中系泊1~4发生蠕变后平台艏摇时域响应见图 6。由图 6可知,各系泊蠕变状态下平台艏摇响应微弱,时域图差异甚微,难以判断系泊蠕变位置。
|
图 6 5种系泊状态下平台艏摇响应时域 Fig. 6 Time response in yaw of platform under five mooring states |
采用VMD方法对5种系泊状态下平台艏摇响应信号进行分解,每种响应信号均具有3个模态分量。因盒维数可表征信号间的自相似性,故以其作为筛选特征分量的依据。结果见图 7。
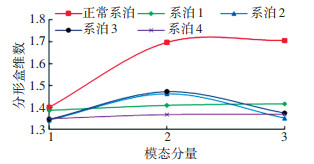
|
图 7 各模态分量分形盒维数 Fig. 7 Fractal box dimension of each modal component |
因盒维数越小表明信号非线性越弱,越规则[24]。故以其值最小的为特征信号,计算原始信号与采用本文方法所选取信号的盒维数,结果见表 4。
| 表 4 5种系泊状态下分形盒维数对比 Tab. 4 Comparison of fractal box dimension under five mooring states |
由表 4可知,各系泊状况下平台艏摇响应原信号分形盒维数较大,自相似性弱;经本文方法处理后所提取信号盒维数小,自相似性强。表明经VMD方法可较大程度滤除噪声,信号中非线性特征可得到有效提取。
5.3 多重分形特性分析非线性特征经VMD捕捉后采用MF-DFA方法进行多重分形分析,求取各多重分形参数与波动函数阶数q的变化关系曲线。5种系泊状态下平台艏摇响应信号的τq与波动函数阶数q的变化曲线见图 8。
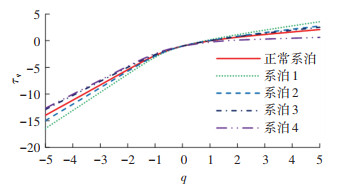
|
图 8 平台响应信号标度指数变化曲线 Fig. 8 Scale index curves of platform response signals |
由图 8可知,5种系泊状态下,τq在取值范围内,其值均随q值增大而呈非线性增加。q < 0时,系泊4状态下τq最大,系泊1最小,系泊3、正常系泊和系泊2的τq依次减小;q>0时,系泊1状态下τq最大,系泊4最小,系泊2、系泊3及正常系泊状态下τq顺序减小;当波动函数阶数=0时,各信号标度指数均为0.6,进一步说明5种系泊状态下平台响应信号具有多重分形特征。
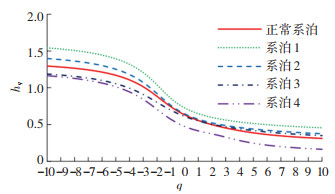
图 9为5种系泊状态下平台响应信号Hurst数与q的关系曲线。
|
图 9 平台响应信号Hurst指数变化曲线 Fig. 9 Hurst exponent variation curves of platform response signals |
由图 9可知,5种系泊状态下hq与q的变化曲线呈非线性变化。在全取值范围内,随q增加,hq持续减小,由此进一步表明各信号均为多重分形序列。当q>0时,系泊1状态下hq随q降速最大呈弱非线性,系泊3状态下降速最小呈强非线性;当q>0时,系泊1状态下hq降速最小呈强非线性,系泊4状态下降速最大呈弱非线性。由此表明,不同系泊状态下的广义Hurst指数存在较大差异,通过hq与q的斜率关系可判断各系泊状态下平台响应信号具备不同的非线性特征。
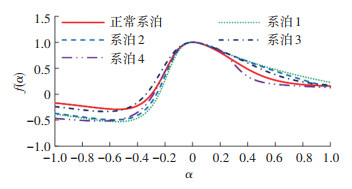
图 10为5种系泊状况下平台响应信号的奇异谱函数f(α)与奇异指数α的关系曲线。
|
图 10 平台响应信号多重分形谱变化曲线 Fig. 10 Multifractal spectrum variation curves of platform response signals |
由图 10可知,5种系泊状态下平台响应信号多重分形谱均呈几字形,曲线峰值处大致相同,各系泊状态下分形谱变化存在差异,说明各系泊状态下平台响应信号具备多重分形特征。
α0为变化关系曲线峰值的横坐标,其可说明信号在q=0下的不均匀程度[25]。文献[26]研究表明信号非线性状况可通过分析α0得到有效判断。因此本文对5种系泊状况下平台响应信号各随机选取30组数据,计算并分析其α0值,解析各系泊状态下平台响应信号的非线性特征。
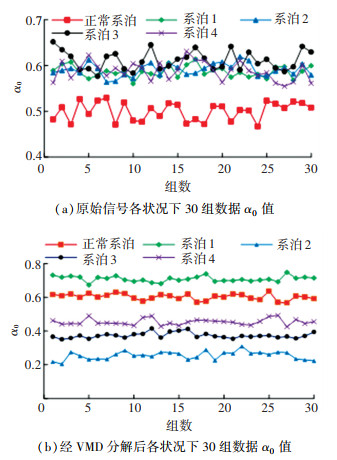
原信号与经VMD处理后5种系泊状态下各30组平台响应信号α0值变化趋势见图 11。
|
图 11 各系泊状况下30组数据的α0值对比 Fig. 11 Comparison of α0 values of 30 groups of data under different mooring states |
由图 11可知,各系泊状态下平台响应信号的α0值各异。系泊1状态下α0最大,说明该信号包含复杂的数据模式。而系泊2状态下α0最小,可见此数据模式单调,整体系泊系统受非线性作用较小。但α0在噪声环境下无法准确描述系统非线性状况。因此,当系泊处于不同状况时,α0值在图 11(a)中出现了交叉现象,系泊1~4的α0值无法准确描述信号不规则程度。但采用VMD方法后,提取信号的非线性特征更具代表性,能够精准刻画信号规则状况,消除曲线交织。由此可依靠数据复杂度判断系泊状态。
6 结论1) 在系泊由蠕变至失效过程中,平台六自由度动态响应均产生不同程度增大。系泊蠕变后,平台响应幅值增加极小;系泊失效后,响应幅值急剧增大。不同位置系泊状态变化对平台动态响应影响不同,靠近迎风浪侧的系泊对平台影响较大,远离迎风浪侧的系泊影响较小。
2) 采用VMD法分解平台响应信号,通过分形盒维数选取最优分量,可得到最具代表性的非线性特征,其分形盒维数低,不规则程度低,自相似性强。
3) 标度指数、广义Hurst指数和多重分形谱均表明各状况下平台响应信号具有多重分形特征。
4) 通过MF-DFA法分析VMD所提取的非线性特征,可根据数据复杂度较好地判断系泊状态,而仅通过原始信号无法判断系泊状态。
| [1] |
刘桢, 俞炅旻, 黄德财, 等. 海上风电发展研究[J]. 船舶工程, 2020, 42(8): 20. LIU Zhen, YU Jiongmin, HUANG Decai, et al. Research on development of offshore wind power[J]. Ship Engineering, 2020, 42(8): 20. |
| [2] |
GAO Kun, LI Chun, GAO Wei, et al. Research on new offshore wind power generation and its key technologies[J]. Energy Research and Information, 2010, 26(2): 110. DOI:10.3969/j.issn.1008-8857.2010.02.009 |
| [3] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531. DOI:10.1109/TSP.2013.2288675 |
| [4] |
WANG Yanxue, MARKERT R, XIANG Jiawei, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 243. DOI:10.1016/j.ymssp.2015.02.020 |
| [5] |
ZHANG Ming, JIANG Zhinong, FENG Kun. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump[J]. Mechanical Systems and Signal Processing, 2017, 93: 460. DOI:10.1016/j.ymssp.2017.02.013 |
| [6] |
郑小霞, 周国旺, 任浩翰. 基于变分模态分解和排列熵的滚动轴承故障诊断[J]. 振动与冲击, 2017, 36(22): 22. ZHENG Xiaoxia, ZHOU Guowang, REN Haohan. Rolling bearing fault diagnosis based on variational modal decomposition and permutation entropy[J]. Journal of Vibration and Shock, 2017, 36(22): 22. |
| [7] |
许子非, 李春, 杨阳, 等. 基于改进小波阈值及多重分形的风力机轴承振动信号分析[J]. 热能动力工程, 2019, 34(9): 191. XU Zifei, LI Chun, YANG Yang, et al. Vibration signal analysis of wind turbine bearing based on improved wavelet threshold and multifractal[J]. Journal of Thermal Energy and Power Engineering, 2019, 34(9): 191. DOI:10.16146/j.cnki.rndlgc.2019.09.022 |
| [8] |
TANG Baoping, LIU Wenyi, SONG Tao. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution[J]. Renewable Energy, 2010, 35(12): 2862. DOI:10.1016/j.renene.2010.05.012 |
| [9] |
郝研, 王太勇, 万剑, 等. 分形盒维数抗噪研究及其在故障诊断中的应用[J]. 仪器仪表学报, 2011, 32(3): 540. HAO Yan, WANG Taiyong, WAN Jian, et al. Fractal box dimension denoising and its application in fault diagnosis[J]. Chinese Journal of Scientific Instrument, 2011, 32(3): 540. |
| [10] |
HUANG Huafang, SONG Xiaolong, LIU Chun, et al. A novel fractal method for fault diagnosis and signal measurements[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(16): 6805. DOI:10.1016/j.ijleo.2015.10.113 |
| [11] |
韩东颖, 李庚, 时培明. 基于EMD和分形盒维数的旋转机械耦合故障诊断方法研究[J]. 振动与冲击, 2013, 32(15): 209. HAN Dongying, LI Geng, SHI Peiming. Research on fault diagnosis method of rotating machinery coupling based on EMD and fractal box dimension[J]. Journal of Vibration and Shock, 2013, 32(15): 209. DOI:10.3969/j.issn.1000-3835.2013.15.037 |
| [12] |
KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A: Statistical Mechanics and its Applications, 2002, 316(1): 87. DOI:10.1016/S0378-4371(02)01383-3 |
| [13] |
JONKMAN J, MATHA D. Quantitative comparison of the responses of three floating platforms[J]. Australian Historical Studies, 2010, 32(3): 351. |
| [14] |
王兴刚. 深海浮式结构物与其系泊缆索的耦合动力分析[D]. 大连: 大连理工大学, 2011 WANG Xinggang. Coupling dynamic analysis of deep-sea floating structures and mooring cables[D]. Dalian: Dalian University of Technology, 2011 |
| [15] |
JONKMAN J M, MATHA D. Dynamics of offshore floating wind turbines-analysis of three concepts[J]. Wind Energy, 2011, 14(4): 557. DOI:10.1002/we.442 |
| [16] |
HALL M, GOUPEE A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data[J]. Ocean Engineering, 2015, 104: 590. DOI:10.1016/j.oceaneng.2015.05.035 |
| [17] |
YE Kan, JI Jinchen. Current, wave, wind and interaction induced dynamic response of a 5 MW Spar-type offshore direct-drive wind turbine[J]. Engineering Structures, 2019, 178: 395. DOI:10.1016/j.engstruct.2018.10.023 |
| [18] |
MORIARTY P J, HANSEN A C. AeroDyn theory manual: NREL/TP-500-36881[R]. Golden: National Renewable Energy Laboratory, 2005
|
| [19] |
王博, 丁勤卫, 李春, 等. 普通海况下驳船式平台漂浮式风电场平台动态响应研究[J]. 机械工程学报, 2021, 57(6): 171. WANG Bo, DING Qinwei, LI Chun, et al. Dynamic response of floating wind farm platform based on Barge platform under common sea conditions[J]. Journal of Mechanical Engineering, 2021, 57(6): 171. DOI:10.3901/JME.2021.06.171 |
| [20] |
JONKMAN B J, BUHL M L. TurbSim user's guide: NREL/TP-500-39797[R]. Golden: National Renewable Energy Laboratory, 2005
|
| [21] |
成曙, 张振仁. 发动机现代诊断技术[M]. 西安: 西安交通大学出版社, 2006: 188. CHENG Shu, ZHANG Zhenren. Modern diagnosis technology for engine[M]. Xi'an: Xi'an Jiaotong University Press, 2006: 188. |
| [22] |
李舜酩. 振动信号的现代分析技术与应用[M]. 北京: 国防工业出版社, 2008: 234. LI Shunming. Modern analysis technique and application of vibration signal[M]. Beijing: National Defense Industry Press, 2008: 234. |
| [23] |
王浩天, 段修生, 单甘霖, 等. 一种基于ILCD融合与多重分形去趋势波动分析的退化特征提取方法[J]. 振动与冲击, 2019, 38(6): 233. WANG Haotian, DUAN Xiusheng, SHAN Ganlin, et al. Method for degradation feature extraction based on the ILCD fusion and multi fractal detrended fluctuation analysis[J]. Journal of Vibration and Shock, 2019, 38(6): 233. DOI:10.13465/j.cnki.jvs.2019.06.035 |
| [24] |
许子非, 缪维跑, 李春, 等. 流场非线性特征提取与混沌分析[J]. 物理学报, 2020, 69(24): 344. XU Zifei, MIAO Weipao, LI Chun, et al. Nonlinear feature extraction and chaos analysis of flow field[J]. Acta Physica Sinica, 2020, 69(24): 344. DOI:10.7498/aps.69.20200625 |
| [25] |
付晓强, 杨仁树, 崔秀琴, 等. 冻结立井爆破振动信号多重分形去趋势波动分析[J]. 振动与冲击, 2020, 39(6): 51. FU Xiaoqiang, YANG Renshu, CUI Xiuqin, et al. Multi-fractal detrended fluctuation analysis of the blasting vibration signal in a frozen shaft[J]. Journal of Vibration and Shock, 2020, 39(6): 51. |
| [26] |
李洋, 李春, 杨阳. 基于多重分形去趋势波动分析的风力机轴承故障诊断[J]. 太阳能学报, 2019, 40(11): 3235. LI Yang, LI Chun, YANG Yang. Fault diagnosis of wind turbine bearing based on multi-fractal de-trend fluctuation analysis[J]. Acta Energiae Solaris Sinica, 2019, 40(11): 3235. |
 2023, Vol. 55
2023, Vol. 55


