2. 航天发射场可靠性重点实验室,海口 570100
2. Key Laboratory of Space Launching Site Reliability Technology, Haikou 570100, China
异常检测是数据挖掘领域一项非常重要的技术,广泛应用于金融、网络、保险、股票等多个领域[1]。基于相对密度的局部异常因子(local outlier factor, LOF)[2]算法是目前应用最广泛且最有效的无参数异常检测算法之一,尤其是对于呈偏态分布的数据集。有鉴于此,相关文献[3-12]开展了大量基于LOF的研究,但对于LOF的局限性,人们依然没有找到较好的改进方法,这使得该算法无法拓展到数据规模更大以及检测精度需求更高的应用场景中。第一, 其时间复杂度较高, 由于LOF要分别对n个样本点进行k近邻搜索,因此使用线性扫描方法的时间复杂度为O(n2)。第二, 其空间复杂度较高, 由于LOF算法需要存储每对数据点的距离信息,因此其空间复杂度也为O(n2)。这使得该算法无法应用于数据流处理中,因为随着数据源源不断的到达,LOF所需内存将持续增大,直到无法处理[8]。第三, LOF对交叉异常以及低密度簇周围异常点识别不敏感。在真实场景中,正异常点通常不是泾渭分明而是交错在一起的,LOF对这种紧邻正常数据簇且与其存在一定交叉的异常点的识别不敏感,最差情况下LOF将退化为随机检测器。同时在真实数据集中,正常数据的分布不会只集中在一个区域,而是分布在多个密度不同的簇中,虽然与多数算法相比,LOF可以较为有效地检测出这种存在于非均匀密度数据中的异常点,但其仍存在局限性,即相比于高密度簇,低密度簇正常点周围的异常点更容易被LOF算法忽略。
1 理论基础LOF算法通过计算局部离群因子来衡量每个数据点的异常程度,数据点a局部离群因子的计算以及分析需要以下定义以及定理,其中定理1的具体证明过程参见文献[2]。
定义1 点a与其第k邻域点之间的欧氏距离为dk(a)。
定义2 点o到点a的可达距离为
| $ d_{\text {reach }, k}(a, o)=\max \left\{d_k(o), d(a, o)\right\} $ | (1) |
式中d(a, o)为点a和点o之间的欧氏距离。
定义3 点a的局部可达密度为
| $ d_{\mathrm{lr}, k}(a)=\frac{1}{\left[\frac{\sum _{o \in N_k(a)} d_{\text {reach }, k}(a, o)}{\left|N_k(a)\right|}\right]} $ | (2) |
式中Nk(a)为a点k近邻数据点的集合。
定义4 点a的局部离群因子为
| $ F_{\mathrm{lo}, k}(a)=\frac{\sum _{o \in N_k(a)} \frac{d_{\mathrm{lr}, k}(o)}{d_{\mathrm{lr}, k}(a)}}{\left|N_k(a)\right|} $ | (3) |
定义5 点a第k邻域中一点到点a可达距离的最小值以及最大值为
| $\begin{aligned} F_{\text {min }}(a)=\min \left\{d_{\text {reach }, k}(a, b) \mid b \in N_k(a)\right\} \end{aligned} $ | (4) |
| $ F_{\text {max }}(a)=\max \left\{d_{\text {reach }, k}(a, b) \mid b \in N_k(a)\right\} $ | (5) |
定义6 点a第k邻域中一点b的第k邻域中一点到点b可达距离的最小值以及最大值为
| $S_{\text {min }}(a)=\min \left\{d_{\text {reach }, k}(b, o) \mid b \in N_k(a) \text { 且 } o \in N_k(b)\right\} $ | (6) |
| $S_{\max }(a)=\max \left\{d_{\text {reach }, k}(b, o) \mid b \in N_k(a) \text { 且 } o \in N_k(b)\right\} $ | (7) |
定理1 假设a为数据集D中的一个样本点,并且1≤k≤|D|,则点a局部离群因子的范围为
| $ \frac{F_{\text {min }}(a)}{S_{\text {max }}(a)} \leqslant F_{10, k}(a) \leqslant \frac{F_{\text {max }}(a)}{S_{\text {min }}(a)} $ | (8) |
iDELOF异常检测算法,将iKSSE前置于LOF算法,高效剪切掉大量无用及干扰数据,获得更加精准的搜索空间,极大提升LOF异常检测算法的效率及效果。算法分为近邻搜索空间提取(iKSSE)、异常分数计算(anomaly score calculation, ASC)两个阶段,每个阶段又分为两步。
2.1 第一阶段iKSSEiKSSE分为构造数据提取森林、提取近邻搜索空间两步。
第一步, 构造数据提取森林。利用孤立森林[13]提出的隔离思想对数据随机选择属性、随机设定阈值分隔为左右叶子节点,不断迭代重复,直到叶子节点中只有一个样本点或所有样本点取值相同,或者提取树到达最大设定阈值l。与IF算法建立的隔离树一样,提取树也为二叉树,其中每个节点又分为拥有两个叶子节点的内部节点以及没有叶子节点的外部节点两种类型;与隔离树的区别在于,提取树中每个外部节点的存储内容不再是数据点的数量,而是所有被分割到此节点的数据点以及数据点在树中对应的深度,即数据点被分割的次数。按上述方法,在多个随机抽取的样本子集上建立t棵提取树,组合成为数据提取森林。构建数据提取森林的具体细节见算法1、2。
算法1 iDETree (X, c, l)
Input:X-input data, c-current tree depth, l-depth limit Output:an iDETree 1:if c≥l or |X|≤1 then 2: return exNode{data←X, depth←c} 3:else 4: let A be a list of attributes in X 5: randomly choose an attribute a∈A 6: randomly choose a divide point b from min and max value of attribute a in X 7: Xl←filter(X, a≤b) 8: Xr←filter(X, a>b) 9: return 10:end if
算法2 iDEForest (X, t, φ) Input:X-input data, t-number of trees, φ-subsample size Output:a group of iDETrees 1:Initialize iDEForest 2:set depth limit l=ceiling(log2φ) 3:for i=1∶ t do 4: 5: iDEForest=iDEForest∪iDETree( 6:end for 7:return iDEForest
第二步, 提取近邻搜索空间。遍历提取森林中的所有外部节点,取出每棵树中深度位于设定的深度阈值Ct以下的外部节点中的所有样本,即位于数据集全局较中心的数据,并且将在所有树中提取到的数据合并得到候选数据。最后根据设定的次数阈值N,在候选数据中筛选出提取次数超过N的所有数据,作为第二阶段近邻数据的搜索空间。从构建好的森林中提取近邻数据搜索空间的具体细节见算法3、4。
算法3 DataExtraction (T, Ct) Input:T-an iDETree, Ct-depth threshold Output:candidate_data from an iDETree 1:if T is an external node 2:if T.depth>Ct then 3: return T.data 4: end if 5:else 6: return combine(DataExtraction(T.left, Ct), DataExtraction(T.right, Ct)) 7:end if
算法4 DataFilter (F, Ct, N) Input:F-an iDEForest, Ct-depth threshold, N-filter threshold Output:KNN search_space 1:Initialize candidate_data, search_space 2:for T in F do 3: candidate_data=candidate_data∪DataExtraction(T, Ct) 4:end for 5:(value, counts)←count(condidate_data) 6:if counts≥N then 7: search_space=search_space∪value 8:end if 9:return KNN search_space
根据LOF的思想,计算每个测试点的局部利群因子,其中k近邻的搜索空间不再是全部数据集而是由iKSSE提取所得的子集。异常分数计算分为两步:
第一步, 在iKSSE提取所得搜索空间中实例化每个样本点的k近邻数据,以及他们到样本点的距离,将所得结果保存在数据库M中;
第二步, 根据第一步所得数据库M,计算每个样本点的局部离群因子作为异常分数,并且据此对所有样本进行排序,挑选出异常点。
3 前置iKSSE的优越性相对于LOF算法,iDELOF算法前置iKSSE,借助隔离的思想快速提取位于簇中心的子集作为ASC近邻数据搜索空间,具有以下优越性。
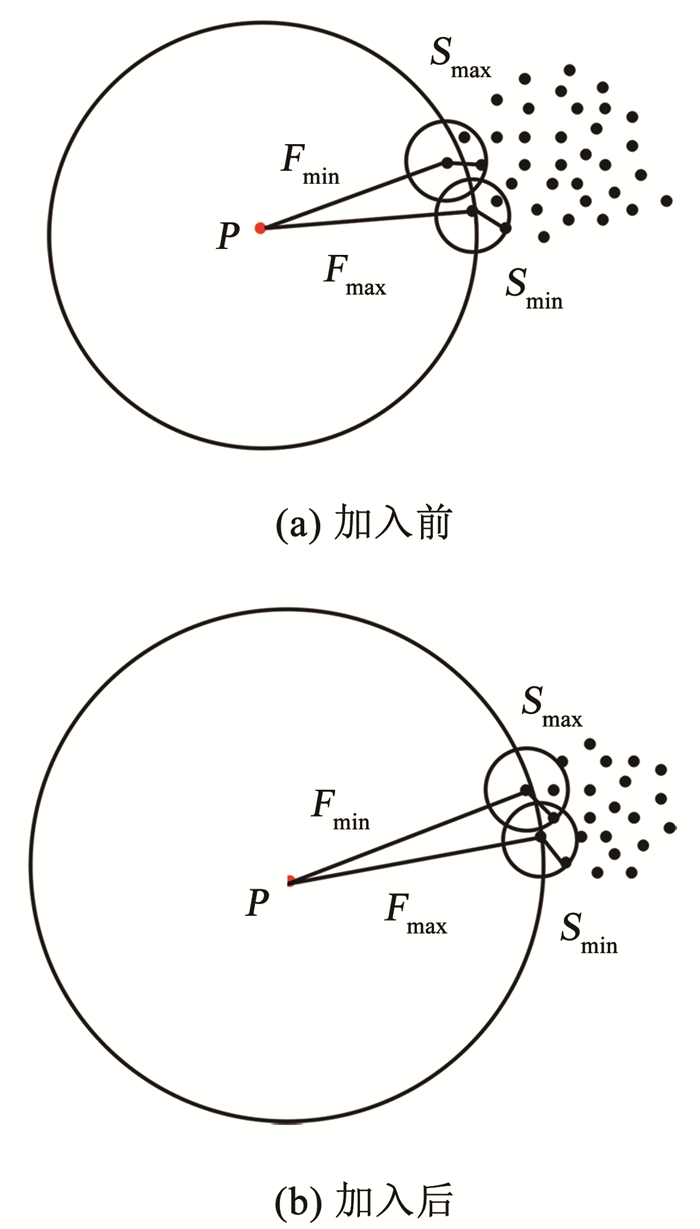
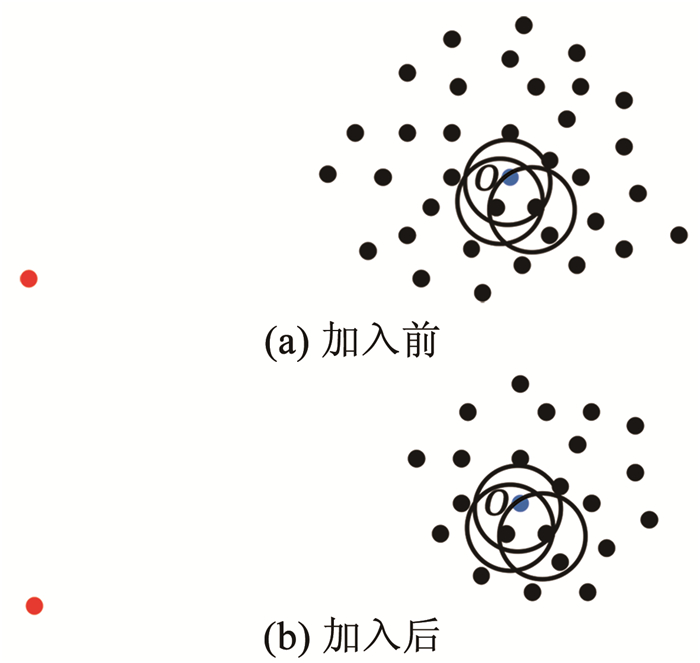
3.1 拉大正异常点局部离群因子之间的差距对位于簇周围的异常点p,其Fmin(p)、Fmax(p)增大,而Smin(p)、Smax(p)不变,因此异常点的LOF值增大;而对位于簇深处的正常点o,即其所有k近邻都在簇中,并且其k近邻的所有k近邻点也都在簇中的点,其Fmin(o)、Fmax(o)和Smin(o)、Smax(o)均改变不大,因此正常点的LOF值也变化不大。因此iDELOF算法拉大了正异常点LOF值之间的差距,使异常检测变得更容易。为进一步说明,图 1和图 2列举了一个简单的例子,其中k取2。
|
图 1 加入iKSSE前后p点LOF的取值范围 Fig. 1 LOF value range of p before and after adding iKSSE |
|
图 2 加入iKSSE前后o点LOF的取值范围 Fig. 2 LOF value range of o before and after adding iKSSE |
对于LOF算法,簇中心与边缘样本点的LOF值相差不大,因此该算法无法有效识别此类交叉异常,当簇的密度变化不大时,LOF将退化为随机检测器。对于iDELOF算法,只有位于簇深处样本点o的LOF值是相同的,而簇内其余点p的Smin(p)、Smax(p) 虽然变化不大,但Fmin(p)、Fmax(p)随着与中心距离由近至远逐渐增加,因此LOF值也随之增加,呈阶梯分布,这使得算法更有可能将位于数据集边缘的样本点识别为交叉异常,而不是盲目地从整个数据集中随机识别。为进一步说明,图 3和图 4列举了一个简单的例子,其中k取2,红色点为交叉异常点,黑色点为正常点。

|
图 3 加入iKSSE前后p点LOF的取值范围 Fig. 3 LOF value range of p before and after adding iKSSE |

|
图 4 加入iKSSE前后o点LOF的取值范围 Fig. 4 LOF value range of o before and after adding iKSSE |
对于LOF算法,在Fmin(a)、Fmax(a)相同的前提下,显然低密度簇周围异常点比高密度簇周围异常点的Smin(a)、Smax(a)更高,其LOF值相应的更小,因此也更容易被LOF忽略。对于iDELOF算法,图 5为数据提取森林中深度的等高线图,从图中可以看出当深度阈值Ct固定时,加入iKSSE后,对于近邻数据的搜索空间,其低密度簇半径的缩减量大于高密度簇,也就是说在Smin(a)、Smax(a)不变的情况下,显然低密度簇周围异常点比高密度簇周围的异常点的Fmin(a)、Fmax(a)增加的更多,因此两者LOF值之间的差距减小,改善了LOF对存在于不同密度簇周围异常点的识别偏差。

|
图 5 各数据点在数据提取森林中的深度等高线 Fig. 5 Depth contour plot of each datapoint in iDEForest |
对于iKSSE阶段:假设建立t棵树,每棵树的采样大小为ψ,则时间复杂度为O(tψlog ψ),独立于样本大小以及空间维度,只在模型训练时提取一次。
对于ASC阶段:不同于LOF算法,iDELOF算法是在iKSSE提取到的子集上进行k近邻搜索,因此每个估计器的时间成本是O(n · m),并且iDELOF只有一个基估计器,因此算法的时间成本就是O(n · m),其中n为数据集大小,m为iKSSE提取到的子集的大小(0 < m < n)。通过实验可知m的取值独立于样本大小及空间维度,取决于数据集的分布特征,并且m通常远远小于n,从多数数据集提取到的最优子集的大小还不到整个数据集的1%。因此该阶段的时间复杂度与样本大小呈线性关系,且该线性关系的斜率m很小,也就是算法的运行时间随着样本数量的增加而上涨缓慢。
综上算法的整体时间复杂度为O(tψlog ψ)+O(n · m),可以看出iDELOF有效地将LOF的时间复杂度降低到与样本数量呈线性关系且该线性关系的斜率很小,并且样本数量越大,iKSSE的时间耗费相较于其他算法就变得越微不足道,整个算法在时间复杂度上的优越性也就越明显。因此本文算法更适合应用于超大规模的数据中。
3.4.2 空间复杂度对于iKSSE阶段:假设建立t棵树,每棵树的采样大小为ψ=2a, 则每棵树最大的节点数为Nnode=2a+2a-1+…+20, 因此所需内存为O(t · Nnode),独立于样本数量,对于计算机来说微不足道。对于ASC阶段:iDELOF算法是在iKSSE提取到的样本子集上进行k近邻搜索,因此可以有效地将所需内存减小到O(m2)。
综上,算法整体的空间复杂度为O(t · Nnode)+O(m2),远小于LOF,且不会随着样本数量的增加而持续上涨,因此算法可以很容易加入在线学习的模块,应用于数据流中。
4 实验验证进行了4组实验,每组实验分别进行iDELOF算法与LOF、IF、iNNE(isolatin using nearest neighbour ensemble) [14]3种典型算法的对比分析,以验证iDELOF算法的优越性及其应对真实数据集的能力。其中前2组实验采用合成数据集,验证iDELOF算法在识别交叉异常以及轴平行异常方面的优越性;第3组实验采用Backblaze上公开的磁盘数据集,验证当数据集规模不断增大时iDELOF算法在时间复杂度上的优越性;第4组实验采用Backblaze和UCI上多个公开数据集,测试iDELOF应对不同维度、异常比例及数量级的真实数据集的能力。各种算法的超参数均根据数据集调整到最佳组合,其中iDELOF、IF以及iNNE为随机算法,他们的AUC值(AAUC)均采用10次不同的随机数种子计算所得平均值。
4.1 交叉异常的识别主要测试各种算法对交叉异常的识别能力。采用合成数据集,包括2个密度不同的正常数据簇,异常数据分布在正常簇周围并且存在一定交叉。其中低密度簇包含200个样本点,周围存在20个异常点;高密度簇包含500个样本点,周围存在40个异常点。异常点在固定环宽的圆环中随机生成,根据圆环边界与正常数据边界圆环交叉程度的不同,生成5组不同的数据集,分别表示不同的正异常数据交叉比例,见图 6。

|
图 6 不同交叉比例的测试数据集 Fig. 6 Test datasets with different crossover ratios |
图 7为4种算法的AAUC随着交叉比例的变化趋势。从图中可以看出随着交叉比例的增大,各个算法的识别能力都有所下降,其中iDELOF一直拥有着最高的AAUC,且随着交叉比例越大,iDELOF与其他算法之间的差距也越大,识别优越性越明显。

|
图 7 各算法在不同交叉比例下的AAUC Fig. 7 AAUC of each algorithm under different crossover ratios |
主要测试各种算法对轴平行异常的识别能力。实验采用2组轴平行异常的数据集,数据集1见图 8(a),正常数据呈螺旋形分布,其中隐藏着6个异常点,数据集2见图 3(b),图中左下和右上角为2个呈高斯分布的密度不同的正常数据簇,左上和右下角为2个异常数据簇。

|
图 8 轴平行异常测试数据 Fig. 8 Test datasets of axis parallel anomaly |
图 9为各数据点在不同算法下所得LOF值的等高线图。从图中可以看出,RC(robust covariance) 及IF算法的识别效果非常差,这是由于IF基于正常数据点的投影进行分割,因此对此类隐藏在轴平行中的异常点无能为力,iNNE的识别效果也不理想。而对于iDELOF以及LOF算法,只要调整好近邻数据k的大小便可以很好刻画出正异常点的分界。因此虽然加入iKSSE,iDELOF本质上依然为基于相对密度的算法,与LOF算法一样在识别轴平行异常方面具有明显优越性。

|
图 9 各数据点在不同算法下LOF值的等高线 Fig. 9 LOF values contour map of each datapoint under different algorithms |
主要验证iDELOF算法在时间复杂度方面优越性。采用的数据集为Backblaze 2015年ST4000DM000型号的磁盘数据,数据集规模为1 000~250 000。采用的方法为对比各算法检测磁盘异常所需运行时间随样本数量的变化情况,其中LOF算法根据是否使用R_tree[15]分为LOFIndexed以及LOF算法。
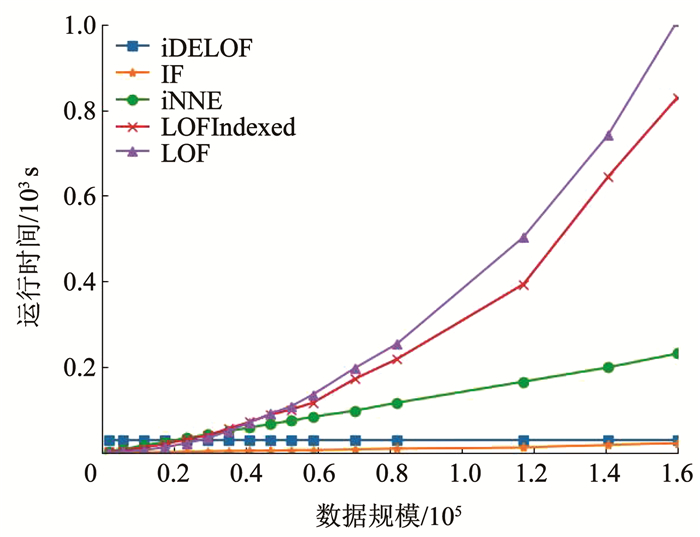
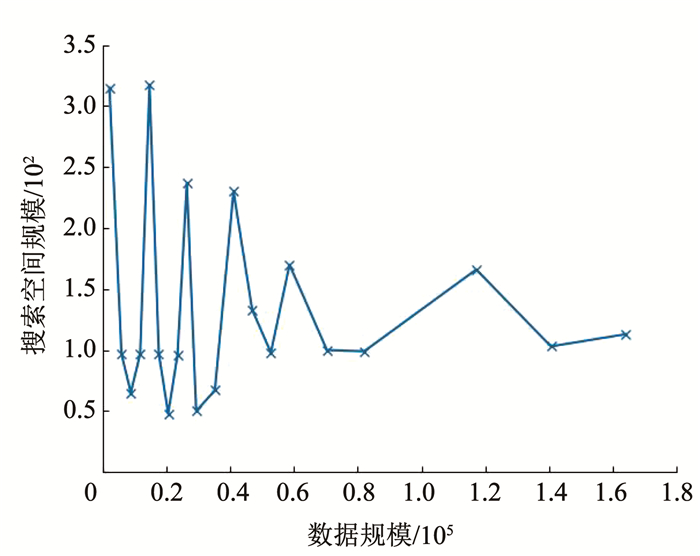
图 10记录了各算法的运行时间随数据集规模的变化趋势,图 11记录了iKSSE在不同规模磁盘数据集下提取到的子集的大小。从图 10可以看出IF、iNNE以及iDELOF算法的时间复杂度与数据集大小呈线性关系,LOF算法的时间复杂度则与数据集大小的二次方成正比,而LOFIndexed算法利用R_tree对k近邻进行快速检索,时间复杂度相比线性扫描方法有所降低,但当样本数据量增大时,运行时间依然很大。从图 11可以看出随着磁盘数据集规模的扩大,iKSSE提取到的子集的大小m不会随之增加,而是稳定在100附近。因此虽然在数据量较小时,iDELOF由于加入iKSSE步骤,运行时间比其他几个算法略长,但是当样本数量逐渐增多时,算法在时间复杂度上的优越性就体现出来了:iDELOF的运行时间随着样本规模增大而增加缓慢,其时间曲线的斜率m比最有效率的IF算法都要小。当样本的数量达到25 000时,iDELOF算法的运行时间已经远远小于LOF算法;当样本数量达到250 000时,iDELOF算法的运算速度已经逼近IF算法,并且可以预测随着样本规模的进一步扩大,iDELOF算法在时间复杂度上的优越性也会体现得越明显,成为最有效率的算法。
|
图 10 各算法在不同规模数据集下的运行时间 Fig. 10 Running time of each algorithm on different scale datasets |
|
图 11 iKSSE在不同规模数据集下获得子集的大小 Fig. 11 Size of subsets extracted by iKSSE under different scale datasets |
主要验证iDELOF算法应对真实数据集的能力。采用包括Backblaze和UCI上不同维度、异常比例及数量级共5个公开数据集。每个数据集的大小、纬度、处理方式以及异常比例见表 1。各个算法的超参数采用网格搜索法得到最佳组合见表 2。不同算法在不同数据集上的AAUC值以及对应的运行时间记录见表 3和表 4。iKSSE在不同数据集上提取到的子集大小记录见表 4。
| 表 1 实验数据集信息 Tab. 1 Experimental dataset information |
| 表 2 各算法在不同数据集上的最佳参数 Tab. 2 Optimal parameters of each algorithm on different datasets |
| 表 3 各算法在不同数据集上的AAUC Tab. 3 AAUC of each algorithm on different datasets |
| 表 4 各算法的运行时间以及iKSSE提取到的子集大小 Tab. 4 Running time of each algorithm and size of subsets extracted by iKSSE |
对于检测精度,从表 3中可以看出iDELOF在多个不同真实数据集上均被证实拥有最优的AAUC,在离群点检测精度方面优越性明显。对于运行效率,从表 2中可以看出LOF算法在多数大规模数据集上都需要很大k值才可以达到较好的检测效果,因此该算法的时间复杂度是所有算法中最高的。iDELOF算法由于前置了iKSSE,从各个数据集中提取到的子集的大小只占整个数据集的1%左右(见表 4),这使得算法仅需要个位数的k值(见表 2)就可以达到很好的效果。因此iDELOF在多数数据集上都保持着较小的时间复杂度(见表 4),只在最后3个数据集上运行时间比IF算法稍慢,这主要是数据集规模较小,算法的优越性没有完全体现的原因。
5 结论iDELOF异常检测算法将基于隔离思想的近邻搜索空间提取前置于LOF算法,高效剪切掉大量无用及干扰数据,获得更加精准的搜索空间。研究表明:
1) iDELOF异常检测算法拉大了正异常点局部利群因子的差距,增强了对交叉异常及低密度簇周围异常点的识别能力,提升了检测效果。
2) iDELOF异常检测算法在识别轴平行异常方面,与LOF一致,具有明显的优越性。
3) iDELOF异常检测算法通过iKSSE获得的子集显著小于原数据集,且多数子集数据量小于原数据集的1%,因此iDELOF的时间空间复杂度显著降低。
4) 原数据集数据量越大,iDELOF异常检测算法在时间复杂度上的优越性越明显;当样本数量达到一定数值时,iDELOF算法的运行时效将高于IF算法。
5) 不同纬度、规模、异常比例真实数据集实验表明:iDELOF算法在异常点检测精度及运行效率方面显著优于其他先进算法。
| [1] |
KELLER F, MULLER E, BOHM K. HiCS: High contrast subspaces for density-based outlier ranking[C]//2012 IEEE 28th International Conference on Data Engineering. Arlington: IEEE, 2012: 1037. DOI: 10.1109/ICDE.2012.88
|
| [2] |
BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: Identifying density-based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York: Association for Computing Machinery, 2000: 93. DOI: 10.1145/335191
|
| [3] |
SHARFY R, GHARAEI R H, TAHERI S M. Improved LOF algorithm using random point[C]//2022 9th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS). Bam: IEEE, 2022: 1. DOI: 10.1109/CFIS54774.2022.9756488
|
| [4] |
XU Siying, LIU Huiyi, DUAN Liting, et al. An improved LOF outlier detection algorithm[C]//2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA). Dalian: IEEE, 2021: 113. DOI: 10.1109/ICAICA52286.2021.9498181
|
| [5] |
FAN Linchang, MA Jinqiang, TIAN Junjing, et al. Comparative study of isolation forest and LOF algorithm in anomaly detection of data mining[C]//2021 International Conference on Big Data, Artificial Intelligence and Risk Management (ICBAR). Shanghai: IEEE, 2021: 1. DOI: 10.1109/ICBAR55169.2021.00008
|
| [6] |
CHENG Geyao, GUO Deke, LUO Lailong, et al. Lofs: A lightweight online file storage strategy for effective data deduplication at network edge[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 33(10): 2263. DOI:10.1109/TPDS.2021.3133098 |
| [7] |
ZIMEK A, GAUDET M, CAMPELLO R J G B, et al. Subsampling for efficient and effective unsupervised outlier detection ensembles[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2013: 428. DOI: 10.1145/2487575
|
| [8] |
NA G S, KIM D, YU H. Dilof: Effective and memory efficient local outlier detection in data streams[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: Association for Computing Machinery, 2018: 1993. DOI: 10.1145/3219819
|
| [9] |
SALEHI M, LECKIE C, BEZDEK J C, et al. Fast memory efficient local outlier detection in data streams[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3246. DOI:10.1109/TKDE.2016.2597833 |
| [10] |
PAPADIMITRIOU S, KITAGAWA H, GIBBONS P B, et al. Loci: Fast outlier detection using the local correlation integral[C]//Proceedings 19th International Conference on Data Engineering. Bangalore: IEEE, 2003: 315. DOI: 10.1109/ICDE.2003.1260802
|
| [11] |
ANGIULLI F, FASSETTI F. Dolphin: An efficient algorithm for mining distance-based outliers in very large datasets[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2009, 3(1): 1. DOI:10.1145/1497577 |
| [12] |
LAZAREVIC A, KUMAR V. Feature bagging for outlier detection[C]//Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining. New York: Association for Computing Machinery, 2005: 157. DOI: 10.1145/1081870.1081891
|
| [13] |
LIU F, TING Kaiming, ZHOU Zhihua. Isolation forest[C]//2008 Eighth IEEE International Conference on Data Mining. Pisa: IEEE, 2008: 413. DOI: 10.1109/ICDM.2008.17
|
| [14] |
BANDARAGODA T R, TING K M, ALBRECHT D, et al. Efficient anomaly detection by isolation using nearest neighbour ensemble[C]//2014 IEEE International Conference on Data Mining Workshop. Shenzhen: IEEE, 2014: 698. DOI: 10.1109/ICDMW.2014.70
|
| [15] |
BECKMANN N, KRIEGEL H P, SCHNEIDER R, et al. The R*-tree: An efficient and robust access method for points and rectangles[C]//Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data. New York: Association for Computing Machinery, 1990: 322. DOI: 10.1145/93605
|
| [16] |
NA G S, KIM D, YU H. Dilof: Effective and memory efficient local outlier detection in data streams[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: Association for Computing Machinery, 2018: 1993. DOI: 10.1145/3219819.3220022
|
| [17] |
SALEHI M, LECKIE C, BEZDEK J C, et al. Fast memory efficient local outlier detection in data streams[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3246. DOI:10.1109/ICDE.2017.32 |
| [18] |
ZHAO Jian, HE Yongzhan, LIU Hongmei, et al. Disk failure early warning based on the characteristics of customized smart[C]//2020 19th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm). Orlando: IEEE, 2020: 1282. DOI: 10.1109/ITherm45881.2020.9190324
|
 2023, Vol. 55
2023, Vol. 55


