2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
软件系统复杂性日益增加,手动创建测试用例效率低,难以满足测试要求,自动生成测试用例无疑对提高软件测试效率具有重要意义。扩展有限状态机(extended finite state machine, EFSM)是一种可同时携带控制流和数据流信息的软件描述模型,常用于基于模型的软件测试用例的自动生成[1-2]。在EFSM测试用例生成过程中,需要首先生成测试序列再生成测试数据,因此快速地生成高质量的测试序列是自动化测试用例生成的关键。然而,高性能自动化测试序列集生成算法需同时满足以下条件:1)测试序列集内每个序列均是可行的;2)测试序列集满足全迁移覆盖;3)测试序列集规模小;4)测试序列生成算法效率高。这对自动化测试序列生成任务提出了挑战。因此,本文开展了快速生成小规模测试序列集算法的研究。
遗传算法(genetic algorithm, GA)作为目前较为流行的启发式搜索算法,可用于求解迁移覆盖的测试序列生成问题。文献[3-5]首次提出了一种有效生成可行迁移路径的方法,该方法根据控制流和数据流的依赖关系评估路径的可行性,针对模型中的每一条迁移,通过多次执行GA算法指导路径的搜索。虽能以较高概率生成可行迁移路径,但对于具有“计数器变量问题”的路径,仅是采取了“绕过”的策略,因此最终生成的测试序列集无法满足全迁移覆盖。针对该问题,文献[6-7]利用分组遗传算法,通过绑定依赖计数器变量的迁移,使生成的序列集很好地满足了全迁移覆盖,但由于生成单个序列的计算量较大,算法整体运算效率较低。文献[8]提出了一种先利用图遍历搜索算法得到满足控制流的候选序列集,再筛选满足数据流序列的方法,该方法生成的测试序列集存在冗余序列,导致测试序列集规模较大。文献[9-10]利用多目标搜索算法,综合考虑了序列的可行性和迁移覆盖率,以及序列集的规模,但过多的优化目标也降低了成功搜索到最优解的概率。文献[11-12]通过引入种群多样性度量方法增加个体间差异,压缩了测试序列集规模,但仍存在因早熟收敛导致的无法满足全迁移覆盖的问题,且仅是在种群初始化阶段就要生成大量的可行迁移路径,极大增加了算法的时间开销。自适应多种群遗传算法可有效克服传统遗传算法早熟收敛和搜索能力弱的缺陷,如文献[13-14]根据种群多样性自适应调整交叉和变异算子,一定程度上克服了早熟问题,文献[15-16]通过引入多种群机制并行搜索,加快了收敛速度等,但将自适应多种群遗传算法应用在EFSM测试序列生成问题上的研究较少。
针对以上问题,本文尝试将改进的自适应多种群遗传算法(improved adaptive multi-population genetic algorithm, IAMGA)应用到EFSM测试序列生成问题中,意在探索一种面向全迁移的一次性快速生成较小规模的测试序列集方法。为了使测试序列集更好地满足全迁移覆盖,引入多种群机制,以增加种群的多样性;为了提高序列集生成效率,引入自适应方法,根据种群进化程度动态地调整交叉和变异概率;为了压缩序列集规模,先正向生成能产生迁移增益的可行序列,再反向去除未产生增益的冗余序列。经实验验证,IAMGA算法在不同EFSM模型下,均能以较高的成功率生成满足全迁移覆盖的小规模测试序列集。
1 EFSM模型 1.1 EFSM模型描述与符号定义EFSM可形式化地表示为一个六元组M=(S, s0, I, O, V, T),其中S为一组有限状态集合;s0为模型的初始状态(s0∈S);I为输入集合;O为输出集合;V为内部变量的有限集合;T为迁移集合。迁移集合T的每个迁移变量t可以用一个五元组表示(ss, i, g, Oop, se),其中ss为t的源状态;i为输入(i∈I);g为守卫,是当前变量的谓词判定条件,可以为空,也可以是一个逻辑表达式的集合;Oop为该迁移触发后的一系列操作,由输出语句、变量赋值语句组成;se为t的目的状态。
为便于说明,对EFSM模型中的相关术语作出如下规定和解释:
定义1 迁移路径(transition path, TP): 可能生成的测试序列,由若干个迁移组成的但无法被EFSM模型成功执行的迁移路径,表示为TP=(t1, t2, …, ti, tj, …, tn),其中ti的目的状态是tj的源状态。
定义2 可行迁移路径(feasible transition path, FTP): 生成的测试序列,由若干个迁移组成的且可被EFSM模型成功执行的迁移路径,表示为FTP=(t1, t2, …, ti, tj, …, tn),t1的源状态是模型的初始状态,tn的目的状态是模型的终止状态,且至少存在一组测试数据,能触发该序列中的所有迁移。
定义3 可行迁移路径集合(feasible transition path set, FTPS): 生成的测试序列集,由若干个FTP组成的集合,表示为FTPS=(FTP1, FTP2, …, FTPm),其中m表示生成的测试序列集的规模。
定义4 迁移覆盖增益: TP中含有未覆盖迁移集合中的迁移在未覆盖迁移集合中的占比。
定义5 冗余序列: FTPS中相对于其他FTP未能产生迁移覆盖增益的序列。
1.2 EFSM测试序列生成问题分析为保证EFSM测试序列生成的效率和质量,需考虑以下方面:1)序列的可行性;2)测试序列集的迁移覆盖率;3)测试序列集的规模。以当前较为典型的EFSM模型——ATM[17]为例,对EFSM测试序列生成问题进行分析,ATM模型见图 1。

|
图 1 ATM模型 Fig. 1 Diagram of ATM model |
由于EFSM模型中含有控制流信息和数据流信息,因此在生成测试序列时,既要考虑有向图中的可行性,又要考虑迁移间的数据流依赖。当一个序列中的两个迁移上的动作和谓词判定之间存在矛盾,即无法找到满足谓词条件的输入时,该序列是不可行的。如图 1中的一条测试序列TP1=(t1, t4, t5, t7, t11, t15, t9, t23),迁移t5对变量l的赋值操作为l=′e′,而t11的谓词判定条件为l=′s′,则此时二者发生冲突,导致TP1不可行。在进行测试序列生成时,应避免产生存在迁移冲突的测试序列。
1.2.2 序列集覆盖性分析为保证测试的充分性,常采用全迁移覆盖(all transitions coverage, ATC)准则指导测试序列生成。然而,在EFSM模型中存在一类问题——“计数器变量问题”,影响了序列集的迁移覆盖率。如图 1中一条包含计数器变量a的测试序列FTP1=(t1, t2, t2, t2, t3),由于迁移t3的谓词判定条件为a=3,需执行3次t2才能触发t3,概率为1/8,而触发t4的概率为7/8。因此在一般情况下,含有被计数器变量触发迁移的FTP的生成难度更大。
1.2.3 序列集规模分析测试序列集中的冗余序列会导致测试效率下降。如图 1中的测试序列FTP2=(t1, t2, t4, t5, t23)、FTP3=(t1, t2, t4, t6, t23)和FTP4=(t1, t4, t6, t7, t9, t23),可知FTP3为冗余序列,因为FTP3不能对FTP2和FTP4所包含的迁移集合产生迁移覆盖增益,因此在测试时,只需测试FTP2和FTP4即可,不需要测试FTP3。
1.3 序列可行性度量方法为模拟被测系统的动态行为,利用transitions工具包[18]建立EFSM可执行模型,根据控制流信息定义模型的状态和迁移,根据数据流信息定义绑定在迁移上的条件约束和行为。为判断被EFSM模型执行的TP是否为FTP,需对序列的可行性进行度量,序列可行性度量方法如下:
Step1 初始化EFSM模型的变量和状态,在模型中动态执行TP中的迁移。
Step2 判断当前迁移是否满足数据流约束,若变量的当前值符合当前迁移的谓词判定条件,则执行Step3,否则执行Step4。
Step3 判断当前迁移是否满足控制流约束,若满足,则将模型的当前状态设为当前迁移的目的状态,执行迁移上绑定变量的更新等操作,再将当前迁移设为TP中的下一个迁移,执行Step2。若不满足,则执行Step4。
Step4 若模型当前状态为“exit”,则将该TP作为FTP加入到FTPS中;否则直接返回第一个不可行迁移的位置。
2 IAMGA算法 2.1 种群初始化为直观地表示测试序列和EFSM模型中迁移的逻辑关系,采用符号编码,符号集代表EFSM模型中的迁移集合,一个基因位代表一个迁移,个体代表一个可能生成的序列。为简化研究问题,个体长度固定为符号集大小。
种群采用随机初始化的方式,假定个体长度为L,种群规模为N,从符号集中随机选择L个迁移组成一个个体,并重复上述操作N次,完成种群初始化。
2.2 适应度函数适应度函数用于评估TP与FTP的接近程度。大多数测试序列生成任务的目标仅是生成满足全迁移覆盖的测试序列集,因此很多研究在设计适应度函数时只考虑了迁移覆盖率,这存在两点问题:1)具有较高迁移覆盖率的个体未必具有较高的路径通过率,难以进化为FTP,导致全局收敛速度下降;2)具有较高迁移覆盖率的个体进化为FTP后,未必能对测试序列集的迁移覆盖率产生增益,这将导致测试序列集规模增加。针对以上问题,为提高全局收敛速度引入了个体的路径通过率,为减小测试序列集规模引入了个体的迁移覆盖增益。
假定个体的长度为L,对于第i个个体,可行迁移的个数为ca1(i),不可行迁移的个数为ca0(i),可行迁移中能产生覆盖增益的有效迁移个数为ce1(i),不可行迁移中能产生覆盖增益的有效迁移个数为ce0(i),则个体的路径通过率γp(i)可表示为
| $ \gamma_{\mathrm{p}}(i)=\frac{c_{\mathrm{a}}^1(i)}{L}=\frac{c_{\mathrm{a}}^1(i)}{c_{\mathrm{a}}^1(i)+c_{\mathrm{a}}^0(i)} $ | (1) |
式中:L为个体的长度,ca1(i)为可行迁移的个数,ca0(i)为不可行迁移的个数。
个体的迁移覆盖增益Gn(i)可表示为
| $ G_{\mathrm{n}}(i)=G_{\mathrm{n}}^1(i)+G_{\mathrm{n}}^0(i)=\frac{c_{\mathrm{e}}^1(i)}{\sum _{n=1}^N c_{\mathrm{e}}^1(n)}+\frac{c_{\mathrm{e}}^0(i)}{\sum _{n=1}^N c_{\mathrm{e}}^0(n)} $ | (2) |
式中:N为种群规模,Gn1(i)为路径可行迁移的覆盖增益,Gn0(i)为路径不可行迁移的覆盖增益,ce1(i)为可行迁移中能产生覆盖增益的有效迁移个数,ce0(i)为不可行迁移中能产生覆盖增益的有效迁移个数。
在进化前期,为加快收敛速度,需优先保留Gn1(i)较大而Gn0(i)较小的个体。在进化后期,为提高迁移覆盖增益以减小测试序列集规模,需优先保留Gn1(i)较小而Gn0(i)较大的个体。因此,个体的适应度函数设计如下:
| $\begin{aligned} f(i)= & \left(1-\gamma_{\mathrm{p}}(i)\right) \times \frac{c_{\mathrm{e}}^1(i)}{\sum _{n=1}^N c_{\mathrm{e}}^1(n)}+ \\ & \gamma_{\mathrm{p}}(i) \times \frac{c_{\mathrm{e}}^0(i)}{\sum _{n=1}^N c_{\mathrm{e}}^0(n)} \end{aligned} $ | (3) |
式中:N为种群规模,γp(i)为个体的路径通过率,ce1(i)为可行迁移中能产生覆盖增益的有效迁移个数,ce0(i)为不可行迁移中能产生覆盖增益的有效迁移个数。
图 2实例演示种群规模为3的个体适应度计算过程。由式(3)可知,个体适应度f(i)由个体的路径通过率γp(i)、个体的路径可行迁移覆盖增益Gn1(i)和路径不可行迁移覆盖增益Gn0(i)表示。其中,γp(i)度量了个体的进化程度,当种群刚初始化时,γp(i)为0,此时f(i)仅由Gn1(i)表示。随着个体不断进化,Gn1(i)的占比逐渐下降,Gn0(i)的占比逐渐增加,以此来生成更高质量的序列和更小规模的测试序列集。

|
图 2 个体适应度计算过程 Fig. 2 Calculation process of individual fitness |
选择算子用于在种群进化过程中保留适应度较高的个体,淘汰适应度较低的个体。然而,传统GA的选择算子针对整个种群进行选择,这会使种群多样性变差,导致“早熟”问题。针对该问题,本文通过改进传统的多种群遗传算法(multi-population genetic algorithm, MGA),将其应用在测试序列生成任务的选择过程中。
图 3实例演示了某代种群的选择过程。首先根据个体的可行迁移将整个种群划分为若干个子种群,使可行迁移完全相同的个体组成一个子种群,在每个子种群内使用轮盘赌选择法对个体进行选择,不同子种群的选择操作互不影响。个体被选择的概率P(i)可表示为
| $ P(i)=\frac{f(i)}{\sum _{m=1}^M f(m)} $ | (4) |

|
图 3 选择过程 Fig. 3 Process of selection |
式中:M为子种群规模,f(i)为个体的适应度函数。
2.4 交叉算子交叉算子用于个体间基因重组以推动种群进化。在测试序列生成任务中,该过程对应于TP通过彼此间交换迁移,以逐步收敛为FTP。然而,传统GA的交叉算子通常存在以下问题:1)交叉概率是固定的,不能动态地反映不同种群进化阶段对交叉的需求;2)交叉的基因位是随机的,不能有效提高后代个体的适应度。
针对问题1,为度量种群的进化程度,引入了种群的平均路径通过率
| $ \bar{\gamma}_{\mathrm{p}}=\frac{1}{N} \sum\limits_{i=1}^N \gamma_{\mathrm{p}}(i) $ | (5) |
式中:N为种群规模,γp(i)为个体的路径通过率。
针对问题2,为了简化问题,仅是针对由序列可行性度量所反馈的第一个不可行迁移进行交叉,即只是考虑基因位的交叉,而不考虑基因片段的交叉。
此外,种群进化后期基因多样性变差,为克服迭代过程中无效的交叉操作对运算效率的影响,引入了交叉进化函数fc(k),用于度量种群的进化停滞程度。交叉进化函数fc(k)由正弦函数经三角平移变换后得到,可表示为
| $ f_{\mathrm{c}}(k)=\left\{\begin{array}{lc} \frac{1}{2}+\frac{1}{2} \sin \left(\frac{\pi}{\tau}\left(-k+\frac{\tau}{2}\right)\right) & 0<k<\tau \\ 0 & k>\tau \end{array}\right. $ | (6) |
式中:k为距离上一次产生FTP所经历的种群迭代次数,τ为进化停滞代数的门限。
因此,种群内每个个体的交叉概率Pc可表示为
| $ P_{\mathrm{c}}=\alpha_{\mathrm{c}}\left(1-\bar{\gamma}_{\mathrm{p}}\right)+\left(1-\alpha_{\mathrm{c}}\right) f_{\mathrm{c}}(k) $ | (7) |
式中:αc(0 < αc < 1)为交叉系数,
由式(7)可知,种群初始化完成后,
为避免“近亲繁殖”,选取不同子种群的个体进行交叉。图 4实例演示了某次交叉过程。对于个体i,交叉点C1为第一个不可行迁移的位置。首先,随机选择一个与i在不同子种群的个体j,分别计算出两个体的路径通过率γp(i)、γp(j)。然后,比较γp(i)和γp(j),若γp(i)≥γp(j),认为个体i的进化程度较高,已经包含了个体j的可行迁移,因此从个体j的不可行迁移中随机选择一个交叉点C2;反之,若γp(i) < γp(j),认为个体j的进化程度较高,选择个体j中的可行迁移能使个体i有效进化,因此从个体j的可行迁移中随机选择一个交叉点C2。最后,将C1与C2的基因位进行交换。

|
图 4 交叉过程 Fig. 4 Process of crossover |
变异用于个体内基因突变以丰富种群多样性。在测试序列生成任务中,当TP无法通过交叉进化时,则从符号集中随机选择迁移,以加速进化为FTP。本文对变异算子的设计与交叉算子类似。变异进化函数fm(k)可表示为
| $f_{\mathrm{m}}(k)=\left\{\begin{array}{lc} \frac{1}{2}+\frac{1}{2} \sin \left(\frac{\pi}{\tau}\left(k-\frac{\tau}{2}\right)\right) & 0<k<\tau \\ 0 & k>\tau \end{array}\right. $ | (8) |
式中:k为距离上一次产生FTP所经历的种群迭代次数,τ为进化停滞代数的门限。
由式(8)可知,fm(k)与fc(k)在[0, τ]区间内关于τ/2对称,即fc(k)+fm(k)=1(k>0)。
因此,种群内每个个体的变异概率Pm可表示为
| $ P_{\mathrm{m}}=\alpha_{\mathrm{m}} \bar{\gamma}_{\mathrm{p}}+\left(1-\alpha_{\mathrm{m}}\right) f_{\mathrm{m}}(k) $ | (9) |
式中:αm(0 < αm < 1)为变异系数,
由式(9)可知,种群初始化完成后,
图 5实例演示了某次变异过程。对于个体i,变异点M1为第一个不可行迁移的位置,并从符号集中随机选择一个迁移替换M1的基因位。
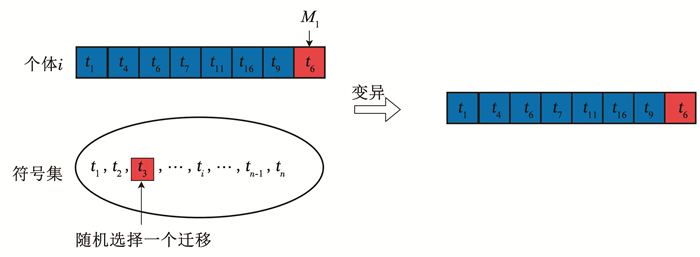
|
图 5 变异过程 Fig. 5 Process of mutation |
算法流程见图 6。具体步骤如下:

|
图 6 IAMGA算法流程图 Fig. 6 Flow chart of IAMGA algorithm |
Step1 对种群进行初始化。
Step2 根据序列可行性度量方法,将生成的FTP加入到FTPS中。判断当前FTPS是否满足ATC,若满足,则执行Step7,否则执行Step3。
Step3 判断当前种群代数是否达到最大迭代次数,若未达到,则执行Step4,否则算法结束。
Step4 根据个体的可行迁移将整个种群划分为若干个子种群,在各子种群内计算所有个体的个体适应度,并使用轮盘赌选择法对个体进行选择。
Step5 根据式(7)计算个体的交叉概率,若满足交叉条件,则采用交叉策略对不同子种群间的个体进行交叉操作。
Step6 根据式(9)计算个体的变异概率,若满足变异条件,则采用变异策略对个体进行变异操作。种群个体全部更新完成后,返回Step2。
Step7 倒序遍历生成的测试序列集并压缩规模,若该测试序列产生迁移覆盖增益,则保留;否则将其剔除。遍历完成后,得到最终的测试序列集。
由以上过程可知,IAMGA算法生成的测试序列集没有冗余序列,证明过程见表 1。
| 表 1 测试序列集不存在冗余序列的证明 Tab. 1 Proof of no redundant sequences in FTPS |
实验选取2种典型的具有“计数器变量问题”的模型ATM模型和Cashier模型[19],并将全迁移覆盖成功率、满足全迁移覆盖的测试序列集规模和收敛时的迭代次数作为评价指标,对IAMGA算法的有效性和性能进行分析和验证,实验参数设置见表 2。
| 表 2 实验参数设置 Tab. 2 Experimental parameter settings |
为验证IAMGA算法的有效性,分别在8组不同的种群规模下对2种模型各实验100次,仿真结果见图 7和图 8,具体统计结果见表 3和表 4。

|
图 7 不同种群规模下的仿真结果(ATM) Fig. 7 Simulation results under different population sizes(ATM) |

|
图 8 不同种群规模下的仿真结果(Cashier) Fig. 8 Simulation results under different population sizes(Cashier) |
| 表 3 不同种群规模下的统计结果(ATM) Tab. 3 Statistical results under different population sizes(ATM) |
| 表 4 不同种群规模下的统计结果(Cashier) Tab. 4 Statistical results under different population sizes(Cashier) |
图 7为ATM模型的仿真结果。由图 7(a)可知,在不同种群规模下的平均迁移覆盖率均能达到95%以上,但当种群规模为250时,不同实验的迁移覆盖率分布较为分散。由图 7(b)可知,当种群规模在500以上时,全迁移覆盖成功率可达80%以上;当种群规模在750以上时,全迁移覆盖成功率可达90%以上;当种群规模在1 500以上时,全迁移覆盖成功率可达到100%。由图 7(c)可知,不同种群规模下所生成的测试序列集规模都在5~6之间,差异较小;种群规模越大,生成的测试序列集规模的平均值也越大;当种群规模在1 000以下时,可搜索到达到最小测试序列集规模的序列组合。由图 7(d)可知,不同种群规模下达到收敛时迭代次数的平均值分布在100~400之间,且随着种群规模增加,达到收敛时的迭代次数也随之减小。
图 8为Cashier模型的仿真结果。由图 8(a)可知,在不同种群规模下的平均迁移覆盖率均能达到95%以上,但当种群规模为250时,相对于ATM模型分布更加集中。由图 8(b)可知,当种群规模在1 000以上时,全迁移覆盖成功率可达90%以上,但均无法达到100%。由图 8(c)可知,不同种群规模下所生成的测试序列集规模也都在5~6之间,差异较小;种群规模越大,生成的测试序列集规模的平均值也越大;在不同种群规模下均可搜索到达到最小测试序列集规模的序列组合。由图 8(d)可知,不同种群规模下达到收敛时迭代次数的平均值分布在150~300之间,且随着种群规模增加,达到收敛时的迭代次数同样也随之减小。
由以上仿真结果和分析知,在选取适当的种群规模的条件下,IAMGA算法在2种模型上均能以较高的全迁移覆盖成功率生成较小规模的测试序列集,且均能搜索到最小测试序列集规模的序列组合。但IAMGA算法在2种模型上的表现存在差异,需对其进一步分析。
表 3和表 4分别给出了全迁移覆盖成功率达到80%以上的未覆盖迁移的统计结果。可知Cashier模型未覆盖的迁移全部为属于“计数器变量问题”的迁移t15,而ATM模型未覆盖的迁移除了具有“计数器变量问题”的迁移t3,还有具有“并联关系”的迁移组合{t11, t12}、{t19, t20}等。由ATM和Cashier的模型图可知,相比于ATM模型,Cashier模型的“计数器变量问题”位置更深,算法搜索到越深位置的路径时,由于种群规模一定,而子种群数量变多,因此子种群的规模变小,导致在选择个体时,具有“计数器变量问题”的个体更难被选到。同理,ATM模型具有“并联关系”的迁移组合的位置更深,因此当种群规模较小时,具有较深的“并联关系”迁移的个体很难被选到。
此外,相较于ATM模型,Cashier模型更加简单,因此在同一种群规模下收敛时的平均迭代次数更小。由于种群规模越大,单次迭代的计算量越多,因此应根据不同的模型和任务类型,选择合适的种群规模。
3.2 算法性能对比与分析为验证IAMGA算法的性能优势,选取AGA[20]、MGA[21]、AMGA[22]算法进行对比,各算法的实现方式及对比维度见表 5,实验参数设置与表 2一致。根据上文分析结论,将种群规模设为1 000,分别使用4种算法对2种模型实验100次。为尽可能减少种群初始化的随机性对结果的影响,提前缓存100个随机初始化的种群,以保证每次实验各算法的初始种群相同。仿真结果见图 9和图 10,具体统计数据见表 6和表 7。
| 表 5 各算法实现方式 Tab. 5 Implementation of each algorithm |

|
图 9 各算法性能对比(ATM) Fig. 9 Performance comparison of algorithms(ATM) |

|
图 10 各算法性能对比(Cashier) Fig. 10 Performance comparison of algorithms(Cashier) |
| 表 6 各算法性能仿真结果对比(ATM) Tab. 6 Comparison of simulation results of algorithms (ATM) |
| 表 7 各算法性能仿真结果对比(Cashier) Tab. 7 Comparison of simulation results of algorithms (Cashier) |
图 9为ATM模型的仿真结果。由图 9(a)可知,AGA算法的迁移覆盖率均未达到100%,全迁移覆盖的成功率为0。而IAMGA算法的全迁移成功率高达97%,未满足全覆盖的3次实验的迁移覆盖率也在90%以上,均优于AGA算法。这是因为AGA算法未使用多种群策略,进化过程中种群多样性逐渐变差,最终导致“早熟”;由图 9(b)可知,MGA算法的平均迭代次数为250,最小迭代次数为100。而IAMGA算法的平均迭代次数192,最小迭代次数为66,均优于MGA算法。这是因为MGA算法未使用自适应方法,交叉和变异的概率未能适应种群的进化程度,导致收敛速度变慢;由图 9(c)可知,在迁移覆盖率较低时,IAMGA算法的收敛速度略优于MGA算法,而在迁移覆盖率较高时,IAMGA算法的收敛速度明显优于MGA算法。这是因为在种群进化初期,两种算法的交叉概率均较高,因此种群进化速度差异较小,而在种群进化后期,IAMGA算法的变异概率远大于MGA算法,因此种群进化速度更快;由图 9(d)可知,AMGA算法生成的测试序列集规模全部在9~16之间,而IAMGA算法生成的测试序列集规模全部在3~8之间,这是因为IAMGA算法优先选择了能够产生迁移覆盖增益的个体,并通过对结果集倒序遍历,保证了集合内两两序列之间均能产生迁移覆盖增益,有效去除了未产生迁移覆盖增益的冗余序列。
图 10为Cashier模型的仿真结果。由图 10可知,各算法在Cashier模型上的表现与ATM结果相似,因此均可得出类似的分析结论,这表明IAMGA算法在不同模型上的性能均优于其他3种算法。
表 6和表 7分别为ATM模型和Cashier模型的仿真结果统计。由表 6可知,在ATM模型上,与AGA算法相比,IAMGA算法的平均迁移覆盖率提高了134%;与MGA算法相比,IAMGA算法的平均迭代次数减少了23%;与AMGA算法相比,IAMGA算法的测试序列集平均规模减少了52%。由表 7可知,在Cashier模型上,与AGA算法相比,IAMGA算法的平均迁移覆盖率提高了54%;与MGA算法相比,IAMGA算法的平均迭代次数减少了20%;与AMGA算法相比,IAMGA算法的测试序列集平均规模减少了48%。因此,相比于以往的遗传算法,IAMGA在迁移覆盖率、收敛速度、序列集规模等方面的性能均有所提升。
4 结论1) 对EFSM测试序列生成问题进行了分析,提出了IAMGA算法,根据迁移覆盖增益设计了适应度函数,引入多种群机制改进了选择过程,引入自适应机制改进了交叉变异过程,最后通过回溯去除冗余序列压缩了测试序列集规模。
2) 仿真结果表明,与传统遗传算法相比,IAMGA算法能以90%以上的成功率生成满足全迁移覆盖的测试序列集,生成的测试序列集规模减小了50%,收敛速度提升了20%。本文提出的测试序列生成方法可有效提高EFSM测试序列集生成的效率和质量。
| [1] |
REN Chengqian, SHANG Ying. Bug reproduction based on EFSM model[C]//2021 IEEE International Conference on Information Communication and Software Engineering(ICICSE). Chengdu: Institute of Electrical and Electronics Engineers Inc, 2021: 217. DOI: 10.1109/icicse52190.2021.9404112
|
| [2] |
ALBAHLI A, ANDREWS A. Model-based testing of smart home systems using EFSM and CEFSM[C]//2021 International Conference on Computational Science and Computational Intelligence. Las Vegas: Institute of Electrical and Electronics Engineers Inc, 2021: 1824. DOI: 10.1109/CSCI54926.2021.00345
|
| [3] |
KALAJI A S, HIERONS R M, SWIFT S. Generating feasible transition paths for testing from an extended finite state machine(EFSM)[C]//2009 International Conference on Software Testing Verification and Validation. Denver: IEEE, 2009: 230. DOI: 10.1109/ICST.2009.29
|
| [4] |
KALAJI A S, HIERONS R M, SWIFT S. Generating feasible transition paths for testing from an extended finite state machine (EFSM) with the counter problem[C]//2010 Third International Conference on Software Testing, Verification, and Validation Workshops. Paris: IEEE, 2010: 232. DOI: 10.1109/ICSTW.2010.25
|
| [5] |
KALAJI A S, HIERONS R M, SWIFT S. An integrated search-based approach for automatic testing from extended finite state machine (EFSM) models[J]. Information and Software Technology, 2011, 53(12): 1297. DOI:10.1016/j.infsof.2011.06.004 |
| [6] |
CHOI Y M, LIM D J. Automatic feasible transition path generation from UML state chart diagrams using grouping genetic algorithms[J]. Information and Software Technology, 2018, 94: 38. DOI:10.1016/j.infsof.2017.09.013 |
| [7] |
张毅伟, 贲可荣. 基于状态图测试的迁移路径生成方法[J]. 计算机科学与探索, 2019, 13(6): 961. ZHANG Yiwei, BEN Kerong. Transition path generation method based on state diagram test[J]. Journal of Frontiers of Computer Science and Technology, 2019, 13(6): 961. DOI:10.3778/j.issn.1673-9418.1807035 |
| [8] |
YANG Rui, CHEN Zhenyu, XU Baowen, et al. Improve the effectiveness of test case generation on EFSM via automatic path feasibility analysis[C]//2011 IEEE 13th International Symposium on High-Assurance Systems Engineering. Boca Raton: IEEE, 2011: 17. DOI: 10.1109/HASE.2011.12
|
| [9] |
ASOUDEH N, LABICHE Y. Multi-objective construction of an entire adequate test suite for an EFSM[C]//2014 IEEE 25th International Symposium on Software Reliability Engineering. Naples: IEEE, 2014: 288. DOI: 10.1109/ISSRE.2014.14
|
| [10] |
YANO T, MARTINS E, SOUSA F. MOST: A multi-objective search-based testing from EFSM[C]// 2011 IEEE Fourth International Conference on Software Testing, Verification and Validation Workshops. Berlin: IEEE, 2011: 164. DOI: 10.1109/ICSTW.2011.37
|
| [11] |
宋雨琪, 尚颖, 赵瑞莲. 基于遗传算法的面向多样性EFSM测试序列生成方法[J]. 东南大学学报(自然科学版), 2017, 47(Sup.1): 176. SONG Yuqi, SHANG Ying, ZHAO Ruilian. Automatic generation of diversity-oriented EFSM test sequence suite based on genetic algorithm[J]. Journal of Southeast University: Natural Science Edition, 2017, 47(Sup.1): 176. DOI:10.3969/j.issn.1001-0505.2017.S1.033 |
| [12] |
ZHAO Ruilian, WANG Weiwei, SONG Yuqi, et al. Diversity-oriented test suite generation for EFSM model[J]. IEEE Transactions on Reliability, 2020, 69(2): 611. DOI:10.1109/TR.2020.2971095 |
| [13] |
包晓安, 熊子健, 张唯, 等. 一种基于改进遗传算法的路径测试用例生成方法[J]. 计算机科学, 2018, 45(8): 174. BAO Xiaoan, XIONG Zijian, ZHANG Wei, et al. Approach for path-oriented test cases generation based on improved genetic algorithm[J]. Computer Science, 2018, 45(8): 174. |
| [14] |
刘芳, 马玉磊, 周慧娟. 基于种群多样性的自适应遗传算法优化仿真[J]. 计算机仿真, 2017, 34(4): 250. LIU Fang, MA Yulei, ZHOU Huijuan. An adaptive genetic algorithm based on population diversity[J]. Computer Simulation, 2017, 34(4): 250. DOI:10.3969/j.issn.1006-9348.2017.04.053 |
| [15] |
ZHANG Na, WU Biao, BAO Xiaoan. Automatic generation of test cases based on multi-population genetic algorithm[J]. International Journal of Multimedia and Ubiquitous Engineering, 2015, 10(6): 113. DOI:10.14257/ijmue.2015.10.6.11 |
| [16] |
吕卉, 周聪, 邹娟, 等. 基于多种群进化的遗传算法[J]. 计算机工程与应用, 2010, 46(28): 57. LÜ Hui, ZHOU Cong, ZOU Juan, et al. Genetic algorithm based on multi-population evolution[J]. Computer Engineering and Applications, 2010, 46(28): 57. DOI:10.3778/j.issn.1002-8331.2010.28.017 |
| [17] |
KOREL B, SINGH I, TAHAT L, et al. Slicing of state-based models[C]//International Conference on Software Maintenance. Amsterdam: IEEE, 2003: 34. DOI: 10.1109/icsm.2003.1235404
|
| [18] |
TEREKHOV M, NEUMANN A. Transitions 0.8.11[EB/OL]. (2022-02-24)[2022-05-01]. https://github.com/pytransitions/transitions
|
| [19] |
WANG Yue, LI Zheng, ZHAO Ruilian. Dependence based model-healing[C]//2015 IEEE 39th Annual Computer Software and Applications Conference. Taichung: IEEE, 2015: 556. DOI: 10.1109/compsac.2015.274
|
| [20] |
杨博, 刘树东, 鲁维佳, 等. 改进遗传算法在机器人路径规划中的应用[J]. 现代制造工程, 2022, 2022(6): 9. YANG Bo, LIU Shudong, LU Weijia, et al. Application of improved genetic algorithm in robot path planning[J]. Modern Manufacturing Engineering, 2022, 2022(6): 9. DOI:10.16731/j.cnki.1671-3133.2022.06.002 |
| [21] |
ZHOU Xiaofei, ZHAO Ruilian, YOU Feng. EFSM-based test data generation with multi-population genetic algorithm[C]//2014 5th IEEE International Conference on Software Engineering and Service Science (ICSESS). Beijing: IEEE Computer Society, 2014: 925. DOI: 10.1109/ICSESS.2014.6933716
|
| [22] |
CAO Zhiqi, WANG Yichen, GUO Peng, et al. EFSM test data generation based on fault propagation and multi-population genetic algorithm[C]//2020 7th International Conference on Dependable Systems and Their Applications (DSA). Xi'an: Institute of Electrical and Electronics Engineers Inc, 2020: 240. DOI: 10.1109/DSA51864.2020.00042
|
 2023, Vol. 55
2023, Vol. 55


