2. 广东海洋大学 船舶与海运学院,广东 湛江 524088
2. Naval Architectureand Shipping College, Guangdong Ocean University, Zhanjiang 524088, Guangdong, China
永磁同步电机(permanent magnet synchronous motor,PMSM)具有效率高、体积小、功率密度大和调速范围宽等优点,在生产生活中有着广泛的应用。但是电机长时间运行可能会出现电气故障、退磁故障、机械故障等[1]。电机故障具有偶发性,传统的故障诊断方法难以满足高效快速诊断的要求。深度学习凭借其良好的特征提取能力被应用在故障诊断领域[2-3],但足量且均衡的数据集是保证基于深度学习的故障诊断方法发挥其性能的前提[4]。通过试验平台采集数据难以模拟所有故障类型和故障程度,而实际应用中采集的电机故障样本又偏少,与正常样本相比严重失衡。
过采样方法是目前解决样本数量缺失的思路之一。传统的随机过采样算法(random oversampling,ROS)[5]通过简单复制使数据集各类样本达到均衡,但这种方式得到的数据集样本重叠严重,随着生成数据的增多,导致诊断模型泛化性弱。合成少数类过采样技术(synthetic minority oversampling technique,SMOTE)[6]、自适应合成样本方法(adaptive synthetic,ADASYN)[7]在少数类样本中通过线性插值生成样本,缓解了ROS导致的模型泛化性弱的问题。但是此类方法并未考虑到原始数据的整体分布特性,所以对模型性能的提升有限[8]。
大数据的驱动下,深度学习算法在数据扩张领域取得了一定成果。文献[9-10]在自编码的基础上对样本进行了重建,生成了效果不错的数据,但是概率计算复杂,样本的重构精度偏低。文献[11]提出的生成对抗网络(generative adversarial nets,GAN)利用两个神经网络对抗有效地提升了生成图像的质量。文献[12-13]提出了超分辨GAN(super-resolution generative adversarial network,SRGAN),提高了对低分辨率图像的超分辨率重建效率。文献[14-15]考虑到数据的相关性,在模型中添加上下文约束条件,生成了高质量的重建图像。以上研究表明GAN能够通过训练学习到原始样本的特征分布[16]。
鉴于采集到的电机故障数据是一维时间序列,研究表明GAN的衍生模型具有生成一维时间序列数据的潜力。文献[17]提出了一种基于GAN的多优化数据插补方法解决了风力涡轮机大规模数据丢失的问题;文献[18]利用ACGAN对心电信号进行了有效扩张。
PMSM故障数据是变化波动大且分布多样的离散数据,直接将ACGAN用于生成电机故障数据存在生成效率低、重建损失大、训练不稳定等情况。鉴于此,本文提出了一种基于改进ACGAN的数据扩张方法, 对电机故障数据进行扩充。首先使用Wasserstein距离约束生成数据的重建损失,利用梯度惩罚代替权值剪裁对模型进行优化;然后,考虑到电机发生故障时数据的时序特性和相关性,在生成器中引入循环神经网络;最后将BP神经网络作为诊断模型,对比数据扩张前后的分类结果验证本文所提方法的有效性。
1 改进ACGAN算法 1.1 GAN生成对抗网络由生成器和判别器两部分组成[19],且两者处于博弈对抗关系。生成器的目的是生成尽量逼真的数据骗过判别器的甄别;判别器的目的是将真实数据和生成数据准确区分,并且最大化判别概率。其结构见图 1。

|
图 1 GAN结构示意 Fig. 1 GAN structure |
假设n组电机故障样本,则故障数据集为X={x1, x2, …, xn},xn为第n组故障样本的特征向量。随机噪声z服从Pz分布,即z~Pz为生成器的输入;真实数据X满足客观真实分布Pdata,即X~Pdata。
通过对生成器和判别器进行交替迭代训练,建立Pz和Pdata之间的映射关系。将生成器生成的样本和原始故障样本一同输入到判别器中,通过神经网络计算获得样本为真实样本的概率,将输出结果反馈给生成器使得生成更加逼真的数据,达到以假乱真的地步。
最终当生成器生成的数据分布和故障数据分布一致时,达到纳什均衡点。则GAN的目标函数为
| $ \begin{aligned} \min _G \max _D V(G, D)= & E_{x \sim P_{\text {data }}}[\ln D(x)]+ \\ & E_{z \sim P_z}[\ln (1-D(G(z)))] \end{aligned} $ | (1) |
式中:
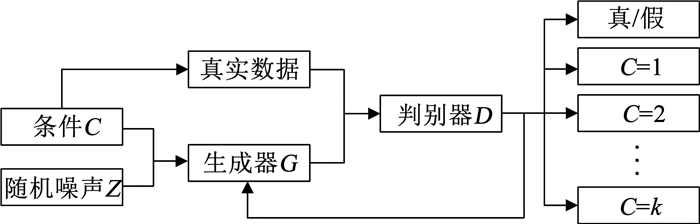
ACGAN[20]通过在生成器和判别器中引入类别标签,用来引导样本的生成,解决了传统GAN无法控制生成数据类别的缺陷。同时ACGAN模型具备生成指定类别故障数据的特性,减少了训练时间。其结构见图 2。
|
图 2 ACGAN结构示意 Fig. 2 ACGAN structure |
保持生成器G不变,训练判别器D的目的是使Ls+Lc最大化;保持判别器D不变,训练生成器G的目的是使Ls-Lc最大化。ACGAN的目标函数为:
| $ L_s=E_{x \sim P_{\text {data }}}\left[\log _2(D(x))\right]+E_{z \sim P_z}\left[\log _2(1-D(G(z)))\right] $ | (2) |
| $ L_c=E_{c \sim P_{\mathrm{data}}}\left[\log _2(D(c))\right]+E_{c \sim P_z}\left[\log _2(1-D(G(c)))\right] $ | (3) |
式中:Ls为判别器输出数据为真的概率,Lc为判别器输出数据分类正确的概率。
1.3 改进ACGAN选用Wasserstein距离来度量实际电机故障数据分布与合成电机故障数据分布之间的差异,避免了ACGAN由于采用JS散度或者KL散度来衡量实际分布和生成分布的距离时产生的训练不稳定。Wasserstein距离[21]定义为
| $ W\left(P_{\text {data }}, P_g\right)=\inf\limits _{\gamma \in \Pi\left(P_{\text {data }}, P_g\right)} E_{(x, \tilde{x}) \sim \gamma}[\|x-\tilde{x}\|] $ | (4) |
式中:∏(Pdata, Pg)为Pdata与Pg的联合概率分布γ的集合;
| $ W\left(P_{\text {data }}, P_g\right)=\frac{1}{K} \sup\limits _{\|f\|_{\mathrm{L}}<K} E_{x \sim P_{\text {data }}}[f(x)]-E_{x \sim P_g}[f(x)] $ | (5) |
式中:K为常数;sup为上确界;‖f‖L≤K表示函数f(x)满足K-Lipschitz连续,保证其导函数在一定范围。即在训练时网络更新的权重被限定在一定区间内,保证正常的梯度优化,使得网络权值在每一轮迭代中不会有较大的变化,有效解决ACGAN训练不稳定的问题。
为了避免权值范围设置不恰当导致梯度爆炸或梯度消失这一问题,本文在原有的损失函数中添加梯度惩罚项[22],以提高网络训练的稳定性。其表达式为
| $ L_{\mathrm{gp}}=\lambda E_{\hat{x} \sim P_{\hat{x}}}\left[\left(\left\|\nabla_{\hat{x}} D(\hat{x})\right\|_2-1\right)^2\right] $ | (6) |
式中:▽为梯度; ‖·‖2为2范数; λ为正则项系数;
由此可知,基于梯度惩罚优化的改进ACGAN网络模型总损失函数为:
| $ \begin{aligned} L_s= & E_{x \sim P_{\text {data }}}\left[\log _2(D(x))\right]+E_{z \sim P_z}\left[\log _2(1-D(G(z)))\right]+ \\ & \lambda E_{\hat{x} \sim P_{\hat{x}}}\left[\left(\left\|\nabla_{\hat{x}} D(\hat{x})\right\|_2-1\right)^2\right] \end{aligned} $ | (7) |
| $ L_c=E_{c \sim P_{\text {data }}}\left[\log _2(D(c))\right]+E_{c \sim P_z}\left[\log _2(1-D(G(c)))\right] $ | (8) |
结合变量之间潜在的相关性及历史数据变化规律,本文在生成器中引入循环神经网络[23],结构见图 3。

|
图 3 改进ACGAN的生成器 Fig. 3 Generator of improved ACGAN |
生成器由一系列相同的结构单元组成,每个结构包含g(·)、f(·)两部分。全局变量时间步骤T控制生成器的大小。
首先从先验分布中采样得到一个样本zt,zt与此时对应的标签拼接成变量hz, c, t;然后将hz, c, t缩放至与hy, t相同维度并组成[hz, c, t, hy, t],hy, t为t-1时刻f(·)的输出结果;最后输入到f(·),经过多层卷积操作之后得到当前t时刻的生成数据,输出结果为yt;同样的, 遍历所有的时间步骤,最终输出结果yT。
2 改进ACGAN模型结构及训练过程 2.1 模型网络结构改进ACGAN生成器网络整体架构见图 4,网络的超参数是在文献[18]的基础上进行实验所得的结果。卷积核大小和归一化时采用的动态均值动量大小为原文献的默认数值;由于电机故障数据是一维的时间序列,所以采用1D卷积来进行数据维度上的处理;滤波器的数量以2为倍数,在结果重构误差相近的情况下选择较小的数值,以减少网络参数,优化模型提高训练速度;为了充分学习到数据潜在的内部特征,将步长设置为1;采用ReLU激活函数提高训练速度。生成器在每个时间步长处,添加长度为128的潜变量与上一个步长的结果拼接。

|
图 4 基于改进ACGAN的电机数据扩张方法框架 Fig. 4 Framework of motor data expansion method based on improved ACGAN |
为保证生成数据与输入数据的维度一致,f(·)网络的输出层滤波器的个数设置为4,分别对应A相电流、B相电流、负序电流、电磁转矩4类数据。生成器基本单元里g(·)、f(·)的详细网络参数见表 1、2。g(·)、f(·)的输出层分别采用tanh、sigmoid激活函数,其他卷积层及全连接层采用ReLU激活函数。
| 表 1 g(·)网络结构参数 Tab. 1 Structure parameters of g(·) network |
| 表 2 f(·)网络结构参数 Tab. 2 Structure parameters of f(·) network |
改进ACGAN模型的判别器网络结构与生成器的编码g(·)基本类似,不同之处在于, 为了提高判别器对于数据真伪的判别能力,卷积层的激活函数采用LeakyReLU以提高识别性能。输出层为2个并列结构的全连接: 一个为能够判定样本类别的softmax输出层;另一个为鉴别样本真假的全连接,采用sigmoid激活函数。最终判别器输出的值是Wasserstein距离,并且对整个判别模型采用梯度惩罚提升训练稳定性。
2.2 模型训练过程基于改进ACGAN的损失函数,对模型参数进行迭代更新。在每个训练单元中,训练过程可以分为2个步骤。
1) 判别器的训练:首先从高斯分布取样生成数据和原始数据,组成一个批次的训练数据m;然后将其生成数据和原始数据一同输入到判别器中,通过对判别器损失函数求导来对判别器网络参数进行优化,使用Adam算法作为梯度优化算法。
2) 生成器的训练:判别器训练完成后,开始生成器的训练。将判别器的输出结果用来反馈给生成器,指导生成器生成质量更高的数据。通过对生成器损失函数求导对生成器网络参数进行优化,同样使用Adam算法作为梯度优化算法。
准确的判别器梯度信息会促进生成器性能的提升,本文先预训练判别器300次,然后在每一轮正式训练过程中采取先训练判别器nD次再训练生成器1次的方式来提高模型的整体性能。在一轮训练完后,训练过程重新开始,通过反复迭代训练,使整个模型在判别器和生成器损失函数的损失值上达到纳什均衡。最后生成器可以根据给定的标签控制和高斯噪声生成PMSM不同故障类型的数据。
改进ACGAN的训练过程如下所示:
算法 改进ACGAN
默认参数:学习率l=0.000 5;λ=5;m=128;nD=5;β1=0.9;β2=0.999;w,判别器初始参数;θ,生成器初始参数。
步骤1:while网络不满足收敛要求
步骤2:For t=0, …, nD do
步骤3:For i=1, …, m do
步骤4:x~Pdata//(从真实样本中取样)
步骤5:z~Pz(z)//(从潜在分布中取随机噪声)
步骤6:ε~U[0, 1]//(随机参数服从均匀分布)
步骤7:
步骤8:
步骤9:
| $ \begin{aligned} L_s \longleftarrow & E_{x \sim P_{\text {data }}}\left[\log _2(D(x))\right]+E_{z \sim P_z}\left[\log _2(1-D(G(z)))\right]+ \\ & \lambda E_{\hat{x} \sim P_{\hat{x}}}\left[\left(\left\|\nabla_{\hat{x}} D(\hat{x})\right\|_2-1\right)^2\right] \\ L_c \leftarrow & E_{c \sim P_{\text {data }}}\left[\log _2(D(c))\right]+E_{c \sim P_z}\left[\log _2(1-D(G(c)))\right] \end{aligned} $ |
步骤10:end for
步骤11:
步骤12:end for
步骤13:Samples {z(i)}i=1m~Pg(z)//(从潜在分布中取一个批次的训练量)
步骤14:
步骤15:end while
步骤16:输出网络模型参数
3 算例分析 3.1 数据集的获取及分布情况本文所采用的车用永磁同步电动机性能参数如下:额定功率12 kW,额定转速为1 500 r/min,电机极数为10,定子槽数为45,冷却方式为水冷。电机控制系统的参数:电机控制器型号KTZ54X32SAN,额定电压540 V,额定功率90 kW。
选用了A相电流、B相电流、负序电流、电磁转矩来形成电机故障的组合特征,通过设置不同的并联短路匝数来模拟不同程度的匝间短路故障,实验采集的部分数据见表 3。
| 表 3 部分实验数据 Tab. 3 Partial experimental data |
电机不同状态对应的编码见表 4。其中,所有状态下,输入电压的不平衡度控制在0~4%范围内。健康状态为电机正常,无匝间故障;允许状态、故障状态A、故障状态B分别为短路程度为5%、10%、15%时发生的匝间短路。
| 表 4 电机状态编码 Tab. 4 Motor status code |
本文构建的数据集样本总数为2 382。其中,健康状态、允许状态、故障状态A、故障状态B样本数据量分别为1 675、358、226、123。将每一类别样本按照3∶1分为训练集和测试集,各类别样本的训练集和测试集数量见表 5。
| 表 5 样本分布状态 Tab. 5 Sample distribution status |
为了更加直观了解在训练过程中生成数据的动态变化,采用主成分分析法(principal component analysis,PCA)将生成数据映射到二维空间,观察其在二维空间的分布,其结果见图 5。其中在改进ACGAN的训练过程中,保持各类别生成数据和原始数据数量一致;状态编码1、2、3、4分别为健康状态、允许状态、故障状态A、故障状态B 4类电机状态;图 5(a)、(b)、(c)分别为模型迭代了1 000次、5 000次、10 000次时生成数据的分布结果,图 5(d)为原始数据的分布结果。

|
图 5 生成数据和原始数据分布 Fig. 5 Distribution of generated and original data |
由图 5可知,当迭代次数较少时,模型还未充分学习到原始数据的潜在特征,导致改进ACGAN训练生成的数据分布和原始数据分布相差较远;随着迭代次数的增加,模型逐渐学习到变量之间的相关性和历史变化规律,改进ACGAN生成的数据分布和原始数据分布越来越相似。
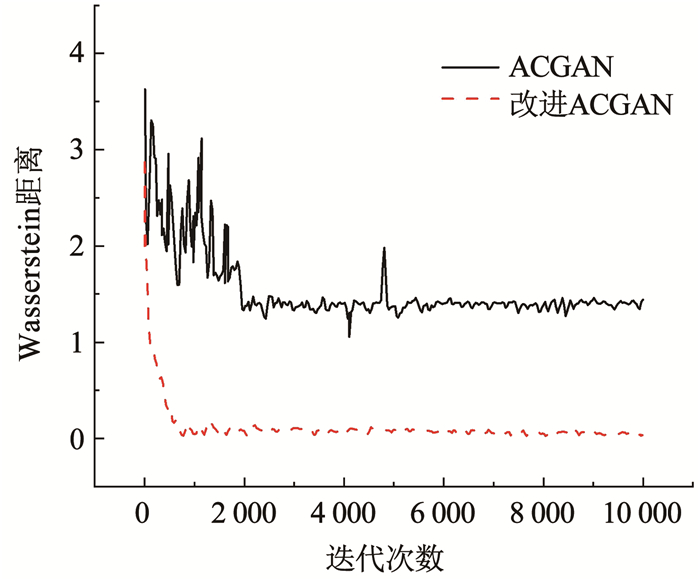
为验证基于梯度惩罚优化的ACGAN模型具有更好的收敛性和训练稳定性, 本文选用的基于权值裁剪的传统方法作为对比[21],实验结果见图 6。
|
图 6 基于不同方法的Wasserstein距离变化 Fig. 6 Wasserstein distance variation based on different methods |
由图 6可知,在迭代次数处于0~2 000之间,基于权值裁剪的传统方法训练极不稳定,当训练到6 000次后才相对稳定,且最终未达到全局最优。相比之下,基于梯度惩罚优化的改进ACGAN训练过程中收敛速度和收敛结果都有显著提升。当训练轮数为2 000时模型逐步开始收敛且在后续迭代过程中平稳收敛到0.03左右,此时的生成器已具有良好的衍生能力。相比于ACGAN,基于梯度惩罚的改进ACGAN模型最终的Wasserstein距离更小,学习到的数据分布与真实数据更为接近。
3.2.2 数据有效性分析实验基于2 382组真实样本进行数据扩张,最终扩张优化后的训练集中各类别的样本数量相同,将训练数据输入到隐含层大小为20、50、30的BP神经网络,最大迭代次数为1 000,参数更新算法为Adam,损失函数为交叉熵,小批量训练样本为32。优化网络参数,得到训练后的诊断模型。
图 7(a)为无数据扩张下故障诊断模型损失函数变化趋势,可以看到训练集的损失函数最终近似收敛到0,而测试集的损失函数一直在0.9左右振荡,则表明此时模型因训练数据不足出现了过拟合现象。图 7(b)为经改进ACGAN数据扩张后故障诊断模型的损失函数变化趋势,其损失函数值在训练集和测试集上均近似收敛到0,说明改进ACGAN模型产生的样本具有多样性,使得诊断模型过拟合现象基本消失,具有更强的泛化能力。

|
图 7 扩张前后的诊断情况 Fig. 7 Diagnosis before and after expansion |
为了能够在各类别数据量相差较大的情况下全面有效地综合评价分类模型的性能,本文引入分类模型的精度指标和召回率指标对诊断网络的泛化能力进行评价。其中Pi精度衡量的是系统的查准率,召回率Ri衡量的系统的查全率。见式(9)、(10):
| $ P_i=\frac{n_{i i}}{\sum\limits_{j=1}^L n_{j i}} $ | (9) |
| $ R_i=\frac{n_{i i}}{\sum\limits_{j=1}^L n_{i j}} $ | (10) |
式中:L为样本总类别数;nij为实际样本类别为i被预测为类别j的样本。
为综合评估分类模型的性能,本文选用分类准确率、F1度量、G-mean来综合评价分类模型的分类性能。其公式见式(11)~(13):
| $ \lambda_{\text {Acc }}=\frac{\sum\limits_{i=1}^L n_{i i}}{\sum\limits_{i=1, j=1}^L n_{i j}} $ | (11) |
| $ \lambda_{\mathrm{F} 1}=\frac{2}{L} \frac{\sum\limits_{i=1}^L R_i \sum\limits_{i=1}^L P_i}{\sum\limits_{i=1}^L R_i+\sum\limits_{i=1}^L P_i} $ | (12) |
| $ \lambda_{\mathrm{G} \text {-mean }}=\prod\limits_{i=1}^L R_i \square^{-1 / L} $ | (13) |
为了检验本文提出方法生成数据的质量,选用了ROS、SMOTE、ADASYN 3种传统过采样方法进行对比分析,每一种方法均保证训练集中各类别的样本数量相同。所有方法在测试集上的结果见表 6。
| 表 6 不同数据扩张方法下的故障诊断结果 Tab. 6 Fault diagnosis results using different data expansion methods |
由表 6可知,相比于原始数据集,采用不同方法扩张后的数据集都会使得模型的诊断性能得到一定的提升。其中,BP神经网络与ROS算法结合时,其λAcc、λF1、λG-mean指标较扩张前分别提高了4.5%、3.8%、4.8%;BP神经网络在与SMOTE算法结合时,其λAcc、λF1、λG-mean指标较扩张前分别提高了5.5%、5.3%、14%;BP神经网络在结合ADASYN算法时,其λAcc、λF1、λG-mean指标较扩张前分别提高了6.5%、7.8%、17%;与改进ACGAN结合时,其λAcc、λF1、λG-mean指标较扩张前分别提高了9%、15%、18%。因此,与传统过采样方法相比,在数据合成方式和合成性能方面,改进ACGAN更加适合用于改善电机故障数据的不平衡问题,进而提升模型的综合分类性能。
4 结论针对PMSM故障数据集样本数量少、各类别样本数量不平衡的问题,本文提出了一种基于改进ACGAN模型的数据扩张方法,通过实际算例,与传统过采样方法相比,得到如下结论:
1) 利用PCA降维可视化对所提模型进行评估,结果表明改进ACGAN模型能够学习到原始数据的分布特征,生成数据与原始数据的分布相似。
2) 改进ACGAN在ACGAN模型中使用Wasserstein距离衡量实际分布与生成分布之间的差异,并进一步引入梯度惩罚项进行改进, 提升了网络训练的稳定性。
3) 考虑到变量之间的相关性和历史变化规律,在基于改进ACGAN的电机故障数据扩张方法中引入循环神经网络,提高了生成数据的质量,使得诊断模型在分类准确率、F1度量、G-mean指标上较传统过采样方法提升效果更为明显。
| [1] |
孙文珺, 邵思羽, 严如强. 基于稀疏自动编码深度神经网络的感应电动机故障诊断[J]. 机械工程学报, 2016, 52(9): 65. SUN Wenjun, SHAO Siyu, YAN Ruqiang. Induction motor diagnosis based on deep neural network of sparse auto-encoder[J]. Journal of Mechanical Engineering, 2016, 52(9): 65. DOI:10.3901/JME.2016.09.065 |
| [2] |
彭彬森, 夏虹, 王志超, 等. 深度神经网络在滚动轴承故障诊断中的应用[J]. 哈尔滨工业大学学报, 2021, 53(6): 155. PENG Binsen, XIA Hong, WANG Zhichao, et al. Rolling bearing fault diagnosis using deep neural network[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 155. DOI:10.11918/201909062 |
| [3] |
赵书涛, 王二旭, 陈秀新, 等. 声振信号联合1D-CNN的大型电机故障诊断方法[J]. 哈尔滨工业大学学报, 2020, 52(9): 116. ZHAO Shutao, WANG Erxu, CHEN Xiuxin, et al. Fault diagnosis method for large motor based on sound-vibration signal combined with 1D-CNN[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 116. DOI:10.11918/201901221 |
| [4] |
雷亚国, 贾峰, 孔德同, 等. 大数据下机械智能故障诊断的机遇与挑战[J]. 机械工程学报, 2018, 54(5): 94. LEI Yaguo, JIA Feng, KONG Detong, et al. Opportunities and challenges of machinery intelligent fault diagnosis in big data era[J]. Journal of Mechanical Engineering, 2018, 54(5): 94. DOI:10.3901/JME.2018.05.094 |
| [5] |
BATISTA G E, PRATI R C, MONARD M C, et al. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6(1): 20. DOI:10.1145/1007730.1007735 |
| [6] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321. DOI:10.1613/jair.953 |
| [7] |
HE Haibo, YANG Bai, GARCIA E A, et al. ADASYN: Adaptive synthetic sampling approach for imbalanced learning[C]//IEEE 2008 IEEE International Joint Conference on Neural Networks. Hong Kong: IEEE World Congress on Computational Intelligence, 2008: 1322. DOI: 10.1109/ijcnn.2008.4633969
|
| [8] |
ZHU Lipeng, LU Chao, DONG Z Y, et al. Imbalance learning machine-based power system short-term voltage stability assessment[J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2533. DOI:10.1109/TII.2017.2696534 |
| [9] |
陈海燕, 杜婧涵, 张魏宁. 基于深度降噪自编码网络的监测数据修复方法[J]. 系统工程与电子技术, 2018, 40(2): 435. CHEN Haiyan, DU Jinghan, ZHANG Weining. Monitoring data repair method based on deep denoising autoencoder network[J]. Systems Engineering and Electronic Technology, 2018, 40(2): 435. DOI:10.3969/j.issn.1001-506X.2018.02.28 |
| [10] |
张周磊, 李垣江, 李梦含, 等. 基于深度学习的永磁同步电机故障诊断方法[J]. 计算机应用与软件, 2019, 36(10): 123. ZHANG Zhoulei, LI Yuanjiang, LI Menghan, et al. Fault diagnosis method of permanent magnet synchronous motor based on deep learning[J]. Computer Application and Software, 2019, 36(10): 128. DOI:10.3969/j.issn.1000-386x.2019.10.022 |
| [11] |
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2014: 354
|
| [12] |
张杨忆, 林泓, 管钰华, 等. 改进残差块和对抗损失的GAN图像超分辨率重建[J]. 哈尔滨工业大学学报, 2019, 51(11): 128. ZHANG Yangyi, LIN Hong, GUAN Yuhua, et al. GAN image super-resolution reconstruction model with improved residual block and adversarial loss[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 128. DOI:10.11918/j.issn.0367-6234.201812115 |
| [13] |
DOU Xinyu, LI Chenyu, SHI Qian, et al. Super-resolution for hyperspectral remote sensing images based on the 3D attention-SRGAN network[J]. Remote Sensing, 2020, 12: 1203. DOI:10.3390/rs12071204 |
| [14] |
YEH R A, CHEN C, LIM T Y, et al. Semantic image inpainting with deep generative models[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE Computer Society, 2017: 6882. DOI: 10.1109/CVPR.2017.728
|
| [15] |
LI Yijun, LIU Sifei, YANG Jimei, et al. Generative face completion[C]//Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE Computer Society, 2017: 5892. DOI: 10.1109/CVPR.2017.624
|
| [16] |
GOU Chaowu, WU Yue, WANG Kang, et al. A joint cascaded framework for simultaneous eye detection and eye state estimation[J]. Pattern Recognition, 2017, 67: 23. DOI:10.1016/j.patcog.2017.01.023 |
| [17] |
QU Fuming, LIU Jinhai, MA Yanjuan, et al. A novel wind turbine data imputation method with multiple optimizations based on GANs[J]. Mechanical Systems and Signal Processing, 2020, 139: 106610. DOI:10.1016/j.ymssp.2019.106610 |
| [18] |
WANG Pu, HOU Borui, SHAO Siyu, et al. ECG arrhythmias detection using auxiliary classifier generative adversarial network and residual network[J]. IEEE Access, 2019, 7: 100910. DOI:10.1109/ACCESS.2019.2930882 |
| [19] |
史丹青. 生成对抗网络入门指南[M]. 北京: 机械工业出版社, 2018: 14. SHI Danqing. Generative adversarial network: A primer[M]. Beijing: Machinery Industry Press, 2018: 14. |
| [20] |
DENA A, OLAH C, SHLENS J, et al. Conditional image synthesis with auxiliary classifier gans[C]//Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR, 2017: 2642
|
| [21] |
ARJOVSKY M, CHINTALA S, BOTTOU L, et al. Wasserstein generative adversarial networks[C]//International Conference on Machine Learning. [S. l. ]: PMLR, 2017: 214
|
| [22] |
GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of wasserstein gans[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. [S. l. ]: Long Beach, 2017: 314
|
| [23] |
WANG Qiang, FAN Huijie, SUN Gan, et al. Recurrent generative adversarial network for face completion[J]. IEEE Transactions on Multimedia, 2021, 23: 429. DOI:10.1109/TMM.2020.2978633 |
 2023, Vol. 55
2023, Vol. 55


