2. 内蒙古交通设计研究院有限责任公司, 呼和浩特 010011
2. Inner Mongolia Transportation Design and Research Institute Co., Ltd., Hohhot 010011, China
正交异性钢桥面板(orthotropic steel deck,OSD),由于其焊缝众多,构造复杂,且局部应力明显,在交通荷载反复作用下,正交异性钢桥面板极易发生疲劳破坏[1-6]。自20世纪80年代年起,国内外学者便对OSD结构开展了大量的实验和理论研究。文献[7]对欧洲三座桥梁的焊接开裂情况进行总结,发现在OSD结构的分析中应适当考虑桥面板和加劲肋中的应力流,以及桥面板构件结合处和桥面板支撑处的局部应力;文献[8]通过数值分析的方法对纵肋和横隔板连接处(rib-floorbeam,RF)的面内变形、面外变形的机理和疲劳特性进行研究,发现横隔板和纵肋的变形会导致加劲肋与横隔板上产生次内力;文献[9]对威廉堡大桥进行全面的实验研究和有限元分析,测量并计算横隔板上面内应力和面外应力的分配情况,发现横隔板疲劳问题主要由面内应力控制,在此基础上提出了横隔板疲劳设计方法;文献[10]总结了美国钢桥的焊接历史,并与现有钢桥抗疲劳设计方法进行比较,提出了超声波冲击方法对焊接位置进行加强处理,根据两次足尺模型试验验证该方法的有效性;文献[6]利用有限元方法对U肋和顶板的残余应力分布进行分析,发现顶板与U肋的厚度比以及U肋的厚度对于焊接残余应力的分布有较大影响;文献[11]在断裂力学的基础上对RF处的疲劳特性、寿命预测进行研究,并提出了栓接角钢的装配式快速加固方法,通过足尺试验研究和有限元计算,发现RF处的疲劳裂纹程度随裂纹扩展逐渐加剧,装配式加固方法能有效抑制疲劳的进一步扩展;文献[12]利用有限元分析的方法对RF处的不同设计方案进行分析计算,比较横隔板上弧形开口形状构造的合理性,选定最优的几何参数设计;文献[13-14]利用有限元方法对OSD结构进行分析计算,发现随着横隔板弧形缺口曲率比增加,弧形切口起始处的计算寿命增加,而自由边的计算寿命减小,对比多个优化方案,最终提出合理的弧形切口形式。
对于OSD结构的疲劳问题,学者们已经提出多种构造形式的优化设计方法,其中部分方法对于解决顶板与纵肋之间的疲劳问题有良好的效果[15-18]。但仍然存在着一些问题,如纵肋与横隔板连接处的疲劳开裂问题仍然未得到解决。根据日本学者对东京两座采用OSD结构的钢桥进行的疲劳病害统计分析发现:发生在纵肋与横隔板连接处(含开口部位)的疲劳开裂可能性最高,比例高达38.2%。该部位是OSD结构中构造最为复杂的位置,应力集中程度大、交叉焊接复杂,故该部位容易发生疲劳破坏。本文在既有研究的基础上,对横隔板厚度、内隔板构造形式与横隔板开口形式对纵肋与横隔板连接处的主应力极值的影响进行细致研究分析,并基于理论分析结果提出了若干合理的构造措施。
1 有限元计算模型研究依托辽宁省铁岭新区凡河四桥,凡河四桥主桥结构为跨径140 m+110 m的梭型独塔斜拉桥,其跨径分布为2×30 m+140 m+110 m+3×30 m=400 m。主梁为单箱五室薄壁钢箱梁,全桥钢材采用Q345q。该桥在实际运营之后出现了顶板-纵肋连接焊缝出现疲劳裂纹等病害。由于钢箱梁尺寸较大,采用整体有限元模型分析效率较低。选择子模型建模的方式是较合理的方式,即整体采用网格较为粗糙的板壳单元建模,关注位置采用网格较为精细的实体单元建模。整体模型包含3个横隔板和7个闭口加劲肋,横隔板间距为4.5 m,U肋间距为600 mm。横隔板高度取1 m,子模型截取整体模型中间1.8 m×0.6 m(横桥向×纵桥向)部分,横隔板高度截取500 mm,具体包括3个U肋及附近顶板和横隔板(图 1)。U肋具体细节如图 2所示。在整体模型的横隔板底部施加约束,约束其x、y、z三个方向的平动和转动自由度。模型采用的钢材为Q345,密度ρs=7.8×10-9 kg/m3,弹性模量Es=2×105 MPa,泊松比μ=0.3。

|
图 1 OSD结构尺寸图(mm) Fig. 1 Dimension of OSD (mm) |

|
图 2 U肋和弧形开口示意图(mm) Fig. 2 Schematic diagram of U rib and arc opening (mm) |
采用有限元软件ANSYS进行建模和分析,单元类型选取实体单元solid45,单元尺寸约为6 mm×6 mm×6 mm,子模型轮廓图如图 3所示。

|
图 3 子模型网格划分轮廓图 Fig. 3 Outline diagram of submodel meshing |
由于研究的核心内容是构造细节的优化设计,以应力为指标,因此采用单轮加载的方式,轮重70 kN,接触面积为600 mm×200 mm。计算模型考虑铺装层厚度为50 mm,由于铺装层的扩散作用,荷载在铺装层以45°进行扩散,实际接触面积为700 mm×300 mm。
2 控制应力选取在横向上取9个具有代表性的位置进行横向布载,如图 4所示,将车轮加载位置从横隔板上中间U肋的正上方开始向左横向移动,移动间距为150 mm,移动至1 200 mm为止,即中间U肋的左侧的第2个U肋正上方为终点位置。以此9个横向位置为起始位置,纵向移动至边跨横隔板附近。轮载纵向移动范围为一个横隔板间距,横向移动范围为两个纵肋间距。研究各控制应力在轮载移动时的变化规律。

|
图 4 轮载作用工况示意图(mm) Fig. 4 Schematic diagram of wheel load (mm) |
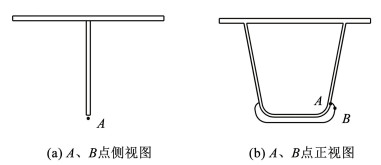
在轮载作用下,U肋上A点和横隔板上B点有应力集中现象,A、B两点位置如图 5所示,以这两点的主应力为控制应力,绘制影响面,如图 6所示。轮载横向移动300 mm,纵向移动1.8 m时,A点达到最大控制应力;轮载横向移动150 mm,纵向移动600 mm时,B点达到最大控制应力。
|
图 5 分析点相对位置图 Fig. 5 Analysis point relative position diagram |

|
图 6 A、B两点主应力影响面 Fig. 6 Principal stress influence surfaces of point A and B |
在钢箱梁桥中,由于活载的偏心加载作用以及轮载直接作用在箱梁的顶板上,使得箱梁断面发生畸变与横向弯曲变形,为减少钢箱梁的这种变形,增加整体刚度,防止过大的局部应力,需要在箱梁的支点处和跨间设置横隔板。
3.1 横隔板厚度参数分析依托工程钢箱梁横隔板厚度按照现行钢桥设计规范取值仅需2.66 mm。而实际工程中采用的横隔板厚度在8~14 mm之间,偏于安全,因此本节以横隔板厚度为研究对象进行参数分析,变化为8~16 mm,变化梯度为2 mm,其余参数不变,考察横隔板厚度变化对关注点的控制应力的影响。
B点内侧为轮载纵向移动中靠近轮载的横隔板一侧,B点外侧为背离轮载的横隔板一侧(图 7)。B点面内、外应力依据祝志文等[13]建议的方法对横隔板上点的应力进行面内应力和面外应力分解所得,即
| $ \sigma_{\text {in }}=\left(\sigma_{\text {inp }}+\sigma_{\text {onp }}\right) / 2 $ | (1) |
| $ \sigma_{\text {on }}=\left(\sigma_{\text {inp }}-\sigma_{\text {onp }}\right) / 2 $ | (2) |

|
图 7 B点内外侧示意图(mm) Fig. 7 Interior and exterior diagram of point B(mm) |
式中:σin、σon分别为B点内侧和外侧应力;σinp、σonp分别为B点面内和面外应力。
从图 8中可以看出随着横隔板厚度的增加,B点的控制应力即B点外侧应力呈现稳定减小的趋势:横隔板从8 mm变化到16 mm,B点控制应力减小了34.29 MPa,减小幅度高达38.11%;将上述应力分解为面内应力和面外应力,结果表明随着横隔板厚度的增加,B点的面内应力减小了39.54 MPa,面外应力增大了5.25 MPa。

|
图 8 B点控制应力随横隔板厚度变化 Fig. 8 Control stress variation with diaphragm thickness at point B |
显然横隔板厚度对横隔板的应力影响主要影响体现在对面内应力的影响,增大板厚大幅降低了横隔板的面内应力,这是由于横隔板对于U肋主要起支撑作用,增加板厚必然会减小其面内应力;而增大板厚对于面外应力有不利影响,是因为增大板厚,横隔板刚度增加,分配的弯矩也随之增加,导致面外应力有所增大。
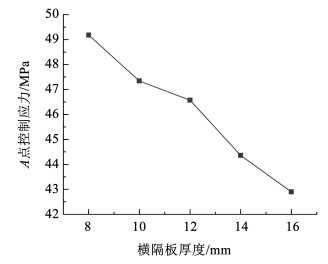
根据图 9可知面外应力占总应力的比值有限,对于控制应力的影响较小。故可知增大横隔板厚度可以明显降低横隔板面内应力,进而减小B点的疲劳控制应力,降低横隔板上疲劳裂纹开展的可能性,对于缓解弧形开口处疲劳问题具有明显效果。如图 10所示,给出了A点控制应力随横隔板厚度的变化情况,从图中可以看出随着横隔板厚度的增加,A点的控制应力呈现稳定减小的趋势,横隔板从8 mm变化到16 mm,A点控制应力减小了6.29 MPa,减小幅度仅为12.78%,这是由于A点的控制应力主要由面外效应引起,增大横隔板厚度对于缓解U肋的畸变效应不明显。显然增大横隔板厚度对于改善B点的疲劳性能效果明显,对应A点的疲劳性能改善不明显。横隔板依据抗畸变效应计算的最小厚度对于疲劳计算是不利的,考虑横隔板的疲劳性能不宜采用该最小厚度。

|
图 9 B点面外应力占总应力比值随横隔板厚度变化 Fig. 9 The ratio of out-of-plane stress to total stress at point B variation with the thickness of diaphragm |
|
图 10 A点控制应力随横隔板厚度变化 Fig. 10 Control stress variation with diaphragm thickness at point A |
以上分析表明增大横隔板厚度对于改善B点的疲劳性能效果明显,因此在保持整体厚度不变的前提下提高U肋所在区域横隔板的厚度,从而提高横隔板局部抗疲劳性能,由此提出一种新型变截面厚度横隔板设计,即与U肋、顶板交接区处横隔板厚度与其他区域厚度不同。
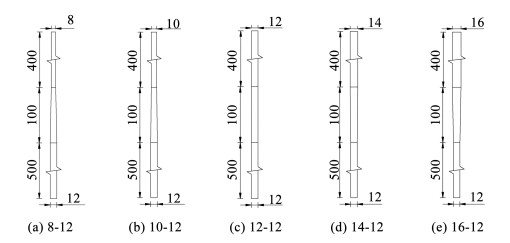
参考箱梁顶板的变截面设计进行横隔板的变截面设计,当坡口焊缝两侧构件的宽度不同或者厚度相差4 mm以上时,为使传力平顺减少应力集中应将较宽或者较厚构件加工成小于1∶4的坡度平滑过渡;当厚(或宽)差不超过4 mm时,则可采用焊缝表面斜度来过渡。进行变截面厚度横隔板设计如图 11所示,为满足横隔板抗畸变设计要求,横隔板下部厚度依然采用12 mm,上部400 mm部分采用8~16 mm厚度,上下部分之间统一采用100 mm的变化过渡段。进行有限元计算分析,绘制B点控制应力随横隔板上部厚度变化关系如图 12所示。
|
图 11 变厚度横隔板设计图示(mm) Fig. 11 Diagram of diaphragm of variable thickness (mm) |

|
图 12 B点控制应力随变厚度横隔板厚度变化 Fig. 12 Diaphragm of the control stress at point B varies with the thickness |
从图 12可知,随着横隔板厚度的增加,B点的控制应力即B点外侧应力呈现稳定减小的趋势,横隔板从8 mm变化到16 mm,B点控制应力减小了36.53 MPa,减小幅度达到40.45%;分析分解得到的面内应力和面外应力可知随着横隔板厚度的增加,B点的面内应力减小了39.25 MPa,而面外应力增大了2.73 MPa。可见增大横隔板上部分厚度能够有效地降低B点的面内应力,对于弧形开口处疲劳改善有明显效果。
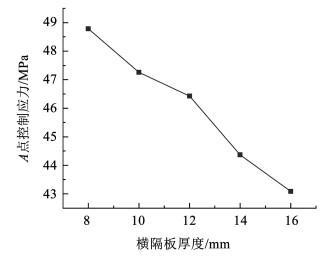
从图 13可知,A点控制应力随着横隔板厚度增加有减小趋势,横隔板从8 mm变化到16 mm,A点控制应力减小了5.70 MPa,减小幅度仅为11.68%,由于该部位控制应力主要由面外应力组成,增加横隔板厚度对改善该疲劳细节效果不明显。换言之,如不考虑计算误差,对于以面外控制应力为主的疲劳细节,增加横隔板板厚是不适合的。
|
图 13 A点控制应力随变厚度横隔板厚度变化 Fig. 13 Diagram of diaphragm thickness variation of control stress with varying thickness at point A |
由于RF处的疲劳问题是局部问题,通过调整该部位的横隔板厚度缓解该位置的疲劳问题是完全可行的。建议采用上部横隔板16 mm厚,下部横隔板12 mm厚的变横隔板设计方法,该方法可有效降低弧形开口最大控制应力,降幅可达到40.45%。
4 内隔板构造形式优化分析早期,美国学者Fisher和Bocchieri提出内隔板结构,并做了相关疲劳试验,试验结果表明,在U肋内部焊接内横隔板可以增强局部构件的刚度,限制U肋的扭转变形,进而有效降低了U肋与横隔板连接处的应力集中,之后研究人员对其外形进行了不断的优化(图 14)。

|
图 14 利用内隔板消除梯形加劲肋开口处的应力集中 Fig. 14 The stress concentration at the opening of trapezoidal stiffening rib was eliminated by internal baffle |
中国目前对U肋内隔板的构造形式、尺寸以及疲劳性能研究较少。现行规范中对于内隔板的设计方法没有明确规定,目前随着焊接技术的进步,这一构造可以实施。因此有必要对内隔板的疲劳性能进行相应研究,并提出具有实际意义的构造措施。
在U肋内部建立内隔板,内隔板的厚度与横隔板一致,均为12 mm,且二者在同一平面上,依据美国AASHTO规范,设计内隔板尺寸如图 15所示,分别建立有内隔板和无内隔板两种有限元模型进行对比分析。分别计算在不同轮载情况下A、B两点的控制应力。

|
图 15 内隔板尺寸(mm) Fig. 15 Internal partition size (mm) |
无内隔板时,A、B点的控制应力分别为-65.51 MPa和46.57 MPa;单内隔板时,A、B点的控制应力分别为-60.06 MPa和33.59 MPa;B点控制应力增设内隔板后减小了8.32%,这是由于增设内隔板后,改变了U肋与横隔板的作用方式,由原来的U肋与横隔板相互作用转变为内隔板与横隔板相互作用。在没设置内隔板的情况下,A点控制应力最大增设内隔板后,减小幅度达到27.87%,效果明显,能够有效地减小该位置疲劳开裂的可能性,这是由于增设内隔板后加强了U肋的局部刚度,有效削弱了U肋扭转畸变效应,减小了畸变引起的次内力。
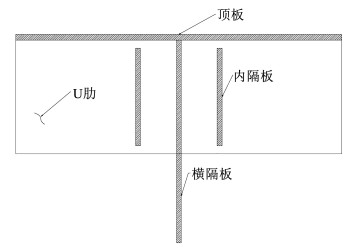
在U肋内部增设内隔板对于解决纵肋与横隔板连接处的疲劳问题效果明显,但也存在一定不足。首先在纵肋与横隔板连接处,由于焊接问题存在着较大的焊接残余应力,如果继续在该位置焊接内隔板,焊接残余应力叠加会使得该处疲劳问题更严重;其次,即使目前可以采用机器人技术焊接内隔板,但是焊接过程未必能达到足够精细,无法完全保证内隔板与横隔板在同一平面上。依据以上两点,提出新型的双内隔板构造形式,即在横隔板前后分别设置内隔板,将内隔板设置在横隔板前后100 mm位置处,如图 16所示,进行有限元分析,得到结果与无内隔板结果进行比较。
|
图 16 双内隔板布置示意图 Fig. 16 Layout diagram of double internal partitions |
双内隔板时,A、B点的控制应力分别为-62.78 MPa和32.44 MPa。在设置双内隔板后B点控制应力减小了4.17%,相比于单内隔板,双内隔板对于减小B点控制应力的效果不明显。在设置双内隔板后A点控制应力减小了30.34%,与单内隔板相近,效果明显,这同样是由于增设内隔板使得U肋的局部刚度得到加强,畸变效应得到削弱,而且由于采用双内隔板,加强效果更加明显。
综上所述,增设内隔板虽然对于降低弧形开口处的疲劳应力效果不明显,但是能够大幅降低纵肋与横隔板连接处纵肋上的疲劳应力。本文提出的新型双内隔板构造形式可以起到与单内隔板一样甚至更好的效果。
5 横隔板开口形式优化设计文献[19]的研究发现纵肋连续通过横隔板会引起纵肋底部焊接部位的疲劳裂纹,因此对纵肋底部的横隔板进行开口来消除该位置的集中应力,这种方法虽然有效地解决了纵肋底部的应力集中问题,却在弧形开口处引入了新的应力集中和疲劳问题。各国学者为解决这一问题进行了大量的实验,提出了不同的开口形式。
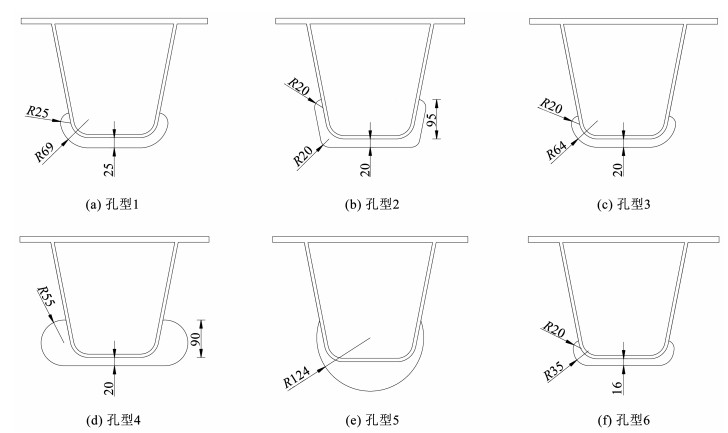
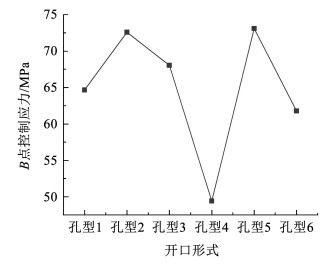
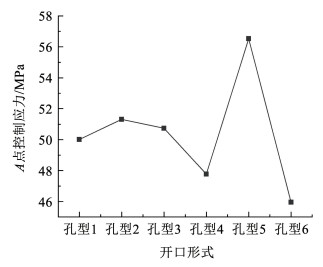
本文选取6种典型的横隔板弧形开口形式进行对比分析,如图 17所示。孔型1为欧洲钢桥规范Eurocode推荐的公路桥开口形式;孔型2为美国钢桥公路桥梁规范AASHTO推荐的开口形式;孔型3为日本钢桥规范推荐的开口形式;孔型4为美国的Williamsburge桥采用的开口形式;孔型5为典型的圆形开口形式;孔型6为铁岭凡河四桥所采用的开口形式。结合6种不同的开口形式建立有限元模型,提取计算结果中的控制应力,绘制不同开口形式下各点的控制应力对比图见图 18和图 19。
|
图 17 不同横隔板弧形开口形式(mm) Fig. 17 Different diaphragm arc opening forms (mm) |
|
图 18 不同开口形式下B点控制应力 Fig. 18 Controlled stress of point B under different opening forms |
|
图 19 不同开口形式下A点控制应力 Fig. 19 Controlled stress of point A under different opening forms |
B点控制应力为压应力,为方便比较,取绝对值绘入图中。从图 18可以看出,孔型4的B点控制应力最小(-49.4 MPa),孔型5的B点控制应力最大(-73.1 MPa),除了孔型4以外,其余5种孔型的B点控制应力相近,就B点控制应力而言,孔型4最为理想。故在孔型设计时应使圆形开口半径尽量大,以减少构造细节过渡,减小集中应力。从图 19可以看出,孔型6的A点控制应力最小(46.0 MPa),孔型5的A点控制应力最大(56.5 MPa),除了孔型5以外,其余5种孔型的A点控制应力相近,就A点控制应力而言,孔型6最为理想。值得注意的是孔型5这种特殊的圆形开口形式对于RF处疲劳较为不利。
通过比较A、B两点控制应力可以发现,增大弧形开口的半径可以使几何过渡更加平顺,有效降低集中应力的大小,因此在设计时应考虑采用大半径弧形切口;依据美国规范AASHTO,底部切口深度C>H/3,C为弧形开口起始点到U肋底部的垂直距离,H为U肋的高度,如果切口深度C很小,则会限制肋的旋转,由于横隔板和腹板之间相互作用力以及由于切口C的较小深度而产生的二次效应,会在纵肋中引入局部二次应力,故应尽量提高切口深度;在横隔板与纵肋连接处采用反向圆弧进行平滑过渡,可以使几何线形更加平顺,减小几何不连续导致的应力集中。综合以上三点,提出一种半径和切口深度均有所增加的开口形式,其中C=90 mm,H=277 mm,如图 20所示。
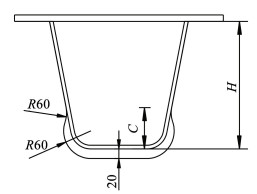
|
图 20 建议弧形开口形式(mm) Fig. 20 Recommended curved opening form (mm) |
对该开口形式进行有限元分析计算,得到A、B两点控制应力值。其中B点的控制应力最大为-42.4 MPa,比上述6种开口形式中最小控制应力-49.4 MPa(开口形式4)降低14.2%;A点的控制应力最大,为34.7 MPa,比上述6种开口形式中最小控制应力46.4 MPa(开口形式6)降低25.2%。通过对比分析A、B两点的控制应力结果可以判定,该新型开口形式可以明显减小A、B两点的疲劳控制应力,从而较大幅度提升该疲劳细节的疲劳性能。
6 结论本文以实际桥梁为原型,采用有限元方法对纵肋与横隔板连接处的疲劳性能进行优化设计研究,从横隔板厚度、内隔板的设置及横隔板开口形式这3个角度,进行合理的参数分析,提出能够提升疲劳性能的新型构造细节。结论如下:
1) 基于疲劳裂纹受力局部性机理,提出变厚度横隔板的构造形式,横隔板与U肋连接厚度区域加厚,其余不变。设计多种变厚度横隔板下的OSD结构,结果表明控制应力下降明显,可有效改善疲劳性能。
2) 考虑到施工难度与局部焊接残余应力过度集中,提出双内隔板的方案。在两道内隔板之间可以填充减振材料,计算结果表明双内隔板构造形式可以有效改善疲劳性能,且便于施工。
3) 提出的反圆弧过渡下的大半径开口形式,计算结果表明该方案可以有效改善该细节疲劳性能。
| [1] |
卜一之, 金正凯, 黄云, 等. 钢桥面板纵肋顶板焊缝疲劳裂纹扩展的关键影响因素[J]. 中国公路学报, 2019, 32(9): 61. BU Yizhi, JIN Zhengkai, HUANG Yun, et al. Key influencing factors of fatigue crack propagation in rib-to-deck welded joints of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2019, 32(9): 61. DOI:10.19721/j.cnki.1001-7372.2019.09.006 |
| [2] |
LEONETTI D, MALJAARS J, SNIJDER H H. Probabilistic fatigue resistance model for steel welded details under variable amplitude loading-Inference and uncertainty estimation[J]. International Journal of Fatigue, 2020, 135. DOI:10.1016/j.ijfatigue.2020.105515 |
| [3] |
黄云, 张清华, 郭亚文, 等. 钢桥面板纵肋与横隔板焊接细节表面缺陷及疲劳效应研究[J]. 工程力学, 2019, 36(3): 203. HUANG Yun, ZHANG Qinghua, GUO Yawen, et al. Research on surface defects and effects and fatigue effects at rib-to-crossbeam welded joints of orthotropic steel bridge decks[J]. Engineering Mechanics, 2019, 36(3): 203. DOI:10.6052/j.issn.1000-4750.2017.12.0973 |
| [4] |
KAINUMA S, YANG Muye, JEONG Y S, et al. Experimental investigation for structral parameter effects on fatigue behavior of rib-to-deck welded joints in orthotropic steel decks[J]. Engineering Failure Analysis, 2017, 79: 520. DOI:10.1016/j.engfailanal.2017.04.028 |
| [5] |
LI Datao, ZHANG Chunguo, LU Pengming. Fatigue property and improvement of a rounded welding region between the diaphragm plate and closed rib of an orthotropic steel bridge deck[J]. Metals, 2020, 10(2): 161. DOI:10.3390/met10020161 |
| [6] |
ZHAO Qiu, ZHAI Zhansheng, NIE Yu. Distribution of welding residual stress of mixed steel U-rib-stiffened plates[J]. Transactions of Tianjin University, 2018, 24(5): 489. |
| [7] |
WOLCHUK R. Steel orthotropic decks: developments in the 1990s[J]. Transportation Research Record, 1999, 1688(1): 30. DOI:10.3141/1688-04 |
| [8] |
LEENDERTZ J S, KOLSTEIN M H, WARDENIER J, et al. Numerical analyses of the trough to crossbeam connections in orthotropic steel bridge decks[C]//Nordic Steel Construction Conference'95. Malmo: Swedish Institute of Steel Construction, 1995
|
| [9] |
CONNOR R J. A comparison of the in-service response of an orthotropic steel deck with laboratory studies and design assumptions[D]. Bethlehem: Lehigh University, 2002
|
| [10] |
FISHER J W, ROY S. Fatigue of steel bridge infrastructure[J]. Structure and Infrastructure Engineering, 2011, 7(7/8): 457. DOI:10.1080/15732479.2010.493304 |
| [11] |
张清华, 卜一之, 李乔. 正交异性钢桥面板疲劳问题的研究进展[J]. 中国公路学报, 2017, 30(3): 14. ZHANG Qinghua, BU Yizhi, LI Qiao. Review on fatigue problems of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2017, 30(3): 14. DOI:10.3969/j.issn.1006-3897.2017.03.002 |
| [12] |
鞠晓臣, 曾志斌, 方兴, 等. 正交异性钢桥面板U形肋与横隔板连接处弧形缺口几何参数优化研究[J]. 钢结构, 2016, 31(11): 19. JU Xiaochen, ZENG Zhibin, FANG Xing, et al. The geometric parameters optimization study of arc profile crossconnection between floor-beam web and U-shaped rib in orthotropic steel deck[J]. Steel Construction, 2016, 31(11): 19. DOI:10.13206/j.gjg201611005 |
| [13] |
祝志文, 黄炎, 李健朋, 等. 正交异性钢桥面板横隔板弧形切口疲劳评价的热点应力法[J]. 交通运输工程学报, 2018, 18(5): 25. ZHU Zhiwen, HUANG Yan, LI Jianpeng, et al. Fatigue assessment of floorbeam cutout in orthotropic steel bridge deck base on hot-spot stress method[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 25. DOI:10.3969/j.issn.1671-1637.2018.05.003 |
| [14] |
何志刚, 蔺鹏臻. 钢箱梁横隔板弧形切口疲劳性能及构造优化研究[J]. 桥梁建设, 2021, 51(1): 37. HE Zhigang, LIN Pengzhen. Study of fatigue performance and structural optimization of arc shaped notch in diaphragm of steel box girder[J]. Bridge Construction, 2021, 51(1): 37. |
| [15] |
YUAN Yuan, WU Chong, JIANG Xu. Experimental study on the fatigue behavior of the orthotropic steel deck rehabilitated by UHPC overlay[J]. Journal of Constructional Steel Research, 2019, 157: 1. DOI:10.1016/j.jcsr.2019.02.010 |
| [16] |
KINOSHITA K, BANNO Y, ONO Y, et al. Fatigue strength improvement of welded joints of existing steel bridges by shot-peening[J]. International Journal of Steel Structres, 2019, 19(2): 495. DOI:10.1007/s13296-018-0140-9 |
| [17] |
DE FREITAS S T, KOLSTEIN H, BIJLAARD F. Fatigue assessment of full-scale retrofitted orthotropic bridge decks[J]. Journal of Bridge Engineering, 2017, 22(11): 04017092. DOI:10.1061/(ASCE)BE.1943-5592.0001115 |
| [18] |
祝志文, 李健朋, 黄炎, 等. 2种弧形切口对RF构造细节疲劳性能影响的现场监测[J]. 中国公路学报, 2020, 33(1): 87. ZHU Zhiwen, LI Jianpeng, HUANG Yan, et al. Investigation on fatigue performance of rib-to-floorbeam connection with two cutout geometries based on field monitoring[J]. China Journal of Highway and Transport, 2020, 33(1): 87. DOI:10.19721/j.cnki.1001-7372.2020.01.009 |
| [19] |
JONG F B P D. Overview fatigue phenomenon in orthotropic bridge decks in the netherlands[C]//2004 Orthotropic Bridge Conference. Sacramento: ASCE, 2004: 489
|
 2023, Vol. 55
2023, Vol. 55


