2. 四川省公路规划勘察设计研究院有限公司, 成都 610041
2. Sichuan Highway Planning, Survey, Design and Research Institute Ltd., Chengdu 610041, China
在使用寿命周期内,桥梁不可避免地会遭受环境侵蚀和重载交通作用,同时也可能遭受冲击、爆炸和火灾等极端作用[1-2]。如2007年因重载交通作用而坍塌的I-35W密西西比河大桥[3],2013年因爆炸而坍塌的河南连霍高速大桥,2018年因斜拉索锈蚀断裂而坍塌的莫兰迪大桥[4]以及2019年因货车超载而发生侧翻的无锡独柱墩高架桥。桥梁体系的非线性冗余为结构应对此类非对称极端作用提供了必要的内部防灾缓冲机制[5],通过应力塑性重分布丰富了结构的传力路径,增加了体系承载的平衡状态数[6]。为了应对桥梁在各类非对称极端作用下发生连续倒塌,美国已于2010年将体系冗余性纳入AASHTO LRFD桥梁设计规范[7],并在钢桥设计手册中将冗余划分为荷载路径冗余、体系冗余和内部构件冗余3种类型,明确提出了冗余性的设计要求[8],且在2018年针对缺少荷载路径冗余的钢桥发布了用于识别临界断裂构件(FCM)和体系冗余构件(SRM)的AASHTO指南[9]。
近年来,由于结构性能优势和市场政策的双重推动,中国钢板组合梁桥在中小跨径桥梁中的应用快速增加。随着桥梁工业化建造技术的进步,更适应现场快速装配需求的少主梁或少横联结构形式应用也越来越广泛。如淮河特大桥引桥采用双主梁钢板组合梁[10];长益高速采用Π形钢板组合梁桥,减少了Π形梁之间的横向联系[11]。值得注意的是,钢板组合梁桥的少主梁或少横联形式,可能减少体系的备用荷载传力路径,降低体系的非线性冗余;而随着服役年限的增长,钢板延性也会因锈蚀而明显退化[12],其应对非对称极端作用的内部缓冲性能可能愈发缺失。
目前,考虑材料劣化效应的钢板组合梁桥时变体系冗余性研究成为了国内外学者关注的热点。文献[13]将结构简化成串-并联系统,通过假定多根主梁失效来评估钢板组合梁桥在腐蚀和车辆荷载共同作用下的体系时变冗余性;文献[14]通过量化构件损伤尺寸和位置对体系承载性能的影响,提出了公路典型钢板组合梁桥结构时变体系冗余性的简化计算方法。然而,这些研究均假设体系承载机制不变,未考虑材料劣化对体系传力格局的改变,材料劣化引发的构件延性退化会降低体系的再平衡能力,改变内力塑性再分配机制,甚至阻断传力路径,减少体系承载机制的状态数。如何在钢板组合梁桥时变冗余性评估过程中考虑体系传力格局的经时变异性,目前尚鲜有相关研究。
在目前有关钢板组合梁桥的数值模拟和试验研究中,材料劣化对其结构状态的影响已分别在构件、体系层次取得了丰富成果,如文献[15]针对钢板组合梁的典型腐蚀损伤部位,采用数值模拟方法研究了腐蚀对构件抗弯和抗剪承载性能的影响;文献[16-17]基于中性盐雾试验和多尺度精细化数值模型,研究了腐蚀对钢板组合梁体系抗弯性能的影响;这些研究侧重材料劣化对结构承载强度、刚度的影响,而对因材料劣化引发的构件延性降低、体系传力机制和内力重分配机制的改变尚未予以对称性重视。关于这方面的初步探索,文献[18]开发了一种基于钢梁厚度退化模式的时变体系非线性冗余数值模拟方法,探索了材料劣化对主要构件失效后承载机制的影响规律;但其假设钢梁的腐蚀沿构件长度和截面厚度方向均匀变化,在考虑材料劣化位置非均匀性对体系承载机制的影响方面具有一定的局限性。可见,聚焦钢板组合梁桥材料劣化过程的体系再平衡和内力重分配性能,围绕材料劣化位置的非均匀性,建立高效稳定的时变体系非线性冗余数值模拟方法,亟待进一步开展。
综上,材料劣化会改变体系的传力格局,本文通过考虑构件和体系两个层面的3种失效模式,在应变能时变预期值的基础上推导了定量评估体系荷载弹性分配和塑性再分配能力的新指标,提出了考虑承载机制经时变异性的时变体系冗余性评估新方法。聚焦钢板组合梁桥材料劣化过程的体系再平衡和内力重分配性能,围绕材料劣化位置的非均匀性,利用MATLAB/OpenSEES编制了基于纤维宏单元的时变演化参数组管理程序,采用数值增量算法,开展了结构在非对称荷载下的弹塑性全过程分析,并通过与构件-体系层次的破坏性试验对比验证了数值模型的准确性,进而建立了高效稳定的时变体系非线性冗余数值模拟方法。此外,采用拆除构件法进行了构件的敏感性分析,识别了钢板组合梁桥的关键构件。
1 多梁式钢板组合梁桥的时变体系冗余性 1.1 弯曲失效模式如图 1所示,在外荷载作用下,钢板组合梁桥的主梁易损部位依次从弹性向弹塑性状态演变,进而屈服而产生塑性铰,变成瞬变机构,此时主梁将产生大变形,形成悬链线效应,主梁通过轴力和大变形形成的力矩来抵抗外荷载,直至主梁达到极限承载力而破坏[19]。

|
图 1 钢板组合梁桥的弯曲失效模式 Fig. 1 Bending failure modes of steel plate composite girder bridge |
值得注意的是,钢板组合梁的弯曲延性比混凝土梁好得多,在产生塑性铰后,钢梁仍然有很大的抗弯刚度,与同跨度的混凝土梁相比,钢混组合梁可以产生更大的跨中位移[20]。而多梁式钢板组合梁桥的特点是通过横向联系使得多片主梁共同受力,更大的跨中位移会使多梁式钢板组合桥横向传力效果更明显;正是由于这个特点,可将多梁式钢板组合梁桥横向联系失效与否分为单梁和多梁3种典型的弯曲失效模式。
1) 单梁失效模式(SGFM)。相邻主梁之间的传力路径被切断,这将导致相邻各主梁之间的协同承载机制不复存在。在这种情况下,体系中任一主梁达到极限状态,体系将以存粹意义上的简支梁形态发生破坏,这种结构的失效模式称为单梁失效模式。荷载-位移曲线与横坐标轴围成的面积,可表征应变能,因此SGFM应变能可描述为
| $ C_{\mathrm{fe}, \mathrm{c}}=\int\limits_0^{\delta_{\mathrm{cm}}} L_{\mathrm{f}, \mathrm{c}}(\delta) \mathrm{d} \delta $ | (1) |
式中:Lf, c(δ)为SGFM单梁荷载-位移曲线位移为δ时对应的荷载系数,δcm为单梁达到极限承载力时对应的位移。
2) 荷载弹性分布下的多梁失效模式(MGFM-ED)。当横向连接完好时,多个主梁协同作用承担荷载,现行规范下的车辆荷载会根据初始弹性阶段内的构件刚度在各个主梁之间进行分配,一旦体系中的最不利主梁达到极限状态,整个桥梁体系可被视作失效,这种结构失效模式可称为MGFM-ED。结合荷载横向分布系数[21],MGFM-ED的极限车辆荷载Lf, e可表示为
| $ L_{\mathrm{f}, \mathrm{e}}=\frac{L_{\mathrm{f}, \mathrm{c}}}{m} $ | (2) |
式中m为经结构体系弹性分析所确定的最不利构件的内力分布系数。则MGFM-ED的体系应变能可表示为
| $ C_{\mathrm{fe}, \mathrm{e}}=\int\limits_{0}^{\delta_{\mathrm{em}}} L_{\mathrm{f}, \mathrm{e}}(\delta) \mathrm{d} \delta $ | (3) |
式中:Lf, e(δ)为MGFM-ED荷载-位移曲线位移为δ时对应的荷载系数,δem为MGFM-ED体系达到极限承载力时对应的位移。
3) 考虑塑性重分布的多梁失效模式(MGFM-PR)。随着外部车辆荷载得增加,荷载在梁间的分布逐渐从基于刚度的弹性分布转变为考虑延性的塑性重分布,一旦体系超过极限状态,体系将会失效,这种失效模式定义为MGFM-PR。其体系应变能可表示为
| $ C_{\mathrm{fe}, \mathrm{u}}=\int\limits_{0}^{\delta_{\mathrm{um}}} L_{\mathrm{f}, \mathrm{u}}(\delta) \mathrm{d} \delta $ | (4) |
式中:Lf, u(δ)为MGFM-PR下体系荷载-位移曲线位移为δ时对应的荷载系数,δum为MGFM-PR体系达到极限承载力对应的位移。
1.2 主梁的延性退化就多梁式钢板组合梁桥而言,材料劣化除了会导致构件的抗力降低,更重要的是会导致构件延性的退化,使得协同承载机制和失效模式发生改变,进而影响体系冗余性。所以构件层面的延性至关重要,考虑到材料退化,本文将构件的时变延性系数ηc(t)表示为
| $ \eta_{\mathrm{c}}(t)=\varphi_{\mathrm{u}}(t) / \varphi_{\mathrm{y}}(t) $ | (5) |
式中φu(t)和φy(t)分别为截面材料非线性分析得到的MCR曲线破坏曲率与屈服曲率。
对于钢板组合梁桥,钢筋和钢材的腐蚀是结构性能退化的主要来源之一。随着腐蚀在使用寿命周期内不断发展,除了钢筋和钢材的剩余面积会不断减少,还会降低钢筋和钢材的延性,具体表现为应力-应变曲线屈服平台的缩短直至消失[22]。
需要强调的是,不同厚度钢板和不同直径钢筋在腐蚀后本构衰减程度具有差异性[12]。根据第3节算例的环境和尺寸,本文给出如下的钢板和钢筋时变退化本构模型。
1) 钢材的退化模型。本文采用石永久等[23]提出的本构模型来模拟,如图 2(a)所示,其钢材的应力-应变关系可表示为
| $ \sigma=\left\{\begin{array}{l} E_{\mathrm{s}} \varepsilon, \varepsilon \leqslant \varepsilon_{\mathrm{ys}} \\ f_{\mathrm{ys}}, \varepsilon_{\mathrm{ys}} \leqslant \varepsilon \leqslant k_{1 \mathrm{s}} \varepsilon_{\mathrm{ys}} \\ k_{2} f_{\mathrm{ys}}+\frac{E_{s}\left(1-k_{2}\right)}{\varepsilon_{\mathrm{ys}}\left(\frac{\varepsilon_{\mathrm{us}}}{\varepsilon_{\mathrm{y}}}-k_{1 \mathrm{s}}\right)^{2}}\left(\varepsilon-\varepsilon_{\mathrm{us}}\right)^{2}, k_{1 \mathrm{s}} \varepsilon_{\mathrm{ys}} \leqslant \varepsilon \leqslant \varepsilon_{\mathrm{us}} \\ f_{\mathrm{us}}, \varepsilon \geqslant \varepsilon_{\mathrm{us}} \end{array}\right. $ | (6) |
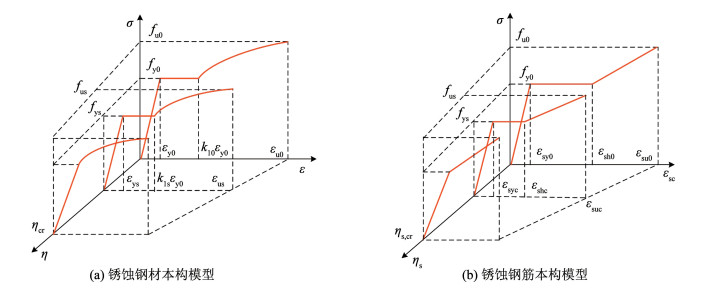
|
图 2 锈蚀钢材和锈蚀钢筋的本构模型 Fig. 2 Constitutive model of corroded steel and corroded steel bars |
式中:锈蚀钢材的弹性模量Es,极限应变εus,屈服强度fys和极限强度fus可分别表示[24]为
| $ f_{\mathrm{ys}} =(1-0.8943 \eta) f_{\mathrm{y} 0} $ | (7) |
| $ f_{\mathrm{us}} =(1-0.8797 \eta) f_{\mathrm{u} 0} $ | (8) |
| $ \varepsilon_{\mathrm{us}} =(1-0.01637 \eta) \varepsilon_{\mathrm{u} 0} $ | (9) |
| $ E_{\mathrm{s}} =(1-0.8752 \eta) E_{0} $ | (10) |
式中:k1s和k2分别为应力-应变曲线的形状控制参数,本文保持k2不变,k2取1.4;控制屈服平台的参数k1s随着锈蚀率η的退化规律可表示为
| $ k_{1 \mathrm{s}}=9.57-35.95 \eta $ | (11) |
2) 钢筋的退化模型。本文选用张伟平等[25]总结的普通钢筋锈蚀本构模型,如图 2(b)所示,当锈蚀率ηs小于临界锈蚀率ηs, cr时,锈蚀钢筋应力应变关系采用三线型模型;当锈蚀率ηs高于临界锈蚀率ηs, cr时采用双线型模型,可表示为
| $ \sigma_{\mathrm{sc}}=\left\{\begin{array}{l} E_{\mathrm{s} 0} \varepsilon_{\mathrm{sc}}, \varepsilon_{\mathrm{sc}} \leqslant f_{\mathrm{yc}} / E_{\mathrm{s} 0} \\ f_{\mathrm{yc}}, f_{\mathrm{yc}} / E_{\mathrm{s} 0}<\varepsilon_{\mathrm{sc}} \leqslant \varepsilon_{\mathrm{shc}} \\ f_{\mathrm{yc}}+\left(\frac{\varepsilon_{\mathrm{sc}}-\varepsilon_{\mathrm{shc}}}{\varepsilon_{\mathrm{suc}}-\varepsilon_{\mathrm{shc}}}\right) \cdot\left(f_{\mathrm{uc}}-f_{\mathrm{yc}}\right), \varepsilon_{\mathrm{sc}}>\varepsilon_{\mathrm{shc}} \end{array}\right. $ | (12) |
式中σsc和εsc分别为受腐蚀钢筋的拉应力和应变。
强化应变εshc的演变规律可表示为
| $ \varepsilon_{\mathrm{shc}}=\left\{\begin{array}{l}\frac{f_{\mathrm{yc}}}{E_{\mathrm{s} 0}}+\left(\varepsilon_{\mathrm{sh} 0}-\frac{f_{\mathrm{y} 0}}{E_{\mathrm{s} 0}}\right) \cdot\left(1-\frac{\eta_{\mathrm{s}}}{\eta_{\mathrm{s}, \mathrm{cr}}}\right), \eta_{\mathrm{s}} \leqslant \eta_{\mathrm{s}, \mathrm{cr}} \\ \varepsilon_{\mathrm{syc}}=\frac{f_{\mathrm{yc}}}{E_{\mathrm{s} 0}}, \eta_{\mathrm{s}}>\eta_{\mathrm{s}, \mathrm{cr}}\end{array}\right. $ | (13) |
式中:Es0、fy0、εsh0分别为未锈蚀钢筋的弹性模量、屈服强度和强化应变,根据文献[5],锈蚀钢筋的屈服强度fyc和极限强度fuc可分别表示为
| $ f_{\mathrm{yc}}=\frac{1-1.049 \eta_{\mathrm{s}}}{1-\eta_{\mathrm{s}}} f_{\mathrm{y} 0} \\ $ | (14) |
| $ f_{\mathrm{uc}}=\frac{1-1.119 \eta_{\mathrm{s}}}{1-\eta_{\mathrm{s}}} f_{\mathrm{u} 0} $ | (15) |
3) 混凝土的退化模型。尽管钢筋和钢材的腐蚀是钢板组合梁桥的主要病理表现,但还应考虑混凝土碳化后的力学性能。本文采用张建仁等[26]提出的的混凝土强度的时变退化模型,该模型基于长期暴露试验数据和旧桥的测量结果,其中一般大气环境下混凝土强度平均值和标准差可分别表示为
| $ m_{\mathrm{c}}(t)=\eta_{\mathrm{c}}(t) m_{\mathrm{c} 0} $ | (16) |
| $ \sigma_{\mathrm{c}}(t)=\zeta_{\mathrm{c}}(t) \sigma_{\mathrm{c} 0} $ | (17) |
式中mc0和σc0分别为混凝土28 d强度的平均值和标准差,ηc(t)和ζc(t)可分别表示为
| $ \eta_{\mathrm{c}}(t)=1.3781 \exp \left[-0.0187(\ln t-1.7282)^{2}\right] $ | (18) |
| $ \zeta_{\mathrm{c}}(t)=0.0347 t+0.9772 $ | (19) |
钢板组合梁体系冗余性定义为体系在主要构件失效后,具有备用荷载传递路径,可以继续承担荷载的能力[5]。随着使用寿命周期内构件延性的不断退化,体系冗余性也在随时间不断变化。为分析本文聚焦的多梁式钢板组合梁桥弯曲失效模式,定量评价体系荷载弹性分配和塑性再分配的能力,本文提出“主梁有效使用根数”这一指标,其含义为多梁式桥体系在达到极限状态时充分使用的主梁根数。结合式(1)、(3)、(4)可将3种弯曲失效模式下应变能描述为时间t的函数,MGFM-ED的“主梁有效使用根数”Ne(t)可以表示为
| $ N_{\mathrm{e}}(t)=\frac{C_{\mathrm{fe}, \mathrm{e}}(t)}{C_{\mathrm{fe}, \mathrm{c}}(t)} $ | (20) |
MGFM-PR的“主梁有效使用根数”Nu(t)可以表示为
| $ N_{\mathrm{u}}(t)=\frac{C_{\mathrm{fe}, \mathrm{u}}(t)}{C_{\mathrm{fe}, \mathrm{c}}(t)} $ | (21) |
结合应变能的物理含义,可推导出钢混组合钢板梁桥体系冗余性Ru(t)的定量表达式为
| $ R_{\mathrm{u}}(t)=\frac{C_{\mathrm{fe}, \mathrm{u}}(t)}{C_{\mathrm{fe}, \mathrm{e}}(t)}=\frac{C_{\mathrm{fe}, \mathrm{u}}(t) / C_{\mathrm{fe}, \mathrm{c}}(t)}{C_{\mathrm{fe}, \mathrm{e}}(t) / C_{\mathrm{fe}, \mathrm{c}}(t)}=\frac{N_{\mathrm{u}}(t)}{N_{\mathrm{e}}(t)}=\lambda(t) $ | (22) |
式中λ(t)为t时刻结构体系的塑性重分布系数。
由式(22)推导可见,多梁式钢板组合梁桥的体系冗余度Ru(t)与其塑性重分布系数λ(t)具有相同的物理内涵,都可用主梁有效使用根数比Nu(t)/Ne(t) 来确定。
值得注意的是,即使桥梁是不冗余的,但只要构件设计保守,体系安全水平仍有可能很高,反之亦然。因此,构件和体系的安全性与体系冗余性共同构成了内部防灾缓冲性能的科学内涵。为量化体系和构件的安全性,结合1.1节的弯曲失效模式,本文引入全概率公式来描述体系的失效概率,即
| $ \begin{aligned} P_{\mathrm{S}}^{\mathrm{f}}(t)= & P_{\mathrm{r}}\left\{R_{\mathrm{S}}(t)<\left.S_{\mathrm{S}}(t)\right|_{R_{\mathrm{T}}(t)<S_{\mathrm{T}}(t)}\right\} \cdot \\ & P_{\mathrm{r}}\left(R_{\mathrm{T}}(t)<S_{\mathrm{T}}(t)\right)+P_{\mathrm{r}}\left\{R_{\mathrm{S}}(t)<\right. \\ & \left.\left.S_{\mathrm{S}}(t)\right|_{R_{\mathrm{T}}(t) \geqslant S_{\mathrm{T}}(t)}\right\} \cdot P_{\mathrm{r}}\left(R_{\mathrm{T}}(t) \geqslant S_{\mathrm{T}}(t)\right)= \\ & P_{\mathrm{c}}^{\mathrm{f}}(t) \cdot P_{\mathrm{T}}^{\mathrm{f}}(t)+P_{\mathrm{s}, \mathrm{u}}^{\mathrm{f}}(t) \cdot\left(1-P_{\mathrm{T}}^{\mathrm{f}}(t)\right) \end{aligned} $ | (23) |
式中:PTf(t)为横向连接的失效概率;Pcf(t)为SGFM的失效概率;Ps, uf(t)为MGFM-PR的失效概率;RT(t)和ST(t)分别为横向连接的抗力和效应;RS(t)和SS(t)分别为桥梁体系的抗力和效应;Pr{E}为事件E发生的概率。在计算过程中涉及的极限状态方程汇总为
| $ \left\{\begin{array}{l} Z_{\mathrm{T}}(t)=R_{\mathrm{T}}(t)-S_{\mathrm{T}}^{\mathrm{G}}(t)-S_{\mathrm{T}}^{\mathrm{V}}(t) \\ Z_{\mathrm{c}}(t)=R_{\mathrm{c}}(t)-S_{\mathrm{c}}^{\mathrm{G}}(t)-S_{\mathrm{c}}^{\mathrm{V}}(t) \\ Z_{\mathrm{s}, \mathrm{e}}(t)=R_{\mathrm{s}, \mathrm{e}}(t)-S_{\mathrm{s}}^{\mathrm{G}}(t)-S_{\mathrm{s}, \mathrm{e}}^{\mathrm{V}}(t) \\ Z_{\mathrm{s}, \mathrm{u}}(t)=R_{\mathrm{s}, \mathrm{u}}(t)-S_{\mathrm{s}}^{\mathrm{G}}(t)-S_{\mathrm{s}, \mathrm{u}}^{\mathrm{V}}(t) \end{array}\right. $ | (24) |
式中:ZT(t)为横向连系的极限状态方程, RT(t)、STG(t)和STV(t)分别为横向联系的抗力、恒载效应和汽车活载效应; Zc(t)为SGFM的极限状态方程, Rc(t)、ScG(t)和ScV(t)分别为单梁的抗力、恒载效应和汽车活载效应; Zs, e(t)为MGFM-ED的极限状态方程, Rs, e(t)、Ss, eG(t)和Ss, eV(t)分别为MGFM-ED的抗力、恒载效应和汽车活载效应; Zs, u(t)为MGFM-PR的极限状态方程, Rs, u(t)、Ss, uG(t)和Ss, uV(t)分别为MGFM-PR的抗力、恒载效应和汽车活载效应。
结合主梁的有效使用根数,体系抗力Rs, e(t)和Rs, u(t)可表示为
| $ R_{\mathrm{s}, \mathrm{e}}(t)=N_{\mathrm{e}}(t) \cdot R_{\mathrm{c} 0} $ | (25) |
| $ R_{\mathrm{s}, \mathrm{u}}(t)=N_{\mathrm{u}}(t) \cdot R_{\mathrm{c} 0}=R_{\mathrm{u}}(t) \cdot N_{\mathrm{e}}(t) \cdot R_{\mathrm{c} 0} $ | (26) |
式中:Rc0为设计状态下的单梁弯曲抗力;Ss, eV和Ss, uV为最不利车辆荷载作用下多梁失效模式下每根主梁的汽车活载效应之和∑MiV。
同时根据Bayes定律,SGFM与MGFM-PR对体系失效的概率贡献分别表示为
| $ P_{\mathrm{I}, \mathrm{c}}=\frac{P_{\mathrm{c}}^{\mathrm{f}} \cdot P_{\mathrm{T}}^{\mathrm{f}}}{P_{\mathrm{S}}^{\mathrm{f}}} $ | (27) |
| $ P_{\mathrm{Is}, \mathrm{u}}=\frac{P_{\mathrm{s}, \mathrm{u}}^{\mathrm{f}} \cdot\left(1-P_{\mathrm{T}}^{\mathrm{f}}\right)}{P_{\mathrm{S}}^{\mathrm{f}}} $ | (28) |
综上,时变体系冗余性评估对于防灾减灾工作而言至关重要,但如何科学高效地评估在役钢板组合梁桥的时变体系冗余性将在下节进一步研究。
2 基于纤维宏单元的时变体系冗余性评估 2.1 数值模拟方法如图 3所示,本文聚焦钢板组合梁桥材料劣化过程的体系再平衡和内力重分配性能,围绕材料劣化的非均匀性,利用MATLAB编制了考虑材料退化的参数组管理程序,用于自动输入与时变更新核心物理量(纤维网格划分、连接单元的刚度参数等)和纤维本构的时空四维(x, y, z, t)描述矩阵,并调用基于纤维宏单元的OpenSEES嵌入平台,采用增量数值算法,开展构件及体系在非对称荷载下的非线性全过程分析,实现使用寿命周期非均匀材料劣化的宏观模拟。纤维宏单元模型与传统杆系模型相比,可以将截面沿长度方向划分为若干纤维,提高分析精度;同时与由实体单元或板壳单元等组成的微观模型相比,可以提高分析效率[27]。本文纤维宏单元模型采用非线性纤维梁单元,每个单元设置4个积分点,每个积分点表征该处截面,将截面离散为若干混凝土纤维和钢纤维,并对不同的纤维赋予不同的单轴本构。采用6个自由度空间梁单元组成的梁格模型,纵向梁格构件和横向梁格构件之间采用刚性连接。为了使混凝土板和钢梁在截面中协调变形,通过赋予连接单元的非线性属性来模拟两种构件之间的滑移行为。
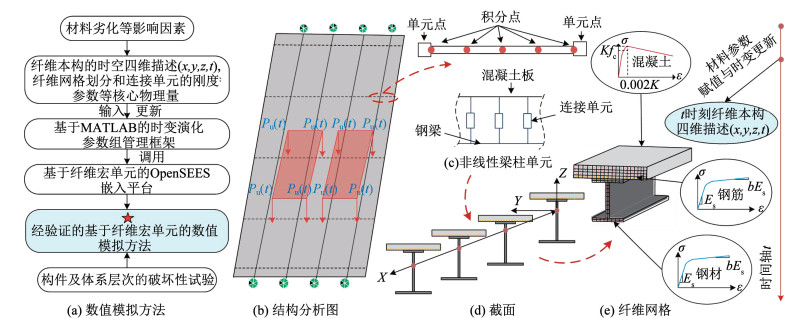
|
图 3 基于纤维宏单元的数值模拟方法 Fig. 3 Numerical simulation method based on fiber macro-elements |
结合上述模拟方法,通过与构件-体系层次的破坏试验进行比对,并基于校验结果进一步优化相关参数,进而建立基于纤维宏单元的时变体系非线性冗余数值模拟方法。因此,构件-体系层次破坏性试验对数值模型的验证对于钢板组合梁桥时变体系冗余性的评估至关重要。
2.2 试验数据校验为验证基于OpenSEES纤维宏单元模拟方法应用于钢板组合梁构件-体系层次数值模型的精度和效率,本文分别选取了一根钢板组合简支梁和一座三主梁钢板组合梁桥进行了分析。其中构件层次参考Chen等[28]开展的不同剪力钉锈蚀率下钢板组合梁的弯曲试验研究,选取剪力钉未腐蚀条件下的弯曲试验梁验证构件层次数值模型精度和效率,该弯曲试验梁全长3 m,计算跨径2.8 m。试验梁在位移控制下进行了单调加载,获得了在不同剪力钉锈蚀率下试验梁的极限承载力,具体尺寸及加载情况如图 4(a)、4(c)所示。体系层次参考文献[29]中Kathol开展的钢板组合梁桥全尺寸破坏性试验研究,该桥跨径为21.34 m,单跨横向设置3片钢板组合梁,桥宽7.92 m,采用12根后张拉杆对桥梁体系施加垂直集中载荷,以模拟两辆并排的的HS-20卡车,单调加载直至桥梁破坏,该桥细部尺寸及加载情况如图 4(b)、4(d)、4(e)所示。用于构件及体系层次试验中钢材、钢筋和混凝土的材料力学性能参数见表 1、2。

|
图 4 试验模型的尺寸及加载情况(mm) Fig. 4 Dimensions and loading of test model(mm) |
| 表 1 混凝土的力学性能参数 Tab. 1 Mechanical property parameters of concrete |
| 表 2 钢筋和钢材的力学性能参数 Tab. 2 Mechanical property parameters of reinforcement and steel |
用2.1节提出的基于OpenSEES纤维宏单元的模拟方法对构件及体系层次的破坏全过程进行了数值模拟,其中主梁和横向连接均采用考虑弹塑性行为的dispBeamColumn纤维单元模拟,剪力连接件采用elasticBeamColumn模拟,利用连接单元的非线性属性来模拟两种构件之间的滑移行为。混凝土单轴本构采用Kent-Park-Scott模型[30],不考虑混凝土的抗拉强度。钢筋和钢材采用1.2节的时变退化本构模型,将数值模型分析结果与试验数据进行了比对,其中构件层次的试验和数值模型分析结果如图 5(a)所示,体系层次中梁和边梁的试验和数值模型分析结果如图 5(b)、5(c)所示。结果表明,构件层次和体系层次中梁试验结果与数值模拟结果吻合度较高,体系层次边梁在小于50 mm试验结果与数值模拟结果存在一定差异,这是由于体系层次模型采用中载加载,边梁对加载量的敏感性低于中梁,而随着加载量的增加,试验的极限承载力与数值模拟结果趋于一致,可认为本文数值模拟方法能够准确地模拟钢板组合梁的破坏全过程。
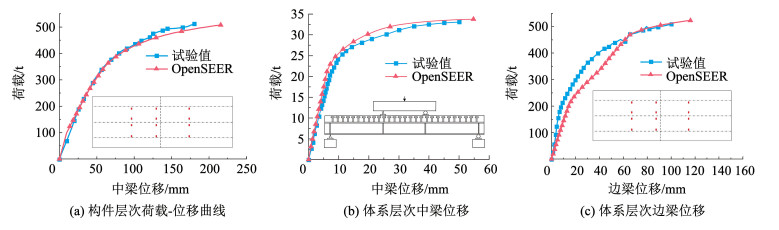
|
图 5 构件及体系的荷载位移曲线 Fig. 5 Applied load versus deflection of member and system |
此外,构件及体系计算耗时分别为2 s和6 s,为与2.1节数值模拟方法进行效率比较,采用ABAQUS建立了体系层次钢板组合梁桥的精细化模型,得到分析时间为1 776 s(处理器为Intel(R) Core(TM) i5-8265U),可见,本文的数值模拟方法耗时远低于精细化分析方法,提高了分析效率。因此,本文提出的数值模拟方法在钢板组合梁构件-体系层次的分析中获得了满意的精度和效率,可为体系时变冗余性的研究提供可靠保证。
2.3 评估框架基于上述理论和方法,构建在役钢板组合梁桥时变体系冗余性的评估框架,如图 6所示,具体步骤如下:

|
图 6 体系时变冗余性的评估框架 Fig. 6 Framework of time-varying system redundancy |
1) 采用2.1节基于纤维宏单元的数值模拟方法以10 a为时间间隔进行使用寿命周期内主梁截面材料非线性分析、线性分析和体系的非线性分析,其中服役时间与锈蚀率的转换参考文献[24]中式(4)。本步骤采用欧拉-贝努利梁[5]进行线性分析,采用非线性纤维梁柱单元并选用梁格法进行体系非线性分析,得到主梁截面的弯矩-曲率曲线,SGFM的荷载-位移曲线,MGFM-PR的荷载-位移曲线。
2) 确定构件的抗力Rc(t),其在数值上等于弯矩-曲率曲线的极限弯矩Mu(t);同时得到屈服曲率φy(t) 和极限曲率φu(t),得到构件的延性系数ηc(t)。
3) 确定SGFM下的应变能Cfe, c(t),SGFM下的恒载效应ScG(t)和车辆荷载效应ScV(t);MGFM-ED的应变能Cfe, e(t),恒载效应SsG(t)和车辆荷载效应Ss, eV(t);MGFM-PR的应变能Cfe, u(t),以及恒载效应SsG(t)和车辆荷载效应Ss, uV(t)。
4) 计算出MGFM-ED和MGFM-PR体系的“主梁的有效使用根数”Ne(t)、Nu(t)和体系的冗余度Ru(t)。
5) 基于主梁的抗力Rc(t),MGFM-ED和MGFM-PR的“主梁有效使用根数”Ne(t)、Nu(t),根据式(25)、(26)可计算得到桥梁体系抗力Rs, e(t)和Rs, u(t)。
6) 采用FORM求解极限状态方程进行可靠度计算得到相应的可靠度指标βT(t)、βc(t)、βs, e(t)、βs, u(t)和βS(t);进而得到SGFM与MGFM-PR对体系失效的概率贡献PI, c和PIs, u;重复以上步骤2~6直至服役年限达到100 a结束。
3 算例分析 3.1 算例概况选取国内某座钢混组合钢板梁桥,其桥跨布置为5×30 m,其中主梁根数为4根,桥宽为12.75 m,具体尺寸及加载情况如图 7所示。混凝土等级为C50,普通钢筋采用HRB400,工字钢梁采用Q345钢。在使用年限内正常养护条件下,选取桥梁的第一跨,用第2节的评估方法对钢板组合梁桥时变体系冗余性进行研究。使用基于纤维宏单元的数值模拟方法建立上部结构三维模型。其中主梁和横向连接均采用弹塑性纤维单元dispBeamColumn模拟,剪力连接件采用弹性梁柱单元elasticBeamColumn模拟,采用连接单元的非线性属性来模拟两种构件之间的滑移行为。混凝土本构采用Kent-Park-Scott模型,不考虑混凝土的抗拉强度,钢筋和钢材采用1.2节的时变退化本构模型。

|
图 7 算例模型的尺寸及加载情况(mm) Fig. 7 Dimensions and loading of example model(mm) |
如1.2节所述,钢板组合梁的时变材料特性如图 8(a)所示,可以看出,随着锈蚀的发展,工字钢梁的应力-应变曲线屈服平台不断减少,直至锈蚀率30%时消失,参数比率Es,fys,fus和εus的参数比率均近似按线性关系退化,其中,极限应变εus的退化较Es,fys,fus退化明显。普通钢筋屈服强度fyc,极限强度fuc以及强化应变εshc的时变预期值作为锈蚀率ηs的函数,变化规律如图 8(b)所示,随着钢筋锈蚀的发展,在ηs达到ηs, cr之前,fyc,fuc的相对值均近似按线性关系退化;在整个锈蚀区间内,两者相对值的变化程度都很小。值得注意的是在整个锈蚀区间中,fuc的相对值比fyc的相对值退化更为明显,这将导致屈强比增大,发生脆性破坏的概率会相应增大。对于εshc,在ηs达到ηs, cr之前,εshc的相对值急速下降,而在ηs达到ηs, cr之后,屈服应变εsyc与强化应变εshc合为一体,屈服平台消失。
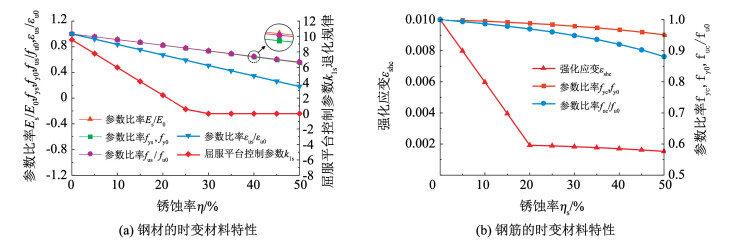
|
图 8 钢材及钢筋的时变材料特性 Fig. 8 Time-varying material properties of steel and reinforcement |
考虑钢板组合梁的时变材料特性,以10 a为时间间隔对主梁截面进行材料非线性分析得到MCR曲线,如图 9(a)所示;MCR曲线中的屈服曲率φy(t),极限曲率φu(t)和构件延性系数μc(t)的时变预期值的变化规律如图 9(b)所示。

|
图 9 主梁的时变延性 Fig. 9 Time-varying ductility of main beam |
随着钢材和钢筋锈蚀的发展,其力学性能参数的退化将越来越严重,屈服弯矩My(t)和极限弯矩Mu(t)也开始降低,而相应的屈服曲率φu(t)则几乎保持不变,φy(t)急剧下降,φy(t)和φu(t)变化情况的不一致使得构件的延性急剧降低。截面延性系数μc(t)从21.66降低到4.01,导致钢板组合梁在整个服役年限内由高延性向低延性过渡。
3.3 体系的时变冗余性在图 7(b)的偏载加载方式下,采用2.1节的模拟方法可以得到使用寿命周期内单梁的荷载-位移曲线如图 10(a)所示;同时,以t=0时刻为例,体系G1~G4梁的荷载-位移曲线如图 10(b)所示。

|
图 10 服役年限内主梁及体系的荷载-位移曲线 Fig. 10 Applied load versus deflection of member and system in service life |
在整个服役年限将不同失效模式下的应变能时变预期值绘总于图 11(a),可以看到,体系和构件的应变能随时间不断降低。例如t=100 a时刻SGFM和MGFM-PR下的应变能预期值为t=0时刻的69.3%和60.8%。由于MGFM-ED失效后体系还能继续承载,所以MGFM-ED应变能的退化程度比SGFM和MGFM-PR要轻。采用2.3节的评估框架获得使用寿命周期MGFM-ED和MGFM-PR的“主梁有效使用根数”Ne(t),Nu(t)和Ru(t)的时变预期值如图 11(b)所示。以t=0为例,由于塑性重分布的影响,最脆弱构件失效以后,由于体系塑性重分配,剩余桥梁体系仍能具有50.68%的应变能。t=100 a时,Ne(t)、Nu(t)和Ru(t)为t=0时的89.1%、69.3%和77.7%。当服役年限超过80 a后,Ru(t)小于1.3[5],此时该桥冗余性能不充分。
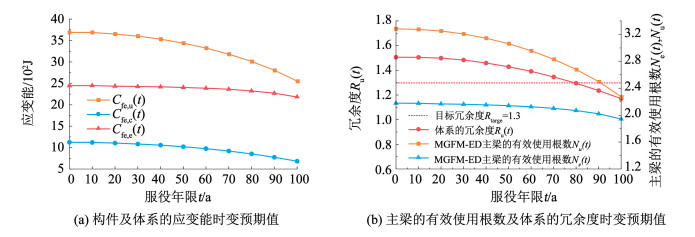
|
图 11 体系的时变冗余性 Fig. 11 Time-varying redundancy of system |
构件和体系的安全性与体系冗余性共同构成了内部防灾缓冲性能的科学内涵。采用2.3节的评估框架,可以得出3种失效模式的可靠度指标,如图 12所示。其中,由于横向联系弹性分布的影响,MGFM-ED的可靠度指标βs, e大于SGFM的可靠度指标βc;由于塑性重分布的影响,MGFM-PR的可靠度指标βs, u大于MGFM-ED的可靠度指标βs, e。同时,当横向连接不退化,体系的可靠性βs与βs, u非常接近,然而,随着横向连接的不断退化,体系的可靠度βs逐渐向βc靠近,也就意味着体系失效逐渐转变为单梁失效。值得注意的是,单梁的可靠度指标在50 a左右退化到阈值(即4.2)。因此,体系的可靠性是构件及体系安全性的保证,时变承载机制会影响桥梁体系的可靠性。

|
图 12 体系的时变可靠性 Fig. 12 Time-varying reliability of system |
为进一步探索承载机制对桥梁体系可靠性的影响,本文以t=50 a为例,研究了考虑横向连接退化和不考虑横向连接退化对桥梁体系可靠性的影响,如图 13(a)所示,可以看出,考虑横向连接退化,桥梁体系的承载机制逐渐从MGFM转变为SGFM。SGFM和MGFM对体系失效的贡献率如图 13(b)所示,横向连接的可靠度指标越大,MGFM-PR的贡献概率越大,反之则SGFM的贡献概率大。

|
图 13 横向连接对体系承载机制的影响 Fig. 13 Influence of transverse connection on bearing mechanism of system |
将由横向连接构件和主梁组成的钢板组合梁桥某构件失效后与初始状态体系最不利车辆荷载的比值定义为构件的敏感性指标[31],即
| $ S_{I}=\frac{L_{\mathrm{f}, \mathrm{u}}(t)-L_{\mathrm{f, d}}(t)}{L_{\mathrm{f}, \mathrm{u}}(t)} $ | (29) |
将本桥的不同构件移除分为8个工况,如图 14所示,采用OpensSEES中remove element生死单元模拟方法对损伤构件进行移除,进而对钢混组合钢板梁桥初始状态和构件失效后体系非线性全过程进行模拟。以t=0为例,由式(29)计算可得到构件的敏感性指标,如图 15所示,可以看出,在车辆偏载作用下,G1~G4主梁是整个体系的敏感构件,其敏感性指标从G1主梁0.38到G4主梁0.153逐渐降低。此外,较为敏感的构件依次为中部横向联系和端部横向联系,其敏感性指标为分别为0.11和0.062,其他横梁的敏感性指标相对较低。
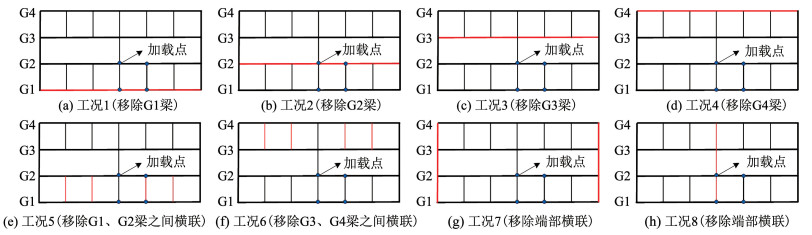
|
图 14 构件的敏感性分析工况 Fig. 14 Component sensitivity analysis conditions |
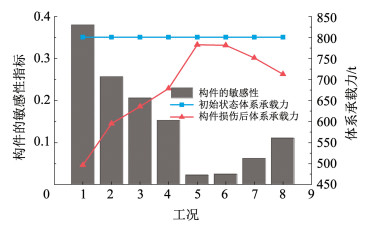
|
图 15 构件的敏感性 Fig. 15 Sensitivity of components |
材料劣化会改变体系的再平衡和内力重分配机制。本文提出了考虑承载机制经时变异性的时变体系冗余性评估新方法;聚焦材料劣化过程的体系再平衡和内力重分配性能,围绕材料劣化位置的非均匀性,建立了高效稳定的时变体系非线性冗余数值模型,并进行了构件的敏感性分析,得出以下结论:
1) 通过考虑构件和体系两个层面的3种失效模式,在应变能时变预期值的基础上推导了定量评估体系荷载弹性分配和塑性再分配能力的新指标,提出了考虑承载机制经时变异性的时变体系冗余性评估新方法。
2) 利用MATLAB/OpenSEES编制了基于单元纤维的时变演化参数组管理程序,采用数值增量算法,开展了结构在非对称荷载下的弹塑性全过程分析,并通过与构件-体系层次的破坏性试验对比验证了数值模型的准确性,进而建立了高效稳定的时变体系非线性冗余数值模拟方法。并通过与构件-体系层次的破坏性试验对比验证了数值模型的准确性,进而在宏观尺度实现对钢板组合梁桥时变体系冗余性的精准高效模拟。
3) 材料劣化会改变体系的协同承载机制,导致构件延性、体系冗余性和体系可靠性发生不同程度的退化, 更适应现场快速装配需求时少主梁或少横联形式容易在使用寿命周期内出现构件安全性和体系冗余性不足的情况。
4) 通过构件的敏感性分析发现,主梁、中部横联和端部横联对体系承载性能影响较大,为钢板组合梁桥的关键构件;其他横联敏感性极低,对体系承载性能影响可忽略,为非关键构件。
| [1] |
刘洋, 吕大刚, 于晓辉. 近场地震作用下型钢-混凝土组合结构桥易损性分析[J]. 土木工程学报, 2016, 49(增刊1): 6. LIU Yang, LÜ Dagang, YU Xiaohui. Seismic fragility analysis of steel-concrete composite bridges excited by near-fault ground motions[J]. China Civil Engineering Journal, 2016, 49(Sup.1): 6. DOI:10.15951/j.tmgcxb.2016.s1.010 |
| [2] |
蒋翔, 童根树, 张磊. 耐火钢-混凝土简支组合梁抗火性能[J]. 哈尔滨工业大学学报, 2017, 49(12): 68. JIANG Xiang, TONG Genshu, ZHANG Lei. Fire-resistance performance of simply supported fire-resistant steel-concrete composite beams[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 68. DOI:10.11918/j.issn.0367-6234.201610101 |
| [3] |
HAO S. I-35W bridge collapse[J]. Journal of Bridge Engineering, 2010, 15(5): 608. DOI:10.1061/(ASCE)BE.1943-5592.0000090 |
| [4] |
MORGESE M, ANSARI F, DOMANESCHI M, et al. Post-collapse analysis of Morandi's Polcevera viaduct in Genoa Italy[J]. Journal of Civil Structural Health Monitoring, 2020, 10(1): 69. DOI:10.1007/s13349-019-00370-7 |
| [5] |
WANG Xiaoming, MAO Xiangyuan, FRANGOPOL D M, et al. Full-scale experimental and numerical investigation on the ductility, plastic redistribution, and redundancy of deteriorated concrete bridges[J]. Engineering Structures, 2021, 234: 111930. DOI:10.1016/j.engstruct.2021.111930 |
| [6] |
DONG You, AKIYAMA M, FRANGOPOL D M, et al. Risk-, resilience-, and sustainability-informed assessment and management of civil infrastructure in a life-cycle context[J]. Structure and Infrastructure Engineering, 2020, 17(4): 1. DOI:10.1080/15732479.2020.1845754 |
| [7] |
American Association of State Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. Washington DC: AASHTO, 2010
|
| [8] |
HARTMANN J L. Steel bridge design handbook: redundancy[R]. Washington DC: Department of Transportation Federal Highway Administration, 2015
|
| [9] |
American Association of State Highway and Transportation Officials. AASHTO guide specifications for analysis and identification of fracture critical members and system redundant members[S]. Washington DC: AASHTO, 2018
|
| [10] |
石雪飞, 马海英, 刘琛. 双工字钢组合梁桥钢梁设计参数敏感性分析与优化[J]. 同济大学学报(自然科学版), 2018, 46(4): 444. SHI Xuefei, MA Haiying, LIU Chen. Parametric study and optimization on behavior of twin-Ⅰ girder composite bridges[J]. Journal of Tongji University (Natural Science), 2018, 46(4): 444. DOI:10.11908/j.issn.0253-374x.2018.04.004 |
| [11] |
贺耀北, 方博夫, 刘榕, 等. 中小跨整体预制Π形钢板组合梁力学与经济性研究[J]. 公路交通科技, 2019, 36(12): 62. HE Yaobei, FANG Bofu, LIU Rong, et al. Study on mechanics and economy of small and medium-span overall prefabricated Π-shaped steel plate composite beams[J]. Journal of Highway and Transportation Research and Development, 2019, 36(12): 62. DOI:10.3969/j.issn.1002-0268.2019.12.008 |
| [12] |
徐善华, 李柔, 苏超, 等. 锈损冷弯薄壁型钢材料力学性能试验[J]. 哈尔滨工业大学学报, 2018, 50(12): 74. XU Shanhua, LI Rou, SU Chao, et al. Mechanical property tests on cold-formed thin-walled steel materials with rust loss[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 74. DOI:10.11918/j.issn.0367-6234.201805156 |
| [13] |
ZHU Benjin, FRANGOPOL D M. Effects of post-failure material behaviour on redundancy factor for design of structural components in nondeterministic systems[J]. Structure and Infrastructure Engineering, 2015, 11(4): 466. DOI:10.1080/15732479.2014.951864 |
| [14] |
FIORILLO G, GHOSN M. Structural redundancy, robustness, and disproportionate collapse analysis of highway bridge superstructures[J]. Journal of Structural Engineering, 2022, 148(7): 04022075. DOI:10.1061/(ASCE)ST.1943-541X.0003369 |
| [15] |
GHEITASI A, HARRIS D K. Redundancy and operational safety of composite stringer bridges with deteriorated girders[J]. Journal of Performance of Constructed Facilities, 2016, 30(2): 04015022. DOI:10.1061/(ASCE)CF.1943-5509.0000764 |
| [16] |
朱劲松, 郭晓宇, 亢景付, 等. 耐候桥梁钢腐蚀力学行为研究及其应用进展[J]. 中国公路学报, 2019, 32(5): 1. ZHU Jinsong, GUO Xiaoyu, KANG Jingfu, et al. Research on corrosion behavior, mechanical property, and application of weathering steel in bridges[J]. China Journal of Highway and Transport, 2019, 32(5): 1. DOI:10.19721/j.cnki.1001-7372.2019.05.001 |
| [17] |
ZHU Jinsong, GUO Xiaoyu, KANG Jingfu, et al. Numerical and theoretical research on flexural behavior of steel-UHPC composite beam with waffle-slab system[J]. Journal of Constructional Steel Research, 2020, 171: 106141. DOI:10.1016/j.jcsr.2020.106141 |
| [18] |
SAYDAM D, FRANGOPOL D M. Time-dependent performance indicators of damaged bridge superstructures[J]. Engineering Structures, 2011, 33(9): 2458. DOI:10.1016/j.engstruct.2011.04.019 |
| [19] |
张建春, 张大山, 董毓利, 等. 火灾下钢-混凝土组合梁内力变化的试验研究[J]. 工程力学, 2019, 36(6): 183. ZHANG Jianchun, ZHANG Dashan, DONG Yuli, et al. Experimental study on internal force variation of steel-concrete composite beam under fire[J]. Engineering Mechanics, 2019, 36(6): 183. DOI:10.6052/j.issn.1000-4750.2018.05.0281 |
| [20] |
聂建国, 陶慕轩. 体外预应力钢-混凝土组合梁受力性能的研究现状与展望[J]. 工程力学, 2011(增刊2): 129. NIE Jianguo, TAO Muxuan. Research status and perspective on externally prestressed steel-concrete composite beams[J]. Engineering Mechanics, 2011(Sup.2): 129. |
| [21] |
贺拴海, 陈杰, 朱钊, 等. 无湿接缝高强混凝土工字组合梁桥荷载横向分配试验[J]. 中国公路学报, 2021, 34(11): 83. HE Shuanhai, CHEN Jie, ZHU Zhao, et al. Experiment on load transversal distribution of high strength concrete Ⅰ-beams without wet joints[J]. China Journal of Highway and Transport, 2021, 34(11): 83. DOI:10.3969/j.issn.1001-7372.2021.11.007 |
| [22] |
王友德, 李超, 史涛, 等. 循环荷载作用下锈蚀钢材滞回性能与本构模型[J]. 建筑结构学报, 2021, 42(12): 162. WANG Youde, LI Chao, SHI Tao, et al. Hysteretic behavior and constitutive model of corroded steel under cyclic loading[J]. Journal of Building Structures, 2021, 42(12): 162. DOI:10.14006/j.jzjgxb.2020.0073 |
| [23] |
石永久, 王萌, 王元清. 结构钢材循环荷载下的本构模型研究[J]. 工程力学, 2012, 29(9): 92. SHI Yongjiu, WANG Meng, WANG Yuanqing. Study on constitutive model of structural steel under cyclic loading[J]. Engineering Mechanics, 2012, 29(9): 92. DOI:10.6052/j.issn.1000-4750.2010.09.0711 |
| [24] |
KONG Zhengyi, JIN Ya, HOSSEN G M S, et al. Experimental and theoretical study on mechanical properties of mild steel after corrosion[J]. Ocean Engineering, 2022, 246: 110652. DOI:10.1016/j.oceaneng.2022.110652 |
| [25] |
张伟平, 李崇凯, 顾祥林, 等. 锈蚀钢筋的随机本构关系[J]. 建筑材料学报, 2014, 17(5): 920. ZHANG Weiping, LI Chongkai, GU Xianglin, et al. Stochastic model of constitutive relationship for corroded steel bars[J]. Journal of Building Materials, 2014, 17(5): 920. DOI:10.3969/j.issn.1007-9629.2014.05.028 |
| [26] |
张建仁, 刘扬. 混凝土桥梁构件服役期的抗力概率模型[J]. 长沙理工大学学报(自然科学版), 2004, 1(1): 27. ZHANG Jianren, LIU Yang. Statistical models for the lifetime resistance of concrete bridges[J]. Journal of Changsha University of Science and Technology (Natural Science), 2004, 1(1): 27. DOI:10.3969/j.issn.1672-9331.2004.01.005 |
| [27] |
韩小雷, 陈学伟, 林生逸. 基于宏观单元的结构非线性分析方法、算例及工程应用[J]. 工程力学, 2010, 27(增刊1): 59. HAN Xiaolei, CHEN Xuewei, LIN Shengyi. Nolinear structure analysis methods, examples and engineering applications based on macroscopic elements[J]. Engineering Structures, 2010, 27(Sup.1): 59. |
| [28] |
CHEN Ju, ZHANG Haipeng, YU Qianqian. Monotonic and fatigue behavior of steel-concrete composite beams subjected to corrosion[J]. Structures, 2021, 34: 1973. DOI:10.1016/j.istruc.2021.08.110 |
| [29] |
GHEITASI A, HARRIS D K. Failure characteristics and ultimate load-carrying capacity of redundant composite steel girder bridges: case study[J]. Journal of Bridge Engineering, 2015, 19(3): 1. DOI:10.1061/(ASCE)BE.1943-5592.0000667 |
| [30] |
孙宝印, 古泉, 张沛洲, 等. 钢筋混凝土框架结构弹塑性数值子结构分析方法[J]. 工程力学, 2016, 33(5): 44. SUN Baoyin, GU Quan, ZHANG Peizhou, et al. Elastoplastic numerical substructures method of reinforced concrete frame structures[J]. Engineering Structures, 2016, 33(5): 44. DOI:10.6052/j.issn.1000-4750.2015.07.ST08 |
| [31] |
朱南海, 李杰明. 基于构件冗余度均衡化的单层网壳结构优化研究[J]. 工程力学, 2021, 38(12): 73. ZHU Nanhai, LI Jieming. Study on optimization design of single-layer reticulated shell based on the homogenization of component redundancy[J]. Engineering Structures, 2021, 38(12): 73. DOI:10.6052/j.issn.1000-4750.2020.10.0758 |
 2023, Vol. 55
2023, Vol. 55


