中国地震频发,地震触发的边坡滑坡造成了大量的人员伤亡和经济损失[1]。土工格室挡墙结构因其结构巧、施工易、造价低等优势,在公路、铁路、机场、电力和冶金矿山等工程领域中得到了广泛的应用[2]。通过土工格室挡墙对边坡进行支护其抗震性能得到显著提高[3-4],然而,目前关于土工格室挡墙支护边坡的动力问题研究较少,地震作用下土工格室挡墙支护边坡的稳定性研究远落后于工程实践,因此对其进行研究十分必要且迫切。
目前,前人对静力条件下土工格室挡墙支护边坡的稳定性研究已经取得丰硕的成果[5-7]。文献[8]采用梁模型来模拟土工格室的柔性板基础,对加固边坡的土工格室层不同位置,不同层数以及加固层之间的垂直间距、长度、厚度、土工格室的杨氏模量进行了研究;文献[9]通过室内模型试验研究了土工格室参数对挡墙支护边坡稳定性的影响;文献[10]采用有限元软件对不同高宽比和不同土体强度下的土工格室挡墙的破坏模式进行了研究,给出了不同工况下土工格室挡墙破坏模式的数学表达式;文献[11]基于极限平衡法,提出了一种分析土工格室加筋边坡稳定性的方法;文献[12]采用极限平衡分析方法,提出了路堤临界高度的计算模型,并讨论了格室参数对路堤临界高度的影响规律。
迄今为止,人们对于地震荷载作用下土工格室挡墙支护边坡的稳定性研究却鲜有涉及。鉴于此,本文利用FLAC3D数值软件建立土工格室挡墙支护边坡数值模型[13-14], 系统分析了不同位置和不同数量的拉筋带对边坡动力响应的影响,以期为土工格室挡墙结构的抗震设计提供可靠的依据。
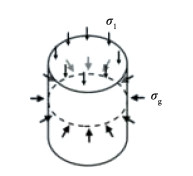
1 格室约束围压理论解土工格室内部充填料在外荷载σ1作用下将产生轴向压缩和侧向膨胀变形,引起格室产生拉伸应变和拉应力,而格室的拉应力对于格室内充填料产生侧向约束力,如图 1所示,这种侧向约束力称为约束围压[15]。
|
图 1 土工格室约束机制示意图 Fig. 1 Schematic diagram ofgeocell constraint mechanism |
格室对于充填料的约束围压可按照式(1)进行计算[15], 即
| $ \sigma_{\mathrm{g}}=\frac{2 M_t}{D_{\varepsilon}} \frac{\varepsilon_{\mathrm{c}}}{\left(1-\varepsilon_1\right)} $ | (1) |
| $ D_{\varepsilon}=\frac{D_0}{\sqrt{1-\varepsilon_1}} $ | (2) |
| $ \varepsilon_{\mathrm{c}}=\frac{1-\sqrt{1-\varepsilon_1}}{\sqrt{1-\varepsilon_1}} $ | (3) |
式中:σg为格室约束围压;Mt为格室条带刚度;εc为格室周向应变;Dε为格室在周向应变εc时等效直径;D0为格室初始等效直径;ε1为格室轴向应变。
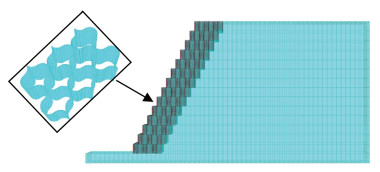
2 边坡模型建立 2.1 数值模型建立参考文献[13-14]建立土工格室挡墙支护边坡数值模型,如图 2所示。该模型由基底和边坡两部分组成,基底长×宽×高=7.0 m×0.4 m×0.2 m,边坡由格室挡墙和墙后坡体两部分组成,挡墙由14层土工格室及格室内充填料组成,格室内充填料为砾石,基底和坡体填料均为砂土,每个格室单元的高度和等效直径均为20 cm,格室厚度为0.12 cm, 边坡高为2.8 m,厚为0.4 m,坡比为1∶ 0.5。由于FALC3D中前处理建模具有一定的局限性,为了体现土工格室单元的曲面效应,本文利用Rhino软件建立土工格室单元,应用Rhino To Flac3D接口程序将土工格室单元导入到FALC3D中进行动力计算。
|
图 2 边坡数值模型(m) Fig. 2 Slope numerical model (m) |
边坡数值模型共1 338个单元,2 235个节点,土工格室与坡体、填料之间均设置接触面,该接触面服从Mohr-Coulomb准则。文献[13]通过对土工格室条带和节点进行拉伸试验,测得节点强度和条带屈服强度接近。基于本文数值模拟提取的格室应变计算得到格室拉力均小于格室条带屈服强度和节点强度。本文数值模拟中砾石和砂土采用弹塑性本构关系,屈服准则均采用适用于岩土体力学行为的Mohr-Coulomb准则[16-20],土工格室采用弹塑性本构关系。模型中材料物理力学参数[13-14]如表 1、2所示。
| 表 1 材料物理力学参数 Tab. 1 Physical and mechanical parameters of materials |
| 表 2 接触面力学参数 Tab. 2 Mechanical parameters of contact surface |
为了避免地震波传播时产生的反射及能量耗散,本次数值模型的四周及底部边界均设置为自由场边界。阻尼选取局部阻尼,阻尼系数为0.158。
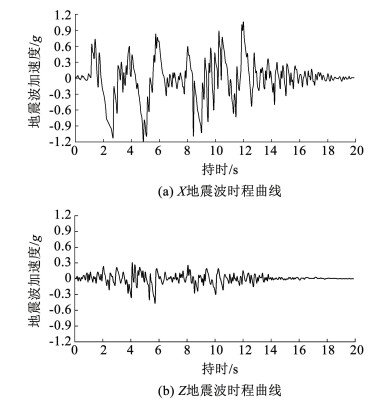
选取日本神户海洋气象台观测点记录的近场脉冲地震波Kobe波作为输入地震波[13-14],XZ双向耦合施加于模型底部,Z向加速度为X向加速度的0.38倍,其中X向地震波加速度峰值为1.193g,卓越频率为1.9 Hz,主频为1~3.8 Hz;Z向地震波加速度峰值为0.463g,卓越频率为1.18 Hz,主频为0.9~5 Hz,持时为20 s,如图 3所示。
|
图 3 Kobe波加速度时程曲线 Fig. 3 Time history curve of Kobe wave acceleration |
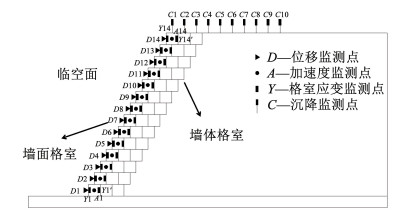
为了便于分析,对不同位置的土工格室进行定义,将临空面处的格室定义为墙面格室,将墙体内的格室定义为墙体格室。
在墙面自坡脚至坡顶布置14个位移监测点(编号依次为D1~D14);在墙面格室自坡脚至坡顶布置14个加速度监测点(编号依次为A1~A14);在墙面格室的内壁布置应变监测点,每个格室单元前后对称位置各布设一个监测点,计算时取二者的平均值作为最终应变值(编号依次为Y1~Y14,Y1′~Y14′);在坡顶自坡肩向坡体深处共布置10个沉降监测点(编号依次为C1~C10),各监测点布置如图 4所示。
|
图 4 监测点布置 Fig. 4 Monitoring points layout |
不同位置的拉筋带,自墙面向坡体方向,均为9个格室单元长度(包括墙体3个格室单元)。为了研究拉筋带的力学特性,在9个格室单元内均布置应变监测点和加速度监测点,其中应变监测点在每个格室单元前后对称位置各布设一个,计算时取二者的平均值作为最终应变值,拉筋带及其监测点布置如图 5所示。
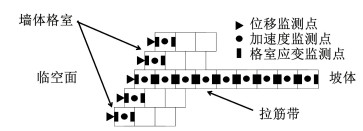
|
图 5 拉筋带及其监测点布置示意图 Fig. 5 Layout diagram of lacing belt and its monitoring points |
为了验证数值模型的准确性,建立与文献[13-14]中的5个试验模型对应的数值模型,数值模型中的参数设置、试验条件、试验要素、监测点布设、监测指标以及地震波选取均按照试验[13-14]提供的设置。图 6和图 7分别为第1次和第3次振动的数值计算结果与振动台试验结果对比,通过对比可以看出,第1次振动和第3次振动的数值模拟计算结果与振动台试验结果及变化规律相似,说明数值计算与试验结果相吻合,数值模拟计算结果是准确可靠的。

|
图 6 第1次振动数值模拟与试验结果对比 Fig. 6 Comparison of the first vibration numerical simulation and test results |

|
图 7 第3次振动数值模拟与试验结果对比 Fig. 7 Comparison of the third vibration numerical simulation and test results |
根据文献[21]的研究,本文选择0、H/3、H/2、3H/4、H(H为边坡高度)这5个位置作为边坡拉筋带的布设位置。以图 2所示模型为基本模型,首先布设两层拉筋带,通过计算确定两层拉筋带布设最优位置;基于两层拉筋带最优位置,进行3层拉筋带的布设,最后,进行4层拉筋带的布设。
3.2.1 拉筋带位置对格室约束围压的影响图 8(a)为布设两层拉筋带墙面格室约束围压沿高程分布。由图可知,当在(0, H/3)、(0, H/2)和(0, 3H/4)布设拉筋带时,格室约束围压的最大值依次出现在H/3、H/2和3H/4处,说明在坡体中布设拉筋带对该位置附近的坡体起到了有效的锚固作用,而在(0, H)布设拉筋带时,格室约束围压的最大值出现在约H/3处,这是由于土压力合力作用点位置大约在距离墙底约H/3处,且坡顶处拉筋带紧靠坡顶临空面,在地震作用下,格室内填料将向临空面运动,格室约束效果减弱;当在(H/3, H/2)和(H/3, 3H/4)布设拉筋带时,二者中下部的格室约束围压值基本接近,中上部的格室约束围压差值增大,且在(H/3, H)布设时,格室约束围压达到所有布设方案的最大值,说明在(H/3, H)处布设拉筋带对于墙体的整体稳定最为有利;当在(H/2, 3H/4)布设拉筋带时,与(H/3, 3H/4)相比,中上部格室约束围压二者基本接近,但中下部前者远小于后者,说明在H/3处布设拉筋带对于提高挡墙稳定具有重要作用;当在(3H/4, H)布设拉筋带时,与(0, H)相比,坡脚附近格室约束围压前者小于后者,中上部却相反。
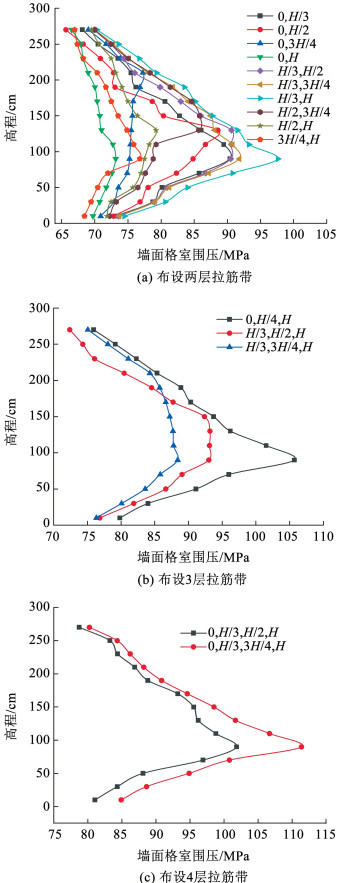
|
图 8 拉筋带位置对格室约束围压的影响 Fig. 8 Effect of the location of the tension band on cell confining pressure |
图 8(b)为布设3层拉筋带时墙面格室约束围压沿高程分布。由图可知,当在(0, H/3, H)布设拉筋带时格室约束围压最大,最大值相较于(H/3, H),格室约束围压由97.61 kPa增加至105.71 kPa,增幅达到8.29%,说明在坡脚处布设拉筋带对于提高墙体稳定同样具有重要作用;当在(H/3, H/2, H)和(H/3, 3H/4, H)布设拉筋带时,中下部格室约束围压前者大于后者,而中上部却相反。可见,布设拉筋带虽然在一定程度上能够提高边坡稳定,但其布设位置不合理时将不能充分发挥格室力学性能,造成材料浪费。此外,3种方案下格室约束围压的最大值均出现在H/3处,说明在H/3处布设拉筋带是必要且合理的。
图 8(c)为布设4层拉筋带时墙面格室约束围压沿高程分布。由图可知,在(0, H/3, 3H/4, H)布设拉筋带时,格室约束围压大于(0, H/3, 3H/4, H),对应的最大值为111.39 kPa,相较于(0, H/3, H),增幅达到5.38%,可见,在边坡中下部和中上部合理布设拉筋带,能够显著增强边坡抗震性能。
综上所述,在实际工程中应优先考虑在0, H/3, 3H/4和H这4个位置布设拉筋带。
3.2.2 拉筋带位置对挡墙位移的影响图 9(a)为布设两层拉筋带时墙面永久水平位移沿高程变化。由图可知,当在(0, H/3)和(0, H/2)布设拉筋带时,位移沿高程呈非线性增加,在坡顶处位移达到最大值;而在(0, 3H/4)和(0, H)布设拉筋带时,位移沿高程呈“增加-减小”的两段形态,最大位移出现在H/3处,说明拉筋带布设位置上移能够对坡顶附近的位移起到有效遏制作用;当在(H/3, H/2)布设拉筋带时,位移最大值出现在坡顶处,而在(H/3, 3H/4)和(H/3, H)布设拉筋带时,位移最大值又出现在H/3处,由此说明,仅在边坡中下部布设拉筋带时最大位移出现在坡顶附近,而仅在边坡中上部布设拉筋带时最大位移出现在H/3处;当在(H/2, 3H/4)和(H/2, H)布设拉筋带时,边坡中下部位移值二者基本接近,但中上部位移逐渐减小,而在(3H/4, H)布设拉筋带时,坡脚附近的位移大于坡顶附近。

|
图 9 拉筋带位置对墙面位移的影响 Fig. 9 Influence of the location of tension belt on wall displacement |
图 9(b)为布设3层拉筋带时墙面永久水平位移沿高程变化。由图可知,当在(0, H/3, H)布设拉筋带时,墙面永久水平位移值最小,其位移值相较于(H/3, H),由19.78 cm减小至18.65 cm,减幅达到5.68%;而在(H/3, H/2, H)和(H/3, 3H/4, H)布设拉筋带时,二者中上部位移逐渐减小,中下部位移基本不变。
图 9(c)为布设4层拉筋带时墙面永久水平位移沿墙高变化。由图可知,当在(0, H/3, 3H/4, H)布设拉筋带时位移最小,最小值为18.06 cm,相较于(0, H/3, H),减幅达到5.16%;而在(0, H/3, H/2, H)布设拉筋带时,其位移值小于(0, H/3, 3H/4, H),坡脚附近二者位移差值量较小,但在坡顶附近位移差值量较大,可见保持边坡中下部拉筋带位置和数量不变的情况下,在3H/4处布设拉筋带更能有效提高边坡的整体稳定。
综上所述,在坡脚和坡顶附近布设拉筋带更有助于提高边坡的抗震性,这是由于边坡破坏时,在坡脚发生剪切破坏,坡顶发生张拉破坏,当在0和H/3布设拉筋带时可阻止坡脚处剪切破坏的发生,在3H/4和H布设拉筋带时可阻止坡顶张拉破坏的发生,因此在这4个位置布设拉筋带是合理的。
3.2.3 拉筋带位置对挡墙加速度的影响图 10(a)为布设两层拉筋带时墙面水平峰值加速度沿高程变化。由图可知,峰值加速度沿墙高表现为“增加-减小-增加”的三段形态,在坡顶处峰值加速度达到最大值。具体来看,当在(0, H/3)、(0, H/2)、(0, 3H/4)和(0, H)布设拉筋带时,边坡中下部峰值加速度逐渐增大,而中上部逐渐减小,说明随着拉筋带布设位置的上移,坡顶附近加速度放大效应减弱;当在(H/3, H/2)、(H/3, 3H/4)和(H/3, H)布设拉筋带时,峰值加速度逐渐减小,且在(H/3, H)处布设时峰值加速度达到所有方案的最小值,说明在该处布设拉筋带加速度放大效应最弱;当在(H/2, 3H/4)和(H/2, H)布设拉筋带时,在边坡中下部二者峰值加速度接近,中上部逐渐减小,而在(3H/4, H)布设拉筋带时,坡脚附近峰值加速度大于坡顶附近,说明在坡顶处布设拉筋带,对于减小坡顶附近的加速度放大效应更为有利。
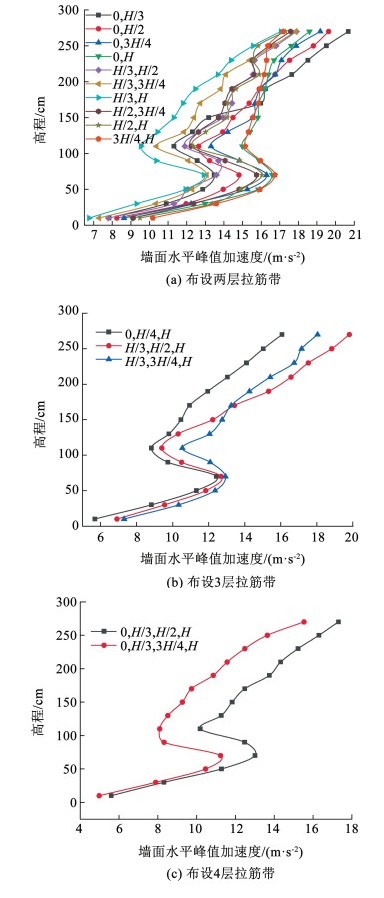
|
图 10 拉筋带位置对加速度的影响 Fig. 10 Influence of reinforced belt at different positions on acceleration |
图 10(b)为布设3层拉筋带时墙面水平峰值加速度沿墙高变化。由图可知,当在(0, H/3, H)布设拉筋带时,峰值加速度最小,相较于(H/3, H)峰值加速度的最大值由17.05 m/s2减小至16.07 m/s2,减幅达到5.77%;而在(H/3, H/2, H)和(H/3, 3H/4, H)布设拉筋带时,边坡中下部二者峰值加速度接近,而上部逐渐减小,说明在保持边坡中下部布设位置不变的情况下,拉筋带位置越靠近坡顶,加速度放大效应越小。
图 10(c)为布设4层拉筋带时墙面水平峰值加速度沿墙高变化。由图可知,当在(0, H/3, 3H/4, H)布设拉筋带时,峰值加速度最小,峰值加速度最大值为15.53 m/s2,相较于(0, H/3, H),减幅达到3.36%;而在(0, H/3, H/2, H)布设拉筋带时,在坡脚处二者数值相近,在坡顶处二者差值量增大。
综上所述,在0、H/3、3H/4和H处布设时,峰值加速度放大效应最小,边坡最为稳定。
3.2.4 拉筋带位置对坡顶沉降的影响图 11为不同拉筋带布设时坡顶沉降分布。由图可知,不同布设方案下,坡顶沉降自坡肩向坡体延伸,均表现为先增加后减小的“V”型分布。具体来看,由图 11(a)可知,当在(0, H/3)、(0, H/2)、(0, 3H/4)和(0, H)处布设拉筋带时,坡顶沉降值在(0, H) 较小,最小值为18.41 cm;当在(H/3, H/2)、(H/3, 3H/4)和(H/3, H)布设拉筋带时,坡顶沉降值在(H/3, H)较小,最小值为17.08 cm;当在(H/2, 3H/4) 和(H/2, H)布设拉筋带时,坡顶沉降值在(H/2, H)较小,最小值为17.59 cm,可见,在(H/3, H)布设拉筋带坡顶沉降最小,边坡最为稳定。由图 11(b)可知,在(0, H/3, H)布设拉筋带时沉降最小,最小值为16.01 cm,相较于(H/3, H),减幅达到6.26%;而在(H/3, H/2, H)和(H/3, 3H/4, H)布设拉筋带时,二者差值不大。由图 11(c)可知,在(0, H/3, 3H/4, H)布设拉筋带时沉降最小,最小值为15.28 cm, 相较于(0, H/3, H),减幅达到4.51%。
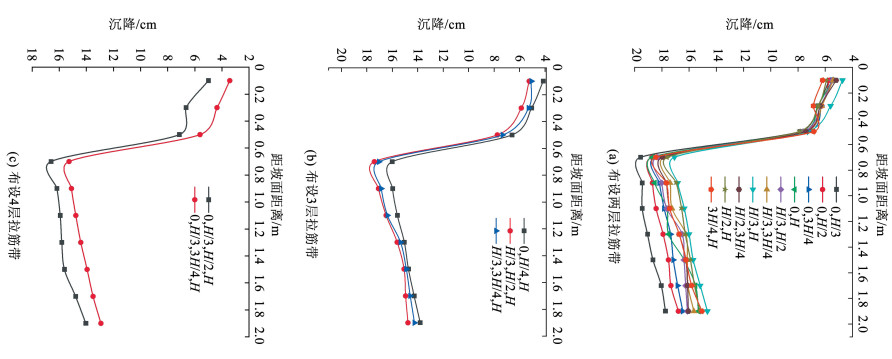
|
图 11 拉筋带位置对坡顶沉降的影响 Fig. 11 Influence of the location of tension belt on the settlement of slope top |
综上所述,在0, H/3, 3H/4, H处布设拉筋带对于减小坡顶沉降具有显著作用。
3.3 拉筋带数量对边坡动力响应的影响基于上述分析,选取两层拉筋带、3层拉筋带和4层拉筋带布设的最优位置,以此来研究不同数量拉筋带对于边坡动力响应的影响,选取工况如表 3所示。
| 表 3 拉筋带数量计算工况 Tab. 3 Calculation conditions of the number of tensile strips |
图 12展示了计算终态时各工况的塑性云图。由图可知,在未布设拉筋带时(工况1),边坡的塑性区较小,主要出现在坡面附近,边坡滑裂面近似于圆弧形;当在H/3和H处布设拉筋带时(工况2),坡脚和坡顶附近的边坡塑性区向坡体发展较为明显,塑性区域增大,边坡滑裂面向坡体转移,但H/3~H高程之间的塑性区并未得到明显的发展;当在0、H/3和H处布设拉筋带时(工况3),坡脚附近的塑性区进一步向坡体延伸,且H/3~H之间的塑性区也有进一步向坡体发展的趋势,但坡顶处的塑性区未得到明显发展,滑裂面位置仅在坡脚处向坡体转移;当在0、H/3、3H/4和H处布设拉筋带时(工况4),边坡塑性区整体向坡体明显发展,塑性区域增大,滑裂面整体转移至拉筋带末端,边坡稳定性得到提高。
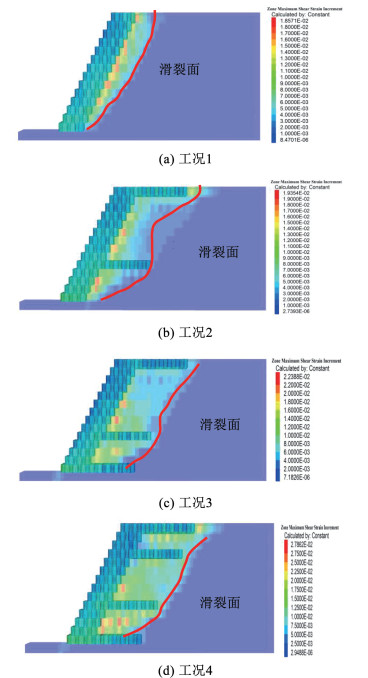
|
图 12 各工况下边坡塑性云图 Fig. 12 Plastic cloud map of slope under different working conditions |
综合而言,在选择拉筋带布设位置时,应优先考虑坡脚,坡顶以及H/3~H高程之间的塑性区发展情况,从而确定最优布设位置。
3.3.2 拉筋带数量对格室约束围压的影响图 13为不同工况下墙面格室约束围压沿高程分布。由图可知,不同工况下墙面格室约束围压沿高程均呈“增加-减小”的两段形态,在H/3处达到最大值,由于底层格室内充填料受到上部格室及其内充填料的压重作用较大,对于格室内充填料的变形具有一定的限制作用,而边坡中部受到上部格室及其充填料的压重作用减小,且H/3处土压力最大,沿墙高,格室压重作用减弱,顶层格室内部充填料在地震力作用下,向坡顶临空面运动,格室约束围压较小。另外,工况1中,格室约束围压峰值为88.92 kPa;工况2中,格室约束围压峰值为97.61 kPa,相较于工况1,增幅为9.77%,且H/3~H高程格室约束围压增幅大于0~H/3高程;工况3中,格室约束围压峰值为105.71 kPa,相较于工况2,增幅为8.29%,且0~H/3高程和H/3~H高程格室约束围压增幅基本一致;工况4中,格室约束围压峰值为108.39 kPa, 与工况3相比,增幅为2.54%,且0~H/3高程格室约束围压增幅较小,而H/3~H高程增幅较为明显,说明在3H/4处设置拉筋带对于增强边坡上部稳定性具有重要作用。

|
图 13 不同工况墙面格室约束围压沿高程变化 Fig. 13 Changes of wall cell confining pressure along elevation under different working conditions |
图 14展示了不同工况下拉筋带格室约束围压沿水平方向变化。由图可知,格室约束围压自墙面向坡体延伸呈先增大后减小的“人”字形分布,最大值均出现在挡墙与坡面交界处,由于在地震作用下,与坡面交界处的拉筋带格室单元受到拉筋带上下坡体的推压作用较大,该处格室单元需要发挥更大的约束作用以低抗坡体的推压作用,此处格室约束围压最大;向坡体延伸,拉筋带格室单元受到坡体的压重作用较大,起到主要作用,因此越向坡体格室约束围压越小。此外,不同工况下墙面格室约束围压小于墙体格室约束围压,由于墙体格室受到周边格室及坡体填料的相互挤压作用较大,限制了格室的拉伸变形,而墙面格室紧靠临空面,在地震力作用下,受到周边格室挤压作用时,将向临空面方向产生变形,因此墙体格室约束围压大于墙面格室约束围压。不同工况下格室约束围压由大到小依次为H/3>3H/4>H>0,说明H/3处格室受力最大。
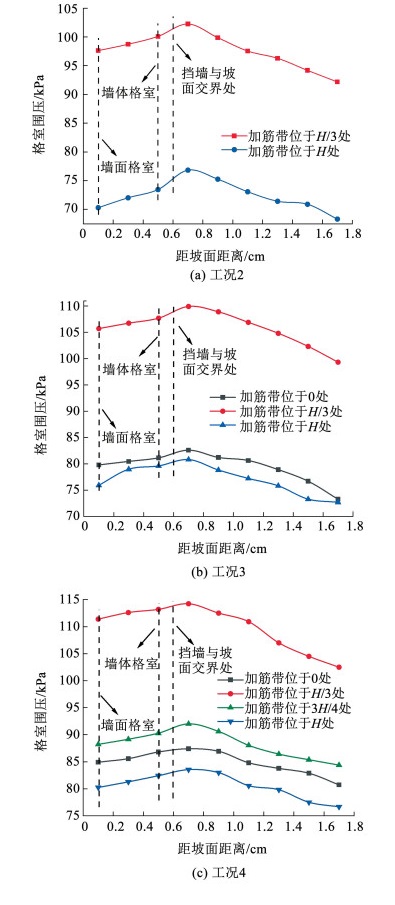
|
图 14 拉筋带处格室约束围压沿水平方向变化 Fig. 14 Confining pressure at the lacing zone changes along the horizontal |
综合而言,拉筋带布设位置合理时,随着拉筋带数量的增加边坡的整体稳定性得到显著提高。但拉筋带数量布设较多时,施工难度加大,工时较长。
3.3.3 拉筋带数量对挡墙位移的影响图 15展示了不同工况下墙面永久水平位移沿高程变化。由图可知,不同工况下位移沿高程均表现出明显的非线性,在H/3处位移达到最大值。此外,工况1中,最大位移为22.02 cm,墙顶位移小于墙脚位移;工况2中,最大位移为19.93 cm,相较于工况1,减幅达到9.46%,且墙脚处位移由19.56 cm减小至8.11 cm,减幅达到58.56%;工况3中,最大位移为19.93 cm,相较于工况2,减幅达到6.44%,且0~H/3减幅最大,H/3~H高程减幅较小;工况4中,最大位移为17.51 cm,相较于工况3,0~H/3减幅较小,H/3~H高程减幅较大。4种工况下位移由大到小依次为工况1、工况2、工况3、工况4,即随着拉筋带数量的增加,墙面永久水平位移逐渐减小,且减幅趋弱。
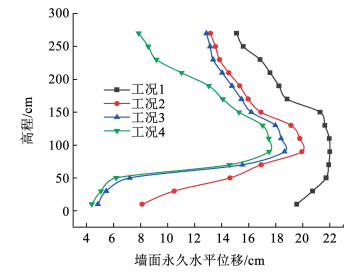
|
图 15 不同工况下墙面永久水平位移沿高程变化 Fig. 15 The permanent horizontal displacement varies along the elevation |
图 16展示了不同工况下边坡水平位移云图。由图可知,不同工况下边坡水平位移最大值均出现在H/3处。未布设拉筋带时(工况1),坡面和坡体均出现了位移,说明挡墙结构抗震性能较弱;当在H/3和H布设拉筋带时(工况2),位移仅出现在墙体及拉筋带锚固区域,坡脚处水平位移得到明显减小;当在0、H/3和H布设拉筋带时(工况3),墙脚水平位移进一步减小,H/3~H高程之间的位移等势线向坡体发展;当在0、H/3、3H/4和H处布设拉筋带时(工况4),墙脚附近水平位移未得到明显改变,H/3~3H/4高程之间的位移等势线继续向坡体发展。综合而言,拉筋带数量增加,墙面永久水平位移逐渐减小,边坡抗震性得到显著提高。

|
图 16 不同工况下边坡水平位移云图 Fig. 16 Slope displacement nephogram under different working conditions |
图 17展示了墙面水平峰值加速度沿高程分布。由图可知,不同工况下峰值加速度沿高程分布大体相同,均表现为“增加-衰减-增加”的三段形态,这与文献[22]研究结果一致。这是由于在墙脚附近(H < 50 cm),挡墙结构对地震波的衰减效应并不明显,临空面放大效应仍占据主导因素,从而出现了加速度随高程而增加的现象;墙高到达一定高度时(H=50 cm左右),随着高程增加,土工格室及内部充填料对地震波的阻尼增大,滤波作用增强,入射波经过格室内充填料的吸收滤波后,阻尼衰减效应明显增高,从而超过临空面放大效应而占据主导地位,此时加速度随高程增加而减小;当高程增加至H=110 cm时,沿高程至墙顶,由于墙顶临空面的存在,入射波在临空面处经过多次反射、折射和叠加,临空面放大效应超过阻尼衰减效应再次占据主导因素,从而加速度沿高程的增加而增加。另外,4种工况下,峰值加速度由大到小依次为工况1、工况2、工况3、工况4,即随着加筋带数量的增加,峰值加速度逐渐减小。
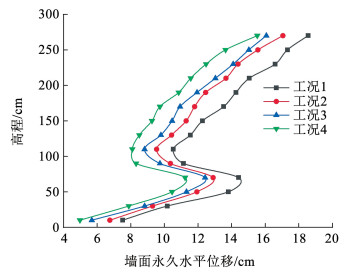
|
图 17 墙面水平峰值加速度沿高程变化 Fig. 17 The horizontal peak acceleration varies along the elevation |
图 18为不同工况下拉筋带处峰值加速度沿水平分布。由图可知,不同工况下峰值加速度自墙面向坡体延伸,均表现为先增大后减小的“人”字形分布,最大值出现在墙体与坡面交界处。这是由于地震波沿水平方向穿过土工格室单元时,土工格室及其内部充填料将会对地震波进行反射和透射,从而造成地震能量的衰减,出现了墙面峰值加速度小于墙体峰值加速度;而位于坡体内部的拉筋带,其四周被坡体材料所包裹,地震波沿水平方向传播至坡面时,坡面放大效应占据主导位置,出现了坡面峰值加速度大于坡体峰值加速度。不同位置的拉筋带,峰值加速度由高到低依次为H>3H/4>H/3>0,说明在坡顶处加速度放大较为显著。综上所述,随着拉筋带数量的增加,峰值加速度逐渐减小;不同位置的拉筋带,坡顶处峰值加速度最大。

|
图 18 不同工况下拉筋带加速度沿水平方向变化 Fig. 18 The acceleration of the tension band varies horizontally |
图 19为不同工况坡顶沉降分布。由图可知,不同工况下,自坡肩向坡体深处延伸,沉降均呈先增大后减小的“V”型分布,在墙体与坡体交界处沉降最大;由于格室的约束作用以及下层格室挡墙的阻碍作用,坡肩处沉降最小;向坡体延伸,与挡墙接触处的坡体填料随墙体位移最先向下滑落,使得坡体顶部与顶层格室之间产生空腔,在地震荷载作用下,顶层格室及其内充填料整体下沉,并达到最大值;继续向坡体深处延伸,坡体填料滑落趋势渐缓,沉降减小。4种工况下,沉降由大到小对应的沉降值依次为18.28、17.08、16.01、15.29 cm,减幅依次为6.56%、6.28%、4.51%。可见,沉降随拉筋带数量的增加而降低,但减幅逐渐减小。
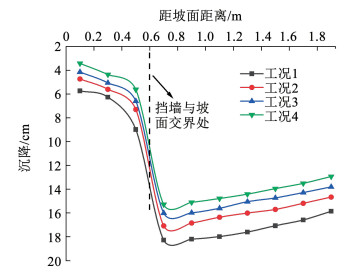
|
图 19 不同工况坡顶沉降分布 Fig. 19 Settlement distribution of hilltop under different working conditions |
土工格室挡墙是将土工格室和充填料组成的结构层按照一定的坡度层层叠加组合而成。格室挡墙的格室本身、充填料与格室之间、层与层之间,具备可靠的抗震构造措施[23]。
土工格室挡墙具有足够的竖向承载能力,土工格室对充填料有着较好的约束作用,使得挡墙结构整体刚度较大,结构稳定性较好,在地震时能够支撑上部结构的所有重量和使用载荷;土工格室挡墙结构具有可变的水平刚度,地震力较小时格室层间摩阻力以及格室与充填料的相互作用具有足够的刚度,以抵抗边坡的破坏,地震力较大时,挡墙水平刚度较小,格室层间产生水平滑动,随地震动发生协调变形;格室挡墙结构具有一定的水平弹性恢复力,地震中格室层间的咬合摩阻力作用,使挡墙结构具有自动复位功能,地震力结束后,挡墙中下部发生挠曲变形,挡墙整体结构未发生坍塌等工程事故;土工格室挡墙结构具有足够的阻尼,土工格室及其充填料对地震能量具有显著耗能作用。
4 结论本文利用FLAC3D软件,建立土工格室挡墙支护边坡数值模型,系统分析了拉筋带位置和拉筋带数量对边坡动力响应的影响,得到主要结论如下:
1) 不同方案下,格室约束围压沿墙高均表现为“增加-减小”的两段形态;拉筋带布设位置合理时,位移最大值出现在H/3处;水平峰值加速度沿墙高呈“增加-减小-增加”的三段分布,坡顶处加速度最大;沉降自坡肩向坡体延伸呈先增加后减小的“V”形分布,在墙体与坡面交界处沉降最大。
2) 布设两层拉筋带时,在(H/3,H)处为最优位置;布设3层拉筋带时,在(0,H/3,H)处为最优位置;布设4层拉筋带时,在(0,H/3,3H/4,H)处为最优位置。
3) 不同工况下,拉筋带处格室约束围压和水平峰值加速度自墙面向坡体延伸均表现为先增大后减小的“人”字形分布,最大值均出现在挡墙和坡面交界处;且墙面加速度小于墙体加速度,土工格室及其填料对于加速度的传播具有一定衰减作用。
4) 不同工况下,拉筋带位置处格室约束围压最大值出现在H/3处,峰值加速度最大值出现在H处;不同布设方案下,在H/3和H处布设拉筋带时,边坡位移和沉降最小,实际工程中应优先考虑在H/3和H处布设。
| [1] |
CHEN Z, SONG D Q, HU C, et al. The September 16, 2017, Linjiabang landslide in Wanyuan County, China: preliminary investigation and emergency mitigation[J]. Landslides, 2020, 17(1): 191. DOI:10.1007/s10346-019-01309-1 |
| [2] |
宋飞, 谢永利, 杨晓华, 等. 填土面作用荷载时土工格室柔性挡墙破坏模式研究[J]. 岩土工程学报, 2013, 35(增刊1): 152. SONG Fei, XIE Yongli, YANG Xiaohua, et al. Failure mode of geocell flexible retaining wall with surcharge acting on backfill surface[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Sup.1): 152. |
| [3] |
LATHA M G, MANJU S G. Seismic response of geocell retaining walls through shaking table tests[J]. International Journal of Geosynthetics and Ground Engineering, 2016, 2(1): 1. DOI:10.1007/s40891-016-0048-4 |
| [4] |
LATHA M G, SANTHANAKUMAR P. Seismic response of reduced-scale modular block and rigid faced reinforced walls through shaking table tests[J]. Geotextiles and Geomembrances, 2015, 43(4): 307. DOI:10.1016/j.geotexmem.2015.04.008 |
| [5] |
LESHCHINSKY D, LING I H, WANG J P, et al. Equivalent seismic coefficient in geocell retention systems[J]. Geotextiles and Geomembranes, 2008, 27(1): 9. DOI:10.1016/j.geotexmem.2008.03.001 |
| [6] |
SONG F, XIE Y L, YANG Y F, et al. Analysis of failure of flexible geocell-reinforced retaining walls in the centrifuge[J]. Geosynthetics International, 2014, 21(6): 342. DOI:10.1680/gein.14.00022 |
| [7] |
宋飞, 许伟强, 张鲁渝, 等. 土工格室柔性挡墙变形规律数值模拟研究[J]. 岩土力学, 2011, 32(增刊1): 738. SONG Fei, XU Weiqiang, ZHANG Luyu, et al. Numerical analysis of deformation behavior of geocell flexible retaining wall[J]. Rock and Soil Mechanics, 2011, 32(Sup.1): 738. DOI:10.16285/j.rsm.2011.s1.134 |
| [8] |
MEHDIPOUR I, GHAZAVI M, MOAYED Z R. Numerical study on stability analysis of geocell reinforced slopes by considering the bending effect[J]. Geotextiles and Geomembranes, 2013, 37: 23. DOI:10.1016/j.geotexmem.2013.01.001 |
| [9] |
LATHA M G, RAJAGOPAL K, KRISHNASWAMY R N. Experimental and theoretical investigations on geocell-supported embankments[J]. International Journal of Geomechanics, 2006, 6(1): 30. DOI:10.1061/(ASCE)1532-3641(2006)6:1(30) |
| [10] |
SONG F, LIU H B, MA L Q, et al. Numerical analysis of geocell-reinforced retaining wall failure modes[J]. Geotextiles and Geomembranes, 2018, 46(3): 284. DOI:10.1016/j.geotexmem.2018.01.004 |
| [11] |
NARIMAN K, MAHMOUD G. Static stability analysis of geocell-reinforced slopes[J]. Geotextiles and Geomembranes, 2021, 49(3): 852. DOI:10.1016/J.geotexmem.2020.12.012 |
| [12] |
梁程, 徐超. 土工格室加筋土垫层路堤临界高度研究[J]. 岩土力学, 2018, 39(8): 2984. LIANG Cheng, XU Chao. Study on critical height of reinforced embankments with geocell layer[J]. Rock and Soil Mechanics, 2018, 39(8): 2984. DOI:10.16285/j.rsm.2016.2875 |
| [13] |
WANG J P. Large-scale shaking table tests of reinforced soil retaining walls with geocell facing[D]. New York: Columbia University, 2007
|
| [14] |
LING I H, LESHCHINSKY D, WANG J P, et al. Seismic response of geocell retaining walls: experimental studies[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(4): 515. DOI:10.1061/(ASCE)1090-0241(2009)135:4(515) |
| [15] |
SONG F, LIU H, YA NG, B, et al. Large-scale triaxial compression tests of geocell-reinforced sand[J]. Geosynthetics International, 2019, 26(4): 1. DOI:10.1680/jgein.19.00019 |
| [16] |
张江伟, 李小军, 齐剑峰, 等. 地震动参数对土坡地震响应的影响权重研究[J]. 振动与冲击, 2018, 37(6): 225. ZHANG Jiangwei, LI Xiaojun, QI Jianfeng, et al. Effect of influence weights of ground motion parameters on soil slope seismic responses[J]. Journal of Vibration and Shock, 2018, 37(6): 225. DOI:10.13465/j.cnki.jvs.2018.06.036 |
| [17] |
蔡晓光, 徐洪路, 李思汉, 等. 地震作用下返包式加筋土挡墙数值模拟[J]. 吉林大学学报(地球科学版), 2021, 51(5): 1416. CAI Xiaoguang, XU Honglu, LI Sihan, et al. Numerical simulation of reinforced soil retaining wall with wrapped face under seismic effects[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(5): 1416. DOI:10.13278/j.cnki.jjuese.20200313 |
| [18] |
蒋建清, 杨果林. 格宾加筋土挡墙抗震性能及数值分析[J]. 土木工程学报, 2012, 45(1): 100. JIANG Jianqing, YANG Guolin. Numerical analysis of seismic behaviour of gabion-reinforced soil retaining wall[J]. China Civil Engineering Journal, 2012, 45(1): 100. DOI:10.15951/j.tmgcxb.2012.01.022 |
| [19] |
LIU H, YANG G, LING I H. Seismic response of multi-tiered reinforced soil retaining walls[J]. Soil Dynamics and Earthquake Engineering, 2014, 43(2): 1. DOI:10.1016/j.soildyn.2014.01.012 |
| [20] |
UJIAWAL K, VENKATESWARLU H, HEGDE A. Vibration isolation using 3D cellular confinement system: a numerical investigation[J]. Soil Dynamics and Earthquake Engineering, 2019, 119: 220. DOI:10.1016/j.soildyn.2018.12.021 |
| [21] |
李永亮. 土工格室挡墙优化断面型式及其在延安机场迁建工程中的应用[D]. 西安: 长安大学, 2016 LI Yongliang. Relocation project retaining wall and application in Yan'an airport study on the optimum sectional form of geocell[D]. Xi'an: Chang'an University, 2016 |
| [22] |
言志信, 郭斌, 段建. 黄土边坡地震动力响应探讨[C]//第3届全国工程安全与防护学术会议论文集. 武汉: 中国工程院土木、水利与建筑工程学部、中国岩石力学与工程学会安全与防护分会, 2012: 383 YAN Zhixin, GUO Bin, DUAN Jian. Study on seismic dynamic response of loess slope[C]//Proceedings of the 3th National Engineering Safety and Protection Academic Conference. Wuhan: Department of Civil, Hydraulic and Construction Engineering, Chinese Academy of Engineering, Safety and Protection Branch of Chinese Society of Rock Mechanics and Engineering, 2012: 383 |
| [23] |
李昀, 杨果林, 林宇亮, 等. 水平地震作用下加筋格宾挡土墙动力特性试验研究[J]. 岩土工程学报, 2009, 31(12): 1930. LI Yun, YANG Guolin, LIN Yuliang, et al. Dynamic characteristics of reinforced gabion walls subjected to horizontal seismic loading[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1930. |
 2023, Vol. 55
2023, Vol. 55


