城市土地利用长期属性,使得城市居民出行需求具有相对稳定性。随着移动互联网时代的到来,可通过各式无线终端设备获取居民的出行规律[1-3]。并以居民的出行规律为基础,分时段地制定相应的交通网络管理控制方法,尤其是交叉口信号灯控制方法。以往的研究往往聚焦于单个交叉口[4-6]或者某一干道[7]的信号灯控制时段划分方法,而缺乏对整个网络进行整体性地分析。本文以实时的道路交通数据为基础,以分类的方式判断城市道路交通运行状态,提出针对整个交通网络的控制时段划分方法。
城市道路交通运行状态是网络供给能力和交通需求两方面共同作用的结果。面对波动的交通需求,产生了点、线、面3种不同层级上的交通信号优化控制方法,以达到交通供给和需求的平衡。点层面上信号优化控制主要为交叉口单点信号优化控制,线层面上信号优化控制为干道交叉口群信号优化协调,面层面上信号优化控制为区域间信号控制策略制定与协调,以达到提高通行能力或安全性等目标。3种不同层级上的控制优化,都需要精准把握城市道路网络实时运行状态,然而它们对运行状态时效性要求不一样。交叉口单点信号控制要求在分钟尺度的交通流量信息基础上进行优化控制;干道交叉口群需要以5~30 min时段长度尺度上干道交叉口群的交通流特征变化趋势规律,判断是否调整协调控制参数;由于控制范围扩大的原因,区域间信号控制策略制定与协调需在30~60 min尺度上进行。目前普遍使用的地面线圈、激光雷达、交叉口或路段上视频等设备都是采集地点交通状态数据,可直接用于交叉口单点信号优化控制。地点交通状态数据只有通过二次加工之后,才能用于线和面层级上的交通信号优化控制。目前探索高效、准确、服务于线和面层级上交通信号优化控制的路网交通状态辨识方法,仍然是当今热门的研究课题。
国内外关于交通网络供给能力的研究主要从交通网络可靠性评价角度展开。交通网络可靠性评价方法主要可分为以下3类:连通可靠性[8-9],行程时间可靠性[10-12],道路网络容量可靠性[13-15]。从理论上看,交通管理者可依据上述评价方法,制定交通管控方案。但是传统的交通可靠性评价方法没有结合实时真实数据,往往假定交通需求、路段容量、旅行时间变化服从某种数学概率分布,再加上道路系统是人、车和非机动混合使用场景,其复杂性难以用简单数学概率分布概括,致使分析结果偏离实际甚远。
近年来虽然有研究使用GPS数据[16]、电子车牌数据[17]等来获取某些路段的行程时间可靠性。但其存在车辆GPS数据与地图匹配问题以及数据只能覆盖部分路段等原因,致使基于车辆GPS数据的该方法缺乏普适性。如果以数据拥有无壁垒、使用简易等标准来筛选多种路况信息检测手段的数据,道路车牌识别监控数据无疑是最佳候选。这是因为道路车牌识别监控数据相比于其他类型数据,不存在车辆数据与地图匹配问题,且能涵盖整个路网。因此,基于道路车牌识别监控数据,以5 min为一个步长,滚动式构建出各时间段上路段旅行时间分布,使用基于平均最短路径长度的拥堵指标评价路网实时运行状态及状态的持续时间,并依据谱距离指标确定分类数,使用K-means聚类算法辨识路网运行状态类型。在此基础上制定针对性交通管控措施,以缓解交通拥堵。
本文从数据处理、拥堵指标、路网运行状态识别3个方面介绍了研究方法;然后通过长沙市中心城区道路网络实例验证了所提出的方法的有效性;最后总结了本文研究结论与未来研究方向。
1 研究方法本文提出的方法可分为以下几步:首先基于道路车牌识别系统数据,得到道路网络每天各时段道路网络路况特征数据,包括路段行程时间和路网实时OD交通量等数据;其次,基于路网平均最短路径长度的拥堵指标衡量不同时段路网拥堵状况;然后,基于谱距离指标确定分类数,依据拥堵指标结果,使用K-means聚类算法对于不同时段路网交通状况进行分类,不同类别表示不同程度的剩余供给能力。剩余供给能力是指当前交通状况下,道路网络仍能继续承担交通流量的能力,并保持一定的服务水平;最后,依据实时路况数据和训练后的K-means分类器来评价不同时段道路网络的运行状态,为制定交通管控措施提供依据。方法流程如图 1所示。

|
图 1 方法流程 Fig. 1 Process of method |
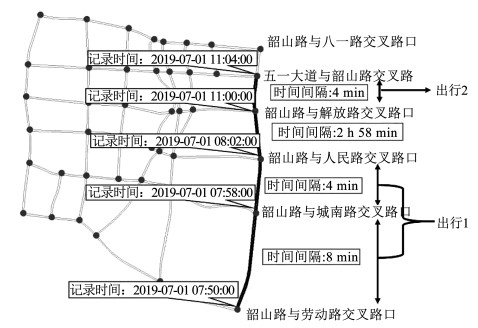
本文数据处理的对象是道路电子卡口经过脱敏之后的监控数据,也称为道路车牌识别系统数据。本文约定,以交叉口前停车线划分路径为路段;以道路围合的自然区域为交通小区,因而交叉口就视为临近小区的起讫点;按1 h时间长度把每一天划分成24个时段;研究网络共有N条边。以道路车牌识别系统数据得到路段实时行程时间分布和路网实时OD出行量。处理过程:依据道路车牌识别系统数据,获取各时段路段上所有车辆行驶时间数据,即获取在时段p(p∈{0, 1, 2, …, 23})内途经路段a(a∈ {1, 2, …, N})上每辆车路段行驶时间tap以及各个时段路网OD出行量,数据处理过程如图 2所示。
|
图 2 数据处理示意图 Fig. 2 Data process |
从图 2可以看出,首先提取车辆1 d中在区域内途经交叉口的轨迹数据,依据时间间隔是否大于某一阈值(例如30 min),把1 d的行驶轨迹划分为不同的出行OD对,并按照右手边规则,把前、后交叉口记录时间间隔大于阈值路段右手边小区看成前一次出行的终点,同时该小区又是下一次出行的起点。然后在同一次出行路径上,通过路段两端卡口监控记录数据的时间间隔获得车辆在该路段的行程时间,以及所有车辆各时段的平均行程时间。最后统计每个OD对的出行交通量。
1.2 基于平均最短路径长度的拥堵指标本文结合道路实际行程时间、路网OD交通出行量,构建基于平均最短路径长度的拥堵指标。平均最短路径是衡量网络传输效率的指标,在平均最短路径的基础上,结合实际交通数据能更真实地衡量路网传输效率,反映路网运行状态,指标计算公式为
| $ T^p=\sum\limits_{i=1}^n \sum\limits_{j \neq i} \frac{q_{i j}^p t_{i j}^p}{Q^p t_{i j}^{\min }}, i \in N, j \in N $ | (1) |
这里交叉口节点将简称为节点。式(1)中Tp表示时段p期间路网拥堵指标。qijp表示时段p内从节点i到节点j的交通出行量,Qp表示时段p内路网总交通出行量。tijp表示时段p内节点i到节点j的最短路的实际所需时长,该值由实时路况数据确定;tijmin表示节点i到节点j的最短路自由流时长,该值由路段自由流速度确定或通过历史路况数据出现的最短时长确定。
拥堵指标是所有OD对之间最短路径的实际行程时间和自由流时间的比值的加权和,权重为对应的交通需求在总交通需求中的比例。其物理意义:1)该指标通过实际行程时间和自由流时间的比值,反映了每条最短路径在研究时刻的拥堵情况;2)该指标通过计算最短路径所承担的交通需求比例,来体现某条最短路径的拥堵情况对整个路网的影响。
1.3 路网运行状态类型识别使用K-means聚类算法对不同时段的路网进行分类。K-means算法是无监督的聚类算法,应用广泛。待分类的路网数据为路网于不同时段的基于平均最短路径长度的拥堵指标结果。
K-means聚类算法需预先确定类别数量。考虑到分类目的为区分不同剩余供给能力的路网结构,即聚类相似剩余供给能力的路网结构。这里基于归一化谱距离(normalized spectral distance, NSD)指标[18]衡量不同类别数下的分类结果,归一化谱距离是侧重于比较网络整体结构差异的指标。
对于路网不同时段的剩余供给能力网络结构差异,可通过去除劣化路段来体现。劣化路段是指在某一时段内该路段的平均行程时间大于该路段的自由流时间乘以劣化系数。可依据路段a的自由流时间ta0和劣化系数δ,判断时段p内路段a是否处于劣化状态:若tap>δta0,则表示时段p内路段a处于劣化状态;若tap≤δta0,则表示时段p内路段a不处于劣化状态。进而得到不同道路劣化情况下的交通网络拓扑结构——对于交通网络G(N, A),将劣化路段从路网路段集合A中去除,且不影响任何OD对的连通性;若不然,仍将保留该路段,得到新的路网路段集合A′,更新得到交通网络G(N, A′)。故原路网与新路网的节点集合不变。劣化系数的取值应由所研究的城市道路发生交通拥堵时,路段实际行程时间和自由流时间的比值来确定。本文通过对长沙市五一广场周边道路网络的实地调查,建议城市道路的劣化系数取值为2。
对于网络Gm=G(N, A)和Gn=G(N, A′),N指代路网节点集合,A和A′指代路网路段集合。网络Gm和Gn之间归一化谱距离计算公式为
| $ d_{\mathrm{NSD}}\left(G_m, G_n\right)=\sqrt{\frac{\sum\nolimits_{i=1}^N\left(\lambda_i^n-\lambda_i^m\right)^2}{\min \left\{\sum\nolimits_{i=1}^N\left(\lambda_i^n\right)^2, \sum\limits_{i=1}^N\left(\lambda_i^m\right)^2\right\}}} $ | (2) |
式中:λm、λn分别表示邻接矩阵Xm和Xn的特征值,Xm和Xn分别表示网络Gm和Gn的邻接矩阵。
通过计算归一化谱距离的平均值来衡量K-means聚类结果,归一化谱距离的平均值的计算公式为
| $ \begin{gathered} d_{\mathrm{NSD}}^{\mathrm{mean}, h}=\frac{1}{k_h\left(k_h-1\right)} \sum\limits_{m=1}^{k_h} \sum\limits_{n \neq m}^{k_h} d_{\mathrm{NSD}}\left(G_m, G_n\right), \\ G_m \in C_h, G_n \in C_h \end{gathered} $ | (3) |
| $ d_{\mathrm{NSD}}^{\mathrm{mean}}=\frac{1}{H} \sum\limits_{h=1}^H d_{\mathrm{NSD}}^{\mathrm{mean}, h} $ | (4) |
式中:Ch表示第h类路网,kh表示第h类路网包含的路网个数,H表示类别数量。
本文基于归一化谱距离平均值,使用肘部法则确定K-means聚类算法的类别数量。对于分类结果,依据该类别所代表的路网可能的路段劣化情况,标定该类路网的供给能力,并针对不同类别路网实施不同程度的交通管控方案。
2 实例分析本节依据长沙市城市道路车牌识别系统数据,得到研究区域内道路网络半个月内的实时路况数据。基于车辆道路旅行时间数据分析的结果以及第2节所提出的拥堵指标计算方法,得到路网在不同时段的拥堵指标。基于归一化谱距离平均值指标确定合适分类数为4。依据拥堵指标使用K-means分类器将不同时段的路网分为4类,各类分别表示路网供给能力良好、一般、较差、极差。最终依据路网实时路况数据,评价研究区域内路网供给能力,依此提出合理的交通管控方案。
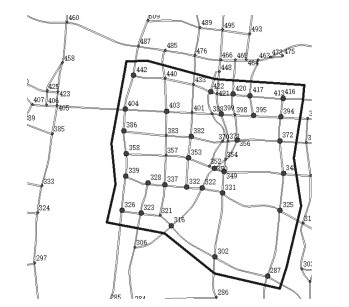
2.1 卡口数据分析依据长沙市城市道路车辆车牌识别系统数据,分析长沙市五一广场周边道路网络2019年7月1日—2019年7月13日的交通状况。研究区域内(框内区域)的道路交通网络包含有44个节点,146条有向路段,如图 3所示。
|
图 3 研究区域示意图 Fig. 3 Case of area studied |
区域内设有卡口监控的节点有31个(粗黑点位置),长沙市道路卡口监控系统平均每日记录数据约有2 200万条,所分析数据的数据结构见表 1。通过卡口数据分析得出的路段行程时间分布可以看出,研究区域内交通流量有明显的早晚高峰拥挤现象,如图 4所示。
| 表 1 部分数据 Tab. 1 Part of data |
|
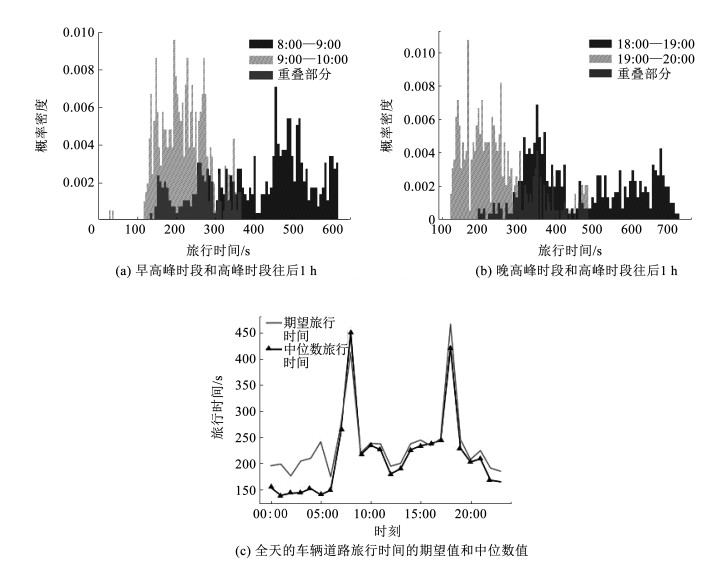
图 4 2019年7月1日(325, 331)路段道路旅行时间情况 Fig. 4 Road travel time of the section (325, 331) on July 1, 2019 |
图中以(325, 331)路段为例,图 4(a)展示了早高峰时期及其往后1 h的车辆道路旅行时间概率密度分布,早高峰时段向后1 h内的车辆旅行时间相比于早高峰时段有了明显下降, 早高峰时段旅行时间最大值可达600 s;图 4(b)展示了晚高峰时期及其往后1 h的车辆道路旅行时间概率密度分布,晚高峰时段向后1 h内的车辆旅行时间相比于早高峰时段同样有明显下降,并且相比于早高峰时段,晚高峰时段更为拥堵,旅行时间最大值可达700 s;图 4(c)展示了路段在2019年7月1日全天的车辆道路旅行时间的期望值和中位数值。
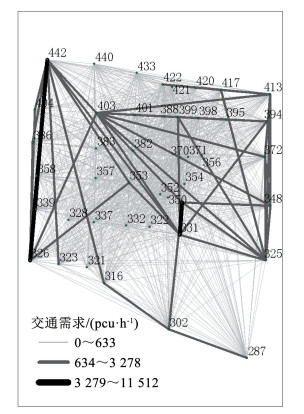
本文以道路围合区域作为自然的交通小区,依据交叉口监控数据可得到路网实时OD数据,如图 5所示。图 5展示了路网8日18时的交通需求结果。表 2展示了高峰时段(8日18时)和平峰时段(8日6时)交通需求前十的OD对的交通流量和最短路径时间。
|
图 5 交通需求结果(8日18时) Fig. 5 Traffic demand results (18:00 on the 8th) |
| 表 2 交通需求前十的OD对的交通数据 Tab. 2 Traffic data of the top ten OD pairs by traffic demand |
基于长沙市2019年7月1日—2019年7月13日的城市道路卡口监控数据,得到每天每时研究区域内道路网络的道路行程时间和路网OD数据,进而可分析得出拥堵指标结果,如图 6所示。图 6展示了拥堵指标最大值于2019年7月8日18时出现,值为3.492 4,最小值出现于2019年7月2日23时,值为1.312 8。总的来说,早晚高峰时段路网拥堵指标有明显增大,并且晚高峰时段路网拥堵指标增长更为显著。在周末(6日、7日、13日)的早晚高峰时段,路网拥堵指标增长幅度相对较小。

|
图 6 拥堵指标结果 Fig. 6 Results of congestion index |
使用K-means聚类算法,依据拥堵指标数据,进行路网分类。为确定合适的类别数量,计算类别为1至7,步长为1,劣化系数δ取2时,归一化谱距离的平均值,如图 7所示。图 7表示当类别为4时归一化谱距离的平均值下降幅度最大。

|
图 7 不同类别的分类结果 Fig. 7 Classification results for different categories |
依据肘部法则,取类别为4进行分类,K-means分类器训练结果将路网划分成了4类,中心点拥堵指标分别为1.522、1.823、2.207、3.069,拥堵指标从小到大依次确定为类1、2、3、4。
根据拥堵指标可将路网划分成了4类,依据各类别对应的中心点拥堵指标来衡量不同类别的路网供给能力:拥堵指标越接近于1,其供给能力越好;拥堵指标越大,其供给能力越差。类1表示路网供给能力良好;类2表示路网供给能力一般;类3表示路网供给能力较差;类4表示路网供给能力极差。
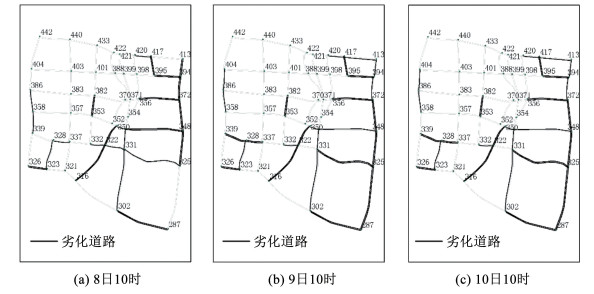
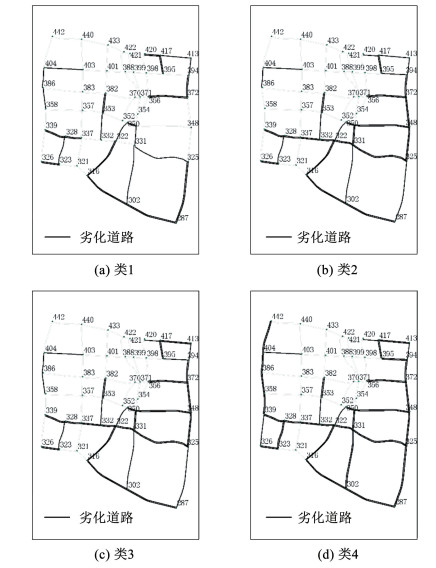
以类3为例,可知同一类路网于不同时段的路网劣化结构大致是一样的,如图 8所示,并且各类归一化谱距离的平均值为1.438。统计同一类型内的所有路网,记录劣化可能性超过50%的路段,得到各类型道路网络路段劣化情况如图 9所示。
|
图 8 不同时段的同一类路网结构(以类3为例) Fig. 8 The road network structure of the same type in different time periods (take class 3 as an example) |
|
图 9 各类道路网络路段劣化情况 Fig. 9 Deterioration of sections of various road network |
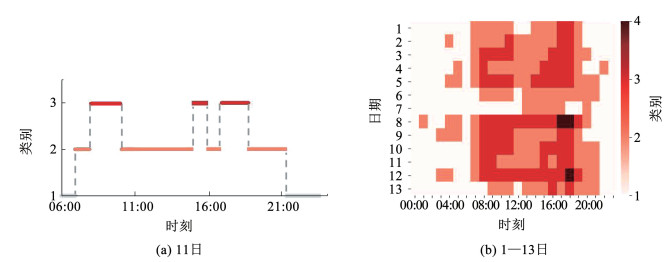
依据道路网络实时路况数据以及训练后的K-means分类器,可得2019年7月1日研究区域内交通网络剩余供给能力变化过程如图 10(a)所示,2019年7月1日—7月13日研究区域内交通网络供给能力变化过程如图 10(b)所示。
|
图 10 交通网络供给能力变化 Fig. 10 Change of transportation network supply capacity |
图 10表明,早晚高峰时段路网剩余供给能力有明显劣化,即路网剩余供给能力较差,路网多为类3状态,并且晚高峰时路网有可能处于剩余供给能力极差状态(即路网为类4)。并且相比于工作日,在周末(6日,7日、13日)的早晚高峰时段,路网剩余供给能力表现较为良好,这与实际情况相一致。
2.5 交通管控实施效果本文针对路网在不同时段所属的类别,建议使用不同的交通管控方式,如表 3所示。
| 表 3 各类别道路网络应采取的交通管控方式 Tab. 3 Traffic control methods that should be adopted in various types of road networks |
为体现针对不同类型路网实施管控方案的效果,本文选用1日18时以及1日19时的路网为例,路网分别处于类2状态、类3状态。对上述两类路网实施对应的管控措施,计算仿真结果见表 4、5。表 4展示了1日18时,当路网处于类3状态时,对路径1(287, 325, 348, 372, 394)施行交通信号控制优化后——依据车流量比值调整其直行方向上的绿信比,路径拥堵缓解情况,结果表明实施信号优化控制后,路径1的社会总成本下降了5.1%;同样,表 5展示了1日19时,当路网处于类2状态时,对路径1施行信号优化控制后的效果,路径1社会总成本下降了6.3%。
| 表 4 类3路网实施管控的效果 Tab. 4 The effect of implementing traffic control method for class 3 road network |
| 表 5 类2路网实施管控的效果 Tab. 5 The effect of implementing traffic control method for class 2 road network |
1) 基于道路车辆车牌识别系统数据,分析得到路网实时路况数据,包括道路行程时间和路网OD需求数据,并使用基于平均最短路径长度的拥堵指标衡量道路网络运行情况。依据指标结果构成的数据集,基于谱距离指标确定分类数,训练K-means分类器,不同类别表示不同程度的剩余供给能力。最终依据训练后的K-means分类器和实时路网指标结果,对路网进行分类以评价其剩余供给能力。
2) 以长沙市五一广场附近的道路网络为实例,研究结果与实际情况相符,即早晚高峰时段路网供给能力有明显劣化,路网多为类3状态,晚高峰时路网甚至会处于剩余供给能力极差状态(类4),并且相比于工作日,周末的早晚高峰时段,路网剩余供给能力表现较为良好。针对路网不同时段所处的剩余供给能力状态,针对性使用交通管控方案,能有效缓解交通拥堵,仿真结果表示拥堵路径社会总成本下降5%以上。
3) 以往的交通可靠性研究要么需将车辆数据与地图数据相匹配,存在滞后性,要么只能涵盖路网部分路段,难以于实践中应用。本文运用实时交叉口车牌识别数据,高效,准确,真实地反映了网络交通状态。相比于传统交通网络可靠性评价研究,避免了数据与地图匹配问题,使得本文提出的方法能实时地反映网络交通状态。
| [1] |
SONG Chaoming, QU Zehui, BLUMM N, et al. Limits of predictability in human mobility[J]. Science, 2010, 327(5968): 1018. DOI:10.1126/science.1177170 |
| [2] |
王璞, 鲁恒宇, 谭倩, 等. 手机信令与出租车GPS数据融合车源定位方法[J]. 哈尔滨工业大学学报, 2018, 50(9): 96. WANG Pu, LU Hengyu, TAN Qian, et al. A data fusion approach for locating driver sources using mobile phone signaling data and taxi GPS data[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 96. |
| [3] |
JENELIUS E, KOUTSOPOULOS H N. Travel time estimation for urban road networks using low frequency probe vehicle data[J]. Transportation Research Part B: Methodological, 2013, 53: 64. DOI:10.1016/j.trb.2013.03.008 |
| [4] |
于德新, 田秀娟, 杨兆升. 基于改进FCM聚类的交通控制时段划分[J]. 华南理工大学学报(自然科学版), 2016, 44(12): 53. YU Dexin, TIAN Xiujuan, YANG Zhaosheng. Division of traffic control periods based on improved FCM clustering[J]. Journal of South China University of Technology, 2016, 44(12): 53. |
| [5] |
姚佼, 徐洁琼. 基于混合聚类的城市道路多时段控制研究[J]. 计算机应用研究, 2016, 33(11): 3274. YAO Jiao, XU Jieqiong. Mixed clustering based time of day control study in urban road[J]. Application Research of Computers, 2016, 33(11): 3274. |
| [6] |
别一鸣, 姜凯, 汤茹茹, 等. 考虑方案过渡影响的单点交通控制时段划分方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1844. BIE Yiming, JIANG Kai, TANG Ruru, et al. Time of interval partition for traffic control at isolated intersection considering impacts of plan transition[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(6): 1844. DOI:10.13229/j.cnki.jdxbgxb20181119 |
| [7] |
徐洁琼, 姚佼, 倪枫. 城市干道的多时段协调控制优化[J]. 公路交通科技, 2017, 34(8): 114. XU Jieqiong, YAO Jiao, NI Feng. Arterial time-of-day coordinated control optimization in urban area[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 114. |
| [8] |
IIDAY. Basic concepts and future directions of road network reliability analysis[J]. Journal of Advanced Transportation, 1999, 33(2): 125. |
| [9] |
LIAN Qiang, ZHANG Penghui, LI Huaifeng, et al. Adjustment method of bridge seismic importance factor based on bridge network connectivity reliability[J]. Structures, 2021, 32: 1692. DOI:10.1016/j.istruc.2021.03.113 |
| [10] |
ASAKURA Y. Reliability measures of an origin and destination pair in a deteriorated road network with variable flows[C]//Transportation Networks: Recent Methodological Advances, Selected Proceedings of the 4th EURO Transportation Meeting. Newcastle, England: Pergamon Press, 1996: 273
|
| [11] |
陈喜群, 刘教坤, 胡浩强, 等. 网络行程时间可靠性评价方法与影响因素[J]. 交通运输工程学报, 2018, 18(4): 132. CHEN Xiqun, LIU Jiaokun, HU Haoqing, et al. Evaluation method and influence factors of network travel time reliability[J]. Journal of Traffic and Transportation Engineering, 2018, 18(4): 132. DOI:10.19818/j.cnki.1671-1637.2018.04.014 |
| [12] |
张琦, 陈红, 刘至真, 等. 降雨量对OD行程时间可靠性影响分析[J]. 交通运输系统工程与信息, 2019, 19(6): 243. ZHANG Qi, CHEN Hong, LIU Zhizhen, et al. Analysis of effects of rainfall on origin-destination based travel time reliability[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(6): 243. DOI:10.16097/j.cnki.1009-6744.2019.06.035 |
| [13] |
CHEN A, YANG Hai, LO H K, et al. A capacity related reliability for transportation networks[J]. Journal of Advanced Transportation, 1999, 33(2): 183. DOI:10.1002/atr.5670330207 |
| [14] |
方雅君, 郑长江, 马庚华, 等. 基于路段服务水平约束的路网容量可靠性分析[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(3): 502. FANG Yajun, ZHENG Changjiang, MA Genghua, et al. Reliability analysis of road network capacity based on service level constraints[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2019, 43(3): 502. |
| [15] |
马庚华, 杜牧青, 张小丽. 不确定因素下的综合运输网络容量可靠性分析[J]. 郑州大学学报(工学版), 2018, 39(1): 1. MA Genghua, DU Muqing, ZHANG Xiaoli. Capacity reliability of comprehensive transportation network under uncertainties[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(1): 1. DOI:10.13705/j.issn.1671-6833.2018.01.021 |
| [16] |
LI Huiping, HE Fang, LIN Xi, et al. Travel time reliability measure based on predictability using the Lempel-Ziv algorithm[J]. Transportation Research Part C, 2019, 101: 58. |
| [17] |
ZHONG Siyuan. RFID E-plate data based travel time reliability estimation of urban expressway[C]//4th International Symposium on Big Data and Applied Statistics (ISBDAS 2021). Dali, China: IOP Publishing Ltd., 2021: 012010. DOI: 10.1088/1742-6596/1955/1/012010
|
| [18] |
王佳. 动态网络的结构相似性度量方法与应用研究[D]. 北京: 北京交通大学, 2019 WANG Jia. Research on structural similarity measurement method and application for dynamic networks[D]. Beijing: Beijing Jiaotong University, 2019. DOI: 10.26944/d.cnki.gbfju.2019.000616 |
 2023, Vol. 55
2023, Vol. 55


