2. 宁波大学 海运学院,浙江 宁波 315211
2. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, Zhejiang, China
栓钉连接件具有施工简便、受力无方向等优点,是目前钢-混凝土组合梁中应用最广泛的一种连接件,也是保证混凝土板和钢梁共同作用的关键部件[1]。然而,在实际组合桥梁运营过程中,由于车辆、温度等可变荷载的反复作用,使得组合梁中栓钉连接件性能发生退化,混凝土与钢梁的交界面产生相对滑移,进而导致组合梁整体受力性能降低[2-3]。随着全寿命周期理念的不断深入[4],栓钉连接件在整个寿命周期内由于疲劳损伤造成滑移量不断累积以及滑移性能不断变化的现象越来越受到关注[5]。所以,研究全寿命周期内组合梁中栓钉连接件在疲劳荷载作用下的滑移性能对于掌握组合梁整体力学性能演化规律具有重要意义。
目前,已有大量学者针对栓钉连接件的疲劳滑移性能开展研究工作。文献[6]研究了在静力和疲劳荷载作用组合桥梁中大栓钉的滑移性能;文献[7]通过推出试验研究了不同型号栓钉连接件在疲劳荷载作用下滑移量的增长规律,并提出了基于全寿命周期的组合结构设计概念;文献[8]通过推出试验研究了组合梁中群钉的滑移性能,发现将栓钉成组布置会加速其刚度的退化和滑移增长,从而降低栓钉的疲劳寿命;文献[9]针对轻型组合桥面板中小栓钉在疲劳荷载作用下的滑移行为进行了分析,发现在试件疲劳破坏阶段,滑移量增速较快且增量明显;文献[10]对单调和重复荷载作用下的滑移行为进行了分析对比,分析了栓钉直径、混凝土强度等参数对栓钉的疲劳性能和抗剪性能的影响,发现相同荷载下的滑移量重复加载要比单调加载多出60%以上。可见,目前这些研究主要针对于在疲劳荷载作用下栓钉连接件滑移量的累积增长情况,但对于经历一定次数疲劳荷载作用后的栓钉荷载-滑移模型的研究尚属空白。
本文基于三组栓钉推出试验,以指数型荷载-滑移模型为基准,分析其关键参数对模型曲线的影响,进而通过试验数据拟合,确定其关键参数,并根据拟合得到的静力作用下的极限滑移量计算公式,提出改进的栓钉指数型荷载-滑移曲线模型。在此基础上,考虑疲劳损伤对栓钉直径及滑移量的折减,同时考虑栓钉连接件在疲劳加载过程中的累积滑移量和疲劳加载后的剩余滑移量,建立在任意次数疲劳荷载循环下栓钉连接件全过程荷载-滑移计算模型,并通过试验值进行对比验证。
1 试验及结果分析 1.1 试验设计本试验共设计11个栓钉推出试件,试件参考欧洲规范EC4[11]进行设计,两侧混凝土翼板尺寸为450 mm×500 mm×150 mm,强度等级为C50,中间钢梁采用Q345的H型钢,尺寸为250 mm×200 mm×14 mm,构造钢筋为Ф10 mm的HPB300钢筋,栓钉为强度ML-15的Ф13 mm×70 mm,布置于距钢梁顶端350 mm处,栓钉横向间距为80 mm,通过测试得到栓钉极限强度平均值为525 MPa,试件具体尺寸构造如图 1所示。

|
图 1 栓钉推出试件尺寸(mm) Fig. 1 Size of the stud push-out specimen (mm) |
为了得到不同疲劳加载次数下的栓钉连接件荷载-滑移情况,推出试验共分为3组,包括静力滑移量试验3个试件、疲劳滑移量试验3个试件及部分疲劳加载后的剩余滑移量试验5个试件。测试内容主要包括试验过程中所加的荷载值(包括荷载幅值、极限荷载值和荷载变化范围),钢板与混凝土间的相对滑移量及疲劳寿命。其中荷载值由加载端作动器内置的力传感器读取,相对滑移量由位移计采集得到,位移计针头布置于和栓钉平行的位置处。同时,为了保证荷载的竖直加载,设置了可调平底座,如图 2所示。

|
图 2 试件加载过程 Fig. 2 Specimen loading process |
在静力试验中,初始每级荷载增量为20 kN,加载速率为10 kN/min。当加载至极限荷载的60%时,改为位移控制加载,加载速率为2 mm/min,直至试件破坏。在疲劳试验中,在试件首次加载及在疲劳加载至1、5、10、25、⋯、万次时停机卸载,并进行一次静力测试,加载至疲劳上限值,直至完成疲劳循环次数n,之后进行静力加载,整个过程如图 3所示。本次疲劳试验加载波形为正弦线,加载频率为4 Hz,加载具体参数见表 1。表 1中,SCP-1~3为静力推出试件,FCP-1~3为疲劳推出试件,SFCP-1~5为部分疲劳加载的推出试件,Pmax为疲劳加载幅值上限,Pmin为疲劳加载幅值下限,ΔP为疲劳加载幅值,Pu为静力极限承载力,n为疲劳加载次数,N为试件疲劳寿命。

|
图 3 疲劳试验加载程序 Fig. 3 Loading procedure for fatigue test |
| 表 1 三组试件加载参数 Tab. 1 Loading parameters of three groups of specimens |
通过3个推出试件的静力试验,得到3个推出试件单个栓钉的极限承载力分别为68.6、70.7、71.7 kN,因试验值较为接近,取三者的平均值70.2 kN作为单钉的极限承载力。
图 4给出了栓钉推出试件在静力荷载作用下的荷载-滑移曲线,最大滑移量在5~6 mm之间。3个试件的曲线基本一致,曲线的相关系数在0.97~0.98之间,表明试验值具有较高的可靠性。现根据曲线的斜率变化情况,将栓钉连接件的荷载-滑移曲线分为4个阶段:1)线性段,即荷载与滑移量成正比;2)弹塑性段,荷载与滑移量呈非线性增长,且增长速率逐渐降低;3)塑性段,荷载基本保持不变,滑移量不断增加;4)下降段,随着滑移量的增加,荷载出现了负增长。

|
图 4 静力荷载作用下SCP-1~3的荷载-滑移曲线 Fig. 4 Load-slip curves of SCP-1~3 under static load |
3个推出试件疲劳试验结果的离散性相对较大,试件FCP-1和试件FCP-3的疲劳寿命分别为274.2万次和261.8万次,而试件FCP-2在加载中发生侧向偏转而提前破坏,因而其结果不予采用。取试件FCP-1和试件FCP-3的疲劳寿命得平均值268万次作为推出试件的疲劳寿命。
图 5给出了推出试件(FCP-1、FCP-3)在疲劳加载过程中栓钉累积滑移量的增长情况。如图 5所示,栓钉的累积滑移量的增长可以大体划分为3个阶段:在第1个阶段,累积滑移量随着疲劳加载次数的增加而迅速增长,且增长速率较快,该阶段约仅占总疲劳寿命的10%;在第2个阶段,累积滑移量的增长速率减慢,增长速率相对稳定,该阶段约占总疲劳寿命的80%;在第3个阶段,疲劳加载次数逐渐趋近于疲劳寿命,累积滑移量快速增长,直至栓钉发生突然断裂破坏,该阶段约占总疲劳寿命的10%。

|
图 5 疲劳累积滑移量增长与拟合曲线 Fig. 5 Growth and fitting curve of fatigue accumulative slip |
为获得不同疲劳加载次数后栓钉连接件的荷载-滑移曲线,对在经历了一定疲劳加载循环后的5个推出试件(SFCP-1~SFCP-5)进行静力破坏试验,得到其荷载-滑移曲线,如图 6所示。

|
图 6 剩余滑移量试验的荷载-滑移曲线 Fig. 6 Load-slip curve from residual slip test |
由图 6可知,在经历了不同疲劳循环后,荷载-滑移曲线的整体形状和静力滑移量试验类似。但随着循环次数的增加,由于疲劳累积滑移的存在,使得栓钉的初始滑移量不断增加,同时栓钉的承载力也逐渐下降。另外,通过进一步对比发现,虽然栓钉的累积滑移量在不断增加,但总滑移量却在减少。可见,随着疲劳加载次数的增加,由于疲劳损伤的存在,导致栓钉连接件整体变形性能越来越差。
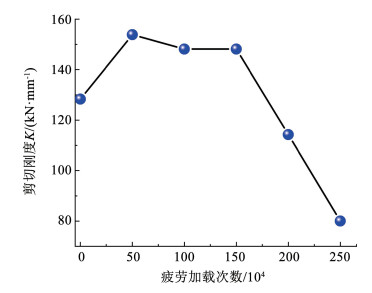
另外,在不同疲劳加载次数后,栓钉的剪切刚度也发生了退化现象,这里将栓钉的剪切刚度定义为K=Pmax/δmax,其中δmax为疲劳荷载上限值Pmax对应的滑移量。图 7给出了栓钉剪切刚度随疲劳加载次数的变化特征。由图 7可知,栓钉的剪切刚度随疲劳加载次数表现出先升后降的变化特征,造成这种现象的原因可能是因为在疲劳加载初期,栓钉与周边混凝土接触不紧密,导致剪切刚度较小;随着加载次数的增加,栓钉与混凝土之间逐渐密实,剪切刚度逐渐增大;然而随着疲劳加载次数的持续增加,疲劳损伤不断累积,导致剪切刚度逐渐退化。
|
图 7 剪切刚度随疲劳加载次数的变化 Fig. 7 The variation of shear stiffness with loading times |
已有许多学者对栓钉连接件在单调荷载作用下的荷载-滑移模型进行了研究,并提出了各式模型,主要有指数型、分式型等[12],其中,文献[13]提出的指数型荷载-滑移模型应用较为广泛,具体公式为
| $ P=P_{\mathrm{u}} \times\left(1-\mathrm{e}^{-\beta|\delta|}\right)^\alpha $ | (1) |
式中:P为荷载值,δ为相对滑移量,α、β为影响参数,Pu为栓钉极限承载力,同时当栓钉破坏时,单钉极限承载力Pu可表示为
| $ P_{\mathrm{u}}=k_{\mathrm{s}} A_{\mathrm{s}} f_{\mathrm{u}}=k_{\mathrm{s}} \frac{\pi d_{\mathrm{s}}^2}{4} f_{\mathrm{u}} $ | (2) |
式中:ks为系数,通过对比发现,当ks=1时,式(2)计算结果和试验结果吻合良好;As为栓钉横截面积,ds为栓钉直径;fu为栓钉极限抗拉强度。
对于指数型荷载-滑移模型(式(1))而言,只要给定合适的α和β值,便可以较好地模拟出不同情况下栓钉的荷载-滑移曲线。但该模型仍存在一些缺陷,主要表现为其无法对滑移量极限值进行有效限定。如当加载值P无限接近于栓钉极限承载Pu时,其滑移量δ则趋向于无限大,这显然与实际情况不符。因而需要对原有经典的荷载-滑移模型的极限滑移量进行相应限制。
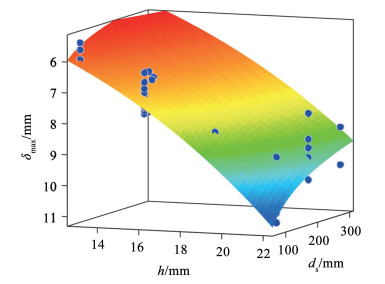
目前国内外关于极限滑移的研究相对较少,文献[6]定义极限滑移为当荷载从峰值降低10%时的滑移,并提出了与圆柱体混凝土抗压强度及栓钉直径有关的极限滑移的计算公式。文献[10]通过试验发现,对于相同直径的栓钉,混凝土强度的增强对极限承载力及所对应的位移影响较小;文献[14]研究了单调荷载下,栓钉连接件受力性能,结果表明,栓钉直径和高度对极限滑移都有较大影响。基于此,本文统计了国内外学者共计50个试验数据[14-23],以栓钉的直径ds、高度h为自变量,构造模型(式(3))进行参数拟合,以确定模型参数a、b、c的值。为提高精度,在模型初次拟合后,根据数据残差以平均值加减2倍的标准差μ±2σ为界剔除离群值,最后根据剩余的32个数据得到模型拟合的决定系数R2=0.833 1,拟合结果较好。此时拟合得到a=2.633,b=0.078,c=-0.119。图 8为极限滑移量模型曲面拟合结果。
| $ \delta_{\max }=a\left(1+\mathrm{e}^{b d_{\mathrm{s}}}\right) h^c $ | (3) |
|
图 8 极限滑移量模型曲面拟合结果 Fig. 8 Surface fitting results of limit slip model |
因此,考虑极限滑移量的栓钉指数型荷载-滑移曲线模型可写为
| $ P=P_{\mathrm{u}} \times\left(1-\mathrm{e}^{-\beta|\delta|}\right)^\alpha, \delta \leqslant \delta_{\max } $ | (4) |
其中δmax=2.633(1+e0.078ds)h-0.119
将本文试验所用栓钉的相关数据代入式(3)中,可以得到极限滑移量为5.97 mm。进而基于静力荷载作用下SCP-1~3的荷载-滑移曲线的试验结果,用式(4)进行拟合,如图 4中所示,得到α=0.85,β=1.78,R2=0.973,拟合精度较好。
3 疲劳荷载作用下栓钉荷载-滑移模型 3.1 模型建立思路由试验结果分析可知,对于经历一定疲劳循环次数后静载破坏的栓钉推出试件而言,其总滑移量由两部分组成(见图 9):一是在疲劳加载循环n次中产生的累积滑移量,记为s(n);二是经历n次疲劳循环荷载后的静力加载中产生的滑移量,记为δ(n)。则总滑移量su(n)可表示为
| $ s_{\mathrm{u}}(n)=s(n)+\delta(n) $ | (5) |

|
图 9 疲劳荷载作用下总滑移量组成示意图 Fig. 9 Composition diagram of total slip under fatigue load |
如图 9所示,若完全静载作用下的滑移量为δ(0),那么栓钉在经历n次疲劳循环荷载作用后,由于疲劳损伤的影响,其结构刚度、承载力、极限滑移量等力学性能指标均会出现一定程度的退化,此时静载作用下的滑移量记为δ(n)。同时,考虑在疲劳加载过程中,经历n次循环所产生的累积滑移量s(n)。将两者相加即可得到栓钉在整个阶段的滑移量总和su(n)。因此只需要分别确定s(n)和δ(n)的计算模型,便可得到经历任意次数疲劳加载作用后直至静载破坏的整个过程中栓钉滑移量的分布情况。
3.2 累积滑移量计算模型文献[7]根据大量推出试验并结合理论推导,得出了n次疲劳荷载作用下栓钉的累积滑移量计算公式:
| $ s(n)=\left\{\begin{array}{l} C_1-C_2 \times \ln \left(\frac{N-n}{n}\right), 0 <\frac{n}{N}<0.9 \\ 0, \frac{n}{N}=0 \end{array}\right. $ | (6) |
其中:
通过本文试验数据与式(6)进行对比,如图 5所示,得到曲线的相关系数在0.96~0.98之间,吻合较好,说明该公式可较好地模拟出疲劳过程中栓钉连接件的累积滑移量增长情况。
3.3 疲劳作用后的荷载-滑移模型由图 6可知,在经历一定疲劳循环荷载作用后,栓钉的整体力学性能指标均发生了下降,结合式(4)的模型中,体现力学性能的参数为栓钉的极限承载力,因而只要将栓钉的极限承载力替换为栓钉的剩余承载力,即可得到经历一定疲劳荷载后的静载荷载-滑移模型:
| $ P=P_{\mathrm{s}}(n) \times\left(1-\mathrm{e}^{-1.78 \delta(n)}\right) 0.85, \delta(n) \leqslant \delta_{\max }(n) $ | (7) |
式中:Ps(n)表示经过n次荷载循环后栓钉连接件剩余承载力,δmax(n)为栓钉剩余极限滑移量。
上述中Ps(n)可根据基于“二元疲劳失效判据”建立的栓钉剩余承载力计算模型[24]得到,计算公式为
| $ P_{\mathrm{s}}(n)=P_{\mathrm{u}}-\left(P_{\mathrm{u}}-P_{\max }\right)\left(\frac{n}{N}\right)^c $ | (8) |
式中:Pu为栓钉的极限承载力(静力试验所得值);Pmax为疲劳荷载上限值;n为实际荷载循环次数;N为试件的疲劳寿命;
由此,在式(7)中,仅需要确定栓钉在疲劳作用后静载的极限滑移量δmax(n)。假设栓钉强度fu不变,参考式(2),n次荷载循环后,栓钉连接件的直径可表示为
| $ d_{\mathrm{s}}^{\prime}=2 \sqrt{\frac{P_{\mathrm{s}}(n)}{\pi f_{\mathrm{u}}}} $ | (9) |
同时,随着疲劳加载次数的增加,栓钉的脆性不断增加[25],表现为其滑移量不断减少,所以在考虑栓钉直径折减的同时,还要考虑滑移量下降。因此,可将δmax(n)表示为
| $ \delta_{\max }(n)=2.633\left(1+\mathrm{e}^{0.078 d_{\mathrm{s}}^{\prime}}\right) h^{-0.119}-k_n \frac{n}{N}(10) $ | (10) |
通过本文SFCP-1~55组试验数据对其进行拟合,得到kn=0.678,R2=0.858,即拟合效果较好,此公式可确定栓钉在疲劳作用后静力加载中的极限滑移量。
3.4 栓钉全过程荷载-滑移模型由此,栓钉在疲劳荷载作用下的全过程荷载-滑移模型可分为3个步骤来计算:第1步,通过式(6)计算在n次疲劳加载过程中栓钉的累积滑移量s(n);第2步,利用式(8)和式(10)分别计算栓钉在疲劳加载后的剩余承载力Ps(n)和剩余极限滑移量δmax(n);第3步,将栓钉疲劳过程中的累积滑移量s(n)计入栓钉荷载-滑移模型(式(7)),就得到了栓钉全过程荷载-滑移模型(式(11))。具体计算流程如图 10所示。
| $ P=\left\{\begin{array}{l} 0, s_{\mathrm{u}}(n) \leqslant s(n) \\ P_{\mathrm{s}}(n) \times\left(1-\mathrm{e}^{-1.78(s(n)+\delta(n))}\right)^{0.85}, s_{\mathrm{u}}(n)>s(n) \end{array}\right. $ | (11) |

|
图 10 栓钉全过程荷载-滑移模型计算流程 Fig. 10 Calculation flow of load-slip model for the whole process of stud |
其中δ(n)≤δmax(n)。
值得说明的是,在式(11)中,当n=0时,即为单调荷载作用下栓钉的荷载-滑移计算模型。
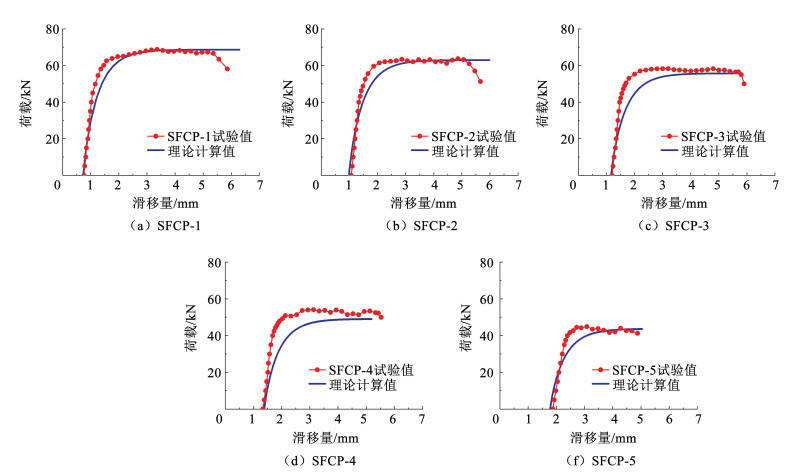
3.5 模型验证为验证本文所提模型的正确性,按图 10的计算流程对本文试验试件SFCP-1~5进行计算。首先,计算栓钉在经历50万次、100万次、150万次、200万次以及250万次荷载循环后累积滑移量分别是0.74、0.98、1.17、1.39、1.78 mm;其次,计算栓钉的剩余承载力分别是68.68、62.98、55.73、49.06、43.71 kN,剩余极限滑移量分别是5.56、5.00、4.39、3.80、3.25 mm;最后通过式(11)得到每个试件栓钉的全过程荷载-滑移模型,将其与试验结果进行对比,对比结果如图 11所示。
|
图 11 不同疲劳加载次数下栓钉全过程荷载-滑移曲线试验值与理论值对比 Fig. 11 Comparison of calculated and experimental values of load-slip curves in the whole process of stud under different load cycles |
由图 11可知,试验值和理论值总体来说吻合较好,主要误差出现在荷载-滑移曲线的屈服段,实际栓钉试件表现出更好的刚度。另外,随着疲劳加载次数的增加,理论值与试验值之间误差增大,这主要是因为随着加载次数的增加,疲劳损伤的离散性也不断增大所致。
此外,基于式(5)可进一步分析栓钉在疲劳加载直至最后静力破坏的整个过程中,总滑移量、累积滑移量及剩余滑移量三者的变化趋势,如图 12所示。

|
图 12 栓钉总滑移量、累积滑移量及剩余滑移量的变化 Fig. 12 Variation of total slip, cumulative slip and residual slip of stud |
由图 12可知,随着疲劳加载次数的增加,栓钉累积滑移量不断增加,剩余滑移量不断减少,总滑移量先缓慢增加而后不断减少,该趋势和图 6的试验结果吻合。说明在疲劳荷载作用下,由于栓钉内部的疲劳损伤不断增加导致其整体变形性能逐渐变差。因此,在实际工程中,需要关注由于疲劳损伤导致栓钉变形能力下降,导致滑移量不足的情况。
4 结论本文基于11个栓钉推出试件进行了静力滑移量试验、疲劳滑移量试验及剩余滑移量试验,通过试验结果分析了栓钉连接件在疲劳及静力作用下全过程的滑移量增长和分布特征。在此基础上,建立了在单调荷载作用下及疲劳荷载作用下栓钉的荷载-滑移计算模型,具体研究结论如下:
1) 在单调荷载作用下,选用指数型荷载-滑移模型,并基于本文及文献统计数据,拟合出了栓钉极限滑移量的计算公式,提出了改进的栓钉荷载-滑移计算模型。
2) 在疲劳荷载作用下,栓钉连接件的滑移量可分为疲劳加载过程中的累积滑移量和疲劳加载后的剩余滑移量。栓钉累积滑移量呈“快速-缓慢-急速”的三阶段增长。在疲劳加载作用后栓钉剩余滑移量和总滑移量均随着疲劳循环次数增加而减少,说明随着栓钉的疲劳损伤不断增加导致其整体变形性能逐渐变差。
3) 基于改进的栓钉指数型荷载-滑移模型,考虑疲劳损伤对栓钉直径及滑移量的折减,得出栓钉疲劳作用后静力的极限滑移量表达式,在此基础上考虑栓钉连接件的累积滑移量和剩余滑移量,建立了栓钉全过程荷载-滑移计算模型,并验证了该模型的准确性。
| [1] |
聂建国, 王宇航. 钢-混凝土组合梁疲劳性能研究综述[J]. 工程力学, 2012, 29(6): 1. NIE Jianguo, WANG Yuhang. Research status on fatigue behavior of steel-concrete composite beams[J]. Engineering Mechanics, 2012, 29(6): 1. DOI:10.6052/j.issn.1000-4750.2010.08.0587 |
| [2] |
宋爱明, 李志聪, 徐洪涛, 等. 钢-混凝土组合梁负弯矩区裂缝宽度数值计算模型[J]. 哈尔滨工业大学学报, 2021, 53(3): 75. SONG Aiming, LI Zhicong, XU Hongtao, et al. Numerical calculation model of crack width in negative moment regions of steel-concrete composite beams[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 75. |
| [3] |
曹国辉, 廖世杰, 彭鹏, 等. 腐蚀与荷载耦合作用下钢-混凝土组合梁长期变形研究[J]. 土木工程学报, 2022, 55(1): 32. CAO Guohui, LIAO Shijie, PENG Peng, et al. Long-term deformation of steel-concrete composite beams subjected to coupling effect of corrosion and loading[J]. China Civil Engineering Journal, 2022, 55(1): 32. DOI:10.15951/j.tmgcxb.2022.01.002 |
| [4] |
张清华, 劳武略, 崔闯, 等. 钢结构桥梁疲劳2020年度研究进展[J]. 土木与环境工程学报(中英文), 2021, 43(增刊1): 79. ZHANG Qinghua, LAO Wulue, CUI Chuang, et al. State-of-the-art review of fatigue of steel bridge in 2020[J]. Journal of Civil and Environmental Engineering, 2021, 43(Sup. 1): 79. |
| [5] |
ZHANG Zhigang, XU Xiaoqing. Static and fatigue behavior of rubber-sleeved stud shear connectors as part of field-cast ultra-high performance concrete connections[J]. Materials, 2020, 13(10): 2269. DOI:10.3390/ma13102269 |
| [6] |
LEE P G, SHIM C S, CHANG S P. Static and fatigue behavior of large stud shear connectors for steel-concrete composite bridges[J]. Journal of Constructional Steel Research, 2005, 61(9): 1270. DOI:10.1016/j.jcsr.2005.01.007 |
| [7] |
HANSWILLE G, PORSCH M, USTUNDAG C. Resistance of headed studs subjected to fatigue loading Part Ⅱ: analytical study[J]. Journal of Constructional Steel Research, 2007, 63(4): 485. DOI:10.1016/j.jcsr.2006.06.036 |
| [8] |
XU Chen, SUGIURA K, SU Qingtian. Fatigue behavior of the group stud shear connectors in steel-concrete composite bridges[J]. Journal of Bridge Engineering, 2018, 23(8): 04018055. DOI:10.1061/(ASCE)BE.1943-5592.0001261 |
| [9] |
张士红, 邵旭东, 黄细军, 等. 轻型组合桥面板中小栓钉连接件的静力及疲劳性能[J]. 公路交通科技, 2016, 33(11): 111. ZHANG Shihong, SHAO Xudong, HUANG Xijun, et al. Static and fatigue behaviors of small stud shear connector for lightweight composite bridge deck[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 111. DOI:10.3969/j.issn.1002-0268.2016.11.017 |
| [10] |
赵根田, 章燚, 江伟, 等. 重复荷载下栓钉抗剪连接件的性能研究[J]. 建筑结构, 2019, 49(23): 97 ZHAO Gentian, ZHANG Yi, JIANG Wei, et al. Performance study on stud shear connectors under repeated loads[J]. Building Structure, 2019, 49(23): 97. DOI: 0.19701/j.jzjg.2019.23.018 |
| [11] |
BENG S H, PARK S. EN 1994-Eurocode 4: design of composite steel and concrete structures[J]. Retrieved May, 1994, 10: 2022. |
| [12] |
BUTTRY K E. Behavior of stud shear connectors in lightweight and normal-weight concrete[D]. Columbia: University of Missouri, 1965
|
| [13] |
ZONA A, RANZI G. Shear connection slip demand in composite steel-concrete beams with solid slabs[J]. Journal of Constructional Steel Research, 2014, 102: 266. DOI:10.1016/j.jcsr.2014.07.018 |
| [14] |
XUE Weichen, DING Min, WANG Hua, et al. Static behavior and theoretical model of stud shear connectors[J]. Journal of Bridge Engineering, 2008, 13(6): 623. DOI:10.1061/(ASCE)1084-0702(2008)13:6(623) |
| [15] |
LIN Zhaofei, LIU Yuqing, HE Jun. Behavior of stud connectors under combined shear and tension loads[J]. Engineering Structures, 2014, 81: 362. DOI:10.1016/j.engstruct.2014.10.016 |
| [16] |
张琪. 钢-混凝土组合梁纵向抗剪的试验研究[D]. 南京: 南京工业大学, 2005 ZHANG Qi. Experimental study on longitudinal shear steel-concrete composite beams[D]. Nanjing: Nanjing University of Technology, 2005 |
| [17] |
严永红, 邓芃, 侯和涛, 等. 钢-混凝土组合梁螺栓连接件抗剪性能的试验研究[J]. 山东科技大学学报(自然科学版), 2021, 40(2): 51. YAN Yonghong, DENG Peng, HOU Hetao, et al. Experimental study on shear resistance of bolt connector in steel-concrete composite beam[J]. Journal of Shandong University of Science and Technology(Natural Science), 2021, 40(2): 51. DOI:10.16452/j.cnki.sdkjzk.2021.02.006 |
| [18] |
PAVLOVIC M, MARKOVIC Z, VELJKOVIC M, et al. Bolted shear connectors vs. headed studs behaviour in push-out tests[J]. Journal of Constructional Steel Research, 2013, 88: 134. DOI:10.1016/j.jcsr.2013.05.003 |
| [19] |
JAYAS B S, HOSAIN M U. Behaviour of headed studs in composite beams: push-out tests[J]. Canadian Journal of Civil Engineering, 1988, 15(2): 240. DOI:10.1139/l88-032 |
| [20] |
GATTESCO N, GIURIANI E. Experimental study on stud shear connectors subjected to cyclic loading[J]. Journal of Constructional Steel Research, 1996, 38(1): 1. DOI:10.1016/0143-974X(96)00007-7 |
| [21] |
孙建营. 考虑侧压作用剪力连接件结构行为分析研究[D]. 成都: 西南交通大学, 2017 SUN Jianying. Structural behavior analysis of shear connectors under lateral pressure[D]. Chengdu: Southwest Jiaotong University, 2017 |
| [22] |
姬同庚. 栓钉连接件剪切刚度试验研究[J]. 世界桥梁, 2013, 41(6): 62. JI Tonggeng. Experimental study of shear stiffness of shear bolt studs[J]. World Bridges, 2013, 41(6): 62. DOI:10.3969/j.issn.1671-7767.2013.06.014 |
| [23] |
陈攀. 带约束构造的栓钉剪力连接件受力性能研究[D]. 湘潭: 湖南科技大学, 2019 CHEN Pan. Research on the mechanical properties of stud shear connectors with constrained structure[D]. Xiangtan: Hunan University of Science and Technology, 2019. DOI: 10.27738/d.cnki.ghnkd.2019.000655 |
| [24] |
汪炳, 黄侨, 刘小玲. 疲劳荷载作用下栓钉连接件的抗剪承载力退化规律[J]. 哈尔滨工业大学学报, 2016, 48(9): 76. WANG Bing, HUANG Qiao, LIU Xiaoling. Shear capacity degradation law of stud connectors under fatigue loading[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 76. DOI:10.11918/j.issn.0367-6234.2016.09.014 |
| [25] |
李萌, 邵旭东, 曹君辉, 等. UHPC中短栓钉抗剪性能试验及理论分析[J]. 中国公路学报, 2021, 34(8): 191. LI Meng, SHAO Xudong, CAO Junhui, et al. Performance of experimental and theoretical analysis on shear short headed studs embedded in UHPC[J]. China Journal of Highway and Transport, 2021, 34(8): 191. DOI:10.19721/j.cnki.1001-7372.2021.08.016 |
 2023, Vol. 55
2023, Vol. 55


