2. 江西省地下空间技术开发工程研究中心(华东交通大学),南昌 330013;
3. 江西省岩土工程基础设施安全与控制重点实验室(华东交通大学),南昌 330013;
4. 滨海和城市岩土工程研究中心(浙江大学),杭州 310058;
5. 江西省交通科学研究院有限公司,南昌 330013
2. Engineering Research & Development Centre for Underground Technology of Jiangxi Province(East China Jiaotong University), Nanchang 330013, China;
3. Jiangxi Key Laboratory of Infrastructure Safety Control in Geotechnical Engineering(East China Jiaotong University), Nanchang 330013, China;
4. Research Center of Coastal and Urban Geotechnical Engineering (Zhejiang University), Hangzhou 310058, China;
5. Jiangxi Transportation Institute Co., Ltd., Nanchang 330013, China
在岩土工程中常采用地下降水的方式对施工条件进行改善,如为了开挖基坑及加固软土地基等[1-2]。而地下水位下降会引起原水位下方土体的有效应力增加,导致邻近土体及既有管线产生变形[3]。地下管线作为城市的生命线,其服役状态稍有差池便可造成巨大的生命财产损失[4]。因此如何准确预测地下降水对邻近管线的影响,已成为城市地下空间建设亟待解决的问题。
目前已有众多学者对地下降水引起的邻近地下管线变形问题展开研究[5-14]。文献[5]结合工程实例建立三维有限元模型模拟了降水引起的邻近管线不均匀沉降。文献[7]结合有限差分法与流固耦合理论研究了降水施工中,市政管线产生的受力变形。文献[9]采用多种方法对基坑降水引起邻近地下管线变形问题进行研究。文献[10]结合天津西站基坑工程,建立数值模型研究了降水对邻近地铁隧道的影响。文献[13]采用两阶段分析法,基于Pasternak地基梁模型,推导了地下降水引起邻近管线变形的解析解。文献[14]采用两阶段分析法,基于Pasternak地基梁模型,分析了基坑正下方隧道因开挖与降水引起的变形,结果表明降水对下卧隧道的影响不应被忽视。
在针对既有管线与土相互作用的现有研究中,弹性地基梁是较为常见的理论方法,常用的地基模型有Winkler地基[16]与Pasternak地基[17]。如图 1所示,Winkler模型将土体视作相互独立的弹簧,是仅考虑土体弹簧刚度的单参数模型;Pasternak模型在Winkler模型基础上通过将弹簧单元与一层只能产生剪切变形的剪切层连接,采用土体弹簧刚度与剪切层刚度两个参数考虑土体变形的连续性[18]。三参数的Kerr地基梁模型[19]是对双参数模型的进一步深化[20],如图 1(c)所示,该模型具有两个弹簧层(刚度为c,k)分别位于剪切层两侧,可以更好地考虑土体的剪切变形。文献[21]采用了Kerr地基模型研究盾构隧道下穿引起上覆既有隧道的竖向位移,结果表明Kerr地基模型计算结果更为准确。

|
图 1 弹性地基梁模型示意图 Fig. 1 Elastic foundation beam model diagram |
综上,为准确预测管线因单井降水引起的竖向变形,本文采用两阶段法在第一阶段结合有效应力原理与Dupuit假定计算出降水引起邻近管线受到的附加应力,在第二阶段采用三参数Kerr地基梁模型模拟管线与土的相互作用,得到了单井降水引起邻近管线的竖向位移。随后将本文所提方法与既有文献结果及原位试验结果进行对比,验证了本文方法的准确性,并深入研究了土体弹性模量Es、渗透系数kt、管线与降水井间距d以及水位降深sw变化对管线竖向位移的影响。
1 方程的建立地下降水将不可避免地引起周围地下水位发生变化,地下水位受到影响范围的半径称为降水半径。根据萨库金公式[22],降水半径R的计算公式为
| $ R=2 s_{\mathrm{w}} \sqrt{k H_0} $ | (1) |
式中:sw为降水井的水位降深,sw=H0-Ht,H0为潜水含水层的初始水位高度,Ht为降水后井中的水位高度。
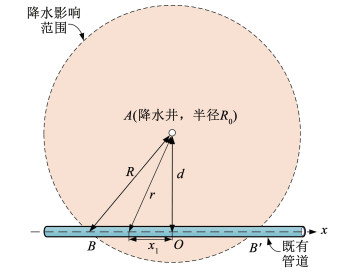
在降水半径内,水位下降会导致土中孔隙水压力下降,进而引起有效应力增加,此时降水半径范围内存在的既有管线会受到降水的影响。如图 2所示,A为降水井,半径为R0,既有管线与降水井垂直水平距离为d。以管线轴线上距降水井最近的O点为原点,沿管线方向建立x轴。B点,B′点为降水半径与管线的交点。
|
图 2 降水半径 Fig. 2 Radius of dewatering |
如图 3所示,降水会使在地下水位形成漏斗形状的降水曲线,基于Dupuit假定,某一水位高度的过水流量等于井的抽水量[22],即
| $ Q=2 \pi r h k_{\mathrm{t}} \frac{\mathrm{d} h}{\mathrm{~d} r} $ | (2) |

|
图 3 降水曲线 Fig. 3 Curve of water level |
式中:r为某点与降水井的水平距离,h为该位置的水位高度,kt为土体的渗透系数。
降水井与降水半径位置的水位边界条件为
| $ \left\{\begin{array}{l} h=H_0, r=R \\ h=H_{\mathrm{t}}, r=R_0 \end{array}\right. $ | (3) |
将式(3)代入式(2),可得降水曲线公式:
| $ \begin{aligned} h(r)= & \sqrt{H_0^2-\frac{Q}{\pi k} \ln \frac{R}{r}}= \\ & \sqrt{H_0^2-\left(H_0^2-H_{\mathrm{t}}^2\right) \frac{\ln \frac{R}{r}}{\ln \frac{R}{R_0}}} \end{aligned} $ | (4) |
如图 3中所示,根据与计算点的相对位置,预降水引起的有效应力可分为两种情况计算。C1点与C2点在降水后分别位与水位的上方和下方,两点的有效应力增量Δσ1,Δσ2计算公式分别为
| $ \begin{aligned} \Delta \sigma_1= & \sigma_{\mathrm{t} 1}-\sigma_{01}=\left(h_0+h_1\right) \gamma-\left(h_0 \gamma+h_1 \gamma_{\mathrm{s}}-h_1 \gamma_{\mathrm{w}}\right)= \\ & h_1\left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right) \end{aligned} $ | (5) |
| $ \begin{aligned} \Delta \sigma_2= & \sigma_{\mathrm{t}2}-\sigma_{02}= \\ & {\left[\left(h_0+H_0-h\right) \gamma+\left(h_2-H_0+h\right)\left(\gamma_{\mathrm{s}}-\gamma_{\mathrm{w}}\right)\right]-} \\ & \left(h_0 \gamma+h_2 \gamma_{\mathrm{s}}-h_2 \gamma_{\mathrm{w}}\right)=\left(H_0-h\right)\left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right) \end{aligned} $ | (6) |
式中:σt,σ0分别为降水前后C1点与C2点的有效应力,h0为初始水位距离地表的埋深,h1和h2分别为C1点、C2点与初始水位的高差。γ、γs和γw分别为土体重度、土体饱和重度以及水的重度。
根据管线与水位的相对位置不同,降水引起的管线附加应力也有所区别,因此可分为两种情况进行计算:1)降水后,部分水位降至管线下方;2)降水后,地下水位均高于管线。两种情况下管线所受到的附加应力如图 4所示。

|
图 4 水位及附加荷载分布 Fig. 4 Water level and additional load distribution |
1) 降水后,部分水位降至管线下方时管线受到的附加应力分为两部分计算。首先,由图 2可知,管线上任意点横坐标x1与降水井的水平距离r=
| $ \begin{aligned} \sigma(x)= & \left(H_0-\sqrt{H_0-\left(H_0^2-H_{\mathrm{t}}^2\right) \frac{\ln \frac{R}{\sqrt{x^2+d^2}}}{\ln \frac{R}{R_0}}}\right)\cdot \\ & \left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right) \end{aligned} $ | (7) |
其次,处于水位上方的管线受到的附加应力一定值,此时可视为管线轴线位于图 3中C1点的情况,因此降水后,位于水位上方管线的附加应力为
| $ \sigma=h_1\left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right) $ | (8) |
需要注意的是,此时h1为初始水位与管线轴线的距离。当h(r)=H0-h1时,正好为水位与管线的交点,因此可以得到该点x的坐标为
| $ x=\sqrt{\left(R^{\frac{\left(H_0-h_1\right)^2-H_{\mathrm{t}}{ }^2}{H_0{ }^2-H_{\mathrm{t}}{ }^2}} \cdot R_0^{\frac{\left(2 H_0 h_1-h_1{ }^2\right)}{H_0 H_0-H_{\mathrm{t}}{ }^2}}\right)^2-d^2} $ | (9) |
基于此,降水后部分水位降至管线下方时,管线附加应力的计算公式为
| $ \sigma(x)=\left\{\begin{array}{l} \left(\begin{array}{l} H_0-\sqrt{H_0^2-\left(H_0^2-H_{\mathrm{t}}^2\right) \frac{\ln \frac{R}{\sqrt{x^2+d^2}}}{\ln \frac{R}{R_0}}} \end{array}\right)\cdot \\ \quad\quad\quad\left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right), \\ \quad\quad\quad x^2>\left(R^{\frac{\left(H_0-h_1\right)^2-H_{\mathrm{t}}^2}{H_0^2-H_{\mathrm{t}}^2}} \cdot R_0^{\frac{\left(2 H_0 h_1-h_1^2\right)}{H_0 0^2-H_{\mathrm{t}}^2}}\right)^2-d^2 \\ h_1\left(\gamma-\gamma_{\mathrm{s}}+\gamma_{\mathrm{w}}\right), \\ \quad\quad\quad x^2 \leqslant\left(R^{\frac{\left(H_0-h_1\right)^2-H_{\mathrm{t}}^2}{H_0^2-H_{\mathrm{t}}^2}} \cdot R_0^{\frac{\left(2 H_0 h_1-h_1^2\right)}{H_0 2-H_{\mathrm{t}}^2}}\right)^2-d^2 \end{array}\right. $ | (10) |
2) 当降水后地下水位均高于管线时,管线任意位置都处于水位下方,因此可采用式(7)计算此时管线的附加应力。
1.2 基于Kerr地基模型的管线控制方程基于Kerr地基管线与土相互作用模型,作出如下假设:1)管线周围土体为均质弹性土体;2)假设管线为一根搁置在Kerr地基上的Euler-Bernoulli梁,Kerr地基模型的剪切层只产生剪切变形;3)管线与地基土始终保持接触,两者的变形在接触面协调。
假设在附加荷载p(x)的作用下,Kerr地基上的管线产生了竖向位移,则其竖向位移w(x)可表示为
| $ w(x)=w_1(x)+w_2(x) $ | (11) |
式中:w1(x)与w2(x)分别为第一层弹簧和土体剪切层的变形量。
管线以及剪切层下方的应力分别为
| $ q_1(x)=c w_1(x)=c\left[w(x)-w_2(x)\right] $ | (12) |
| $ q_2(x)=k w_2(x) $ | (13) |
此外,对于剪切层有
| $ q_1(x)=-g \frac{\mathrm{d}^2 w_2(x)}{\mathrm{d} x^2}+k w_2(x) $ | (14) |
式中:k为第二层土体弹簧的刚度,c为第一层土体弹簧的刚度,g为土体剪切层的剪切刚度。
联立式(12)与式(14)可得
| $ w(x)=\left(1+\frac{k}{c}\right) w_2(x)-\frac{g}{c} \frac{\mathrm{d}^2 w_2(x)}{\mathrm{d} x^2} $ | (15) |
管线在降水引起的附加荷载作用下的位移控制方程为
| $ E I \frac{\mathrm{d}^4 w(x)}{\mathrm{d} x^4}+q_1(x) D=p(x) D $ | (16) |
式中:EI为管线的抗弯刚度,D为管线外直径。
将式(14)与式(15)代入式(16)后可得到
| $ \begin{array}{l} \frac{E I g}{D c} \frac{\mathrm{d}^6 w_2(x)}{\mathrm{d} x^6}-\frac{E I(c+k)}{D c} \frac{\mathrm{d}^4 w_2(x)}{\mathrm{d} x^4}+ \\ g \frac{\mathrm{d}^2 w_2(x)}{\mathrm{d} x^2}-k w_2(x)=-p(x) \end{array} $ | (17) |
式(17)写成差分形式为
| $ \begin{array}{l} \alpha\left(w_2\right)_{i+3}+\beta\left(w_2\right)_{i+2}+\chi\left(w_2\right)_{i+1}+\delta\left(w_2\right)_i+ \\ \chi\left(w_2\right)_{i-1}+\beta\left(w_2\right)_{i-2}+\alpha\left(w_2\right)_{i-3}=-p_i \end{array} $ | (18) |
式中:
为了方便计算,管线两端各增加3个虚拟节点(分别为节点-3,-2,-1与节点n+1,n+2,n+3)。结合边界条件,消去节点节点-3,-2,-1与节点n+1,n+2,n+3,可得到剪切层位移方程:
| $ \left\{W_2\right\}=\{K\}^{-1} \cdot\{P\} $ | (19) |
式中:{W2}=[(w2)0,(w2)1,⋯,(w2)n-1,(w2)n]T,{P}=[-p0,-p1,⋯,-pn-1,-pn]T。
对于管线两端无约束的情况下,两端剪力Qp弯矩Mp均为0,位于管线两端的土体剪切层弯矩Ms也为0,即
| $ \left\{\begin{array}{l} M_{p 0}=M_{p n}=-\left.E I \frac{\mathrm{d}^2 w(x)}{\mathrm{d} x^2}\right|_{i=0, i=n}=0 \\ M_{s 0}=M_{s n}=-\left.E I \frac{\mathrm{d}^2 w_2(x)}{\mathrm{d} x^2}\right|_{i=0, i=n}=0 \\ Q_{p 0}=Q_{p n}=-\left.E I \frac{\mathrm{d}^3 w_2(x)}{\mathrm{d} x^3}\right|_{i=0, i=n}=0 \end{array}\right. $ | (20) |
式中:
| $ \left\{\begin{array}{l} \frac{\mathrm{d}^2 w_2(x)}{\mathrm{d} x^2}=\frac{\left(w_2\right)_{i+1}-2\left(w_2\right)_i+\left(w_2\right)_{i-1}}{l^2} \\ \frac{\mathrm{d}^3 w_2(x)}{\mathrm{d} x^3}=\frac{\left(w_2\right)_{i+2}-2\left(w_2\right)_{i+1}+2\left(w_2\right)_{i-1}-\left(w_2\right)_{i-2}}{2 l^3} \end{array}\right. $ | (21) |
因此,可得
| $ \{K\}=\left[\begin{array}{ccccccccc} A_1 & A_3 & A_6 & 2 \alpha & & & & & \\ A_2 & A_5 & A_7 & \beta & \alpha & & & & \\ A_4 & A_7 & \delta & \chi & \beta & \alpha & & & \\ \alpha & \beta & \chi & \delta & \chi & \beta & \alpha & & \\ & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \\ & & \alpha & \beta & \chi & \delta & \chi & \beta & \alpha \\ & & & \alpha & \beta & \chi & \delta & A_7 & A_4 \\ & & & & \alpha & \beta & A_7 & A_5 & A_2 \\ & & & & & 2 \alpha & A_6 & A_3 & A_1 \end{array}\right]_{(n+1) \times(n+1)} $ | (22) |
式中:
| $ \left\{\begin{array}{l} A_1=\delta+2 \chi+4 \beta+8 \alpha \\ A_2=\chi+2 \beta+2 \alpha \\ A_3=-4 \beta-10 \alpha \\ A_4=\beta+2 \alpha \\ A_5=\delta-\beta \\ A_6=2 \beta+2 \alpha \\ A_7=\chi-\alpha \end{array}\right. $ | (23) |
在得出{W2}后,代入式(15)便可得出管线的竖向位移{W}。
1.3 Kerr地基模型参数的选取根据简化弹性空间法,文献[21]给出了Kerr地基模型中两层土体弹簧的刚度c与k以及土体剪切层的刚度g的计算方法,即
| $ \left\{\begin{array}{l} c=3 k \\ k=4 E_{\mathrm{s}} /(3 T) \\ g=2 E_{\mathrm{s}} T /(9+9 v) \end{array}\right. $ | (24) |
式中:Es为土体的弹性模量; T为地基厚度,取2.5倍的管线直径[22]; v为土体的泊松比。由于简化弹性空间法存在大量假设,文献[23]在进一步研究后,修正了第一层土体弹簧刚度的取值:c=1.9k。
2 算例验证为了验证本文方法的准确性,收集了单井降水试验[24]下邻近既有管线的监测数据,与本文计算方法所得结果进行对比。文献[24]报道了原位单井降水试验案例,试验场地含水层厚度为20.0~26.4 m,水位位于地表以下1.3~2 m,取平均值可得初始水位高度H0=23.2 m,初始水位埋深h0=1.65 m。加权平均得到的土体天然重度γ=18 kN/m3,饱和重度γs=18.5 kN/m3,渗透系数kt=4.32 m/d,泊松比vs=0.3,土体弹性模量Es=10 MPa。降水试验中一次性水位下降sw=12 m,与降水井垂直水平距离d=10 m处存在一条既有管线,埋深z0=6 m,直径D=1 m,壁厚0.1 m,管线弹性模量Et=30 GPa。
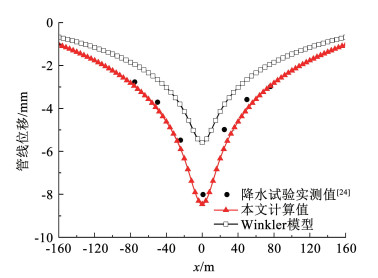
图 5为本文方法计算的管线竖向位移与降水试验结果的对比。
|
图 5 与降水试验结果对比 Fig. 5 Comparison with dewatering test results |
从图 5可以看出,由于Winkler地基模型(当g=0,c=∞时,本文模型即退化为Winkler模型)在受到外力作用时,地基上某点的变形只与该点的受力有关而不受周围土体的影响,与实际土体变形情况不同,因此计算结果与实测值存在偏差。而本文方法采用的Kerr地基模型引入了土体剪切刚度g与第二层土体弹簧刚度c,可以更好地考虑土体的剪切变形以模拟地基土变形的连续性,故本文方法计算结果与降水试验结果更为吻合。本文计算所得管线位移最大值为8.46 mm,略大于试验值8.01 mm。通过与原位试验的实测数据对比,说明了本文方法具有较好的合理性与准确性。
3 参数分析为了研究各因素对降水引起管线位移的影响,假设以下工程概况进行分析:地下初始水位H0=30 m,初始水位埋深h0=2 m,降水井半径R0=0.1 m,降水后井中水位Ht=20 m,预降水后水位下降sw=10 m;土体参数:渗透系数kt=1 m/d,弹性模量Es=50 MPa,泊松比v=0.3,土体重度γ=18 kN/m2,饱和重度γs=20 kN/m2;管线参数:轴线与降水井的垂直水平距离d=12 m,埋深z0=8 m,h2=6 m,直径D=6 m,壁厚0.3 m,抗弯刚度EI=7.548×105 MN · m2。在针对某一参数进行分析时,只有该参数取值发生变化,其他参数不变。
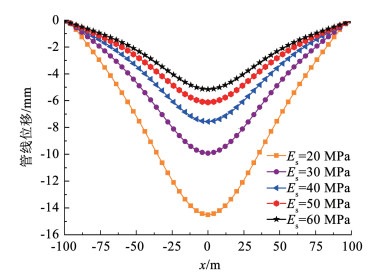
3.1 土体弹性模量Es为研究土体弹性模量Es对管线变形的影响,取5组土体弹性模量Es进行分析,分别为10 MPa、20 MPa、30 MPa、40 MPa以及50 MPa。在5组土体弹性模量Es下,采用本文方法计算所得预降水引起的管线位移曲线如图 6所示。从图 6可看出随着土体弹性模量Es从60 MPa减小到20 MPa时,管线的最大竖向位移从5.15 mm迅速增加到14.50 mm。这是因为土体弹性模量Es增大时,地基更不容易产生变形,而且当管线变形时,地基能提供更大的反力阻止管线变形。因此在软土地区进行降水施工前,可以通过对管线周边土体进行加固,进而达到减小管线变形的目的。
|
图 6 不同土体弹性模量下管线的位移曲线 Fig. 6 Curves of pipeline displacement under different elastic modulus of soil Es |
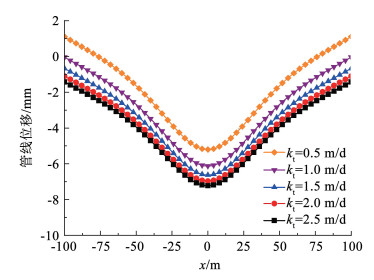
为研究渗透系数kt对管线变形的影响,取5组渗透系数kt进行分析,分别为0.5 m/d、1 m/d、1.5 m/d、2 m/d以及2.5 m/d。在5组渗透系数kt下,采用本文方法计算所得预降水引起的管线位移曲线如图 7所示。从图 7可看出管线竖向位移随着渗透系数的增大而增大,随着渗透系数kt从0.5 m/d增大到2.5 m/d时,管线的最大竖向位移从5.02 mm增大到7.22 mm,增大的幅度逐渐减小。同时可以看出当渗透系数kt=0.5 m/d时,管线竖向位移在|x|≥77的部分出现隆起。这是因为当土体渗透系数kt=0.5 m/d时,降水半径R=77.56 m,根据勾股定理可以计算管线受到附加荷载的范围为|x|≤76.63(图 2中的BB′段),因此管线在未受到附加荷载的部分由于自身抗弯刚度的原因出现隆起。
|
图 7 不同渗透系数kt下的管线位移曲线 Fig. 7 Curves of pipeline displacement under different permeability coefficient of soil kt |
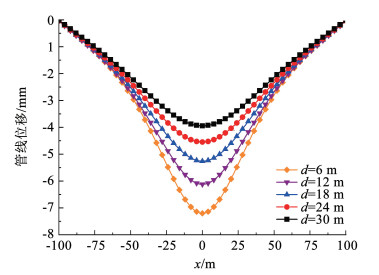
为研究管线与降水井的间距d对管线变形的影响,取5组间距进行分析,分别为6 m、8 m、10 m、12 m以及14 m。采用本文所提方法计算所得的5组间距d时,预降水引起的管线位移曲线如图 8所示。从图 8可看出管线产生的竖向位移随着间距d的增加而减小。当间距d从6 m增大到30 m时,管线的最大竖向位移从7.20 mm减小到3.95 mm。这是由于降水过程中距离降水井越远的位置水位变化的越小,因此对管线造成的影响也较小,即管线距离降水井越远,受到降水的影响减弱。
|
图 8 不同间距d时的管线位移曲线 Fig. 8 Curves of pipeline displacement under different spacing d |
为研究土体中水位降深sw对管线变形的影响,取5组降水后井中水位Ht进行分析,分别为20 m、15 m、10 m、5 m以及0 m,与之对应的水位降深sw分别为10 m、15 m、20 m、25 m以及30 m。在5组水位降深sw时,本文方法计算所得预降水后的地下水位如图 9所示。从图 9中可以看出随着井中水位降深sw的增加,周围地层中的水位随之整体下降,下降的幅度逐渐减少。当降水井内水位降深sw达到20 m时,管线轴线仍然处于地下水位的下方,此时管线上所受到的附加应力采用式(7)计算即可。但随着水位降深sw达到25 m后,与降水井垂直水平距离d=12 m处的水位从初始水位H0=30 m下降到23.56 m,即此处地下水位埋深是8.44 m,此时管线上距离降水井位置最近的部分,已经处于水位上方,此时该部分所受到的附加应力采用式(8)计算。

|
图 9 不同水位降深sw时的地下水位曲线 Fig. 9 Curves of water level under different water level drawdown sw |
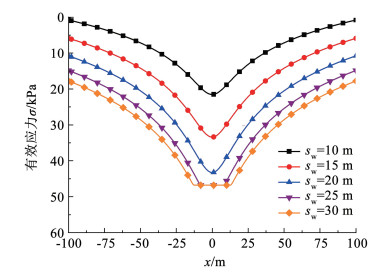
图 10为不同水位降深sw情况下,管线所受到的附加应力。从图中可以看出管线受到的附加应力随着水位降深sw的增加而增加,这是由于水位下降的越多,管线上方土体受到水浮力就越小。但水位下降到管线下方时,管线所受到的附加应力则不再增加,如图 10所示,当降水井内的水位降深sw达到25 m和30 m时,所受到的附加应力最大值不再增加,但附加应力最大值的范围扩大。
|
图 10 不同水位降深sw时的有效应力曲线 Fig. 10 Curves of effective stress under different water level drawdown sw |
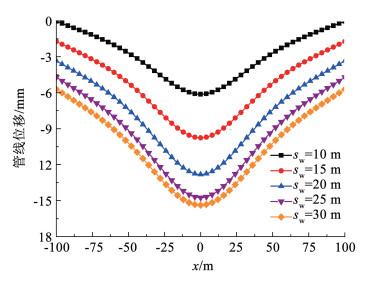
图 11为不同水位降深sw情况下,预降水引起的管线位移曲线。从图 11可看出在水位降深sw从10 m增加到30 m时,管线的最大竖向位移从6.12 mm增加到15.38 mm,但增加的幅度逐渐减弱。结合不同水位降深sw下的地下水位曲线与有效应力曲线不难分析出,周围水位下降的程度随着降水井内水位降深sw的增加而增加,降水在管线上引起的附加荷载也随之增加,最终导致管线因降水引起的位移整体增大。
|
图 11 不同水位降深sw时的管线位移曲线 Fig. 11 Curves of pipeline displacement under different water level drawdown sw |
根据相关规程[27]中的规定,煤气、供水管线(刚性管道)位移累计值的控制指标为10 mm。通过参数分析,可以得出不同参数情况下的管线最大位移,如图 12所示。从图中可以看出,渗透系数和间距对管线最大位移值的影响较小,且在本文分析算例中,这两个参数在常规取值范围内不会导致管线最大位移值超过10 mm。此外,土体弹性模量与降水井内的水位降深对管线最大位移值的影响较大,当土体弹性模量、水位降深分别为30 MPa与15 m时,管线的最大位移值已达到了9.92 mm与9.76 mm。即当土体弹性模量小于30 MPa或降水井内水位降深大于15 m时,单井降水引起的管线变形将超过控制指标。因此从本工程算例出发,为保证邻近管线在降水过程中位移值不超过控制指标,降水井内的水位降深不宜超过15 m。若水位降深大于15 m,则应对管线周围土体进行加固。

|
图 12 不同情况下的管线最大变形值 Fig. 12 The maximum deformation value of the pipeline under different conditions |
本文基于两阶段法提出了单井降水引起邻近既有管线竖向位移的理论计算方法。在第一阶段采用有效应力原理与Dupuit假定计算了降水对管线产生的附加荷载,第二阶段采用Kerr地基模型模拟管线与土的相互作用推导出了管线位移。经过深入分析后,得出以下结论:
1) 通过与现场试验数据的对比验证,显示了本文方法针对单井降水引起的邻近管线变形预测具有一定优越性。相较于Winkler地基模型,本文方法采用的Kerr地基模型考虑了土体剪切变形,可以更好地模拟土体变形的连续性,计算精度更高。
2) 参数分析表明, 土体渗透系数kt及管-井间距d对管线变形的影响较小,土体渗透系数的增大与间距的减小均导致管线变形增大;土体弹性模量Es与降水井内水位降深sw对管线变形的影响较大,土体弹性模量的降低与水位降深的增加均导致管线变形增大。
3) 随着降水井内水位降深的增加,管线受到的附加荷载存在两种形式。在水位降至管线轴线之前,管线受到的附加荷载随着水位降深sw增大而增大,管线产生的位移也随之增加。当水位降到管线轴线以下时,管线处于水位上方的部分受到的附加荷载相同,且不随着水位降深sw的增加而增加。
4) 在本文分析算例中,kt和d在常规取值范围内不会导致管线位移累计值超过相关规程的控制指标。而当Es < 30 MPa或sw>15 m时, 单井降水引起的管线变形将超过控制指标,届时应采取相应的防控措施。
| [1] |
郑刚, 赵悦镔, 程雪松, 等. 复杂地层中基坑降水引发的水位及沉降分析与控制对策[J]. 土木工程学报, 2019, 52(增刊1): 135. ZHENG Gang, ZHAO Yuebin, CHENG Xuesong, et al. Strategy and analysis of the settlement and deformation caused by dewatering under complicated geological condition[J]. China Civil Engineering Journal, 2019, 52(Sup. 1): 135. |
| [2] |
杨海旭, 王海飙, 董希斌. 真空井点降水联合加固软土地基的试验[J]. 哈尔滨工业大学学报, 2008, 40(12): 2044. YANG Haixu, WANG Haibiao, DONG Xibin. Experimental study on the combined method of vacuum well-point dewatering and preloading[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 2044. |
| [3] |
葛照国. 长江漫滩地区基坑施工对周边地表沉降及地下管线影响的现场试验研究[J]. 现代隧道技术, 2014, 51(5): 205. GE Zhaoguo. Field test on the impacts of foundation pit construction on ground settlement and underground utilities in the Yangtze River floodplain area[J]. Modern Tunnelling Technology, 2014, 51(5): 205. |
| [4] |
李锦强, 钟紫蓝, 史跃波, 等. 考虑土体参数不确定性的供水管道地震响应分析[J]. 哈尔滨工业大学学报, 2023, 55(2): 45. LI Jinqiang, ZHONG Zilan, SHI Yuebo, et al. Seismic analysis of water pipeline considering uncertainty of soil properties[J]. Journal of Harbin Institute of Technology, 2023, 55(2): 45. |
| [5] |
宋建学, 聂贤辉, 张建煜. 基坑降水引起的邻近地下管线破坏预测技术研究[J]. 建筑科学, 2014, 30(7): 74. SONG Jianxu, NIE Xianhui, ZHANG Jianyu. Prediction technology of adjacent underground pipelines damage caused by excavations dewatering[J]. Building Science, 2014, 30(7): 74. |
| [6] |
郑刚, 邓旭, 刘庆晨. 承压含水层减压降水对既有盾构隧道影响研究[J]. 岩土力学, 2015, 36(1): 178. ZHENG Gang, DENG Xu, LIU Qingchen. Analysis of responses of existing shield tunnel to pressure-relief in confined aquifer[J]. Rock and Soil Mechanics, 2015, 36(1): 178. |
| [7] |
贾媛媛, 路军富, 魏龙海, 等. 隧道降水施工对既有市政管线隧道影响研究[J]. 水文地质工程地质, 2010, 37(6): 7. JIA Yuanyuan, LU Junfu, WEI Longhai, et al. Research on the influence of the tunnel dewatering construction on existed municipal pipeline tunnel[J]. Hydrogeology & Engineering Geology, 2010, 37(6): 7. |
| [8] |
聂贤辉. 基坑降水引起的邻近地下管线破坏预测技术研究[D]. 郑州: 郑州大学: 2014 NIE Xianhui. Prediction technology of adjacent underground pipelines damage caused by excavations dewatering[J]. Zhengzhou: Zhengzhou University, 2014 |
| [9] |
刘运生. 深大型基坑降水引起地铁隧道沉降的控制措施分析[J]. 土工基础, 2013(1): 4. LIU Yunsheng. Impact of the deep excavation dewatering on the settlement of a subway tunnel[J]. Soil Engineering and Foundation, 2013(1): 4. |
| [10] |
李文广. 邻近基坑降水对运营地铁隧道竖向变形的影响研究[D]. 上海: 同济大学, 2008 LI Wenguang. Influence of dewatering of adjacent foundation pit on longitudinal deformation of metro tunnel in operation[D]. Shanghai: Tongji University, 2008 |
| [11] |
许言. 基于分层标组沉降监测的基坑工程降水对邻近地铁隧道的影响分析[J]. 上海国土资源, 2020, 41(3): 78. XU Yan. Analyzing extensometer group monitoring of metro tunnel subsidence affected by adjacent dewatering engineering work[J]. Shanghai Land & Resources, 2020, 41(3): 78. |
| [12] |
徐长节, 曾怡婷, 田威, 等. Pasternak地基降水对邻近管线影响的解析研究[J]. 上海交通大学学报, 2021, 55(6): 11. XU Changjie, ZENG Yiting, TIAN Wei, et al. Analytical analysis of the influence on adjacent pipelines induced by dewatering based on Pasternak model[J]. Journal of Shanghai Jiaotong University, 2021, 55(6): 11. |
| [13] |
欧雪峰, 张学民, 刘学勤, 等. 基坑开挖与降水引起下卧隧道变形的解析计算方法[J]. 铁道学报, 2019(3): 8. OU Xuefeng, ZHANG Xuemin, LIU Xueqin, et al. Analytic calculation method of underlying tunnel deformation caused by excavation and dewatering of upper pit[J]. Journal of the China Railway Society, 2019(3): 8. |
| [14] |
程霖, 杨成永, 王伟, 等. 考虑轴力的管线变形控制微分方程及其优化解[J]. 华中科技大学学报(自然科学版), 2021, 49(3): 126. CHENG Lin, YANG Chengyong, WANG Wei. Governing differential equations and optimal solution for deformation of jointless pipeline considering axial force[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(3): 126. |
| [15] |
WINKLER E. Dielehre von der elastizitat und festigkeit[M]. Prague: Dominicus, 1867.
|
| [16] |
WINKLER E. Theory of elasticity and strength[M]. Prague: Dominicus, 1867.
|
| [17] |
PASTERNAK P L. On a new method of analysis of an elastic foundation by means of two-constants[D]. Moscow: Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu Ⅰ Arkhitecture, 1954
|
| [18] |
可文海, 管凌霄, 刘东海, 等. 盾构隧道下穿管线施工引起的管-土相互作用研究[J]. 岩土力学, 2020, 41(1): 221. KE Wenhai, GUAN Lingxiao, LIU Donghai, et al. Research on upper pipeline-soil interaction induced by shield tunnelling[J]. Rock and Soil Mechanics, 2020, 41(1): 221. |
| [19] |
KERR A D. A study of a new foundation model[J]. ActaMechanica, 1965, 1(2): 135. |
| [20] |
冯国辉, 徐兴, 侯世磊, 等. 基于Kerr地基模型的基坑开挖引起下卧既有隧道受力变形[J]. 上海交通大学学报, 2022, 56(4): 474. FENG Guohui, XU Xing, HOU Shilei, et al. Deflections of adjacent underground tunnel induced by excavation based on Kerr foundation model[J]. Journal of Shanghai Jiao Tong University, 2022, 56(4): 474. |
| [21] |
ZHANG D M, HUANG Z K, LI Z L, et al. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath[J]. Computers and Geotechnics, 2019, 108(4): 197. |
| [22] |
VERRUIJT A. Theory of groundwater flow[M]. New York: Macmillan Education UK, 1982.
|
| [23] |
MORFIDIS K. Research and development of methods for the modeling of foundation structural elements and soil[D]. Thessaloniki: Aristotle University of Thessaloniki, 2003
|
| [24] |
徐凌. 软土盾构隧道竖向沉降研究[D]. 上海: 同济大学, 2005 XU Ling. Research of the longitudinal settlement of soft soil shield tunnel[D]. Shanghai: Tongji University, 2005 |
| [25] |
KLAR A, VORSTER TE B, SOGA K, et al. Soil-pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions[J]. Geotechnique, 2005, 55(6): 461. |
| [26] |
曾怡婷. 基坑降水及开挖对周边管线影响的研究[D]. 杭州: 浙江大学, 2020 ZENG Yiting. Study on the influence of foundation pit dewatering and excavation on surrounding pipelines[D]. Hangzhou: Zhejiang University, 2020 |
| [27] |
基坑工程施工监测规程: DG/TJ 08-2001—2016[S]. 上海: 同济大学出版社, 2016 Specification for foundation excavation monitoring: DG/TJ 08-2001—2016[S]. Shanghai: Tongji University Press, 2016 |
 2023, Vol. 55
2023, Vol. 55


