2. 中铁二院工程集团有限责任公司,成都 610031
2. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China
渝昆高速铁路是京昆高铁的重要组成部分,其设计时速350 km/h。其中渝昆高铁寻甸蒲草塘至昆明南,正线全长约118 km,拟建造50余座桥梁,该段线路3次跨越了现今非常活跃的地震带——小江断裂带,其中38 km位于九度0.4g地震区,桥梁总长约14.7 km,桥梁沿线区域现今地壳变形十分强烈、地震活动频繁,地质条件十分复杂,小江断裂带与其诱发大地震灾害已经成为影响渝昆高铁运行安全的主要因素。因此,渝昆高铁是集“高速铁路、近断层、高烈度”特征于一体,其运营安全将面临九度近断层地震的严峻挑战。考虑到渝昆高铁穿越近断层九度地震区,为降低风险该段线路主要采用32 m简支梁桥跨越,为了保证渝昆高铁九度地震区桥梁的运营安全,急需研究经济合理、安全可靠的减隔震体系。
近年来许多学者对高烈度地震区桥梁合理减隔震体系开展了相关研究,文献[1]针对跨越地震区高速铁路简支梁,通过时程分析方法,结合抗震设计规范,研究了4种减隔震措施下桥梁结构的抗震性能。文献[2]针对铁路简支梁桥,研究了摩擦摆支座在不同地震烈度下对桥梁结构性能的影响,分析了摩擦摆支座的合理性。文献[3]针对高铁简支梁,采用数值仿真分析法,开展了3种支座(LRB支座、FPB支座、HDR支座)、黏滞阻尼器与钢挡块组合体系下桥梁横向地震碰撞效应及减震性能的分析,比选了几种组合体系的合理性。文献[4]针对地震区客货共线32 m简支梁桥,开展了摩擦摆支座对3~60 m墩高简支梁桥适用范围影响分析研究,提出了摩擦摆支座合理的墩高适用范围。文献[5]针对中国高速铁路32 m简支梁桥,提出了一种新型金属弹塑性装置与支座组合形成减隔震体系,研究了桥梁的抗震性能。然而目前研究主要是针对不同减隔震体系,开展时程分析,通过减震率评估各种减隔震体系的合理性,但对于像九度地震区的高速铁路桥梁研究较少,减隔震体系选取方法过于简单(用减震率等指标简单比选),未综合考虑多种因素的影响(如桥址地震发生概率、桥梁易损性概率),因此急需通过更加合理可行的方法来研究适用于九度地震区的减隔震体系。
本文以渝昆高铁九度地震区32 m跨度简支梁桥为工程背景,构建了一种桥址区地震危险性贡献参数分析方法,运用核密度估计理论推导了桥梁地震易损性计算方法,建立了一种基于地震风险评估的近断层铁路桥梁抗震分析方法,利用建立的方法对5种减隔震体系下九度区高速铁路简支梁桥开展了对比分析,全面分析评估了桥梁构件的地震风险情况,通过综合比较桥梁结构地震风险,比选出适用于九度地震区高速铁路简支梁的减隔震体系。
1 基于地震风险评估的近断层铁路桥梁抗震分析方法 1.1 地震风险分析概述地震风险分析就是利用地震危险性的分析结果,结合对受灾物体和有关社会累计的知识,对特定区域、特定结构物可能遭受的地震灾害程度进行量化分析。地震风险评估可用如下形式表达:
地震风险=地震危险性H(a)×地震易损性PF(a)
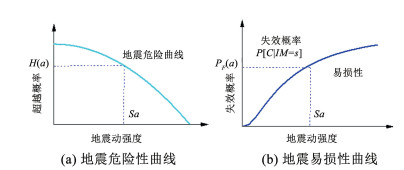
图 1给出了桥梁结构的地震动的危险性函数和地震易损性函数。
|
图 1 地震危险性和地震易损性曲线 Fig. 1 Seismic hazard and seismic vulnerability curves |
地震风险分析主要是桥址区地震危险性函数与桥梁结构地震易损性函数通过积分求解得到,但实际应用过程中会发现,地震危险性函数与地震易损性函数较复杂,积分求解十分困难,只能通过数值分析方法[6]并借助MALTAB等商用软件或自编程序求解地震风险值,根据分析结果评估桥梁抗震性能。
上述方法计算过程复杂,不便于工程应用,故本文提出了一种简化的基于地震风险分析的桥梁抗震分析方法,下文将详细介绍该方法。
1.2 概率地震危险性曲线及地震危险贡献参数建立 1.2.1 地震危险性曲线的建立方法目前研究人员通常按照国家标准《工程场地地震安全性评价》(GB17741—2005)[7]的要求,采用综合概率分析方法,对桥梁工程场区进行地震危险性分析。
地震危险性综合概率分析方法的主要特点是考虑了地震活动的时空不均匀性,确定桥址区不同地震带对桥址工程场地地震危险性超越概率。参考文献[8]基于分段泊松分布模型和全概率公式,可计算出桥址区域内某一断裂带发生地震,导致桥址场地地震动强度值A超越给定值a的年超越概率,具体公式为
| $ \begin{aligned} P_k(A \geqslant a)=&1-\exp \left\{-\frac{2 v_0}{\beta} \cdot \sum_{j=1}^{N_m} \sum_{i=1}^{N_s}\left[\iiint P(A \geqslant a / E) \cdot \right.\right. \\ & \left.\left.f(\theta) \cdot \frac{f_{i, m j}}{A\left(S_i\right)} \cdot f\left(m_j\right) \cdot \operatorname{sh}\left(\frac{1}{2} \beta \Delta m\right) \mathrm{d} x \mathrm{d} m \mathrm{d} \theta\right]\right\} \end{aligned} $ | (1) |
式中:A(Si)为工程场地地震区内第i个潜在震源区的面积; P(A≥a|E)为地震区第i个潜在震源区内发生某一特定地震事件(震级mj+0.5Δm、震中位置、破裂方向确定)时给定地震动值a被超过的概率; f(θ)为破裂方向的概率密度函数; v0为t年内发生在M0~Muz之间地震震级的年平均发生率; β=bln 10,b为震级频度关系的斜率。实际工作中,震级m分成Nm档,mj表示震级为(mj+0.5Δm)的震级档,Ns为地震统计区内共划分出的潜在震源区数量{S1, S2, ⋯, SNs};fi, mj为潜在震源区的空间分布函数;f(mj)为震级概率密度函数。
若桥址区域内有N个地震带对桥梁场地有影响,则桥址场地总的地震危险超越概率为
| $ P(A \geqslant a)=1-\prod\limits_{k=1}^N\left\{1-P_k(A \geqslant a)\right\} $ | (2) |
运用式(2)便可得到桥梁地震危险性函数曲线,但可以发现地震危险性函数十分复杂,若用其来求解地震风险概率比较困难。
1.2.2 各种地震设防水准下的地震危险性贡献率参数ΔλH在实际应用过程中,地震安评报告一般仅提供桥址区50 a超越概率63%、10%、2%和100 a超越概率63%、10%、3%六个水准下的地震危险发生概率,而将6组数据进行拟合可获得一条光滑的地震危险性曲线。为了使工程应用更加方便,参考文献[9]的思路,本文构建了一种桥址区工程场地各地震水准对应地震危险性贡献参数分析方法,通过构造地震危险贡献参数ΔλH,表征不同水准地震对工程场地的贡献大小。
构造方法如下:图 2为渝昆高铁某特大桥地震安评报告给出的6种水准地震危险性发生概率值,通过拟合得到地震危险性曲线。其横坐标为PGA,竖坐标表示地震危险年平均超越概率,PGA的波动在0.08g~0.8g之间,图中共有6个地震水准等级的数据(PGAi, λi),i=1, 2, ⋯, 6,求解相邻两个水准等级PGAi的加速度峰值中位值,并对应在危险曲线上找到这些点,即图中7个红色空心圆点(PGAi′, λi′),i=1, 2, ⋯, 7,于是在地震危险曲线上便可定义6个峰值加速度间隔ΔPGAi=PGAi+1′-PGAi′(i=1, 2, ⋯, 6),这7个空心圆点将地震危险性曲线的年发生概率值分割成了6个范围,计算出相邻两个空心圆点对应的地震年超越概率的差值,即可得到各种地震设防水准下的地震危险性贡献率ΔλH, i(i=1, 2, ⋯, 6),按照上述方法得到的贡献率参数可知:小震(PGAi较低时),地震危险性贡献参数较大,说明发生该水准的地震概率较大,反之对于大地震(PGAi较高),地震危险工程参数值较小,说明发生大地震的概率较低,地震危险性贡献参数表征的物理意义与实际情况相符合。

|
图 2 地震危险贡献参数示意图 Fig. 2 Schematic diagram of seismic hazard contribution parameters |
地震易损性分析是从概率层面对地震作用下的桥梁损伤进行评估,即具体反应某强度地震下,桥梁达到或超过某种损伤状态的发生概率[10],易损函数求解公式为
| $ P_f(\mathrm{IM}, C)=P[D \geqslant C \mid \mathrm{IM}] $ | (3) |
式中:C、D分别为桥梁抗震承载力和地震需求值,IM表示地震的强度值。若已知桥梁抗震承载力的条件概率密度函数fD,则易损性函数可通过积分求解得到, 即
| $ P_f(a, C)=\int_C^{+\infty} f_D(c \mid \mathrm{IM}=a) \mathrm{d} c $ | (4) |
由文献[11]可知,条件概率密度函数可按下式进行求解:
| $ f_D(c \mid \mathrm{IM}=a)=\frac{f_{D, \mathrm{IM}}(c, a)}{f_{\mathrm{IM}}(a)} $ | (5) |
式中:fD, IM(·)为D和IM两个变量的联合概率密度分布函数, fIM(·)为IM变量的边缘分布函数[11]。由上述公式可知,若得到两种分布函数fD, IM(·)和fIM(·)的表达式,便能够积分求解式(5)得到易损性曲线。
为了求解两种分布函数,本文采用了一种非参数检验的方法——核密度估计[12-13],基于桥梁时程分析结果{(IMi, Di), i=1, 2, ⋯, n}求解fD, IM(·)和fIM(·)两种分布函数,从而得到桥梁结构地震易损性函数。
假设多元变量 X有n个样本点{x1, x2, ⋯, xn},由核密度估计的定义[14]可知,采用标准正态核函数时,联合分布函数的核密度估计:
| $ \begin{aligned} \hat{f}_{\mathrm{X}}(x)= & \frac{1}{n|\boldsymbol{H}|^{1 / 2}} \sum\limits_{i=1}^n \frac{1}{(2 \pi)^{d / 2}} \times \\ & \exp \left[-\frac{1}{2}\left(\boldsymbol{x}-x_i\right)^{\mathrm{T}} \boldsymbol{H}^{-1}\left(\boldsymbol{x}-x_i\right)\right] \end{aligned} $ | (6) |
式中(·)T为转置矩阵。带宽矩阵 H为多元矩阵,其具体取值和计算方法参考文献[15]。
利用桥梁时程分析获得的地震响应结果{(IMi, Di), i=1, 2, ⋯, n},代入式(6)得到桥梁联合概率密度分布函数:
| $ \begin{aligned} \hat{f}_{D, \mathrm{IM}}(c, a)= & \frac{1}{2 \pi n|\boldsymbol{H}|^{1 / 2}} \cdot \\ & \sum\limits_{i=1}^n \exp \left[-\frac{1}{2}\left(\begin{array}{l} c-D_i \\ a-\mathrm{IM}_i \end{array}\right)^{\mathrm{T}} \boldsymbol{H}^{-1}\left(\begin{array}{l} c-D_i \\ a-\mathrm{IM}_i \end{array}\right)\right] \end{aligned} $ | (7) |
基于时程分析中地震强度样本{IMi, i=1, 2, ⋯, n}。采用高斯密度函数作为核函数,即K(x)= φ(x)=exp
| $ \hat{f}_{\mathrm{IM}}(a)=\frac{1}{n h_{\mathrm{IM}}} \sum\limits_{i=1}^n \varphi\left(\frac{a-\mathrm{IM}_i}{h_{\mathrm{IM}}}\right) $ | (8) |
式中hIM为IM的最优带宽参数。
将式(7)、(8)代入式(5),得到条件概率密度函数fD(c|IM=a),从而通过式(4)得到桥梁易损性函数数值计算式,即
| $ \begin{array}{l} P_f(a, C)=P[D \geqslant C \mid \mathrm{IM}=a]=\int_C^{+\infty} f_D(c \mid \mathrm{IM}=a) \mathrm{d} c= \\ \frac{h_{\mathrm{IM}}}{2 \pi|H|^{1 / 2}} \frac{\int\limits_C^{+\infty} \sum\limits_{i=1}^n \exp \left[-\frac{1}{2}\left(\begin{array}{l} c-D_i \\ a-\mathrm{IM}_i \end{array}\right)^{\mathrm{T}} \boldsymbol{H}^{-1}\left(\begin{array}{l} c-D_i \\ a-\mathrm{IM}_i \end{array}\right)\right] \mathrm{d} c}{\sum\limits_{i=1}^n \varphi\left(\frac{a-\mathrm{IM}_i}{h_{\mathrm{IM}}}\right)} \end{array} $ | (9) |
运用式(9)可求解出桥梁结构地震易损性函数,开展桥梁地震易损性分析。
1.4 铁路桥梁结构地震风险计算方法考虑到传统地震风险分析需要多重积分求解结构地震风险概率,求解难度大,求解过程复杂。因此本文为解决现有方法的不足,建立了一种新的铁路桥梁结构地震风险分析方法。方法分析流程如下:1)计算特定强度地震作用下的桥梁结构地震损伤破坏概率,采用1.3节的方法,建立桥梁结构损伤破坏概率Pf(PGAi)随地震动强度PGAi变化的关系曲线;2)计算各水准地震作用下地震危险性贡献参数。根据工程场地相关参数并结合规范[7]采用综合概率分析方法,求解桥梁工程场区地震危险性曲线。当无相关工程场地参数不能直接求解时,可采用地震安评报告获得各种地震水准对应的地震年超越概率(即年平均发生概率λH, i),并计算各地震水准对应的地震峰值加速度PGAi,然后建立各工程场地的地震危险性曲线,参考1.2节方法计算出各地震设防水准下的地震危险性贡献参数ΔλH, i;3)计算各水准地震(即地震峰值加速度为PGAi)作用下,桥梁地震损伤概率Pf(PGAi)和地震危险性贡献参数ΔλH, i的乘积值,然后将各水准地震的乘积值进行求和,得到桥梁结构综合地震风险概率值为
可以通过上述方法,求解出桥梁各危险构件的地震风险值,根据结构风险评估结果,研究桥梁各构件的抗震性能,还可以对比研究不同桥梁减隔震措施下各构件的地震风险值,评估不同桥梁减隔震措施的可行性和适用性。
1.5 建立基于地震风险评估的铁路桥梁抗震分析方法基于1.2~1.4节的分析理论,本文提出了一种基于地震风险评估的铁路桥梁抗震分析方法,方法的具体分析流程如图 3所示。

|
图 3 一种基于地震风险的铁路桥梁抗震分析方法流程图 Fig. 3 The flow chart of seismic analysis method for railway bridge based on seismic risk |
运用图 3桥梁抗震分析方法,可分析各类典型铁路桥梁地震风险和抗震性能,但分析结果数据量大,同时需要绘制海量的分析结果图,为了提高分析效率和分析的可操作性,简化分析过程,可快速得到分析结果。
基于1.2~1.4节的分析方法和图 3的分析流程,并结合桥梁相关设计规范,应用MATLAB软件GUI技术,编制了铁路桥梁抗震风险评估分析软件,软件界面如图 4所示。将全桥模型时程分析计算结果导入本文研发的软件后,可自动绘制桥梁构件地震易损性曲线、地震风险评估分析柱状图,还可生成桥梁结构风险评估报告。利用桥梁抗震风险评估分析软件,便可开展各种桥梁结构的抗震性能分析。

|
图 4 软件操作界面 Fig. 4 Software operation interface |
本文以重庆至昆明高速铁路跨越9度地震区典型32 m双线铁路简支梁桥为工程背景,研究对象桥跨布置为5×32 m,采用等墩高形式,墩高分别为10、20、30 m,梁体为预制单箱单室箱梁截面(参考《通桥(2016)2322A-Ⅱ-1》图执行),桥宽12.6 m,梁高3.05 m,主梁为C50混凝土,桥墩采用圆端形墩,15 m以下为实心墩,15~30 m采用空心墩,具体构造见表 1,墩为C35混凝土,钢筋采用HRB400,桥墩桩基础采用9-ϕ1.25 m,一跨简支梁一端采用固定支座,另一端采用纵向活动支座,具体布置如图 5所示。桥址区域为9度0.4g,Ⅱ类场地。
| 表 1 桥墩设计构造参数 Tab. 1 Bridge pier design and construction parameters |

|
图 5 桥跨及支座布置图(cm) Fig. 5 Schematic diagram of bridge and bearing layout (cm) |
针对九度地震区高速铁路桥梁面临的抗震及减震技术难题,拟研究适用于九度地震区高速铁路典型简支梁桥的合理减隔震方案,结合已有的高烈度地震区桥梁抗震及减震研究成果[16-17],拟定了5种减隔震方案作为九度地震区高速铁路简支梁桥的比选方案,具体方案如下:方案1,球型钢支座(传统硬抗型);方案2,普通抗震支座+型钢挡块;方案3,双曲面减隔震支座+ 型钢挡块;方案4,普通抗震支座+ 榫形金属减震耗能装置+型钢挡块;方案5, 双曲面减隔震支座+榫形金属减震耗能装置+型钢挡块。5种措施效果实物如图 6所示。

|
图 6 各种措施效果实物图 Fig. 6 Renderings of various measures |
双曲面减隔震支座、球型钢支座、防落梁挡块力学参数详见表 2~4。榫形金属减震耗能装置初始刚度为15 328 kN/m,屈服强度为376 kN,屈服后刚度比取0.1,初始间隙为20 mm,极限位移≥210 mm。
| 表 2 双曲面减隔震支座参数 Tab. 2 Double spherical aseismic bearing parameters |
| 表 3 球型钢支座参数 Tab. 3 Spherical steel bearing parameters |
| 表 4 防落梁力学参数 Tab. 4 Mechanical parameters of anti-falling beam |
本文采用OpenSees建立全桥模型,主梁不考虑地震损伤,采用梁单元模拟,考虑二期恒载、列车活载对桥梁的影响,圆端形桥墩采用OpenSees中dispBeamColumn基于位移的纤维单元模拟,参考文献[15, 18]考虑混凝土和钢筋的非线性本构,普通抗震支座、减隔震支座分别采用OpenSees中flatSliderBearing和singleFPBearing支座单元模拟[15],型钢挡块采用ElasticPPGap材料本构模型进行模拟[15],榫形金属减震装置采用带间隙的双折线本构模型模拟其力学性能[1],支座、钢挡块模拟参数详见表 2~4,采用ImpactMaterial材料本构模拟相邻梁之间的碰撞效应[19]。桩基础等效土弹簧进行模拟,依据规范[20]附录D求解桩基等效土弹簧刚度,全桥有限元模拟情况如图 7所示。

|
图 7 桥梁有限元模拟示意图 Fig. 7 Finite element model of bridge |
根据渝昆高铁九度地震区安全评估报告,得到了重点工程场地的50 a超越概率63%、10%、2%,100 a超越概率63%、10%、3%六种概率水平下的地震动,每种水准地震动各8条,共计48条地震波。图 8给出了6种水准地震动的反应谱曲线,由图分析可知,随着地震水准年发生概率的逐渐降低,地震动的特征周期逐渐增大,地震的破坏能量越来越强。

|
图 8 6种地震水准下各地震动反应谱 Fig. 8 Seismic response spectra at six seismic levels |
对48条地震动进行调幅,得到10个PGA等级,从0.1g至1.0g,调幅步长0.1g,生成480组地震分析样本用于开展时程分析,地震输入方向分别为纵向+竖向、横向+竖向,依据地震安评报告,竖向与水平向地震动PGA强度比为1∶ 1。同时根据渝昆高铁安评报告可得到桥址区工程场地地震危险性发生概率,如图 2所示,依据1.2节提出的工程场地地震危险性贡献率参数分析方法,得到桥址工程场地地震风险贡献参数见表 5。
| 表 5 桥址区工程场地地震风险贡献参数 Tab. 5 Project site seismic risk contribution parameters |
在建立易损性曲线以前,首先要确定各种损伤状态的损伤指标临界值,本文参考文献[15]关于桥梁结构损伤指标的定义及损伤状态的划分方法,桥墩损伤指标采用曲率延性比,支座损伤指标采用相对位移,计算得到不同墩高各关键构件的损伤指标在4种损伤状态下对应的临界值见表 6。
| 表 6 桥梁构件损伤指标临界值 Tab. 6 Critical value of damage index of bridge members |
基于1.3节的分析方法,便可计算各墩高简支梁桥在各种减隔震方案条件下各种损伤状态对应的地震易损性曲线。由于篇幅有限,本文仅给出10 m墩高简支梁桥在纵向+竖向地震作用下的易损性分析结果,如图 9所示。由图 9分析可知:1)在多遇地震作用下(PGA=0.14g),各减隔震体系下桥墩的地震破坏概率较低,桥墩处于弹性状态;而各体系下支座构件损伤概率低,支座变形在容许范围内。2)在设计地震作用下(PGA=0.4g),减隔震方案1对应桥墩发生严重损伤概率达25%,发生中等损伤概率超过95%,桥墩屈服,进入塑性阶段,其他减隔震方案下桥墩发生严重破坏的概率小于15%,发生中等损伤破坏的概率在35%~65%之间,损伤破坏概率最低的是减隔震方案5。3)在罕遇地震作用下(PGA=0.64g),采用方案1~4桥墩发生严重损伤破坏的概率均大于65%,桥墩构件进入塑性状态,发生完全破坏的概率大于20%;减隔震方案5发生严重损伤破坏的概率为49%,发生完全破坏的概率为10%左右,方案5比其他方案更合理。

|
图 9 纵+竖向地震下10 m墩高简支梁支座地震易损性曲线 Fig. 9 Seismic vulnerability curve of simply supported beam support of 10 m pier under earthquake |
支座构件在5种减隔震方案下的计算结果与桥墩类似,这里不再详述,方案1因为采用的是传统的硬抗体系,故支座均未超过自身容许地震位移,所以易损性概率接近为零。
为了更好地比较各减隔震体系下桥梁结构的地震易损性情况,参考文献[15]采用超越概率地震动强度指标中位值来对比不同减隔震方案下桥梁关键构件的地震易损性(由于篇幅有限图 10仅给出10 m墩高计算结果),各种损伤状态下中位值越小桥梁结构越容易发生损伤破坏。由于方案1采用硬抗体系,支座地震位移小,其PGA中位值远大于其他方案,此时将5种方案放置同一图中将无法区分其他4种方案的差异,因此未在图 10(b)和10(d)中绘制方案1结果。

|
图 10 不同减隔震方案下桥梁结构PGA中位值分布图 (10 m墩高简支梁计算结果) Fig. 10 The median PGA distribution of bridge structures under different vibration reduction and isolation schemes (calculation result of 10 m pier height) |
由图 10给出的10 m墩高简支梁结果可知:1)从轻微损伤到完全破坏,不同减隔震方案的桥梁结构构件其地震易损性函数中位值变化规律是一致的,在数值上都是随着损伤程度的增加逐渐增大。2)对于桥墩构件,在纵、横向地震作用下,方案1条件下其构件地震易损性中位值均小于其余4种方案下的计算结果,且从轻微损伤到完全破坏这4种损伤状态下,中位值的差距逐渐增大,在相同损伤状态下,方案5的地震易损性中位值最大,这表明方案5对桥梁构件的减震效果最好。3)对于支座,在纵+竖向、横+竖向地震作用下,轻微和中等损伤状态下,方案2易损性中位值最小,严重和完全破坏状态下,方案3地震易损性中位值最小。
2.6 桥梁结构地震风险评估分析及减隔震方案比选以上从桥梁结构自身抗震性能的角度对比分析了各种减隔震方案的合理性,为了进一步综合考虑地震发生概率与桥梁结构损伤下减隔震方案的合理性,利用本文提出的分析方法开展了各减隔震体系下桥梁地震风险评估分析。基于2.4节计算50 a和100 a超越概率为63%、10%、2%、3%对应的各地震水准下的风险贡献参数,并结合2.5节各减隔震方案下结构地震易损性分析结果,参照1.4节对各减隔震方案下桥梁关键构件的地震风险进行计算评估,便可得到10 m墩高简支梁桥在4种损伤状态下的年平均风险发生概率,由于篇幅有限,这里仅给出10 m墩高简支梁桥在纵向+竖向地震作用下桥墩计算结果见表 7,最终得到桥墩轻微、中等、严重、完全破坏的风险概率分别为5.99%、4.68%、1.01%、0.15%。图 11给出了5种减隔震体系下纵+竖、横+竖向地震对渝昆高铁典型10 m墩高32 m跨度简支梁的地震风险评估3D柱状图,图 12对应给出了各减隔震方案下风险累计柱状图。
| 表 7 纵+竖向地震作用下渝昆高铁10 m墩高简支梁采用减隔震方案5时对应桥墩风险评估计算 Tab. 7 Risk assessment calculation table corresponding to piers when seismic isolation scheme 5 was adopted for 10 m piers of Chongqing-Kunming high-speed railway |

|
图 11 地震作用下各减隔震体系下简支梁桥关键构件风险分析3D柱状图 Fig. 11 The 3D histogram of risk analysis of key components of simply supported beam bridge under various seismic isolation systems |
|
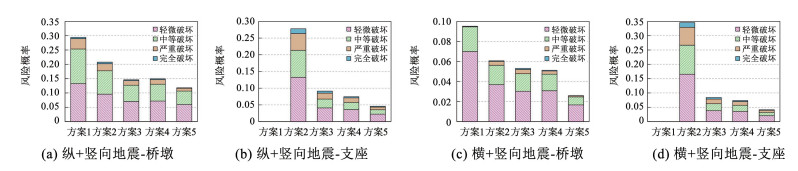
图 12 地震作用下10 m墩高简支梁桥关键构件各减隔震方案对应的风险累计柱状图 Fig. 12 The 2D histogram of risk analysis of key components of simply supported beam bridge under various seismic isolation systems |
图 11(a)和图 12(a)给出了10 m墩高简支梁在纵+竖向地震作用下桥墩地震风险分析柱状图,对于桥墩构件采用方案1(传统硬抗)时,桥墩发生轻微损伤的地震风险概率13.3%,发生中等损伤的地震风险概率12.1%,发生严重破坏的地震风险概率3.6%,发生完全破坏的地震风险概率0.45%,方案1是各方案中地震风险概率最大的方案。对于减隔震方案2~5,各方案发生轻微损伤的地震风险概率分别为9.59%、7.02%、7.2%、5.99%,各方案发生中等损伤的地震风险概率分别为8.17%、5.69%、5.87%、4.68%,各方案发生严重损伤的地震风险概率分别为2.43%、1.57%、1.58%、0.16%,各方案发生完全破坏的地震风险概率分别为0.56%、0.31%、0.32%、0.15%。由各减隔震方案计算结果表明:减隔震方案5对桥墩构件的地震风险破坏概率最低,采用减隔震方案5后,其地震风险相比方案1将下降50%,这说明采用减隔震方案5后,整个桥墩的安全性能提高了50%。此外,分析可知,减隔震方案5条件下,发生严重和完全破坏的地震风险概率均低于0.2%,这也充分说明减隔震方案5条件下桥墩抗震性能良好。
图 11(b)和图 12(b)给出了纵+竖向地震作用下支座构件地震风险分析柱状图,因方案1为传统硬抗型抗震方案,支座位移变形小,无损伤,故图中未给出方案1的计算结果。对于支座构件,采用减隔震方案2时,支座发生轻微损伤的地震风险概率13.26%,发生中等损伤的地震风险概率8.09%,发生严重破坏的地震风险概率5.04%,发生完全破坏的地震风险概率1.38%,方案2在4种损伤状态下的地震风险概率相比其他方案都大,方案2不合理。对于减隔震方案3~5,各方案支座发生轻微损伤的地震风险概率分别为4.11%、3.6%、2.24%,各方案发生中等损伤的地震风险概率分别为2.66%、2.16%、1.33%,各方案发生严重损伤的地震风险概率分别为1.77%、1.33%、0.81%,各方案发生完全破坏的地震风险概率分别为0.58%、0.36%、0.21%。相比4种减隔震方案,减隔震支座+榫形金属减震耗能装置+防落梁方案使支座构件在纵向地震作用下的地震风险最低,相比减隔震方案2,方案5使地震风险降低了65%~85%。
由图 11(c)、11(d)、12(c)、12(d)可知,横向+竖向地震作用下各减隔震方案计算结果的规律与纵向+竖向结果类似,这里不再详细论述。
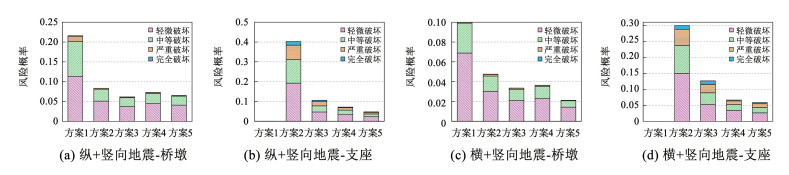
图 13和图 14分别给出了20 m和30 m墩高典型高速铁路简支梁桥,各减隔震方案下风险累计柱状图,分析结果表明:1)在纵向+竖向地震作用下,对于20 m墩高简支梁,其减隔震方案3~5对应的桥墩构件风险概率在6%~8%之间,3种方案差异不明显,但减隔震方案5条件下支座构件的地震风险概率相比其他方案最低;对于30 m墩高简支梁,其在减隔震方案5条件下,桥墩和支座构件的地震风险概率相比其他方案更低,更具优势。2)在横向+ 竖向地震作用下,20 m和30 m墩高简支梁桥,其桥墩构件在方案5下地震风险概率最低,控制在2%左右,而支座构件在方案4和方案5时地震风险概率较低,优于其他方案。
|
图 13 地震作用下20 m墩高简支梁桥关键构件各减隔震方案对应的风险累计柱状图 Fig. 13 The 2D histogram of risk analysis of key components of simply supported beam bridge under various seismic isolation systems |

|
图 14 地震作用下30 m墩高简支梁桥关键构件各减隔震方案对应的风险累计柱状图 Fig. 14 The 2D histogram of risk analysis of key components of simply supported beam bridge under various seismic isolation systems |
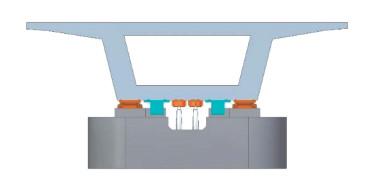
综上所述,在综合考虑地震危险性和桥梁结构地震易损性基础上,通过对5种减隔震方案条件下典型10、20、30 m墩32 m简支梁桥墩、支座构件在纵+竖向、横+竖向地震作用下桥梁关键构件地震风险概率进行分析表明:减隔震方案5(双曲面减隔震支座+榫形金属减震耗能装置+钢防落梁)可以有效提高桥梁抗震性能,耗散地震能量,减少桩基地震力,同时可以有效限制主梁位移,防止发生落梁震害,方案5条件下桥梁各关键构件的地震风险最低,推荐减隔震方案5作为10~30 m墩高32 m简支梁桥在九度地震区的减隔震方案(图 15)。
|
图 15 减隔震体系空间布置示意图 Fig. 15 Schematic diagram of spatial layout of seismic isolation system |
1) 建立了一种基于地震风险评估的铁路桥梁抗震分析方法,提出了不同地震水准等级对应的地震危险性贡献率计算方法,将传统风险分析方法中复杂积分求解转化为了简单、便捷的求解方法,便于工程应用,实现了桥梁结构地震风险及抗震性能评估。并利用MATLAB软件GUI编程方法编写了铁路桥梁地震风险评估分析软件,实现了铁路桥梁抗震性能的高效、快速评估。
2) 对5种减隔震方案下九度地震区典型高速铁路32 m简支梁桥各关键构件地震风险分析表明:减隔震方案5(减隔震支座+榫形金属减震耗能装置+钢防落梁)条件下桥梁各关键构件的地震风险最低,桥墩构件发生轻微、中等、严重和完全损伤的地震风险概率分别为5.9%、4.7%、1.01%、0.15%,支座构件发生轻微、中等、严重和完全损伤的地震风险概率分别为2.24%、1.33%、0.81%、0.21%。
3) 减隔震方案5可以提高桥墩抗震性能,耗散地震能量,减少桩基地震力,同时可以有效限制主梁位移,防止发生落梁震害。因此推荐减隔震方案5作为典型高速铁路32 m简支梁桥在九度地震区的减隔震方案。
| [1] |
曾永平, 董俊, 陈克坚, 等. 九度地震区高铁简支梁减隔震体系适应性分析[J]. 铁道工程学报, 2020, 257(2): 46. ZENG Yongping, DONG Jun, CHEN Kejian, et al. Adaptability analysis of the seismic isolation system for high-speed railway simply supported beam bridge in nine-degree seismic regions[J]. Journal of Railway Engineering Society, 2020, 257(2): 46. |
| [2] |
魏标, 刘义伟, 蒋丽忠, 等. 地震作用下双曲面球型减隔震支座在铁路简支梁桥中的动力行为[J]. 土木工程学报, 2019, 52(6): 110. WEI Biao, LIU Yiwei, JIANG Lizhong, et al. Dynamic behaviors of double spherical isolation bearing in simply-supportedrailway bridges under earthquakes[J]. China Civil Engineering Journal, 2019, 52(6): 110. |
| [3] |
杨孟刚, 孟栋梁, 卫康华, 等. 高铁简支梁桥横向地震碰撞效应及减震研究[J]. 西南交通大学学报, 2020, 55(1): 110. YANG Menggang, MENG Dongliang, WEI Kanghua, et al. Transverse seismic pounding effect and pounding reduction of simply-supported girder bridge for high-speed railway[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 110. |
| [4] |
陈克坚, 李吉林, 魏标, 等. 双线铁路简支梁桥的摩擦摆支座适用墩高范围研究[J]. 铁道科学与工程学报, 2020, 17(2): 364. CHEN Kejian, LI Jilin, WEI Biao, et al. Research on applicable pier height range of friction pendulum bearing of simply supported bridges in a double line railway[J]. Journal of Railway Science and Engineering, 2020, 17(2): 364. |
| [5] |
白全安. 新型减隔震装置在高速铁路桥梁中的应用研究[J]. 铁道工程学报, 2019, 36(10): 66. BAI Quanan. Application research on the new elastic-plastic limit seismic isolation device in high-speed railway simple supported girder bridges[J]. Journal of Railway Engineering Society, 2019, 36(10): 66. |
| [6] |
罗亮生, 包雪松, 王国英. 数值分析[M]. 北京: 科学出版社, 2002. LUO Liangsheng, BAO Xuesong, WANG Guoyin. Numerical analysis[M]. Beijing: Science Press, 2002. |
| [7] |
中国国家标准化管理委员会. 工程场地地震安全性评价: GB 17741—2005[S]. 北京: 中国标准出版社, 2005 Standardization Administration of China. Evaluation of seismic safety for engineering sites: GB 17741—2005[S]. Beijing: China Standards Press, 2005 |
| [8] |
吴果. 基于自适应空间光滑模型和三维断层模型的概率地震危险性分析方法研究[D]. 北京: 中国地震局地质研究所, 2018 WU Guo. The method research of probabilistic seismic hazard analysis based on adaptively smoothed seismicity model and 3-dimensional fault model[D]. Beijing: Institude of Geology, China Earthquake Administration, 2018 |
| [9] |
HUANG Y N, WHITTAKER A S, LUCO N. A probabilistic seismic risk assessment procedure for nuclear power plants: (Ⅱ)application[J]. Nuclear Engineering & Design, 2011, 241(9): 3985. DOI:10.1016/j.nucengdes.2011.06.051 |
| [10] |
董俊, 单德山, 张二华, 等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 159. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Jouranal of Harbin Institute of Technology, 2016, 48(3): 159. |
| [11] |
DEGROOT M H, SCHERVISH M J. Probability and statistics[M]. Englewood Cliff: Pearson Higher Isia Education, 2010.
|
| [12] |
ROSENBLATT M. Remarks on some non-parametric estimates of a density function[J]. Annuals of Mathematical Statistics, 1956, 27(3): 832. |
| [13] |
董俊, 曾永平, 单德山. 核密度估计的桥梁结构地震易损性分析[J]. 哈尔滨工业大学学报, 2018, 50(3): 109. DONG Jun, ZENG Yongping, SHAN Deshan. Seismic fragility analysis of railway bridge using kernel density estimation[J]. Jouranal of Harbin Institute of Technology, 2018, 50(3): 109. |
| [14] |
WAND M, JONES M C. Kernel smoothing[M]. Calabas: Chapman and Hall, 1994.
|
| [15] |
董俊. 铁路高墩大跨刚构-连续组合体系桥梁近场地震易损性分析研究[D]. 成都: 西南交通大学, 2016 DONG Jun. Fragility analysis of railway long span rigid frame-continuouscombination system bridge with high pier subjected to near-fault ground motion[D]. Chengdu: Southwest Jiaotong University, 2016 |
| [16] |
崔靓波. 高烈度地区铁路简支梁桥隔震研究[D]. 兰州: 兰州交通大学, 2016 CUI Jingbo. Study on seismic isolation of railway simple supported beam bridge in high seismic intensity region[D]. Lanzhou: Lanzhou Jiaotong University, 2016 |
| [17] |
董俊, 陈克坚, 曾永平, 等. 高烈度地震区铁路32 m预应力混凝土简支梁摩擦摆支座减震性能研究[J]. 铁道标准设计, 2020, 64(增刊1): 63. DONG Jun, CHEN Kejian, ZENG Yongping, et al. Study on vibration mitigation property of railway 32 m prestressed concrete simply-supported gierder with friction pendulum bearings in highly seismic area[J]. Railway Standard Design, 2020, 64(Sup. 1): 63. |
| [18] |
董俊, 单德山, 张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5): 845. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic fragility of irregularcontinuous rigid frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 845. |
| [19] |
吴文朋. 考虑不确定性的钢筋混凝土桥梁地震易损性研究[D]. 长沙: 湖南大学, 2016 WU Wenpeng. Seismic fragility of reinforced concrete bridges with consideration of various sources of uncertainty[D]. Changsha: Hunan University, 2016 |
| [20] |
国家铁路局. 铁路桥涵地基和基础设计规范: TB 10093—2017[S]. 北京: 中国铁道出版社, 2017 National Railway Administration. Code for design on subsoil and foundation of railway bridge and culvert: TB 10093—2017[S]. Beijing: China Railway Publishing House, 2017 |
 2023, Vol. 55
2023, Vol. 55


