2. 中国人民解放军32382部队, 武汉 430311
2. People's Liberation Army of China, 32382 Troops, Wuhan 430311, China
当舰船服役年限增加,船壳防腐涂层出现破损时,钢制船体与铜合金螺旋桨通过海水-轴系-船壳电路导通发生电偶腐蚀,海水中的腐蚀电流会在舰船周围产生腐蚀静电场[1]。当舰船处于航行状态时,电化学腐蚀回路的腐蚀电流受螺旋桨及轴系旋转调制产生舰船混合电场[2]。该信号被广泛应用于水下目标远距离探测。除海水电导率、温度、氧含量等海洋环境因素外[3],混合电场的大小与舰船航行状态密切相关,包括腐蚀介质流动状态、氧的传质过程、螺旋桨转速等[4-5]。
舰船腐蚀混合电场包括静电场(static electric field)和轴频电场(shaft-rate electric field)。当前对舰船电场的建模方法主要有边界元法、有限元法及等效源法。针对舰船电场,文献[6]采用了水平时谐电偶极子建模。文献[7]通过绘制产生轴频电场的等效电路,分析了轴系内调制等效阻抗。文献[8-9]用数值计算法计算了层流条件下平板及螺旋桨旋转的腐蚀静电场,耦合了多物理场。文献[10-11]在三维建模的基础上采用边界元法计算腐蚀静电场。以上团队采用多种建模方法研究了舰船电场,但针对舰船航行时复杂流体流动状态下的混合电场模型建立,及对不同流速下舰船混合电场变化规律的分析,仍需进一步探索研究。
由于不同舰船及螺旋桨表面形状不规则且差异较大,计算其在不同航速下表面流体流动状态较为困难,更难以计算电极表面电化学反应局部电流密度,因此采用的电偶极子模型等等效源法计算舰船电场,计算过程较为繁琐。针对以上问题,为研究湍流条件下氧的传质过程对舰船混合电场的影响,本文使用Solidworks软件对潜艇进行三维建模,结合流体力学和电化学腐蚀相关理论,分析湍流流场、舰船电场等多物理场建模理论基础,结合舰船轴系机械结构等效电阻变化规律,采用边界元法计算舰船电场。并使用COMSOL Multiphysics仿真软件进行多物理场耦合仿真,最终分析氧的传质过程控制下不同螺旋桨转速及航速对静电场及轴频电场的影响。
1 湍流条件下的舰船电场模型建立 1.1 湍流物理场建模流体由于存在黏滞性而存在两种流动情况,包含层流和湍流,其流动状态由雷诺数Re决定。雷诺数有多种表示方法,舰船航行时螺旋桨的雷诺数在1×107上下,应采用湍流物理场进行建模[12]。Re可表示为
| $ R e=\frac{n D^2}{\mu} $ | (1) |
式中: n为螺旋桨转速,D为螺旋桨直径,μ为流体的运动黏性系数。
湍流是流场的一种状态,螺旋桨旋转使水流流速增加且产生涡流。对轴频电场建模需首先对海水流动状态进行仿真建模。当前,主要的流体数值模拟方法为雷诺时均的Navier-Stockes(RANS)方程[13]。假设流体不可压缩,连续性方程及动量方程的形式为
| $ \rho \frac{\partial \boldsymbol{U}}{\partial t}+\rho \boldsymbol{U} \cdot \nabla \boldsymbol{U}=\nabla\left[-\boldsymbol{p} I+\mu\left(\nabla \boldsymbol{U}+(\nabla \boldsymbol{U})^{\mathrm{T}}\right)\right]+\boldsymbol{F} $ | (2) |
| $ \rho \nabla \cdot \boldsymbol{U}=0 $ | (3) |
式中: μ、ρ分别为流体的黏性系数、密度,不可压缩流体中密度ρ为恒定常数, U为速度矢量, p为压力,I为作用单元的面积, F为体积力矢量。
舰船表面流体流速为
| $ \boldsymbol{u}=\boldsymbol{U} \cdot \vec{u} $ | (4) |
式中
当流动变为湍流,湍流流速U可分解为平均值U′和波动部分u′。RANS方程可改写为式(5)。主要区别为等式左侧最后一项,该项表示速度场波动部分的相互作用,称为雷诺应力张量,该量可表示为式(6)。RANS方法的关键是雷诺应力的准确表示。由于缺少描述雷诺应力的物理定律,所以必须引入某些设定来建立关于雷诺应力的数学模型,因此产生了不同的湍流模型。
| $ \begin{gathered} \rho \frac{\partial \boldsymbol{U}^{\prime}}{\partial t}+\rho \boldsymbol{U}^{\prime} \cdot \nabla \boldsymbol{U}^{\prime}+\nabla \cdot\left(\rho \boldsymbol{u}^{\prime} \times \boldsymbol{u}^{\prime}\right)= \\ \nabla\left[-\boldsymbol{p} I+\mu\left(\nabla \boldsymbol{U}^{\prime}+\left(\nabla \boldsymbol{U}^{\prime}\right)^{\mathrm{T}}\right)\right]+\boldsymbol{F} \end{gathered} $ | (5) |
| $ \nabla \cdot\left(\rho \boldsymbol{u}^{\prime} \times \boldsymbol{u}^{\prime}\right)=\frac{2}{3} \rho k-\mu_{\mathrm{T}}\left(\nabla \boldsymbol{U}^{\prime}+\left(\nabla \boldsymbol{U}^{\prime}\right)^{\mathrm{T}}\right) $ | (6) |
标准k-ε模型是工业应用中最常见的湍流模型之一,该模型额外的引入了两个补充运输方程及两个因变量:湍流动能k及湍流耗散速率ε。并利用k、ε表示湍流黏度,进而实现雷诺时均模拟的两方程湍流模型。湍流黏度表示为
| $ \mu_{\mathrm{T}}=\rho C_\mu \frac{k^2}{\varepsilon} $ | (7) |
式中Cμ为模型常数。
引入的湍流动能k的运输方程:
| $ \rho \frac{\partial k}{\partial t}+\rho \boldsymbol{U} \cdot \nabla k=\nabla \cdot\left[\left(\mu+\frac{\mu_{\mathrm{T}}}{\sigma_{\mathrm{k}}}\right) \nabla k\right]+p_{\mathrm{k}}-\rho \varepsilon $ | (8) |
式中
| $ \begin{aligned} p_{\mathrm{k}}= & \mu_{\mathrm{T}}\left(\nabla \boldsymbol{U}:\left(\nabla \boldsymbol{U}+(\nabla \boldsymbol{U})^{\mathrm{T}}\right)-\right. \\ & \frac{2}{3}(\nabla \cdot \boldsymbol{U})^2-\frac{2}{3} \rho k \nabla \cdot \boldsymbol{U} \end{aligned} $ | (9) |
湍流耗散率ε的运输方程为
| $ \begin{gathered} \rho \frac{\partial \varepsilon}{\partial t}+\rho \boldsymbol{U} \cdot \nabla \varepsilon=\nabla \cdot\left[\left(\mu+\frac{\mu_{\mathrm{T}}}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right]+ \\ C_{\varepsilon 1} \frac{\varepsilon}{k} P_k-C_{\varepsilon 2} \rho \frac{\varepsilon^2}{k} \end{gathered} $ | (10) |
式中模型常数由实验数据确定。Cμ、Cε1、Cε2、σk、σε分别为0.09、1.44、1.92、1.0和1.3。
1.2 湍流条件下螺旋桨表面氧浓度求解海水中氧的传质过程控制着金属腐蚀强度,而氧浓度分布受流体流速分布的影响,需与流速变量耦合计算。
稳态传质过程中模拟化学物质通过对流和扩散传递机制的质量守恒方程为
| $ \nabla \cdot \left( { - {D_{\text{O}}}\nabla {c_{\text{O}}}} \right) + {\boldsymbol{u}} \cdot \nabla {c_{\text{O}}} = {R_{\text{O}}} $ | (11) |
式中:DO表示反应物的扩散系数,cO为物质浓度,本文研究氧的传质过程对电场的影响,故cO即为氧浓度。表面流速u可由式(4)求得。RO为该物质的反应速率,可表示为
| $ {R_{\text{O}}} = \frac{{{v_{\text{O}}} \cdot {i_{{\text{loc}}}}}}{{nF}} $ | (12) |
式中:iloc为化学反应的局部电流密度,可由后文中电极表面电极动力学方程求得;vO为化学反应参与电子数,吸氧腐蚀参与的电子数为4个;F为法拉第常数。
1.3 电场边界元法建模基本理论本文采用边界元法对三维模型下的舰船电场进行建模,针对阴极螺旋桨处在湍流物理场中,氧浓度与腐蚀电化学反应互相影响耦合,电极动力学方程采用浓度依赖性巴特勒-褔尔默方程(Butler-Volmer equation)[14-15], 即
| $ {i_{{\text{loc}}}} = {i_0}\left[ {\frac{{{C_{\text{R}}}}}{{{C_{{\text{R}},{\text{ ref }}}}}}\exp \left( {\frac{{{\alpha _{\text{a}}}F\eta }}{{RT}}} \right) - \frac{{{C_{\text{O}}}}}{{{C_{{\text{O}},{\text{ ref }}}}}}\exp \left( {\frac{{ - {\alpha _{\text{c}}}F\eta }}{{RT}}} \right)} \right] $ | (13) |
式中:i0为交换电流密度,仿真采用的B10铜合金表面氧还原反应的i0为1×10-6A/m2; αa、αc分别为阳极、阴极传递系数; R为气体常数; F为法拉第常数; η为活化过电位,为电极电位与平衡电位Eeq间的差值,阴极氧的平衡电位为0.189 V; cR、cO及cR, ref、cO, ref分别为还原物浓度和氧化物浓度及其初始参考值, 螺旋桨表面氧浓度cO由1.2节得到。最终得到电极表面局部电流密度[16]。
依据电极动力学方程计算电极(即涂层破损位置及螺旋桨表面)表面电位及局部电流密度分布后,可由边界积分方程计算求解域内的任意场点i处的电位φ(i), 即
| $ \begin{array}{*{20}{c}} {\varphi (i) + \int\limits_S \varphi (\xi )\frac{{\partial {\varphi ^*}(i,\xi )}}{{\partial n(\xi )}}{\text{d}}S = } \\ {\int\limits_S J (\xi ){\varphi ^*}(i,\xi ){\text{d}}S} \end{array} $ | (14) |
式中:φ(ξ)、J(ξ)分别为边界表面S上任意点ξ处的电位及电流密度;n为边界外法线,三维介质基本解∂φ*(i, ξ)可表示为
| $ \partial \varphi^*(i, \xi)=\frac{1}{4 {\rm{\mathsf{π}}} \sigma r} $ | (15) |
式中:r为i、ξ间的距离,σ为海水电导率。
边界元法是对边界积分方程进行离散的一种数值计算方法,将边界S离散为N个单元,则边界积分方程变换为
| $ \varphi(i)+\sum\limits_{j=1}^N \varphi_i \int_{S_j} \frac{\partial \varphi^*}{\partial n} \mathrm{~d} S_j=\sum\limits_{j=1}^N J_j \int_{S_j} \varphi^* \mathrm{~d} S_j $ | (16) |
通过解析矩阵方程,计算得到电位电流的基础上,即可计算水下电场分量及其模量[17]:
| $ \left\{\begin{array}{l} E_x=-\frac{\partial \varphi}{\partial x} \\ E_y=-\frac{\partial \varphi}{\partial y} \\ E_z=-\frac{\partial \varphi}{\partial z} \end{array}\right. $ | (17) |
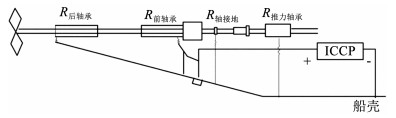
轴频电场是在螺旋桨及轴系机械结构调制作用下的腐蚀电场,在频域上轴频电场信号是与舰船主轴转动频率相同的低频线谱。因其特征明显被广泛应用于舰船的远距离探测与定位。轴频电场的产生机理是腐蚀电流从阳极(船壳破损位置)通过海水流向阴极(螺旋桨)。如图 1所示,通过船体内部的主轴、轴承、联轴器、齿轮箱等机械结构接地回到船壳破损位置形成电流回路。要对轴频电场建模,须首先分析船体内部“螺旋桨→主轴→轴接地→船壳破损处”的等效电阻。
|
图 1 船体内部机械结构 Fig. 1 Internal mechanical structure of the hull |
文献[7]中分析得出等效回路电流为
| $ I=\frac{\varphi_{\mathrm{a}}-\varphi_{\mathrm{c}}}{Z+R_{\mathrm{b}}} $ | (18) |
| $ \frac{1}{R_{\mathrm{b}}}=\frac{1}{R_{\mathrm{FB}}}+\frac{1}{R_{\mathrm{RB}}}+\frac{1}{R_{\mathrm{SG}}}+\frac{1}{R_{\mathrm{TB}}} $ | (19) |
等效回路电流表达式中Z为外调制阻抗,包含船体和螺旋桨的极化阻抗及船体涂层阻抗等。Rb为船体内部等效电路阻抗。RFB、RRB、RSG、RTB分别为前轴承、后轴承、轴接地、推力轴承的电阻。由舰船尾部结构可将Rb等效为如式(19)所示。经分析,Rb所代表的内调制是产生轴频电场的主要因素。其中,轴接地设备的电阻远小于其他设备电阻值,即Rb≈RSG=20 mΩ±(2~6)mΩ,波动系数约为10%~30%。即可设置为
| $ R_{\mathrm{b}}=(20+5 \sin 2 {\rm{\mathsf{π}}} f t) \times 10^{-3} \Omega $ | (20) |
式中f为螺旋桨转速。
在Solidworks软件中建立潜艇三维几何模型。考虑到舰船靠泊时船舷两侧磨损易导致消声瓦及防腐涂层破损,设定破损位置为对称分布的左右舷两侧(破损率为2%左右)。将几何模型导入至COMSOL Multiphysics多物理场仿真软件中,以螺旋桨端点为坐标轴原点,设置“电流分布,边界元”接口建立舰船腐蚀电场边界元模型,由于本模型主要研究静电场及轴频电场,故不考虑设置补偿阳极及牺牲阳极等防腐及电场补偿装置[18]。
将潜艇螺旋桨桨叶及桨毂设置为旋转机械,转速分别设置为0、1、2、3、4 r/s,并在潜艇周围一定空域内设置“湍流”物理场,如图 2所示。湍流模型采用标准k-ε模型,在物理场内分别设置对应螺旋桨转速的0、1、4、7、10 m/s流场,以模拟潜艇不同航速的运动状态。并设置“稀物质传递”物理场计算不同表面流速下的氧浓度。仿真计算时首先使用“湍流”物理场计算潜艇表面流体流速,再对“稀物质传递”及“电流分布,边界元”进行多物理场耦合仿真。并在螺旋桨表面设置随时间t变化的表面电阻Rb,以模拟内调制轴-地等效电阻。

|
图 2 潜艇腐蚀电场三维模型 Fig. 2 Three-dimensional model of submarine corrosion electric field |
通过建立湍流物理场下的混合电场仿真模型,可以分析潜艇在不同运动状态下的表面流速、电场分布及静电场、轴频电场等物理量的变化情况。
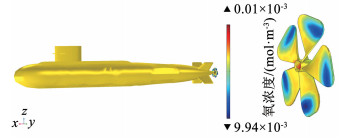
3.1 表面流速及氧浓度分布当螺旋桨转速为4 r/s、航速为10 m/s时,潜艇表面流速分布如图 3所示。可见潜艇表面流速与海水流速接近,螺旋桨桨叶表面呈现为旋转方向边缘流速高于内部流速的状态。最大表面流速约为28 m/s。如图 4为对应流速下潜艇表面氧浓度分布图。其表面分布状态与表面流速分布类似。表面流速较快的位置更多的氧参与到还原反应,使其表面氧分子浓度降低。依据电极动力学方程中浓度依赖性巴特勒-褔尔默方程,螺旋桨表面氧浓度cO/cO, ref比值较低时,局部电流密度较高,最终使得潜艇腐蚀电场强度增大。

|
图 3 潜艇表面流速分布 Fig. 3 Velocity distribution on the surface of submarine |
|
图 4 潜艇表面氧浓度分布 Fig. 4 Distribution of oxygen concentration on the surface of submarine |
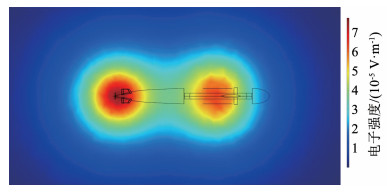
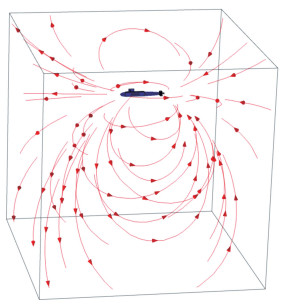
当螺旋桨转速为4 r/s、航速为10 m/s时,在Z=-16 m平面上潜艇电场模量分布如图 5所示,电场模量在螺旋桨及舰船破损处出现峰值。海水域中腐蚀电流密度矢量分布如图 6所示,电流密度矢量的方向由船壳破损位置处经海水域指向螺旋桨。两者之间发生了的电偶腐蚀。本文建立的腐蚀电场模型真实有效。
|
图 5 潜艇电场模量分布图 Fig. 5 Distribution diagram of electric field modulus of submarine |
|
图 6 潜艇电流密度矢量分布 Fig. 6 Submarine current density vector distribution |
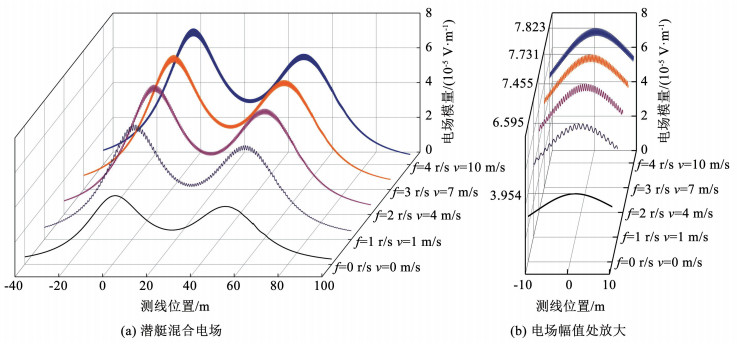
本文设定电场测线位于原点(螺旋桨端点)下方2倍船宽(2B)处即Z=-16 m,点A(-40 m, 0 m, -16 m)至B(100 m, 0 m, -16 m)之间的连线,测点以1 m/s的速度由A至B点移动,测量的舰船电场模量。并通过改变螺旋桨转速及对应的水流流速以模拟潜艇不同的航行状态。可得到舰船静电场及轴频电场叠加而成的混合电场信号。如图 7所示,电场模量在x=0 m即阴极螺旋桨处及x=52 m即潜艇船壳破损位置处分别达到双峰值。截取x在-10~10 m处混合电场信号并放大。可观察到受舰船轴系等效电阻周期性变化的影响,舰船轴电流亦发生周期性变化,进而导致舰船电场模量在一定范围内波动,波动频率与螺旋桨转动频率一致。
|
图 7 潜艇混合电场分布 Fig. 7 Submarine hybrid electric field distribution |
参照设计的螺旋桨转速及对应航速,混合电场模量的幅值出现在螺旋桨正下方2B处,分别为3.954×10-5 V/m、6.595×10-5 V/m、7.455×10-5 V/m、7.731×10-5 V/m、7.823×10-5 V/m,螺旋桨转速由静止每提升1 r/s,电场模量分别依次提高66.5%、13%、3.7%、1.19%。舰船混合电场在螺旋桨开始旋转初始即大幅度增长,较静止状态下电场值增大66.5%。随着航速的提高,舰船混合电场呈现增长率逐渐降低的趋势。至螺旋桨转速为3 r/s以上时,增长率较小可忽略不计。螺旋桨正下方2B处电场强度与转速的变化规律如图 8所示。

|
图 8 电场变化规律 Fig. 8 Electric field change trend |
采用低通滤波器对混合电场进行滤波,得到不同航行状态下的舰船静电场模量分布曲线,如图 9所示。静电场在x=0 m处的幅值为3.954×10-5 V/m、6.437×10-5 V/m、7.256×10-5 V/m、7.515×10-5 V/m、7.604×10-5 V/m。静电场增长率分别为62.8%、12.7%、3.57%、1.18%。增长趋势与混合电场幅值一致。

|
图 9 静电场分布 Fig. 9 Static electric field distribution |
采用带通滤波器对混合电场进行滤波,得到不同航行状态下舰船轴频电场分布曲线,如图 10所示。轴频电场随测线方向呈纺锤形状。轴频电场幅值分别为1.573×10-6 V/m、2×10-6 V/m、2.14×10-6 V/m、2.18×10-6 V/m。轴频电场幅值与静电场幅值的比例低于3%,且增长率显著低于舰船静电场, 可见轴频电场并非混合电场的主要部分。

|
图 10 轴频电场分布 Fig. 10 Shaft-rate electric field distribution |
以上结果表明,舰船腐蚀电场的幅值受到舰船航行状态的影响,即航速与螺旋桨转速的影响。舰船航行状态的变化使得螺旋桨表面介质流速发生变化,表面流速较快的位置有更多氧分子参与到还原反应,增大了腐蚀电流密度,最终影响舰船腐蚀电场分布。
4 结论本文分析了湍流流场、舰船电场等多物理场建模理论基础,结合腐蚀电流回路中舰船轴系机械结构等效电阻变化规律,采用边界元法建立潜艇腐蚀电场模型,通过改变潜艇三维模型中螺旋桨转速及腐蚀介质流速以模拟潜艇不同的航行状态,分析了腐蚀介质中氧的传质过程对舰船腐蚀混合电场的影响。主要结论如下:
1) 本文建立的舰船腐蚀电场模型耦合了湍流流场、舰船腐蚀电场等多物理场,可较好地模拟不同运动状态下的舰船腐蚀混合电场,包含舰船静电场及轴频电场。该建模方法对不同舰船腐蚀电场测量有较强针对性,较传统舰船轴频电场数值计算法更加直观可靠。
2) 当螺旋桨转速分别为0、1、2、3、4 r/s,对应航速分别为0、1、4、7、10 m/s时,螺旋桨转速每提升1 r/s,螺旋桨正下方2B处舰船混合电场幅值依次提高66.5%、13%、3.7%、1.19%。航速及转速的提高增大了介质流速及介质中氧向桨叶表面的传递速率,流速越快的位置有更多的氧分子参与到腐蚀反应中,增大了腐蚀电流密度进而使舰船电场增大。经滤波后的舰船静电场变化趋势与混合电场基本一致。而舰船轴频电场幅值较小,并非混合电场主要部分。
| [1] |
蔡岳丰, 范啸平, 邰能灵. 船舶水中电场分析方法研究综述[J]. 上海交通大学学报, 2018, 52(10): 1410. CAI Yuefeng, FAN Xiaoping, TAI Nengling. Review of analytical methods for underwater electric field in ships[J]. Journal of Shanghai Jiao Tong University, 2018, 52(10): 1410. DOI:10.16183/j.cnki.jsjtu.2018.10.033 |
| [2] |
张立琛, 王英民, 陶林伟. 舰船腐蚀相关轴频电磁场场源建模[J]. 哈尔滨工程大学学报, 2017, 38(10): 1525. ZHANG Lichen, WANG Yingmin, TAO Linwei. Modeling of ship corrosion related shaft-rate electromagnetic field[J]. Journal of Harbin Engineering University, 2017, 38(10): 1525. |
| [3] |
王向军, 张建春, 嵇斗, 等. 浅海中电导率对同一水平面轴频电场的影响[J]. 海军工程大学学报, 2018, 30(2): 6. WANG Xiangjun, ZHANG Jianchun, JI Dou, et al. Conductivity's influence on shaft-rate electric field in shallow sea[J]. Journal of Naval University of Engineering, 2018, 30(2): 6. |
| [4] |
SCHAEFER D, DOOSE J, PICHLMAIER M, et al. Conversion of UEP signatures between different environmental conditions using shaft currents[J]. IEEE Journal of Oceanic Engineering, 2016, 41(1): 105. DOI:10.1109/JOE.2015.2401991 |
| [5] |
KIM Y S, LEE S K, CHUNG H J, et al. Influence of a simulated deep sea condition on the cathodic protection and electric field of an underwater vehicle[J]. Ocean Engineering, 2018, 148: 223. DOI:10.1016/j.oceaneng.2017.11.027 |
| [6] |
熊露, 姜润翔, 龚沈光. 浅海中船舶轴频电场建模方法[J]. 国防科技大学学报, 2014, 36(1): 98. XIONG Lu, JIANG Runxiang, GONG Shenguang. Ship modeling method of shaft-ELFE in shallow sea[J]. Journal of National University of Defense Technology, 2014, 36(1): 98. |
| [7] |
姜润翔, 张伽伟, 陈新刚. 舰船轴频电场产生机理及控制技术[J]. 国防科技大学学报, 2019, 41(6): 111. JIANG Runxiang, ZHANG Jiawei, CHEN Xingang. Ship's shaft-related electric field mechanism of production and countermeasure technology[J]. Journal of National University of Defense Technology, 2019, 41(6): 111. |
| [8] |
王向军, 张建春, 徐庆林. 层流介质中曲面螺旋桨旋转对腐蚀静电场的影响[J]. 电子学报, 2019, 47(11): 7. WANG Xiangjun, ZHANG Jianchun, XU Qinglin. The influence of rotating curved surface propeller on the corrosion electrostatic field in laminar medium[J]. Acta Electronica Sinica, 2019, 47(11): 7. |
| [9] |
张建春, 王向军. 层流介质中金属板腐蚀电位分布研究[J]. 国防科技大学学报, 2018, 40(6): 157. ZHANG Jianchun, WANG Xiangjun. Corrosion potential distribution research of metal plate in laminar flow[J]. Journal of National University of Defense Technology, 2018, 40(6): 157. |
| [10] |
徐庆林, 王向军, 张建春, 等. 温度对舰船阴极保护和腐蚀静电场的影响[J]. 国防科技大学学报, 2019, 41(4): 182. XU Qinglin, WANG Xiangjun, ZHANG Jianchun, et al. Influence of temperature on the cathodic protection and corrosion electrostatic field of ships[J]. Journal of National University of Defense Technology, 2019, 41(4): 182. |
| [11] |
徐庆林, 王向军, 张建春, 等. 补偿阳极位置对舰船腐蚀电场防护效果的影响[J]. 哈尔滨工业大学学报, 2020, 52(9): 123. XU Qinglin, WANG Xiangjun, ZHANG Jianchun, et al. Influence of compensation anode position on corrosion electric field damping effect of ship[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 123. |
| [12] |
盛振邦, 刘应中. 船舶原理(下)[M]. 上海: 上海交通大学出版社, 2004: 34. SHENG Zhenbang, LIU Yingzhong. Principles of ships[M]. Shanghai: Shanghai Jiao Tong University Press, 2004: 34. |
| [13] |
王福军. 流体机械旋转湍流计算模型研究进展[J]. 农业机械学报, 2016, 47(2): 1. WANG Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 1. |
| [14] |
XING S H, LI Y, SONG H Q, et al. Optimization the quantity, locations and output currents of anodes to improve cathodic protection effect of semi-submersible crane vessel[J]. Ocean Engineering, 2016, 113: 144. |
| [15] |
姜润翔, 陈新刚, 张伽伟. 舰船电场及其应用[M]. 北京: 国防工业出版社, 2020: 46. JIANG Runxiang, CHEN Xingang, ZHANG Jiawei. Ship electric field and its application[M]. Beijing: National Defense Industry Press, 2020: 46. |
| [16] |
ZHANG H, WANG X, SHAN C, et al. Electric field distribution measurement equipment calibration based on electric field calculation of space[J]. International Journal of Digital Content Technology & Its Applications, 2012, 6(16): 524. |
| [17] |
XU Q, WANG X, TONG Y, et al. The effect of hydrostatic pressure on corrosion electric field considering the mechanochemical coupling effect[J]. Chemical Physics Letters, 2020, 754: 137761. |
| [18] |
LAN Z, WANG X, HOU B, et al. Simulation of sacrificial anode protection for steel platform using boundary element method[J]. Engineering Analysis with Boundary Elements, 2012, 36(5): 903. |
 2023, Vol. 55
2023, Vol. 55


