具有强突防和快速反应能力的高超声速飞行器,为确保其飞行安全,针对高超声速飞行器整体结构进行可靠性分析显得十分必要。
对于结构可靠性的研究,主要分为静态可靠性和动态可靠性。文献[1-8]应用不同的方法对静态可靠性进行研究并取得一定成果。文献[9]分析了时变性主要来源于材料属性随时间的退化以及随时间变化的载荷。文献[10-12]分别基于跨越率法、极值法以及代理模型法对不同模型的动态可靠性进行求解。文献[13]首次提出基于凸集合模型的非概率可靠性概念。文献[14-15]应用非概率可靠性方法分析了杆系结构的可靠性取得不错效果。而目前关于飞机的可靠性研究,主要集中在飞机的机翼。文献[16]采用区间模型表征系统各组件失效概率,研究了基于故障树的系统可靠性分析方法,并用于分析飞机襟翼机构不对称运动故障。
综上所述,在文献[17-19]的基础上,本文针对高超声速飞行器纵向模型,结合活塞理论、激波-膨胀理论分析飞行器飞行过程中的各主要受力面的结构受力情况,并用区间分布表示飞行器纵向平面所受力矩的不确定性。同时,考虑各种复杂条件引起的机身材料的强度退化,引入指数退化来描述机身强度的变化。然后,基于区间可能度,建立应力-强度干涉动态非概率可靠性模型,提出基于子域子区间的高超声速飞行器非概率可靠性计算的新方法,并分析了在强度退化的情况下,飞行速度、高度以及迎角对飞行器可靠性的影响,为今后结构可靠性控制器设计提供重要参考。
1 高超声速飞行器纵向模型受力分析近年来,针对高超声速飞行器可靠性的研究取得了一些成果。但大都将机翼作为主要研究对象,而未考虑飞行器整体在飞行过程中的可靠性。鉴于此,本文以典型的吸气式高超声速飞行器纵向几何模型为研究对象,并基于活塞理论以及激波-膨胀波理论,分析飞行器飞行过程中全机身结构实时受力情况。
图 1给出了吸气式高超声速飞行器纵向几何模型。

|
图 1 AHFV纵向几何模型 Fig. 1 Longitudinal geometric model |
如图 1所示,该纵向模型由5个受力面组成:飞行器上表面(定义为cf),前体下表面(定义为cd),发动机下表面(定义为gh),后体下表面(定义为ef),控制面(定义为rs)。α为迎角,M∞为无穷远处未扰动流马赫数,xb、zb为机体坐标轴,θs为气流偏转角。表 1给出了剩余参数的定义以及取值。
| 表 1 飞行器结构参数 Tab. 1 Aircraft structure parameters |
结合一阶活塞理论和激波-膨胀波理论对飞行器各个面进行气动力分析, 限于篇幅,这里仅给出上表面的受力分析,其余面的受力分析可参考文献[20]。
1.1 飞行器上表面受力分析首先,以上表面某一单位面积为研究对象,根据力学定律可得
| $ \mathrm{d} \boldsymbol{F}_{c f}=-p_{c f}^{\prime} \mathrm{d} A_{c f} \boldsymbol{n}_{c f} $ | (1) |
式中:dFcf为上表面单位面积的应力矢量,pcf′为上表面受到的压力,dAcf为单位面积,ncf为垂直上表面向外的单位向量。具体地,dAcf可表示为
| $ \begin{aligned} \mathrm{d} A_{c f}= & \sqrt{\mathrm{d} x_1^2+\tan ^2 \tau_{1, \mathrm{u}} \mathrm{d} x_1^2}=\mathrm{d} x_1 \sqrt{1+\tan ^2 \tau_{1, \mathrm{u}}}= \\ & \sec \tau_{1, \mathrm{u}} \mathrm{d} x_1 \end{aligned} $ | (2) |
式中,x1为值在-xa到xf之间的积分变量,即-xa≤ x1≤xf。另外,ncf可表示为
| $ \boldsymbol{n}_{c f}=\sin \tau_{1, \mathrm{u}} \boldsymbol{i}-\cos {\tau}_{1, \mathrm{u}} \boldsymbol{j} $ | (3) |
式中,i、j分别为沿xb轴和zb轴的单位矢量。
根据活塞理论可得
| $ p_{c f}^{\prime}=p_{c f}+\rho_{c f} a_{c f} v_{c f} $ | (4) |
式中:pcf为上表面的当地压力, acf为上表面的当地声速,vcf为上表面的下洗速度。而vcf可表示为
| $ v_{c f}=\boldsymbol{V}_{c f} \cdot \boldsymbol{n}_{c f} $ | (5) |
且
| $ \boldsymbol{V}_{c f}=\left(V \cos \tau_{1, \mathrm{u}}+v_{b x}\right) \boldsymbol{i}+\left(V \sin \tau_{1, \mathrm{u}}+v_{b z}\right) \boldsymbol{j}+\boldsymbol{\omega} \times \boldsymbol{r}_{c f} $ | (6) |
式中:Vcf为上表面运动速度矢量,V为飞行速度,vbx、vbz分别为上表面振动速度在机体坐标轴xb轴和zb轴上的分量,ω为飞行器在纵向平面内的转动角速率矢量,rcf为飞行器质心指向单位面积的矢量。且有:
| $ \boldsymbol{\omega}=q \boldsymbol{k} $ | (7) |
| $ \boldsymbol{r}_{c f}=x \boldsymbol{i}+\tan \tau_{1, \mathrm{u}}\left(x-\bar{x}_f\right) \boldsymbol{j} $ | (8) |
式中:k为角速率单位向量,q为俯仰角速率,将式(7)、(8)代入式(6)可得
| $ \begin{aligned} \boldsymbol{V}_{c f}= & \left(V \cos \tau_{1, \mathrm{u}}+v_{b x}\right) \boldsymbol{i}+\left(V \sin \tau_{1, \mathrm{u}}+v_{b z}\right) \boldsymbol{j}+ \\ & q \boldsymbol{k} \times\left(x_1 \boldsymbol{i}+\tan \tau_{1, \mathrm{u}}\left(x_1-\bar{x}_f\right) \boldsymbol{j}\right) \end{aligned} $ | (9) |
飞行速度 V在垂直于上表面方向上的分量为0,即有
| $ \boldsymbol{V} \cdot \boldsymbol{n}_{c f}=0 $ | (10) |
即式(9)可进一步表示为
| $ \boldsymbol{V}_{c f}=\left(v_{b x} \boldsymbol{i}+v_{b z} \boldsymbol{j}\right)+q \boldsymbol{k} \times\left(x_1 \boldsymbol{i}+\tan \tau_{1, \mathrm{u}}\left(x_1-\bar{x}_f\right) \boldsymbol{j}\right) $ | (11) |
结合式(4)、(5)和式(11)可得
| $ \begin{aligned} p_{c f}^{\prime}= & p_{c f}+\rho_{c f} a_{c f}\left[\left(v_{b x}+q \tan \tau_{1, \mathrm{u}}\left(x-\bar{x}_f\right)\right) \sin \tau_{1, \mathrm{u}}-\right. \\ & \left.\left(v_{b z}-q x\right) \cos \tau_{1, \mathrm{u}}\right] \end{aligned} $ | (12) |
进一步将式(2)~(4)代入到式(1)中可得
| $ \begin{aligned} \mathrm{d} \boldsymbol{F}_{c f}= & \left\{-p_{c f}-\rho_{c f} a_{c f}\left[\left(v_{b x}+q \tan \tau_{1, \mathrm{u}}\left(x_1-\right.\right.\right.\right. \\ & \left.\left.\left.\left.\bar{x}_f\right)\right) \sin \tau_{1, \mathrm{u}}-\left(v_{b z}-q x_1\right) \cos \tau_{1, \mathrm{u}}\right]\right\}\left(\sin \tau_{1, \mathrm{u}} \boldsymbol{i}-\right. \\ & \left.\cos \tau_{1, \mathrm{u}} \boldsymbol{j}\right) \sec \tau_{1, \mathrm{u}} \mathrm{d} x_1 \end{aligned} $ | (13) |
则Fcf为
| $ \begin{aligned} \boldsymbol{F}_{c d}= & \int_{\bar{x}_a-L_f}^{\bar{x}_f}\left\{-p_{c d}-\rho_{c d} a_{c d}\left[\left(v_{b x}-q \tan \tau_{1, \mathrm{u}}\left(x_2-\right.\right.\right.\right. \\ & \left.\left.\left.\left.\bar{x}_f\right)\right) \sin \tau_{1, \mathrm{l}}-\left(v_{b z}-q x_2\right) \cos \tau_{1, \mathrm{l}}\right]\right\}\left(\sin \tau_{1, \mathrm{l}} \boldsymbol{i}+\right. \\ & \left.\cos \tau_{1, \mathrm{l}} \boldsymbol{j}\right) \sec \tau_{1, \mathrm{l}} \mathrm{~d} x_2 \end{aligned} $ | (14) |
式中:ρcf、acf、pcf分别为飞行器上表面的当地气流密度、当地声速、当地压力。
1.2 前体下表面受力和发动机下表面受力前体下表面受力Fcd和发动机下表面受力Fgh分别为:
| $ \begin{aligned} \boldsymbol{F}_{c d}= & \int_{\bar{x}_a-L_f}^{\bar{x}_f}\left\{-p_{c d}-\rho_{c d} a_{c d}\left[\left(v_{b x}-q \tan \tau_{1, \mathrm{u}}\left(x_2-\right.\right.\right.\right. \\ & \left.\left.\left.\left.\bar{x}_f\right)\right) \sin \tau_{1, 1}-\left(v_{b z}-q x_2\right) \cos \tau_{1, 1}\right]\right\}\left(\sin \tau_{1, 1} \boldsymbol{i}+\right. \\ & \left.\cos \tau_{1, 1} \boldsymbol{j}\right) \sec \tau_{1, 1} \mathrm{~d} x_2 \end{aligned} $ | (15) |
| $ \boldsymbol{F}_{g h}=\int_{-x_a}^{\bar{x}_f}\left[-p_{g h}-\boldsymbol{\rho}_{g h} a_{g h}\left(v_{b z}-q x_3\right) \boldsymbol{j}\right] \mathrm{d} x_3 $ | (16) |
式中: x2为xa-Lf到xf之间的积分变量,x3为-xa到xf之间的积分变量,ρcd、acd、pcd分别为前体下表面气流密度、当地声速、当地压力,ρgh、agh、pgh分别为发动机下表面气流密度、当地声速、当地压力。
1.3 后体下表面受力后体下表面受力Fef为
| $ \boldsymbol{F}_{e f}=\frac{\ln \left(p_{e f} / p_{\infty}\right) p_{e f} \bar{x}_f}{\cos \left(\tau_{1, \mathrm{u}}+\tau_2\right)\left(p_{e f} / p_{\infty}-1\right)} $ | (17) |
式中:p∞为无穷远处气流压强,ρef、aef、pef分别为后体下表面气流密度、当地声速、当地压力。
1.4 控制面的受力为控制面的受力为Frs,Frs=Fkx-Fks,其中控制面的上、下表面受力分别为Fks、Fkx分别为:
| $ \begin{aligned} \boldsymbol{F}_{k s}= & \int_{-x_s-L_s \cos \delta_\mathrm{e} / 2}^{-x_s+L_s \cos \delta_\mathrm{e} / 2}\left(-p_{k s}-\rho_{k s} a_{k s} v_{k s}\right)\left(-\sin \delta_{\mathrm{e}} \boldsymbol{i}-\right. \\ & \left.\cos \delta_{\mathrm{e}} \boldsymbol{j}\right) \sec \delta_{\mathrm{e}} \mathrm{d} x \end{aligned} $ | (18) |
| $ \begin{aligned} \boldsymbol{F}_{k x}= & \int_{-x_s-L_s \cos \delta_\mathrm{e} / 2}^{-x_s+L_s \cos \delta_\mathrm{e} / 2}\left(-p_{k x}-\rho_{k x} a_{k x} v_{k x}\right)\left(\sin \delta_{\mathrm{e}} \boldsymbol{i}+\right. \\ & \left.\cos \delta_{\mathrm{e}} \boldsymbol{j}\right) \sec \delta_{\mathrm{e}} \mathrm{d} x \end{aligned} $ | (19) |
式中:vks、vkx分别为控制面上、下表面下洗速度,xs为控制面长度上的积分变量,ρks、aks、pks分别为控制面上表面气流密度、当地声速、当地压力,ρkx、akx、pkx分别为控制面下表面气流密度、当地声速、当地压力。
1.5 飞行器表面的总受力飞行器表面的总受力Ftotal为
| $ \boldsymbol{F}_{\text {total }}=\boldsymbol{F}_{c f}+\boldsymbol{F}_{c d}+\boldsymbol{F}_{g h}+\boldsymbol{F}_{e f}+\boldsymbol{F}_{r s}=\boldsymbol{F}_{t x}+\boldsymbol{F}_{t z} $ | (20) |
式中:Ftotal为总气动力,Ftx为总气动力沿xb轴方向上的分量,Ftz为沿zb轴方向上的分量。
2 高超声速飞行器可靠性建模由于高超声速飞行器在飞行过程中受到复杂的气动力影响,载荷很难通过服从正态分布或者截尾正态分布来描述。面对具有未确知性的气动载荷,本文通过分析得到飞行器各个面受到的气动载荷大小,并在合理范围内假设载荷所属区间范围。在考虑强度随时间退化服从指数分布的情况下,利用应力-强度干涉模型建立非概率可靠性状态极限方程。最后通过子域子区间抽样法来计算飞行器的非概率可靠性。
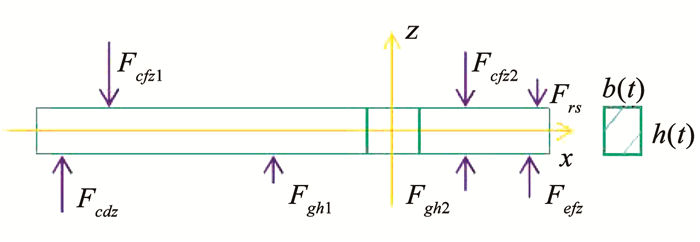
为方便建立飞行器纵向模型的非概率可靠性状态极限方程,将飞行器机身前体和后体等效为质量均匀分布的悬臂梁结构,以质心为固支点,如图 2所示。
|
图 2 悬臂梁受力示意 Fig. 2 Schematic diagram of force on cantilever beam |
根据应力-强度干涉公式,建立飞行器机身结构的非概率可靠性状态极限方程如下:
| $ G(t)=R(t)-6 \frac{M}{b h^2} $ | (21) |
式中:b、h、t分别为等效悬臂梁的宽度、高度以及飞行时间,R(t)为高超声速飞行器的结构强度,M为悬臂梁所受的力矩,可以表示为
在实际飞行过程中,控制面受力Frs远小于其他4个面受力,故在下文的受力分析中忽略控制面受力。对图 2中等效的两个悬臂梁进行受力分析。
图 2中,Fcfz1、Fcfz2分别为飞行器前体上表面受力Fcf沿z轴方向上作用在前、后悬臂梁上的分力,Fcdz为飞行器前体下表面受力Fcd沿z轴的分力,Fgh1、Fgh2分别为飞行器发动机受力Fgh在前、后悬臂梁上的分力,Fefz为飞行器后体下表面所受力Fef在z轴上的分力。图 2中平行于z轴方向作用在悬臂梁上的力的作用点分别为:
| $ \begin{aligned} M= & \mid \boldsymbol{F}_{c f z 1} \bar{x}_f / 2-\boldsymbol{F}_{c d z}\left(\bar{x}_f-L_f / 2\right)- \\ & \boldsymbol{F}_{g h 1}\left(\bar{x}_f-L_f\right) / 2-\boldsymbol{F}_{c f z2} \bar{x}_a / 2+ \\ & \boldsymbol{F}_{g h 2}\left(L_n+L_f-\bar{x}_f\right) / 2+\boldsymbol{F}_{e f z}\left(L_z-\bar{x}_f\right) / 2 \mid \end{aligned} $ | (22) |
由于目前高超声速飞行器主要受力结构的材料为Ti6Al4V,因此本文以Ti6Al4V为强度支撑材料进行分析研究。考虑高超声速飞行器在执行任务过程中经历的复杂环境,飞行器复合材料的强度会随着时间的推移逐渐退化。目前,常见的强度退化方式有:文献[21-22]中采用的指数退化方式,文献[23-24]中采用的Gamma退化方式和文献[25]中采用的基于P-S-N随机退化方式。其中强度随时间指数退化方式相比于其他退化方式,在满足机械零部件强度单向退化的同时,又满足了在高超声速飞行器执行任务的极端复杂条件下材料强度会发生强退化的特点。综合考虑以指数退化过程来描述强度随时间的变化,其表达形式如下:
| $ R(t)=R_0 \exp (-\zeta t) $ | (23) |
式中:ζ为退化指数,这里文献[18]取ζ=0.000 008,R0为初始材料强度。
根据飞行器质量、长度以及Ti6Al4V的密度并考虑所给的参数的不确定性,其中R0给定不确定性为10%,1/bh2的不确定性为60%。式(21)中部分参数所给区间范围和均值见表 2。
| 表 2 随机参数区间分布 Tab. 2 Random parameter interval distribution |
飞行器在执行任务过程中,随着飞行高度、迎角及速度的变化,极限状态方程中的力矩M也会发生改变。通过仿真分析,表 3给出了在考虑随机参数的影响下,飞行器所受力矩M随飞行高度、迎角以及速度变化的区间值。
| 表 3 M随飞行高度、迎角以及马赫数的变化 Tab. 3 M varies with flight altitude, angle of attack and Mach number |
对比表 3中数据可知,力矩的平均数随着马赫数的增加而增加,随飞行高度的增加而减小,随迎角的增加而增加。与文献[26]实际飞行试验结果对比可知,表 3的分析结果是合理的。
3 高超声速飞行器结构非概率可靠性分析 3.1 标准化状态极限方程为计算状态极限方程的非概率可靠度,需对状态极限方程中任意不确定参数X进行标准化处理。假设X变化范围为X∈[Xl, Xu],且在区间内服从均匀分布,对应的区间中点Xc和区间半径Xr分别表示为:
| $ X_c=\frac{X_1+X_{\mathrm{u}}}{2} $ | (24) |
| $ X_r=\frac{X_{\mathrm{u}}-X_1}{2} $ | (25) |
对X进行标准化处理为
| $ X=X_c+X_r \delta_x $ | (26) |
式中δx∈[-1, +1]为强度标准化区间变量。式(21)中,由于R(t)会随时间逐渐减小,R(t)c以及R(t)r都会随之一起变化,但相对R(t)c变化范围而言,R(t)r变化范围可以忽略。本文在保证计算准确性的同时,以初始时刻强度R0的区间半径作为整个强度变化时间内的区间半径R(t)r=55 MPa,R(t)c=R0exp(-ζt)。
同理,不确定参数1/bh2和M的标准化处理与R(t)类似。根据表 3可得1/bh2标准化处理结果为(1/bh2)c=2.5 m-3,(1/bh2)r=1.5 m-3。根据表 3可得Mr=106 N·m,Mc=(Ml+Mu)/2,其中Ml、Mu分别为M∈[Ml, Mu]区间的左、右端点值。将标准化后的不确定参数代入式(21),得到标准状态极限方程:
| $ \begin{aligned} G(\delta, t)= & R(t)_c+R(t)_r \delta_{\mathrm{r} 1}- \\ & 6\left(M_c+M_r \delta_{\mathrm{s} 1}\right)\left(\left(1 / b h^2\right)_c+\right. \\ & \left.\left(1 / b h^2\right)_r \delta_{\mathrm{s} 2}\right) \end{aligned} $ | (27) |
式中:δs1、δs2分别为M和1/bh2的标准区间变量,δr1为R(t)的标准区间变量。
3.2 蒙特卡罗法根据标准化状态极限方程,得出3个未知量的标准区间图,如图 3所示。

|
图 3 功能函数标准化区间 Fig. 3 Functional function standardization interval |
图 3中坐标轴从-1到+1的正方体边界为区域边界,表示结构不确定性参数要求波动范围,阴影部分为失效面即G(δ, t)=0,正方体内阴影的下半部分为失效域即G(δ, t) < 0,正方体阴影的上半部分为安全域即G(δ, t)>0。A(-δr1, 1, 1)为失效面与区域边界沿δr1轴方向的交点,B(-1, δs1, 1)、C(-1, 1, δs2)为失效面与区域边界沿δs1、δs2轴方向的交点。
结合文献[19]利用蒙特卡罗法的子区间法(subset simulation of Monte Carlo simulation, SSMCS)求解高超声速飞行器非概率可靠性计算步骤如下:
1) 失效面与区域边界沿δr轴正向平行方向的交点为(-δr1, 1, 1),则失效域沿δr方向的边长lr1为
| $ l_{\mathrm{r} 1}=1-\delta_{\mathrm{r} 1}=6 M_{\mathrm{u}}\left(1 / b h^2\right) u-R(t)_1 / R_r $ | (28) |
式中, (1/bh2)u为1/bh2的对应区间[(1/bh2), (1/bh2)u]的右端点值。
失效面与区域边界沿δs轴的交点为(-1, δs1, 1),(-1, 1, δs2),则失效域沿δs1,δs2轴的边长ls1和ls2分别为:
| $ l_{\mathrm{s} 1}=1-\delta_{\mathrm{s} 1}=\frac{6 M_{\mathrm{u}}\left(1 / b h^2\right)_{\mathrm{u}}-R(t)_{\rm l}}{6 M_r\left(1 / b h^2\right)_{\mathrm{u}}} $ | (29) |
| $ l_{\mathrm{s} 2}=1-\delta_{\mathrm{s} 2}=\frac{6 M_{\mathrm{u}}\left(1 / b h^2\right)_{\mathrm{u}}-R(t)_{\rm l}}{6 M_{\mathrm{u}}\left(1 / b h^2\right)_r} $ | (30) |
2) 求解失效域体积V失效域:
| $ V_{\text {失效域 }}=\frac{l_{\mathrm{rl}} l_{\mathrm{s} 1} l_{\mathrm{s} 2}}{2^3}=\frac{\left(6 M_{\mathrm{u}}\left(1 / b h^2\right)_{\mathrm{u}}-R(t)_1\right)^3}{288 M_r M_{\mathrm{u}} R_r\left(1 / b h^2\right)_{\mathrm{u}}\left(1 / b h^2\right)_r} $ | (31) |
3) 在抽样域子集区间内进行蒙特卡罗抽样,设抽样点为N,落在失效域内的点数为N1,则非概率可靠度为
| $ P=1-\frac{N_1\left(6 M_{\mathrm{u}}\left(1 / b h^2\right)_{\mathrm{u}}-R(t)_1\right)^3}{288 N M_r M_{\mathrm{u}} R_r\left(1 / b h^2\right)_{\mathrm{u}}\left(1 / b h^2\right)_r} $ | (32) |
当功能函数非线性程度较高时,SSMCS法计算结果误差较大,且该方法不满足区间服从均匀分布。为进一步提高可靠度的计算精度,在基于SSMCS法基础上提出了子域子区间抽样法(subset simulation- subinterval,SSS法),其具体描述如下。
为满足均匀取点,先将强度变量的取值区间[-1, -δr1]和应力变量的取值区间[δs1, 1],[δs2, 1]分别均分为K等分,K+1个边界点和K个子区间,抽样域D划分为Kn+m个子区间。沿δr方向的第k个子区间可表示为(δr1I)k=[δr1, k, δr1, k+1],δr1, k、δr1, k+1分别为失效域内第k个子区间左、右端点,任意子区间宽度为(1-δr)/K,其中δr1, k=-1+(k-1)(1-δr1)/K,δr1, k+1=-1+k(1-δr1)/K,(k=1, 2, …, K)。在任意子区间内抽样,当K取值足够大时,可认为状态极限方程最大值、最小值可在区间端点上取得。同理,(δs1I)k、(δs2I)k子区间内最大、最小值也出现在区间端点上。(δs1I)k、(δs2I)k的第k个子区间可按上述方法类推。当取区间端点值时,以此可满足区间的均匀取点。
为满足不重复取点且区间端点能用于取点。在子区间(δr1I)k=[δr1, k, δr1, k+1]、(δs1I)k=[δs1, k, δs1, k+1]、(δs2I)k=[δs2, k, δs2, k+1]内极限状态方程取得的最大值和最小值可表示为:
| $ \begin{aligned} G_{\max }= & \max \left\{G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 2, k+1}, \delta_{\mathrm{s} 1, k}\right), \right. \\ & G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k}\right), \\ & G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k}, \delta_{\mathrm{s} 2, \mathrm{k}}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 2, k+1}, \delta_{\mathrm{s} 1, k}\right), \\ & \left.G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right)\right\} \end{aligned} $ | (33) |
| $ \begin{aligned} G_{\min }= & \min \left\{G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 2, k+1}, \delta_{\mathrm{s} 1, k}\right), \right. \\ & G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s1} 1, k}, \delta_{\mathrm{s} 2, k}\right), \\ & G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k}, \delta_{\mathrm{s} 2, k+1}\right), \\ & \left.G\left(\delta_{\mathrm{r} 1, k}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right)\right\} \end{aligned} $ | (34) |
由子区间端点函数的取值,子区间可以分为以下3种模型:
1) 若Gmin>0,则子区间安全可靠;
2) 若Gmax < 0,则子区间失效;
3) 若Gmax>0,Gmin < 0,则子区间为干涉区间。
同样,在子区间(δr1I)k+1=[δr1, k+1, δr1, k+2]、(δs1I)k+1=[δs1, k+1, δs1, k+2]、(δs2I)k+1=[δs2, k+1, δs2, k+2]内状态极限方程取得的最大值和最小值可表示为:
| $ \begin{aligned} G_{\mathrm{max}}= & \max \left\{G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+2}\right), \right. \\ & \left.G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+2}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+2}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+2}\right)\right\} \end{aligned} $ | (35) |
| $ \begin{aligned} G_{\mathrm{min}}= & \min \left\{G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+1}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+2}\right), \right. \\ & \left.G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+1}, \delta_{\mathrm{s} 2, k+2}\right), G\left(\delta_{\mathrm{r} 1, k+1}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+2}\right), G\left(\delta_{\mathrm{r} 1, k+2}, \delta_{\mathrm{s} 1, k+2}, \delta_{\mathrm{s} 2, k+2}\right)\right\} \end{aligned} $ | (36) |
根据式(33)~(36)可知,相邻子区间的端点值存在交叉,利用子区间端点值G(δr1, δs1, δs2)的正、负来判断抽样点是否落入失效域,抽样点可直接采用区间端点代替,同时可避免SSMCS中可能出现重复抽样的缺点。
综上所述,均匀且不重复取点的SSS法具体步骤如下:
1) 标准化各区间变量,依次求解出失效面与区域边界沿δs轴和δr的交点值δs1、δs2、δr1和失效域沿δs,δr的边长lj和li以及抽样域V抽样域。
2) 确定抽样域子集区域D, δri的取值区间为[-1, -δr1],δsj的取值区间为[δsj1, 1]。
3) 计算子区间抽样域占标准化基本变量域的比值P1为
| $ P_1=\frac{V_{\text {抽样域 }}}{V_{\text {总 }}}=\frac{l_{\mathrm{r} 1} l_{\mathrm{s} 1} l_{\mathrm{s} 2}}{2^3} $ | (37) |
4) 将提取的区间分别均分为K1等分,分别得到K1+1个边界点和K1个子区间,抽样域D1被划分为K13个小等超长方盒、(K1+1)3个端点,提取(K1+1)3个端点函数值,计算满足G(δi) < 0的点数N2, 则失效可能度P2为
| $ P_2=N_2 /\left(K_1+1\right)^3 $ | (38) |
相比于SSMCS法,这里对抽样域进行区间端点均匀取样,符合区间均匀分布。
5) 非概率的可靠度为
| $ P=1-P_1 P_2=1-\frac{l_{\mathrm{r}} l_{\mathrm{s} 1} l_{\mathrm{s} 2}}{2^3} \times \frac{N_2}{\left(K_1+1\right)^3} $ | (39) |
为验证建立的子域子区间法的合理性和正确性,在考虑强度退化的基础上,分析子域子区间法相对子区间法的优势。选取α=6°, H=25 km, V=6 Ma,SSMCS采样点个数为1×105和1×106,SSS采样点个数为1×106,对比分析高超声速飞行器的可靠性,如图 4所示。

|
图 4 子域子区间法与子区间法对比 Fig. 4 Comparison between subdomain subinterval method and subinterval method |
从图 4中可以看出:
1) 根据蒙特卡罗法性质可知,随着取样点数的增加,计算精度会随之增加。子区间法(SSMCS(1× 106))比子区间法(SSMCS(1×105))采样点数多。故可得,SSMCS(1×106)比SSMCS(1×105)精度更高。由此可得随着精度增加,可靠性值逐渐减小。
2) 采用相同的抽样点数,SSS法可靠度数值更低,说明落入失效域内的点数大于SSMCS(1×106),即SSS抽样结构可靠性精度更高,SSS法与SSMCS法相比具有精度优势。
3) 相比于SSMCS法,SSS法计算所得结果波动性更小,可避免由于随机取点所造成的计算结果异常。
在明确子域子区间抽样法的优势,应用其分析迎角、飞行高度以及马赫数的变化对飞行器可靠度的影响,通过仿真得到如图 5所示结果。

|
图 5 可靠度随时间变化 Fig. 5 Reliability changes with time |
从图 5(a)中对比看出,随着迎角的增加,飞行器的可靠度有着明显的下降。这说明在实际飞行过程中,要尽量避免更大迎角的出现。这主要是由于:迎角的大小和气动力密切相关,更大的迎角意味着飞行器将受到更大的气动力,进而影响结构受力和可靠性,因此大迎角会降低飞行器的可靠性。
由图 5(b)所示,随着飞行高度增加,飞行器的可靠度下降的趋势在逐渐延缓。主要原因在于:随着飞行高度的增加,大气密度逐渐下降,使得各个平面受到的气动力逐渐减小,从而使得飞行器受到的载荷变小。
从图 5(c)中对比看出,随着马赫数的增加,飞行器整体可靠度有着明显的下降。这主要是因为随着速度的增加,机身受到的气动力也随之增大,机身结构的可靠度随之降低。
除此以外,控制面、滚转角和侧滑角等飞行动态都会对可靠度有一定的影响,但与马赫数、飞行高度和迎角相比,它们的影响较小。因此,综合上述分析,在实际飞行中若要保证飞行器的结构可靠性,应尽量做到:避免飞行速度过快增加,避免大迎角,条件允许的情况下适当增加飞行高度。
5 结论1) SSS法的均匀取样比SSMCS法任意取样更符合区间采样所要求的均匀性,同时在相同采样点数下,SSS法具有更高的精度。
2) 飞行器的迎角对飞行器的可靠性有较大影响,且随着迎角增大,可靠性逐渐减小;飞行高度对可靠性有一定影响,且随着飞行高度的增大,可靠性逐渐增大;飞行速度对可靠性有较大影响,且随着速度增加,可靠性逐渐减小。
3) 飞行器机身强度的退化反映出飞行器抵抗应力的能力变弱,在应力载荷作用下,更小的机身强度,使得结构可靠性更小,降低了飞行器飞行安全系数。
4) 基于此,在执行飞行任务时,更快的飞行速度会降低飞行器整体可靠度,较低的飞行高度也会降低飞行器的可靠度,而过大的迎角的出现都会降低机身可靠度。通过对机身整体可靠性的影响因素与动态特性进行定性地分析,不仅可以为可靠性控制提供基础,还可以为飞行器结构可靠性设计提供有价值的参考依据。
| [1] |
DER KIUREGHIAN A, DE STEFANO M. Efficient algorithm for second-order reliability analysis[J]. Journal of Engineering Mechanics, 1991, 117(12): 2904. DOI:10.1061/(ASCE)0733-9399(1991)117:12(2904) |
| [2] |
ZHAO Yangang, ONO T. New approximations for SORM: Part 1[J]. Journal of Engineering Mechanics, 1999, 125(1): 79. DOI:10.1061/(ASCE)0733-9399(1999)125:1(79) |
| [3] |
ZHANG Tianxiao. An improved high-moment method for reliability analysis[J]. Structural and Multidisciplinary Optimization, 2017, 56(6): 1225. DOI:10.1007/s00158-017-1715-3 |
| [4] |
ZHANG Xufang, PANDEY M D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method[J]. Structural Safety, 2013, 43(9): 28. DOI:10.1016/j.strusafe.2013.03.001 |
| [5] |
GROOTEMAN F. Adaptive radial-based importance sampling method for structuralreliability[J]. Structural Safety, 2008, 30(6): 533. DOI:10.1016/j.strusafe.2007.10.002 |
| [6] |
LU Zhenzhou, SONG Shufang, YUE Zhufeng, et al. Reliability sensitivity method by line sampling[J]. Structural Safety, 2008, 30(6): 517. DOI:10.1016/j.strusafe.2007.10.001 |
| [7] |
ZHANG Leigang, LU Zhenzhou, WANG Pan. Efficient structural reliability analysis method based on advanced Kriging model[J]. Applied Mathematical Modelling, 2015, 39(2): 781. DOI:10.1016/j.apm.2014.07.008 |
| [8] |
LV Zhaoyan, LU Zhenzhou, WANG Pan. A new learning function for Kriging and its applications to solve reliability problems in engineering[J]. Computers & Mathematics with Applications, 2015, 70(5): 1182. DOI:10.1016/j.camwa.2015.07.004 |
| [9] |
ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 method: A way to compute time-variant reliability[J]. Reliability Engineering & System Safety, 2004, 84(1): 75. DOI:10.1016/j.ress.2003.10.005 |
| [10] |
张德权, 韩旭, 姜潮, 等. 时变可靠性区间PHI2分析方法[J]. 中国科学: 物理学 力学 天文学, 2015, 45(5): 41. ZHANG Dequan, HAN Xu, JIANG Chao, et al. The interval PHI2 analysis method for time-dependent reliability[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2015, 45(5): 41. DOI:10.1360/SSPMA2014-00419 |
| [11] |
LI Jie. Probability density evolution method: Background, significance and recent developments[J]. Probabilistic Engineering Mechanics, 2016, 44: 111. DOI:10.1016/j.probengmech.2015.09.013 |
| [12] |
HU Zhen, MAHADEVAN S. A single-loop kriging surrogate modeling for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2016, 138(6): 061406. DOI:10.1115/1.4033428 |
| [13] |
BEN-HAIM Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227. DOI:10.1016/0167-4730(94)90013-2 |
| [14] |
朱增青, 陈建军, 宋宗凤, 等. 区间参数杆系结构非概率可靠性指标的改进仿射算法[J]. 工程力学, 2010, 27(2): 49. ZHU Zengqing, CHEN Jianjun, SONG Zongfeng, et al. Non-probabilistic reliability index of bar structures with interval parameters based on modified affine arithmetic[J]. Engineering Mechanics, 2010, 27(2): 49. |
| [15] |
乔心州, 王兵, 彭先龙. 桁架结构非概率可靠性形状优化设计[J]. 应用力学学报, 2020, 37(1): 176. QIAO Xinzhou, WANG Bing, PENG Xianlong. Non-probabilistic reliability-based shape optimization design of truss structures[J]. Chinese Journal of Applied Mechanics, 2020, 37(1): 176. DOI:10.11776/cjam.37.01.D116 |
| [16] |
周长聪, 常琦, 周春苹, 等. 基于非概率模型的飞机襟翼故障树分析[J]. 清华大学学报(自然科学版), 2021, 61(6): 636. ZHOU Changcong, CHANG Qi, ZHOU Chunping, et al. Fault tree analysis of an aircraft flap system based on a non-probability model[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(6): 636. DOI:10.16511/j.cnki.qhdxxb.2020.22.44 |
| [17] |
OPPENHEIMER M, DOMAN D. A hypersonic vehicle model developed with piston theory[C]//Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston, Virigina: AIAA, 2006: AIAA2006 -6637. DOI: 10.2514/6.2006-6637
|
| [18] |
周泽宇, 王玉惠, 吴庆宪. 近空间飞行器机翼动态可靠性分析[J]. 吉林大学学报(信息科学版), 2020, 38(3): 272. ZHOU Zeyu, WANG Yuhui, WU Qingxian. Dynamic reliability analysis of wing for near space vehicles[J]. Journal of Jilin University (Information Science Edition), 2020, 38(3): 272. DOI:10.19292/j.cnki.jdxxp.2020.03.006 |
| [19] |
王敏容. 基于区间模型的非概率结构可靠性分析及优化设计[D]. 武汉: 华中科技大学, 2019 WANG Minrong. Non-probabilistic reliability analysis and optimization design of the structure based on the interval model[D]. Wuhan: Huazhong University of Science and Technology, 2019. DOI: 10.27157/d.cnki.ghzku.2019.003983 |
| [20] |
李云鑫. 基于气动弹性模型的高超声速飞行器减损控制研究[D]. 南京: 南京航空航天大学, 2020 LI Yunxin. Damage-mitigating control for the hypersonic flight vehicle based on aeroelastic model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020. DOI: 10.27239/d.cnki.gnhhu.2020.001107 |
| [21] |
李莉, 谢里阳, 何雪浤, 等. 疲劳加载下金属材料的强度退化规律[J]. 机械强度, 2010, 32(6): 967. LI Li, XIE Liyang, HE Xuehong, et al. Strength degradation law of metallic material under fatigue loading[J]. Journal of Mechanical Strength, 2010, 32(6): 967. DOI:10.16579/j.issn.1001.9669.2010.06.005 |
| [22] |
吕海波, 姚卫星. 元件疲劳可靠性估算的剩余强度模型[J]. 航空学报, 2000, 21(1): 74. LV Haibo, YAO Weixing. Residual strength model of elements' fatigue reliability evaluation[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(1): 74. DOI:10.3321/j.issn:1000-6893.2000.01.017 |
| [23] |
VANNOORTWIJK J M. A survey of the application of Gamma processes in maintenance[J]. Reliability Engineering & System Safety, 2009, 94(1): 2. DOI:10.1016/j.ress.2007.03.019 |
| [24] |
吕昊, 张义民, 王倩倩. 基于Gamma退化过程的机械零部件可靠性灵敏度方法[J]. 东北大学学报(自然科学版), 2013, 34(11): 1610. LV Hao, ZHANG Yimin, WANG Qianqian. Reliability sensitivity analysis method of mechanical parts based on Gamma process strength degradation[J]. Journal of Northeastern University (Natural Science), 2013, 34(11): 1610. DOI:10.3969/j.issn.1005-3026.2013.11.022 |
| [25] |
安宗文, 高建雄, 刘波. 基于P-S-N曲线的强度退化随机模型[J]. 计算力学学报, 2015, 32(1): 118. AN Zongwen, GAO Jianxiong, LIU Bo. Stochastic model of strength degradation based on P-S-N curve[J]. Chinese Journal of Computational Mechanics, 2015, 32(1): 118. DOI:10.7511/jslx201501020 |
| [26] |
JOYCE P, POMROY J, GRINDLE L. The hyper-X launch vehicle: Challenges and design considerations for hypersonic flight testing[C]//Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies. Reston, Virigina: AIAA, 2005: AIAA2005-3333. DOI: 10.2514/6.2005-3333
|
 2023, Vol. 55
2023, Vol. 55


