抓取对于机器人而言是一项非常重要的能力。如今,机器人在工业生产、医疗、军事等领域正在扮演越来越重要的角色,其中实现更精准快速的机器人抓取是不可或缺的能力。当人类看到一个未知物体,就可以直觉般的知道如何拿起它。即使已经有很多关于机器人抓取检测领域的工作[1-5],但对于机器人而言,如何实现鲁棒的目标抓取仍是个挑战。整个抓取流程主要分为抓取检测、轨迹规划和执行。抓取检测是机器人通过光学[3]或者触觉[6-7]等传感器获取周围环境的信息,并从中发现可抓取物体的过程。后续的抓取步骤需要使用抓取检测获得的物体坐标,所以准确的抓取检测结果是顺利实现整个抓取流程的前提和关键。
抓取检测主要分为分析法[8]和数据驱动法[9],分析法要求物体几何、物理模型和力学分析等数据已知,通过这些已知信息进行抓取检测。然而,对于实际需求场景来说,这些信息会经常变化,因此分析法无法成为一种好的通用性方案。数据驱动法利用先前的成功抓取经验数据,可以学习到通用的抓取能力。基于此,本文采用数据驱动法,利用深度学习方法提取物体的抓取信息。有代表性的工作之一是滑动窗口法[10],此方法需要一个分类器来预测每一个小区域是否含有抓取可能,其主要缺点是检测速率过低,很难在现实中使用。另一种代表性的工作是基于锚框的方法[11-13],该方法需要预测很多候选抓取框,通过评分选取最优的候选框。与基于锚框的抓取检测算法不同,本文基于关键点的算法直接通过中心点、宽度图、角度图来预测最优抓取,减少了计算步骤并且可以提高性能。
随着计算机视觉领域的发展,为了更好地利用数据,出现了很多注意力机制算法,例如基于通道的SE(squeeze-and-excitation)注意力[14]和基于空间的SK(selective kernel)注意力[15]。通道注意力通过显式地学习不同通道的权重信息,动态调整每个通道的权重。而空间注意力机制,则可显式地学习不同空间区域的权重。本文采用基于包含空间和通道注意力的CA(coordinate attention)注意力[16]作为特征提取模块的补充,能够结合两种注意力机制的优点,并且避免了混合注意力机制CBAM(convolutional block attention module)注意力[17]在空间上只关注局部位置关系的不足。对于一个抓取检测任务,需要分别学习抓取中心点坐标、角度、抓手开合宽度3种信息[10]。为了能够更好的权衡3种信息在抓取检测任务中所起的作用,本文引入多任务权重学习算法[18]自动学习这几种信息(即任务)的权重。该算法通过概率建模的思想来学习任务的最佳权重,根据任务不同,利用同方差不确定性[19]刻画多任务学习问题中损失函数的权重。本文设计了一个基于关键点检测算法的模型,其中引入了包含通道和空间注意力的CA注意力机制以及多任务权重学习算法。在流行的Cornell数据集以及更大规模的Jacquard数据集上对所设计的模型进行测试,分别获得了98.8%和95.7%的抓取检测成功率。对模型模块进行鲁棒性测试和消融实验,分析研究了所设计模型的不同模块对于整体性能的影响程度。
1 问题描述给定一个物体,本文希望找到一种精确的方法来表示物体的抓取配置,通常用五维抓取来表示[10]。五维表示是七维表示[20]的简化版,在简化维度的同时保留了有效信息,通过抓取点坐标、抓取角度、抓手开合宽度来定义五维抓取表示:
| $ \boldsymbol{g}=(x, y, \theta, h, w) $ | (1) |
式中:(x, y) 对应于抓取矩形的中心点,θ为抓取矩形关于水平方向的角度,h为夹持器的高度,w为抓取手的开合宽度。一个五维表示的例子如图 1(a)所示。因为本文的模型基于像素点,所以本文使用中心点图像、角度图像和宽度图像来定义一个新的抓取表示[21],如图 1(b)所示。
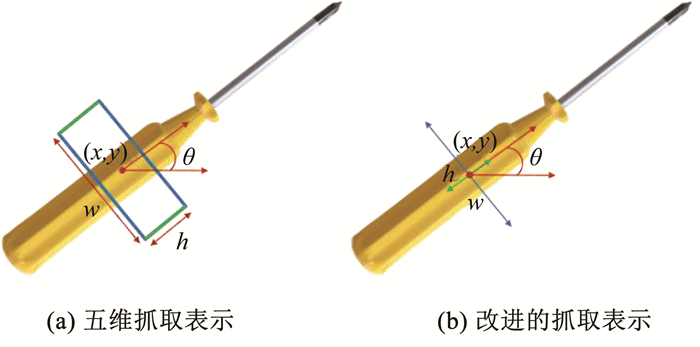
|
图 1 抓取表示对比 Fig. 1 Comparison of grasp representations |
具体地,中心点图中的像素数值表示此点作为可抓取点的可能性,用 Q来表示中心点图像,其中每个像素的取值范围为[0, 1],该值表示该点的抓取成功率,设数值最大点的坐标为(x, y),其即为抓取中心点。W为宽度图像,其中的像素数值对应以所在位置为抓取中心时,抓手的开合宽度信息。Θ为角度图,其中的像素数值对应以所在位置为抓取中心时,夹具与水平方向之间的夹角。因为抓手是对称的,所以角度只需要取
| $ \boldsymbol{g}=(\boldsymbol{Q}, \boldsymbol{W}, \boldsymbol{\varTheta}) \in {{\mathbf{R}}}^{3 \times h \times w} $ | (2) |
本文使用的是基于关键点的检测算法,其中的代表是CenterNet[22]。不同于基于锚框的检测算法,此类算法使用物体边界框的中心点来表示物体。该方法是端到端的,不需要非极大值抑制的过程。原CenterNet的上采样率为4,可能会造成信息丢失,为了避免信息丢失,本文使用转置卷积[23]操作来生成与输入图像大小相同的特征图,从而实现更准确的像素级抓取检测。原始CenterNet的预测参数为中心点坐标,中心点偏移以及目标尺寸,考虑到在抓取检测任务中需要通过五维抓取表示定义抓取,即回归中心点坐标、抓手的旋转角度以及抓取器的开合宽度,本文将可以表示上述变量的中心图、角度图和宽度图作为新模型的预测参数。
2.2 模型结构概述模型的总体结构如图 2所示。先将3×224×224的RGB和1×224×224深度图在特征通道的维度拼接得到多模态的4×224×224尺度RGB-D图像,再将其输入到模型中。模型先通过3个卷积层进行下采样,然后经过带有注意力机制的残差网络组成的特征提取模块,再通过3个转置卷积层上采样,得到与输入图片同样大小的224特征热力图,随后通过4个卷积操作分别得到中心点坐标、以正弦和余弦表示的物体旋转角度以及抓取器的开合宽度。最后,经过后处理模块就能得到该物体的抓取表示。
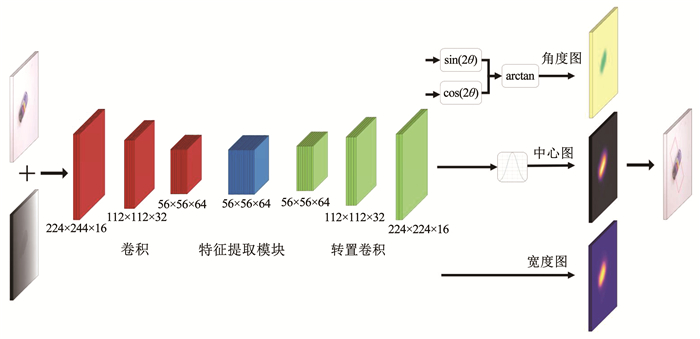
|
图 2 关键点检测模型结构 Fig. 2 Architecture of key point estimation model |
经过转置的操作后,本文得到了4个维度为H×W×C的特征热力图。对于中心点热力图,本文采用两维的高斯核进行平滑操作,将集中的热力标签分散在其周边。这样可以提高模型的抗随机噪声能力,从而帮助本文提取到最佳的抓取点位置。两维高斯核可以表示为
| $ G(x, y)=\frac{1}{\sqrt{2 \sigma^2}} \exp \left(-\frac{x^2+y^2}{2 \sigma^2}\right) $ | (3) |
式中σ=2。由于网络输出的角度特征图分别为cos(2θ)和sin(2θ),所以本文使用下式得到抓取角度为
| $ \theta=\frac{1}{2} \arctan \left(\frac{\sin (2 \theta)}{\cos (2 \theta)}\right) $ | (4) |
式中,左边的θ为通过角度特征图所取的角度值。利用获取的中心点坐标(x, y),角度和宽度特征图,本文可以通过下式得到抓取角度和宽度值为
| $ [\theta, W]=\left[\text {feature}_{\text {angle}}(x, y), \text { feature}_{\text {width}}(x, y)\right] $ | (5) |
本文选择可以充分利用小误差和控制梯度爆炸的Smooth L1函数[24]作为损失函数,Smooth L1损失函数定义为
| $ L\left(\boldsymbol{G}_l, \hat{\boldsymbol{G}}_l\right)=\frac{1}{n} \sum\limits_{l=1}^n x_l $ | (6) |
其中xl定义如下:
| $ x_l=\left\{\begin{array}{l} 0.5\left(\boldsymbol{G}_l-\hat{\boldsymbol{G}}_l\right)^2, \text { when }\left|\boldsymbol{G}_l-\hat{\boldsymbol{G}}_l\right|<1 \\ \left|\boldsymbol{G}_l-\hat{\boldsymbol{G}}_l\right|-0.5, \text { otherwise } \end{array}\right. $ |
式中:Gl为模型输出的抓取表示,
| $ \begin{aligned} L_{\text {total }}= & \lambda_{\text {center }} L_{\text {center }}+\lambda_{\cos (2 \theta)} L_{\cos (2 \theta)}+ \\ & \lambda_{\sin (2 \theta)} L_{\sin (2 \theta)}+\lambda_{\text {width }} L_{\text {width }} \end{aligned} $ | (7) |
式中: λcenter为中心点的损失权重,λcos(2θ)、λsin(2θ)分别为正、余弦角度的损失权重,λwidth为末端夹持器宽度的损失权重。
3 模型改进 3.1 引入通道和空间注意力机制本文使用RGB-D多模态信息作为输入,与只有一个通道的神经网络相比,多模态信息会使特征通道上的信息更加丰富。同时,原始的CenterNet是针对RGB输入设计的,没有考虑RGB-D的输入情况。因此,如何充分利用这些高维度信息非常重要。此外,在抓取检测场景中,物体的摆放间距不确定,不同物体的尺寸也可能相差较大,长条形物体笔、圆形物体盘子或者不规则图形门锁等,故对抓取检测识别的精度要求高。根据上述两个问题,可以使用通道注意力机制来充分利用高维信息,以及空间注意力机制来利用整体图像上长程信息。因此,本文引入CA注意力模块来提高模型的综合性能。
CA注意力机制是一种混合注意力机制,包括通道和空间两种注意力机制。SE注意力模块为仅使用通道注意力的模块,在一定程度上提高了模型性能,但是忽略了空间位置信息,而CA注意力机制则可以将其有效利用。虽然CBAM这一混合注意力机制可以同时利用通道和空间信息,但其在空间注意力的学习中使用了固定大小的7×7卷积核来学习空间维度上的特征权重,从而在注意力过程中加入了超参数,并且固定大小的卷积核只能学习到局部相关性,无法学习超过这个范围的长程相关性。
全局池化通常用于通道注意力机制中以编码各个通道的整体信息,但同时也会将该通道下整体的空间信息压缩,从而很难获取空间信息。然而,空间信息对学习空间注意力机制非常重要。为了更好对比,先介绍SE模块,其从结构上可以分为压缩和激发两个步骤,全局池化对应压缩步骤。设输入特征图X的尺寸为C×H×W,其中C为特征通道数,H为高度,W为宽度。对于第c个通道的全局池化可以表示为
| $ r_c=\frac{1}{H \times W} \sum\limits_{i=1}^H \sum\limits_{j=1}^W x_c(i, j) $ | (8) |
式中rc为第c个通道的全局信息。从式中可以看出其通过压缩空间信息得到的通道信息,无法同时保留两者。CA注意力机制通过以下两步将通道和空间信息同时编码:坐标信息植入模块和注意力生成模块。CA注意力模块和残差模块一起组成了模型的特征提取网络,对于其中一层输入Hk,输出为Y的层级展开,其详细组成结构如图 3所示。

|
图 3 特征提取模块结构 Fig. 3 Architecture of feature extraction module |
为了强化注意力模块通过精确的位置信息来捕捉长距离的空间关系,此方法分解了式(8)中的二维全局池化,将其变为一对沿着水平方向和垂直方向的一维特征编码操作。对于输入X来说,本文使用两个空间延展形池化核(H, 1)和(1, W)来分别沿着水平和垂直方向进行池化操作。对于水平方向来说,第c个通道的高度h输出信息可以表示为
| $ \boldsymbol z_c^h(h)=\frac{1}{W} \sum\limits_{0 \leqslant i<W} x_c(h, i) $ | (9) |
同理,第c个通道在宽度w的输出信息可以表示为
| $ \boldsymbol z_c^w(w)=\frac{1}{H} \sum\limits_{0 \leqslant j<H} x_c(j, w) $ | (10) |
上述两个转换分别聚合了沿着两个空间方向的特征,产生了一对内含方向信息的特征图。
3.1.2 注意力生成模块此模块的设计需要尽量简单和低复杂度且能充分利用通道和空间信息。特别地,对于通过式(9)、(10)得到的聚合特征图,首先将其沿着通道维度拼接起来,并且用C/r个1×1的卷积核对其进行卷积操作,此卷积操作表示为Conv1,此过程如下:
| $ \boldsymbol{t}={\delta}\left(\operatorname{Con} v_1\left(\left[\boldsymbol z^h, \boldsymbol z^w\right]\right)\right) $ | (11) |
式中:[·, ·]为沿着通道维度的拼接操作,δ为非线性激活函数操作,
| $ \boldsymbol{u}^h =\delta\left(\operatorname{Con} v_h\left(\boldsymbol{t}^h\right)\right) $ | (12) |
| $ \boldsymbol{u}^w =\delta\left(\operatorname{Con} v_w\left(\boldsymbol{t}^w\right)\right) $ | (13) |
式中: uh∈ RC×H×1,uw∈ RC×1×W,δ为非线性激活函数。参考文献[16]中讨论的结果,为了在保证性能的同时减低计算复杂度,本文采用r=32。输出uh和uw即为注意力权重,CA注意力模块输出 Y可以表示为
| $ y_c(i, j)=x_c(i, j) \times u_c^h(i) \times u_c^w(j) $ | (14) |
CA注意力机制同时考虑了空间信息的编码,从而可以更精确地定位物体的位置。
3.2 引入多任务学习框架在抓取检测任务中,模型需要输出抓取中心点坐标、抓手旋转角度以及开合宽度。模型的多种输出可看作不同的子任务,其中子任务间的数值差异较大,会导致总损失函数在每个周期梯度下降时偏向于数值较大的子任务,从而影响抓取检测结果。通常的做法是通过穷举法人工调节参数,然而人为调节参数费时,且最终性能对参数权重的选择敏感。为此,本文参考文献[18]提出的方法,通过引入同方差不确定性,使得不同子任务损失函数的损失权重参数可学习。在贝叶斯模型中,主要有两种不确定性可以建模,第1种是由于缺少训练数据导致的认知不确定性,第2种是由于噪声导致的偶然不确定性。偶然不确定又可以分为数据相关的不确定性,以及任务相关的不确定性即同方差不确定性。对于多任务学习问题,可以使用同方差不确定性作为加权损失的基础。
设模型的输入为x,网络参数W,输出为fW(x)。对于回归任务,本文将似然定义为以模型输出作为平均值的高斯函数:
| $ p\left(\boldsymbol{y} \mid f^\boldsymbol W(\boldsymbol{x})\right)=N\left(f^\boldsymbol W(\boldsymbol{x}), \sigma^2\right) $ | (15) |
式中σ为噪声参数。对于多输出模型,本文定义fW(x)为充分统计量,根据独立性假设,故可通过因式分解得到多任务可能性:
| $ \begin{gathered} p\left(\boldsymbol{y}_1, \cdots, \boldsymbol{y}_K \mid f^\boldsymbol W(\boldsymbol{x})\right)=p\left(\boldsymbol{y}_1 \mid f^\boldsymbol W(\boldsymbol{x})\right) \cdots \\ p\left(\boldsymbol{y}_k \mid f^\boldsymbol W(\boldsymbol{x})\right) \end{gathered} $ | (16) |
式中,y1, …, yK为不同任务的输出。对数似然估计为
| $ p\left(\boldsymbol{y} \mid f^\boldsymbol W(\boldsymbol{x})\right) \propto-\frac{1}{2 \sigma^2} \boldsymbol{y}-f^\boldsymbol W(\boldsymbol{x})^2-\log \sigma $ | (17) |
假设模型输出由两个向量y1和y2组成:
| $ \begin{gathered} p\left(\boldsymbol{y}_1, \boldsymbol{y}_2 \mid f^\boldsymbol W(\boldsymbol{x})\right)=p\left(\boldsymbol{y}_1 \mid f^\boldsymbol W(\boldsymbol{x})\right) \cdots p\left(\boldsymbol{y}_2 \mid f^\boldsymbol W(\boldsymbol{x})\right)= \\ N\left(\boldsymbol{y}_1 ; f^\boldsymbol W(\boldsymbol{x}), \sigma_1^2\right) N\left(\boldsymbol{y}_2 ; f^\boldsymbol W(\boldsymbol{x}), \sigma_2^2\right) \end{gathered} $ | (18) |
在上述条件下,为了最小化损失函数L(W, σ1, σ2),有下列推导:
| $ \begin{aligned} L\left(\boldsymbol{W}, \sigma_1, \sigma_2\right)= & -\log p\left(\boldsymbol{y}_1, \boldsymbol{y}_2 \mid f^\boldsymbol W(\boldsymbol{x})\right) \propto \\ & \frac{1}{2 \sigma_1^2} \boldsymbol{y}_1-f_1^\boldsymbol W(\boldsymbol{x})^2+\frac{1}{2 \sigma_2^2} \boldsymbol{y}_2- \\ & f_2^\boldsymbol W(\boldsymbol{x})^2+\log \sigma_1 \sigma_2=\frac{1}{2 \sigma_1^2} L_1(\boldsymbol{W})+ \\ & \frac{1}{2 \sigma_2^2} L_2(\boldsymbol{W})+\log \sigma_1 \sigma_2 \end{aligned} $ | (19) |
式中:L1(W)、L2(W)分别为两个任务的损失函数,σ1、σ2可以基于数据自适应的分别学习到L1(W)和L2(W)的相对权重。σ1作为y1变量的噪声参数,当其增加时,L1(W)的权重会减少。从另一个角度来说,当噪声减少的时候,相对应的损失权重就会增加。由于式(19)中log σ1σ2正则项的存在,也会抑制噪声数值相对过大。在实践中,本文采用s=log σ2作为学习参数,避免了直接学习σ的值,因σ在训练过程中可能会出现0值,导致式(19)中出现被除数为0的问题,从而可获得更强的数值稳定性。针对本文的任务,结合式(7),增加可学习噪声参数后的损失函数为
| $ \begin{aligned} L_{\text {total }}= & \exp \left(-s_{\text {center }}\right) L_{\text {center }}+\exp \left(-s_{\cos }\right) L_{\cos (2 \theta)}+ \\ & \exp \left(-s_{\text {sin }}\right) L_{\sin (2 \theta)}+\exp \left(-s_{\text {width }}\right) L_{\text {width }}+ \\ & s_{\text {center }}+s_{\text {cos }}+s_{\text {sin }}+s_{\text {width }} \end{aligned} $ | (20) |
由式(20)可知,该方法通过引入4个可学习权重参数,可以在反向传播中自动更新权重,与其他模型参数同时训练。相较于原CenterNet模型,增加的参数数量和计算量低。
4 结果和分析 4.1 实验条件本文实验使用的GPU为NVIDIA RTX2060,NVIDIA CUDA版本为11.6.134,处理器型号为AMD RyzenTM 7 4800HS,操作系统是Window 11,版本号21H2。
4.2 数据集具有代表性的公开数据集基本情况见表 1。
| 表 1 抓取检测数据集比较 Tab. 1 Comparison of grasp detection datasets |
由于本文需要使用RGB-D数据训练模型,故选用其中两种包含RGB-D信息的抓取检测数据集。
4.2.1 Cornell数据集,Cornell数据集部分样例如图 4(a)所示。该数据集是抓取检测领域最流行的数据集,包含240个不同物体的885张RGB-D图片,分辨率为640×480。每张图片都有正向和负向抓取标签,一共有8 019个标签,其中5 110个正标签和2 909个负标签,在训练过程中,本文只使用正标签。考虑到图片数量相对较少,为了能更好训练,本文利用了随机裁剪、放缩和旋转等图片增强手段。与其他工作一样,本文通过以下两种方式对数据集进行分割。

|
图 4 Cornell和Jacquard数据集样例 Fig. 4 Examples from Cornell and Jacquard dataset |
1) 图像分割。图像分割随机打乱数据集中的图片进行训练,可检测模型对于不同位姿下的之前见过物体的抓取生成能力。
2) 对象分割。对象分割根据不同物体的种类进行分割。有助于检测模型对于未知物体的抓取能力,具有更强的现实意义,更能体现模型的鲁棒性。
4.2.2 Jacquard数据集Jacquard数据集部分样例如图 4(b)所示。该数据集是通过CAD模型建立的数据集,包含11 619个不同物体的54 485张RGB-D图片,分辨率为1 024× 1 024。图片的正标签是通过在仿真环境中的成功抓取获得的,约含有一百万个抓取标签。由于此数据集已经足够大,训练时并不需要采用数据增强。
4.3 模型训练评估标准为了便于与之前的研究工作比较,本文采用文献[20]提出的矩形抓取标准作为判定条件。一个成功的抓取检测需要满足以下两个判定条件:
1) 预测抓取矩形和真实标签抓取矩形之间的夹角应小于30°;
2) 预测抓取矩形和真实标签抓取矩形的Jaccard相似系数应该大于25%。
Jaccard相似系数定义如下:
| $ \operatorname{Jaccard}(\boldsymbol{g}, \hat{\boldsymbol{g}})=\frac{|\boldsymbol{g} \cap \hat{\boldsymbol{g}}|}{|\boldsymbol{g} \cup \hat{\boldsymbol{g}}|} $ | (21) |
式中:g为模型预测的抓取矩形区域,
模型在Cornell数据集上的检测结果示例如图 5所示。第1、2列分别为RGB和深度图,第3列为模型生成的热力图,第4列为角度图,第5列为宽度图。通过热力图定位抓取中心并结合对应坐标下的角度图和宽度图信息,得到最后1列的抓取表示。从图 5中例子可以看出模型在面对锁型等不规则物体时也有良好表现。
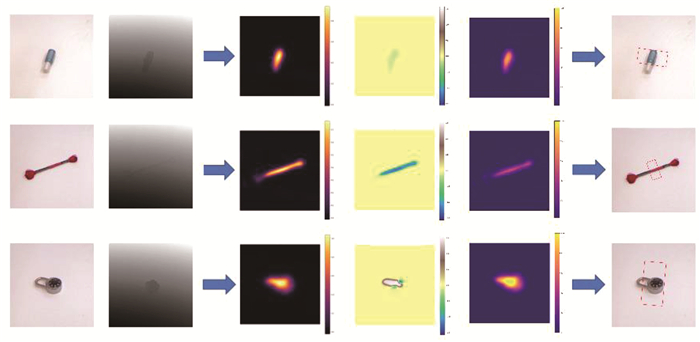
|
图 5 Cornell数据集的抓取检测结果 Fig. 5 Detection results on Cornell dataset |
表 2展现了本文在康奈尔数据集下与其他模型的性能对比。本文采用图像和对象分割方法分别对数据集分割,主要检测准确率和检测速率。在图像和对象分割条件下,本文获得了98.8%的准确率和25.30 fps的检测速率。可以发现,与其他工作相比,本文的检测准确率和检测速率都有一定提升。其中与基于锚框的检测算法相比,见表 2中的Fast-RCNN,本文改进的CenterNet模型在取得相近抓取准确率的同时,由于不需要生成候选锚框和非极大值抑制等操作,在检测速率上有明显优势。
| 表 2 康奈尔数据集下模型精度对比 Tab. 2 Comparison of model prediction accuracy on Cornell dataset |
为了进一步验证本模型的性能和鲁棒性,本文在更加严苛的条件下与其他模型进行对比。如表 3所示,本文测试了本模型在Jaccard相似系数以0.05为梯度、从0.25~0.45等梯度变化时的对象分割准确率。在系数小于0.45时,随着Jaccard相似系数的提高,本模型可以保持在超过90%的准确率。在0.45时,本模型的准确率和其他工作相比也能获得更好的结果。表 3的结果对比表明本模型在更严苛条件下具有较强的性能和鲁棒性。
| 表 3 在不同Jaccard系数下的检测准确率 Tab. 3 Prediction accuracy at different Jaccard thresholds |
除此之外,本文希望验证本模型在更大规模数据集上的效果,故对其在Jacquard数据集上进行训练,相应的检测结果示例如图 6所示。第1行显示的陀螺物体,其在纵向的空间上有一定高度,在倾斜放置时会给抓取检测带来一定挑战。Jacquard数据集是通过CAD模型建立的,其中的物体有一定的随机性,相对于现实情况更加苛刻,如第2行中的盆栽,但本文的模型仍获得了准确的抓取结果。
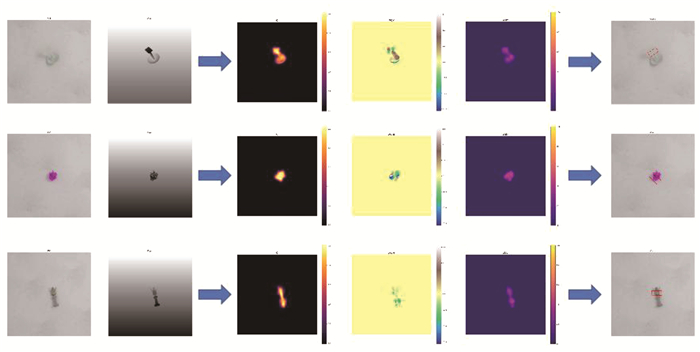
|
图 6 Jacquard数据集的抓取检测结果 Fig. 6 Detection results on Jacquard dataset |
表 4表明本模型不仅在康奈尔数据集上取得出色性能,并且在规模更大的Jacquard数据集上也能取得优秀结果。
| 表 4 Jacquard数据集下模型精度对比 Tab. 4 Comparison of model prediction accuracy in Jacquard grasp dataset |
关于可学习权重的实验,通常仅考虑初始权重为0的情况[18]。为了更好地验证本模型的鲁棒性和适用性,本文将每个子任务的初始权重设定为相差很大的初值,这样中心点、正、余弦角度、抓手开合宽度一共包含16种初始权重组合情况。同时本文也随机交换了不同任务间的学习权重作为初始权重。权重参数随着训练进行的变化情况如图 7所示,可以看出其收敛效果对于初始值不敏感,反应了本算法的鲁棒性。
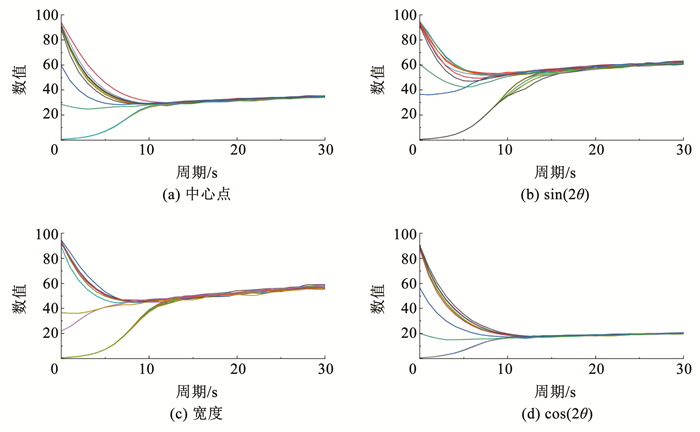
|
图 7 不同初始权重下参数变化情况 Fig. 7 Detection results on Jacquard dataset |
为了进一步验证本方法各模块的有效性,以及其对于整体性能的影响,本文对模型进行消融实验,实验结果见表 5。
| 表 5 消融实验结果 Tab. 5 Results from ablation experiment |
从表 5实验结果可以看出,CA注意力机制和权重学习机制的引入,可有效提升抓取检测的准确率,且由于实现过程中需要的参数较少,对检测速率的影响较小。
5 结论1) 针对抓取检测任务,本文结合CA注意力机制和多任务学习提出了一种新的抓取检测模型。模型利用RGB-D图像作为输入信息,根据输出的中心图、宽度图、角度图,生成像素级别的抓取表示,在Cornell和Jacquard数据集上分别实现了98.8%和95.7%的准确率。
2) 从充分利用高维信息角度出发,本文引入CA注意力机制,其使用通道注意力机制来充分利用高维信息,以及空间注意力机制来利用整体图像上长程信息,从而可以更精确地定位物体的位置。消融实验证明其对于图像分割和对象分割可以达到2%以上的性能提升。
3) 从损失函数优化角度出发,本文引入多任务学习框架,能根据任务特点自动获取不同子损失函数的权重,无需对权重进行人为选定。鲁棒性实验进一步证明此方法可以稳定学习到任务的最优权重,对于初始值的干扰不敏感。
4) 本文通过在不同数据集、不同精度要求以及干扰下进行的实验,验证了所提出的抓取检测模型在各项指标下的良好表现。同时,通过消融实验,从模型组成方面证明了各模块在提升抓取检测性能方面的有效性。在未来的工作中,本文将尝试搭建闭环抓取系统,通过对真实世界中物体的抓取,进一步验证模型的性能表现。
| [1] |
AINETTER S, FRAUNDORFER F. End-to-end trainable deep neural network for robotic grasp detection and semantic segmentation from RGB[C]//2021 IEEE International Conference on Robotics and Automation (ICRA). Xi'an, China: IEEE, 2021: 13452. DOI: 10.1109/ICRA48506.2021.9561398
|
| [2] |
BICCHI A, KUMAR V. Robotic grasping and contact: A review[C]//Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065). San Francisco, CA: IEEE, 2002: 348. DOI: 10.1109/ROBOT.2000.844081
|
| [3] |
KUMRA S, KANAN C. Robotic grasp detection using deep convolutional neural networks[C]//2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver, BC, Canada: IEEE, 2017: 769. DOI: 10.1109/IROS.2017.8202237
|
| [4] |
MORRISON D, CORKE P, LEITNER J. Closing the loop for robotic grasping: A real-time, generative grasp synthesis approach[EB/OL]. 2018: arXiv: 1804.05172. https://arxiv.org/abs/1804.05172.pdf
|
| [5] |
KUMRA S, JOSHI S, SAHIN F. Antipodal robotic grasping using generative residual convolutional neural network[C]//2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas, NV: IEEE, 2021: 9626. DOI: 10.1109/IROS45743.2020.9340777
|
| [6] |
KOLAMURI R, SI Zilin, ZHANG Yufan, et al. Improving grasp stability with rotation measurement from tactile sensing[C]//2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Prague, Czech Republic: IEEE, 2021: 6809. DOI: 10.1109/IROS51168.2021.9636488
|
| [7] |
张建军, 刘卫东, 张溢文, 等. 基于微机电系统的水下灵巧手触觉力测量传感器[J]. 上海交通大学学报, 2018, 52(1): 76. ZHANG Jianjun, LIU Weidong, ZHANG Yiwen, et al. Tactile force sensor of underwater dexterous hand based on micro electromechanical system[J]. Journal of Shanghai Jiao Tong University, 2018, 52(1): 76. DOI:10.16183/j.cnki.jsjtu.2018.01.012 |
| [8] |
BOHG J, MORALES A, ASFOUR T, et al. Data-driven grasp synthesis—a survey[J]. IEEE Transactions on Robotics, 2014, 30(2): 289. DOI:10.1109/TRO.2013.2289018 |
| [9] |
CALDERA S, RASSAU A, CHAI D. Review of deep learning methods in robotic grasp detection[J]. Multimodal Technologies and Interaction, 2018, 2(3): 57. DOI:10.3390/mti2030057 |
| [10] |
LENZ I, LEE H, SAXENA A. Deep learning for detecting robotic grasps[J]. International Journal of Robotics Research, 2015, 34(4/5): 705. DOI:10.1177/0278364914549607 |
| [11] |
ZHOU Xinwen, LAN Xuguang, ZHANG Hanbo, et al. Fully convolutional grasp detection network with oriented anchor box[C]//2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Madrid, Spain: IEEE, 2019: 7223. DOI: 10.1109/IROS.2018.8594116
|
| [12] |
CHU F J, XU Ruinian, VELA P A. Real-world multiobject, multigrasp detection[J]. IEEE Robotics and Automation Letters, 2018, 3(4): 3355. DOI:10.1109/LRA.2018.2852777 |
| [13] |
REDMON J, ANGELOVA A. Real-time grasp detection using convolutional neural networks[C]//2015 IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA: IEEE, 2015: 1316. DOI: 10.1109/ICRA.2015.7139361
|
| [14] |
HU Jie, SHEN Li, SUN Gang. Squeeze-and-excitation networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT: IEEE, 2018: 7132. DOI: 10.1109/CVPR.2018.00745
|
| [15] |
LI Xiang, WANG Wenhai, HU Xiaolin, et al. Selective kernel networks[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, CA: IEEE, 2020: 510. DOI: 10.1109/CVPR.2019.00060
|
| [16] |
HOU Qibin, ZHOU Daquan, FENG Jiashi. Coordinate attention for efficient mobile network design[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville, TN: IEEE, 2021: 13708. DOI: 10.1109/CVPR46437.2021.01350
|
| [17] |
WOO S, PARK J, LEE J Y, et al. Cbam: Convolutional block attention module[C]//Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018: 3. DOI: 10.1007/978-3-030-01234-2_1
|
| [18] |
CIPOLLA R, GAL Y, KENDALL A. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT: IEEE, 2018: 7482. DOI: 10.1109/CVPR.2018.00781
|
| [19] |
KENDALL A, GAL Y. What uncertainties do we need in Bayesian deep learning for computer vision?[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 5580. DOI: 10.5555/3295222.3295309
|
| [20] |
JIANG Yun, MOSESON S, SAXENA A. Efficient grasping from RGBD images: Learning using a new rectangle representation[C]//2011 IEEE International Conference on Robotics and Automation. Shanghai, China: IEEE, 2011: 3304. DOI: 10.1109/ICRA.2011.5980145
|
| [21] |
MORRISON D, CORKE P, LEITNER J. Learning robust, real-time, reactive robotic grasping[J]. The International Journal of Robotics Research, 2020, 39(2/3): 183. DOI:10.1177/0278364919859066 |
| [22] |
ZHOU Xingyi, WANG Dequan, KRÄHENBÜHL P. Objects as points[EB/OL]. 2019: arXiv: 1904.07850. https://arxiv.org/abs/1904.07850.pdf
|
| [23] |
DUMOULIN V, VISIN F. A guide to convolution arithmetic for deep learning[EB/OL]. 2016: arXiv: 1603.07285. https://arxiv.org/abs/1603.07285.pdf
|
| [24] |
GIRSHICK R. Fast r-CNN[C]//2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile: IEEE, 2016: 1440. DOI: 10.1109/ICCV.2015.169
|
| [25] |
ASIF U, BENNAMOUN M, SOHEL F A. RGB-D object recognition and grasp detection using hierarchical cascaded forests[J]. IEEE Transactions on Robotics, 2017, 33(3): 547. DOI:10.1109/TRO.2016.2638453 |
| [26] |
GUO Di, SUN Fuchun, LIU Huaping, et al. A hybrid deep architecture for robotic grasp detection[C]//2017 IEEE International Conference on Robotics and Automation (ICRA). Singapore: IEEE, 2017: 1609. DOI: 10.1109/ICRA.2017.7989191
|
 2023, Vol. 55
2023, Vol. 55


