随着通信技术的快速发展，通信设备的数量和数据流量都呈指数型增长，有限的频谱资源越发拥挤，同时较窄的频谱带宽极大的限制了通信传输速率，难以满足人们对于高速率、低时延的通信需求。双功能雷达通信(dual function radar-communication, DFRC)系统通过雷达和通信系统共享频谱资源，使频谱拥堵问题得以缓解，有效提升了通信传输速率^[1-5]。DFRC系统利用同一硬件平台上发射的双功能信号来进行目标探测和信息传输，将通信和探测功能集于一身，不仅能减小设备体积，而且还能提高系统的资源利用率。在传统通信系统设计中，资源利用率会影响系统的信息传输性能^[6]，而在DFRC系统中，如果不对有限的功率、载波等系统资源进行合理分配，可能会导致DFRC系统在信道较差的载波上分配过多的功率资源，从而对雷达和通信系统的性能产生制约。因此，如何对有限的系统资源进行分配以提高雷达探测能力和通信传输能力，进而提高系统的资源利用率具有重要的研究价值^[7-8]。

为解决上述问题，需要根据不同设计准则来对有限的资源进行合理分配。文献[9]在满足雷达和通信系统性能的前提下，以最小化发送功率为目标构造优化函数，并利用卡罗需-库恩-塔克(Karush-Kuhn-Tuckers，KKT)条件得到其闭式解，有效降低了系统能量消耗。文献[10]进一步研究了雷达和通信系统载波不重叠条件下的资源分配问题，在满足雷达和通信系统性能的前提下，以总功率最小为优化目标对载波资源和功率资源进行联合分配，从而减小DFRC系统的能量消耗。为提高雷达或通信系统性能，文献[11]以雷达系统为核心，将信道增益较大的载波优先分配给雷达使用，使其性能达到最优，再将剩余载波分配给通信使用。文献[12]以通信系统性能为核心，通过联合分配功率和载波资源使得系统在满足雷达性能下界的条件下通信和速率最大，并且分别利用分支定界和惩罚顺序凸规划方法得到优化问题的最优解和次优解。文献[13]在文献[12]的基础上，进一步考虑雷达杂波对通信系统的干扰，并通过将两个功率向量组合成一个功率矩阵的方式对目标函数进行化简，从而绕开了传统的交替迭代算法，极大降低了计算复杂度。不同于文献[11-13]以雷达或通信其中一方为核心，文献[14]提出了联合设计这一概念，将雷达互信息和通信信道容量的加权和作为目标函数，通过改变加权因子来调节功率分配方式，从而实现雷达和通信性能的均衡。然而，上述文献仅对单用户场景下的资源分配算法进行设计，未对更具有现实意义的多用户场景进行研究。在多用户场景中，通信接收机不仅可能会接收到雷达的干扰信号，同时也会受到用户间干扰的影响。文献[15]研究了多用户场景下的资源分配问题，将发送的通信信号用于目标探测，通过分配功率和载波资源不仅可以消除用户间干扰，而且还能提高雷达系统性能。文献[16]进一步考虑了多用户场景下的用户公平性问题，以确保每个用户能正常通信为优化目标进行资源分配。在上述多用户资源分配中，通常采用载波分配的方式来消除多用户干扰，但是这种方式强制令单一载波只能服务于单个用户，降低了载波的利用率，势必会导致总的通信性能降低。因此，需要对多用户场景下的资源分配问题做进一步研究。

针对多用户场景下因载波分配导致通信性能下降的问题，本文提出通信用户载波共享的DFRC系统模型，将下行的多载波信号同时用于雷达目标探测和通信信息传输。在满足雷达系统性能下界、用户功率约束和总功率约束的条件下，以通信和速率最大为目标来构造优化问题。在优化问题求解时因引入多用户干扰导致其非凸，利用二次转换将目标函数进行等效变换，使得优化问题能够通过交替迭代进行求解。仿真结果表明，所提模型功率分配方案能增大通信和速率，有效提高了系统资源利用率。

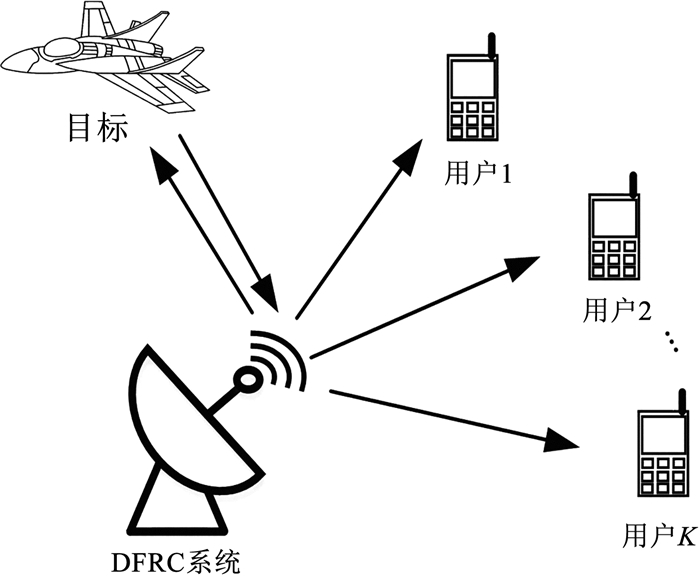
1 信号模型

DFRC系统在同一硬件平台上发送一个带宽为BHz的多载波信号来同时实现雷达目标探测和多用户下行通信功能，如图 1所示。

系统在时刻t发送的多载波基带信号可表示为

$ \begin{aligned} x(t)= & \sum\limits_{n=1}^{N_{\mathrm{c}}} x_n(t)= \\ & \frac{1}{\sqrt{N_{\mathrm{c}}}} \sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \sqrt{p_{k, n}} s_{k, n} \exp \{\mathrm{j} 2 {\rm{ \mathsf{ π} }}(n-1) \Delta f t\} \end{aligned} $

(1)

式中：N_c为载波数，K为用户数，功率矩阵 P中第k行第n列个元素p_{k, n}为在第n个载波上分配给第k个用户的功率，s_{k, n}为携带的通信信息，服从均值为0，方差为1的复高斯分布，Δf=B/N_c为载波间隔。式(1)的离散时间表达式为

$ \boldsymbol{x}=\boldsymbol{Q}_{N_{\mathrm{c}}} \boldsymbol{m} $

(2)

式中：$\boldsymbol{m} \in \mathbf{C}^{N_{\mathrm{c}} \times 1}$，m中第n个值为$\sum\limits_{k=1}^K \sqrt{p_{k, n}} s_{k, n}$, $\boldsymbol{Q}_{N_{\mathrm{c}}} \in \mathbf{C}^{N_{\mathrm{c}} \times N_{\mathrm{c}}}$为逆离散傅里叶变换矩阵，其满足$\boldsymbol{Q}_{N_{\mathrm{c}}}^{\mathrm{H}} \boldsymbol{Q}_{N_{\mathrm{c}}}=\boldsymbol{I}_{N_{\mathrm{c}}}, (\cdot)^{\mathrm{H}}$为复共轭操作，I_Nc为N_c×N_c的单位阵，Q_Nc可表示为

$ \boldsymbol{Q}_{N_{\mathrm{c}}}=\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & Q_{N_{\mathrm{c}}} & \cdots & Q_{N_{\mathrm{c}}}^{N_{\mathrm{c}}-1} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & Q_{N_{\mathrm{c}}}^{N_{\mathrm{c}}-1} & \cdots & Q_{N_{\mathrm{c}}}^{\left(N_{\mathrm{c}}-1\right)\left(N_{\mathrm{c}}-1\right)} \end{array}\right] $

(3)

式中Q_Nc=e^j2π/N_c。

假设存在一个距离为R的静止扩展目标。DFRC系统发射的多载波信号经目标反射后被系统的接收机接收，接收到的回波信号$\tilde{y}_{\mathrm{r}}(t)$可以表示为

$ \tilde{y}_{\mathrm{r}}(t)=\sum\limits_{n=1}^{N_{\mathrm{c}}} \alpha_n x_n(t-\tau)+\tilde{v}(t) $

(4)

式中：α_n为第n个载波的信道系数，主要包含雷达反射截面积和路径衰减系数，其表达式为$\bar{\alpha}_n \sqrt{G_{\mathrm{t}} G_{\mathrm{r}} \lambda^2 /(4 {\rm{ \mathsf{ π} }})^3 R^4}, \bar{\alpha}_n$为第n个载波的雷达反射截面积，G_t、G_r分别为发射天线增益和接收天线增益，λ为信号波长，τ=2R/c为信号路径时延，c为光速，$\tilde{v}(t)$为加性高斯白噪声。

将$\tilde{y}_{\mathrm{r}}(t)$采样后并进行离散傅里叶变换可得

$ \boldsymbol{y}_{\mathrm{r}}=\boldsymbol{A B \boldsymbol { m }}+\boldsymbol{v} $

(5)

式中：A=diag(α)，α=[α₁, …, α_Nc]^T，T为转置操作，$\boldsymbol{B}=\operatorname{diag}\left\{1, \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }} \Delta f \tau}, \cdots, \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }}\left(N_{\mathrm{c}}-1\right) \Delta f \tau}\right\}$，v为$\tilde{\boldsymbol{v}}$的离散傅里叶变换，v中第n个元素的方差为σ_{v, n}²。

第k个用户接收机处的接收信号$\tilde{\boldsymbol{y}}_{\mathrm{c}, k}$可表示为

$ \tilde{\boldsymbol{y}}_{\mathrm{c}, k}=\tilde{\boldsymbol{h}}_k * \boldsymbol{x}+\tilde{\boldsymbol{w}}_k $

(6)

式中：*为卷积操作，$\tilde{\boldsymbol{h}}_k=\left[\tilde{h}_{k, 1}, \cdots, \tilde{h}_{k, N_{\mathrm{c}}}\right]^{\mathrm{T}}$为通信信道单位脉冲响应，$\tilde{\boldsymbol{w}}_k$为加性高斯白噪声。

将$\tilde{\boldsymbol{y}}_{\mathrm{c}, k}$进行离散傅里叶变换后可表示为

$ \boldsymbol{y}_{\mathrm{c}, k}=\boldsymbol{H}_k \boldsymbol{m}+\boldsymbol{w}_k $

(7)

式中：H_k=diag(h_k)为通信信道频域响应系数，$\boldsymbol{h}_k=\left[h_{k, 1}, \cdots, h_{k, N_{\mathrm{c}}}\right]^{\mathrm{T}}$为$\tilde{\boldsymbol{h}}_k$的离散傅里叶变换，w_k为$\tilde{\boldsymbol{w}}_k$的离散傅里叶变换，w_k中第n个元素的方差为σ²_{ωk, n}。

在给出信号模型之后，需要用合适的指标来衡量雷达和通信系统的性能优劣。本文分别采用雷达信噪比R_SN(signal-to-noise ratio，SNR)、通信和速率C_s来衡量雷达感知能力和通信传输能力。雷达信噪比定义为有用信号功率与噪声功率的比值，R_SN越大表示雷达的探测概率越大，探测精度越高。通信和速率定义为在信道上进行无差错传输所能达到的最大传输速率，其值越大表示通信系统信息传输质量越高、速度越快。根据式(5)和式(7)，雷达信噪比R_SN、通信和速率C_s可以分别表示为^[17]：

$ R_{\mathrm{SN}}=\sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \frac{\left|\alpha_n\right|^2 p_{k, n}}{\sigma_{v, n}^2} $

(8)

$ C_{\mathrm{s}}=\sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \log _2\left(1+\frac{\left|h_{k, n}\right|^2 p_{k, n}}{\left|h_{k, n}\right|^2 \sum\limits_{i \neq k} p_{i, n}+\sigma_{\omega_k, n}^2}\right) $

(9)

为便于后续理论分析，令$\sigma_{v, n}^2=\sigma_{\omega_k, n}^2=\sigma^2$，得到归一化的信道增益为:

$ \beta_n=\frac{\left|\alpha_n\right|^2}{\sigma^2}, \gamma_{k, n}=\frac{\left|h_{k, n}\right|^2}{\sigma^2} $

(10)

此时，雷达信噪比R_SN、通信和速率C_s可以分别简化为：

$ R_{\mathrm{SN}}=\sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \beta_n p_{k, n} $

(11)

$ C_{\mathrm{s}}=\sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \log _2\left(1+\frac{\gamma_{k, n} p_{k, n}}{\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1}\right) $

(12)

2 多用户功率分配算法 2.1 优化问题建模

在传统的通信用户载波分配方案中，其任意载波只能分配给其中一个用户，相当于功率矩阵P中任意列中只能有一个非零元素，本文提出通信用户载波共享模型，通过共享载波资源的方式使得功率P中任意元素均能非零，等效于对P进行松弛处理，所以，在其他约束条件和目标函数相同的优化问题中，通信用户载波共享模型能得到更优的目标函数值。为对比两种模型条件下的通信性能优劣，以通信系统为核心，拟构建满足雷达探测性能约束条件下系统通信和速率最大的优化问题，从而有效提高系统资源利用率。基于以上准则，优化问题构建为

$ \begin{aligned} \max\limits_{\boldsymbol{P}} \ &C_{\mathrm{s}} \\ \text { s.t. } &\mathrm{C} 1: R_{\mathrm{SN}} \geqslant R_{\mathrm{SN}, \mathrm{t}} \\ & \mathrm{C} 2: \sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K p_{k, n} \leqslant P_{\mathrm{tol}} \\ & \mathrm{C} 3: 0 \leqslant p_{k, n} \leqslant \xi_{\mathrm{c}} \end{aligned} $

(13)

式中：C1为雷达性能下界约束，R_{SN, t}为SNR下界阈值，C2为DFRC系统总功率约束，P_tol为DFRC系统总功率，C3为用户功率约束，ξ_c为用户功率上界阈值，其有助于防止系统将功率集中在一个或几个子载波上，从而失去频率分集的优势，使得DFRC系统的距离分辨率降低。

2.2 可行性分析

为防止约束间的交集为空，现对给定的优化问题进行可行性分析。根据式(13)可得，优化问题是否存在可行解的关键在于雷达SNR上界R_{SN, max}是否大于阈值R_{SN, t}，即

$ R_{\mathrm{SN}, \text { max }}= \begin{cases}\geqslant R_{\mathrm{SN}, \mathrm{t}}, & \text { 存在可行解 } \\ <R_{\mathrm{SN}, \mathrm{t}}, & \text { 无可行解 }\end{cases} $

(14)

雷达R_{SN, max}可以通过下式求解得到:

$ \begin{aligned} & \max\limits_{\boldsymbol{P}} \sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K \beta_n p_{k, n} \\ & \text { s. t. C2, C3 } \end{aligned} $

(15)

上述优化问题为一个凸线性规划问题，可以根据定理1求得其闭式解。

定理1  令$q_n=\sum\limits_{k=1}^K p_{k, n}$, 若$P_{\mathrm{tol}} \geqslant N_{\mathrm{c}} K \xi_{\mathrm{c}}$, 最优解$q_n^*=K \xi_{\mathrm{c}}$，进一步可得

$ R_{\mathrm{SN}, \max }=K \xi_{\mathrm{c}} \sum\limits_{n=1}^{N_{\mathrm{e}}} \beta_n $

(16)

反之，最优解如下:

$ \begin{cases}q_n^*=0, & \beta_n<\psi \\ q_n^*=\frac{P_{\mathrm{tol}}-N_1 K \xi_{\mathrm{c}}}{N_0}, & \beta_n=\psi \\ q_n^*=K \xi_{\mathrm{c}}, & \beta_n>\psi\end{cases} $

(17)

式中：ψ为β_n, ∀n中第M+1大的信道增益值，$M=\left\lfloor P_{\mathrm{tol}} / K \xi_{\mathrm{c}}\right\rfloor$，N₁为满足β_n>ψ的载波数，N₀为满足β_n=ψ的载波数，进一步可得

$ R_{\mathrm{SN}, \text { max }}=K \xi_{\mathrm{c}} \sum\limits_{n: \beta_n>\psi} \beta_n+\psi\left(P_{\mathrm{tol}}-N_1 K \xi_{\mathrm{c}}\right) $

(18)

下面给出定理1的证明思路。

令$q_n=\sum\limits_{k=1}^K p_{k, n}$为向量q∈R^N_c×1中第n个元素，则式(15)可以简化为

$ \begin{aligned} \max\limits_\boldsymbol q & \sum\limits_{n=1}^{N_{\mathrm{c}}} \beta_n q_n \\ \text { s. t. } & \text { C4 }: \sum\limits_{n=1}^{N_{\mathrm{c}}} q_n \leqslant P_{\mathrm{tol}} \\ & \text { C5: } 0 \leqslant q_n \leqslant K \xi_{\mathrm{c}} \end{aligned} $

(19)

式(19)中约束和目标函数均是线性的。先考虑特殊情况P_tol≥N_cKξ_c，此时C4属于松弛约束，优化问题可以转化为

$ \begin{aligned} & \max\limits_\boldsymbol q \sum\limits_{n=1}^{N_{\mathrm{e}}} \beta_n q_n \\ & \text { s.t. } \mathrm{C} 5: 0 \leqslant q_n \leqslant K \xi_{\mathrm{c}} \end{aligned} $

(20)

显然令q_n=Kξ_c, ∀n，即可最大化雷达信噪比。

若P_tol < N_cKξ_c，应将功率优先分配给信道增益大的载波，即根据信道增益从大到小将载波进行排序，将总功率依照排序先后进行分配直至载波满足功率上界Kξ_c或剩余功率为零。

2.3 问题求解

根据上述可行性分析判定优化问题存在可行解，接下来则对优化问题(13)进行求解。由于其是一个非凸的多比值分式规划问题，可以采用二次转换的方法将分子和分母进行解耦^[18]。引入辅助变量y_{k, n}后，目标函数可以转化为

$ \begin{aligned} f(\boldsymbol{P}, \boldsymbol{Y})= & \sum\limits_{n=1}^{N_{\mathrm{c}}} \sum\limits_{k=1}^K f_{k, n}\left(p_{k, n}, y_{k, n}\right)= \\ & \sum\limits_{n=1}^{N_c} \sum\limits_{k=1}^K \log _2\left(1+2 y_{k, n} \sqrt{\gamma_{k, n} p_{k, n}}-\right. \\ & \left.y_{k, n}^2\left(\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1\right)\right) \end{aligned} $

(21)

下面给出目标函数的等效性证明。

证明   令$\boldsymbol{Y}^*=\underset{\boldsymbol{Y}}{\operatorname{argmax}} f(\boldsymbol{P}, \boldsymbol{Y}), f(\boldsymbol{P}, \boldsymbol{Y})$的最优值在其偏导值为零时可得

$ \begin{aligned} & \frac{\partial f(\boldsymbol{P}, \boldsymbol{Y})}{\partial y_{k, n}}=0 \Rightarrow \\ & \frac{2 \sqrt{\gamma_{k, n} p_{k, n}}-2 y_{k, n}\left(\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1\right)}{1+2 y_{k, n} \sqrt{\gamma_{k, n} p_{k, n}}-y_{k, n}^2\left(\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1\right)}=0 \end{aligned} $

(22)

将式(22)化简可得

$ y_{k . n}^*=\frac{\sqrt{\gamma_{k, n} p_{k, n}}}{\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1} $

(23)

将求解得到的Y^*代入式(21)中，可进一步推出:

$ \begin{aligned} f(\boldsymbol{P})= & f\left(\boldsymbol{P}, \boldsymbol{Y}^*\right)= \\ & \sum\limits_{n=1}^{N_c} \sum\limits_{k=1}^K \log _2\left(1+\frac{\gamma_{k, n} p_{k, n}}{\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}+1}\right) \end{aligned} $

(24)

式(24)与原优化问题(13)中的目标函数表达式相同。证毕。

将优化问题(13)中的目标函数用式(21)替换，则其可以转化为

$ \begin{aligned} & \max \limits_{\boldsymbol{P}, \boldsymbol{Y}}f\left(\boldsymbol{P}, \boldsymbol{Y}\right) \\ & \text { s. t. } \mathrm{C} 1, \mathrm{C} 2, \mathrm{C} 3 \end{aligned} $

(25)

此时，优化问题(25)可以通过交替迭代进行求解。令l为迭代次数，将第l－1次迭代得到的Y^l－1代入式(23)，可以得到:

$ \begin{aligned} & \max\limits _{\boldsymbol{P}} f\left(\boldsymbol{P}, \boldsymbol{Y}^{l-1}\right) \\ & \text { s. t. C1, C2, C3 } \end{aligned} $

(26)

式(26)中约束均是线性的，且目标函数是一个关于变量P的凹函数。因此，优化问题(26)是一个典型的凸优化问题，可以直接利用数值工具包如CVX等求解得到P^l。将计算得到的P^l用于固定变量P，优化问题可以进一步转化为

$ \max\limits_{\boldsymbol{Y}} f\left(\boldsymbol{P}^l, \boldsymbol{Y}\right) $

(27)

式(27)是一个关于变量Y的无约束凸优化问题，且目标函数由多个单调递增的对数函数求和组成。令$\mathrm{d} f\left(\boldsymbol{P}^{l-1}, \boldsymbol{Y}\right) / \mathrm{d} y_{k, n}=0$，则y_{k, n}的闭式解可表示为

$ y_{k, n}^l=\frac{\sqrt{\gamma_{k, n} p_{k, n}^l}}{\gamma_{k, n} \sum\limits_{i \neq k} p_{i, n}^l+1} $

(28)

重复迭代求解式(26)、(27)直至目标函数f(P, Y)收敛。为了更为清晰的描述整个多用户功率分配算法过程，其算法流程如下。

算法   多用户功率分配算法

输入   归一化信噪比β_n、γ_{k, n}，总功率P_tol，收敛阈值ε，雷达信噪比阈值R_{SN, t}，用户功率阈值ξ_c

输出   功率P

Step 1   初始化P⁰，迭代次数l=0

Step 2   若|f(P^l, Y^l)－f(P^l－1, Y^l－1)|≤ε，跳至Step5，否则重复Step3、Step4

Step 3   固定P，根据式(27)求解Y

Step 4   固定Y，根据式(26)求解P

Step 5   将P^l赋值给P

结束

为证明多用户功率分配算法能收敛至固定值，下面给出其收敛性证明。

证明   在第l次迭代中，在给定Y^l－1的条件下，通过求解式(26)可以得到最优功率分配P^l，此时有

$ f\left(\boldsymbol{P}^l, \boldsymbol{Y}^{l-1}\right) \geqslant f\left(\boldsymbol{P}^{l-1}, \boldsymbol{Y}^{l-1}\right) $

(29)

同理，在给定P^l的条件下，通过求解式(27)可以得到最优Y^l，此时有

$ f\left(\boldsymbol{P}^l, \boldsymbol{Y}^l\right) \geqslant f\left(\boldsymbol{P}^l, \boldsymbol{Y}^{l-1}\right) $

(30)

利用递推的方式可以得到在第l次迭代中，目标函数满足:

$ f\left(\boldsymbol{P}^l, \boldsymbol{Y}^l\right) \geqslant f\left(\boldsymbol{P}^{l-1}, \boldsymbol{Y}^{l-1}\right) $

(31)

因此，由于式(25)在每次迭代过程中是非递减的且目标函数存在上界，可以推出在给定收敛阈值的条件下，式(25)经过有限次迭代后能收敛于某一定点，确保了多用户功率分配算法的收敛性。证毕。

2.4 复杂度分析

本文在复杂度分析中仅考虑对算法影响较大的部分。对于多用户功率分配算法而言，其被分成两个子问题进行求解。式(26)优化问题中总共有KN_c个优化变量和KN_c+2个线性约束，所以，其计算复杂度可以表示为O((KN_c)³(KN_c+2))^[19]。式(27)能直接得到闭式解，该部分的计算复杂度可以忽略不计。因此，式(25)经过一次迭代运算的计算复杂度为O((KN_c)³(KN_c+2))。基于通信用户载波分配模型的BLSM算法经过一次迭代运算的计算复杂度为O((2KN_c)³(2KN_c+N_c+2))^[16]。结合上述分析，通信用户载波共享模型不仅能进一步提高通信速率，而且当用户数和载波数较多时，求解算法具有更低的计算复杂度。

3 仿真分析

为验证所提算法的有效性，本文利用MATLAB仿真工具来进行仿真分析。为了简化，设置噪声方差σ²=1，雷达信道系数α_n和通信载波信道系数h_{k, n}均是服从CN(0, 1)的复高斯分布。载波数目N_c=8，用户数K=2，总功率P_tol=20 W，雷达信噪比阈值R_{SN, t}=14.0 dB，用户功率约束ξ_c=7 W。为方便叙述，分别用所提模型来指代本文提出的通信用户载波共享模型，对比模型指代传统的通信用户载波分配模型。

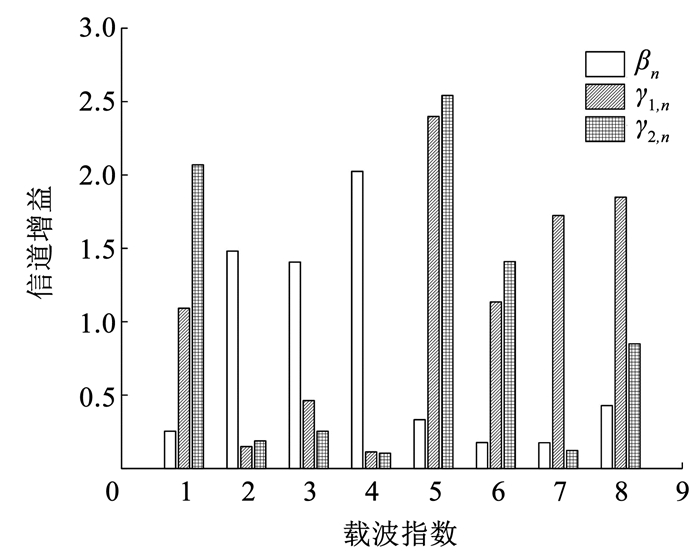
由上述给定的信道条件，利用MATLAB仿真工具随机产生一组雷达和通信信道，并根据式(10)对雷达和通信信道进行归一化处理，最终得到一组归一化信道增益β_n和γ_{k, n}，如图 2所示。从图 2中可以看出，雷达在第2, 3, 4个载波上的信道增益较大；通信用户在第1, 5, 8个载波上的信道增益较大。因此，在后续的功率分配中，DFRC系统会在信道增益较大的载波上分配较多功率以满足雷达和通信系统的性能需求。

首先，图 3给出了迭代次数与通信和速率的关系，用于对算法的收敛性进行验证。从图 3中可以看出，随着迭代次数的增加，通信和速率也随之增大，并且能在第12次左右时收敛。

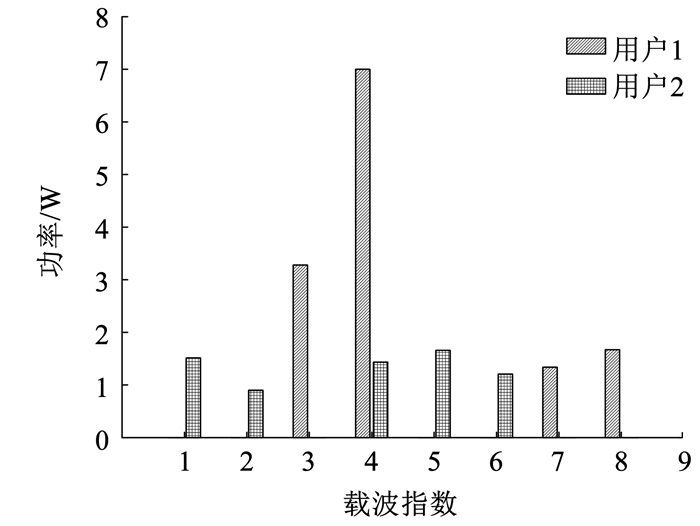
接着，图 4给出了图 2信道增益条件下的各载波用户功率分配情况。从图 4中可以看出，为了降低多用户干扰以提高通信和速率，各载波上的功率都趋向于分配给信道增益较大的用户，且信道增益越大，用户分配到的功率越多。但是，第4个通信信道增益较差的载波也分配了较多的功率。这是因为雷达在该载波上的信道增益最大，为满足雷达性能要求，不得不为其分配较多功率，使得DFRC系统的通信性能有所损失。

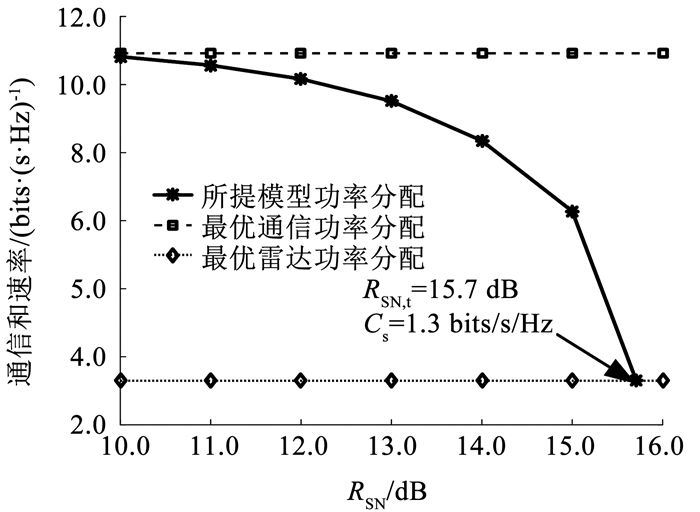
为了进一步分析雷达对通信性能的影响，图 5给出了R_{SN, t}与通信和速率的关系。图 5中最优通信功率分配指在不考虑雷达性能约束条件下，最大化通信和速率的功率分配方式。最优雷达功率分配指在不考虑通信性能要求条件下，最大化雷达信噪比的功率分配方式。可以看出，当R_{SN, t}较小时，所提模型功率分配相对最优通信功率分配来说通信和速率损失较小，随着R_{SN, t}的不断增加直至15.7 dB，所提模型功率分配对应的通信和速率不断减小，最终等效于最优雷达功率分配时的通信和速率，即会牺牲更多通信性能来满足雷达的性能要求。

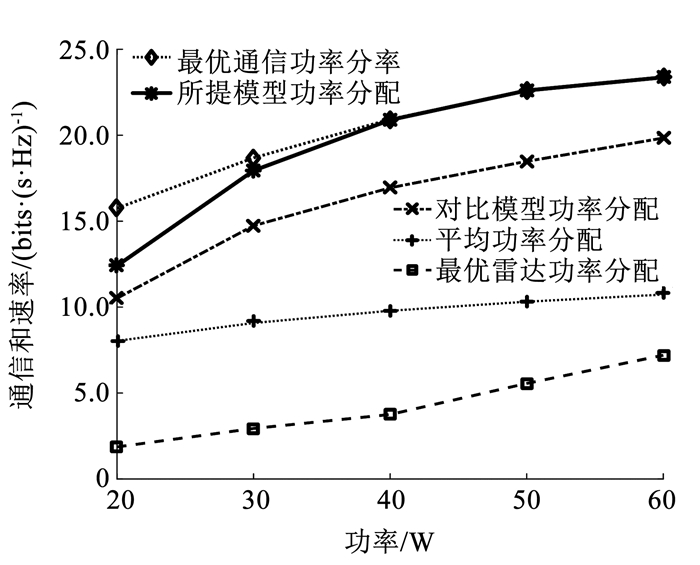
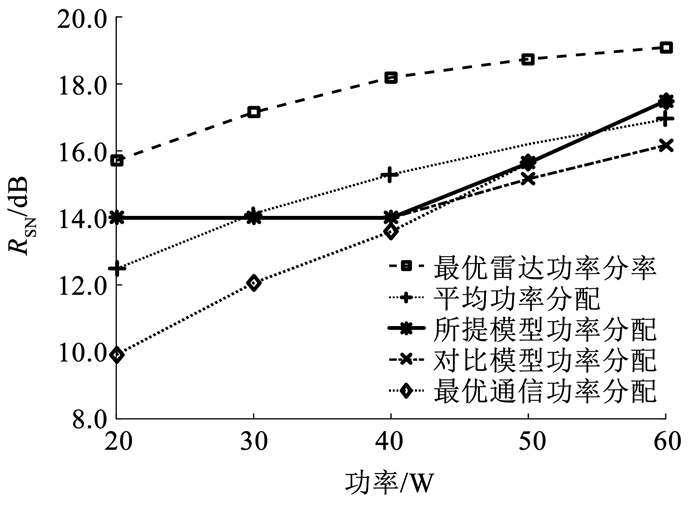
最后，为分析总功率变化对系统性能的影响，图 6、7给出了通信和速率、雷达信噪比与总功率的关系，并且图中还加入了平均功率分配和对比模型功率分配的通信和速率及雷达信噪比变化曲线。

从图 6、7中可以看出，随着总功率的增加，5种分配方式的通信和速率和雷达信噪比都会随之增加，并且最优通信功率分配的通信和速率总是大于另外4种分配方式。然而，最优通信功率分配只考虑通信性能最优，在总功率较小时，R_SN小于R_{SN, t}要求，不满足设计需求，而当功率足够大时，其通信和速率和雷达信噪比与所提模型功率分配相同。这是因为DFRC系统在总功率较小时，不得不牺牲一部分通信性能来满足雷达性能要求；而随着总功率提升，各载波都能分配到更多功率，并不需要牺牲通信性能来满足雷达的性能要求，最优通信功率分配与所提模型功率分配结果相同。最优雷达功率分配的R_SN总是大于另外4种分配方式，也远超R_{SN, t}的要求，但是，其通信和速率远小于另外4种分配方式，同样不满足文中的设计要求。平均功率分配在总功率较大时R_SN能满足R_{SN, t}要求，但是其通信和速率始终小于所提模型功率分配，方案性能较差。最后，将所提模型功率分配与对比模型功率分配进行比较，所提模型功率分配的通信和速率提高约40%。从雷达信噪比来看，两者在总功率较小时均会牺牲一部分通信性能来满足雷达性能下界要求，两者的R_SN等于R_{SN, t}，但是当总功率较大时，两种功率分配方式都等效于各自模型下的最优通信功率分配，功率分配结果只与各通信用户载波信道增益有关，此时只能确保两者的R_SN一直增大，但具体增益大小与当前各载波雷达信道增益有关。

4 结论

1) 传统通信用户载波分配模型因载波分配导致通信性能较差，针对这一问题提出通信用户载波共享模型，构建满足雷达信噪比、总功率以及用户功率约束条件的通信和速率最大问题，并设计一种基于二次转换的多用户功率分配算法。

2) 多用户功率分配算法将原多比值分式非凸优化问题分解为辅助变量优化子问题和功率分配矩阵优化子问题，然后通过交替迭代方式得到问题的优化解。

3) 实验结果表明，相较于通信用户载波分配模型，所提模型的通信和速率提高了约40%，该模型对提高双功能雷达通信系统的通信性能具有较高的使用价值。