抗毁性是发射平台系统结构和功能对于毁伤破坏的敏感程度,用于表征发射平台抵抗毁伤破坏、保持系统运行功能的能力[1]。究竟发射平台在战场打击威胁下的功能保持效果如何,是发射平台抗毁性评估所要研究的关键问题[2-3]。
目前,评估研究大多选取表征发射平台系统分级分层的概念类指标,而忽略了表征发射平台抗毁响应机理的技术类指标的构建,造成了评估指标体系侧重统计归纳,缺乏更为客观的物理描述;在评估方法上,目前评估研究基本采用层次分析法[4]、熵权法[5]、灰色关联法[6]、TOPSIS法[7]、ADC法[8]等及其相关的改进方法[9],重点都是在克服评估指标体系在定量化描述中面临的模糊性和随机性问题;在评估等级判据方面,目前评估研究基本采用了试验法[10]和评分法[11],试验法判据可信度高,但需要进行多组次大量试验;可见现阶段评估体系研究中,存在着主观性较强、偏重统计而缺乏物理逻辑关联等问题。
评估指标体系是评估问题研究的基础,在现有的各类评估研究中,也是人为主观影响最大的部分[12-13]。常见的指标体系构建方法是基于评估对象的特征信息分类,不同评估角度会提取不同特征信息,主观性最强。还有基于因果关联的评估指标体系构建方法和基于系统动力学的指标构建方法[14],这类方法根据因果影响机理,主观性较低,但模型构建复杂,指标体系庞大。
评估方法是评估问题研究的核心,也是现阶段评估问题的研究热点。现有的评估方法主要有两大类:1)以层次分析和熵权值为代表的数理统计方法,目前武器装备领域相关的评估方法主要以数理统计方法为主,这类评估方法物理关联性较差;2)以D-S证据理论[15]和马氏链[16]为代表的知识推论方法,这类方法引入概率论和模糊理论来处理指标量化的随机性,对样本数据和专家经验的要求较高。
基于此,为提高发射平台抗毁性评估的客观性和逻辑关联性,本文从评估指标体系、评估方法和评估等级判据3个方面对发射平台抗毁性评估进行研究。
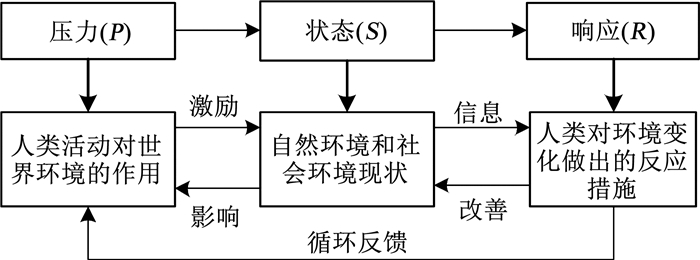
1 评估指标体系 1.1 PSR框架理论概念压力-状态-响应框架(pressure-state-response framework,PSR)理论最早是由联合国经济合作与发展组织为了评价世界环境状况提出并建立的[17]。该理论以因果关联为基础,通过分析系统内在的因果联系,明确影响系统的指标因素。其中,“压力(P)”为人类活动对环境的影响和激励;“状态(S)”为一定时期内世界自然环境和社会环境的综合反映;“响应(R)”为人类为促进环境可持续发展所采取的政策措施。PSR框架理论概念如图 1所示。
|
图 1 PSR框架理论概念 Fig. 1 Pressure-state-response framework |
由于发射平台定型列装后作战价值和结构功能的确定,使得发射平台在战场打击威胁下保持其运行功能的过程,呈现出基本的客观性。为了合理的对发射平台的抗毁性进行评估,就需要对这一客观过程进行分解, 并做出如下假设:
假设1 战场上的攻守双方不再出现新型超高性能的武器装备,评估环境保持稳定性;
假设2 发射平台不再进行总体结构和功能改造,评估对象保持稳定性;
假设3 忽略特殊毁伤工况的影响,评估过程保持稳定性。
即有发射平台在战场打击威胁下的抗毁性演化逻辑如图 2所示。

|
图 2 发射平台抗毁性演化逻辑 Fig. 2 Development process of invulnerability for launch platform |
基于PSR框架理论,从压力、状态和响应3方面分目标层、准则层和指标层构建发射平台抗毁性评估指标体系、评估指标含义说明、评估指标效应见表 1。
| 表 1 发射平台抗毁性评估指标体系 Tab. 1 Evaluation index system of invulnerability for launch platform |
发射平台结构部件复杂繁多,需要对表 1所示的指标体系进行筛选,以简化评估模型的指标复杂度。本文根据发射平台的结构总体布置和系统功能分析,以毁伤传递为关联路径,基于复杂网络理论,将部件或者子系统、功能模块视为复杂网络的节点,将功能关联路径和毁伤传导路径视为边,建立了发射平台异质网络模型如图 3所示。如驾驶室内布置有各种操作装置、驾驶仪表板以及计算机等设备,在这些设备的下方安装有发动机和分动器等装置,在毁伤过程中,毁伤源需要经过驾驶室等外部设备,才能传导作用在发动机等内部装置上。

|
图 3 发射平台拓扑网络模型 Fig. 3 Topological network model of launch platform |
设发射平台结构功能异质网络为
采用节点介数(betweenness)来表征经过某节点处的最短路径数目和网络中最短路径数目之比,用来研究各节点在拓扑网络中的影响,进而筛选出影响较大的节点作为主要的指标部件构建评估指标体系。即节点介数Bi为
| $ B_i=\sum\limits_j \sum\limits_{k \neq j} n_{j k}^i / n_{j k} $ | (1) |
式中: njki为节点j和k之间经过i的最短路径边数, njk为节点j和k之间的最短路径的边数。
然后采用k-means算法对拓扑网络G中的各部件节点介数进行划分聚类,按照各聚类层级筛选节点介数簇中心值占比较高、且节点数量较少的聚类层级所对应的部件。
欧式距离k-means算法的准则函数S为
| $ S=\min \sum\limits_{j=1}^\alpha \sum\limits_{x \in c_\gamma} \operatorname{dist}\left(c_\gamma, x\right)^2 $ | (2) |
式中: α为簇的个数,cγ为第γ个簇的中心点,dist(cγ, x)为cγ到x的距离。
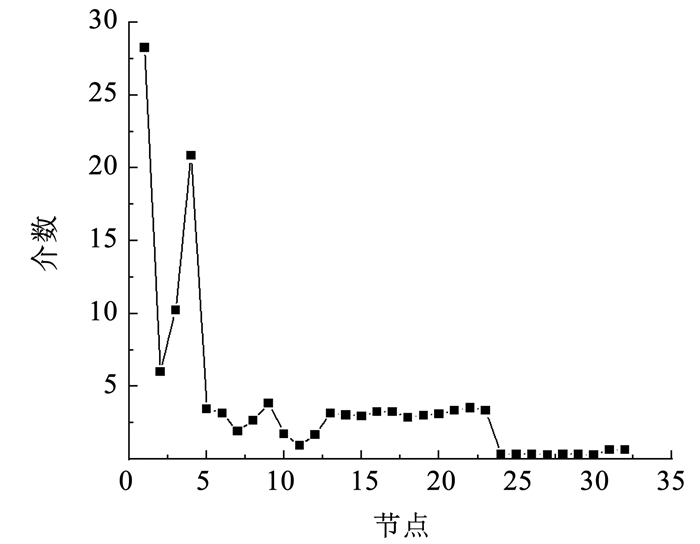
计算可得发射平台拓扑网络模型中各节点的介数值如图 4所示。
|
图 4 拓扑网络节点介数值 Fig. 4 Node-mediated values of topological network |
由图 4可知:介数值越大,该节点对拓扑网络的影响就越大,反之则影响越小。其中介数值大于5的节点有4个,占节点总数的12.500%,节点介数最大值为28.254,为代表发射筒的节点1,表明发射筒在拓扑网络中影响力最大;介数值大于1但小于5的节点有19个,占节点总数的59.380%,这些节点代表的部件和子系统主要集中在次外层;介数小于1的节点所代表的部件主要布置在内层,占节点总数的28.120%;
采用k-means算法对节点介数值进行划分聚类如图 5所示,图中Cmn为簇中心,m为簇数,n为类数。

|
图 5 拓扑网络节点介数聚类分析 Fig. 5 Clustering of node-mediated for topological network |
由图 5可知:随着划分簇数的增加,最高簇的个数和节点不变,剩余节点逐渐划分聚类,呈现出较为明显的分类现象。且随着划分簇数的增加,最低类和最高类的簇中心趋于稳定,分别为0.709和24.550,这说明发射平台拓扑网络模型中的各节点介质存在一定规律的划分聚类,可以采用成类剔除的筛选方法来优化抗毁性评估指标体系。当簇数为4时,剔除最低类的9个节点,剩余节点的介数值占总介数值的91.950%,剩余簇中心值占总簇中心值的98.030%,剩余的23个节点能够较为完整的表达拓扑网络的主要信息;当剔除最低类和第2类的节点时,剩余节点的介数值占总介数值的52.990%,剩余簇中心值占总簇中心值的90.550%,剩余的4个节点虽然表达拓扑网络的完整性相对降低,但剩余簇对总簇的信息保留仍然较为完整,达到90.000%以上;当剔除最低类和第2、3类的节点时,剩余节点的介数值占总介数值的36.970%,剩余簇中心值占总簇中心值的67.130%,剩余的2个节点已经无法较为完整的表达拓扑网络的主要信息。
因此,本文选择剔除簇数为4时的最低类和第2类的节点,以布置在发射平台最外层的发射筒、驾驶室、设备舱和轮胎系统的功能失效容限和失效响应程度为评估指标。则经过筛选后的抗毁性评估指标体系有3类共计9个指标,分别反映发射平台抗毁性的压力属性、状态属性和响应属性。
2 评估方法 2.1 基于量纲分析的DA-PSR评估模型构建本文针对压力指标P、响应指标R和状态指标S之间的管理属性,基于量纲分析(dimensional analysis),提出了发射平台抗毁性DA-PSR评估模型。
PSR框架理论涉及有3个物理量,则有函数:
| $ f(P, S, R)=0 $ | (3) |
由表 1可知,压力指标P为量纲一的量,响应指标和状态指标具有相关性,则有
| $ I=P^\sigma \cdot\left(S R^{-1}\right) $ | (4) |
压力指标P衡量的是发射平台被敌方发现后判别打击的可能,有P∈[0, 1],可令σ=1,有
| $ I=P \cdot \sum\limits_{i=1}^\theta \omega_i \left(\frac{S_i^*}{R_i^*}\right) $ | (5) |
式中: ωi为第i个指标的权重,θ为指标数,*为标准化。
2.2 基于互信息理论的指标赋权本文引入复杂网络中的互信息理论[18]对拓扑网络中关键节点的权重进行客观计算。
对于有向网络,节点存在接收信息和输出信息的双重特征,在互信息理论中,定义节点i的出边概率为
| $ p_{i \rightarrow j}=\frac{1}{k_{\text {out }}(i)} $ | (6) |
定义节点j的入边概率为
| $ p_{j \leftarrow i}=\frac{1}{k_{\text {in }}(j)} $ | (7) |
式中kin、kout分别为节点的入度和出度。
则节点i到节点j的互信息M(i, j)为
| $ M(i, j)=\begin{array}{ll} \ln \frac{1}{p_{i \rightarrow j}}-\ln \frac{1}{p_{j \leftarrow i}}, & i \sim j \text { 有连边 } \\ 0, & \text { 其他 } \end{array} $ | (8) |
定义节点i的信息量是节点i到所有i指向节点的互信息之和减去所有指向i的节点到节点i的互信息之和,即有
| $ M(i)=\sum\limits_{j \in V_{\text {out }}(i)} M(i, j)-\sum\limits_{l \in V_{\text {in }}(i)} M(l, i) $ | (9) |
式中: Vout(i)为节点所指向的节点集合,Vin(i)为指向节点的节点集合。
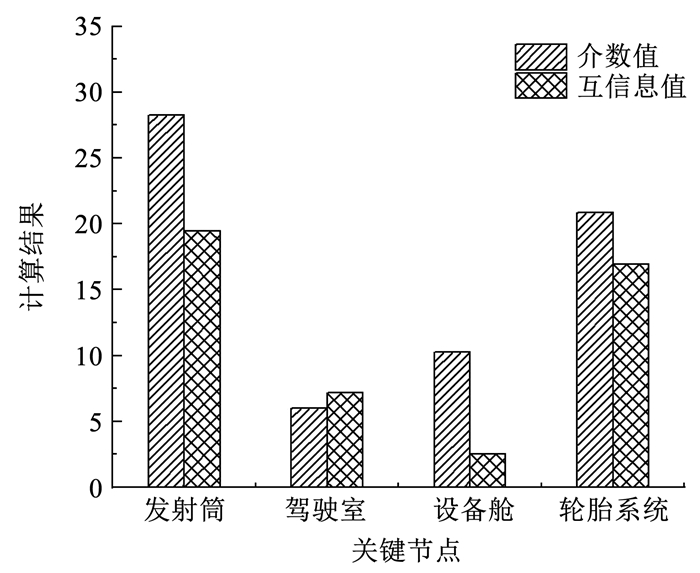
计算拓扑网络中关键节点的介数值和互信息值比较如图 6所示,归一化权重值见表 2。
|
图 6 介数值与互信息值比较 Fig. 6 Comparison of mediated and mutual information value |
| 表 2 关键节点的互信息值与归一化权重值 Tab. 2 Mutual information value and normalized |
由图 6和表 2可知,发射平台关键节点的互信息值最大为发射筒,互信息值是19.442,然后依次是轮胎系统16.950、驾驶室7.167和设备舱2.530,而且发射筒和轮胎系统的互信息值相近。互信息值计算结果与节点介数相比,分布规律大体一致。对关键节点的互信息值进行归一化处理以后即可作为各自的权重,用于发射平台抗毁性评估的指标赋权计算。
2.3 基于极限损毁量化的指标量化本文采用LS-Dyna仿真软件分别对某型发射平台抗毁性评估指标的功能失效容限和失效响应程度进行量化计算,关键节点发射筒、驾驶室、设备舱和轮胎系统的分析内容如图 7所示,计算结果见表 3。

|
图 7 评估指标量化仿真计算 Fig. 7 Simulation calculation of components |
| 表 3 评估指标计算结果 Tab. 3 Calculation results of evaluation index |
发射平台的本质是用来作战的,脱离作战任务的发射平台评估是不完整的。设武器装备完成某任务所需的最低性能状态为任务状态,添加有任务状态的性能损毁过程如图 8所示。

|
图 8 添加任务状态的性能损毁过程 Fig. 8 Performance degradation process after adding the battle status |
由图 8可知,武器装备从服役后的完整状态C开始,性能损毁过程存在两个关键节点:满足作战任务需求的状态节点B和满足基本运行需求的状态节点L,这两个节点将武器装备实际状态A所处的位置分成了3个阶段。可建立抗毁性评估等级判据表(见表 4)。
| 表 4 抗毁性等级判据表 Tab. 4 Rating criterion of invulnerability |
1) 当A∈[C, B],有I(A→L)≥I(B→L),此阶段能够满足作战任务对抗毁性的要求;
2) 当A∈[B, L],有I(A→L) < I(B→L),且I(A→L)>0,此阶段无法满足作战任务对抗毁性的要求,但能够满足基本的运行需求;
3) 当A∈[L, 0],有I(A→L)≤0,此阶段无法满足基本的运行需求。
假设有3种作战任务:1)20 min内占领15 km处的某处混凝土阵地并完成发射任务;2)20 min内机动至15 km处的某处沙土阵地并完成发射任务;3)附近混凝土阵地被摧毁,1 h内机动抢占65 km外的某发射阵地并完成发射任务;则表 3所示的某型发射平台,在上述3种作战任务要求下分别需要达到不同规定的机动速度和弹射压力要求,即有该型发射平台的抗毁性评估等级如图 9所示。

|
图 9 抗毁性评估等级 Fig. 9 Assessment level of invulnerability |
由图 9可知,当该型发射平台执行任务1时,对机动速度和弹射压力要求相对较低,满足作战需求的最低性能指标为0.648,该型发射平台评估技术结果0.737大于该值,因而其抗毁性在任务1下的评估等级为“优”;当该型发射平台执行任务2时,与任务1相比,对弹射压力的要求提高,满足作战需求的最低性能指标为0.824,该型发射平台评估技术结果0.737小于该值,但大于运行需求的最低性能指标0.648,因而其抗毁性在任务2下的评估等级为“中”;当该型发射平台执行任务3时,与任务1相比,对机动速度的要求提高,满足作战需求的最低性能指标为0.836,该型发射平台评估技术结果0.737小于该值,因而其抗毁性在任务3下的评估等级为“中”。
4 结论1) 在评估指标体系构建方面。提出了基于PSR框架理论的发射平台抗毁性评估指标体系构建方法,以及基于复杂异质网络理论节点介数和k-means算法的评估指标体系筛选方法。构建并筛选出了剩余节点介数值占总介数值52.990%、剩余簇中心值占总簇中心值90.550%的精简评估指标体系。与传统评估指标体系的构建方法相比,克服了指标构建主观性强的问题。
2) 在评估方法方面。提出了基于互信息理论的指标赋权方法和基于极限损毁量化的指标量化方法,并通过量纲分析对PSR框架理论进行了改进,构建了抗毁性DA-PSR评估模型,基于本文提出的评估方法,计算得该型发射平台的抗毁性评估值为0.737。与传统评估方法相比,该方法受主观因素影响小,物理逻辑关联性强。
3) 在评估等级判据方面。根据任务状态下的性能损毁过程,提出了面向作战任务需求的等级判据方法,将发射平台的等级划分为“满足作战”,“满足运行”和“无法满足”3个等级,分别对应“优、中、差”。并计算得出该型发射平台在不同作战任务下,评估等级分别呈现出“优、中、中”的差别。评估等级判据的构建受主观因素影响较小,与作战需求联系紧密。
4) 尽管与传统评估模型相比,基于DA-PSR模型和复杂网络的抗毁性评估模型能够克服主观因素的影响,增加物理逻辑关联性,且与作战需求联系紧密。但是采用该模型需要对评估对象的总体结构和应用具有深刻的认知,下一步需要对模型的通用性进行优化。
| [1] |
邹宾. 目标易损性概念和相关理论的探讨[J]. 四川建筑, 2016, 36(4): 134. ZOU Bin. Discussion on the concept of target vulnerability and related theories[J]. Sichuan Architecture, 2016, 36(4): 134. DOI:10.3969/j.issn.1007-8983.2016.04.049 |
| [2] |
ZHAI Chenglin, CHEN Xiaowei. Damage assessment of the target area of the island/reef under the attack of missile warhead[J]. Defence Technology, 2020, 16(1): 18. DOI:10.1016/j.dt.2019.06.022 |
| [3] |
王杰, 丁达理, 陈诚, 等. 导弹攻击状态评估下的UCAV试探机动决策[J]. 哈尔滨工业大学学报, 2021, 53(6): 118. WANG Jie, DING Dali, CHEN Cheng, et al. UCAV trial maneuvering decision under missile attack state assessment[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 118. DOI:10.11918/201908046 |
| [4] |
LUO Ruining, HUANG Shucai, ZHAO Yan, et al. Threat assessment method of low altitude slow small (LSS) targets based on information entropy and AHP[J]. Entropy, 2021, 23(10): 1292. DOI:10.3390/e23101292 |
| [5] |
ZHOU Shijie. Research on safety evaluation of nuclear power plant based on entropy weight method[J]. Canadian Social Science, 2021, 17: 82. DOI:10.3968/12236 |
| [6] |
李想, 黄胜, 张修远. 应用改进TOPSIS法的舰船气流场方案评价[J]. 哈尔滨工业大学学报, 2016, 48(4): 133. LI Xiang, HUANG Sheng, ZHANG Xiuyuan. Evaluation of airflow on warship deck based on improved TOPSIS method[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 133. DOI:10.11918/j.issn.0367-6234.2016.04.022 |
| [7] |
靳崇, 孙娟, 王永佳, 等. 基于直觉模糊TOPSIS和变权VIKOR的防空目标威胁综合评估[J]. 系统工程与电子技术, 2022, 44(1): 172. JIN Chong, SUN Juan, WANG Yongjia, et al. Threat comprehensive assessment for air defense targets based on intuitionistic fuzzy TOPSIS and variable weight VIKOR[J]. Systems Engineering and Electronics, 2022, 44(1): 172. DOI:10.12305/j.issn.1001-506X.2022.01.22 |
| [8] |
刘仕雷, 李昊. 改进ADC方法及其在武器装备系统效能评估中的应用[J]. 国防科技大学学报, 2017, 39(3): 130. LIU Shilei, LI Hao. Modified ADC method and its application for weapon system effectiveness evaluation[J]. Journal of National University of Defense Technology, 2017, 39(3): 130. DOI:10.11887/j.cn.201703020 |
| [9] |
ABBASI S, SARABADAN S. Evaluating tactical missile systems by using fuzzy AHP and TOPSIS technique[J]. Journal of Military and Information Science, 2015, 3(2): 28. DOI:10.17858/jmisci.69912 |
| [10] |
LEE G, NA O. Assessment of mechanical, thermal and durability properties of high-volume GGBS blended concrete exposed to cryogenic conditions[J]. Materials, 2021, 14(9): 2129. DOI:10.3390/ma14092129 |
| [11] |
JESÚS C, KING DANIEL L, STEIN DAN J, et al. Expert appraisal of criteria for assessing gaming disorder: An international Delphi study[J]. Addiction (Abingdon, England), 2021, 116(9): 2463. DOI:10.1111/add.15411 |
| [12] |
LI Xianguo, ZHANG Qian. AHP-based resources and environment efficiency evaluation index system construction about the west side of Taiwan Straits[J]. Annals of Operations Research, 2015, 228(1): 97. DOI:10.1007/s10479-012-1072-y |
| [13] |
肖勇, 陆文升, 李云涛, 等. 城市配电网发展形态指标体系及其评估方法研究[J]. 电力系统保护与控制, 2021, 49(1): 62. XIAO Yong, LU Wensheng, LI Yuntao, et al. Research on index system and its evaluation methods of urban distribution network development form[J]. Power System Protection and Control, 2021, 49(1): 62. DOI:10.19783/j.cnki.pspc.200803 |
| [14] |
MANDI N M, ALI M, ALI REZA MASSAH B, et al. System dynamics simulation of regional water supply and demand using a food-energy-water nexus approach: Application to Qazvin Plain, Iran[J]. Journal of Environmental Management, 2021, 280: 111843. DOI:10.1016/j.jenvman.2020.111843 |
| [15] |
SUN Tanghui, LIU Bailin. Health assessment based on D-S evidence theory of equipment[J]. International Journal of Advanced Network, Monitoring and Controls, 2020, 5(4): 15. DOI:10.21307/ijanmc-2020-033 |
| [16] |
HABBEN JANSEN A C, DUCHATEAU E A E, KANA A A, et al. Assessing complex failure scenarios of on-board distributed systems using a Markov chain[J]. Journal of Marine Engineering & Technology, 2020, 19(Sup.1): 45. DOI:10.1080/20464177.2019.1673032 |
| [17] |
WANG Yutu, WANG Youshao, WU Meilin, et al. Assessing ecological health of mangrove ecosystems along South China Coast by the pressure-state-response (PSR) model[J]. Ecotoxicology, 2021, 30(4): 622. DOI:10.1007/s10646-021-02399-1 |
| [18] |
马润年, 王班, 王刚, 等. 基于互信息的通信网络节点重要性度量方法[J]. 电子学报, 2017, 45(3): 747. MA Runnian, WANG Ban, WANG Gang, et al. Evaluation method for node importance in communication network based on mutual information[J]. Acta Electronica Sinica, 2017, 45(3): 747. DOI:10.3969/j.issn.0372-2112.2017.03.035 |
 2023, Vol. 55
2023, Vol. 55


