2. 海军研究院空中所, 上海 200436;
3. 92283部队,上海 201900
2. Institute of Air Combat, Naval Research Academy, Shanghai 200436, China;
3. Unit No.92283 of PLA, Shanghai 201900, China
由于受到航空母舰着舰甲板尺寸的限制、海上环境的干扰以及“反区”操纵特性的影响,舰载机下滑着舰是一项复杂度极高、困难度极大的任务,是航空母舰舰载机作战任务环节中事故率最高的阶段。在传统的着舰过程中,飞行员必须不断调整飞机的迎角和下滑道高度,使飞机的尾钩对准甲板上的拦阻索,一次完整的进近过程往往需要上百次对姿态、速度等要素的修正,飞行员需要精神高度紧张,往往不堪重负。为了减轻飞行员的操纵负担、缩短培训周期并降低训练成本,美国海军提出了“魔毯”(MAGIC CARPET)着舰技术的概念,其核心是集成直接升力控制技术。这是由于直接升力控制可以实现独特的运动模式,有良好的迎角保持和轨迹修正能力,并且控制响应快,恰好可以满足进近时的轨迹调节和对中修正的操纵需求。这主要体现在下滑着舰阶段,将飞行员“保角”、“对中”、“看灯”这3项相互耦合的操纵进行解耦,以实现驾驶杆操纵到控制目标一一对应,即“纵向驾驶杆操纵”对应“轨迹高度”,“横向驾驶杆操纵”对应“对中修正”,从而显著降低操纵难度[1-5]。
直接升力控制的概念最早是英国人提出来的,早期主要是为了解决大型运输飞机着陆轨迹控制问题[6]。20世纪70年代以前,主要限于从飞行力学角度进行理论上的分析和讨论。到了20世纪70年代后期,进入应用研究阶段,主要应用于各种验证机的试飞。进入80年代后,主要集中于研究运用现代控制理论进行控制律和控制系统的设计,例如线性二次型法、系统特征结构配置方法、奇异摄动方法、高增益串联解耦等方法,后来逐渐将非线性的控制方法应用于直接升力控制系统中,如动态逆控制[7-8]、自抗扰控制等[9]。中国对主动控制技术的研究开展较晚,上世纪70年代开始对主动控制技术进行规划,并拟定一些预研课题。在歼-8 ACT验证机上实现了放宽静稳定性设计,对直接升力控制进行了初步研究,直到90年代,西北工业大学专门对直接升力控制进行了一些研究,但不够深入[10-11]。近年来,朱玉莲等[12]采用PID控制方法设计了直接升力着舰控制律,考虑了甲板运动与舰尾流的影响,对下滑道高度进行了控制,不过采用的是线性化模型和静态解耦手段,对于真实系统的非线性以及环境干扰因素的应对还可改进。罗飞等[13-14]采用常规的动态逆方法设计了直接升力着舰轨迹控制律,实现了纵向解耦控制,不过其指令跟踪存在较为明显稳态误差,而且其采用的是直接升力控制模式中的垂直平移模式,即在调节轨迹时保持俯仰角不变,这在下滑着舰阶段并非最好的方式,由于下滑着舰时的三大任务之一“保角”需要保持舰载机迎角不变,因此保持舰载机迎角不变是更好的方式,但迎角相比于俯仰角而言所受的干扰因素更多,因而对迎角进行精确控制的难度也相对较大。
此外,“魔毯”着舰系统具有横、纵向综合解耦的特性,而现有研究仅是针对纵向控制进行设计,尚未有对于结合横航向的综合控制器的设计研究。本文在综合考量舰载机下滑着舰控制阶段的操纵特点及难点,为了实现简化飞行员操纵难度并提升控制精度的目标,充分结合直接升力控制及非线性动态逆的优势特点,设计了舰载机着舰综合控制律,搭建了完整的横、纵向着舰控制器,不仅在纵向运动中实现了姿态和轨迹控制的解耦,还实现了横航向控制与纵向轨迹控制间的解耦,对飞行员“保角”、“看灯”、“对中”3项操纵任务实现一一解耦。由于直接升力控制需要多个操纵面共同完成,为了使舵面协调搭配,结合了加权伪逆控制分配的方法实现舵面的合理优化分配,使用了分段衔接控制的方式,构建了两层级联式控制结构,通过设置中间虚拟控制变量,将动态逆与控制分配两种控制方法有机地结合,设计了基于“直接爬升模式”(直接升力控制的一种运动模态,即保持飞行迎角不变的前提下实现飞行轨迹调节)的精确着舰综合控制律。此外,由于下滑着舰过程对控制响应的快速性要求比较高,基于预设加权误差向量约束方程改写系统动态,并利用非线性动态逆方法求解控制律,提升动态逆控制环节的综合控制性能,加快跟踪速度并消除稳态误差。
1 舰载机模型建立以F-18舰载机为研究对象,建立6自由度飞行动力学模型,为后续仿真研究奠定基础[15]。
舰载机受到的气动力和力矩主要由各操纵面及机体产生,将气动力系数转化到机体坐标系下,可以得到升力、侧力和阻力,分别表示为:
| $ L=\frac{1}{2} \rho V^2 S C_{\mathrm{L}} $ | (1) |
| $ Y=\frac{1}{2} \rho V^2 S C_{\mathrm{Y}} $ | (2) |
| $ D=\frac{1}{2} \rho V^2 S C_{\mathrm{D}} $ | (3) |
式中:ρ为空气密度,V为舰载机空速,CL为舰载机总升力系数,CD为舰载机总阻力系数,CY为舰载机总侧力系数,S为舰载机机翼参考面积。CL、CD和CY用气动力导数表达为[16]
| $ \left\{\begin{array}{l} C_{\mathrm{L}}=c_{\mathrm{L}_0}+c_{\mathrm{L}_\alpha} \alpha+c_{\mathrm{L}_q} \frac{c}{2 V} q+c_{\mathrm{L}_{\delta_{\mathrm{e}}}} \delta_{\mathrm{e}}+c_{\mathrm{L}_{\delta_{\mathrm{f}}}} \delta_{\mathrm{f}} \\ C_{\mathrm{D}}=c_{\mathrm{D}_0}+c_{\mathrm{D}_\alpha} \alpha+c_{\mathrm{D}_q} \frac{c}{2 V} q+c_{\mathrm{D}_{\delta_{\mathrm{e}}}} \delta_{\mathrm{e}}+c_{\mathrm{D}_{\delta_{\mathrm{f}}}} \delta_{\mathrm{f}} \\ C_{\mathrm{Y}}=c_{\mathrm{Y}_0}+c_{\mathrm{Y}_\beta} \beta+c_{\mathrm{Y}_p} \frac{b}{2 V} p+c_{\mathrm{Y}_{r}} \frac{b}{2 V} r+c_{\mathrm{Y}_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{\mathrm{Y}_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} \end{array}\right. $ | (4) |
式中:
而滚转力矩 Lroll,俯仰力矩 M和偏航力矩 N分别为:
| $ \boldsymbol{L}_{\text {roll }}=\frac{1}{2} \rho V^2 b s C_l $ | (5) |
| $ \boldsymbol{M}=\frac{1}{2} \rho V^2 c s C_M $ | (6) |
| $ \boldsymbol{N}=\frac{1}{2} \rho V^2 b s C_N $ | (7) |
其中,总力矩系数分别为
| $ \left\{\begin{array}{l} C_l=c_{l_0}+c_{l_\beta} \beta+c_{l_p} \frac{b}{2 V} p+c_{l_r} \frac{b}{2 V} r+c_{l_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{l_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} \\ C_M=c_{M_0}+c_{M_\alpha} \alpha+c_{M_q} \frac{c}{2 V} q+c_{M_{\delta_{\mathrm{e}}}} \delta_{\mathrm{e}}+c_{M_{\delta_{\mathrm{f}}}} \delta_{\mathrm{f}} \\ C_N=c_{N_0}+c_{N_\beta} \beta+c_{N_p} \frac{b}{2 V} p+c_{N_{r}} \frac{b}{2 V} r+c_{N_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{N_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} \end{array}\right. $ |
在机体坐标系上,飞机动力学与运动学方程组如下:
1) 线动力学方程组:
| $ \left\{\begin{array}{l} \dot{u}=v r-w q-g \text{sin} \;\theta+\frac{F_x}{m} \\ \dot{v}=-u r+w p+g \text{cos}\; \theta \text{sin} \;\phi+\frac{F_y}{m} \\ \dot{w}=u q-v p+g \text{cos}\; \theta \text{cos} \;\phi+\frac{F_z}{m} \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} F_x=T \text{cos}\; \sigma-D \text{cos} \;\alpha \text{cos} \beta-m g \text{sin}\; \theta \\ F_y=Y \text{cos} \;\alpha \text{cos} \beta+m g \text{cos} \;\theta \text{sin} \; \phi \\ F_z=-T \text{sin} \; \sigma-L \text{cos} \;\alpha+m g \text{cos} \;\theta \text{cos}\; \phi \end{array}\right. $ | (9) |
2) 角动力学方程组:
| $ \left\{\begin{array}{l} \dot{p}=\left(c_1 r+c_2 p\right) q+c_3 \boldsymbol{L}_{\mathrm{roll}}+c_4 \boldsymbol{N} \\ \dot{q}=c_5 p r-c_6\left(p^2-r^2\right)+c_7 \boldsymbol{M} \\ \dot{r}=\left(c_8 p-c_2 r\right) q+c_4 \boldsymbol{L}_{\mathrm{roll}}+c_9 \boldsymbol{N} \end{array}\right. $ | (10) |
式中: ci,i=1, 2, ⋯, 9为飞机的惯性矩常数,c1=
3) 姿态角运动学方程组:
| $ \left\{\begin{array}{l} \dot{\phi}=p+(r \text{cos} \;\phi+q \text{sin}\; \phi) \tan \theta \\ \dot{\theta}=q \text{cos}\; \phi-r \text{sin}\; \phi \\ \dot{\psi}=\frac{1}{\cos \theta}(r \text{cos}\; \phi+q \text{sin}\; \phi) \end{array}\right. $ | (11) |
4) 气流角运动学方程组:
| $ \left\{\begin{aligned} \dot{\alpha}= & \frac{q \text{cos} \; \phi}{\text{cos} \; \psi}+\frac{r \text{sin}\; \phi}{\text{cos} \; \psi}-\frac{T \text{sin}\; \alpha}{m V}+\frac{g \text{cos} \; \alpha \text{cos} \; \theta}{V}-\frac{V c_{l_\alpha} \alpha}{m}+ \\ & \frac{g \text{sin}\; \alpha \text{sin}\; \theta}{V}-\frac{T \delta_{\mathrm{e}} \cos \; \alpha}{2 V m} \\ \dot{\beta}= & r \text{cos} \; \phi-q \text{sin}\; \phi+\frac{V c_{l_\beta} \beta}{m}-\frac{T \delta_{\mathrm{r}} \text{cos} \; \beta}{2 V m}-\frac{T \text{cos} \; \alpha \text{sin}\; \beta}{m V}- \\ & \frac{g \text{cos} \; \alpha \text{cos} \; \beta \text{sin}\; \psi \text{sin}\; \theta}{V}+\frac{g \text{cos} \; \alpha \text{cos} \; \psi \text{sin}\; \beta \text{sin}\; \theta}{V}+ \\ & \frac{g \text{cos} \; \beta \text{sin}\; \alpha \text{cos} \; \theta \text{sin}\; \psi}{V}-\frac{g \text{cos} \; \psi \text{sin}\; \alpha \text{sin}\; \beta \text{cos} \; \theta}{V} \\ \dot{\mu}= & \frac{1}{\text{cos} \; \beta}(p \text{cos} \; \alpha+r \text{sin}\; \alpha)+\frac{L}{m V}(\tan \gamma \text{sin}\; \mu+\tan \beta)+ \\ & \frac{C}{m V} \tan \gamma \text{cos} \; \mu \text{cos} \; \beta-\frac{T \text{cos} \; \alpha}{m V} \tan \gamma \text{cos} \; \mu \text{sin}\; \beta- \\ & \frac{g}{V} \text{cos} \; \gamma \text{cos} \; \mu \text{tan} \beta \end{aligned}\right. $ | (12) |
5) 轨迹运动方程组:
| $ \left\{\begin{aligned} \dot{V}= & \frac{1}{m}(T \cdot \text{cos} \; \alpha \text{cos} \; \beta-D \cdot \text{cos} \; \beta+Y \cdot \text{sin}\; \beta)-g \text{sin}\; \gamma \\ \dot{\gamma}= & \frac{1}{m V}(L \cdot \text{cos} \; \mu-Y \cdot \text{cos} \; \beta \text{sin}\; \mu-D \text{sin}\; \beta \text{sin}\; \mu)+ \\ & \frac{T}{m V}(\text{sin}\; \alpha \text{cos} \; \mu-\text{cos} \; \alpha \text{sin}\; \beta \text{sin}\; \mu)-\frac{g \text{cos} \; \gamma}{V} \\ \dot{\chi}= & \frac{1}{m V \text{cos} \; \gamma}[T(\text{sin}\; \alpha \text{sin}\; \mu+\text{cos} \; \alpha \text{sin}\; \beta \text{cos} \; \mu)+ \\ & Y \text{cos} \; \mu+L \text{sin}\; \mu] \end{aligned}\right. $ | (13) |
根据式(1)~(13)以及飞机的气动参数,利用Matlab中的S函数模块即可建立6自由度动力学模型。
2 控制方法分析 2.1 直接升力控制 2.1.1 基本原理直接升力控制的方式能消除力和力矩耦合的影响,实现对航迹调节和姿态控制的解耦,能提升轨迹控制的快速性和精确性,改善飞行品质,使得飞机具有更优良的轨迹控制性能和更强的抗干扰能力[17-18]。
直接升力操纵面的选取有以下5种搭配方案:
1) 对称襟翼+升降舵;
2) 同步偏转副翼+升降舵;
3) 扰流板+升降舵;
4) 水平鸭翼+襟翼;
5) 水平鸭翼+升降舵。
由于襟翼产生直接升力的能力较大,而且由于襟翼偏转产生气动力的作用点离飞机的重心很近,因此在产生附加升力的同时,本身不会引起明显的力矩变化,升降舵则起到微调配平的作用,这也是目前较为常用的直接升力产生方式,如图 1所示是飞机受力示意图[19]。本文在进行控制律设计时即是采用对称襟翼与升降舵搭配偏转的控制方式。

|
图 1 直接升力操纵面配合偏转示意 Fig. 1 Force balance of the direct life control |
由于直接升力控制可以实现特定的运动模态,因此具有很多独特的优势,可以弥补常规飞行控制方式下着舰的一些不足,主要具有如下优点:
1) 下滑道偏差修正速度快。直接升力控制能产生十分可观的法向过载,而且由于直接升力控制不需要经过改变飞机姿态进而影响飞行迎角来间接改变升力的过渡过程,省去了多个积分环节,显著降低了相位滞后,因此可以更快地修正偏差。
2) 抗舰尾流、阵风干扰能力强。由于在着舰阶段舰尾流或阵风的干扰对舰载机纵向运动的影响主要体现在法向方向上,直接升力操纵面产生的力恰能直接抵消这种法向扰动,且由于响应速度快,在应对高频风扰动时,具有明显的抑制效果[20]。
3) 避免“负调”现象。传统控制方式是通过改变飞机姿态以改变气动力,因此飞行轨迹的调节存在过渡过程,且在控制初期,轨迹会向期望指令的反向响应,称为“负调”现象,这在舰载机着舰特别是临近舰尾时是非常危险的。而直接升力控制操纵面直接产生期望的附加升力,因此不存在轨迹的反向调整问题,能够提高安全性和精确性。
4) 下滑速度保持效果好。采用直接升力控制可以稳定飞行迎角,因此不会引起诱导阻力发生明显的变化,能够较好地保持进近速度。
2.2 非线性动态逆控制通过直接升力控制的方式可以实现轨迹控制与姿态控制间的解耦,除此之外,对非线性舰载机模型来说,系统本身的空气动力学特性同样也具有很强的耦合性,比如横航向运动间的交联以及横滚运动导致纵向升力损失。因此在设计控制律时采用非线性动态逆的控制方法,利用其较好的系统解耦性能实现系统综合控制解耦,从而获得更好的精确控制效果[21]。
2.2.1 基本概念动态逆方法是基于模型论的控制理念,其基本思想是对于给定的系统,先利用对象模型生成一种可用反馈方法实现的原系统的α阶积分逆系统,将对象补偿成为具有线性传递关系且已解耦的一种规范化系统——伪线性系统,再应用线性系统理论完成系统的综合[22]。
2.2.2 优势特点非线性动态逆是利用状态反馈抵消系统内部的非线性特性,从而将系统进行伪线性化解耦,因此具有更好的针对性和精确度,其良好的解耦特性在设计横、纵向综合轨迹控制律时具有显著优势。本文在设计动态逆控制环节时,充分发挥动态逆控制的解耦特性,并提出了预设性能的加权误差参数向量和系统动态约束方程,基于此所解得的控制律,能使闭环系统按照预设的约束性能渐进稳定,并可以通过调节参数,优化控制效果。
2.3 加权伪逆控制分配算法控制分配算法用于解决多操纵面的协调控制问题,根据期望的指令和控制目标,求解各操纵面的控制量[23]。对于形如Be·u=v的控制系统,可以选取Be的伪逆与期望变量的积作为解,即
| $ u=\boldsymbol{B}_{\mathrm{e}}^{+} \cdot v=\boldsymbol{B}_{\mathrm{e}}^{\mathrm{T}}\left(\boldsymbol{B}_{\mathrm{e}} \boldsymbol{B}_{\mathrm{e}}^{\mathrm{T}}\right)^{-1} \cdot v $ | (14) |
式中:Be为系统控制效能矩阵,u为系统控制输入,v为虚拟控制变量,Be+为矩阵 Be的Moore-Penrose广义逆矩阵,Be+=BeT(Be·BeT)-1。
由于一般伪逆法的分配效率较低而且不同的操纵面具有不同的速率限制和频带宽度,在实际的控制律设计中应为不同操纵面设置不同的权重[24]。因此可以采用加权伪逆算法进行分配求解,其分配指标函数为
| $ \begin{array}{ll} & J=\min \left\|W_u u\right\|_2 \\ \text { s. t. } & \boldsymbol{B}_{\mathrm{e}} \cdot u=v \end{array} $ | (15) |
它的解如下式所示:
| $ \begin{array}{c} u=u_d+\boldsymbol{W}_u^{-1}\left(\boldsymbol{B} \boldsymbol{W}_u^{-1}\right)+\left(v-\boldsymbol{B} u_d\right)= \\ \underbrace{\left(I-\boldsymbol{W}_u^{-1}\left(\boldsymbol{B} \boldsymbol{W}_u^{-1}\right)^{+} \boldsymbol{B}\right)}_F \cdot u_d+\underbrace{\boldsymbol{W}_u^{-1}\left(\boldsymbol{B} \boldsymbol{W}_u^{-1}\right)^{+}}_G \cdot v= \\ F \cdot u_d+G \cdot v \end{array} $ | (16) |
本文可以根据需求设置最优化的权值矩阵 Wu来获得较好的分配结果。
3 控制律设计“魔毯”着舰控制技术主要有两个模态,分别是飞行轨迹角速率模态和飞行轨迹增量(delta path,DP)控制模态,都是基于直接升力控制中的直接爬升模式,即对飞行轨迹进行操纵调节的同时,自动飞行控制律能够保持飞机迎角不变。本文设计的横、纵向综合控制律是在第5边下滑进近时使用的DP模态下,纵向修正轨迹高度时,飞行员的杆指令对应控制轨迹角,自动控制器保持迎角和速度稳定;横向对中调节时,杆指令对应控制偏航角,自动控制器保持飞机滚转姿态和轨迹高度的稳定。
纵向控制以期望轨迹角γc作为指令控制输入,反馈量则为飞行轨迹角γ,由于需要在控制轨迹角的同时保持迎角稳定,因此还需引入迎角反馈量α、空速反馈量V和俯仰角速率q,期望指令γc则根据驾驶杆纵向位移转化得到,当杆处于中立位置时,默认理想下滑道角度-3.5°。工程中通过调整合适增益系数使驾驶员的杆位移量与期望指令γc之间为线性变化关系,而使飞行员可以直观恰当地进行下滑道修正。由于在下滑阶段需要“保角”,即保持飞机迎角稳定,于是在控制律中还需给定常值迎角控制信号,以在飞行员操控改变轨迹角时始终保持迎角不变,此外,为了保证舰载机平稳下滑,需要保持飞行速度稳定,同样在控制律中给定常值速度控制信号,自动控制飞机油门功率,保证速度稳定。引入俯仰角速率q信号作为阻尼项,使得控制信号响应更精确。
航向控制以期望偏航角ψc作为指令控制输入,反馈量为飞机偏航角ψ,在控制偏航角时保持滚转姿态的稳定,于是在控制律中还需给定滚转角稳定控制信号,引入滚转角反馈量ϕ,滚转角速率p,偏航角速率r,期望指令ψc根据驾驶杆的横向位移转化得到。不同于常规控制模态下,左、右压杆操控飞机滚转,在该模态中,当飞行员压杆操纵时进行对中修正时,驾驶杆的输入量线性对应偏航角指令,副翼和方向舵联合偏转,舰载机的航向发生改变并伴有同侧滚转,并在达到期望角度后,机身滚转被控制律自动消除,同时在调整的过程中,纵向轨迹高度和迎角则由直接升力控制律来联动保持,实现在对中修正时纵向不掉高。
本文构建了两层递进式的控制架构,既能发挥非线性动态逆在飞机横、纵向运动解耦的优势,又能发挥直接升力控制方式在纵向轨迹和姿态控制上解耦的特性。为了将非线性动态逆控制方法与直接升力控制方式进行有机且协调的结合,设置了虚拟中间控制量作为动态逆控制模块和控制分配模块的衔接,第1层控制环节根据输入的期望控制指令,解算得出期望的虚拟控制量值;第2层控制环节则根据所期望的虚拟控制量解算得到相应操纵面的偏转量并将此控制指令传递给伺服舵机。第1层的控制环节采用预设性能的非线性动态逆控制方法以进行反馈解耦控制,第2层的控制环节采用控制分配的方法是因为直接升力控制需要多个操纵面的共同参与,协调偏转才能实现相应的运动模态。完整的控制律架构原理图如图 2所示。

|
图 2 完整控制器结构原理框图 Fig. 2 Direct lift control system with nonlinear dynamic inversion method |
非线性动态逆的控制原理在前文已做阐述,在此选取慢状态
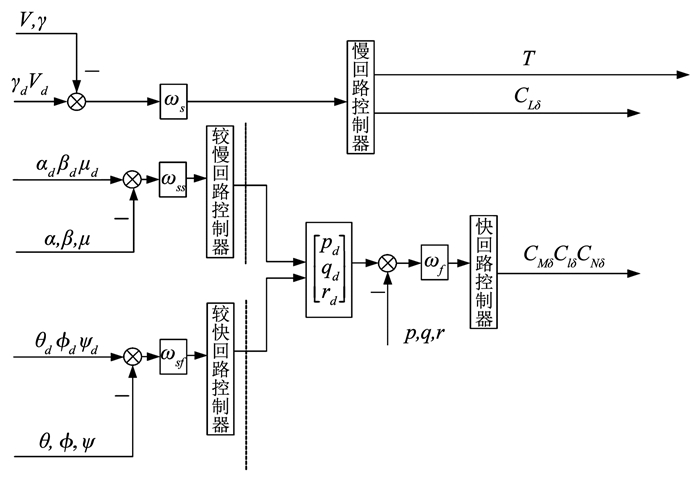
|
图 3 非线性动态逆控制环节简化模型 Fig. 3 Simplified model of nonlinear dynamic inverse control loop |
在应用动态逆控制律时,一般需要求系统控制矩阵的全逆,即求 G-1(x)这就要求在控制系统中,必须满足控制量与状态量数量相同的条件,才能使系统分解成多个线性解耦子系统,在飞行控制系统中,这一条件往往是做不到的。为了避免这种不足,将非线性动态逆方法与奇异摄动理论,即状态变量的时标分离方法相结合,进行近似的求解。
所谓时标分离就是按照被控变量对控制输入量响应快、慢的特点,将它们分成不同的变量组,然后进行分组控制,以简化控制系统设计任务。
1) 状态变量的时标划分。
由前文所介绍的飞机六自由度非线性方程可知:F-18数学模型中有12个状态变量,即
| $ \boldsymbol{x}=\left[\begin{array}{llllllllllll} p & q & r & \varphi & \theta & \psi & \alpha & \beta & \mu & V & \gamma & \chi \end{array}\right]^{\mathrm{T}} $ | (17) |
根据时标分离原理,结合工程实际,可将这12个状态变量划分成为快、慢不同的4组,各组之间存在一定嵌套关系,可以根据需求对相应的变量组设计控制律,这样可以简化控制器的设计任务。
本文以轨迹控制、迎角控制和偏航控制为主要目的,按时标分离原理对状态变量的划分如下。
2) 控制量的描述。
飞机的控制量为
根据时标分离原理,将本文中所建立的飞机数学模型进行合理的划分,从而将整个系统的数学模型分成有着内在联系的4个子系统。本文采用了设置虚拟控制变量的方法,因而可以相对简化回路之间的嵌套结构。
3.1.2 快状态回路设计选取变化最快的角速度式(10)作为快状态回路,将快变量状态方程改写成与飞机状态和控制作用相关的两部分。取总力矩系数中与操纵面偏转量相关的力矩系数作为虚拟控制量,称为操纵力矩系数,可写成
| $ \left\{\begin{array}{l} C_{l \delta}=c_{l_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{l_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} \\ C_{M \delta}=c_{M_{\delta_{\mathrm{e}}}} \delta_{\mathrm{e}}+c_{M_{\delta_{\mathrm{f}}}} \delta_{\mathrm{f}} \\ C_{N \delta}=c_{N_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{N_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} \end{array}\right. $ | (18) |
将气动力矩方程中与控制量(操纵力矩系数)相关的参数分离为单独的控制输入增益矩阵 g(·),并将其他与控制输入无关的项写入f(·),即可得到仿射结构的快状态回路表达式:
| $ \left[\begin{array}{c} \dot{p} \\ \dot{q} \\ \dot{r} \end{array}\right]=f_f\left(\boldsymbol{x}_f\right)+\boldsymbol{g}_f\left(\boldsymbol{x}_f\right)\left[\begin{array}{c} C_{l \delta} \\ C_{M \delta} \\ C_{N \delta} \end{array}\right] $ | (19) |
式中
快回路的误差向量定义为
| $ e_f=\boldsymbol{x}_1-\boldsymbol{x}_{1 d} $ | (20) |
式中x1d为快状态回路的期望指令,且是与t相关的有界函数。为了给控制律附加预设性能,以及可以通过调整权重来选取更关注的主控制变量,则提出定义加权误差范数向量:
| $ \begin{array}{c} \boldsymbol{E}_f=\left\|\boldsymbol{e}_f\right\|_w^2= \\ k_p\left(p-p_d\right)^2+k_q\left(q-q_d\right)^2+k_r\left(r-r_d\right)^2 \end{array} $ | (21) |
在上述误差偏离方程中,kp, kq, kr为正常数,基于此,快回路状态的线性时变约束动态可以表示为
| $ \dot{E}_f+c_1(t) E_f=0 $ | (22) |
式中c1为能使得该约束动态一致渐进稳定的正常数,且
| $ \begin{array}{c} \dot{\boldsymbol{E}}_f=2 \times \boldsymbol{e}_f^{\mathrm{T}} \times \operatorname{diag}\left(k_p, k_q, k_r\right) \times \\ \left(f_f\left(x_f\right)+\boldsymbol{g}_f\left(\boldsymbol{x}_f\right) \cdot \delta-\dot{x}_{1 d}\right) \end{array} $ | (23) |
式中:diag为对角矩阵符号,δ为虚拟控制量,即
| $ \boldsymbol{A}_1\left(\boldsymbol{x}_2, \boldsymbol{x}_3, t\right) \cdot \delta=\boldsymbol{B}_1\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) $ | (24) |
其中:
| $ \begin{array}{c} \boldsymbol{A}_1=2 \boldsymbol{e}_f^{\mathrm{T}} \operatorname{diag}\left(k_p, k_q, k_r\right) \cdot \boldsymbol{g}_f\left(\boldsymbol{x}_f\right) \\ \boldsymbol{B}_1=-2 \boldsymbol{e}_f^{\mathrm{T}} \operatorname{diag}\left(k_p, k_q, k_r\right)\left(f_f-\dot{x}_{1 d}\right)- \\ c_1\left[k_p, k_q, k_r\right] \boldsymbol{e}_f^2 \end{array} $ |
通过求逆,即可解得所需的虚拟控制量δ为
| $ \delta=\boldsymbol{A}_1^{+}\left(\boldsymbol{x}_2, \boldsymbol{x}_3, t\right) \cdot \boldsymbol{B}_1\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) $ | (25) |
式中,
| $ V=\frac{1}{2} \boldsymbol{E}_f^2 $ | (26) |
则求导并代入式(22),可得
| $ \dot{V}=\boldsymbol{E}_f \cdot \dot{\boldsymbol{E}}_f=\boldsymbol{E}_f \cdot\left(-c_1(t) \boldsymbol{E}_f\right)=-c_1(t) \cdot \boldsymbol{E}_f^2 $ | (27) |
式中,c1>0,因此可以得到
快状态理想动态响应
| $ \dot{x}_{1 d}=\operatorname{diag}\left(\omega_p, \omega_q, \omega_r\right) \cdot\left(\boldsymbol{x}_{1 d}-\boldsymbol{x}_1\right) $ | (28) |
式中: 根据实际仿真需要,选取回路带宽ωp=ωq=ωr=15.0 rad/s, 快状态的指令信号向量 x1d由外回路控制器产生。
3.1.3 较快回路控制律设计较快状态控制回路是快状态控制律的外回路。以前述方式对式(11)进行整理,可得
| $ \left[\begin{array}{c} \dot{\theta} \\ \dot{\phi} \\ \dot{\psi} \end{array}\right]=f_{s f}\left(\boldsymbol{x}_{s f}\right)+\boldsymbol{g}_{s f}\left(\boldsymbol{x}_{s f}\right)\left[\begin{array}{c} p \\ q \\ r \end{array}\right] $ | (29) |
式中,
| $ \boldsymbol{e}_{s f}=\boldsymbol{x}_2-\boldsymbol{x}_{2 d} $ | (30) |
如前文定义:
| $ \begin{array}{c} \boldsymbol{E}_{s f}=\left\|\boldsymbol{e}_{s f}\right\|_w^2= \\ k_\theta\left(\theta-\theta_d\right)^2+k_\phi\left(\phi-\phi_d\right)^2+k_\psi\left(\psi-\psi_d\right)^2 \end{array} $ | (31) |
由于纵向运动中的控制变量为迎角和轨迹角,因此较快回路中,不对俯仰角进行干预,重点针对飞机的横航向运动,控制滚转角和偏航角,在上述误差偏离方程中,取
| $ \dot{E}_{s f}+c_2(t) \boldsymbol{E}_{s f}=0 $ | (32) |
| $ \begin{array}{c} \dot{\boldsymbol{E}}_{s f}=2 \times \boldsymbol{e}_{s f}^{\mathrm{T}} \times \operatorname{diag}\left(k_\theta, k_\phi, k_\psi\right) \times \\ \left(f_{s f}\left(\boldsymbol{x}_{s f}\right)+\boldsymbol{g}_{s f}\left(\boldsymbol{x}_{s f}\right) \cdot U-\dot{\boldsymbol{x}}_{2 d}\right) \end{array} $ | (33) |
式中U为中间控制量。然后代入式(32)可得到约束方程的代数形式:
| $ \boldsymbol{A}_2\left(x_1, x_2, t\right) \cdot U=\boldsymbol{B}_2\left(\boldsymbol{x}_1, \boldsymbol{x}_2, t\right) $ | (34) |
其中:
| $ \begin{array}{c} \boldsymbol{A}_2=2 \boldsymbol{e}_{s f}^{\mathrm{T}} \operatorname{diag}\left(k_\theta, k_\phi, k_\psi\right) \cdot \boldsymbol{g}_{s f}\left(\boldsymbol{x}_{s f}\right) \\ \boldsymbol{B}_2=-2 \boldsymbol{e}_{s f}^{\mathrm{T}} \operatorname{diag}\left(k_\theta, k_\phi, k_\psi\right)\left(f_{s f}-\dot{\boldsymbol{x}}_{2 d}\right)- \\ c_2\left[k_\theta, k_\phi, k_\psi\right] \boldsymbol{e}_{s f}^2 \end{array} $ |
通过求逆,即可解得所需的中间控制量U。
| $ U=\boldsymbol{A}_2^{+}\left(\boldsymbol{x}_1, \boldsymbol{x}_2, t\right) \cdot \boldsymbol{B}_2\left(\boldsymbol{x}_1, \boldsymbol{x}_2, t\right) $ | (35) |
同理可得,较快回路系统也是渐近稳定的。则理想动态响应为
| $ \dot{x}_{2 d}=\operatorname{diag}\left(\omega_\theta, \omega_{\varphi}, \omega_\psi\right) \cdot\left(\boldsymbol{x}_{2 d}-\boldsymbol{x}_2\right) $ | (36) |
回路带宽ωθ=ωϕ=ωψ=5.0 rad/s;较快状态的指令信号向量x2d根据需要指定期望的输入。
3.1.4 较慢状态回路设计较慢状态控制回路是快状态控制律的外回路。较慢状态回路主要控制飞机的α,β和μ,同样,通过将角速度量分离为输入变量,即得到仿射结构的较慢状态回路表达式:
| $ \left[\begin{array}{c} \dot{\alpha} \\ \dot{\beta} \\ \dot{\mu} \end{array}\right]=f_{s s}\left(\boldsymbol{x}_{s s}\right)+\boldsymbol{g}_{s s}\left(\boldsymbol{x}_{s s}\right)\left[\begin{array}{c} p_c \\ q_c \\ r_c \end{array}\right]+\boldsymbol{g}_{s s^{\prime}}\left(\boldsymbol{x}_{s s}\right)\left[\begin{array}{c} C_{l \delta} \\ C_{M \delta} \\ C_{N \delta} \end{array}\right] $ | (37) |
式中
| $ \boldsymbol{e}_{s s}=\boldsymbol{x}_3-\boldsymbol{x}_{3 d} $ | (38) |
同理,定义加权误差范数向量为
| $ \begin{array}{c} \boldsymbol{E}_{s s}=\left\|\boldsymbol{e}_{s s}\right\|_w^2= \\ k_\alpha\left(\alpha-\alpha_d\right)^2+k_\alpha\left(\beta-\beta_d\right)^2+k_\alpha\left(\mu-\mu_d\right)^2 \end{array} $ | (39) |
在较慢回路中,主要控制飞机的迎角,不针对侧滑角和航迹滚转角,取kβ = kμ=0,kα为正常数,则较慢回路的一阶约束动态可以表示为
| $ \dot{\boldsymbol{E}}_{s s}+c_3(t) \boldsymbol{E}_{s s}=0 $ | (40) |
式中c3为能使得该约束动态一致渐进稳定的正常数,且
| $ \begin{array}{c} \dot{\boldsymbol{E}}_{s s}=2 \times \boldsymbol{e}_{s s}^{\mathrm{T}} \times \operatorname{diag}\left(k_\alpha, k_\beta, k_\mu\right) \times \\ \left(f_{s s}\left(\boldsymbol{x}_{s s}\right)+\boldsymbol{g}_{s s}\left(\boldsymbol{x}_{s s}\right) \cdot U-\dot{\boldsymbol{x}}_{3 d}\right) \end{array} $ | (41) |
期望输入变量
| $ \boldsymbol{A}_3\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) \cdot \widetilde{U}=\boldsymbol{B}_3\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) $ | (42) |
其中:
| $ \begin{array}{c} \boldsymbol{A}_3=2 \boldsymbol{e}_{s s}^{\mathrm{T}} \operatorname{diag}\left(k_\alpha, k_\beta, k_\mu\right) \cdot \boldsymbol{g}_{s s}\left(\boldsymbol{x}_{s s}\right) \\ \boldsymbol{B}_3=-2 \boldsymbol{e}_{s s}^{\mathrm{T}} \operatorname{diag}\left(k_\alpha, k_\beta, k_\mu\right)\left(f_{s s}-\dot{\boldsymbol{x}}_{3 d}\right)- \\ c_3\left[k_\alpha, k_\beta, k_\mu\right] \boldsymbol{e}_{s s}^2 \end{array} $ |
若忽略快状态回路的动态响应过程,通过对式(42)求逆可得
| $ \widetilde{U}=\boldsymbol{A}_3^{+}\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) \cdot \boldsymbol{B}_3\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) $ | (43) |
满足式(40)所得到的控制律式(43)可以使系统渐进稳定。
| $ \dot{\boldsymbol{x}}_{3 d}=\operatorname{diag}\left(\omega_\alpha, \omega_\beta, \omega_\mu\right) \cdot\left(\boldsymbol{x}_{3 d}-\boldsymbol{x}_3\right) $ | (44) |
式中,ωα=ωβ=ωμ=2.0 rad/s。
至此,由于较快回路与较慢回路均是快回路的外环,且是并联关系,因此令传递给内环快回路的期望信号向量
较慢状态指令向量x3d根据需要给定期望输入。
3.1.5 慢状态回路设计慢状态回路是轨迹控制回路,目标状态向量为 x4,控制输出为发动机推力T和虚拟控制量CLδ,CNδ,分别如下:
| $ C_{L \delta}=c_{L_{\delta_{\mathrm{e}}}} \delta_{\mathrm{e}}+c_{L_{\delta_{\mathrm{f}}}} \delta_{\mathrm{f}} $ | (45) |
| $ C_{N \delta}=c_{N_{\delta_{\mathrm{a}}}} \delta_{\mathrm{a}}+c_{N_{\delta_{\mathrm{r}}}} \delta_{\mathrm{r}} $ | (46) |
则慢状态回路表达式为
| $ \left[\begin{array}{c} \dot{V} \\ \dot{\gamma} \\ \dot{\chi} \end{array}\right]=f_s\left(\boldsymbol{x}_s\right)+\boldsymbol{g}_s\left(\boldsymbol{x}_s\right)\left[\begin{array}{c} T \\ C_{L \delta} \\ C_{N \delta} \end{array}\right] $ | (47) |
式中,
| $ \boldsymbol{e}_s=\boldsymbol{x}_4-\boldsymbol{x}_{4 d} $ | (48) |
同上,定义加权误差范数向量为
| $ \boldsymbol{E}_s=\left\|\boldsymbol{e}_s\right\|_w^2=k_V\left(V-V_d\right)^2+k_\gamma\left(\gamma-\gamma_d\right)^2+k_\chi\left(\chi-\chi_d\right)^2 $ | (49) |
式中,kV, kγ, kχ为正常数,基于慢回路控制的动态特性,采用二阶约束动态,设为
| $ \ddot{\boldsymbol{E}}_s+c_4(t) \dot{E}_s+c_5(t) \boldsymbol{E}_s=0 $ | (50) |
其中c4, c5为使得该二阶约束动态一致渐进稳定的正常数,且:
| $ \begin{aligned} \dot{\boldsymbol{E}}_s= & 2 \times \boldsymbol{e}_s^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times \\ & \left(f_s\left(\boldsymbol{x}_s\right)+\boldsymbol{g}_s\left(\boldsymbol{x}_s\right) \cdot \delta^*-\dot{\boldsymbol{x}}_{4 d}\right) \\ \ddot{\boldsymbol{E}}_s= & 2 \times \boldsymbol{e}_s^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times \\ & \left\{\dot{f}_s\left(\boldsymbol{x}_s\right)+\dot{\boldsymbol{g}}_s\left(\boldsymbol{x}_s\right) \cdot \delta^*-\ddot{\boldsymbol{x}}_{4 d}\right\}+ \\ & 2\left(f_s\left(\boldsymbol{x}_s\right)+\boldsymbol{g}_s\left(\boldsymbol{x}_s\right) \cdot \delta^*-\dot{\boldsymbol{x}}_{4 d}\right)^{\mathrm{T}} \times \\ & \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times\left(f_s\left(\boldsymbol{x}_s\right)+\right. \\ & \left.\boldsymbol{g}_s\left(\boldsymbol{x}_s\right) \cdot \delta^*-\dot{\boldsymbol{x}}_{4 d}\right) \end{aligned} $ |
式中虚拟控制量
| $ \boldsymbol{A}_4\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) \cdot \delta^*=\boldsymbol{B}_4\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, t\right) $ | (51) |
其中:
| $ \begin{aligned} \boldsymbol{A}_4= & 2 \boldsymbol{e}_s^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times \dot{\boldsymbol{g}}_s\left(\boldsymbol{x}_s\right)+ \\ & 2 c_4 \times \boldsymbol{e}_s^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \cdot \boldsymbol{g}_s\left(\boldsymbol{x}_s\right) \\ \boldsymbol{B}_4= & -2 \boldsymbol{e}_s^{\mathrm{T}} \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right)\left(\dot{f}_s\left(\boldsymbol{x}_s\right)-\ddot{\boldsymbol{x}}_{4 d}\right)- \\ & 2\left(f_s\left(\boldsymbol{x}_s\right)-\dot{\boldsymbol{x}}_{4 d}\right)^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times \\ & \left(f_s\left(\boldsymbol{x}_s\right)-\dot{\boldsymbol{x}}_{4 d}\right)-2 c_4 \times \boldsymbol{e}_s^{\mathrm{T}} \times \operatorname{diag}\left(k_V, k_\gamma, k_\chi\right) \times \\ & \left(f_s\left(\boldsymbol{x}_s\right)-\dot{\boldsymbol{x}}_{4 d}\right)-c_5\left[k_V, k_\gamma, k_\chi\right] \boldsymbol{e}_s^2 \end{aligned} $ |
通过求逆可得
| $ \delta^*=\boldsymbol{A}_4^{+}\left(\boldsymbol{x}_s, t\right) \cdot \boldsymbol{B}_4\left(\boldsymbol{x}_s, t\right) $ | (52) |
由式(50)给出的相对于慢状态回路的二阶约束动态是一致渐进稳定的,因而由此得出的控制律式(52)可以使系统渐进稳定。
| $ \dot{\boldsymbol{x}}_{4 d}=\operatorname{diag}\left(\omega_V, \omega_\gamma, \omega_\chi\right) \cdot\left(\boldsymbol{x}_{4 d}-\boldsymbol{x}_4\right) $ | (53) |
式中,ωV=ωγ=ωχ=0.4 rad/s。慢回路的期望状态向量x4d根据需要人为给定。
3.2 控制分配算法本文所设计的直接升力控制系统属于多输入-多输出系统控制问题,因此采用控制分配算法进行操纵面控制量的有效分配,纵向直接升力控制方式需要直接升力操纵面和常规配平舵面的协调偏转,本文选用后缘襟翼与升降舵的搭配方式产生直接升力。在此环节中,控制输入为动态逆环节控制律解算生成cMδ和cLδ期望值,输出即为对应操纵面的控制量。采用加权伪逆控制分配算法,以求解襟翼和升降舵分别所需的偏转量,具有可主动调节分配的优点,可以根据执行器操纵行程及速率限制进行优化定制,使操纵面协调配合,同时选取一个最优函数作为衡量指标,保证实现期望指令的同时满足函数指标最优化。纵向控制分配律表示为:
| $ \boldsymbol{u}_{\text {lon }}=\boldsymbol{P}_{\text {lon }} \cdot \boldsymbol{\delta}_{\text {lon }} $ | (54) |
| $ \boldsymbol{P}_{\text {lon }}=\boldsymbol{W}_{\text {lon }}^{-1} \boldsymbol{B}^{\mathrm{T}}\left[\boldsymbol{B} \boldsymbol{W}_{\text {lon }}^{-1} \boldsymbol{B}^{\mathrm{T}}\right]^{-1} $ | (55) |
式中:ulon为包含襟翼和升降舵的控制量的矩阵; δlon为包含纵向虚拟控制量,即CLδ,CNδ的矩阵; Plon为加权伪逆控制矩阵; Wlon为纵向权值系数矩阵; B为飞机控制效能矩阵。
横航向运动的核心是调节航向时保持滚转角稳定,也需要副翼和方向舵同时参与,与纵向类似,控制分配环节输入为动态逆环节生成的clδ和cNδ的期望值,输出即为方向舵和副翼的控制量。同样,通过设置合适的加权系数以实现控制目标。与纵向类似,横航向控制分配律表示为:
| $ \boldsymbol{u}_{\text {lat }}=\boldsymbol{P}_{\text {lat }} \cdot \boldsymbol{\delta}_{\text {lat }} $ | (56) |
| $ \boldsymbol{P}_{\text {lat }}=\boldsymbol{W}_{\text {lat }}^{-1} \boldsymbol{B}^{\mathrm{T}}\left[\boldsymbol{B} \boldsymbol{W}_{\text {lat }}^{-1} \boldsymbol{B}^{\mathrm{T}}\right]^{-1} $ | (57) |
采用动态逆控制与控制分配方法结合的两层级联式控制架构,这样设计的好处是两种方法有机结合又相对独立,既可以充分发挥每种控制方法的潜能,又可以使后续控制律改进设计(如选取其他的直接升力操纵面搭配方案)更加方便。未来,还可将多种直接升力控制方案集成到控制分配环节中,在首选模式发生舵面故障而失效时,控制分配算法能自动选择其余可用的舵面组合方案,使整体的控制律不会失效,提升系统的余度可靠性,保证着舰控制的安全。
4 仿真分析本文根据前文所设计的级联式非线性动态逆与控制分配结合的直接升力控制律,以F-18舰载机为控制对象,在六自由度非线性方程上搭建Simulink模型,并进行仿真分析。
4.1 纵向轨迹控制仿真舰载机下滑过程中的平衡初始状态,迎角为11°,轨迹角为-3°,速度为69.6 m/s。然后设置轨迹角操纵指令,在2 s时给定-4°的期望轨迹角指令,并在6 s时重新给定-3°的轨迹角指令,以此模拟飞行员进行轨迹高度调整时的操作,在此过程中,迎角指令始终给定11°,速度指令给定69.6 m/s,以保持着舰迎角和速度的稳定。依据舵面偏转速率和幅值限制,取
从图 4中可以看出,在动态逆控制环节采用常规方法时,在给入指令后,轨迹角需要2 s多才能达到期望值,虽然没有超调和稳态误差,但对下滑着舰阶段,跟踪速度不是很理想。而采用本文所设计的预设性能动态逆控制器,轨迹角的跟踪速度很快,约1 s左右就能达到期望值,且几乎没有超调,控制响应的快速性和准确性都比较好,后重新回到理想下滑道的-3°的期望轨迹角同样响应效果很好。

|
图 4 轨迹角跟踪和迎角跟踪曲线 Fig. 4 γ captures and α holds |
与此同时,由于采用了直接升力的控制方式,飞机的迎角几乎没有发生明显变化,在轨迹调整的过程中出现了略微波动,波动值仅0.1°上下,可以认为在控制过程中迎角没有受到影响,实现了良好的纵向解耦效果。通过对比可以看出,采用了预设性能动态逆控制器,迎角波动后恢复稳定耗时更短,缩短了50%,虽然迎角的波动峰值略高于常规方法约15%,相差无几,可以忽略不计。
通过图 5的俯仰角和角速率曲线对比可以看出,本文所设计的控制系统响应效率很高。

|
图 5 俯仰角及角速率变化曲线 Fig. 5 Pitch angle and angular rate |
如图 6所示为襟翼和升降舵偏转曲线,在给入轨迹角指令后,襟翼从配平位置回收,升力系数减小,升力减小,高度降低,同时升降舵也跟随收舵,调整飞机俯仰姿态,使飞机俯仰角跟随速度矢量变化,从而保持迎角始终稳定在期望值。

|
图 6 升降舵和襟翼控制偏转量 Fig. 6 Deflection of elevator and flap |
如图 7所示是油门开度与飞机速度变化曲线,在动态逆自动油门控制律作用下,飞行速度虽有小幅波动,波动幅度不到1 m/s,可以认为基本处于动态稳定的状态。

|
图 7 油门开度与飞行速度跟踪曲线变化 Fig. 7 Throttle and air speed curve |
如图 8所示是采用常规控制而非直接力的方式进行轨迹控制的角度状态响应,可以看出轨迹角从0°~-3°的过渡过程中,最初有一个小幅的反向变化,即“负调”现象,达到期望值所用时间也较长。且在轨迹调节时,迎角和姿态角都有大幅度波动,俯仰姿态不稳定。相比之下,采用直接升力的控制方式调节轨迹,无“负调”,跟踪响应快,控制精度高,且最重要的是能够实现姿态和轨迹控制的解耦,保持迎角稳定。

|
图 8 非直接升力控制方式轨迹调节响应曲线 Fig. 8 γ captures and α holds without DLC |
横航向仿真时,迎角、速度等指令与纵向控制仿真时相同,轨迹角指令为常值-3°,初始滚转角和偏航角均为0。在2 s时给定10°的期望偏航角指令,并在6 s时重新给定0°偏航角指令,以此模拟飞行员进行对中修正时的操纵,在此过程中,滚转角指令始终为0,以保持滚转姿态稳定并削弱对纵向运动的耦合扰动,如图 9所示。

|
图 9 偏航角跟踪和滚转角保持曲线 Fig. 9 ψ captures and ϕ holds |
从图 9中可以看出,在动态逆控制环节采用常规方法时,在给入指令后,偏航角需要2 s多才能达到期望值,虽然没有超调和稳态误差,但跟踪速度并不是很理想。而采用本文所设计的预设性能动态逆控制器,偏航角跟踪速度很快,约1 s左右就能达到期望值,且几乎没有超调,在此过程中,控制初期伴有同向的滚转运动,峰值约为6°滚转角,偏航角达到指令输入后,滚转角在姿态稳定控制律的作用下消除,重新恢复水平状态,以尽可能减少由滚转引起的纵向运动耦合干扰。6 s时模拟对中偏差修正后重新调回对正中心线方向,给入0°偏航角指令,此时系统响应同样快速。虽然采用常规动态逆控制在调节的过程中,滚转角的变化更小,但由于此时主要目标控制量为偏航角,因此偏航角的快速跟踪是更重要的性能,也体现出预设性能动态逆控制对主控量目标性能优先满足的设计优点。
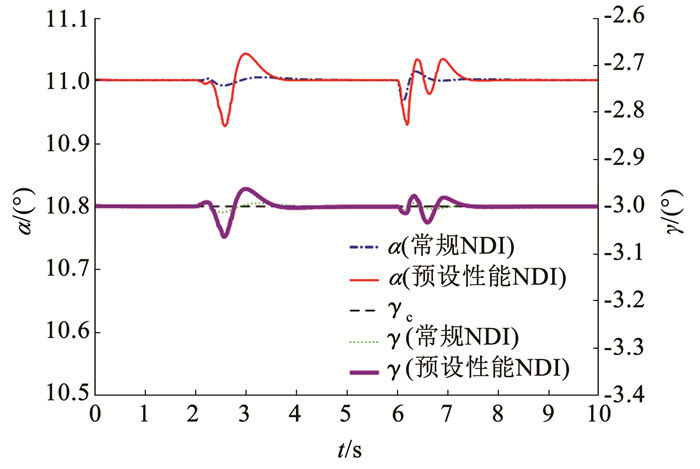
如图 10所示,进行横航向对中操纵的时候,由于直接升力控制方式的作用,两种动态逆控制方法下纵向运动所受的干扰都很小,轨迹角和迎角的波动幅度都在0.1°以内,几乎没有受到影响,下滑道保持稳定,没有出现高度损失,迎角和飞行速度也基本保持稳定。说明采用非线性动态逆方法设计的直接升力控制器对横、纵向运动间的解耦效果良好。
|
图 10 轨迹角、迎角变化曲线 Fig. 10 γ and α holds |
如图 11所示是油门开度与飞行速度变化曲线,飞行速度虽有小幅度波动,可以认为基本处于动态稳定的状态。
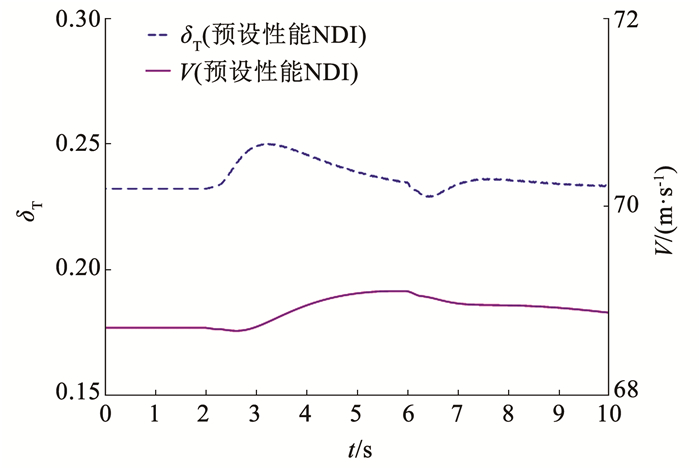
|
图 11 油门开度和空速变化曲线 Fig. 11 Throttle and air speed curve |
如图 12所示是副翼和方向舵偏转曲线,在给入偏航角指令后,副翼和方向舵协调配合偏转,实现横航向对中控制。

|
图 12 副翼与方向舵控制偏转量 Fig. 12 Deflection of aileron and rudder |
1) 对轨迹回路的精确控制难度较大,采用预设性能非线性动态逆方法设计直接升力控制律,可以发挥动态逆方法本身的精确性以及直接升力控制对于姿态和轨迹控制的解耦,提出预设性能的动态逆设计,可以人为突出主控制变量,并且提升跟踪性能,使飞行员的操纵指令得以被有效且迅速的跟踪,仿真效果良好。
2)“魔毯”着舰控制模态不仅局限于纵向控制解耦,发挥非线性动态逆方法对横纵向运动的解耦特性,选取对应状态回路设计了横航向控制器,在综合控制架构下,实现了在对中修正时保证纵向轨迹不掉高且迎角和滚转角都稳定,仿真效果良好。
3) 由于采用直接升力的控制方式,涉及多操纵面的协调控制,采用控制分配方法可以更合理、方便地搭配舵面组合,更充分地发挥舵面效能。
4) 采用两层级联式的控制架构,将动态逆控制与控制分配的方法进行结合,通过虚拟控制量将两层控制结构衔接起来,在后续设计提供便利,如需采用新的直接升力舵面搭配方式,无需对整个控制器进行重新设计,只需要对控制分配部分进行修改,即可适配舵面重新组合的方案。未来,还可在控制分配环节中集成多种舵面组合方案,或采用模糊控制的思想,在发生舵面故障而失效时,控制分配算法能自动调整,使整体的控制律不会失效,增加控制器余度,提升着舰系统的可靠度和安全性。
| [1] |
段卓毅, 王伟, 耿建中, 等. 舰载机人工进场着舰精确轨迹控制技术[J]. 航空学报, 2019, 40(4): 622328. DUAN Zhuoyi, WANG Wei, GENG Jianzhong, et al. Precision trajectory manual control technologies for carrier-based aircraft approaching and landing[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(4): 622328. DOI:10.7527/S1000-6893.2018.22328 |
| [2] |
DENHAM J W. Project MAGIC CARPET: "Advanced controls and displays for precision carrier landings"[C]//Proceedings of the 54th AIAA Aerospace Sciences Meeting. Reston, Virginia: AIAA, 2016. DOI: 10.2514/6.2016-1770
|
| [3] |
SOUSA P, WELLONS L, COLBY G, et al. Test results of an F/A-18 automatic carrier landing using shipboard relative global positioning system[R]. Patuxent River: Naval Air Warfare Center Aircraft Division, 2003: 1. DOI: 10.1007/s10999-010-9147-x
|
| [4] |
TOMCZYK A. Evaluation of maneuverability of aircraft equipped with direct lift control system[C]//Proceedings of the 23rd Atmospheric Flight Mechanics Conference. Reston, Virginia: AIAA, 1998: 4253. DOI: 10.2514/6.1998-4253
|
| [5] |
HESS R A. Analysis of the aircraft carrier landing task, pilot +augmentation/automation[J]. IFAC-PapersOnLine, 2019, 51(34): 359. DOI:10.1016/j.ifacol.2019.01.017 |
| [6] |
LYKKEN L O, SHAH N M. Direct lift control for improved automatic landing and performance of transport aircraft LOWELL[J]. Journal of Aircraft, 1972, 9(5): 325. DOI:10.2514/3.58988 |
| [7] |
杨向忠, 章卫国, 段富海, 等. 动态逆与模糊控制方法在飞控系统中的应用[J]. 西北工业大学学报, 1998, 16(4): 527. YANG Xiangzhong, ZHANG Weiguo, DUAN Fuhai, et al. On making nonlinear dynamic inversion control effective with nonlinear input known only approximately[J]. Journal of Northwestern Polytechnical University, 1998, 16(4): 527. DOI:10.1007/BF02946502 |
| [8] |
徐骋, 强文义, 王长青. 基于逆动力学的飞行器直接力控制系统及其稳定性分析[J]. 宇航学报, 2008, 29(4): 1308. XU Cheng, QIANG Wenyi, WANG Changqing. The direct force flight control systems based on the inversed dynamics and their stability analysis[J]. Journal of Astronautics, 2008, 29(4): 1308. DOI:10.3873/j.issn.1000-1328.2008.04.040 |
| [9] |
王亚龙, 吴欣龙, 郑浩. 菱形翼布局无人机自抗扰直接升力着陆控制[J]. 测控技术, 2017, 36(7): 70. WANG Yalong, WU Xinlong, ZHENG Hao. Landing strategy of diamond-wing unmanned aerial vehicle based on direct lift control[J]. Measurement & Control Technology, 2017, 36(7): 70. DOI:10.19708/j.ckjs.2017.07.017 |
| [10] |
职晓波. 基于多变量解耦的直接升力控制应用与仿真[D]. 西安: 西北工业大学, 2007 ZHI Xiaobo. Application and simulation of direct lift control based on multivariable decoupling[D]. Xi'an: Northwestern Polytechnical University, 2007. DOI: 10.7666/d.y1033903 |
| [11] |
李明, 张汝麟. 我国飞机主动控制技术的开发与验证[C]//新世纪力学研讨会——钱学森技术科学思想的回顾与展望论文集. 北京: 中国力学学会, 2001
|
| [12] |
朱玉莲, 甄子洋, 季雨璇, 等. 舰载飞机着舰直接力控制方法[J]. 电光与控制, 2020, 27(11): 1. ZHU Yulian, ZHEN Ziyang, JI Yuxuan, et al. Direct lift control for auto-landing of shipboard aircraft[J]. Electronics Optics & Control, 2020, 27(11): 1. DOI:10.3969/j.issn.1671-637X.2020.11.001 |
| [13] |
罗飞, 张军红, 王博, 等. 基于直接力的着舰航迹动态逆控制仿真研究[J]. 电光与控制, 2021, 28(9): 103. LUO Fei, ZHANG Junhong, WANG Bo, et al. Simulation research on direct-lift-control based NDI control of landing trajectory based on DLC[J]. Electronics Optics & Control, 2021, 28(9): 103. DOI:10.3969/j.issn.1671-637X.2021.09.022 |
| [14] |
罗飞, 张军红, 王博, 等. 基于非线性动态逆的舰载机直接升力航迹控制[J]. 飞行力学, 2021, 39(1): 40. LUO Fei, ZHANG Junhong, WANG Bo, et al. Direct lift trajectory control for carrier aircraft based on NDI[J]. Flight Dynamics, 2021, 39(1): 40. DOI:10.13645/j.cnki.f.d.20201113.010 |
| [15] |
GREEN B E, FINDLAY D. CFD analysis of the F/A-18E super hornet during aircraft-carrier landing high-lift aerodynamic conditions[C]//Proceedings of the 54th AIAA Aerospace Sciences Meeting. Reston, Virginia: AIAA, 2016: 1768. DOI: 10.2514/6.2016-1768
|
| [16] |
MCNEILL W E, GERDES R M, INNIS R C, ET AL. A flight study of the use of direct-lift-control flaps to improve station keeping during in-flight refueling: NASA-TM-X-2936[P]. 1973-10-01
|
| [17] |
DE SALVO M, HEATHCOTE D, SMITH M J, et al. Direct lift control using distributed aerodynamic bleed[C]//AIAA Scitech 2019 Forum. Reston, Virginia: AIAA, 2019: 0591. DOI: 10.2514/6.2019-0591
|
| [18] |
MERAT R. Study of a direct lift control system based on the A380 aircraft[C]//Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit. Reston, Virginia: AIAA, 2008: 1432. DOI: 10.2514/6.2008-1432
|
| [19] |
JATEGAONKAR R V. Identification of aerodynamic effectiveness and interference effects of direct-lift-control flaps from flight data[C]//Proceedings of the 30th Aerospace Sciences Meeting and Exhibit. Reston, Virginia: AIAA, 1992: 171. DOI: 10.2514/6.1992-171
|
| [20] |
吴文海, 汪节, 高丽, 等. MAGIC CARPET着舰技术分析[J]. 系统工程与电子技术, 2018, 40(9): 2079. WU Wenhai, WANG Jie, GAO Li, et al. Analysis on MAGIC CARPET carrier landing technology[J]. Systems Engineering and Electronics, 2018, 40(9): 2079. DOI:10.3969/j.issn.1001-506X.2018.09.26 |
| [21] |
梁洪瑜, 张勇, 徐鸣. 基于模糊动态逆的飞机直接升力控制[J]. 海军航空工程学院学报, 2019, 34(3): 290. LIANG Hongyu, ZHANG Yong, XU Ming. Direct lift control of aircraft based on fuzzy dynamic inverse[J]. Journal of Naval Aeronautical and Astronautical University, 2019, 34(3): 290. DOI:10.7682/j.issn.1673-1522.2019.03.006 |
| [22] |
DI FRANCESCO G, D'AMATO E, MATTEI M. INDI control with direct lift for a tilt rotor UAV[J]. IFAC-PapersOnLine, 2015, 48(9): 156. DOI:10.1016/j.ifacol.2015.08.076 |
| [23] |
史静平, 屈晓波. 多操纵面飞机控制分配理论与应用[M]. 北京: 国防工业出版社, 2017. SHI Jingping, QU Xiaobo. Control allocation theory and its application for aircraft with multiple control surfaces[M]. Beijing: National Defense Industry Press, 2017. |
| [24] |
申晓明, 吕新波, 黄振威. 多操纵面飞机控制分配方法研究[J]. 航空科学技术, 2016, 27(9): 8. SHEN Xiaoming, LV Xinbo, HUANG Zhenwei. Research on the control allocation for aircrafts with multi-control surfaces[J]. Aeronautical Science & Technology, 2016, 27(9): 8. |
 2023, Vol. 55
2023, Vol. 55


