2. 西安建筑科技大学 理学院, 西安 710055
2. School of Mechatronic Science, Xi'an University of Architecture and Technology, Xi'an 710055, China
以电能为核心的能源市场朝着绿色低碳化、协同多元化稳步发展,深度融合“云大物移智”等新兴技术和新能源技术的新一轮能源革命正助推“双碳”愿景的高质量实现,其中用户侧的用电提质增效是关键环节[1-3]。电力用户作为电力市场体系中重要的有机单元,其用电能效评估是推动自身参与虚拟电厂、移峰填谷、需求响应等新兴业务的必要条件,也是新型电力系统建设中优化电力产业结构、制定差异化节电策略的重要基础。因此,开展以电力用户能效状态评估为核心的智能化数据服务具有重要的现实意义和工程价值。
目前电力用户能效评估分析等常用算法仍以集中计算的方式为主[4]。随着配电系统中海量终端互联化、设备数据高维化和网架层次复杂化的发展,传统依靠单一的云主站信息处理模式存在着数据传输高时延、高拥塞、信息远离设备端,且排队处理缓慢等弊端。而边缘计算技术将计算力部署在近配电终端数据源侧,在控制执行单元侧进行数据分析、系统运行状态态势感知[5-6],并做出自主快速决策,可有效弥补云计算的不足,成为近年来电力能源领域的热点研究。Khan等[7]面向家庭能源门户设计的站点可以用于实施任何特定的需求侧服务。Wei等[8]将边缘计算引入到工厂能源管理场景中以降低电力成本。目前边缘计算技术已在能源优化调度、负荷需求预测、服务分发策略等高级应用场景展开深入实践,边缘智能化的发展为用户的用电能效分析提供了有力支撑。
目前电力用户能效评估方法主要有模糊评价法、数据包络分析法、灰色关联分析法等。吴剑飞等[9]通过对状态因素集、评判集、指标权重分别进行分析,建立模糊综合评估模型,然而评价过程中隶属度函数的选择易受专家经验影响,评估结果有较强的主观偏好性。李金良等[10]提出基于交叉超效率的CCR模型,可有效提高评估方法的客观性,但评估过程较为复杂。罗志坤等[11]将灰色关联分析法与层次分析法相结合进行能效评估,该方法虽然适用性较强,但方法中指标权重的确定采用主观赋权法,所得出的权重客观性不足,进而会降低评估方法的精确性。Kong等[12]基于熵权法与逼近理想解排序法(technique for order preference by similarity to an ideal solution,TOPSIS)计算家庭用户的各时段能效评分,采用客观赋权法能充分利用数据的本质特征,保证赋权的客观性,但由于未考虑到TOPSIS在计算相对优劣性时欧式判据存在的缺陷,对于评估的准确性会产生影响。Zhao等[13]结合灰色关联度改进传统TOPSIS方法,弥补距离判据的不足,但忽视了实际用户数量动态变化时,评估结果会存在不确定性。
基于上述分析,本文提出一种在边缘系统架构下实时动态评估电力用户能效的方法。在研究用户边缘计算能效评估框架的基础上,依据“压力-状态-响应”概念模型构建多维动态能效指标集合,采用相关性定权法(criteria importance though intercrieria correlation, CRITIC),从差异性和冲突性两种角度,更科学、合理的衡量指标蕴含的信息量,并针对TOPSIS在计算过程中存在的逆序现象和距离测度不合理的问题,通过构造绝对理想点和改用灰色关联度判据,有针对性地进行改进,弥补传统方法在判断评估对象相对优劣性上的不足。同时,考虑到边缘节点存储资源的有限性以及数据信息间存在的冗余性,进一步融合指标的重要性、独立性与均衡性三重抽象属性,引入合作博弈论思想优选出精简指标,可减小计算量以及对边缘侧内存的占用。通过试验分析,验证了本文所提方法在评估的可靠性和准确性上具有较大的优势。
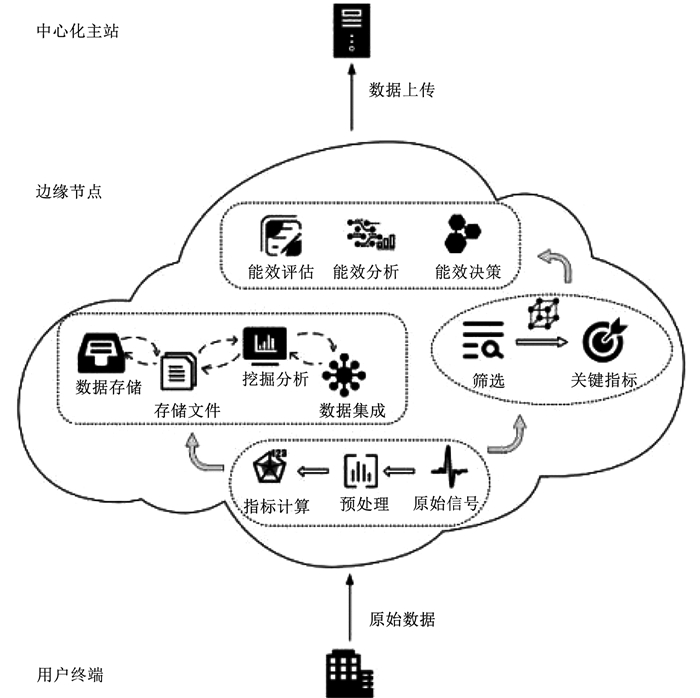
1 边缘能效评估方法本文在边缘计算模式下所构建的用户侧能效评估框架如图 1所示,该框架分为用户终端、边缘节点和中心化主站。用户终端位于框架的最底层,主要包括设备、仪表等,其通过多种通信方式获取并传输采集到的能耗数据信息。边缘节点汇集接收到的用户终端数据后,结合边缘计算模型对缓存在本地的数据进行就地处理和分析,实时计算用户的能效状况,仅将处理后的数据和计算结果发送至中心化主站。顶层的中心化主站负责对所有上传的用户信息进行管理,实现更深层次的分析与决策。
|
图 1 边缘能效评估框架 Fig. 1 Edge energy efficiency evaluation framework |
在该模式框架下,部署开发的边缘节点软、硬件系统架构如图 2所示。软件系统主要包括系统运行环境、协议解析、存储文件以及边缘计算与服务。在Linux Real-Time OS系统环境下,节点支持Labview、MATLAB等语言,开发的边缘感知的数据采集模块可实现信息收集,设计了适用于用户能效数据的存储文件,包括传感数据、指标数值、计算结果等信息的分类存储,同时也能为用户的能效数据分析提供算法模型与决策服务。硬件模块主要包括主控单元、驱动单元、处理单元、存储单元、数据采集接口、内置外设与通信单元。节点采用NI公司的FPGA Kintex-7芯片,配有可重配置的工业级I/O模块,支持WiFi、ZigBee、RJ-45以太网等无线通信形式,也可通过RS232、RS485、CAN总线、USB等与传感器进行有线连接,传感器接入后的采集数据可存储于板载内存或SD卡。

|
图 2 边缘节点软、硬件架构 Fig. 2 Edge node hardware and software architecture |
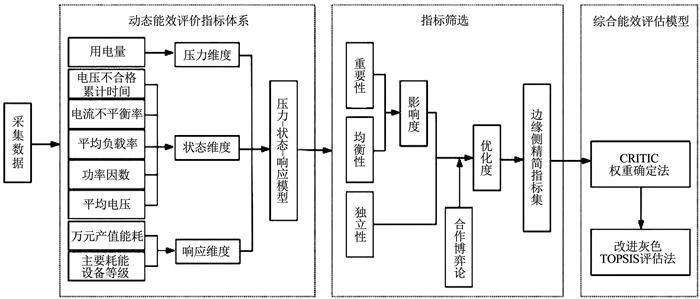
边缘节点作为整个系统框架的核心,其评估方法的逻辑框图如图 3所示,主要包括:
|
图 3 评估方法的逻辑框图 Fig. 3 Logic diagram of evaluation method |
1) 能耗数据预处理。即将采集数据加工计算成实时的指标数值,并根据“压力-状态-响应”概念模型构建电力用户能效评估指标体系,以综合评测用户能效水平。
2) 指标属性特征融合优化。即在构建指标体系的基础上,为优化指标集合、减少边缘存储压力,以影响度、优化度融合各项指标的属性特征——重要性、独立性、均衡性,同时采用合作博弈论避免融合过程中的决策偏好,根据融合后的量化结果筛选指标。
3) 能效评估。即通过CRITIC权重确定方法分配评估指标权重,并由改进灰色TOPSIS评估法对评估对象进行排序,实现不同电力用户在边缘场景下的能效状态评价。
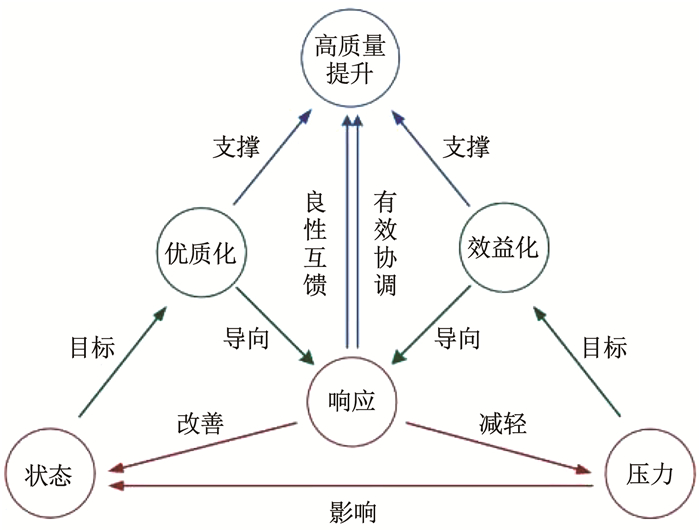
2 构建电力用户能效评估指标体系 2.1 “压力-状态-响应”模型“压力-状态-响应”(Pressure-State-Response, PSR)模型能够清晰阐释系统中因果关系的持续性变化,并通过维度间的动态逻辑关系构建评价指标,在土地集约利用、生态系统健康等评价研究中得到广泛应用[14-15]。在电力领域,可认为外部用电环境与生产活动会对用户施加压力,进而导致用户的用电能效状态发生变化,用户通过改变现有的用电行为方式,可以有针对性地进行节能响应,其模型结构如图 4所示。
|
图 4 用户能效的PSR概念模型 Fig. 4 PSR conceptual model of user energy efficiency |
本文从用户能效的PSR概念模型出发,依据GBT 31960.1—2015《电力能效监测系统技术规范》、GB/T 36714—2018《用能单位能效对标指南》以及国内、外对于电力用户能效评估的现有研究成果,并遵循指标数据的客观性、科学性、可获取性等原则,对用户能效状态评估的相关参数指标进行初步整理和筛选。以用户负荷、电量、电压、电流等运行数据及其衍生数据为基础,选取8项最能反映用户能效水平的指标,构建能效评估指标集合,以实现在边缘节点评测在网电力用户的能效情况,指标体系见表 1。
| 表 1 能效评估指标体系 Tab. 1 Energy efficiency evaluation index system |
实际生产中设备的运行与维护交替进行,生产任务的进度能够对用户能效施加一定的压力,用电量间接反映了生产进程,因此压力指标可用用电量来表示。优质可靠的电能质量可以提高用户电能利用效率并减少经济损失,从该角度出发选取电流不平衡率、平均电压等5项能够反映用户能效状况的指标作为状态指标。用户通过增长产值能耗、使用低功耗设备等调控措施,积极提升自身能效,体现了用户对实现健康用电目标的响应,因此万元产值能耗和主要耗能设备等级可视为响应指标。
2.2 基于指标抽象属性的融合筛选随着能效状态监测趋于全面化和精细化,大量冗余性较高的数据占用了较多的存储资源,导致海量数据对边缘设备存储资源的需求越来越严重,有必要对信息进行进一步的精简与筛选。本文紧密结合指标体系的动态逻辑关系,从指标自身的属性特征出发,对指标的“重要性”、“均衡性”、“独立性”三重属性特征进行量化,以重要性反映指标的信息价值,以均衡性选择最具代表性的指标诠释评价对象最多的属性,以独立性剔除关联程度高的指标,降低指标集维数。定义影响度、优化度对指标的抽象属性进行融合,并基于合作博弈论优化各指标的筛选排序,进而为边缘侧的数据去冗余提供依据。
2.2.1 指标重要性指标重要性表征的是指标对能效数据集合的影响程度。利用主成分分析法将指标在各个主成分上的因子载荷的绝对值作为评价指标重要性的依据。
令n为评估对象的数量,m为评估指标个数,能效评估标准化矩阵可表示为Z=[zij]n×m。对标准化后的指标集Z计算其相关系数rij和协方差矩阵Rm×m。再由矩阵论相关理论得到特征根λ与特征向量α,将特征根λ从大到小依次排序,取λj>0的前j个特征根组成因子载荷矩阵bij,则指标重要性的计算公式为
| $ G_{j}=\max \left(\left|\boldsymbol{b}_{i j}\right|\right)=\max \left(\left|\boldsymbol{\alpha}_{i j} \sqrt{\lambda_{j}}\right|\right) $ | (1) |
指标独立性表征的是指标与指标之间的关联程度。斯皮尔曼等级相关系数用于反映变量间的依赖关系。
设定U和V为两个n维的指标变量,其斯皮尔曼相关系数为ρij,将指标xj对各个指标的相关度表示为tj,则指标独立性的计算公式为
| $ D_{j}=\frac{\mathrm{e}^{\left(1-t_{j}\right)}}{\sum\limits_{j=1}^{m} \mathrm{e}^{\left(1-t_{j}\right)}} $ | (2) |
指标均衡性表征的是指标在能效数据集合中的离散情况。熵是对所量测信息的不确定性或无序状态的度量。
集合中第j个评估指标的熵和熵权分别定义为ej、wj,则指标均衡性的计算公式为
| $ S_{j}=\frac{w_{j}}{e_{j}} $ | (3) |
在计算三重指标属性特征的基础上,为消除指标选取上以单一方法定向筛选可能造成的结果“偏向性”,使用影响度、优化度模型融合指标属性得到筛选结果的综合量化值。
首先构造指标影响度融合模型,指标影响度γj反映指标在集合中的受关注程度,以指标重要性Gj与指标均衡性Sj的度量值来表示:
| $ \gamma_{j}=\frac{G_{j} S_{j}}{\sum\limits_{j=1}^{m} G_{j} S_{j}} $ | (4) |
关键指标筛选由指标优化度Oj确定,指标优化度为指标在整体中的综合表现情况,由指标影响度γj和指标独立性Dj的线性组合来表示:
| $ O_{j}=\alpha_{1} \gamma_{j}+\alpha_{2} D_{j} $ | (5) |
式中, 0<α1<1,0<α2<1,α1+α2=1。
在求解融合模型时,为克服决策者对于筛选结果的主观偏好性,采用合作博弈模型实现对偏好系数α1、α2取值的最优分配。具体如下:通过将指标优化度对指标影响度和指标独立性的差值极小化,对偏好系数α1和α2进行优化,由此建立对策模型:
| $ \min \left\|\sum\limits_{q=1}^{2} \alpha_{q} \gamma_{j}^{\mathrm{T}}-D_{j}^{\mathrm{T}}\right\|_{2} $ | (6) |
式中αq为线性偏好系数。
式(6)的实质即为多目标函数规划模型,将其简化为以偏差最小化为目标的问题进行求解后,根据矩阵的微分性质可得其相应的最优化一阶导数条件为
| $ \sum\limits_{q=1}^{2} \alpha_{q} D_{j} \gamma_{j}^{\mathrm{T}}=D_{j} D_{j}^{\mathrm{T}} $ | (7) |
对应的线性方程组形式为
| $ \left[\begin{array}{cc} \gamma_{j} \gamma_{j}^{\mathrm{T}} & \gamma_{j} D_{j}^{\mathrm{T}} \\ \gamma_{j}^{\mathrm{T}} D_{j} & D_{j} D_{j}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{l} \alpha_{1} \\ \alpha_{2} \end{array}\right]=\left[\begin{array}{c} \gamma_{j} \gamma_{j}^{\mathrm{T}} \\ D_{j} D_{j}^{\mathrm{T}} \end{array}\right] $ | (8) |
对式(8)求得的最优系数α1、α2进行归一化处理后得到偏好系数α1*、α2*,最终指标优化度的组合计算式如下:
| $ O_{j}=\alpha_{1}^{*} \gamma_{j}+\alpha_{2}^{*} D_{j} $ | (9) |
根据上述合成规则融合指标多源属性信息,并对指标优化度进行排序,从而为指标决策优选提供依据。
3 评估模型能效评估是边缘计算的核心,在边缘侧对用户的能效数据进行信息融合,可实现用户的就地能效评估。本文采用CRITIC赋权法计算评估指标的权重,并以改进灰色TOPSIS方法对待评估电力用户进行排序,评估结果在考虑到指标数据的客观信息的基础上,能够避免逆序问题并且更加合理地计算待评电力用户与绝对理想解的距离测度。
3.1 基于CRITIC赋权的改进灰色TOPSIS评估方法TOPSIS法在决策分析时不特殊要求评估对象的样本量、指标多少以及数据分布[16],通过使用函数曲线计算评估对象与理想解之间的距离来排序。但传统TOPSIS法存在一定的缺陷:1)在样本增减时正、负理想解的变化可能会产生逆序现象[17];2)欧式几何距离存在计算评价对象与正、负理想解的距离测度均相接近的情况[18],这时对于评估对象的优劣较难界定,故不能直接用于用户能效分析。近年来,已有一些学者将TOPSIS法应用于能效评估方法的研究,但是存在以下几方面的不足:
1) 没有考虑和处理评估对象数量变化时所带来的决策冲突问题,这会对评估结果产生干扰。
2) 通过各种主、客观方法确定各个指标的权重值,不同的赋权方法会对评估结果造成影响。
3) 如何选取相对距离度量方法,用以得到一个合理有效的距离测度。
针对上述分析,本文综合考虑各方面的影响因素,提出基于CRITIC赋权的改进灰色TOPSIS评估方法,实现用户能效评估,该模型具有如下特点:
1) 通过构造绝对理想解,考虑并处理当用户数量动态变化时,理想解会随之变化的问题,其优点是保证最终评估结果不受决策用户变化的干扰,从而具有一定的保序性。
2) 采用CRITIC赋权法从对比性和冲突性两种信息角度计算各评价指标的权重分配,二者的有效结合能够更好地展现各能效指标的重要度。
3) 将灰色关联度代替原有的欧氏距离,进而根据曲线序列的相似性计算距离测度,可以有效反映用户间的内部发展态势,提高评估的准确性。
CRITIC赋权法的具体步骤如下。
Step1 能效指标同向化处理。求得标准化决策矩阵Z为
| $ x_{i j}^{*}= \begin{cases}\frac{x_{i j}-\min\limits _{i} x_{i j}}{\max\limits _{i} x_{i j}-\min\limits _{i} x_{i j}}, & \text { 效益型 } \\ \frac{\max\limits _{i} x_{i j}-x_{i j}}{\max\limits _{i} x_{i j}-\min\limits _{i} x_{i j}}, & \text { 成本型 } \\ 1-\frac{\left|x_{i j}-v_{j}\right|}{\max\limits _{i}\left|x_{i j}-v_{j}\right|}, &\text { 区间型 }\end{cases} $ | (10) |
式中:xij为原始能效指标数值,xij*为正向化后的能效指标值,υj为区间型能效指标的最佳取值范围。
对能效指标进行标准化处理如下:
| $ z_{i j}=\frac{x_{i j}}{\sqrt{\sum\limits_{j=1}^{m} x_{i j}^{* 2}}} $ | (11) |
Step2 基于CRITIC确定指标权重。
1) 计算指标间的相关系数ζij为
| $ \zeta_{i j}=\frac{\sum\limits_{s=1}^{n}\left(z_{s i}-\bar{z}_{i}\right)\left(z_{s j}-\bar{z}_{j}\right)}{\sqrt{\sum\limits_{s=1}^{n}\left(z_{s i}-\bar{z}_{i}\right)^{2} \sum\limits_{s=1}^{n}\left(z_{s j}-\bar{z}_{j}\right)^{2}}} $ | (12) |
式中:zsi、zsj分别为第s个用户的第i个能效指标和第j个能效指标的值,zi、zj分别为n个待评用户中第i个能效指标和第j个能效指标的均值。
2) 定义指标的信息量Cj为
| $ C_{j}=\sigma_{j} \sum\limits_{i=1}^{m}\left(1-\zeta_{i j}\right) $ | (13) |
式中: σj为第j个能效指标的均方差,表示能效指标的对比强度;
3) 确定指标权重Wj为
| $ W_{j}=\frac{C_{j}}{\sum\limits_{j=1}^{m} C_{j}} $ | (14) |
Step3 构建标准化加权评估矩阵:
| $ \boldsymbol{Y}=\left(y_{i j}\right)_{n \times m}=\left(z_{i j} W_{j}\right)_{n \times m} $ | (15) |
式中yij为标准化加权后的能效指标值。
Step4 构造绝对正、负理想解。在用户能效优劣评估中,将最优用户设为评估标准的正理想解,其各评价属性均为所有待评用户中的最优值,将最远离理想用户的待评用户设为评估标准的负理想解,其各评价属性均为所有待评用户中的最劣值。为避免传统TOPSIS方法中用户正、负理想解的选择存在相对性,对各评价属性值进行归一化处理[17],处理后属性值越大越好,因此待评用户的绝对正、负理想解数据序列分别为
| $ \left\{\begin{array}{l} b^{+}=[1, 1, \cdots, 1] \\ b^{-}=[0, 0, \cdots, 0] \end{array}\right. $ | (16) |
当确定用户的绝对正、负理想解后,待评用户数量的增减并不会影响其与绝对理想解的距离,该值将始终保持不变,可确保待评用户之间优劣关系的稳定。
Step5 计算灰色关联度。第i个待评用户与绝对正、负理想解之间的灰色关联矩阵为R+(R-),其中灰色关联系数为
| $ r_{i j}^{+(-)}=\frac{\min\limits _{i} \min\limits _{j}\left|y_{i j}-b^{+(-)}\right|+\rho \max\limits _{i} \max\limits _{j}\left|y_{i j}-b^{+(-)}\right|}{\left|y_{i j}-b^{+(-)}\right|+\rho \max\limits _{i} \max\limits _{i j}\left|y_{i j}-b^{+(-)}\right|} $ | (17) |
式中:ρ为分辨系数,ρ∈[0, 1.0],一般取ρ=0.5;|yij-b+(-)|为待评用户与绝对理想解相对应指标差的绝对值,正灰色关联系数对应上标“+”, 负灰色关联系数对应上标“-”。
Step6 定义改进后的第i个待评用户与绝对正、负理想解的距离测度为:
| $ S_{i}^{+}=\sum\limits_{j=1}^{m} W_{j} r_{i j}^{+} $ | (18) |
| $ S_{i}^{-}=\sum\limits_{j=1}^{m} W_{j} r_{i j}^{-} $ | (19) |
Step7 求取各待评用户的相对贴近度为
| $ C_{i}=\frac{S_{i}^{-}}{S_{i}^{-}+S_{i}^{+}} $ | (20) |
相对贴近度的大小从一定程度上反映电力用户能效水平的高低,其取值范围为[0, 1.0]。若Ci越大,表明待评用户与用户绝对正理想解越接近,同时越远离用户绝对负理想解时,该待评用户能效水平越好。
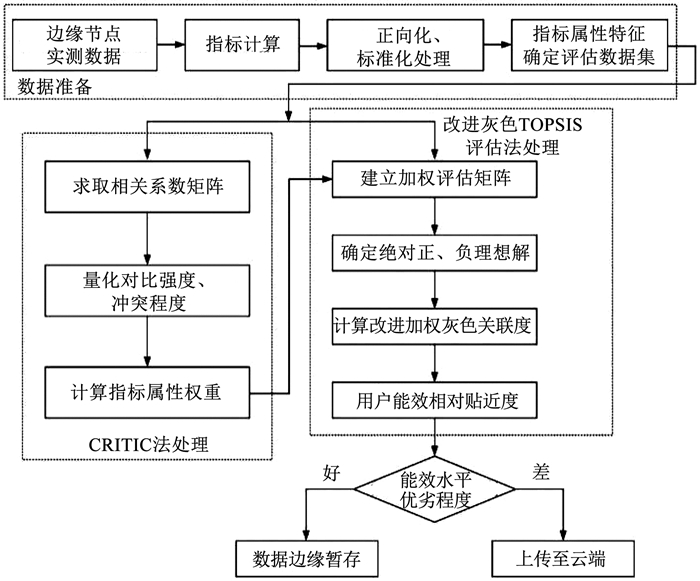
3.2 电力用户边缘能效评估流程为实现在边缘节点对电力用户的能效进行量化,构建能效评估模型,具体流程如图 5所示。
|
图 5 用户边缘能效评估流程 Fig. 5 User energy efficiency edge assessment process |
1) 根据边缘节点采集到的用户能效状态参数,计算出电力用户的能效指标数据,并对数据进行预处理,获取精简数据集。
2) 利用CRITIC赋权法计算指标权重,并在评估过程中引入绝对理想解与灰色关联度来改进TOPSIS评估方法,然后根据相对贴近度评价各电力用户的相对优劣性,实现边缘评估目标。
3) 根据用户的能效评估结果,将现阶段能效水平较差的电力用户的能效数据和评估结果上传至中心化主站,而能效水平较优的用户则将其相关数据结果在边缘侧缓存。
4 试验分析 4.1 能效指标属性特征计算与融合选取某地工业区的10个工业用户,结合用户用电数据的特点,采用模块化设计思路部署开发边缘节点,利用采集到的运行数据对PSR指标体系中的评估指标进行统计和计算,指标预处理后的雷达图如图 6所示。根据指标围成几何封闭区域的面积,可以粗略衡量各个用户的能效水平。

|
图 6 各项指标标准化 Fig. 6 Standardization of indicators |
由指标特征定义公式,对预处理后的能效指标数据计算其重要性、独立性、均衡性3类属性值,见表 2。
| 表 2 初选指标属性计算值 Tab. 2 Calculation value of primary selection index attribute |
由式(4)计算可得指标的影响度γj=[0.007 5, 0.028 6, 0.091 2, 0.132 5, 0.002 1, 0.446 2, 0.117 9, 0.173 9]。
再根据矩阵的微分性质,得到最优化的一阶导数条件的矩阵表示为
| $ \left[\begin{array}{lll} 0.2700 & 0.138 & 6 \\ 0.1386 & 0.142 & 3 \end{array}\right]\left[\begin{array}{l} \alpha_1 \\ \alpha_2 \end{array}\right]=\left[\begin{array}{lll} 0.270 0 \\ 0.1423 \end{array}\right] $ | (21) |
从而得到线性方程组归一化后的最优解为α1=0.949 3,α2=0.050 7。则基于合作博弈论的指标优化度Oj=[0.012 6, 0.034 6, 0.094 8, 0.131 8, 0.007 8, 0.431 8, 0.117 7, 0.172 6]。由此得到能效评价指标的优化度排序为:平均电压>主要耗能设备等级>平均负载率>万元产值能耗>电流不平衡率>电压不合格累计时间>用电量>功率因数。
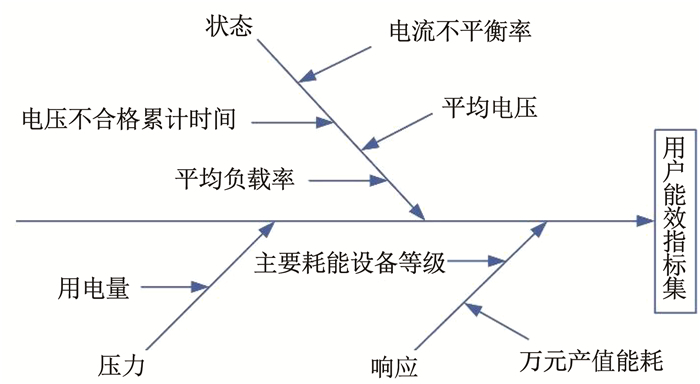
进一步根据统计学基本理论,以数据方差表示各项指标的信息量贡献率,对排序结果中的指标进行末位剔除。为保证评估精度,给定信息贡献率阈值为95.00%。发现当所保留的指标个数为7时,能够反映初选指标集合信息的比率为99.77%,评估信息含量满足需求。对此,将功率因数指标作为冗余指标予以剔除,故最终确定边缘侧评估指标集合如图 7所示。
|
图 7 能效指标集鱼骨图 Fig. 7 Fishbone diagram of energy efficiency index set |
根据CRITIC法的定义计算各指标的权值Wj=[0.121 7, 0.101 2, 0.144 6, 0.173 4, 0.182 7, 0.140 0, 0.136 4]。其中反映用户状态性能的平均负载率和平均电压两项指标的权重较大,分别为0.173 4和0.182 7,突出状态类指标在评估过程中的重要性,也间接反映电能质量对用户的能效水平具有较大的影响。而用电量和电压不合格累计时间两项指标的权重占比相对较小,一方面由于其在整体评估过程中提供的有用信息较少,另一方面也与各用户该方面的能效指标数据差异小有关。
基于评估模型设置电力用户能效水平的绝对理想解,进而计算各用户分别与绝对正、负理想解的加权灰色关联度,在此基础上得到电力用户综合能效状态评分及其优劣排序,其结果见表 3。由表 3可知10个用户的能效水平优劣排序中,用户5的能效水平最优,用户8的能效水平次优。
| 表 3 边缘侧评估结果 Tab. 3 Edge side assessment results |
为更加细致地反映电力用户U1~U10的能效水平,将“压力-状态-响应”模型各维度的相对贴近度值以折线图的形式呈现,如图 8所示。从图 8可以看出:各用户的压力指标评分差异较明显,中间出现较大起伏,状态指标评分值呈波动变化,而响应指标的评估分值相近,整体差异较小。

|
图 8 各子系统评分情况 Fig. 8 Subsystem ratings |
其中U5的状态维度评分在10个用户中最高,3个维度的指标表现均较好,因此最终的综合评估结果最优。U2、U4的响应维度评分值较高,最终其排名靠前。这是由于万元产值能耗等响应指标可以对压力、状态产生正向的反馈,因此优化用户的响应性能可以提高用电能效水平。U9、U10在状态、响应维度上的表现均较差,下一步应努力提升电能质量并尽量选用低耗能设备。U6的压力维度评分与其他用户相比存在较大差距,这与其用电量指标表现较差有关,因此其最终排名略低于U1。
上述分析表明,对电力用户采用PSR模型分析,能够找到用户自身用能的薄弱环节,通过边缘节点将用户的能效信息发送至中心化主站,运维人员通过各项指标可确定电力用户能效异常的原因,并及时对用户给予反馈并确定优化方案。
4.2.2 边云评估对比为了证明本文边缘节点能效评估方法与系统中心化主站指标集合的评估效果一致,对主站能效评估进行检验,计算结果见表 4。
| 表 4 主站侧评估结果 Tab. 4 Main station side evaluation results |
由表 4可知,同一电力用户在边缘侧与主站侧的评估结果排序一致,而本文所提方法只需将计算模式切换到边缘侧执行,即可利用数据冗余性来降低主站存储资源。边缘侧评估结果相对于主站结果的误差百分比,如图 9所示。可以看出误差绝对值皆小于9.5%,符合对于边缘节点的评估要求,进一步证明该评估方法在保证用户优劣排序的基础上,仍具有良好的评估精度,具备一定的可应用性。

|
图 9 能效水平误差分析 Fig. 9 Energy efficiency level error analysis chart |
同时考虑到边云传输的差异性,传统计算方式需要将每个传感器采集到的数据全部传输给主站,数据量庞大,而利用本地边缘节点的计算能力就可以周期性地仅将指标数据与评估结果传输给主站。为进一步说明边缘计算的优势,将边缘计算与传统计算方式进行指标对比,见表 5。
| 表 5 边缘计算与主站计算对比 Tab. 5 Comparison of edge calculation and master station calculation |
由表 5可知,相较于主站计算方式,边缘计算方式下传输给主站的数据量大幅减少,不仅节省了传输网络带宽,也间接减少了程序整体计算耗时,有利于减轻主站的计算复杂度并缓解数据的存储压力。
4.3 评估方法的比较分析 4.3.1 与传统TOPSIS法的比较为验证改进后的TOPSIS方法的有效性,将其与传统TOPSIS法得到的评估结果进行对比,见表 6。可以发现,本文方法和传统方法在用户能效排名上略有差别,主要有以下原因:
| 表 6 评估结果比较 Tab. 6 Comparison of evaluation results |
1) 指标权重层面。传统TOPSIS法使用熵权法计算综合排序,各指标的权值结果为0.089 2, 0.100 3, 0.138 8, 0.136 8, 0.269 2, 0.130 9, 0.134 7。其中平均电压指标所占权重达到0.269 2,远高于用电量指标,且在整体权重分配中该项指标的占比略大。这是因为熵权法利用数据分布状况确定权重,易夸大指标间的权重差距,而改进的TOPSIS法使用CRITIC法依据指标内的对比强度和指标间的冲突程度综合确定权重,在数值上可以均衡各指标的权重值,从而能够更好地弥补这一不足。
2) 理想解计算层面。在删减U2之前,由传统TOPSIS法得到的各用户能效状态优劣排序为U5、U8、U4、U2、U3、U1、U6、U10、U7、U9,在删减U2之后,排序则变为U8、U5、U4、U3、U1、U6、U10、U7、U9。调整前、后,U5和U8两者的优劣顺序发生了逆转,产生了逆排序现象,影响到评估结果的准确性。而本文的改进方法引入了绝对理想解,在删减U2之前,各用户的优劣排序为U5、U8、U4、U2、U3、U1、U6、U10、U7、U9;删减U2后,排序为U5、U8、U4、U3、U1、U6、U10、U7、U9,说明改进后TOPSIS法可有效避免因待评用户数量变化而引起的逆排序问题,在调整待评用户数量的前、后,其余待评用户的优劣顺序没有发生变化,证明所用改进方法的准确性和合理性。
3) 距离测度层面。TOPSIS使用欧氏距离作为距离测度,在判断待评估用户与正、负理想解间的位置关系时存在固有缺陷;而本文采用灰色关联度改进后,一方面对于小样本无规律指标的评估决策准确性更高,另一方面在计算贴近度时更接近待评用户的态势变化。
4.3.2 方法的对比分析为进一步说明本文所提评估算法的有效性,另选用3种典型方法进行对比实验,评估结果见表 6。
表中GRA-TOPSIS和灰色关联分析法与本文改进方法的排序结果基本一致。改进灰色关联投影法的排序与本文方法相差不超过两个排名。因此,在一定程度上表明本文方法可以较好地从用电能效水平差异上对电力用户进行评估,验证了模型的适应性。
相比于上述文献中的方法,本文方法具有以下优势:1)GRA-TOPSIS评估方法未考虑到增减评估方案的情形,而本文的绝对理想解可抑制方案的相对位置关系发生反转的可能,能够适应用户及数据的动态变化。2)在灰色关联分析法中,采用FAHP确定指标权重,包含专家对评价结果的主观偏好,而本文方法充分利用客观数据信息,避免主观因素的影响。3)改进灰色关联投影法中引入马氏距离夸大了微小变量的作用,特别是在与其他方法对比时评估结果的偏差较为明显,而灰色关联度在分析数据特征和相似程度方面均具有较好优势,可靠性更高。因此,本文评估模型基于客观能效数据,采用CRITIC赋权和改进灰色TOPSIS法进行综合能效评估,评估过程中通过构造绝对理想解、引入CRITIC赋权法以及采用改进加权灰色关联度代替欧氏距离,克服了TOPSIS决策分析时存在逆排序现象、权重设定不合理及距离测度度量不准确等固有缺陷,使得结果更具客观性、稳定性。
5 结论1) 通过在边缘侧部署边缘节点,实时分析用户的能效情况,改变传统依赖上传大量原始数据进行分析评估的方法。与主站的信息交互仅以相关数据结果进行传输可实现快速响应。
2) 构建基于PSR模型的多维度电力用户能效评估指标体系,从中抽象出重要性、均衡性、独立性3项数据特征关系,结合融合模型优选出边缘侧精简后的关键性指标,可减少向主站传输数据时对数据通道的占用和数据处理时间。
3) 采用CRITIC权重与改进灰色TOPSIS法相结合的评估模型,对能效状况进行研判分析。利用能效指标的分析结果,用户可以了解自身用能的薄弱环节,有针对性地提高用电效率,形成在边缘侧“用电-监测-评估-节电-改善”的优质循环。
| [1] |
别朝红, 林超凡, 李更丰, 等. 能源转型下弹性电力系统的发展与展望[J]. 中国电机工程学报, 2020, 40(9): 2735. BIE Zhaohong, LIN Chaofan, LI Gengfeng, et al. Development and prospect of resilient power system in the context of energy transition[J]. Proceedings of the CSEE, 2020, 40(9): 2735. DOI:10.13334/j.0258-8013.pcsee.191705 |
| [2] |
黄雨涵, 丁涛, 李雨婷, 等. 碳中和背景下能源低碳化技术综述及对新型电力系统发展的启示[J]. 中国电机工程学报, 2021, 41(Sup.1): 28. HUANG Yuhan, DING Tao, LI Yuting, et al. Decarbonization technologies and inspirations for the development of novel power systems in the context of carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(Sup.1): 28. DOI:10.13334/j.0258-8013.pcsee.211016 |
| [3] |
李扬, 王蓓蓓, 李方兴. 灵活互动的智能用电展望与思考[J]. 电力系统自动化, 2015, 39(17): 2. LI Yang, WANG Beibei, LI Fangxing. Outlook and thinking of flexible and interactive utilization of intelligent power[J]. Automation of Electric Power Systems, 2015, 39(17): 2. DOI:10.7500/AEPS20150730004 |
| [4] |
周峰, 周晖, 刁赢龙. 泛在电力物联网智能感知关键技术发展思路[J]. 中国电机工程学报, 2020, 40(1): 70. ZHOU Feng, ZHOU Hui, DIAO Yinglong. Development of intelligent perception key technology in the ubiquitous internet of things in electricity[J]. Proceedings of the CSEE, 2020, 40(1): 70. DOI:10.13334/j.0258-8013.pcsee.191198 |
| [5] |
唐文虎, 牛哲文, 赵柏宁, 等. 数据驱动的人工智能技术在电力设备状态分析中的研究与应用[J]. 高电压技术, 2020, 46(9): 2985. TANG Wenhu, NIU Zhewen, ZHAO Boning, et al. Research and application of data-driven artificial intelligence technology for condition analysis of power equipment[J]. High Voltage Engineering, 2020, 46(9): 2985. DOI:10.13336/j.1003-6520.hve.20191902 |
| [6] |
赵鹏, 蒲天骄, 王新迎, 等. 面向能源互联网数字孪生的电力物联网关键技术及展望[J]. 中国电机工程学报, 2022, 42(2): 447. ZHAO Peng, PU Tianjiao, WANG Xinying, et al. Key technologies and perspectives of power internet of things facing with digital twins of the energy internet[J]. Proceedings of the CSEE, 2022, 42(2): 447. DOI:10.13334/j.0258-8013.pcsee.211977 |
| [7] |
KHAN R, KHAN S U. Design and implementation of UPnP-based energy gateway for demand side management in smart grid[J]. Journal of Industrial Information Integration, 2017, 8: 8. DOI:10.1016/j.jii.2017.07.001 |
| [8] |
WEI Min, LI Caiqin, YANG Xu. An energy management system with edge computing for industrial facility[C]//2021 15th International Conference on Ubiquitous Information Management and Communication (IMCOM). Seoul, Korea (South): IEEE, 2021: 1. DOI: 10.1109/IMCOM51814.2021.9377419
|
| [9] |
吴剑飞, 姚建刚, 陈华林, 等. 电力客户能效状态模糊综合评估[J]. 电力系统保护与控制, 2010, 38(13): 94. WU Jianfei, YAO Jiangang, CHEN Hualin, et al. Fuzzy comprehensive evaluation of power customer energy efficiency assessment[J]. Power System Protection and Control, 2010, 38(3): 94. DOI:10.3969/j.issn.1674-3415.2010.13.020 |
| [10] |
李金良, 刘怀东, 王睿卓, 等. 基于交叉超效率CCR模型的综合能源系统综合效率评价[J]. 电力系统自动化, 2020, 44(11): 78. LI Jinliang, LIU Huaidong, WANG Ruizhuo, et al. Comprehensive efficiency evaluation of integrated energy system based on cross-super-efficiency CCR model[J]. Automation of Electric Power Systems, 2020, 44(11): 78. DOI:10.7500/AEPS20190805008 |
| [11] |
罗志坤, 刘潇潇, 陈星莺, 等. 变电站能效评估指标体系及建模方法[J]. 电力自动化设备, 2017, 37(3): 132. LUO Zhikun, LIU Xiaoxiao, CHEN Xingying, et al. Energy efficiency evaluation index system and modeling method for substation[J]. Electric Power Automation Equipment, 2017, 37(3): 132. DOI:10.16081/j.issn.1006-6047.2017.03.022 |
| [12] |
KONG Xiangyu, ZHU Shijian, HUO Xianxu, et al. A household energy efficiency index assessment method based on non-intrusive load monitoring data[J]. Applied Sciences, 2020, 10(11): 3820. DOI:10.3390/app10113820 |
| [13] |
ZHAO Hongshan, LI Jingxuan. Energy efficiency evaluation and optimization of industrial park customers based on PSR model and improved grey-TOPSIS method[J]. IEEE Access, 2021, 9: 76423. DOI:10.1109/ACCESS.2021.3081142 |
| [14] |
张博胜, 杨子生. 基于PSR模型的中国人地关系协调发展时空格局及其影响因素[J]. 农业工程学报, 2021, 37(13): 252. ZHANG Bosheng, YANG Zisheng. Spatio-temporal pattern and its influencing factors of coordinated development of man-land relationship in China using PSR model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(13): 252. DOI:10.11975/j.issn.1002-6819.2021.13.029 |
| [15] |
李冲, 张璇, 许杨, 等. 京津冀生态屏障区人类活动对生态安全的影响[J]. 中国环境科学, 2021, 41(7): 3324. LI Chong, ZHANG Xuan, XU Yang, et al. The impacts of human activities on ecological security in the ecological barrier zone in Beijing-Tianjin-Hebei region[J]. China Environmental Science, 2021, 41(7): 3324. DOI:10.19674/j.cnki.issn1000-6923.20210331.007 |
| [16] |
付志扬, 王涛, 孔令号, 等. 基于AHP-TOPSIS算法的重要电力客户用电状态评估[J]. 电网技术, 2022, 46(10): 4095. FU Zhiyang, WANG Tao, KONG Linghao, et al. Power consumption state evaluation of important power customers based on AHP-TOPSIS algorithm[J]. Power System Technology, 2022, 46(10): 4095. DOI:10.13335/j.1000-3673.pst.2021.2280 |
| [17] |
黄德才, 郑河荣. 理想点决策方法的逆序问题与逆序的消除[J]. 系统工程与电子技术, 2001, 23(12): 80. HUANG Decai, ZHENG Herong. Study on the problem and elimination of rank reversal existing in ideal point multiple attribute decision making[J]. Systems Engineering and Electronics, 2001, 23(12): 80. DOI:10.3321/j.issn:1001-506X.2001.12.024 |
| [18] |
田世明, 潘明明, 苑嘉航, 等. 有源重要用户供电风险评估方法研究[J]. 电网技术, 2015, 39(1): 35. TIAN Shiming, PAN Mingming, YUAN Jiahang, et al. Power supply risk element assessment for important consumers equipped with standby power supplies[J]. Power System Technology, 2015, 39(1): 35. DOI:10.13335/j.1000-3673.pst.2015.01.006 |
| [19] |
尹传忠, 刘咪, 武中凯, 等. 区域应急物流中心空间布局规划研究[J]. 铁道科学与工程学报, 2022, 19(6): 1550. YIN Chuanzhong, LIU Mi, WU Zhongkai, et al. On spatial layout planning of regional emergency logistics center[J]. Journal of Railway Science and Engineering, 2022, 19(6): 1550. DOI:10.19713/j.cnki.43-1423/u.T20210690 |
| [20] |
张志飞, 薛昊祥, 陈钊, 等. 基于灰色关联度TOPSIS法的前悬架与转向系统优化[J]. 汽车工程, 2020, 42(8): 1082. |
| [21] |
梁海平, 田圣双, 李秋燕, 等. 基于改进TOPSIS灰色关联投影法的主网网架结构评价[J]. 电力自动化设备, 2019, 39(4): 63. LIANG Haiping, TIAN Shengshuang, LI Qiuyan, et al. Main grid structure evaluation based on improved TOPSIS grey relation projection method[J]. Electric Power Automation Equipment, 2019, 39(4): 63. DOI:10.16081/j.issn.1006-6047.2019.04.010 |
| [22] |
吴波, 陈辉浩, 黄惟, 等. 基于FAHP-GRA理论的深基坑涌水涌砂风险评价[J]. 铁道科学与工程学报, 2021, 18(8): 2209. WU Bo, CHEN Huihao, HUANG Wei, et al. Risk assessment of water and sand gushing in deep foundation pit based on the FAHP-GRA theory[J]. Journal of Railway Science and Engineering, 2021, 18(8): 2209. DOI:10.19713/j.cnki.43-1423/u.t20210198 |
 2023, Vol. 55
2023, Vol. 55


