卷弧翼弹箭自20世纪中期问世以来,由于卷弧翼可以包裹覆盖在弹体外表面的特性,已被广泛应用于各种武器中,许多筒式发射的战术火箭和导弹大都采用折叠卷弧翼作为稳定装置。虽然卷弧翼弹箭在零攻角下产生的自诱导滚转力矩在亚、跨声速下会发生滚转换向,且产生显著的侧向力和偏航力矩,不利于弹箭飞行稳定,但与平直翼相比,卷弧翼可以减小弹的体积以及节省弹内空间,零攻角下产生的自诱导滚转力矩,有利于弹体自旋稳定[1]。为解决卷弧翼弹箭的不足,并有效利用其优势,有必要对其气动力特性开展研究。
从20世纪70年代开始,针对卷弧翼弹箭独特的气动特性及其影响因素,国、内外学者进行了大量的研究。Dahlke[2]利用风洞试验对标准TTCP(The technical cooperation program,由国际技术协作小组设计的标准卷弧翼弹箭)卷弧翼弹箭,在马赫数0.3~3.0范围内的气动特性进行研究,主要研究卷弧翼的外形结构(曲率、边缘锐化角度等)对弹箭气动力的影响;Eastman等[3]对安装卷弧翼的小型导弹在30°攻角及亚、跨、超声速下进行空气动力学试验,发现大攻角下卷弧翼的气动特性与平直翼完全不同,最主要表现在偏航力矩、滚动力矩都与马赫数和攻角强相关;Winchenbach等[4]对卷弧翼导弹进行飞行试验,结果表明马格努斯力矩随俯仰角变化明显;文献[5-6]通过工程算法和数值模拟对标准TTCP卷弧翼弹箭进行气动参数计算,研究了马赫数、翼厚度和雷诺数等对滚转力矩特性的影响,并与实验数据进行对比,结果较为一致。
为有效利用卷弧翼的优势,消除自诱导滚转力矩、侧向力矩等带来的不利影响,国内、外学者就卷弧翼产生这些力的机理也开展了相应研究。Tilmann等[7-8]使用代数涡黏性模型求解N-S(Navier-Stokes)方程的数值模拟方法,在Ma=2.8、4.9条件下进行了单个卷弧翼的流场计算,结果表明在翼体结合处有涡的存在,并且涡的强度和位置随着马赫数的变化而变化,引起滚转力矩显著下降;姜鑫等[9]针对5种不同弯度的卷弧翼,通过风洞试验并采用粒子图像测速仪,测定5°~30°攻角范围内叶片表面压力分布和卷弧翼附面层速度场,发现低速时卷弧翼附面层的流动分离和涡旋运动是影响其空气动力特性的主要原因;郑建[10]采用计算流体力学(CFD)方法对标准TTCP卷弧翼弹箭的气动特性进行数值分析,包括单片翼和翼身组合体;谢志敏等[11]通过数值模拟,对翼片压力进行分析,揭示了卷弧翼产生侧向力的机理。
近年来,学者们通过研究卷弧翼的外形结构以及安装方式等来解决卷弧翼弹箭的飞行稳定性问题。Mclntyre等[12]通过飞行试验,证实了在卷弧翼上开槽可增强其滚转稳定性并减少波阻;Morote等[13]通过140 mm卷弧翼火箭弹飞行试验发现,在马赫数2.5~2.7范围内会出现严重的动态不稳定,发生掉弹现象,后经研究通过改变卷弧翼展弦比和后掠角,减小了侧向力和侧向力矩,从而改善了弹箭的稳定性;向玉伟等[14]利用CFD软件对某卷弧翼弹箭的滚转特性进行了研究,结果表明在卷弧翼正斜置角及后缘凸面斜切对其滚转特性影响显著;张磊等[15]基于Wagner函数,在非定常条件下建立了卷弧翼的滚转模型并开展了数值仿真,并与CFD仿真结果进行对比发现,卷弧翼反装反旋的安装方式能有效减小弹箭的滚转力矩,这对卷弧翼弹箭的颤振分析及锥形运动抑制等有积极的指导效果。
上述文献对卷弧翼的气动特性研究都是针对固定卷弧翼(弹箭飞行时尾翼与弹身固定为一整体),而研究[16]发现,具有差动结构的自由旋转卷弧翼(尾翼与弹身通过一定的机构实现解耦,尾翼可相对弹身差动自由旋转)弹箭能够有效抑制弹箭飞行中的共振不稳定,这是固定卷弧翼所不具备的。国内目前针对差动结构弹箭的研究主要集中在双旋修正弹,如常思江等[17]对固定鸭舵双旋弹进行了七自由度飞行动力学建模与仿真;钱龙等[18]利用CFD方法对某固定鸭舵双旋修正弹的流场进行数值模拟,研究了舵与弹身解耦自由旋转以及舵和弹身存在差动滚转角速度时弹丸的线性与非线性气动特性。国内对自由旋转卷弧翼的研究较为缺乏,故有必要对其开展深入研究。
本文采用滑移网格方法来模拟卷弧翼弹箭的滚转运动,首先对自由旋转卷弧翼与固定卷弧翼弹箭在亚、跨、超声速下进行时间精确非定常动态模拟,将两者的气动特性进行对比分析;其次对自由旋转卷弧翼弹箭在不同的翼、体差动滚转条件下开展数值分析,重点讨论差动滚转角速度对弹箭滚转力矩和马格努斯力矩特性的影响。
1 数值计算方法与研究对象 1.1 数值计算方法为模拟自由旋转卷弧翼弹箭的差动滚转运动,本文采用滑移网格方法,将流场域划分为动、静3个计算域,计算域之间通过交界面进行数据传输,该方法较之多重坐标系法和动网格法精确度高,能获得更高的网格质量。具体为:1)对弹箭相对于自由流速度矢量在选定攻角α下保持静止的定常流动进行求解;2)将该流动解作为时间精确非定常动态模拟的初始条件,其中弹箭保持相同的攻角α,同时以恒定的角速度绕固定x轴(如图 1(a)所示,弹箭的轴向方向即x轴方向)滚转,二者皆选择k-ε(k-epsilon)湍流模型,采用隐式迭代、二阶迎风差分格式。

|
图 1 TTCP卷弧翼弹箭计算模型 Fig. 1 Calculation model of TTCP projectile wraparound fins |
非定常计算时间步长Δt按照下式计算为[19]
| $\Delta t=\frac{1}{N n}$ | (1) |
式中:N为时间步数;n为转速,r/s。
1.2 研究对象为便于开展对比分析,本文以TTCP模型为研究对象,其具体几何参数如图 1所示,所有尺寸均以弹径D表示(1D=101.6 mm),弹箭由2.0D的头部、8.0D的圆柱体和两对1.75D弦长、0.65D展长的卷弧翼构成。卷弧翼厚度为0.05D,曲率45°。
为保证网格质量,本文采用文献[6]中尾翼结构,与标准TTCP的尾翼相比,其尾翼前、后缘稍有钝化。TTCP的重心位于从弹尾起3.9D处,参考长度取为弹径D,参考面积S=πD2/4。
1.3 计算网格和边界条件为模拟自由旋转卷弧翼差动滚转,采用内外嵌套网格,三维六面体网格如图 2所示,计算域边界尺寸参考弹径D。

|
图 2 计算域网格 Fig. 2 Computational domain grids |
外部大流场网格左侧边界距弹头20D,右侧边界距弹尾30D,径向为20D;套内流场网格左侧边界距弹头8D长度,右侧边界距弹尾12D长度,径向为8D。第1层网格高度设置为1×10-5 m,以保证网格在壁面附近y+≤1,总网格数量为3.98×106。
1.4 计算方法验证为了对拟采用的计算方法进行验证,将计算所得TTCP模型的阻力系数CD与文献[10]进行比较,结果如图 3所示;将计算所得TTCP模型的滚转力矩系数Cl与文献[5-6]中的滚转力矩系数进行对比,结果如图 4所示。

|
图 3 阻力系数随马赫数变化关系 Fig. 3 Drag coefficient vs Ma number |

|
图 4 滚转力矩系数随马赫数变化关系 Fig. 4 Roll moment coefficient vs Ma number |
图 3~4所示结果表明,本文计算结果与文献结果总体趋势吻合较好,最大误差约7%,验证了本文拟采用方法的可行性。
1.5 无关性检验本文采用3套不同规格的网格对TTCP模型定常计算的网格无关性进行检验,采用两种时间步数对非定常计算的时间步数无关性进行检验,时间步长由时间步数N和转速n按照式(1)确定。
计算工况为:Ma=1.1、α=4°,3套网格的数量分别为2.01×106、3.98×106、6.12×106,计算结果见表 1。
| 表 1 网格无关性检验 Tab. 1 Mesh irrelevance test |
如表 1所示,2.01×106网格对应的结果与3.98×106网格对应的结果相差较大,阻力系数和升力系数差异在2.00%左右,而6.12×106网格对应的结果与3.98×106网格计算结果更为相近,最大相对误差仅为0.45%。
表 2给出了自由旋转卷弧翼弹箭(n=10 r/s)在两种时间步数下的阻力系数和滚转力矩系数的模拟结果。从表 2中可以看出,两者差异很小,最大相对误差仅为0.50%。因此,从精度和计算成本综合考虑,本文选用网格数量3.98×106和时间步数800的方案对卷弧翼弹箭进行数值模拟。
| 表 2 时间步数无关性检验 Tab. 2 Number step sizes irrelevance test |
本文主要研究固定卷弧翼和自由旋转卷弧翼弹箭在飞行过程中的气动特性,计算模型如图 1所示。由于计算涉及到弹箭绕轴旋转非定常计算,所以采用滑移网格计算,壁面设置为无滑移壁面条件。考虑到非定常计算非常耗费资源和时间,因此只需计算弹箭旋转一周[19],每次旋转使用时间步数N=800次迭代,相当于每个时间步将弹箭滚转了0.45°。弹体转动速度为n1,卷弧翼转动速度为n2,滚转角(弹箭相对于零时刻滚转的角度)为φ(从弹底看,取逆时针旋转为正,顺时针旋转为负)。
考虑到弹箭真实飞行状况,对弹箭在亚、跨、超声速的气动特性进行数值计算,具体工况选取见表 3。
| 表 3 计算工况 Tab. 3 Calculation condition |
本文的定常工况计算结果一方面可作为非定常计算的初始条件,另一方面可与非定常计算结果进行对比。
2.2.1 流场分析通过对卷弧翼弹箭流场流线图的分析,可研究卷弧翼气动特性的机理。图 5给出了两种卷弧翼弹箭(工况2和工况3)在x=8.4D(以弹头为坐标原点)截面处的压力云图和流线图。由于卷弧翼的特殊结构,引起翼体周围流场的不对称,在有攻角情况下,卷弧翼凹、凸表面的流场结构变化更为显著,且当凹、凸表面同为迎风面或背风面时,其流场结构亦有所差异,引起卷弧翼升力、滚转力矩、马格努斯力矩等气动力的变化。

|
图 5 x=8.4D截面处压力云图 Fig. 5 Cross-sectional pressure cloud at x=8.4D |
从图 5可知,有攻角情况下,气流撞击翼体迎风面而受阻,引起气流强烈压缩,压力升高;之后气流翻转向上,在翼体背风面受到扰动,流速增大,压力降低,翼体迎风面和背风面产生的压差提供了弹箭需要的升力。由图 5的对比可知,虽然当凹、凸翼面同为迎风面或背风面时,翼体周围气流流动形式相似,但所受压力载荷差异显著。这是由于翼体凹面的特殊结构,使得气流扰动更为剧烈,所以同为背风面的凹面翼(凹型翼面)区域低压面积远大于凸面翼(凸型翼面)。因此,两片翼面产生的升力大小存在差值,从而产生滚转力矩。
图 5中可以明显看到,虽然随着马赫数的增大,翼体周围的气流扰动变得更为复杂,但其压力不对称性反而在减小,即随着马赫数的增大,卷弧翼的几何结构对弹箭滚转力矩和马格努斯力距的影响在减弱。从流线图来看,凸面翼与弹体连接处产生了涡,这与文献[7]的结果相吻合。涡主要由弹体壁面的黏性作用所引起,随着马赫数的增大,涡的强度变大,且更加靠近弹体区域,从而引起弹体壁面压力载荷的不对称,这可能是造成卷弧翼弹箭滚转力矩和马格努斯力矩随马赫数强烈变化的重要原因。
图 6给出了卷弧翼弹箭在z=0截面和y=0截面处的压力云图。

|
图 6 工况2、3为z=0、y=0截面处压力云图 Fig. 6 Working conditions 2 and 3 are pressure cloud maps at sections z=0 and y=0 |
从图 6(a)~6(c)可知,有攻角情况下,弹体与弹翼部分迎风面压力明显大于背风面,两者的压差提供了全弹的升力。从图 6(d)~6(f)可知,弹体两侧的压力值基本相同,这是由于弹体为旋转体,随着弹箭滚转,气流在弹体周围的扰动为对称分布,所以卷弧翼弹箭的马格努斯力基本由弹翼提供。从图 6中也可以看出,在亚、跨、超声速下,尾翼处于z轴方向上方截面的压力值明显低于下方截面,且压力集中在卷弧翼前缘附近,由此在弹箭z轴方向产生压力差,形成马格努斯力和力矩。产生压差的原因为:1)卷弧翼独特的几何结构造成翼体周围气流的不对称扰动,形成压力差;2)翼、体连接处由于黏性作用而形成涡,产生低压分离区,造成弹体壁面的压力不对称。
2.2.2 气动特性分析 2.2.2.1 阻力系数和升力系数表 3中的3种工况对应的阻力系数CD和升力系数CL数据对比结果见表 4、5。
| 表 4 阻力系数结果对比 Tab. 4 Comparison of drag coefficent results |
| 表 5 升力系数结果对比 Tab. 5 Comparison of lift coefficent results |
由表 4、5可知,翼、体连接方式对弹箭的阻力系数和升力系数的影响较小。阻力系数和升力系数随着马赫数从亚声速到超声速的变化都呈现先增大后减小的趋势,并在跨声速达到峰值。在非定常状态下,两种卷弧翼弹箭的阻力系数在各马赫数处基本一致;在跨声速(Ma=1.1)处,自由旋转卷弧翼的升力系数比固定卷弧翼稍大约1%。
2.2.2.2 俯仰力矩系数两种卷弧翼弹箭(工况2和工况3)的俯仰力矩系数Cmy随滚转角φ的变化关系如图 7所示。

|
图 7 俯仰力矩系数随滚转角变化关系 Fig. 7 Variation of pitching moment coefficient with roll angle |
本文计算为弹箭滚转一周的气动数据,由图 7可知,随着滚转角φ的变化,俯仰力矩系数基本上呈周期性变化,呈现4个峰、谷值。在亚、超声速下,两种卷弧翼弹箭的俯仰力矩系数随滚转角变化在数值和波幅上基本趋于一致,在跨声速下,有较为明显的差别,自由旋转卷弧翼的俯仰力矩系数随着滚转角的变化,波动峰谷值更大,这与其在跨声速下升力系数比固定卷弧翼稍高1%相符。
取后1/2周期的数据平均值作为卷弧翼弹箭的俯仰力矩系数,表 6给出了俯仰力矩系数随马赫数的变化对比结果。
| 表 6 俯仰力矩系数结果对比 Tab. 6 Comparison of pitching moment coefficient results |
由表 6可知,在3种马赫数下,两种卷弧翼弹箭的俯仰力矩系数数值上基本相等,与定常计算结果(工况1)相比,在Ma=0.8和Ma=1.3时有所差异,最大相对误差约4%。
2.2.2.3 滚转力矩系数表 3中的3种工况下卷弧翼弹箭的滚转力矩系数Cl随马赫数Ma的变化对比结果见表 7。
| 表 7 滚转力矩系数结果对比 Tab. 7 Comparison of roll moment coefficient results |
定常状态下,卷弧翼弹箭能够产生自诱导滚转力矩,随着马赫数增加而减小,在Ma=1.1附近跨过零点,出现滚转换向现象。工况2和工况3非定常计算的结果趋势也与定常计算相一致,滚转力矩系数的绝对值随着马赫数的增加而减小。3种马赫数下,自由旋转卷弧翼的滚转力矩系数要比固定卷弧翼数值上平均要小约17%。从图 5中也可以看出,同处背风面的凸面翼,自由旋转卷弧翼翼面低压区面积更大。
2.2.2.4 马格努斯力矩系数两种卷弧翼弹箭(工况2和工况3)的马格努斯力矩系数Cmz随滚转角φ的变化关系如图 8所示。

|
图 8 马格努斯力矩系数随滚转角变化关系 Fig. 8 Variation of Magnus moment coefficient with roll angle |
同样,取后1/2周期气动数据的平均值表示卷弧翼弹箭的马格努斯力矩系数,表 8给出了马格努斯力矩系数随马赫数的变化对比结果。
| 表 8 马格努斯力矩系数结果对比 Tab. 8 Comparison of Magnus moment coefficient results |
从表 8中可以看出,虽然两种卷弧翼弹箭的马格努斯力矩系数都随滚转角呈周期性变化,但自由旋转卷弧翼弹箭的马格努斯力矩系数数值上更小,在Ma=0.8和Ma=1.1处基本接近于零,相较于固定卷弧翼,自由旋转卷弧翼的马格努斯效应较小,这对弹箭的飞行稳定是有利的。从云图来看,其原因是固定卷弧翼弹箭在翼、体连接处受黏性影响更大,气流形成的诱导涡旋强度更强,导致马格努斯效应较强。
3 不同差动滚转对气动特性的影响上述对比分析了两种卷弧翼弹箭的气动特性,其中自由旋转卷弧翼弹箭的弹体转速为零。本文考虑更为真实的工况,即弹体和卷弧翼均存在转速且大小不同,重点研究翼、体差动滚转角速度对自由旋转卷弧翼弹箭滚转力矩特性和马格努斯力距特性的影响。
3.1 工况选取为实现上述目的,这里将计算流场分为3个计算域,如图 9所示,其中计算域3为静止域,计算域1、2为动域。
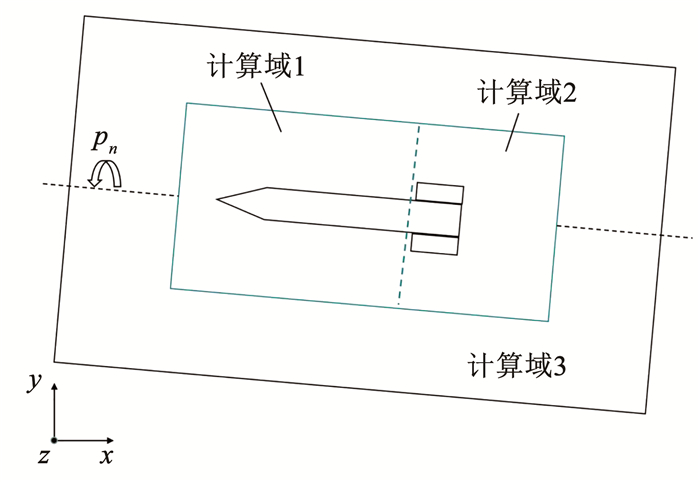
|
图 9 差动滚转模拟示意 Fig. 9 Differential roll simulation schematic |
设置两个动域绕弹箭轴向以指定的转速n旋转:计算域1绕轴旋转转速固定为n1=1 r/s,计算域2绕轴旋转速度分别设为n2=3、5、9、11 r/s,从而使弹身与尾翼产生不同的差动滚转角速度。选取差动滚转角速度分别为Δn=2、4、8、10 r/s。计算马赫数为Ma=0.8、1.1、1.3,攻角α=4°,其中,Δn按照下式计算,即
| $\Delta n=n_2-n_1$ | (2) |
自由旋转卷弧翼弹箭滚转力矩系数Cl随马赫数和差动滚转角速度Δn的变化对比结果见表 9及图 10所示。从表 9和图 10中可知,在亚、跨、超声速下,弹箭的滚转力矩系数数值大小与差动滚转角速度基本呈线性关系,即随Δn的增大而增加,且随着马赫数的增加,滚转力矩系数绝对值随Δn增加的幅度也变大。
| 表 9 滚转力矩系数结果对比 Tab. 9 Comparison of roll moment coefficient results |
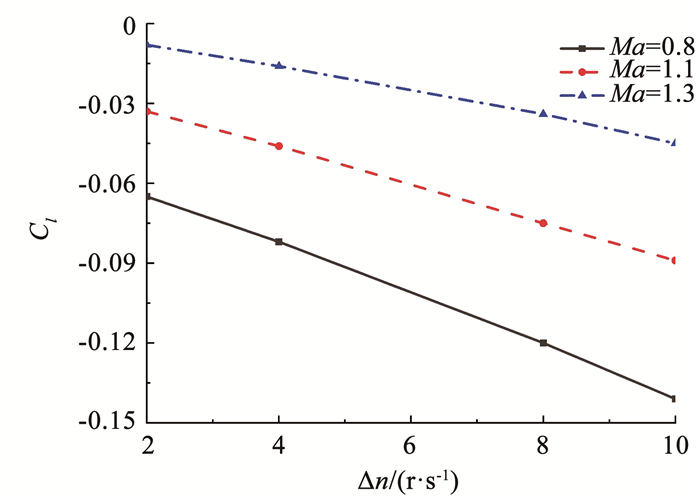
|
图 10 滚转力矩系数随Δn变化关系 Fig. 10 Rolling moment coefficient varies with Δn |
由表 9可知,在不同差动滚转角速度下,滚转力矩系数随着马赫数的变化趋势基本一致,随着马赫数的增加,系数绝对值在降低,且降幅随Δn增大而减小。在Δn=2 r/s时,滚转力矩系数最大降幅在Ma=1.1至Ma=1.3时,达到了76%;在Δn=10 r/s,Ma=1.1至Ma=1.3时,滚转力矩系数降幅最大,仅为49%。其原因是由于翼、体连接处由于黏性作用形成的涡,随着马赫数的增加,涡强度变大,将周围气流卷入弹体壁面附近,形成涡旋诱导的低压区,导致滚转力矩系数随着马赫数的增加急剧降低。
3.2.2 马格努斯力矩特性自由旋转卷弧翼弹箭的马格努斯力矩系数Cmz随滚转角φ的变化关系如图 11所示。

|
图 11 马格努斯力矩系数随滚转角变化关系 Fig. 11 Variation of Magnus moment coefficient with roll angle |
从图 11中可知,马格努斯力矩系数在第1个1/4周期内迅速减小,之后为稳定的周期性变化,呈现4个峰值和4个谷值。随着差动滚转角速度Δn的增加,马格努斯力矩系数随滚转角变化的波动幅度变小,峰值明显降低,在Ma=0.8时差别最为显著。
取后1/2周期的数据平均值作为自由旋转卷弧翼弹箭的马格努斯力矩系数,表 10和图 12给出了马格努斯力矩系数Cmz与马赫数Ma和差动滚转角速度Δn的变化对比结果。
| 表 10 马格努斯力矩系数结果对比 Tab. 10 Comparison of Magnus moment coefficient results |

|
图 12 马格努斯力矩系数随Δn变化关系 Fig. 12 Magnus moment coefficient varies with Δn |
如表 10所示,马格努斯力矩系数绝对值随马赫数的增加先减小后增大,在跨声速下达到最低(接近于0)。从Ma=0.8至Ma=1.1,降幅不明显,而从Ma=1.1至Ma=1.3,马格努斯力矩系数绝对值迅速增大,原因是来流达到超声速后,弹体壁面的黏性作用增强,引起涡旋急剧增强,气流卷向弹体壁面附近,进而形成更大的低压区。
由图 12可知,在亚、跨、超声速下,马格努斯力矩系数随Δn的变化规律基本一致,均呈现先降低后升高的趋势,且在Δn=8 r/s时绝对值达到最低。但在Ma=0.8和Ma=1.1附近,马格努斯力矩系数幅值很小,基本在零值附近。
4 结论1) 翼、体连接方式(固定、自由旋转)对卷弧翼弹箭升力系数、阻力系数和俯仰力矩系数的影响很小,但对滚转力矩和马格努斯力矩特性影响显著。自由旋转卷弧翼弹箭的滚转力矩系数比固定卷弧翼弹箭滚转力矩系数数值上平均要小约17%;自由旋转卷弧翼弹箭的马格努斯力矩系数也较小,在Ma=0.8和Ma=1.1时基本接近于0。这表明,自由旋转卷弧翼弹箭的马格努斯效应较弱,对弹箭的飞行稳定有利。
2) 自由旋转卷弧翼弹箭的滚转力矩系数与翼、体差动滚转角速度Δn基本呈线性关系,而马格努斯力矩系数与差动滚转角速度Δn呈明显的非线性关系,且在Δn=8 r/s时达到极小值,其幅值随滚转角φ的波动幅度也最小。
3) 受弹体壁面黏性作用的影响,来流在卷弧翼与弹身连接处会产生诱导涡,且随着马赫数的增加,涡强度急剧增大,从而造成滚转力矩系数急剧减小和马格努斯力矩系数急剧增大,这些都对卷弧翼弹箭的气动特性影响较大,在气动、弹道设计时须予以着重考虑。
| [1] |
LIAÑO G, MOROTE J. Roll-rate stability limits of unguided rockets with wraparound fins[J]. Journal of Spacecraft and Rockets, 2006, 43(4): 757. DOI:10.2514/1.17775 |
| [2] |
DAHLKE C W. The aerodynamic characteristics of wrap-around fins at Mach numbers of 0.3 to 3.0: RD-77-4[R]. Alabama: US Army Missile Command, 1976
|
| [3] |
EASTMAN D W, WENNDT D L. Aerodynamics of maneuvering missiles with wrap-around fins[C]//Proceedings of the 3rd Applied Aerodynamics Conference. Reston, Virigina: AIAA, 1985: AIAA1985-4083. DOI: 10.2514/6.1985-4083
|
| [4] |
WINCHENBACH G L, BUFF R S, WHYTE R H, et al. Subsonic and transonic aerodynamics of a wraparound fin configuration[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(6): 627. DOI:10.2514/3.20156 |
| [5] |
EDGE H L. Computation of the roll moment for a projectile with warp-around fins[J]. Journal of Spacecraft and Rockets, 1994, 31(4): 615. DOI:10.2514/3.26486 |
| [6] |
PAEK S K, PARK T S, BAE J S, et al. Computation of roll moment for projectile with wraparound fins using Euler equation[J]. Journal of Spacecraft and Rockets, 1999, 36(1): 53. DOI:10.2514/2.3432 |
| [7] |
TILMANN C P, BUTER T A, BOWERSOX R D W. Characterization of the flowfield near a wrap-around fin at Mach 2.8[J]. Journal of Aircraft, 1998, 35(6): 868. DOI:10.2514/2.2406 |
| [8] |
TILMANN C P, BOWERSOX R D W. Characterization of the flowfield near a wrap-around fin at Mach 4.9[C]//Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit. Reston, Virigina: AIAA, 1998: AIAA1998-684. DOI: 10.2514/6.1998-684
|
| [9] |
姜鑫, 宋力, 苏猛, 等. 低速弧形翼气动性能实验研究[J]. 太阳能学报, 2015, 36(2): 325. JIANG Xin, SONG Li, SU Meng, et al. Experimental research on aerodynamic characteristics of curved wing at low speed[J]. Acta Energiae Solaris Sinica, 2015, 36(2): 325. DOI:10.3969/j.issn.0254-0096.2015.02.010 |
| [10] |
郑健. 弧形翼及翼身组合体在超高速下的空气动力学特性研究[D]. 南京: 南京理工大学, 2009 ZHENG Jian. Investigation of aerodynamic characteristics of projectile with WAF at super high speeds[D]. Nanjing: Nanjing University of Science & Technology, 2009. DOI: 10.7666/d.Y1542622 |
| [11] |
谢志敏, 杨树兴, 陈伟. 卷弧尾翼火箭弹侧向气动特性数值计算[J]. 空气动力学学报, 2010, 28(1): 66. XIE Zhimin, YANG Shuxing, CHEN Wei. Numerical investigation of side aerodynamic characteristics of wrap-around fins rocket[J]. Acta Aerodynamica Sinica, 2010, 28(1): 66. DOI:10.3969/j.issn.0258-1825.2010.01.010 |
| [12] |
MCINTYRE T C, BOWERSOX R D W, GOSS L P. Experimental investigation of supersonic wrap-around fin aerodynamic Mach number effects[C]//Proceedings of the 37th AIAA Aerospace Sciences Meeting and Exhibit. Reston, Virigina: AIAA, 1999: AIAA1999-991. DOI: 10.2514/6.1999-991
|
| [13] |
MOROTE J, LIAÑO G. Stability analysis and flight trials of a clipped wrap around fin configuration[C]//Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston, Virigina: AIAA, 2004: AIAA2004-5055. DOI: 10.2514/6.2004-5055
|
| [14] |
向玉伟, 李杰. 卷弧翼弹箭气动外形滚转特性研究[J]. 弹箭与制导学报, 2015, 35(5): 127. XIANG Yuwei, LI Jie. Rolling characteristics investigation on missile with wrap-around fins[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(5): 127. DOI:10.15892/j.cnki.djzdxb.2015.05.031 |
| [15] |
张磊, 高敏, 周布奎, 等. 基于Wagner函数的卷弧翼非定常气动力分析[J]. 计算机仿真, 2020, 37(4): 52. ZHANG Lei, GAO Min, ZHOU Bukui, et al. Unsteady aerodynamic analysis of wrap around wing based on Wagner function[J]. Computer Simulation, 2020, 37(4): 52. |
| [16] |
MOROTE J. Lateral motion of free-rolling tail rockets in free flight[J]. Journal of Spacecraft and Rockets, 2005, 42(5): 873. DOI:10.2514/1.13531 |
| [17] |
常思江, 王中原, 刘铁铮. 鸭式布局双旋弹飞行动力学建模与仿真[J]. 弹道学报, 2014, 26(3): 1. CHANG Sijiang, WANG Zhongyuan, LIU Tiezheng. Modeling and simulation of flight dynamics for dual-spin stabilized projectile equipped with canards[J]. Journal of Ballistics, 2014, 26(3): 1. DOI:10.3969/j.issn.1004-499X.2014.03.001 |
| [18] |
钱龙, 常思江, 杨文龙, 等. 固定鸭舵修正弹非线性与非定常气动数值模拟[J]. 弹道学报, 2020, 32(1): 31. QIAN Long, CHANG Sijiang, YANG Wenlong, et al. Simulation on nonlinear and unsteady aerodynamic characteristics of fixed-canard correction projectile[J]. Journal of Ballistics, 2020, 32(1): 31. DOI:10.12115/j.issn.1004-499X(2020)01-005 |
| [19] |
BHAGWANDIN V A. Numerical prediction of roll damping and Magnus dynamic derivatives for finned projectiles at angle of attack[C]//Proceedings of the 30th AIAA Applied Aerodynamics Conference. Reston, Virigina: AIAA, 2012: AIAA2012-2905. DOI: 10.2514/6.2012-2905
|
 2023, Vol. 55
2023, Vol. 55


