2. 中国空气动力研究与发展中心 超高速空气动力研究所,四川 绵阳 621000;
3. 跨流域空气动力学重点实验室(中国空气动力研究与发展中心),四川 绵阳 621000
2. Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China;
3. Laboratory of Aerodynamics in Multiple Flow Regimes (China Aerodynamics Research and Development Center), Mianyang 621000, Sichuan, China
起重机作为一类广泛应用于港口的专用设备,其防风性能一直备受关注。主梁结构在起重机中起着重要的承载作用,其特点为风力作用位置较高,迎风面积大,因此主梁结构的优化设计对整体起重机的防风性能有着重要影响[1]。传统计算流体力学(computational fluid dynamics, CFD)方法是结构优化设计中风力系数计算的主流方法[2-5],但CFD对网格要求过高且求解步骤复杂等问题限制了其在防风优化设计中的应用[6-7]。
神经网络提出后短短几年便在流体力学领域引起了巨大反响[8-9],越来越多的学者通过神经网络建立了图形与力系数等流场特征量的映射关系。文献[10]采用神经网络创建了预测模型,用以预测翼型的气动参数,并对二维翼型NACA63215进行了预测。文献[11]采用卷积神经网络通过训练后模拟了近似钝体形状和阻力与升力之间的非线性映射。文献[12]基于深度神经网络构建了湍流涡黏系数模型,提升了计算的准确率与效率。文献[13]通过神经网络预测了不同雷诺数下河道水流的雷诺应力,并与数值模拟结果进行了比较。文献[14]提出了一种基于卷积神经网络的数据驱动翼型压力分布预测方法,用于预测给定翼型几何形状的风压。文献[15]通过卷积神经网络预测了翼型在确定的迎风角与雷诺数下的法向力系数。文献[16]利用神经网络方法建立了预测模型,实现了对主梁断面三分力系数的预测。文献[17]基于BP神经网络对扁平与倒梯形状箱形梁这两个种类的断面桥梁主梁的风力系数进行预测。
根据上述研究可知,将神经网络应用到流体力学领域建立新的研究范式受到越来越多的关注[18]。同时,当神经网络加入优化算法后可实现流体机械的快速优化设计。文献[19]基于CFD计算与遗传算法建立了风力机翼型的优化模型,但优化流程过于繁琐。文献[20]将翼型多种工况下升、阻比作为优化目标,基于神经网络与遗传算法创建了优化模型。文献[21]通过深度学习对微藻生物燃料生产和光生物反应器进行了优化设计。文献[22]使用深度卷积研究了UIUC翼型数据库中翼型的分布特征,并对翼型进行了优化。
上述研究皆为将卷积神经网络应用于气动领域的案例,基于神经网络对港口起重机防风性能预测与结构优化设计的相关研究较少。本文以港口起重机主梁作为研究对象,采用卷积神经网络构建了起重机主梁截面风力系数的快速预测模型。在给定流场信息下,以数据集内起重机主梁截面图形作为输入,风力系数作为输出,通过对预测模型不断的训练与优化,最终实现对风力系数的快速精确预测。同时,将预测模型与遗传算法结合建立的结构优化设计方法可实现起重机主梁截面的快速优化设计。
1 卷积神经网络卷积神经网络(convolutional neural networks, CNN)是指具备深度结构的前馈神经网络,是当前图像识别方向引用最为广泛的模型。CNN实质是构建从输入到输出之间的映射关系,具体为通过已知数据集对网络进行训练使其具备输入输出对之间的映射能力[23]。针对本文中起重机主梁截面的风力系数预测问题则是通过CNN建立从主梁截面图形到其风力系数之间的映射关系。
卷积层是CNN最基础的部分。当网络模型进行卷积时,卷积核扫描输入层输入的图像后通过对图像各像素进行局部卷积特征变换得到相应的特征图[24]。尺寸不同的卷积核提取的特征也不同,因此采用不同的卷积核来提取图像多个方向的局部特征。具体的卷积过程如图 1(a)所示。若输入卷积层的第i个特征图为X(i),则输出的第j个特征图为Y(j),其表达式为
| $Y(j)=\sum\limits_i X(i) * \omega_{i j}+b_j$ | (1) |

|
图 1 卷积神经网络中卷积与池化过程示意 Fig. 1 Schematic diagram of convolution and pooling process in convolutional neural network |
式中:*为卷积操作符,ωij为滤波器参数,bj为第j个节点对应的偏置。
卷积层后通常为池化层。池化层作用为通过池化来缩小卷积层生成的特征图尺寸,同时使得特征表示具有不变性,若输入数据的位置发生变化,其对应的特征表示不会受影响。主要的池化操作有平均池化、最大池化等,在实际应用中通常采用最大池化操作[25],最大池化具体为提取图像区域中的最大值来合成新的特征图。最大池化过程如图 1(b)所示。
CNN的后几层为全连接层,用于对前面卷积层输出的特征进行加权和,全连接层会将输入的特征展开为一维的向量,每层的节点都是相连的,输出表示为输入与权重系数相乘加上偏置[26]。
数据预处理,本文中CNN模型的输入是由尺寸为256×256的单通道图像组成,像素值从0~255。为提高神经网络的学习效率且避免异常值和极端值的影响[27],在输入网络模型前需将其尺寸缩小至128×128,然后进行归一化处理,将原始像素值缩放至(0, 1)之间。
激活函数,现在较为常见的激活函数有Tanh、Logistic和Relu函数。由于Tanh与Logistic函数存在梯度消失的问题所以通常不会被采用,Relu函数可以有效解决此问题,实现神经网络的稀疏表达能力,加快网络收敛速度[28]。因此本文选择Relu函数作为神经网络的激活函数,其表达式为
| $f(x)=\max (0, x)$ | (2) |
对于Relu函数而言,当其输入值x>0时,则输出f(x)与x一致,否则输出f(x)为0。
损失函数与反向传播,损失函数衡量了CNN输出值和目标值间的差距。本文选定均方误差函数(mean square error, MSE)作为损失函数,均方误差函数表达式如下式所示。利用损失函数进行反向传播,采用随机梯度下降算法不断更新权重和偏差。
| $\mathrm{MSE}=\frac{1}{m} \sum\limits_{i=1}^m\left(y_i^*-y_i\right)^2$ | (3) |
式中:yi*为输出值,yi为目标值,m为样本个数。
神经网络模型,本文中CNN模型的训练环境为Win10 64位正式版结合Keras库[27](带有Tensorflow后端)运行,基础语言为Python语言,训练使用的硬件主要为Intel Core i9-9900K处理器、32 G内存以及11 G显存的GPU,并在模型训练过程中应用GPU提高网络模型训练效率。
在本文中,首先使用如图 2所示的CNN基础模型进行训练,后续将优化此基础模型。CNN基础模型共有8层卷积、1层全连接与4个池化层,输入层输入起重机主梁截面图形,输出层输出预测的风力系数。卷积层与池化层重复多次,每一层卷积的卷积核数是可变的,为充分提取输入截面图形的特征,前4层卷积的卷积核数为32,后4层卷积的卷积核数为64,全连接层的节点数为64。

|
图 2 CNN基础模型 Fig. 2 CNN basic model |
本文通过自由几何变形方法对基础截面形状进行处理,得到4 000张尺寸为256×256具有丰富几何特征的起重机主梁截面图形集合。同时利用数值模拟方法得出各主梁截面x轴方向(主梁截面的顺风方向)在来流风速为20 m/s的均匀风场环境中的平均风力系数(简称风力系数Xw),并构建主梁截面图形对应的数据标签,最后生成数据集,其中来流风速为F.E.M《欧洲起重机械设计规范》[29]内规定的所有安装在露天的一般起重机进行风压设计时的工作状态风速。风力系数Xw计算公式为
| $X_{\mathrm{w}}=\frac{F}{S \rho V^2 /2}$ | (4) |
式中:S为主梁截面迎风面积,F为作用于主梁截面的风载力,ρ为空气密度,V为来流风速。由于本文主要考虑了x轴方向的来流风,起重机主梁y轴方向所受的风载力较小,故选用Xw为本文的主要研究目标。训练CNN模型时需先将4 000个数据集打乱,随机划分为3个集合:3 200个截面图形样本作为训练集;400个截面图形样本作为验证集;400个截面图形样本作为测试集。
2.1 截面数据获取 2.1.1 截面图形生成选取港口各类起重机内所受风载荷较大的结构,依照这些结构的截面形状建立基础截面形状共21个,围绕此21个基础截面形状通过自由几何变形方法生成截面图形集合,并收集生成的各截面图形坐标点便于后续的风力系数计算工作。为分辨各基础截面形状,将收集的21种截面依次命名为(A, B, …, U),如图 3对其中10种基础形状进行展示,图中可直观看出各类基础截面形状的差异,为数据集的多样性提供了保障。

|
图 3 基础截面形状 Fig. 3 Foundation section shape |
自由几何变形方法具体为通过改变基础截面形状的长、宽比例来生成新的图形。本文采用此方法对21种基础图形类型处理来生成截面图形集合。
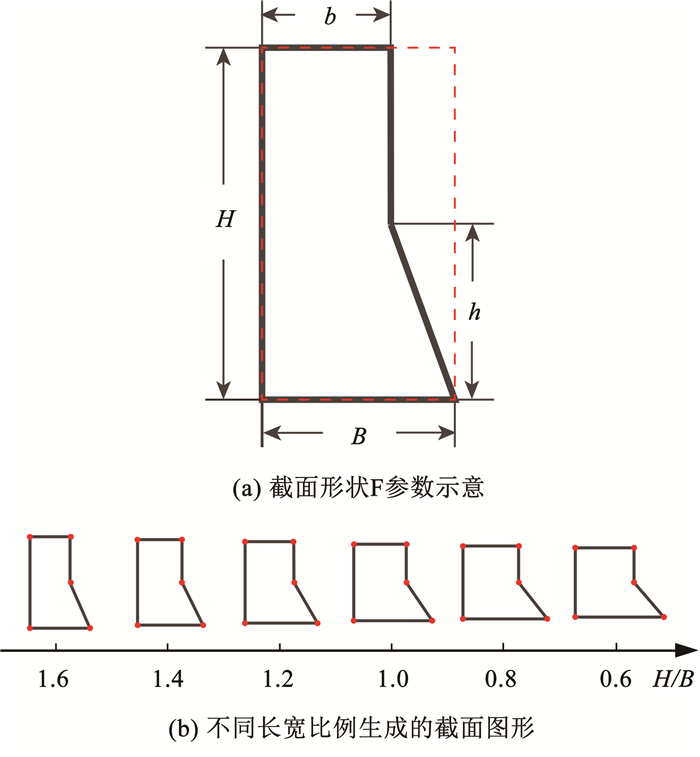
在进行自由几何变形之前需确定各基础截面形状长度与宽度的取值范围,如图 4(a)中基础截面形状F为例,首先固定H×B=10 000不变,由此确定以H和B作为长和宽所构成的矩形截面面积不变,设定长度H的变化范围为[50,200],在此范围内将长度H的变化范围划分为200个增量,每次按照0.75 cm的增量递增,生成不同长宽比例的截面图形,其中H=2h,B=3b/2。最终基础截面形状F共生成200个截面图形,将其命名为F1-F200。图 4(b)展示了不同长宽比例生成的截面图形。
|
图 4 基础截面形状F生成图形集合 Fig. 4 Graphic set generated by basic section shape F |
对剩余的基础截面形状同样使用自由几何变形方法处理,为保证生成截面图形的多样性以及防止生成不规则或不符合实际应用情况的图形,设定各基础截面形状H×B的取值不同,长度H取值变化范围也不同,最终生成不同的截面图形数量,各种截面生成截面图形数量见表 1,最终共计生成4 000个具有丰富几何特征的截面图形,充足的数据集保证了训练样本的多样性,其丰富程度基本满足了CNN模型对训练样本的要求。
| 表 1 各基础截面形状生成截面图形个数 Tab. 1 Number of random section shapes generated by each foundation section shape |
在对基础截面形状进行自由几何变形处理生成截面图形集合后,为避免无效区域的影响,对截面图形进行数据转换,将其颜色填充为黑色并将图像背景替换为灰色,其中截面形状位于整幅图片的中心位置,如图 5(a)、(b)所示。最终由21个基础截面形状生成的截面图形并经过数据转换后的图形集合如图 5(c)所示。

|
图 5 截面图形数据转换与图形集合展示 Fig. 5 Data conversion and graph collection display of sectional graphs |
本文将计算截面图形集合内各截面在均匀风场环境中,来流风速为20 m/s时的风力系数并制作数据标签。风力系数将采用有限元分析软件中的ICEM与FLUENT模块进行数值模拟得出。
2.2.1 数值模拟设置在对各起重机主梁截面进行数值模拟前需先进行流域设计,为了防止流域的边界对截面风力系数Xw的计算产生影响,经过多次实验后本文的流域将按图 6(a)进行设置。图中介绍了流场区域的大小、内、外流域的划分。其中H为主梁截面的高度,x为顺风方向,y为横风方向。

|
图 6 截面的数值模拟设置 Fig. 6 Numerical simulation settings for sections |
本文中各主梁截面图形的风场模拟实质上为高雷诺数下的钝体绕流模拟。整体流域的网格划分方法均使用ICEM中使用较为广泛的自适应网格划分法。图 6(b)展示了整体流域的网格划分示意图。
将整体流域划分为内、外流域分别使用不同尺寸的网格,计算域的外流域入口使用速度入口(velocity-inlet)作为边界条件;顶部与底部使用的是对称边界条件(symmetry)来模仿滑移的壁面;出口使用完全输出流(outflow)作为边界条件;主梁截面图形的边界使用无滑移壁面边界条件(wall);内、外流域采用内部面边界连接(interior)。为了使截面图形附近的网格能够达到更好的贴体效果,本文将内流域网格尺寸设置的较小。
2.2.2 网格无关性验证为了排除网格尺寸对整体数值计算结果的影响,本文采用4套大小不同的网格对流场域进行划分,分别对4套网格进行数值模拟计算,选取主梁截面顺风方向的风力系数Xw作为检测指标,4种网格数量、网格划分的具体设置及其对应的风力系数见表 2。由表 2中可知当网格数量达到19万及以上时,Xw稳定在2.65,其相对误差在0.76%以下,故本文中截面图形均采用19万及以上的网格数进行数值模拟。
| 表 2 4种网格数量计算结果 Tab. 2 Four kinds of grid number calculation results |
将上述收集的各主梁截面图形的坐标点导入ICEM CFD中,然后对整个流域进行网格划分,最终导入FLUENT求解器进行数值模拟后得到作用于主梁截面上的风力系数Xw。在进行数值模拟时选择双精度模式,计算模型选择RNG-ε标准湍流模型,采用稳态模拟,流场计算方法采用压力-速度耦合SIMPLE算法。
通过对数据集内各主梁截面图形的数值模拟,可以得到其对应的风力系数Xw、风压分布云图与流线图。选取截面面积相同的两种截面(A5, F5)的风压分布云图(如图 7所示)进行对比研究。由图 7中可以看出截面F5迎风边的风压较小,两种截面图形的背迎风区都出现了负压区且会有漩涡出现且漩涡的大小与位置有较小的差异。

|
图 7 不同截面图形压力云图 Fig. 7 Pressure nephogram of different cross-section graphics |
最后进行数据标注工作,将数值模拟得出的各截面风力系数Xw与得到的主梁截面图形相对应,制作截面图形的数据标签,最终生成起重机主梁截面数据集。
3 网络模型评测与优化 3.1 网络模型设计本文对前面提出的CNN基础模型进行训练,探究此模型在起重机主梁截面图形风力系数Xw预测上的性能。网络模型的输入为256×256大小的图像,数据集生成制作的起重机主梁截面数据集用以训练模型。经过多次实验本文将学习速率设定为2×10-3,衰减因子设定为5×10-3,为防止训练CNN模型时出现过拟合的情况本文采用早停法[30],为避免模型还在全图搜索阶段就结束训练,将早期停止步数设置为10。网络模型采用随机初始化参数,批处理值设置为256,使用Adams优化器。
3.2 模型性能评估为了评估CNN基础模型的预测能力,选取数据集内未被训练过的400组截面图形作为测试集。网络模型的性能主要通过对测试集风力系数Xw预测值的平均相对误差(average relative error, ARE)与最大相对误差(maximum relative error, MRE)来综合判定,其计算公式为:
| $\mathrm{ARE}=\frac{1}{m} \sum\limits_{i=1}^m\left|\frac{t_i-y_i}{t_i}\right|$ | (5) |
| $\mathrm{MRE}=\max \left|\frac{t_i-y_i}{t_i}\right|, i=1, 2, \cdots, m$ | (6) |
式中:ti为Xw真实值,yi为Xw预测值。
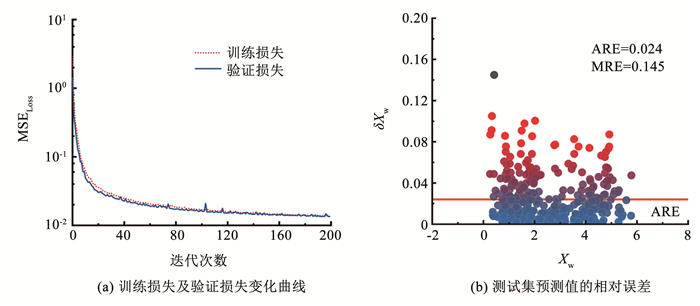
CNN模型训练过程中训练与验证的损失曲线如图 8(a)所示。使用训练好的网络模型对测试集内各截面图形对应的风力系数Xw进行预测,并评估此模型的性能,最终得到主梁截面图形风力系数预测值与真实值之间的相对误差δXw,如图 8(b)所示。
|
图 8 CNN基础模型训练结果 Fig. 8 CNN basic model training results |
从图 8中可以看出,利用此CNN预测模型得到测试集预测值的平均相对误差为2.40%,由此可见网络模型整体的预测性能相对较好。但仍有一些主梁截面图形的相对误差高达14.5%,因此CNN基础模型还需进一步优化,后续本文将展开对模型优化的研究。
3.3 模型优化卷积神经网络模型的结构设计会直接影响到模型的性能,本文将以此展开CNN基础模型的优化,主要通过改变卷积部分(P, N参数)和全连接部分(Q, M参数)来实现对网络结构的寻优。参数具体内容如图 9所示。

|
图 9 卷积部分(P, N参数)和全连接部分(Q, M参数) Fig. 9 Convolution part (P, N parameters) and full connection part (Q, M parameters) |
首先对卷积部分进行研究,将N值的变化范围设定为[2,128],P值的变化范围设定为[1,4],将全连接部分参数设定为(Q, M)=(1, 64)。测试集预测值的相对误差ARE与最大误差MRE作为优化目标。训练CNN模型后最终得到不同P值与N值对模型性能的影响曲线如图 10所示。从图 10中可知,随着N值的增加,网络模型的预测效果趋优。当(P, N)=(3, 64)时,整体模型的预测效果达到最佳,故CNN结构选定(P, N)=(3, 64)。

|
图 10 不同P值与N值对模型性能的影响 Fig. 10 Effect of different P and N values on model performance |
接着对全连接部分进行研究,将Q值的变化范围设定为[1,3],M值的变化范围设定为[2,64],将卷积部分参数设定为最优参数(P, N)=(3, 64)。训练CNN模型后得到不同Q值和M值对模型性能的影响曲线如图 11所示。从图 11中可知,当(Q, M)= (1, 32)时,整体模型的预测效果达到最佳,因此最终的CNN结构选定(Q, M)=(1, 32)。

|
图 11 不同Q值与M值对模型性能的影响 Fig. 11 Effect of different Q and M values on model performance |
经过对CNN基础模型的优化研究,最终本文使用的CNN结构如图 12所示。经过优化的网络结构具有更好地预测性能。其相对误差为1.85%,较优化前降低了23.20%,其最大误差为8.59%,较优化前降低了40.70%,由此可知模型优化取得了较为明显的效果。

|
图 12 优化后的CNN结构 Fig. 12 Optimized CNN structure |
本文统计了当截面数量为1、10、30、100、500时使用有限元分析软件中FLUENT模块进行数值模拟达到收敛条件时所需的时间,同时统计CNN预测方法在输入不同截面数量后进行运算所需的时间并对两种方法进行对比,如图 13所示。通过对比图 13可知CNN预测方法较传统的CFD方法计算效率提高了近100倍,并且随着计算样本数量的增多CNN预测方法的效率会更高。

|
图 13 时间对比 Fig. 13 Time comparison |
起重机主梁截面的防风性能是结构优化设计的重要参考指标。本文将主梁截面的最小风力系数Xw作为目标进行优化设计,基于CNN预测模型与遗传算法建立的主梁截面图形优化设计方法可以大大提升结构优化设计的效率,对提高起重机的防风性能具备重要意义。
4.1 截面参数化模型截面的参数化模型对结构优化设计的质量有着重要的影响,首先设定优化前的起重机主梁截面图形高度为h0,面积为S0。考虑到结构设计的牢固性与合理性,优化设计后的主梁截面靠近中部位置的宽度不宜过小,故将主梁截面图形宽度的自由变形分为3部分进行控制,分别由截面图形上端的控制点pi, qi{i=1, …, (1/20)n}(占总控制点数n的5%) 与图形中部的控制点pk, qk{k=(1/20)n+1, …, (19/20)n-1}(占总控制点数的90%)以及图形下端的控制点pi, qi{i=(19/20)n, …, n}(占总控制点数的5%)进行控制,其中总控制点数n的取值与优化前主梁截面图形高度h0一致,即n=h0,且n、(1/20)n、(19/20)n值皆取整数。为了简化截面优化设计的难度,将截面宽度控制点pi, qi, pk, qk的取值设定为整数。主梁截面控制点图如图 14所示,同时需确定截面各控制点的变化范围,截面优化后的图形高度h与优化前图形高度h0一致,优化后的图形面积S与优化前图形面积S0一致。截面图形上端、中端以及下端控制点取值范围不同,各控制点的变化范围见表 3。

|
图 14 截面图形参数 Fig. 14 Section graphics parameters |
| 表 3 主梁截面参数化变量信息 Tab. 3 Parametric variable information of main beam section |
由本文卷积神经网络可知,CNN预测模型的输入为128×128尺寸的主梁截面图形,并将其像素值进行归一化处理。因此本文中CNN模型的输入可视为128×128的像素值矩阵,图 15为起重机主梁截面图形F11的像素值矩阵示意图。由图 15中可以看出像素矩阵内各个位置的数值都代表着不同的几何意义,因此主梁截面图形通过参数化模型进行自由变化时,像素值也在不断变化。

|
图 15 截面图形F11的像素矩阵 Fig. 15 Pixel matrix of cross-sectional pattern F11 |
本文采用遗传算法[31]进行起重机主梁截面图形的优化设计,其基本流程为:
1) 首先随机产生N个初始种群并使用实数编码的方式进行编码,本文将风力系数Xw作为适应度值,评价种群中每个染色体个体的适应度;
2) 采用轮盘赌法对初始种群按照概率选择染色体个体生成新的种群,概率与适应度值密切相关。最终繁衍得到下一代个体生成新的种群;
3) 确定交叉、变异的概率值以便实现算法的随机性。对得到的新种群进行交叉、变异逐步迭代产生新群体;
4) 重复上述步骤,利用适应度值评价种群的优劣,当输出最优解或者迭代次数达到设置的上限时迭代结束。
本文构建的优化设计方法总体流程图如图 16所示。本优化方法首先采用截面参数化模型生成主梁截面图形,在输入CNN前对其进行像素缩放与像素值归一化处理后生成对应的像素矩阵,从而生成第1代子种群。然后根据生成的像素矩阵将其导入到训练好的CNN预测模型中,基于预测模型对起重机主梁截面图形的风力系数进行预测,并以风力系数Xw最小为目标进行目标优化。

|
图 16 基于CNN预测模型与遗传算法的主梁截面图形优化流程 Fig. 16 Optimization process of main beam section raphics based on CNN prediction model and genetic algorithm |
本文选取F11起重机主梁截面进行优化设计,F11主梁截面优化前高度h0为134 cm,面积S0为8 375 cm2。优化目标为风力系数Xw最小,结合各设计变量的取值范围,优化模型的数学描述为
| ${\rm s.t.}\begin{cases} S=S_0 & \\ p_i, q_i \in[0, 100], & i=1, \cdots, 7, 127, \cdots, 134 \\ p_k, q_k \in[20, 100], & k=8, \cdots, 126 \\ h=h_0\end{cases}$ | (7) |
式中:S为F11截面图形优化后的面积,pi, qi, pk, qk为截面宽度控制变量,h为截面高度设计变量。
在进行目标寻优时,种群初始化大小设置为300,交叉概率设置为0.7,变异概率设置为0.3,迭代次数设置为150。优化收敛过程如图 17所示。

|
图 17 优化收敛曲线 Fig. 17 Optimization convergence curve |
由收敛曲线可知当迭代步数为102时主梁截面F11的风力系数收敛至最小值。优化前、后的风力系数Xw与主梁截面高度、面积的对比见表 4。
| 表 4 优化前、后风力系数、高度与面积对比 Tab. 4 Comparison of wind coefficient, height and area before and after optimization |
由表 4可知,优化后的F11起重机主梁截面风力系数降低了15.89%,主梁截面的变量范围与主梁截面的面积都严格满足约束。优化前、后的截面压力云图如图 18所示,由风压分布云图可以看出,优化后的F11主梁截面迎风边的风压相较于优化前削弱了,因此风力系数Xw减小。同时,优化后截面的背迎风区的负压区中的漩涡的数量与位置也发生了变化。

|
图 18 优化前、后截面图形压力云图 Fig. 18 Pressure nephogram of the cross-section graphics before and after optimization |
1) 本文提出的风力系数快速预测模型在预测各主梁截面的风力系数时,其预测结果相对误差在9%以内,具有较好的可靠性。
2) 本文所提出的风力系数快速预测模型在获取起重机主梁截面风力系数上的效率相比传统CFD方法提升了百倍以上,可以极大地降低风力系数计算的时间和成本。
3) 应用本文所提出的起重机主梁截面优化设计方法优化后的截面,其防风性能较优化前得到了显著提高,证明了本文优化方法的有效性。
| [1] |
刘立成. 基于风洞试验的岸桥风载数值模拟方法研究及应用[D]. 武汉: 武汉理工大学, 2019 LIU Licheng. Research and application of numerical simulation method for wind loads of container cranes based on wind tunnel test[D]. Wuhan: Wuhan University of Technology, 2019. DOI: 10.27381/d.cnki.gwlgu.2019.001111 |
| [2] |
周铸, 黄江涛, 黄勇, 等. CFD技术在航空工程领域的应用、挑战与发展[J]. 航空学报, 2017, 38(3): 020891. ZHOU Zhu, HUANG Jiangtao, HUANG Yong, et al. CFD technology in aeronautical engineering field: Applications, challenges and development[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 020891. DOI:10.7527/S1000-6893.2016.0311 |
| [3] |
张淼, 刘铁军, 马涂亮, 等. 基于CFD方法的大型客机高速气动设计[J]. 航空学报, 2016, 37(1): 244. ZHANG Miao, LIU Tiejun, MA Tuliang, et al. High speed aerodynamic design of large civil transporter based on CFD method[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 244. DOI:10.7527/S1000-6893.2015.0331 |
| [4] |
CARY A W, CHAWNER J, DUQUE E P, et al. Correction: CFD vision 2030 road map: Progress and perspectives[C]//Proceedings of the AIAA Aviation 2021 Forum, Virtual Event. Reston, Virginia: AIAA, 2021: AIAA2021-2726. DOI: 10.2514/6.2021-2726
|
| [5] |
JAMESON A, VASSBERG J C. Computational fluid dynamics for aerodynamic design: Its current and future impact[C]//Proceedings of the 39th Aerospace Sciences Meeting and Exhibit. Reston, Virigina: AIAA, 2001: AIAA2001-538. DOI: 10.2514/6.2001-538
|
| [6] |
RAISSI M, WANG Zhicheng, TRIANTAFYLLOU M S, et al. Deep learning of vortex-induced vibrations[J]. Journal of Fluid Mechanics, 2019, 861: 119. DOI:10.1017/jfm.2018.872 |
| [7] |
HUANG Jianqing, LIU Hecong, CAI Weiwei. Online in situ prediction of 3-D flame evolution from its history 2-D projections via deep learning[J]. Journal of Fluid Mechanics, 2019, 875: R2. DOI:10.1017/jfm.2019.545 |
| [8] |
XIONG H Y, ALIPANAHI B, LEE L J, et al. The human splicing code reveals new insights into the genetic determinants of disease[J]. Science, 2015, 347(6218): 144. DOI:10.1126/science.1254806 |
| [9] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436. DOI:10.1038/nature14539 |
| [10] |
黄继鸿, 苏红莲, 赵新华. 基于BP神经网络的翼型空气动力系数预测[J]. 航空工程进展, 2010, 1(1): 36. HUANG Jihong, SU Honglian, ZHAO Xinhua. Aerodynamic coefficient prediction of airfoil using BP neural network[J]. Advances in Aeronautical Science and Engineering, 2010, 1(1): 36. DOI:10.16615/j.cnki.1674-8190.2010.01.018 |
| [11] |
MIYANAWALA T P, JAIMAN R. An efficient deep learning technique for the navier-stokes equations: Application to unsteady wake flow dynamics[J]. ArXiv preprint: 1710.09099v3, 2017: 1. DOI: 10.48550/arXiv.1710.09099
|
| [12] |
MAULIK R, SHARMA H, PATEL S, et al. Accelerating RANS turbulence modeling using potential flow and machine learning[J]. ArXiv preprint, ArXiv: 1910.10878v2, 2019: 1. DOI: 10.48550/arXiv.1910.10878
|
| [13] |
ZHANG Zhen, SONG Xudong, YE Shuran, et al. Application of deep learning method to reynolds stress models of channel flow based on reduced-order modeling of DNS data[J]. Journal of Hydrodynamics, 2019, 31(1): 58. DOI:10.1007/s42241-018-0156-9 |
| [14] |
HUI Xinyu, BAI Junqiang, WANG Hui, et al. Fast pressure distribution prediction of airfoils using deep learning[J]. Aerospace Science and Technology, 2020, 105: 105949. DOI:10.1016/j.ast.2020.105949 |
| [15] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294. CHEN Hai, QIAN Weiqi, HE Lei. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294. DOI:10.7638/kqdlxxb-2017.0098 |
| [16] |
李乔, 杨兴旺. 桥梁主梁断面空气力学特性分析的人工神经网络方法[J]. 中南公路工程, 2000, 25(3): 56. LI Qiao, YANG Xingwang. Artificial neural network method for aerodynamic characteristics analysis of bridge girder section[J]. Central South Highway Engineering, 2000, 25(3): 56. DOI:10.3969/j.issn.1674-0610.2000.03.024 |
| [17] |
陈讷郁, 葛耀君. 基于人工神经网络的典型桥梁断面气动参数识别[J]. 土木工程学报, 2019, 52(8): 91. CHEN Neyu, GE Yaojun. Aerodynamic parameter identification of typical bridge sections based on artificial neural network[J]. China Civil Engineering Journal, 2019, 52(8): 91. DOI:10.15951/j.tmgcxb.2019.08.008 |
| [18] |
KUTZ J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1. DOI:10.1017/jfm.2016.803 |
| [19] |
杨科, 王会社, 徐建中, 等. 基于CFD技术的高性能风力机翼型最优化设计方法[J]. 工程热物理学报, 2007, 28(4): 586. YANG Ke, WANG Huishe, XU Jianzhong, et al. Optimization and design method research of wind turbine airfoils based on CFD technique[J]. Journal of Engineering Thermophysics, 2007, 28(4): 586. DOI:10.3321/j.issn:0253-231X.2007.04.014 |
| [20] |
琚亚平, 张楚华. 基于人工神经网络与遗传算法的风力机翼型优化设计方法[J]. 中国电机工程学报, 2009, 29(20): 106. JU Yaping, ZHANG Chuhua. Optimal design method for wind turbine airfoil based on artificial neural network model and genetic algorithm[J]. Proceedings of the CSEE, 2009, 29(20): 106. DOI:10.13334/j.0258-8013.pcsee.2009.20.018 |
| [21] |
DELRIO-CHANONA E A, WAGNER J L, ALI H, et al. Deep learning-based surrogate modeling and optimization for microalgal biofuel production and photobioreactor design[J]. AIChE Journal, 2019, 65(3): 915. DOI:10.1002/aic.16473 |
| [22] |
LI Jichao, ZHANG Mengqi, MARTINS J R R A, et al. Efficient aerodynamic shape optimization with deep-learning-based geometric filtering[J]. AIAA Journal, 2020, 58(10): 4243. DOI:10.2514/1.j059254 |
| [23] |
徐健. 基于深度学习的水翼绕流特性预测及结构设计优化研究[D]. 镇江: 江苏大学, 2021 XU Jian. Research on flow characteristics prediction and optimization of hydrofoil based on deep learning[D]. Zhenjiang: Jiangsu University, 2021. DOI: 10.27170/d.cnki.gjsuu.2021.001558 |
| [24] |
VIQUERAT J, HACHEM E. A supervised neural network for drag prediction of arbitrary 2D shapes in laminar flows at low Reynolds number[J]. Computers & Fluids, 2020, 210: 104645. DOI:10.1016/j.compfluid.2020.104645 |
| [25] |
ZHANG Yao, SUNG W J, MAVRIS D N. Application of convolutional neural network to predict airfoil lift coefficient[C]//Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, Virginia: AIAA, 2018: AIAA2018-1903. DOI: 10.2514/6.2018-1903
|
| [26] |
李少鹏, 李海, 李珂. 基于深度学习的钝体断面外形气动性能高效预测方法[J]. 土木与环境工程学报(中英文), 2024, 46(1): 1. LI Shaopeng, LI Hai, LI Ke. An efficient deep learning prediction method for aerodynamic performance based on the shape of the main beam[J]. Journal of Civil and Environmental Engineering, 2024, 46(1): 1. DOI:10.11835/j.issn.2096-6717.2022.025 |
| [27] |
KETKAR N. Deep learning with python[M]. Berkeley, CA: Apress, 2017. DOI:10.1007/978-1-4842-2766-4
|
| [28] |
柴聪聪, 王强, 易贤, 等. 基于卷积神经网络的结冰翼型气动参数预测[J]. 飞行力学, 2021, 39(5): 13. CHAI Congcong, WANG Qiang, YI Xian, et al. Aerodynamic parameters prediction of airfoil ice accretion based on convolutional neural network[J]. Flight Dynamics, 2021, 39(5): 13. DOI:10.13645/j.cnki.f.d.20210811.001 |
| [29] |
M技术委员会F.E. 欧洲起重机械设计规范[S]. 上海: 上海振华港口机械公司译丛, 1998
|
| [30] |
HECKEL R, YILMAZ F F. Early stopping in deep networks: Double descent and how to eliminate IT[J]. ArXiv, 2021, abs/2007.10099v2: 4. DOI: 10.48550/arXiv.2007.10099
|
| [31] |
KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: Past, present, and future[J]. Multimedia Tools and Applications, 2021, 80(5): 8091. DOI:10.1007/s11042-020-10139-6 |
 2023, Vol. 55
2023, Vol. 55


