2. 跨流域空气动力学重点实验室(中国空气动力研究与发展中心),四川 绵阳 621000;
3. 中国空气动力研究与发展中心 超高速空气动力研究所,四川 绵阳 621000
2. Laboratory of Aerodynamics in Multiple Flow Regimes (China Aerodynamics Research and Development Center), Mianyang 621000, Sichuan, China;
3. Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China
锂离子电池生产的核心——电池极片[1],对其原料(涂炭铜箔、涂炭铝箔)有着极高的清洁要求,然而微米、亚微米级的颗粒黏附在边界层中难以去除[2-5],已经成为影响电池极片制造的主要因素之一。近年来,国内、外学者对超声波清洗设备进行了大量研究[6-7],期望通过超声波频率高、方向性强且能量集中等特点将黏附在材料表面的微粒去除[8],其中干式超声清洗设备因为其结构简单、效果稳定、维护成本低等特点,迅速成为清洗电池极片材料的主流[9]。
在实验方面,文献[10]发现高速气流通过矩形空腔可以发生振荡产生强烈的声波能。文献[11-12]提出了预测矩形空腔模型下流激振荡频率的经验公式, 后由文献[13]结合实验进行改进。文献[14]将空腔的振动激励分为:1)流体动力学相互作用;2)流体与声学模态共振;3)流体与弹性壁面作用。文献[15]设计了一种通过结构内流激振荡产生超声波的清洗装置。文献[16]建立模型解释了微粒受力类型和数量以及边界层的影响,并进行实验验证。文献[17]建立了风洞实验平台,研究了管道声学驻波模态与剪切层自激振荡模态的耦合关系。文献[18]设计了干式超声清洗效果评价实验。文献[19]研究了腔体形状变化对超声清洗机构流速的影响,并设计实验测量了结构的超声频率。在数值方面,文献[20]对长宽比为2的空腔流动进行气动声学数值计算,提出腔体前缘二次发声现象。文献[21]结合自激振荡发声机理,提出空腔流场中脱落涡—声波—新脱落涡—新声波的回路特点,指出空腔声压级幅值主要集中在低阶模态、能量主要集中在低频区域。文献[22]分析了腔体结构、压力引起的超声波声压级和频率变化,并利用离散相模型分析了颗粒轨迹。文献[23]建立了微粒的力学模型和颗粒悬浮模型,分析了气流速度和空腔的形状、结构等因素对流激振荡的影响。
然而对干式超声清洗技术,目前还存在以下问题:1)其作为锂电、半导体行业下游企业核心技术,长期由日本、韩国垄断,国内使用的清洗头主要依赖进口,随时面临“卡脖子”风险;2)国内针对该技术的研究鲜有报道,清洗头流道结构加工难度高、精度要求高、工艺成本高。
本文基于CFD技术,对不同尺寸腔体流场、声场特性进行研究,以改进超声清洗头腔体设计。首先对干式超声波清洗技术和空腔发声机理简要阐述,为空腔结构设计提供依据。随后对所设计的腔体进行数值模拟,通过分析其流场和声场特性并与发声机理相互验证,定性地证明了结构的有效性。最后对全文工作进行总结。
1 干式超声清洗技术 1.1 技术原理灰尘附着在被清洗材料表面属于典型的物理吸附过程[24],使用物理的清洗方式即可实现颗粒的定量脱附[25]。传统的干式清洗装置,多采用高速气流(风刀)作为媒介清洗材料表面灰尘,即通过高速气流吹走材料表面的微粒。然而,由于边界层的存在,材料表面的微米级、亚微米级微粒黏附于边界层中,难以被风刀清洗。为了破坏相对稳定的边界层,一种理论上可行的方式是引入超声波发生装置,希望通过超声波的高频振荡,促进微粒与边界层脱离,使其进入高速气流中,达到材料表面清洁的目的。
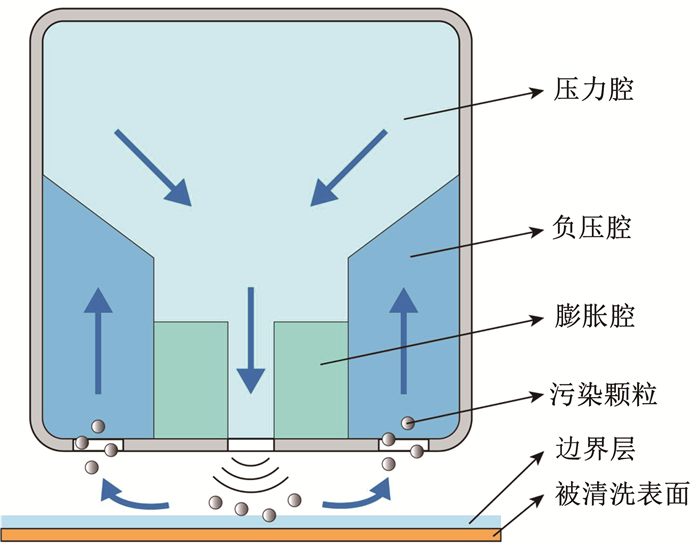
目前,干式超声波清洗技术主要由日本、韩国两国掌握,干式超声清洗头主要依赖于进口。随着近年来中国锂电、半导体行业的发展,对干式超声清洗设备研发的需求愈发紧迫。干式超声波清洗的原理如图 1所示,压力腔内高速气流流经膨胀腔,经过阵列的变截面空腔结构时气体膨胀—压缩—再膨胀—再压缩,在流场和声场的耦合作用下产生强烈超声波[26-28],通过压力腔底部的狭缝出口流出,作用在材料表面的边界层上,边界层内的粒子发生再悬浮作用,跟随气流被吸入负压腔,从而达到除尘效果。
|
图 1 干式超声波清洗机构原理图 Fig. 1 Schematic diagram of dry ultrasonic cleaning mechanism |
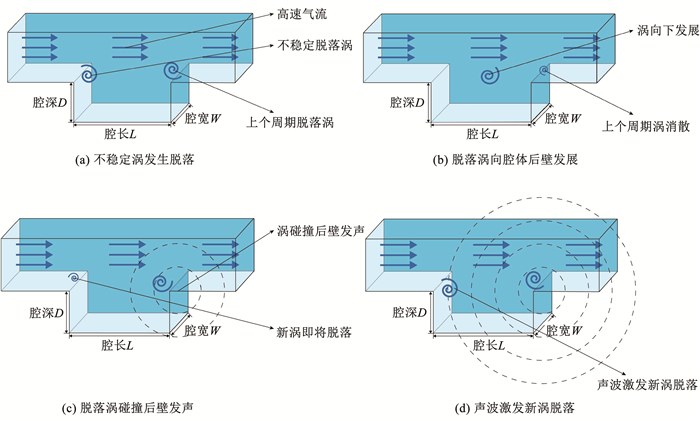
针对长度与深度比值小于10的开放式空腔[29],其自由剪切层[30]激发空腔自激振荡从而诱导空腔噪声产生,其原理如图 2所示。当高速气流流经特殊的阵列变截面流道时,在连续的时间周期中某一时间段内,空腔的前缘剪切层沿腔体深度方向发展形成了涡(如图 2(a)所示),这个涡随着气流向腔体中部发展(如图 2(b)所示),最终与腔体后壁碰撞产生声波(如图 2(c)所示),声波在传到腔口前缘时激发了下一个涡的脱落(如图 2(d)所示),新的脱落涡采用相同方式产生二次噪声,二次噪声波再回传到腔口前缘壁面,继续激发下一个脱落涡生成。故而在腔体内部,不断进行着一次涡脱落——一次声波——二次涡脱落——二次声波的一个反馈机制[21],进而在流场涡的自然频率与空腔的声学共振频率相近时,流场内气体流动形成自激振荡,振荡频率足够高时超声波由此产生。
|
图 2 空腔流激振荡原理图 Fig. 2 Schematic diagram of cavity fluid-induced oscillation |
在文献[11-12]的理论中,假设脱落涡的频率与反馈声波频率相同,则其频率应满足如下关系:
| $f_m=\frac{\kappa u_c}{\lambda_v}=\frac{c}{\lambda_c}$ | (1) |
式中: uc为气流流速, κ为涡迁移速度与自由流速度之比, λv为涡运动的波长, c为声速, λc为反馈声波波长。
根据空腔流激振荡的反馈机制,涡运动的相位、声波运动的相位以及激发新涡产生的相位滞后共同组成一个完整的周期,三者关系可表示为
| $2 \pi \frac{L}{\lambda_v}+2 \pi \frac{L}{\lambda_c}+2 \pi \beta=2 \pi m$ | (2) |
式中: L为图 2所示的空腔长度, β为时间滞后系数, m为空腔流激振荡声学模态阶数,其值为正整数。
联立式(1)、(2)可得到量纲一的频率Sm表达式为
| $S_m=\frac{f_m L}{u_c}=\frac{m-\beta}{M a+1 /\kappa}$ | (3) |
式中Ma为气流马赫数,Ma=uc/c。
文献[13]对文献[11-12]的公式进行了修正,提高了预测精度,其改进后的量纲一的频率Sm的表达式为
| $S_m=\frac{f_m L}{u_c}=\frac{m-0.25 \times\left(1-0.35 \times 10^{(0.8-M a)}\right)}{M a\left(1+0.2 \times M a^2\right)^{-0.5}+1.75}$ | (4) |
利用式(4)可以对不同模态下空腔流激振荡频率做出合理的分析和预估。
1.2.2 流体与声学模态共振相互作用流道中高速气流内不稳定的剪切层在跨出腔口时不断起伏作为振动的激励,使腔体在其特征频率上产生驻波模态振荡[17]。文献[31]指出空腔的壁面会反射腔内产生的声波,在一定条件下形成由空腔几何尺寸确定的声学驻波模态。当空腔的剪切层自激驻波模态振荡频率与声学驻波模态振荡频率接近时,将诱导流场和声场共振,产生流体与声学模态共振相互作用,当振荡频率足够高时超声波由此产生。
由于矩形腔刚性壁面上质点速度为0,则有:
| $\left.u_1\right|_{x_1=0, x_1=L}=0, \left.u_2\right|_{x_2=0, x_2=W}=0, \left.u_3\right|_{x_3=0, x_3=D}=0$ | (5) |
式中:L为腔体长度, W为腔体宽度, D为腔体深度。
空腔内声场的波动方程和其解pn可表达为[23]:
| $\frac{\partial^2 p}{\partial x_1^2}+\frac{\partial^2 p}{\partial x_2^2}+\frac{\partial^2 p}{\partial x_3^2}=\frac{1}{c_0^2} \cdot \frac{\partial^2 p}{\partial t^2}$ | (6) |
| $p_n(x, t)=A_{n_1, n_2, n_3} \cos k_1 x_1 \cos k_2 x_2 \cos k_3 x_3 \cdot \mathrm{e}^{\mathrm{i} \omega_n t}$ | (7) |
式中:k1=n1π/L, k2=n2π/W, k3=n3π/D, ni(i=1, 2, 3)分别为图 3所标注的空腔长度方向、深度方向、宽度方向的轴向波模态阶数; An1, n2, n3cosk1x1cosk2x2cosk3x3为振动的幅值;ωn为空腔内声波的圆频率,通过pn可描述空腔中压力的波动状态。

|
图 3 流体与声学模态共振原理图 Fig. 3 Schematic diagram of fluid and acoustic modal resonance |
根据式(7)和空腔内声波圆频率ωn=2πfn可得
| $f_n=\frac{\omega_n}{2 \pi}=\frac{c}{2} \cdot \sqrt{\left(\frac{n_1}{L}\right)^2+\left(\frac{n_2}{W}\right)^2+\left(\frac{n_3}{D}\right)^2}$ | (8) |
式(8)描述了空腔内驻波共振的频率与腔体长度尺寸、深度尺寸、宽度尺寸以及振动的声学模态的关系。且振动频率的方向由模态阶数值确定,当其中两个方向的模态阶数值为零时,式(8)描述沿腔体某一边界方向的轴向驻波模态简正频率;当其中某一个方向的模态阶数值为零时,该式描述了沿腔体坐标轴的某一个切向方向的驻波模态简正频率;当3个方向的模态阶数值都不为零时,该式描述腔内某一斜向的驻波模态简正频率。
2 空腔数值模拟 2.1 结构设计与模型干式超声清洗头的流道结构如图 4(a)所示。研究拟根据两种不同发声机理,设计两种不同尺寸大小的变截面流道结构模型。腔体采用式(4)所示的发声机理时,若要其在一阶模态下频率fm达到超声频率,需满足如下条件:
| $f_m=\frac{m-0.25 \times\left(1-0.35 \times 10^{(0.8-M a)}\right)}{M a\left(1+0.2 \times M a^2\right)^{-0.5}+1.75} \times \frac{u_c}{L} \geqslant 20 \;\mathrm{kHz}$ | (9) |

|
图 4 腔体结构模型 Fig. 4 Diagram of cavity structure model |
文献[19]给出了气体流速与压强的关系:
| $V=\sqrt{\frac{2 P}{\rho}}$ | (10) |
式中:V为气体流速, P为给定压力, ρ为气体密度。
根据式(10)计算在10 kPa压力下气体流速为124.51 m/s,代入式(9)可得,腔体长度L为2.9 mm。考虑实际工况下压力条件略大,设计3 mm尺寸流道结构(下文简称小腔体)其结构如图 4(b)所示。该结构以双边设计的3 mm尺寸的方形腔为空腔,流道宽度为1 mm,流道下方设计有利于提高清洗效果的0.3 mm的狭缝气流出口[32]。在宽度方向上选取3 mm为计算模型。
腔体采用式(8)所示的发声机理时,由于沿腔体宽度切向方向的驻波模态简正频率清洗效果最强,故取n2=0,若要其在一阶模态下频率fm达到超声频率,需满足如下条件:
| $f_n=\frac{c}{2} \cdot \sqrt{\left(\frac{n_1}{L}\right)^2+\left(\frac{n_3}{D}\right)^2} \geqslant 20\; \mathrm{kHz}$ | (11) |
由于方腔结构L=D且均为一阶模态,可得L<12.02 mm。因此设计10 mm尺寸流道结构(下文简称大腔体),如图 4(c)所示。该结构以双边设计的10 mm尺寸的方形腔为空腔,流道宽度为3 mm,流道下方同样设计0.3 mm的狭缝气流出口。由于两类腔体均为开式空腔,其受宽度影响较小[33],为配合方形腔体,在宽度方向上选取10 mm为计算模型。
腔体部分为超声结构,狭缝正下方区域为清洗区域,流道两侧部分为负压腔入口,流道的下表面为被清洗材料的表面,通过传送带传送被清洗材料经过清洗头下方完成表面清洗。
2.2 计算方法和参数设置计算采用双精度求解器(double precision),密度基求解(density-based)。将计算分为稳态流场计算和瞬态声场计算两步骤进行。
2.2.1 稳态流场计算在定常条件下采用SST k-omega模型,开启能量方程(energe equation)和理想气体(ideal-gas)计算,收敛后得到稳态流场。
2.2.2 瞬态声场计算以稳态流场为初始条件,采用大涡模拟(large eddy simulation, LES)[34]中WALE(wall-adapting local eddy-viscosity)亚格子模型进行瞬态数值计算,采用FW-H(Ffowcs williams-Hawkings)[35]模型收集声压信号。
2.3 流动计算域及边界条件计算流域如图 4(b)、4(c)所示,设定超声结构上表面为压力入口(1号表面),负压腔上表面为压力出口(2号表面),其余面为壁面。出口压力统一设置为0(实际工况下为负压);入口边界压力值分别为10、15、20、25、30 kPa;壁面为绝热壁面、无滑移边界条件。
2.4 网格无关性验证分别为两个结构划分4种流场网格以验证网格无关性。选择流场最大速度变化作为衡量网格无关性因素,不同网格的计算结果如图 5所示。结果表明,在网格数量达到30万以上时,流场内最大流速趋于稳定。因此小腔体网格取31万,如图 6(a)所示;大腔体网格取33万进行计算,如图 6(b)所示。

|
图 5 网格无关性验证结果 Fig. 5 Mesh independence verification results |

|
图 6 腔体三维网格划分 Fig. 6 3D mesh generation of cavity |
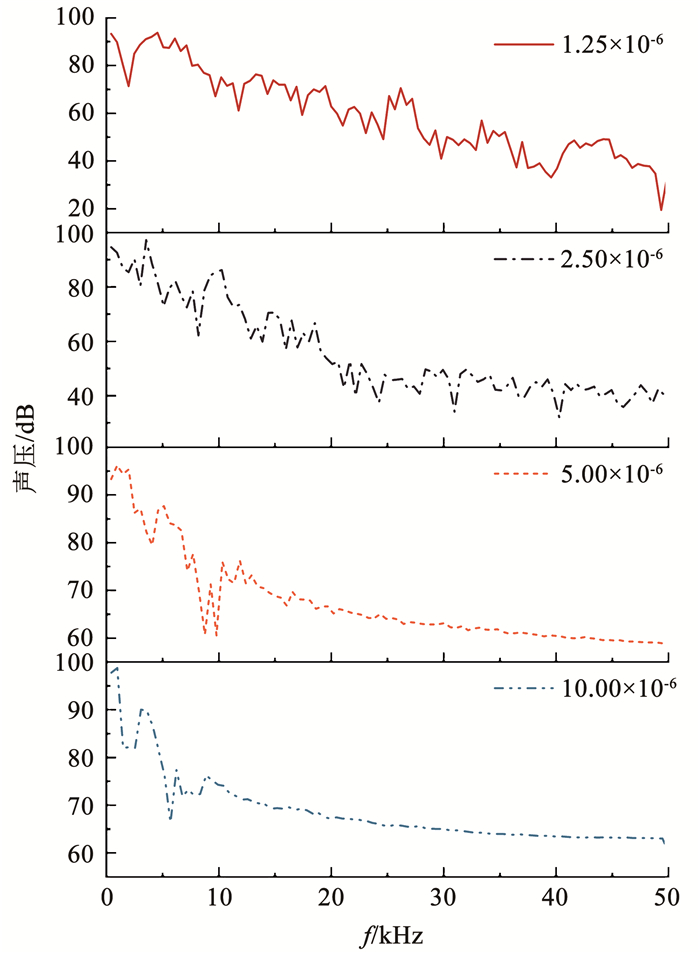
数值模拟时采用4个不同值来验证时间步长独立性。由于对瞬态声场进行分析,因此选择一段时间内流场底部中央点在流场中的声压频谱作为衡量时间步长独立性的关键因素,其结果如图 7所示。结果表明,当时间步长的精度为2.50×10-6 s及以上时,监测点处的声压频域曲线已经可以较好地反映流场的声学状态。因此时间步长选择2.50×10-6 s,以时间步数2 000步进行计算。
|
图 7 时间步长独立性验证结果 Fig. 7 Time step independence verification results |
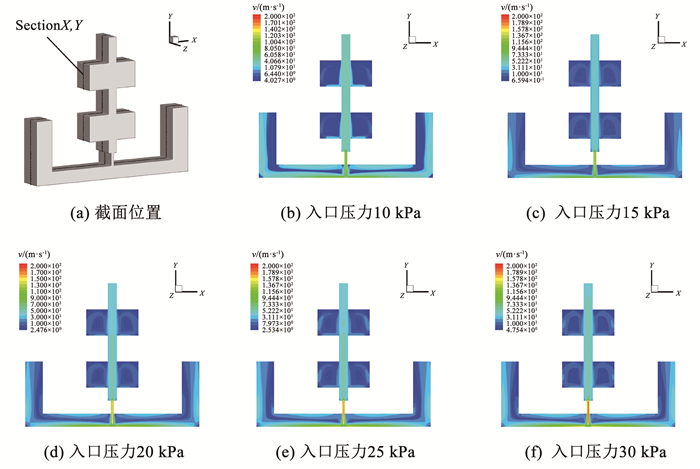
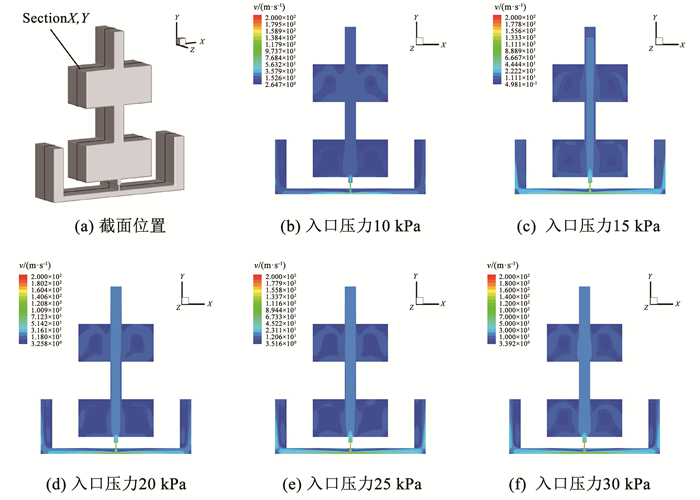
取空腔Z方向中点X、Y截面观察空腔内流场速度云图,截面位置如图 8(a)、图 9(a)所示。图 8(b)~8(f)、图 9(b)~9(f)分别为不同压力条件下X、Y截面的速度云图。从图 8、9中可以看出,两结构有着相似的流场特性,腔体内沿着方腔都形成了不同速度的涡流,随着压力的增加,腔体内的涡流速度增大。
|
图 8 不同压力下小腔体中心截面速度云图不同压力下小腔体中心截面速度云图 Fig. 8 Velocity nephogram of small cavity center section under different pressures |
|
图 9 不同压力下大腔体中心截面速度云图 Fig. 9 Velocity nephogram of large cavity center section under different pressures |
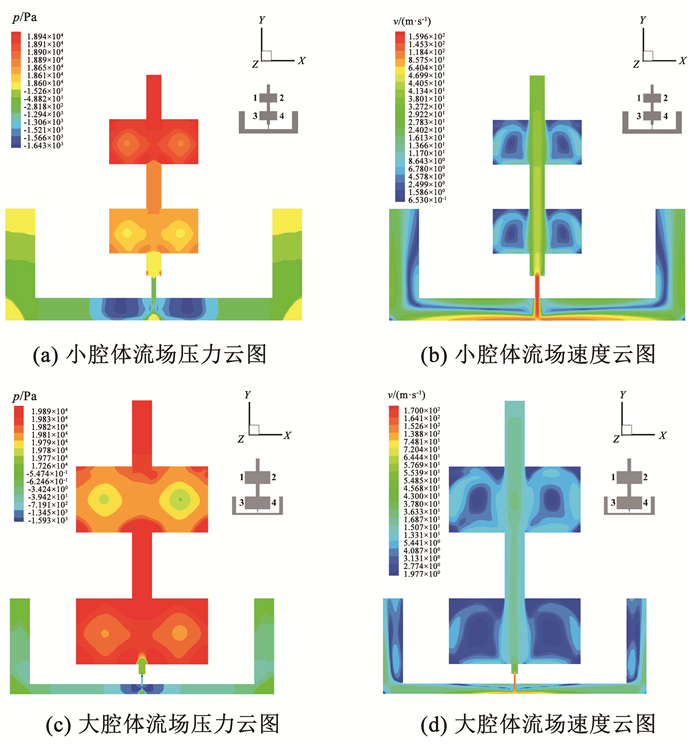
以20 kPa的入口压力条件下两腔体的流场为例进行分析。图 10(a)~10(d)分别给出了两个腔体在X, Y平面内压力分布云图以及速度云图。可以明显观察到,流场内的气流从压力入口进入腔体,经过双边方腔流道形成了一个加速效果,这与文献[19]结论相符,气流在狭缝出口处达到最大速度,最终通过流道两侧设计的负压腔流出结构。两种结构内气流的运动方式相同,Y轴方向上小腔体上方1号、2号方腔与下方3号、4号方腔流速接近,而大腔体上方1号、2号方腔流速略高于与下方3号、4号方腔,X轴方向上,由于腔体为轴对称结构,流场、压力场分布情况高度对称。对比两个结构在相同压力下的速度云图可以得出,大、小腔体内对应编号的方腔流速相差不大,其内部流激振荡情况还应结合声场情况加以分析。
|
图 10 相同压力下腔体中心截面压力云图和速度云图 Fig. 10 Pressurenephogram and velocity nephogram of central section of cavity under same pressure |
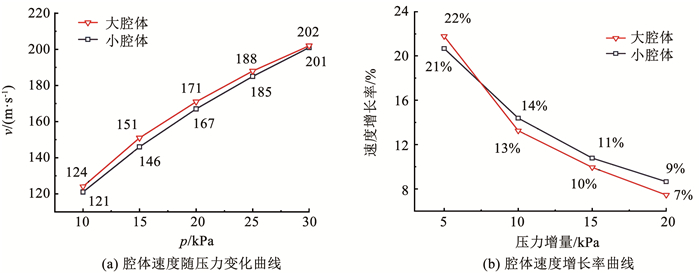
按照时间步长独立性验证中设置的边界条件进行数值计算,并记录两腔体在不同的入口压力条件下流场最大速度值,见表 1。为更直观的反映不同腔体、不同压力条件下流场最大速度的变化情况,根据表 1中的数据绘制两腔体速度随压力变化曲线,如图 11(a)所示。不同压力下速度增长率曲线,如图 11(b)所示。
| 表 1 腔体压力值与最大流速表 Tab. 1 Cavity pressure and maximum flow velocity |
|
图 11 流场速度曲线 Fig. 11 Velocity curve of flow field |
根据表 1中数据和图 11(a)可以得知,腔体内最大流速随压力的增大而增大,当压力达到30 kPa时,腔体气流速度最大,可以达到200 m/s以上。根据图 11(b)可以得知,随着压力的增大,速度的增长率逐渐下降。综合来看,两种不同的腔体在相同压力条件下最大速度相近、最大速度的增长率相近,进一步说明腔体内流场特性相似。
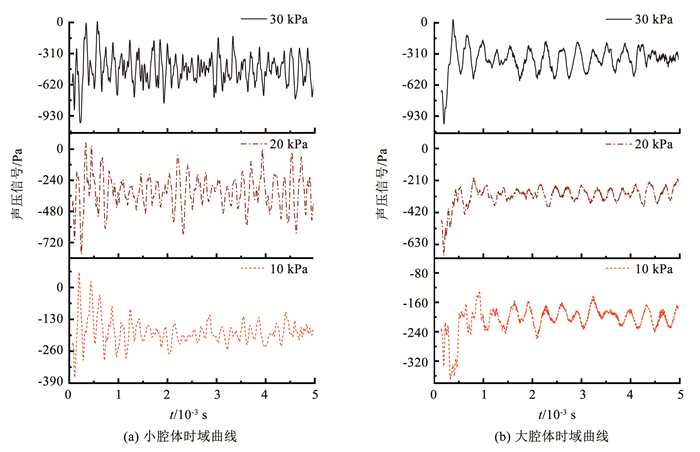
3.2 腔体声场特性分别选择两个腔体狭缝底部中央点布置声压监测点,其空间坐标为(0, 0, 0)。图 12(a)为小腔体监测点声场时域曲线、图 12(b)为大腔体监测点声场时域曲线。从时域曲线可以得出,两种结构流道中的监测点都存在随时间脉动的周期的声压信号,证明结构符合脉动气流破坏边界层除尘的基本构想。随着压力值从10 kPa增加至30 kPa,脉动信号的幅值明显增大,说明压力的增加有助于增强声压脉动强度。通过两腔体时域曲线对比可知,在相同的压力条件下,小腔体内声压脉动的幅值更大、声压变化的频率更快,产生的流激振荡更强烈。
|
图 12 腔体监测点声压时域曲线 Fig. 12 Time domain curve of sound pressure at monitoring points of cavity |
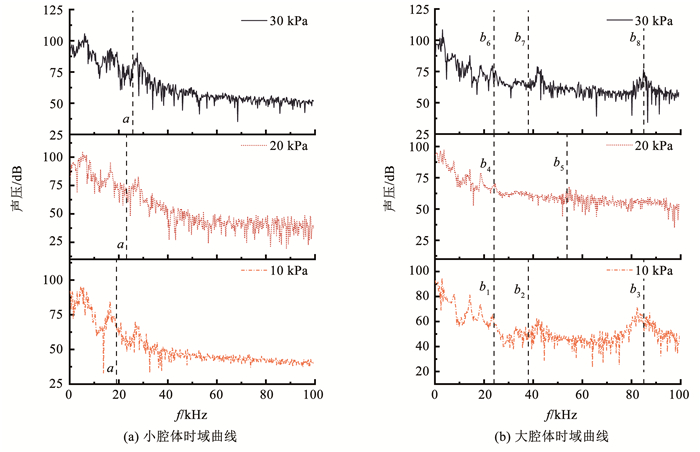
对上述的时域信号进行FFT变换得到腔体声场频域曲线,如图 13(a)、13(b)所示。观察得出,不同压力下两腔体频域曲线均存在声压级峰值,其纵坐标对应了声压级大小,横坐标对应了空腔发声频率,进而通过频谱特性证明了空腔内存在周期性的流激振荡。
|
图 13 腔体监测点声压频域曲线 Fig. 13 Frequency domain curve of sound pressure at monitoring points of cavity |
小腔体的声压级峰值主要出现在前3个峰值频率下,其中第3个峰值频率进入超声范围,证明该腔体可以产生超声波。通过式(4)对小腔体内流体动力学相互作用引起的声压频率进行计算,其预测值与实际值在表 2中给出,预测值位置如图 13(a)中参照线a所示。计算结果表明,式(4)预测频率与小腔体超声峰值频率接近,但存在一定误差,随着压力的增大,误差逐渐减小,此时腔内的超声波由腔内流体间相互作用产生。对比不同压力下小腔体声压频谱得出,压力的增加提高了声压级峰值,而峰值对应的频率并未明显提升。
| 表 2 小腔体预测频率与实际频率验证 Tab. 2 Verification of predicted frequency and actual frequency of small cavity |
大腔体的声压级频域曲线在低频部分与小腔体相似,而在超声频域范围内存在多个高频声压级峰值,证明大腔体可以产生超声波。通过式(8)对大腔体内流体与声学模态共振相互作用引起的声压频率进行计算,在表 3中给出与峰值频率相近的预测值,预测值位置如图 13(b)中参照线b1~b8所示。结果表明,式(8)所得的预测值与腔体内超声频率高度接近,说明此时腔体内超声波由流体与声学模态共振相互作用产生。
| 表 3 大腔体预测频率与实际频率验证 Tab. 3 Verification of predicted frequency and actual frequency of large cavity |
通过对比两腔体声压频域曲线发现,虽然两腔体结构相似、流场特性相似、频域曲线均存在声压级峰值,然而由于两腔体尺寸不同,其超声波产生机理也不同,在声压级峰值频率上存在较大差异。经过预测频率的计算与数值模拟的结果相互验证,说明超声除尘头的声场特性与其腔体尺寸相关,定性的证明了所设计的两种结构均能产生超声波。综合两腔体的流场和声场情况得出,超声波清洗头的流道结构设计并不局限于流体间流体力学相互作用发声的小腔体,而在入口压力与腔体结构的搭配下,其他尺寸的腔体同样可以达到产生强烈、高频超声波破坏边界层除尘的作用。在设计中将超声清洗头腔体合理放大,避免了原本小腔体的加工难、精度要求高、整体结构需要拼接等缺点。
4 结论1) 相同结构的流场特性相似。两种腔体都会在腔内形成涡流,涡流速度随压力增大而增大,当压力条件相同时,小腔体能激发更强烈的流激振荡。
2) 随压力的增加,腔体内最大速度增大,最大速度的增长率减小。当压力条件相同时,两腔体的最大速度和最大速度的增长率接近。
3) 两种结构均能产生超声波,其超声波发声机理与腔体尺寸相关。小腔体由流体间流体动力学相互作用发声,大腔体由流体与声学模态共振相互作用发声,与预测值相符。
4) 经过数值模拟和计算相互验证,干式超声波清洗头的流道结构可以结合空腔发声机理进行设计,为干式超声波清洗头的结构设计提供参考。
| [1] |
李茂源, 张云, 汪正堂, 等. 锂离子电池极片制造中的微结构演化[J]. 科学通报, 2022, 67(11): 1088. LI Maoyuan, ZHANG Yun, WANG Zhengtang, et al. Microstructure evolutions in lithium ion battery electrode manufacturing[J]. Chinese Science Bulletin, 2022, 67(11): 1088. |
| [2] |
QUESNEL D J, RIMAI D S, SCHAEFER D M. Aspects of particle adhesion and removal[M]//QUESNEL D J, RIMAI R S, SHARPE L H, et al. Developments in surface contamination and cleaning. Amsterdam: Elsevier, 2008: 475. DOI: 10.1016/b978-081551555-5.50009-5
|
| [3] |
GOTOH K, MIZUTANI K, TSUBOTA Y, et al. Enhancement of particle removal performance of high-speed air jet by setting obstacle in jet flow[J]. Particulate Science and Technology, 2015, 33(5): 567. DOI:10.1080/02726351.2015.1060653 |
| [4] |
BOWLING R A. An analysis of particle adhesion on semiconductor surfaces[J]. Journal of the Electrochemical Society, 1985, 132(9): 2208. DOI:10.1149/1.2114320 |
| [5] |
AHMADI G, GUO Shiguang, ZHANG Xinyu. Particle adhesion and detachment in turbulent flows including capillary forces[J]. Particulate Science and Technology, 2007, 25(1): 59. DOI:10.1080/02726350601146432 |
| [6] |
HARVEY G, GACHAGAN A, MUTASA T. Review of high-power ultrasound-industrial applications and measurement methods[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(3): 481. DOI:10.1109/TUFFC.2014.2932 |
| [7] |
BRETZ N, STROBEL J, KALTENBACHER M, et al. Numerical simulation of ultrasonic waves in cavitating fluids with special consideration of ultrasonic cleaning[C]//IEEE Ultrasonics Symposium. Rotterdam, Netherlands: IEEE, 2006: 703. DOI: 10.1109/ULTSYM.2005.1602948
|
| [8] |
ITO Y, SUDO M. Study on effectiveness of peeling off adhesion solid particles using high intensity aerial ultrasonic waves[J]. 振動·音響新技術シンポジウム講演論文集, 2001(1): 107. |
| [9] |
蒋旭堂, 郑筵谕, 祝楷博. 乾式清洗机机电系统设计及性能探讨[J]. 先进工程学刊, 2019, 14(2): 85. JIANG Shiutang, ZHENG Yanyu, Jhu Kaipo. An investigate in design and performance of electromechanical system for dry cleaner[J]. Journal of Advanced Engineering, 2019, 14(2): 85. |
| [10] |
KRISHNAMURTY K. Sound radiation from surface cutouts in high speed flow[D]. Pasadena, CA: California Institute of Technology, 1956
|
| [11] |
ROSSITER J E. Wind-unnel experiments on the flow over rectangular cavities at subsonic and transonic speeds: RAE Technical Report No. 64037[R]. Farnborough: Ministry of Aviation, Royal Aircraft Establishment, 1964
|
| [12] |
HELLER H H, BLISS D B. Aerodynamically induced pressure oscillations in cavitiesphysical mechanisms and suppression concepts: AFFDL-TR-74-133[R]. Ohio: Wright-Patterson Air Force Base, 1975
|
| [13] |
张强. 流动诱导空腔振荡频率方程的改进[J]. 振动工程学报, 2004, 17(1): 53. ZHANG Qiang. Development of the frequency equation used for prediction of fluid induced pressure oscillation in cavities[J]. Journal of Vibration Engineering, 2004, 17(1): 53. DOI:10.16385/j.cnki.issn.1004-4523.2004.01.014 |
| [14] |
ROCKWELL D, NAUDASCHER E. Review—self-sustaining oscillations of flow past cavities[J]. Journal of Fluids Engineering, 1978, 100(2): 152. DOI:10.1115/1.3448624 |
| [15] |
TAKADA S. Dust removing system for panellike bodies US5388304[P]. 1995-02-14
|
| [16] |
QI Quan, BRERETON G J. Mechanisms of removal of micron-sized particles by high-frequency ultrasonic waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1995, 42(4): 619. DOI:10.1109/58.393105 |
| [17] |
朱幼君. 管道空腔流声耦合振荡及压电振子流动控制技术的研究[D]. 上海: 上海交通大学, 2010 ZHU Youjun. Research on acoustic oscillation over the duct cavity and suppression with piezoelectric vibrator[D]. Shanghai: Shanghai Jiaotong University, 2010 |
| [18] |
史斐娜. 超声波干式清洗机机械系统设计与研究[D]. 太原: 中北大学, 2015 SHI Feina. Design and study on ultrasonic dry cleaning machine mechanical system[D]. Taiyuan: North University of China, 2015 |
| [19] |
蒋旭堂, 祝楷博, 郑筵谕. 超音波清洗头设计及性能探讨[J]. 先进工程学刊, 2019, 14(2): 93. JIANG Shiutang, JHU Kaipo, ZHENG Yanyu. An investigation in design and performance of an ultrasonic cleaner[J]. Journal of Advanced Engineering, 2019, 14(2): 93. |
| [20] |
李晓东, 刘靖东, 高军辉. 空腔流激振荡发声的数值模拟研究[J]. 力学学报, 2006, 38(5): 599. LI Xiaodong, LIU Jingdong, GAO Junhui. Numerical simulation of flow-induced oscillation and sound generation in a cavity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 599. DOI:10.3321/j.issn:0459-1879.2006.05.004 |
| [21] |
杨党国, 李建强, 梁锦敏. 基于CFD和气动声学理论的空腔自激振荡发声机理[J]. 空气动力学学报, 2010, 28(6): 724. YANG Dangguo, LI Jianqiang, LIANG Jinmin. Sound generation induced by self-sustained oscillations inside cavities based on CFD and aeroacoustic theory[J]. Acta Aerodynamica Sinica, 2010, 28(6): 724. DOI:10.3969/j.issn.0258-1825.2010.06.019 |
| [22] |
CHOI H, KIM T S. Numerical simulation of ultrasonic generator in dust removing system[J]. Advanced Materials Research, 2012, 488/489: 1446. DOI:10.4028/www.scientific.net/amr.488-489.1446 |
| [23] |
庞昊斐. 超声干式清洗技术的理论研究与应用[D]. 太原: 中北大学, 2017 PANG Haofei. Theory research and application of ultrasonic dry cleaning technology[D]. Taiyuan: North University of China, 2017 |
| [24] |
李艳强. 微颗粒在表面的粘附力学及其可视化应用研究[D]. 长沙: 中南大学, 2007 LI Yanqiang. Mechanics and visual application research of micro-particle adhesion on the surface[D]. Changsha: Central South University, 2007 |
| [25] |
崔燕. 微米级固体颗粒的分形及其与界面间粘附力的关系研究[D]. 长沙: 中南大学, 2011 CUI Yan. Investigation on the relationship between adhesion force and the fractal characteristics of solid micro-particle[D]. Changsha: Central South University, 2011 |
| [26] |
BARTEL H W, MCAVOY J M. Cavity oscillation in cruise missile carrier aircraft: AFWALTR-81-3036[R]. Bethesda: Lockheed-Georgia Co Marietta Structures Technology Div, 1981
|
| [27] |
LAMP A M, CHOKANI N. Computation of cavity flows with suppression using jet blowing[J]. Journal of Aircraft, 1997, 34(4): 545. DOI:10.2514/2.2207 |
| [28] |
ARUNAJATESAN S, SINHA N, MENON S. Towards hybrid LES-RANS computations of cavity flowfields[C]//Proceedings of the 38th Aerospace Sciences Meeting and Exhibit. Reston, Virigina: AIAA, 2000: AIAA2000-401. DOI: 10.2514/6.2000-401
|
| [29] |
SAROHIA V, MASSIER P F. Control of cavity noise[J]. Journal of Aircraft, 1977, 14(9): 833. DOI:10.2514/3.58862 |
| [30] |
张强, 李启, 李青. 喷口自由剪切层自激振荡优势频率的预测[J]. 南京航空航天大学学报, 2004, 36(2): 257. ZHANG Qiang, LI Qi, LI Qing. Prediction of dominant frequency of self-sustaining oscillation derived from free shear layer[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(2): 257. DOI:10.16356/j.1005-2615.2004.02.025 |
| [31] |
MCGREGOR O W, WHITE R A. Drag of rectangular cavities in supersonic and transonic flow including the effects of cavity resonance[J]. AIAA Journal, 1970, 8(11): 1959. DOI:10.2514/3.6032 |
| [32] |
LIN Hong. Chemical and particulate contamination removal from patterned and nonpatterned semiconductor surfaces using oscillating flow[D]. Potsdam, NY: Clarkson University, 2001
|
| [33] |
CROW S C, CHAMPAGNE F H. Orderly structure in jet turbulence[J]. Journal of Fluid Mechanics, 1971, 48(3): 547. DOI:10.1017/S0022112071001745 |
| [34] |
SARGHINI F, PIOMELLI U, BALARAS E. Scale-similar models for large-eddy simulations[J]. Physics of Fluids, 1999, 11(6): 1596. DOI:10.1063/1.870021 |
| [35] |
WILLIAMS J E F, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society of London Series A, Mathematical and Physical Sciences, 1969, 264(1151): 321. DOI:10.1098/rsta.1969.0031 |
 2023, Vol. 55
2023, Vol. 55


